Introduction

Lambert’s problem is the classical two-point boundary value problem (TPBVP) in celestial mechanics, that was first posed and solved by Johann Heinrich Lambert in 1761. It is known to have a unique solution for the fractional orbit transfer between prescribed positions in a prescribed “time of flight”. Solving the problem requires determining the orbital arc (typically, solving for the initial velocity) connecting a prescribed initial position and final position, which correspond to the specified flight time. In the modern literature, Richard Battin [1, 2] developed an immortal and the most widely used and general algorithm for solving the unperturbed Lambert’s Problem (Keplerian motion). His algorithm generates not only the unique solution for the fractional orbit case, but also the multiple solutions associated with multiple revolution orbit transfers. Prussing further refined this method and published an elegant formulation and algorithm in 1992 [3].

The most common solution approach for generalizing the Lambert problem to include perturbations is to utilize the state transition matrix sensitivity of the final state with respect to the initial velocity, and iterate via Newton’s method on the three components of initial velocity to “hit” the final desired position at the prescribed final time. Another method for solving the generalized Lambert’s problem that is not as well-known but is also very good is the method of particular solutions (MPS) [4]. MPS makes assumptions based on local-linearity and utilizes a reference trajectory and a set of particular solutions. Variations of the initial velocity to the position of the particular solutions at the final time are used to generate a subspace containing the current “miss vector” at the final time. A linearity assumption for the departure of the desired particular solution relative to the reference trajectory permits an update of the initial velocity via a Newton-type iteration. In both cases the unperturbed Lambert solution can be used as a “warm start” to solve the perturbed problem.

The focus of this paper is the development of the unified Lambert tool (ULT) that consists of three algorithms that solve the perturbed Lambert problem and one that solves the Keplerian problem. The algorithms accommodate state of the art force models and the tool as a whole is implemented in C/C+ +and in parallel, using Message Passing Interface (MPI), for high performance computation on a 192 core computer cluster. Each algorithm that forms part of the ULT is discussed in the section following, with relevant references provided where more details can be found.

One motivation for this research is to respond to the various challenges in Space Situational Awareness (SSA) with a difficult “data association” problem. Short tracks of many newly observed objects, widely separated in time, must be processed to determine orbits and correlate the observations of tracked objects, if possible, with each other and with existing space object data bases. In the current state of the practice, hundreds of thousands of hypotheses must frequently be tested to find feasible preliminary orbits connecting time-displaced short tracks of unknown space objects. These preliminary orbits and the underlying data associations are taken as the starting estimates for further correlation. “Short” tracks may be separated by up to several orbits, so ignoring the effects of perturbations will typically introduce residual errors much larger than the measurement errors, which can corrupt the data association process.

Data association hypotheses are currently tested for preliminary orbit estimation using the Keplerian Lambert solutions for sufficiently short arcs, but higher precision is needed to accommodate hypothesis testing over longer time intervals. When more than several hundred thousand hypotheses are tested daily (including perturbations), the computational cost can exceed many CPU days per month. The anticipation of a new space fence giving an order of magnitude increase to ∼ 200,000 more presently un-trackable debris objects (visible to our sensors) means that already high computational costs are about to dramatically increase [5]. Millions of hypotheses will require testing to solve the data association problems. Also, “all-on-all” conjunction analysis and probability of collisions will be extremely difficult using existing orbit propagation tools. Thus the issue of finding an accurate and efficient solution to a generally perturbed TPBVP lies near the heart of many computational challenges in SSA. The inclusion of perturbations in Lambert’s problem and the development of more efficient and robust methods are therefore of strong interest.

In addition to the data association problem, which deals with tracking, there is also the problem of debris removal that must be considered. The satellite collision of Iridium and Kosmos, in 2009, demonstrated the seriousness of the orbit debris problem. In an instant hundreds of thousands of fragments with much higher than bullet speeds began orbiting the Earth. This debris is hazardous to operational satellites and reducing the risk of future collisions is possible by rendezvous, capture and de-orbit missions to remove the largest derelict objects. There are over 500 USA-launched spent rocket boosters in low Earth orbit [6]. Determining the globally optimal sequence of maneuvers for retrieving orbital debris can require simulating thousands of transfer trajectories. The Δv cost for each must be computed and displayed in an extremal field map (EFM) in order to effectively distinguish globally optimal from infeasible and sub-optimal orbit maneuver regions. We present a case study that illustrates the power of the ULT by generating EFMs in parallel, and we also demonstrate the importance of including perturbations in data association analysis.

Unified Lambert Tool

The ULT is a parallel C/C+ +algorithm that may be used to solve for a set of transfer trajectories between two specified sets of points and the associated times-of-flight (data association type problem), or to simulate transfer trajectories between two orbits (EFM type problem). In each case, the simulation of hundreds of thousands of trajectories may be required.

Sub-algorithms

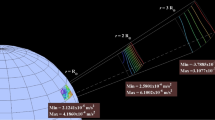
The ULT consists of four Lambert algorithms written in a C/C+ +environment and a suite of MATLAB post-processing tools for plotting and analysis. A schematic of the ULT is shown in Fig. 1. Each Lambert problem that the ULT is tasked with solving is first computed with the Keplerian solver [3], and then if a perturbed trajectory is required the ULT automatically selects the best suited perturbed algorithm for the job. There are three perturbed algorithm choices, and the arc length or true anomaly angle spanned by the Keplerian transfer trajectory is the parameter that governs the automated selection of the appropriate perturbed algorithm. This selection is based on the algorithm convergence characteristics and efficiency of the respective perturbed solvers. More details on the modified Chebyshev-Picard iteration (MCPI) algorithm convergence may be found in the Bai’s [7] and Woollands’ [8] PhD dissertations.

Fig. 1
figure 1

Flow diagram outlining the components in the unified Lambert tool

Full size image

The Keplerian Lambert solver utilized in the ULT is limited to the computation of elliptic orbits only (no parabolic or hyperbolic orbits). This work was originally developed by Battin and published in his book, Astronautical Guidance, in 1964 [2]. Later Prussing, a student of Battin, revisited this work and published his additions and refinements to the method in 1992 [3]. Both algorithms (Battin’s and Prussing’s) consider the multiple possible solutions associated with multiple revolution Lambert problem. Prussing’s version of the algorithm was adopted and re-coded in C and MATLAB for use in the ULT.

The first of the three perturbed Lambert solvers is the MCPI-TPBVP. This algorithm solves the TPBVP without using a shooting method whereby the linearly contained Chebyshev coefficients of the acceleration and the ensuing trajectory (that is iteratively converging to the solution) are formulated in such a way to implicitly determine the unknown initial velocity (constant of integration) using knowledge of the initial and final position only. This is the most efficient of the three perturbed solvers but has the drawback that convergence is limited to about a third of an orbit and the convergence degrades with increasing eccentricity.

The second of the perturbed algorithms is MCPI-TPBVP regularized with the Kustaanheimo-Stiefel (KS) transformation. This method, MCPI-KS-TPBVP, makes use of the KS time transformation [9] as well as a state variable change that rigorously linearizes the two-body problem through a judicious coordinate transformation. Woollands, et al. developed the MCPI-KS-TPBVP algorithm in 2015 [10]. The full derivation of the algorithm is presented in Appendix E of Woollands’ PhD dissertation [8]. Regularization of the equations of motion when solved using the MCPI-TPBVP alters the convergence properties of the problem and as discussed in [10] increases the domain of convergence of the MCPI-TPBVP from about a third of an orbit to 90% of an orbit. Theoretically the MCPI-KS-TPBVP should converge for a full orbit, however as this upper bound is approached the time for the algorithm to converge approaches infinity, and as a practical matter we obtain convergence up to about 90% of an orbit (independent of eccentricity). The MCPI-KS-TPBVP is the second most efficient of the perturbed Lambert solvers in the ULT. This algorithm promises many applications, for example mid-course guidance, wherein no state transition matrix is required.

The third of the perturbed solvers uses MPS [4] and the MCPI initial value problem (IVP) solver. This algorithm, MCPI-MPS-IVP, is a shooting-type method that is a local-linearity based approach that requires a reference trajectory \(\textit {\textbf {r}}_{ref}(t),\dot {\textit {\textbf {r}}}_{ref}(t),\ddot {\textit {\textbf {r}}}_{ref}(t)\) and a set of particular solutions. Variations of the initial velocity to generate particular solutions neighboring the nominal trajectory, for sufficiently small displacements from the reference trajectory, span all positions of the solutions at the final time. This permits the initial velocity to be updated via a Newton-type iteration. The mathematical development for this method is summarized in [11]. The MCPI-MPS-IVP algorithm converges over multiple revolutions, unlike the previous two methods, but it is the most expensive of the three algorithms in the ULT. [11] showed that MPS is at least competitive if not better than the regular Newton shooting method with regard to efficiency, while maintaining the comparable accuracy.

Parallelization

The ULT is implemented in parallel, using MPI, on the 192 core SSA computer cluster at the LASR Lab, Texas A&M University. The nature of the parallelization is general in the sense that the ULT can compute multiple trajectories at any instant in time if they are independent, but it is specific in the sense that a unique “front end” to the ULT is required for solving different types of problems.

For example, to solve a large set of Lambert problems (data association type problem) the ULT will accept a configuration file with a user specified number of position boundary conditions and the corresponding user speficied times-of-flight. All the computations of these potential Lambert transfers will be computed in parallel until the job is completed. If for example, an EFM is required then the parallelization is slightly different as there are two possible layers of parallelization that may be utilized. The first layer involves the number of revolutions (see [3], where 2π is added for each additional revolution) and the second layer of parallelization is related to each “vertical row” (increasing time-of-flight) on the EFM. In both cases the only limitation is the number of compute nodes available for performing the task.

User Input

The user input required by the ULT differs slightly for solving different types of problems. Below is a brief description of the initial conditions and simulation parameters required in the configuration file(s). More details are given in the user manual and code.

  1. 1.

    Keplerian OR Perturbed final solution?

  2. 2.

    Single Trajectory OR Set of Trajectories OR EFM?

    1. (a)

      Single trajectory

      1. (i)

        Specify initial and final position (Cartesian or classical elements).

      2. (ii)

        Specify the desired time-of-flight.

    2. (b)

      Set of Trajectories

      1. (i)

        Specify all initial and final positions (Cartesian or classical elements).

      2. (ii)

        Specify all the corresponding times-of-flight.

    3. (c)

      EFM

      1. (i)

        Specify departure and arrival orbit (Cartesian or classical elements).

      2. (ii)

        Specify EFM dimensions.

        1. (A)

          Maximum time-of-flight (y-axis)

        2. (B)

          Maximum time past arbitrary starting point (x-axis)

  3. 3.

    Force Model

    1. (a)

      Specify spherical harmonic degree and order

    2. (b)

      Specify atmospheric drag parameters

    3. (c)

      Specify third body effects

Parallel Generation of Extremal Field Maps

Orbit debris is not distributed uniformly in space, in fact forty percent of the debris in LEO is located in nine distinct clusters. These clusters contain anywhere from 20 to 150 spent rocket boosters and the bulk of the booster mass is located at inclinations of about 65∘, 71∘, 74∘, 81∘ and 83∘ [12]. Two smaller clusters are near 28∘and 98∘. In addition to these clusters of spent boosters, there are thousands of other small debris objects spanning a range or inclinations. Spent boosters are attractive objects to remove because they all represent potential collisions and removing these large objects has been found to be one of the best ways to mitigate debris growth. Since removing several of these boosters on a given launch is a nonlinear “orbital traveling salesman” optimization problem, hundreds of thousands of trajectories may need to be accurately and efficiently generated to determine the optimal trajectory sequence for rendezvous, docking and de-orbit of these boosters.

The ULT is used to simulate transfer trajectories between a pair of LEO orbits that could represent a retrieval spacecraft seeking to find the optimal maneuver for rendezvous with a piece of orbit debris. Since the debris has typically been in orbit for decades, this is not a fixed time problem. The take-off time is unknown and the time of flight between successive captures may entail many orbits. For each transfer the Δv cost is computed and the results are displayed on an EFM. Each EFM is composed of thousands of possible transfer trajectories, and presenting the data in this way allows mission design engineers to distinguish globally optimal from infeasible and sub-optimal orbit maneuver regions.

Multiple Solutions: Possible vs Feasible

There are 2N + 1solutions to the multiple revolution Lambert’s problem [2, 3]. Figures 2 and 3 are two example test cases that show the multiple ways a spacecraft can transfer from a certain position on the blue orbit to a certain position on the red orbit in a given time of flight. In each of these figures the legend details the number of revolutions (N) and also whether the transfer resides on the upper or lower branch. This terminology is defined and discussed in both [3] and [11]. It is not essential for the reader to have a deep mathematical understanding of the upper and lower branch classifications for understanding the material that follows in this paper, but it is necessary to recognize that multiple solutions do exist and these must be considered when generating EFMs. Note that these figures reveal a number of mathematically possible solutions but not all are physically feasible. Both these examples are for planar orbit transfers and it is clear that some trajectories collide with the Earth.

Fig. 2
figure 2

Possible transfer trajectories between the departure (blue) and arrival (red) orbits. All transfer trajectories have the same time-of-flight and different semimajor axis values, hence each is undergoing some number of revolutions about the Earth. This set of transfers corresponds to the black cross/circle in the EFMs that follow

Full size image
Fig. 3
figure 3

Possible transfer trajectories between the departure (blue) and arrival (red) orbits. All transfer trajectories have the same time-of-flight and different semimajor axis values, hence each is undergoing some number of revolutions about the Earth. This set of transfers corresponds to the magenta cross/circle in the EFMs that follow

Full size image

Over the next few pages a series of figures are presented that display all the possible solutions (left panels) for an orbit transfer between the two specified low Earth orbits, and of those, the ones that are actually physically feasible (right panels). The axes on these figures are departure time past some arbitrary starting time on the x-axis and time-of-flight on the y axis. The integer number of solutions is represented using various colors. Figure 4a and b show the number of solutions for transfers spanning a true anomaly angle range of 0 < f < 2π. This is noted as the N = 0revolution. As is evident, most of the EFM (a) shows that a transfer is “possible” except for a few small regions at the bottom where the time-of-flight is too short to make an elliptic transfer. In contrast, EFM (b) shows the feasible transfers. Note that there are more dark blue regions where a transfer is infeasible. This is due to the fact that certain transfers in the simulation collide with the Earth making them infeasible candidates. Note also the black and magenta cross/circle in these figures, previously mentioned, that represent the set of transfers shown in Figs. 2 and 3 respectively.

Fig. 4
figure 4

Number of possible solutions versus feasible solutions for N = 0

Full size image

Figure 5a and b show the number of solutions for transfers spanning a true anomaly angle range of 0 < f < 4π. Note that the maximum number of solutions is 2N + 1 = 3. The EFM (a) shows regions where 1, 2 or 3 solutions are possible, and the EFM (b) shows regions where 1, 2 or 3 solutions are feasible. The two new solutions corresponding to the N = 1revolution have different semimajor axis values and in certain cases one may collide with the Earth and become an infeasible candidate, as is evident in Figs. 2 and 3. These sets of solutions correspond to the two “branches” of solutions as discussed by [3, 11].

Fig. 5
figure 5

Number of possible solutions versus feasible solutions for N = 1

Full size image

Figures 6, 7 and 8 show the number of possible (a) and feasible (b) solutions for transfers spanning a true anomaly angle range of 0 < f < 6π, 0 < f < 8π and 0 < f < 10π respectively. The maximum number of possible solutions in EFM Fig. 8a is 2N + 1 = 9. The total number of possible solutions for this particular simulation is actually 19, although we have not included figures all the way up to 19. In addition, most of those additional higher N “possible” candidates are physically infeasible solutions and thus we find in this case that the total number of feasible solutions is 9 (as shown in Fig. 8b).

Fig. 6
figure 6

Number of possible solutions versus feasible solutions for N = 2

Full size image
Fig. 7
figure 7

Number of possible solutions versus feasible solutions for N = 3

Full size image
Fig. 8
figure 8

Number of possible solutions versus feasible solutions for N = 4

Full size image

Trajectory Cost Quantification

The Δv cost associated with each feasible transfer solution is computed and the results are presented in a Δv EFM. White represents all infeasible transfers, either that an elliptic transfer could not be computed, a simulated transfer collided with the Earth, or that the Δv exceeded the maximum allowable value that we adopted in this study. In this simulation we arbitrarily selected a maximum allowable Δv of 12 km/s. The various shades represent feasible transfers that become increasingly more expensive as the color changes from blue to red (see colorbar). Note the black cross/circle (Fig. 9), corresponds to the cyan square trajectory in Fig. 2, and the white cross/circle (Fig. 3) corresponds to the cyan triangle trajectory in Fig. 3.

Fig. 9
figure 9

Δv extremal field map for N = 0 transfers

Full size image

Figure 10 shows the Δv cost and infeasible transfer regions for N = 1. The upper and lower branch EFMs are shown in (a) and (b) respectively. Observe that for the upper branch EFM (a) the black cross/circle, corresponding to the “green triangle” trajectory in Fig. 2, lies in an infeasible region. This is because the trajectory collides with the Earth. On the lower branch, EFM (b), the transfer is feasible. That is the “green square” trajectory in Fig. 2 is a feasible transfer. The reverse situation occurs with the magenta cross/circle, and the result can be easily verified by referring to Figs. 2 and 3.

Fig. 10
figure 10

Δv extremal field maps for N = 1 transfers

Full size image

Figures 11, 12 and 13 show the Δv cost and infeasible maneuver regions for larger values of N. Finally in Fig. 14(a), the minimum Δv values from each of the 2N + 1EFMs are extracted and used to construct the “combined” Δv EFM. This is the plot that is most valuable to the user and it allows them to investigate potential maneuver regions that correspond to low Δv cost. In addition, (b) is a “combined” EFM for a set of orbits with the same orbital elements as in (a) but with an inclination change of 40∘. As expected, the overall Δv required for transferring between these orbits is greater due to the required plane change. The MATLAB post-processing tools allow the user to select which information they require to be plotted, if any, or simply to output the information for the optimal (minimum Δv) transfer. More details are given in the code and in the ULT user manual.

Fig. 11
figure 11

Δv extremal field maps for N = 2 transfers

Full size image
Fig. 12
figure 12

Δv extremal field maps for N = 3 transfers

Full size image
Fig. 13
figure 13

Δv extremal field maps for N = 4 transfers

Full size image
Fig. 14
figure 14

“Minimum” Δv extremal field maps for combined (all N) transfers

Full size image

Data Association Application

The U.S. Air Force radar fence that is currently under development will increase the number of trackable objects in low Earth orbit by an order of magnitude (about 20,000 objects to 200,000 objects) [5]. This increased volume of data and the increased statistical ambiguity associated with establishing orbits from the tracking measurements of this population will pose a computational grand challenge for building and maintaining a space object catalog. In this section the ULT is used to address the challenge by demonstrating the importance of including perturbations in data association algorithms. For this study the simulations are performed considering the deterministic Lambert problem only. In reality, estimation theory and uncertainty propagation are key elements in state-of-the-art data association algorithms, as these are required for determining accurate physical approximations of the object prior to solving Lambert’s problem. These aspects of the problem are beyond the scope of this paper and the work presented demonstrates the effectiveness of ULT, and its potential use as an asset to existing operational state-of-the-art data association algorithms.

Radar measurements usually provide the range, elevation, azimuth, and sometimes range-rate of the object relative to the observer location. If all these measurements are available then geometry and trigonometry can be used to extract a position and velocity from this data [13]. Sensor limitations sometimes provide only range, or only range and range-rate measurements. If this occurs then different techniques must be employed for determining the initial position and velocity guess [13]. Orbit determination is not the focus of this paper and thus the assumption is made that adequate information is available from the sensors and that position and velocity is already computed and available for use in the ULT.

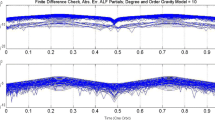
We performed a set of simulations to compare the solution of Lambert’s problem with and without gravity perturbations. Figures 15 and 16 show the maximum absolute position and velocity error along each particular Lambert solution trajectory. A 70thdegree and order spherical harmonic gravity field (EGM2008) is used for propagating the perturbed trajectories. All trajectories preserved the Hamiltonian to 14 digits and meet the final boundary conditions to sub-milimeter precision. Five test cases were done with semimajor axis values of 8000km, 10,000km, 20,000km, 30,000km and 42,000 km (typical geostationary orbit), eccentricity of zero and inclination of 10∘. As expected, Figs. 15 and 16 reveal that with increasing time (and arc length) over which the Lambert problem is solved there is an increase in the error between the perturbed and Keplerian Lambert solutions. The errors are also larger for orbits with smaller semimajor axis values where the trajectory is experiencing greater variations in the gravity field.

Fig. 15
figure 15

Position error between the perturbed and Keplerian Lambert solution for five test cases with with zero eccentricity, 10∘inclination and the range of semimajor axis values shown in the legend

Full size image
Fig. 16
figure 16

Velocity error between the perturbed and Keplerian Lambert solution for five test cases with zero eccentricity, 10∘inclination and the range of semimajor axis values shown in the legend

Full size image

It is clear from these results that neglecting gravity perturbations when propagating trajectories and solving Lambert’s problem will introduce considerable errors (as much as 10 km) that will lead to large uncertainties during the data association process. Including other perturbations such as drag, solar radiation pressure and third body effects would further reveal the discrepancies between the perturbed and Keplerian solutions. The parallel structure of the ULT and ability to efficiently include state of the art force models makes this tool significant and promising for near-term transition to establish a new state of the practice.

Conclusion

We have developed a parallel-compiled tool that combines several of our recently developed methods for solving the perturbed Lambert problem using modified Chebyshev-Picard iteration. This tool is named the unified Lambert tool and consists of four individual algorithms, each of which is unique and better suited for solving a particular type of orbit transfer. The first is a Keplerian Lambert solver that provides a good initial guess (warm start) for solving the perturbed problem and also determines the appropriate algorithm to call for solving the perturbed problem. The arc length or true anomaly angle spanned by the transfer trajectory is the parameter that governs the automated selection of the appropriate perturbed algorithm, and it is based on the respective algorithm convergence characteristics. The second algorithm solves the perturbed problem using the modified Chebyshev-Picard iteration two-point boundary value algorithm. This algorithm does not require a Newton-like shooting method and is the most efficient of the perturbed solvers presented in the paper, however the domain of convergence is limited to about 1/3 of an orbit (varies with varying eccentricity). The third algorithm extends the domain of convergence of the modified Chebyshev-Picard iteration two-point boundary value solver to about 90% of an orbit, through regularization with the Kustaanheimo-Stiefel transformation. This is the second most efficient of the perturbed set of algorithms. The fourth algorithm uses the method of particular solutions and the modified Chebyshev-Picard iteration initial value algorithm for solving multiple-revolution perturbed transfers. This method does require “shooting” but differs from Newton-like shooting methods in that it does not require propagation of a state transition matrix. The unified Lambert tool makes use of the General Mission Analysis Tool and is capable of computing thousands of perturbed Lambert trajectories in parallel on the Space Situational Awareness computer cluster at the LASR Lab, Texas A&M University. We have demonstrated the power of our tool by solving a highly parallel example problem, the generation of extremal field maps for optimal spacecraft rendezvous (and eventual orbit debris removal). In addition we demonstrated the need for including perturbative effects in simulations for satellite tracking or data association. The unified Lambert tool developed in this paper is being used by several industrial partners and we are confident that it will play a significant role in practical applications, including solution of Lambert problems that arise in the current applications focused on enhanced space situational awareness.