An Adaptive Analytic Continuation Method for Computing the Perturbed Two-Body Problem State Transition Matrix

Abstract

In this work, the Taylor series based technique, Analytic Continuation is implemented to develop a method for the computation of the gravity and drag perturbed State Transition Matrix (STM) incorporating adaptive time steps and expansion order. Analytic Continuation has been developed for the two-body problem based on two scalar variables f and g_p and their higher order time derivatives using Leibniz rule. The method has been proven to be very precise and efficient in trajectory propagation. The method is expanded to include the computation of the STM for the perturbed two-body problem. Leibniz product rule is used to compute the partials for the recursive formulas and an arbitrary order Taylor series is used to compute the STM. Four types of orbits, LEO, MEO, GTO and HEO, are presented and the simulations are run for 10 orbit periods. The accuracy of the STM is evaluated via RMS error for the unperturbed cases, symplectic check for the gravity perturbed cases and error propagation for the gravity and drag perturbed orbits. The results are compared against analytical and high order numerical solvers (ODE45, ODE113 and ODE87) in terms of accuracy. The results show that the method maintains double-precision accuracy for all test cases and 1-2 orders of magnitude improvement in linear prediction results compared to ODE87. The present approach is simple, adaptive and can readily be expanded to compute the full spherical harmonics gravity perturbations as well as the higher order state transition tensors.

Introduction

In Astrodynamics, the State Transition Matrix (STM) of the two-body problem works as a sensitivity of the current states to the initial conditions. Hence, it computes the propagation of error of the initial states over time. Computing the STM is ubiquitous to spaceflight dynamics, navigation and control, [20, 21, 26, 32]. Goodyear presented an exact analytical solution of the two-body Cartesian STM and the method is valid for all types of orbits for the attractive force and for the hyperbolic and rectilinear orbits for the repulsive force, [10]. However, it is complicated to introduce third body effect in this method and the method requires transcendental function evaluation, [21]. This method has been simplified to increase the numerical efficiency for the Keplerian elliptical orbit, [6, 19]. However, gravity perturbation was not incorporated in this simplified method, [6]. Recently a decoupled direct method is developed by Hatten and Russel using fixed step size Runge-Kutta method, [13]. In this method, first and second order STM is decoupled from the state propagation to make the procedure computationally efficient. To formulate the STM with Spherical Harmonic Gravity model, Read et al. applied Modified Chebyshev Picard Iteration method, [25]. The method is shown to be well suited for parallel implementation for additional speed of computation. Markley presented a J₂ perturbed approximate Cartesian STM, [21]. This method is also capable of handling the n-body problem. A major drawback of this method is that it is restricted by short time intervals. It can compute the J₂ perturbation term for only up to 6 second time step.

A geometric method is developed by Gim and Alfriend to derive the STM for the relative motion including gravitational perturbation, [9]. This method uses the relationship between the relative states and the differential orbital elements. To implement the STM in practical engineering applications, Yamanaka and Ankersen linearized the differential equations of relative motion on elliptical orbits, [35]. This linearized method is valid for unperturbed elliptical orbits. Koenig et al. derived the STM using classical Keplerian orbit elements, [18]. They introduced J₂ and differential drag perturbation in their work.

In low earth orbit (LEO), there is another inevitable perturbation, which is atmospheric drag. It depends on the shape, size and orientation of the orbiting body. Drag perturbation has been extensively studied, [5, 7, 17]. Mavraganis and Michalakis reviewed drag along with radiation pressure exerted by the major body on the minor one, [22]. Vallado and Finkleman discussed the sources of uncertainty in the drag models and evaluated the interrelation among different parameters of the problem, [34]. The literature is rich with numerical techniques that study the orbit problem in the presence of perturbations, [33]. More recently, parallel implementation of Modified Chebyshev Picard iteration on various gravity fields using multiple cores and Graphic Processing Units (GPUs) are discussed, [1]. Atallah et al. also focused on the comparison among different numerical integrators for perturbed orbit propagation in terms of accuracy and efficiency, [2]. The Analytic Continuation method is a numerical integration method that is based on Taylor series expansion and Leibniz product rule. This method has already been proven to be very precise in solving unperturbed and J₂ − J₆ gravity perturbed two-body problem, [16, 31]. Later on, exponential atmospheric drag model is introduced, [14]. Recently, the method has been further developed to handle the full spherical harmonics gravity potential up to 250 degree and order, [15].

In this paper, the Analytic Continuation Method is used to derive the State Transition Matrix for the perturbed two-body problem. In “STM Derivation Using Adaptive Analytic Continuation”, the procedure to derive the drag and gravity perturbed adaptive STM is discussed. In “Numerical Simulations”, first results for the unperturbed case are compared with Lagrange’s F and G solution. Then the method is expanded for the J₂ − J₆ gravity perturbation terms and compared against ODE45 (based on Runge-Kutta (4,5) integration method, [4, 8]), ODE113 (based on variable order Adams-Bashforth-Moulton predictor corrector method, [27, 28]) and ODE87 (based on 8-7th order Dormand and Prince formulas, [11, 12, 24]). Atmospheric drag model is included and error propagation of the states using Analytic Continuation STM are checked against the results using ODE87. Finally, discussion of the results and concluding remarks are presented in “Discussion” and “Conclusion”, respectively.

STM Derivation Using Adaptive Analytic Continuation

In the Analytic Continuation technique, two scalar variables are defined as, f = r.r and g_p = f^−p/2, where r is the position vector and p is an integer. In the two-body problem, the acceleration vector is defined as,

$$ \mathbf{r}^{(2)}(t) = -\mu \frac{\mathbf{r}(t)}{(\mathbf{r}(t).\mathbf{r}(t))^{3/2}} $$

(1)

where, r(t) is the position vector at current time and μ is the standard gravitational parameter. Next, Leibniz product rule is implemented to derive the recursive formulas for computing the higher order time derivatives of the variables:

$$ \mathbf{r}^{(n+2)}(t) = -\mu \sum\limits_{m=0}^{n}{\binom{n}{m}}\mathbf{r}^{(m)}(t)g_{3}^{(n-m)}(t) $$

(2)

$$ f^{(n)}(t) = \sum\limits_{m=0}^{n}{\binom{n}{m}}\mathbf{r}^{(m)}(t).\mathbf{r}^{(n-m)}(t) $$

(3)

$$ \begin{array}{ll} g_{p}^{(n+1)}(t) = -\frac{1}{f(t)} \left\{\frac{p}{2}f^{(1)}(t)g_{p}^{(n)}(t) + {\sum}_{m=1}^{n}{\binom{n}{m}}\left( \frac{p}{2}f^{(m+1)}(t)g_{p}^{(n-m)}(t) + \right. \right.\\ \left. \left. f^{(m)}(t)g_{p}^{(n-m+1)}(t)\right) \right\} \end{array} $$

(4)

Finally, the higher order time derivatives of the position vector are substituted into the Taylor series expansion to obtain position and velocity of the next time step as shown in Eqs. 5 and 6,

$$ \mathbf{r}(t+dT) = \mathbf{r}(t) + \sum\limits_{m=1}^{n}\mathbf{r}^{(m)}(t)\frac{dT^{(m)}}{m!} $$

(5)

$$ \mathbf{r}^{(1)}(t+dT) = \mathbf{r}^{(1)}(t) + \sum\limits_{m=2}^{n}\mathbf{r}^{(m)}(t)\frac{dT^{(m-1)}}{(m-1)!} $$

(6)

To increase efficiency of computation, adaptive time step and expansion order are applied to the method, [15]. As in embedded Runge-Kutta methods, the adaptation is based on defining absolute and relative tolerances, δ_a and δ_r, respectively. The expansion order is then determined from,

$$ N = round(-\delta_{fac}log(\delta) + k_{inc}) $$

(7)

where, δ is defined as, min(δ_a,|r|δ_r) in the first step and max(δ_a,δ_a × fac) in the subsequent steps. Here, fac for canonical units is defined as,

$$ fac = ||\mathbf{r}(t_{0})| - |\mathbf{r}(t)||\times \frac{DU}{10000} $$

(8)

The time step is then determined using,

$$ dT = h_{fac}\times min(dT_{a},dT_{b}) $$

(9)

where, dT_a and dT_b are calculated from $\frac {\delta \times (N-1)!}{|\mathbf {r}^{(N)}|_{\infty }^{1/(N-1)}}$ and $\frac {\delta \times (N-2)!}{|\mathbf {r}^{(N-1)}|_{\infty }^{1/(N-2)}}$, respectively which represent the last two terms in the Taylor series. The adaptation parameters δ_fac, k_inc and h_fac are tuned towards accuracy or speed and to increase the method robustness to handling different types of orbits.

According to the definition of the STM for the two-body problem, [3, 26]

$$ \phi = \left[\begin{array}{ll} \phi_{11}(t+dT,t) & \phi_{12}(t+dT,t) \\ \phi_{21}(t+dT,t) & \phi_{22}(t+dT,t) \end{array}\right] = \left[\begin{array}{ll} \frac{\partial \mathbf{r}(t+dT)}{\partial \mathbf{r}(t)} & \frac{\partial \mathbf{r}(t+dT)}{\partial \mathbf{r}^{(1)}(t)} \\ \frac{\partial \mathbf{r}^{(1)}(t+dT)}{\partial \mathbf{r}(t)} & \frac{\partial \mathbf{r}^{(1)}(t+dT)}{\partial \mathbf{r}^{(1)}(t)} \end{array}\right] $$

(10)

where, ϕ₁₁ is the sensitivity of the next position to the current position, ϕ₁₂ is the sensitivity of the next position to the current velocity, ϕ₂₁ is the sensitivity of the next velocity to the current position and ϕ₂₂ is the sensitivity of the next velocity to the current velocity. The same approach of the Taylor series expansion of the state variables are followed to expand the elements of the STM, [29]

$$ \phi_{11}(t+dT,t) = \frac{\partial \mathbf{r}(t+dT)}{\partial \mathbf{r}(t)} = \psi_{r} + \sum\limits_{m=1}^{n} \psi_{r}^{(m)} \frac{dT^{(m)}}{m!} $$

(11)

$$ \phi_{12}(t+dT,t) = \frac{\partial \mathbf{r}(t+dT)}{\partial \mathbf{r}^{(1)}(t)} = \psi_{v} + \sum\limits_{m=1}^{n} \psi_{v}^{(m)}\frac{dT^{(m)}}{m!} $$

(12)

$$ \phi_{21}(t+dT,t) = \frac{\partial \mathbf{r}^{(1)}(t+dT)}{\partial \mathbf{r}(t)} = \psi_{r}^{(1)} + \sum\limits\limits_{m=2}^{n} \psi_{r}^{(m)} \frac{dT^{(m-1)}}{(m-1)!} $$

(13)

$$ \phi_{22}(t+dT,t) = \frac{\partial \mathbf{r}^{(1)}(t+dT)}{\partial \mathbf{r}^{(1)}(t)} = \psi_{v}^{(1)} + \sum\limits_{m=2}^{n} \psi_{v}^{(m)} \frac{dT^{(m-1)}}{(m-1)!} $$

(14)

where, dT is the time step between the current position and the next position and $\psi _{r}^{(m)}$ and $\psi _{v}^{(m)}$ are defined as $\frac {\partial \mathbf {r}^{(m)}(t)}{\partial \mathbf {r}(t)}$ and $\frac {\partial \mathbf {r}^{(m)}(t)}{\partial \mathbf {r}^{(1)}(t)}$, respectively. The partial derivatives of r(t), r⁽¹⁾(t), f and g_p with respect to r(t) and r⁽¹⁾(t) can be written as,

$$ \begin{array}{lll} \frac{\partial \mathbf{r}(t)}{\partial \mathbf{r}(t)} = \frac{\partial \mathbf{r}^{(1)}(t)}{\partial \mathbf{r}^{(1)}(t)} = \mathbf{I}_{3\times3} &\quad \frac{\partial \mathbf{r}(t)}{\partial \mathbf{r}^{(1)}(t)} = \frac{\partial \mathbf{r}^{(1)}(t)}{\partial \mathbf{r}^(t)} = \mathbf{0}_{3\times3} & \quad \frac{\partial f(t)}{\partial \mathbf{r}(t)} = 2 \mathbf{r}(t)\\ \frac{\partial g_{p}(t)}{\partial \mathbf{r}(t)} = -p\frac{g_{p}(t)}{f(t)}\mathbf{r}(t) & \quad \frac{\partial f(t)}{\partial \mathbf{r}^{(1)}(t)} = \frac{\partial g_{p}(t)}{\partial \mathbf{r}^{(1)}(t)} = \mathbf{0}_{1\times3} & \end{array} $$

(15)

By substitution, the recursive formulas to calculate partial derivatives of the higher order time derivatives of the variables, with respect to position and velocity are given by,

$$ \frac{\partial \mathbf{r}^{(n+2)}(t)}{\partial \chi} = -\mu\left\{\sum\limits_{m=0}^{n}{\binom{n}{m}}\psi_{\chi}^{(m)}g_{p}^{(n-m)}(t) + \sum\limits_{m=0}^{n}{\binom{n}{m}}\mathbf{r}^{(m)}(t)G_{p\chi}^{(n-m)}\right\} $$

(16)

$$ \frac{\partial f^{(n)}(t)}{\partial \chi} = \sum\limits_{m=0}^{n}{\binom{n}{m}}\psi_{\chi}^{(m)}\mathbf{r}^{(n-m)}(t) + \sum\limits_{m=0}^{n}{\binom{n}{m}}\mathbf{r}^{(m)}(t)\psi_{\chi}^{(n-m)} $$

(17)

$$ \begin{array}{@{}rcl@{}} \frac{\partial g_{p}^{(n+1)}(t)}{\partial \mathbf{\chi}(t)} &=& -\frac{1}{f(t)}\left\{ g_{p}^{(n+1)}F_{\chi} + \frac{p}{2} \left( F_{\chi}^{(1)} g_{p}^{(n)}(t) + f^{(1)}(t)G_{p\chi}^{(n)}\right) \right.\\ &&\left. + \sum\limits_{m=1}^{n}{\binom{n}{m}}\frac{p}{2}\left( F_{\chi}^{(m+1)}g_{p}^{(n-m)}(t) + f^{(m+1)}(t)G_{p\chi}^{(n-m)}\right) \right.\\ &&\left. + \sum\limits_{m=1}^{n}{\binom{n}{m}} \left( F_{\chi}^{(m)}g_{p}^{(n-m+1)}(t) + f^{(m)}(t)G_{p\chi}^{(n-m+1)}\right)\right\} \end{array} $$

(18)

where, χ = r(t) or r⁽¹⁾(t), $F_{\chi }^{(m)} = \frac {\partial f^{(m)}(t)}{\partial \mathbf {\chi }}$ and $G_{p\chi }^{(m)} = \frac {\partial g_{p}^{(m)}(t)}{\partial \mathbf {\chi }}$

Zonal Perturbations

For the J₂ − J₆ zonal perturbations, the higher order partial derivatives are obtained. In this section we show the detailed derivation for the J₂ perturbation and refer the reader to the appendix for the detailed derivation of J₃ − J₆. The J₂ acceleration is given by, [16, 26]

$$ \begin{array}{ll} a_{J_{2}} = \mathbf{r}_{J_{2}}^{(2)}(t) = -\frac{3}{2}J_{2} \left( \frac{\mu}{r^{2}}\right) \left( \frac{r_{eq}}{r}\right)^{2} \left[\begin{array}{lll} \left( 1-5(\frac{z}{r})^{2} \right)\frac{x}{r} \\ \left( 1-5(\frac{z}{r})^{2} \right)\frac{y}{r} \\ \left( 3-5(\frac{z}{r})^{2} \right)\frac{z}{r} \end{array}\right] \\ = -\frac{3}{2}J_{2} \mu r_{eq}^{2} \left[\begin{array}{lll} xg_{5}-5xz^{2}g_{7} \\ yg_{5} - 5yz^{2}g_{7} \\ 3zg_{5} - 5z^{3}g_{7} \end{array}\right] \end{array} $$

(19)

where, r_eq is equatorial radius of earth and J₂ = 1082.63 × 10^− 6, [26]. In order to obtain the recursions for the higher order partials, we define a constant, $C_{J_{2}} = -\frac {3}{2}J_{2} \mu r_{eq}^{2}$, and 2 new variables, B_p and C_α, as,

$$ B_{p} = \mathbf{r}g_{p} \quad C_{\alpha} = z^{\alpha} $$

(20)

The higher order time derivatives of the newly defined variables are given by,

$$ B^{(n)}_{p} = \sum\limits^{n}_{m = 0}{\binom{n}{m}} \mathbf{r}^{(m)}g_{p}^{(n-m)} \quad C^{(n)}_{\alpha} = \sum\limits^{n}_{m = 0}{\binom{n}{m}}C^{(m)}_{\alpha - 1}z^{(n-m)} $$

(21)

Hence, the higher order time derivatives of the J₂ perturbation acceleration is computed as,

$$ \mathbf{a}_{J_{2}}^{(n)} = \mathbf{r}_{J_{2}}^{(n+2)}(t) = C_{J_{2}} \left\{ \left[\begin{array}{lll} 1 \quad 0 \quad 0 \\ 0 \quad 1 \quad 0 \\ 0 \quad 0 \quad 3 \end{array}\right]B^{(n)}_{5} - 5\sum\limits^{n}_{m = 0}{\binom{n}{m}}B^{(m)}_{7}C^{(n-m)}_{2} \right\} $$

(22)

The partial derivatives of Eqs. 21 and 22 with respect to position and velocity are then expressed as,

$$ \frac{\partial B^{(n)}_{p}}{\partial \chi} = \sum\limits^{n}_{m = 0} {\binom{n}{m}}\left( \frac{\partial \mathbf{r}^{(m)}}{\partial \chi}g_{p}^{(n-m)} + \mathbf{r}^{(m)}\frac{\partial g_{p}^{(n-m)}}{\partial \chi} \right) $$

(23)

$$ \frac{\partial C^{(n)}_{\alpha}}{\partial \chi} = \sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial C^{(m)}_{\alpha-1}}{\partial \chi}z^{(n-m)} + C^{(m)}_{\alpha-1}\frac{\partial z^{(n-m)}}{\partial \chi}\right) $$

(24)

$$ \begin{array}{ll} \frac{\partial \mathbf{r}_{J_{2}}^{(n+2)}(t)}{\partial \chi} =C_{J_{2}} \left\{ \left[\begin{array}{lll} 1 \quad 0 \quad 0 \\ 0 \quad 1 \quad 0 \\ 0 \quad 0 \quad 3 \end{array}\right] \frac{\partial B^{(n)}_{5}}{\partial \mathbf{\chi}} - 5{\sum}^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{7}}{\partial \mathbf{\chi}}C^{(n-m)}_{2} \right. \right.\\ + \left. \left. B^{(m)}_{7}\frac{\partial C^{(n-m)}_{2}}{\partial \mathbf{\chi}} \right)\right\} \end{array} $$

(25)

where, χ is r(t) or r⁽¹⁾(t).

Finally, Eq. 25 is added to Eq. 11 through Eq. 14 to obtain the J₂ perturbed STM as,

$$ \phi_{11J_{2}}(t+dT,t) = \psi_{r} + \sum\limits_{m=1}^{n} \psi_{r}^{(m)} \frac{dT^{(m)}}{m!} + \sum\limits_{m=1}^{n}\frac{\partial \mathbf{r}_{J_{2}}^{(m)}(t)}{\partial \mathbf{r}} \frac{dT^{(m)}}{m!} $$

(26)

$$ \phi_{12J_{2}}(t+dT,t) = \psi_{v} + \sum\limits_{m=1}^{n} \psi_{v}^{(m)}\frac{dT^{(m)}}{m!} + \sum\limits_{m=1}^{n} \frac{\partial \mathbf{r}_{J_{2}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m)}}{m!} $$

(27)

$$ \phi_{21J_{2}}(t+dT,t) = \psi_{r}^{(1)} + \sum\limits_{m=2}^{n} \psi_{r}^{(m)} \frac{dT^{(m-1)}}{(m-1)!} + \sum\limits_{m=2}^{n}\frac{\partial \mathbf{r}_{J_{2}}^{(m)}(t)}{\partial \mathbf{r}}\frac{dT^{(m-1)}}{(m-1)!} $$

(28)

$$ \phi_{22J_{2}}(t+dT,t) = \psi_{v}^{(1)} + \sum\limits_{m=2}^{n} \psi_{v}^{(m)} \frac{dT^{(m-1)}}{(m-1)!} + \sum\limits_{m=2}^{n}\frac{\partial \mathbf{r}_{J_{2}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m-1)}}{(m-1)!} $$

(29)

Atmospheric Drag Perturbation

A canon ball drag model is re-derived using analytic continuation method, [14]. The acceleration for the drag model is given by, [34]

$$ a_{dr} = \mathbf{r}_{dr}^{(2)}(t) = -\frac{1}{2}\rho(r)\frac{C_{D}A}{m}v_{rel}^{2}\frac{\mathbf{v}_{rel}}{|\mathbf{v}_{rel}|} = -\tilde{\rho}||\mathbf{v}_{rel}||\mathbf{v}_{rel} $$

(30)

where, ρ(r) is the atmospheric density, C_D is the drag coefficient, A is the reference area, and v_rel is the relative velocity of the satellite with respect to Earth defined as,

$$ \mathbf{v}_{rel} = \mathbf{r}^{(1)} - \omega_{\oplus}\times \mathbf{r} = \left[\begin{array}{lll} x^{(1)} + y\omega_{\oplus} \\ y^{(1)} - x\omega_{\oplus} \\ z^{(1)} \end{array}\right] $$

(31)

From Eq. 31, the higher order time derivatives of the relative velocity is,

$$ \mathbf{v}_{rel}^{(n)} = \left[\begin{array}{lll} x^{(n+1)} + y^{(n)}\omega_{\oplus} \\ y^{(n+1)} - x^{(n)}\omega_{\oplus} \\ z^{(n+1)} \end{array}\right] $$

(32)

To calculate the higher order time derivatives of the relative velocity magnitude, ||v_rel||⁽ⁿ⁾, two new variables similar to f and g_p, Eqs. 3 and 4, are introduced as,

$$ f_{vrel} = \mathbf{v}_{rel}.\mathbf{v}_{rel} \quad g_{vrel} = f_{vrel}^{(1/2)} = ||\mathbf{v}_{rel}|| $$

(33)

Applying Leibniz product rule, the higher order time derivatives of the variables in Eq. 33 are expressed as,

$$ f_{vrel}^{(n)} = \sum\limits_{m=0}^{n}{\binom{n}{m}}\mathbf{v}_{rel}^{(m)}.\mathbf{v}_{rel}^{(n-m)} $$

(34)

$$ \begin{array}{ll} ||\mathbf{v}_{rel}||^{(n+1)} = g_{vrel}^{(n+1)} = \frac{1}{f}_{vrel} \left\{\frac{1}{2}f_{vrel}^{(1)}g_{vrel}^{(n)} + \sum\limits_{m=1}^{n}{\binom{n}{m}}\left( \frac{1}{2}f_{vrel}^{(m+1)}g_{vrel}^{(n-m)} - \right. \right.\\ \left. \left. f_{vrel}^{(m)}g_{vrel}^{(n-m+1)}\right)\right\} \end{array} $$

(35)

ρ(r) is defined according to the Exponential Model of atmospheric density, [33], as

$$ \rho(r) = \rho_{0}e^{-\frac{h_{ellp} - h_{0}}{H}} = \rho_{0}e^{\frac{R_{eq} + h_{0}}{H}} e^{-\frac{|\mathbf{r}|}{H}} $$

(36)

where, ρ₀ is the nominal density, R_eq is the equatorial radius of Earth, h_ellp is the altitude, h₀ is the base altitude, and H is the scale height. From Eqs. 30 and 36, the equation of $\tilde {\rho }$ is given by,

$$ \tilde{\rho} = \frac{1}{2}\frac{C_{d}A}{m}\rho_{0}e^{\frac{R_{eq} + h_{0}}{H}} e^{-\frac{|\mathbf{r}|}{H}}= \upbeta e^{-\frac{|\mathbf{r}|}{H}} $$

(37)

where, β is a constant. The first order time derivative of $\tilde {\rho }$ is,

$$ \tilde{\rho}^{(1)} = -\frac{1}{H}\tilde{\rho}|\mathbf{r}|^{(1)} $$

(38)

Applying Leibniz product rule on Eq. 38 the higher order time derivative of ρ is derived as,

$$ \tilde{\rho}^{(n+1)} = -\frac{1}{H}\sum\limits^{n}_{m = 0}{\binom{n}{m}}\tilde{\rho}^{(m)}|\mathbf{r}|^{(n-m+1)} $$

(39)

The higher order time derivatives of the acceleration due to drag is calculated using, [14]

$$ \mathbf{a}_{dr}^{(n)} = \mathbf{r}_{dr}^{(n+2)}(t) = -\sum\limits^{n}_{i=0}\sum\limits^{n-i}_{j=0}\frac{n!}{i!j!(n-i-j)!}\rho^{(i)}||\mathbf{v}_{rel}||^{(j)}\mathbf{v}_{rel}^{(n-i-j)} $$

(40)

The recursive formula for the partial derivatives of the drag perturbation acceleration with respect to position and velocity is then expressed as,

$$ \begin{array}{@{}rcl@{}} \frac{\partial \mathbf{r}_{dr}^{(n+2)}(t)}{\partial \chi} &=& -\sum\limits^{n}_{i=0}\sum\limits^{n-i}_{j=0}\frac{n!}{i!j!(n-i-j)!}\left( \frac{\partial \rho^{(i)}}{\partial \chi}||\mathbf{v}_{rel}||^{(j)}\mathbf{v}_{rel}^{(n-i-j)} \right.\\ &&\left. +\rho^{(i)}\frac{\partial ||\mathbf{v}_{rel}||^{(j)}}{\partial \chi}\mathbf{v}_{rel}^{(n-i-j)} + \rho^{(i)}||\mathbf{v}_{rel}||^{(j)}\frac{\partial \mathbf{v}_{rel}^{(n-i-j)} }{\partial \chi}\right) \end{array} $$

(41)

where, $\frac {\partial \rho ^{(n)}}{\partial \chi }$, $\frac {\partial \mathbf {v}_{rel}^{(n)} }{\partial \chi }$ and $\frac {\partial ||\mathbf {v}_{rel}||^{(n)} }{\partial \chi }$ are calculated separately as shown in the Appendix. $\frac {\partial \mathbf {r}_{dr}^{(n+2)}(t)}{\partial \mathbf {r}(t)}$ and $\frac {\partial \mathbf {r}_{dr}^{(n+2)}(t)}{\partial \mathbf {r}(t)^{(1)}}$ are then added to Eqs. 26 to 29 to include drag perturbation in computing the STM.

Algorithms 1 – 3 in the Appendix show the steps for the full implementation of the analytic continuation method to compute the J₂ − J₆ and drag perturbed STM for the two-body problem.

Numerical Simulations

In this section, numerical results are presented for the derived STM via the Analytic Continuation technique for 4 orbits as shown in Table 1. Each orbit is propagated for 10 orbit periods.

Table 1 Orbits used for numerical simulation

First, Analytic Continuation is utilized to compute the STM for the unperturbed orbits and compared versus the closed-form solution by Battin, [3], via computing the RMS error. Next, J₂ − J₆ perturbation is added and the STM computed with Analytic Continuation is compared against MATLAB ODE45, ODE113 and ODE87 in terms of accuracy via the symplectic check. Finally, an exponential drag model is added to the J₂ − J₆ perturbed STM and the results are compared against ODE87 via error propagation. All codes are written and compiled using MATLAB R2019a and canonical units. To compare the numerical results, three different methods are used; calculation of RMS error, the symplectic check and error propagation of the states.

RMS Error for the Unperturbed STM

The RMS Error for each element of the STM in the time domain of 10 orbit periods is computed from the difference between the elements of the unperturbed STMs computed using Battin’s method, [3], and the Analytic Continuation technique as shown in Eq. 42.

$$ E_{ij} = \sqrt{\sum\limits_{k=1}^{N}(M_{ijk} - L_{ijk})^{2}/n} $$

(42)

where, M_ijk and L_ijk are (i,j)th terms of the STM at k-th time step from Battin’s method, [3] and Analytic Continuation method, respectively, E_ij is the RMS Error of the (i,j)th term of the unperturbed STM and N is the total number of steps.

The RMS errors for the 36 elements of the STM are calculated using Eq. 42 for the four orbit test cases and the results are shown in Tables 2, 3, 4 and 5, [30].

Table 2 RMS error of the elements of the unperturbed STM of LEO orbit using analytic continuation method

Table 3 RMS error of the elements of the unperturbed STM of MEO orbit using analytic continuation method

Table 4 RMS error of the elements of the unperturbed STM of GTO orbit using analytic continuation method

Table 5 RMS error of the elements of the unperturbed STM of HEO orbit using analytic continuation method

Symplectic Error for the Gravity Perturbed STM

The symplectic nature of the J₂ − J₆ perturbed STM is examined and elements of the error matrix are plotted versus orbital periods. The matrix [ϕ] is called symplectic, if it satisfies Eq. 43, [26]

$$ [\phi]^{T}[J][\phi] = [J] $$

(43)

where, [ϕ] is the STM and [J] is a skew-symmetric matrix defined by,

$$ [J] = \left[\begin{array}{ll} 0_{3\times3} & I_{3\times3}\\ -I_{3\times3} & 0_{3\times3} \end{array}\right] $$

(44)

The absolute error in the symplectic nature of the J₂ − J₆ perturbed STM is calculated by Eq. 45, [25]

$$ [E_{sym.}] = \left|[\phi]^{T}[J][\phi] - [J]\right| $$

(45)

where, [E_sym.] is the symplectic error matrix.

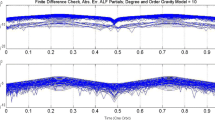
For the J₂ − J₆ perturbed cases, the results of the 10 orbit periods of the elements of the [E_sym.] matrix of every step using Analytic Continuation method are compared with the results using ODE87, ODE113 and ODE45. In this case, the initial and final time is provided to the solvers and the flexibility is given to the methods to select the time steps for the calculation. The results of the four different orbits are plotted as scattered points versus orbital period as shown in Figs. 1, 2, 3, 4, 5, 6, 7 and 8. Next, the gravity perturbed STM is generated up to 1,000 orbit periods using Analytic Continuation and compared against the results of ODE87, ODE113 and ODE45. The comparison results are shown in Figs. 9, 10, 11 and 12 via the average of the 36 elements of the symplectic error matrix, E_sym., versus orbital period. The Analytic Continuation is then used to propagate the STMs of the four orbit types for 10,000 orbit periods. The average symplectic check results at per orbit is used and the results are shown in Fig. 13. When performing these symplectic error calculations, both relative and absolute tolerance are set to 10^− 13 to get the highest possible accurate results for the STM generation from the MATLAB ODE suite.

Fig. 1

STMs symplectic check vs orbital period using Analytic Continuation and ODE87 for gravity perturbed LEO

Fig. 2

STMs symplectic check vs orbital period using ODE113 and ODE45 for gravity perturbed LEO

Fig. 3

STMs symplectic check vs orbital period using Analytic Continuation and ODE87 for gravity perturbed MEO

Fig. 4

STMs symplectic check vs orbital period using ODE113 and ODE45 for gravity perturbed MEO

Fig. 5

STMs symplectic check vs orbital period using Analytic Continuation and ODE87 for gravity perturbed GTO

Fig. 6

STMs symplectic check vs orbital period using ODE113 and ODE45 for gravity perturbed GTO

Fig. 7

STMs symplectic check vs orbital period using Analytic Continuation and ODE87 for gravity perturbed HEO

Fig. 8

STMs symplectic check vs orbital period using ODE113 and ODE45 for gravity perturbed HEO

Fig. 9

STMs average symplectic check vs orbital revolution using Analytic Continuation, ODE87, ODE113 and ODE45 for gravity perturbed LEO

Fig. 10

STMs average symplectic check vs orbital revolution using Analytic Continuation, ODE87, ODE113 and ODE45 for gravity perturbed MEO

Fig. 11

STMs average symplectic check vs orbital revolution using Analytic Continuation, ODE87, ODE113 and ODE45 for gravity perturbed GTO

Fig. 12

STMs average symplectic check vs orbital revolution using Analytic Continuation, ODE87, ODE113 and ODE45 for gravity perturbed HEO

Fig. 13

STMs average symplectic check vs orbital revolution using Analytic Continuation for gravity perturbed LEO, MEO, GTO and HEO

Error Propagation for Gravity and Drag Perturbed STM

To check the error propagation of the states using the STM, first the trajectory, x_i, is computed with a nominal set of initial conditions, Table 1. A perturbation is introduced to the initial states as shown in Table 6. Linear prediction is used to compute the trajectory, $\hat {x}_{i}$, at the desired time steps using the STM as shown in Eq. 46. The “true” trajectory is propagated separately using the perturbed initial conditions. The error is then computed as the difference between the true states, x_⊗i, and the predicted states $\hat {x}_{i}$, [9]. The error propagation compares J₂ − J₆ gravity and drag perturbed Analytic Continuation results for the four orbit types in Table 1 against ODE87 for 10 orbit periods. The results of the error propagation of the position and velocity are shown in Figs. 14, 15, 16, 17, 18, 19, 20, and 21.

$$ \begin{array}{lll} \delta x_{i} = [\phi_{i-1}]\delta x_{i-1}\\ \hat{x}_{i} = x_{i} + \delta x_{i}\\ Error_{i} = x_{\otimes i} - \hat{x}_{i} \end{array} $$

(46)

Fig. 14

Linear prediction position error(m) vs orbital revolution using Analytic Continuation and ODE87 for gravity and drag perturbed LEO

Fig. 15

Linear prediction velocity error(m/s) vs orbital revolution using Analytic Continuation and ODE87 for gravity and drag perturbed LEO

Fig. 16

Linear prediction position error(m) vs orbital revolution using Analytic Continuation and ODE87 for gravity and drag perturbed MEO

Fig. 17

Linear prediction velocity error(m/s) vs orbital revolution using Analytic Continuation and ODE87 for gravity and drag perturbed MEO

Fig. 18

Linear prediction position error(m) vs orbital revolution using Analytic Continuation and ODE87 for gravity and drag perturbed GTO

Fig. 19

Linear prediction velocity error(m/s) vs orbital revolution using Analytic Continuation and ODE87 for gravity and drag perturbed GTO

Fig. 20

Linear prediction position error(m) vs orbital revolution using Analytic Continuation and ODE87 for gravity and drag perturbed HEO

Fig. 21

Linear prediction velocity error(m/s) vs orbital revolution using Analytic Continuation and ODE87 for gravity and drag perturbed HEO

Table 6 Initial states and initial perturbations of the orbits

Discussion

As shown in Tables 2 to 5 the unperturbed STMs computed via the Analytic Continuation technique maintained 11 - 16 digits of accuracy in the RMS error across all 36 elements for all types of orbits when compared against the analytic solution by Battin, [3]. The check is performed for 10 orbit periods and the RMS error is computed for each element at each time step.

The symplectic check is used for accuracy verification when gravitational perturbations, J₂ − J₆, are considered. Analytic Continuation is compared against ODE45, ODE113 and ODE87. For LEO, Figs. 1 and 2, Analytic Continuation, maintained double precision accuracy for the full 10 orbit periods, whereas all other integrators lost between 4 - 6 digits of accuracy towards the end of the simulations. In terms of accuracy, ODE87 performed the best relative to ODE113 and ODE45, and ODE113 marginally outperformed ODE45. However, for ODE87, ODE113 and ODE45, the accumulation of truncation and round-off errors are evident in the loss of accuracy as the simulation time increases, whereas for Analytic Continuation, the ability to adapt to arbitrary order in the Taylor series enabled it to maintain double precision throughout the simulation. As the eccentricity, and consequently the nonlinearity, [23], is increased, the accuracy of ODE87, ODE113 and ODE45 degrades over the 10 orbit periods, whereas Analytic Continuation maintains double precision for MEO, GTO and HEO as shown in Figs. 3 to 8. The Analytic Continuation method is then used to generate STMs up to 1,000 orbit periods and compared against ODE87, ODE113 and ODE45 using the average symplectic error of the STMs, as shown in Figs. 9 to 12. Results for 1000 orbits and beyond (Fig. 13) show that the Analytic Continuation method is able to maintain double precision in the symplectic check whereas the other methods lost between 10 - 12 digits of accuracy at 1000 orbits. It has to be noted that all numerical integration methods, including Analytic Continuation, were set to the lowest absolute and relative tolerance which explains the similarity in results of ODE45, ODE113 and ODE87 at 1000 orbits. If tolerances were to be set to their default values the lower order methods (particularly ODE45) will lose an additional 4-5 orders of magnitude when compared with ODE87. Finally, in the case of drag perturbation, linear prediction is used to verify the results where Analytic Continuation is compared against ODE87 for the four types of orbits. From the results presented in Figs. 14 to 21, Analytic Continuation outperforms ODE87 in linear prediction error in all test cases. For the LEO case, Analytic Continuation is two orders of magnitude more accurate compared to ODE87 in position, Fig. 14, and three order of magnitude in velocity, Fig. 15. For MEO and GTO, Analytic continuation achieved one order of magnitude more accuracy in position and velocity, Figs. 16 to 19. Finally, for HEO, Analytic Continuation is shown to be 3 - 4 times more accurate as shown in Figs. 20 and 21 for position and velocity, respectively. We attribute the significant improvement in LEO results to the higher effect drag perturbation has on LEO versus the other orbits which take advantage of the more accurate STM produced by Analytic Continuation to produce better linear prediction results.

Conclusion

In this work, the State Transition Matrix of the perturbed two body problem is derived using the higher order Analytic Continuation technique. All the higher order partial derivatives are computed recursively by utilizing Leibniz rule and scalar variables transformations. The recursive relations shown for J₂ − J₆ and drag perturbations can be readily generalized for arbitrary order perturbations, [15]. Simulation results are presented for four different types of orbits: LEO, MEO, GTO and HEO, for up to 10,000 orbit periods and compared with ODE45, ODE113 and ODE87. For all cases, Analytic Continuation STM maintains machine precision that is enabled by the adaptation scheme combined with the ability of computing arbitrary higher order partials. The cases presented include unperturbed orbits where the RMS error for each element of the STM is computed and compared against Lagrange’s F and G solution. For the gravity perturbed cases, the accumulation of truncation and round-off errors in ODE45, ODE113 and ODE87 is observed whereas Analytic Continuation maintained double-precision accuracy. Finally, with the introduction of drag, the STM computed via Analytic Continuation is shown to outperform ODE87 (in terms of accuracy) for all the test cases in linear prediction results.

The present method for computing the STM is simple, highly accurate and can be readily expanded to include higher order perturbations. The same recursions can also be expanded to compute the higher order state transition tensors. Areas that will be explored in future research.

Appendix

Recursive Relations for J₂ − J₆ and Drag Perturbations

In this section, the recursive relations of the J₃ − J₆ perturbed acceleration are presented along with the derivation of the partial derivatives for the STM computation. The J₃ − J₆ perturbation accelerations are defined as,

$$ \begin{array}{@{}rcl@{}} \mathbf{r}_{J_{3}}^{(2)} &=& \frac{1}{2}J_{3} \left( \frac{\mu}{r^{2}}\right) \left( \frac{r_{eq}}{r}\right)^{3} \left[\begin{array}{lll} 5\left( 7(\frac{z}{r})^{3} - 3(\frac{z}{r}) \right)\frac{x}{r} \\ 5\left( 7(\frac{z}{r})^{3} - 3(\frac{z}{r}) \right)\frac{y}{r} \\ 3\left( 1 - 10(\frac{z}{r})^{2} + \frac{35}{3}(\frac{z}{r})^{4} \right) \end{array}\right]\\ &=& C_{J_{3}} \left\{ -\left[\begin{array}{lll} 15 \quad 0 \quad 0 \\ 0 \quad 15 \quad 0 \\ 0 \quad 0 \quad 30 \end{array}\right]B_{7}z + 35B_{9}C_{3} + \left[\begin{array}{lll} 0\\ 0\\ 3 \end{array}\right] g_{5}\right\} \end{array} $$

(47)

$$ \begin{array}{@{}rcl@{}} \mathbf{r}_{J_{4}}^{(2)} &=& \frac{5}{8}J_{4} \left( \frac{\mu}{r^{2}}\right) \left( \frac{r_{eq}}{r}\right)^{4} \left[\begin{array}{lll} \left( 3-42(\frac{z}{r})^{2} + 63(\frac{z}{r})^{4}\right)\frac{x}{r} \\ \left( 3-42(\frac{z}{r})^{2} + 63(\frac{z}{r})^{4}\right)\frac{y}{r} \\ \left( 15-70(\frac{z}{r})^{2} + 63(\frac{z}{r})^{4}\right)\frac{z}{r} \end{array}\right]\\ &=& C_{J_{4}} \left\{\left[\begin{array}{lll} 3 \quad 0 \quad 0 \\ 0 \quad 3 \quad 0 \\ 0 \quad 0 \quad 15 \end{array}\right]B_{7} -\left[\begin{array}{lll} 42 \quad 0 \quad 0 \\ 0 \quad 42 \quad 0 \\ 0 \quad 0 \quad 70 \end{array}\right]B_{9}C_{2} + 63B_{11}C_{4}\right\} \end{array} $$

(48)

$$ \begin{array}{@{}rcl@{}} \mathbf{r}_{J_{5}}^{(2)} \!&=&\! \frac{1}{8}J_{5} \left( \frac{\mu}{r^{2}}\right) \left( \frac{r_{eq}}{r}\right)^{5} \left[\begin{array}{lll} 3\left( 35(\frac{z}{r}) - 210(\frac{z}{r})^{3} + 231(\frac{z}{r})^{5} \right)\frac{x}{r} \\ 3\left( 35(\frac{z}{r}) - 210(\frac{z}{r})^{3} + 231(\frac{z}{r})^{5} \right)\frac{y}{r} \\ \left( 693(\frac{z}{r})^{6} - 945(\frac{z}{r})^{4} + 315(\frac{z}{r})^{2} - 15\right) \end{array}\right]\\ \!&=&\! C_{J_{5}} \left\{\!\left[\begin{array}{lll} 105 \quad 0 \quad 0 \\ 0 \quad 105 \quad 0 \\ 0 \quad 0 \quad 315 \end{array}\right]B_{9}z - \left[\begin{array}{lll} 630 \quad 0 \quad 0 \\ 0 \quad 630 \quad 0 \\ 0 \quad 0 \quad 945 \end{array}\right]B_{11}C_{3} + 693B_{13}C_{5} - \left[\begin{array}{lll} 0\\ 0\\ 15 \end{array}\right]g_{7}\!\right\}\\ \end{array} $$

(49)

$$ \begin{array}{@{}rcl@{}} \mathbf{r}_{J_{6}}^{(2)} &=& -\frac{1}{16}J_{6} \left( \frac{\mu}{r^{2}}\right) \left( \frac{r_{eq}}{r}\right)^{6} \left[\begin{array}{lll} \left( 35 - 945(\frac{z}{r})^{2} + 3465(\frac{z}{r})^{4} - 3003(\frac{z}{r})^{6} \right)\frac{x}{r} \\ \left( 35 - 945(\frac{z}{r})^{2} + 3465(\frac{z}{r})^{4} - 3003(\frac{z}{r})^{6} \right)\frac{y}{r} \\ \left( 245 - 2205(\frac{z}{r})^{2} + 4851(\frac{z}{r})^{4} - 3003(\frac{z}{r})^{6} \right)\frac{z}{r} \end{array}\right]\\ &=& C_{J_{6}} \left\{\left[\begin{array}{lll} 35 \quad 0 \quad 0 \\ 0 \quad 35 \quad 0 \\ 0 \quad 0 \quad 245 \end{array}\right]B_{9} -\left[\begin{array}{lll} 945 \quad 0 \quad 0 \\ 0 \quad 945 \quad 0 \\ 0 \quad 0 \quad 2205 \end{array}\right]B_{11}C_{2} \right.\\&&\left.+\left[\begin{array}{lll} 3465 \quad 0 \quad 0\\ 0 \quad 3465 \quad 0\\ 0 \quad 0 \quad 4851 \end{array}\right]B_{13}C_{4} - 3003B_{15}C_{6} \right\} \end{array} $$

(50)

where, $C_{J_{3}}$, $C_{J_{4}}$, $C_{J_{5}}$, and $C_{J_{6}}$ are defined as,

$$ \begin{array}{@{}rcl@{}} &&C_{J_{3}} = \frac{1}{2}J_{3} \mu r_{eq}^{3} \quad C_{J_{4}} = \frac{5}{8}J_{4} \mu r_{eq}^{4}\\ && C_{J_{5}} = \frac{1}{8}J_{5} \mu r_{eq}^{5} \quad C_{J_{6}} = -\frac{1}{16}J_{6} \mu r_{eq}^{6} \end{array} $$

(51)

B_p and C_α are defined in Eq. 20, r_eq is the equatorial radius of the Earth and the values of J₃ − J₆ are given by, [26],

$$ \begin{array}{@{}rcl@{}} J_{3} &=& -2.52\times10^{-6} \quad J_{4} = -1.61\times10^{-6}\\ J_{5} &=& -0.15\times10^{-6} \quad J_{6} = 0.57\times10^{-6} \end{array} $$

(52)

The higher order time derivatives of the J₃ − J₆ perturbation accelerations are derived as,

$$ \begin{array}{@{}rcl@{}} \mathbf{r}_{J_{3}}^{(n+2)} &=& C_{J_{3}} \left\{ -\left[\begin{array}{lll} 15 \quad 0 \quad 0 \\ 0 \quad 15 \quad 0 \\ 0 \quad 0 \quad 30 \end{array}\right]\sum\limits^{n}_{m = 0}{\binom{n}{m}}B_{7}^{(m)}z^{(n-m)} \right.\\ &&\left.+ 35\sum\limits^{n}_{m = 0}{\binom{n}{m}}B_{9}^{(m)}C_{3}^{(n-m)} + \left[\begin{array}{lll} 0\\ 0\\ 3 \end{array}\right]g_{5}^{(n)}\right\} \end{array} $$

(53)

$$ \begin{array}{@{}rcl@{}} \mathbf{r}_{J_{4}}^{(n+2)} &=& C_{J_{4}} \left\{\left[\begin{array}{lll} 3 \quad 0 \quad 0 \\ 0 \quad 3 \quad 0 \\ 0 \quad 0 \quad 15 \end{array}\right]B_{7}^{(n)} -\left[\begin{array}{lll} 42 \quad 0 \quad 0 \\ 0 \quad 42 \quad 0 \\ 0 \quad 0 \quad 70 \end{array}\right]\sum\limits^{n}_{m = 0}{\binom{n}{m}}B_{9}^{(m)}C_{2}^{(n-m)} \right. \\ &&\left. + 63\sum\limits^{n}_{m = 0}{\binom{n}{m}}B_{11}^{(m)}C_{4}^{(n-m)}\right\} \end{array} $$

(54)

$$ \begin{array}{@{}rcl@{}} \mathbf{r}_{J_{5}}^{(n+2)} &=& C_{J_{5}} \left\{\left[\begin{array}{lll} 105 \quad 0 \quad 0 \\ 0 \quad 105 \quad 0 \\ 0 \quad 0 \quad 315 \end{array}\right]\sum\limits_{m = 0}^{n}{\binom{n}{m}}B_{9}^{(m)}z^{(n-m)}\right.\\ &&-\left[\begin{array}{lll} 630 \quad 0 \quad 0 \\ 0 \quad 630 \quad 0 \\ 0 \quad 0 \quad 945 \end{array}\right]\sum\limits_{m = 0}^{n}{\binom{n}{m}}B_{11}^{(m)}C_{3}^{(n-m)} \\ &&\left. + 693\sum\limits_{m = 0}^{n}{\binom{n}{m}}B_{13}^{(m)}C_{5}^{(n-m)} - \left[\begin{array}{lll} 0\\ 0\\ 15 \end{array}\right]g_{7}^{(n)}\right\} \end{array} $$

(55)

$$ \begin{array}{@{}rcl@{}} \mathbf{r}_{J_{6}}^{(n+2)} \!&=&\! C_{J_{6}} \left\{\left[\begin{array}{lll} 35 \quad 0 \quad 0 \\ 0 \quad 35 \quad 0 \\ 0 \quad 0 \quad 245 \end{array}\right]B_{9}^{(n)} -\left[\begin{array}{lll} 945 \quad 0 \quad 0 \\ 0 \quad 945 \quad 0 \\ 0 \quad 0 \quad 2205 \end{array}\right]\sum\limits_{m = 0}^{n}{\binom{n}{m}}B_{11}^{(m)}C_{2}^{(n-m)} \right.\\ &&\left. \!+\left[\begin{array}{lll} 3465 \quad 0 \quad 0\\ 0 \quad 3465 \quad 0\\ 0 \quad 0 \quad 4851 \end{array}\right]\sum\limits_{m = 0}^{n}{\binom{n}{m}}B_{13}^{(m)}C_{4}^{(n-m)} - 3003\sum\limits_{m = 0}^{n}{\binom{n}{m}}B_{15}^{(m)}C_{6}^{(n-m)} \right\}\\ \end{array} $$

(56)

The partial derivatives of the higher order time derivatives in Eqs. 53 to 56 are recursively computed as,

$$ \begin{aligned} \frac{\partial \mathbf{r}_{J_{3}}^{(n+2)}}{\partial \chi} = C_{J_{3}} \left\{ -\left[\begin{array}{lll} 15 \quad 0 \quad 0 \\ 0 \quad 15 \quad 0 \\ 0 \quad 0 \quad 30 \end{array}\right]\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{7}}{\partial \mathbf{\chi}}z^{(n-m)} + B_{7}^{(m)}\frac{\partial z^{(n-m)}}{\partial \mathbf{\chi}}\right) \right.\\ \left. + 35\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{9}}{\partial \mathbf{\chi}}C_{3}^{(n-m)} + B_{9}^{(m)}\frac{\partial C_{3}^{(n-m)}}{\partial \mathbf{\chi}}\right) + \left[\begin{array}{lll} 0\\ 0\\ 3 \end{array}\right]\frac{\partial g_{5}^{(n)}}{\partial \mathbf{\chi}}\right\} \end{aligned} $$

(57)

$$ \begin{aligned} \frac{\partial \mathbf{r}_{J_{4}}^{(n+2)}}{\partial \chi} \!&=\! C_{J_{4}} \left\{\left[\begin{array}{lll} 3 \quad 0 \quad 0 \\ 0 \quad 3 \quad 0 \\ 0 \quad 0 \quad 15 \end{array}\right]\frac{\partial B^{(n)}_{7}}{\partial \mathbf{\chi}} -\left[\begin{array}{lll} 42 \quad 0 \quad 0 \\ 0 \quad 42 \quad 0 \\ 0 \quad 0 \quad 70 \end{array}\right]\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{9}}{\partial \mathbf{\chi}}C_{2}^{(n-m)} \right. \right.\\ &\quad\left. \left.+ B_{9}^{(m)}\frac{\partial C_{2}^{(n-m)}}{\partial \mathbf{\chi}}\right) + 63\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{11}}{\partial \mathbf{\chi}}C_{4}^{(n-m)} + B_{11}^{(m)}\frac{\partial C_{4}^{(n-m)}}{\partial \mathbf{\chi}}\right)\right\} \end{aligned} $$

(58)

$$ \begin{aligned} \frac{\partial \mathbf{r}_{J_{5}}^{(n+2)}}{\partial \chi} = C_{J_{5}} \left\{\left[\begin{array}{lll} 105 \quad 0 \quad 0 \\ 0 \quad 105 \quad 0 \\ 0 \quad 0 \quad 315 \end{array}\right]\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{9}}{\partial \mathbf{\chi}}z^{(n-m)} + B_{9}^{(m)}\frac{\partial z^{(n-m)}}{\partial \mathbf{\chi}}\right) \right.\\ -\left[\begin{array}{lll} 630 \quad 0 \quad 0 \\ 0 \quad 630 \quad 0 \\ 0 \quad 0 \quad 945 \end{array}\right]\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{11}}{\partial \mathbf{\chi}}C_{3}^{(n-m)} + B_{11}^{(m)}\frac{\partial C_{3}^{(n-m)}}{\partial \mathbf{\chi}}\right) \\ \left. + 693\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{13}}{\partial \mathbf{\chi}}C_{5}^{(n-m)} + B_{13}^{(m)}\frac{\partial C_{5}^{(n-m)}}{\partial \mathbf{\chi}}\right) - \left[\begin{array}{lll} 0\\ 0\\ 15 \end{array}\right]\frac{\partial g_{7}^{(n)}}{\partial \mathbf{\chi}} \right\} \end{aligned} $$

(59)

$$ \begin{aligned} \frac{\partial \mathbf{r}_{J_{6}}^{(n+2)}}{\partial \chi} &= C_{J_{6}} \left\{\left[\begin{array}{lll} 35 \quad 0 \quad 0 \\ 0 \quad 35 \quad 0 \\ 0 \quad 0 \quad 245 \end{array}\right]\frac{\partial B^{(n)}_{9}}{\partial \mathbf{\chi}} -\left[\begin{array}{lll} 945 \quad 0 \quad 0 \\ 0 \quad 945 \quad 0 \\ 0 \quad 0 \quad 2205 \end{array}\right]\sum\limits^{n}_{m = 0}{\binom{n}{m}} \right. \\& \quad\times\left( \frac{\partial B^{(m)}_{11}}{\partial \mathbf{\chi}}C_{2}^{(n-m)} +B_{11}^{(m)}\frac{\partial C_{2}^{(n-m)}}{\partial \mathbf{\chi}}\right) +\left[\begin{array}{lll} 3465 \quad 0 \quad 0 \\ 0 \quad 3465 \quad 0 \\ 0 \quad 0 \quad 4851 \end{array}\right]\sum\limits^{n}_{m = 0}{\binom{n}{m}}\\&\quad\times\left( \frac{\partial B^{(m)}_{13}}{\partial \mathbf{\chi}}C_{4}^{(n-m)} + B_{13}^{(m)}\frac{\partial C_{4}^{(n-m)}}{\partial \mathbf{\chi}}\right) \\ &\quad\left. - 3003\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial B^{(m)}_{15}}{\partial \mathbf{\chi}}C_{6}^{(n-m)} + B_{15}^{(m)}\frac{\partial C_{6}^{(n-m)}}{\partial \mathbf{\chi}}\right)\right\} \end{aligned} $$

(60)

where, χ is r(t) or r⁽¹⁾(t).

For the drag perturbation, the partial derivatives of the higher order time derivatives of ρ, v_rel and ||v_rel|| are computed as,

$$ \frac{\partial \rho^{(n+1)}}{\partial \chi} = -\frac{1}{H}\sum\limits^{n}_{m = 0}{\binom{n}{m}}\left( \frac{\partial \rho^{(m)}}{\partial \chi}|\mathbf{r}|^{(n-m+1)} + \rho^{(m)}\frac{\partial |\mathbf{r}|^{(n-m+1)}}{\partial \chi}\right) $$

(61)

$$ \frac{\partial \mathbf{v}_{rel}^{(n)}}{\partial \chi} = \frac{\partial \mathbf{r}^{(n+1)}(t)}{\partial \chi} + \left[\begin{array}{lll} 0 \quad 1 \quad 0 \\ -1 \quad 0 \quad 0 \\ 0 \quad 0 \quad 0 \end{array}\right]\frac{\partial \mathbf{r}^{(n)}(t)}{\partial \chi}\omega_{\oplus} $$

(62)

$$ \frac{\partial f_{vrel}^{(n)}}{\partial \chi} = \sum\limits_{m=0}^{n}{\binom{n}{m}}\left( \frac{\partial \mathbf{v}_{rel}^{(m)}}{\partial \chi}\mathbf{v}_{rel}^{(n-m)} + \mathbf{v}_{rel}^{(m)}\frac{\partial \mathbf{v}_{rel}^{(n-m)}}{\partial \chi}\right) $$

(63)

$$ \begin{aligned} \frac{\partial ||\mathbf{v}_{rel}||^{(n+1)} }{\partial \chi} = \frac{\partial g_{vrel}^{(n+1)}}{\partial \mathbf{\chi}} = -\frac{1}{f_{vrel}}\left\{ g_{vrel}^{(n+1)}F_{{vrel}\chi} + \frac{p}{2} \left( F_{{vrel}\chi}^{(1)} g_{vrel}^{(n)} + f_{vrel}^{(1)}G_{{vrel}\chi}^{(n)}\right)\right.\\ + \left. \sum\limits_{m=1}^{n}{\binom{n}{m}}\frac{p}{2}\left( F_{{vrel}\chi}^{(m+1)}g_{vrel}^{(n-m)} + f_{vrel}^{(m+1)}G_{{vrel}\chi}^{(n-m)}\right) \right.\\ + \left. \sum\limits_{m=1}^{n}{\binom{n}{m}} \left( F_{{vrel}\chi}^{(m)}g_{vrel}^{(n-m+1)} + f_{vrel}^{(m)}G_{{vrel}\chi}^{(n-m+1)}\right)\right\} \end{aligned} $$

(64)

where, $\mathbf {v}_{rel}^{(n)}$, $f_{vrel}^{(n)}$, $g_{vrel}^{(n+1)}$ and ρ^(n+ 1) are defined in Eqs. 32, 34, 35, and 39, respectively. $F_{vrel\chi }^{(m)} = \frac {\partial f_{vrel}^{(m)}}{\partial \mathbf {\chi }}$ and $G_{vrel\chi }^{(m)} = \frac {\partial g_{vrel}^{(m)}}{\partial \mathbf {\chi }}$.

The Taylor series expansions for the perturbed STM sub-blocks can be then expressed as,

$$ \begin{aligned} \phi_{11}(t+dT,t) = \psi_{r} + \sum\limits_{m=1}^{n}\left( \psi_{r}^{(m)} \frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{J_{2}}^{(m)}(t)}{\partial \mathbf{r}} \frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{J_{3}}^{(m)}(t)}{\partial \mathbf{r}} \frac{dT^{(m)}}{m!} \right.\\ + \left. \frac{\partial \mathbf{r}_{J_{4}}^{(m)}(t)}{\partial \mathbf{r}} \frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{J_{5}}^{(m)}(t)}{\partial \mathbf{r}} \frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{J_{6}}^{(m)}(t)}{\partial \mathbf{r}} \frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{dr}^{(m)}(t)}{\partial \mathbf{r}} \frac{dT^{(m)}}{m!}\right) \end{aligned} $$

(65)

$$ \begin{aligned} \phi_{12}(t+dT,t) = \psi_{v} + \sum\limits_{m=1}^{n}\left( \psi_{v}^{(m)}\frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{J_{2}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{J_{3}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m)}}{m!}\right.\\ \left. + \frac{\partial \mathbf{r}_{J_{4}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{J_{5}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{J_{6}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m)}}{m!} + \frac{\partial \mathbf{r}_{dr}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m)}}{m!}\right) \end{aligned} $$

(66)

$$ \begin{aligned} \phi_{21}(t + dT,t) = \psi_{r}^{(1)} + \sum\limits_{m=2}^{n}\left( \psi_{r}^{(m)} \frac{dT^{(m-1)}}{(m - 1)!} + \frac{\partial \mathbf{r}_{J_{2}}^{(m)}(t)}{\partial \mathbf{r}}\frac{dT^{(m-1)}}{(m - 1)!} + \frac{\partial \mathbf{r}_{J_{3}}^{(m)}(t)}{\partial \mathbf{r}}\frac{dT^{(m-1)}}{(m - 1)!}\right.\\ \left. + \frac{\partial \mathbf{r}_{J_{4}}^{(m)}(t)}{\partial \mathbf{r}}\frac{dT^{(m-1)}}{(m - 1)!} + \frac{\partial \mathbf{r}_{J_{5}}^{(m)}(t)}{\partial \mathbf{r}}\frac{dT^{(m-1)}}{(m - 1)!} + \frac{\partial \mathbf{r}_{J_{6}}^{(m)}(t)}{\partial \mathbf{r}}\frac{dT^{(m-1)}}{(m-1)!} + \frac{\partial \mathbf{r}_{dr}^{(m)}(t)}{\partial \mathbf{r}}\frac{dT^{(m-1)}}{(m - 1)!}\right) \end{aligned} $$

(67)

$$ \begin{aligned} \phi_{22}(t+dT,t) = \psi_{v}^{(1)} + \sum\limits_{m=2}^{n}\left( \psi_{v}^{(m)} \frac{dT^{(m-1)}}{(m-1)!} + \frac{\partial \mathbf{r}_{J_{2}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m-1)}}{(m-1)!} \right.\\ + \frac{\partial \mathbf{r}_{J_{3}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m-1)}}{(m-1)!}+ \frac{\partial \mathbf{r}_{J_{4}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m-1)}}{(m-1)!} + \frac{\partial \mathbf{r}_{J_{5}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m-1)}}{(m-1)!} \\\left.+ \frac{\partial \mathbf{r}_{J_{6}}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m-1)}}{(m-1)!} + \frac{\partial \mathbf{r}_{dr}^{(m)}(t)}{\partial \mathbf{r}^{(1)}}\frac{dT^{(m-1)}}{(m-1)!}\right) \end{aligned} $$

(68)

where, $\psi _{r}^{(m)}$ and $\psi _{v}^{(m)}$ are defined as $\frac {\partial \mathbf {r}^{(m)}(t)}{\partial \mathbf {r}(t)}$ and $\frac {\partial \mathbf {r}^{(m)}(t)}{\partial \mathbf {r}^{(1)}(t)}$, respectively.

Algorithms for Implementing Analytic Continuation

In this section, Algorithm 1 - Algorithm 3 are presented for the implementation of the present Analytic Continuation Method. In Algorithm 1 the derivation of the unperturbed STM is shown. Algorithm 2 presents the derivation of the J₂ − J₆ perturbed STM. Finally, Algorithm 3 includes the J₂ − J₆ and drag perturbed STM computation via the Analytic Continuation method.