1 Introduction

The calculated service life of welds can be determined using various concepts, which can be subdivided into global and local assessments. The global assessment is the nominal stress approach and is described in various guidelines and codes, e.g., [1, 2, 3, 4]. Local approaches proceed from local stress or strain parameters. In [5], the different variants are presented and differentiated. For welds in particular, the structural stress approach and the notch stress approach have been used. These approaches can also be found in standards and guidelines, e.g., [1, 3, 6, 7]. The applicability of these assessments is limited to N > 104.

In the low-cycle fatigue (LCF) range, plastic deformation cannot be neglected, and the assessment of elastic material behavior can no longer be performed with sufficient accuracy. For the low-cycle fatigue of welds, there are several approaches, one of which is the notch strain concept [5, 8, 9]. For non-welded components, the German FKM-guideline “nonlinear,” [10], presents a calculation procedure for fatigue assessment. For a short introduction to this new guideline, see also [11]. Although the notch strain approach has been discussed and applied at various times, this is the first time that the calculation procedure is described consistently as a guideline, including a safety concept.

For the application of the notch strain approach to welds, several alternative versions have been published [12, 13, 14, 15, 16]; there are also fracture mechanics-based approaches, as well as combinations of these approaches [17]. But by extending the FKM-guideline “nonlinear” to welds, the same fatigue assessment can be applied to non-welded and welded areas of a component.

Since for the mentioned examples no standardized calculation procedure and safety concept are specified, the transferability of the algorithms of the FKM-guideline “nonlinear” to welded joints is examined in this contribution. In this analytical fatigue assessment, analytical calculation algorithms are used, but information from numerical finite element analysis are also used as input data. The failure criterion is defined as the technical crack initiation, which has a final length of 0.25 < aend < 3 mm [10].

First, in Section 2, the calculation algorithms and the approach are presented. Afterwards, the assessment is applied to a database of fatigue tests of welded joints in Section 3, and the accuracy is evaluated. A conclusion and outlook complete this paper in Section 4. The investigations in this article are limited to the material group of steel and plate thickness of 5 mm ≤ t ≤ 12 mm.

2 Fatigue assessment based on the FKM-guideline “nonlinear” applied to welds

Fatigue assessments according to the FKM-guideline “nonlinear” [10] allow the calculation of the fatigue life up to crack initiation including elastic–plastic material behavior under proportional loading. For non-proportional loading, the algorithms of the FKM-guideline “nonlinear” would show load variations while calculating the equivalent stress. In addition, the cyclic material properties taking into account the elastic–plastic material behavior only apply to proportional loads, since, for example, non-proportional hardening is not taken into account. The procedure for considering non-proportional loads in the FKM-guideline “nonlinear” is currently being researched for non-welded components and may eventually be applied to weld seams in the future. For a better understanding, the complete calculation procedure for the application of the notch strain approach to welds based on [10] is shown in Fig. 1.

Fig. 1
figure 1

Calculation algorithm for the notch strain approach applied to welds

Full size image

The individual modules are explained in more detail in the following sections. The modeling of the weld and determination of local linear-elastic stresses are discussed in Section 2.1, and the subsequent estimation of the local elastic–plastic stresses and strains is explained in Section 2.2. These parameters are then converted into damage parameters, and a linear damage accumulation is performed, as described in Section 2.3. Finally, the safety concept is explained in Section 2.4.

2.1 Modeling of weld seams and determination of local linear-elastic stresses

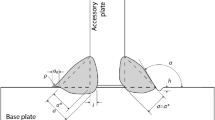
The assessment is based on elastic–plastic stresses, which are estimated from the linear-elastic stresses. These linear elastic stresses are determined in finite element calculations. For this calculation, the load sequence has to be converted into a time sequence of local linear-elastic stresses σe(t) using the transfer factor c. This factor indicates the ratio of the local elastic signed von Mises equivalent stress, Eq. 1 [10], and the external load at the most highly stressed point of the model.

$${\sigma}_{\text{eq}}\text{=} \frac{{\text{sign}}\left({\sigma }_{\text{h}}\right)}{\sqrt{2}}\sqrt{{\left({\sigma }_{\text{xx}}-{ \sigma}_{\text{yy}}\right)}^{2}\text{+}{\left({ \sigma}_{\text{xx}}-{\sigma}_{\text{zz}}\right)}^{2}\text{+}{\left({\sigma }_{\text{zz}}-{ \sigma}_{\text{yy}}\right)}^{2}+ \text{6} \left({{\tau }_{\text{xy}}}^{2}\text{+}{{\tau }_{\text{yz}}}^{2}\text{+}{{ \tau}_{\text{xz}}}^{2}\right)}$$
(1)

The sign of the equivalent stress depends on the hydrostatic stress. If σh > 0, the sign is positive; for hydrostatic stresses σh < 0, the sign is negative. Only by differentiating the sign physically meaningful cycles are generated. The factor c can be determined with the weld seam modeled according to the specifications of the effective notch stress approach [1] by using a linear-elastic finite element analysis. It is defined at the point with the highest stress concentration in terms of amount via the ratio between an applied reference load Lref and the resulting linear elastic stress σeq at the verification point, Eq. 2 [10].

$$\text{c} = \frac{{ \sigma}_{\text{eq}}}{{\text{L}}_{\text{ref}}}$$
(2)

The modeling of the weld seam is thus significantly simplified using the same simplifications as in the assessment with the effective notch stress approach. The weld seams that have been examined in this paper can be modeled with a reference radius rref = 1 mm and a specified dihedral angle of 45°. Models that are already available for verification with the effective notch stress approach can also be used for the assessment of the notch strain approach to determine the factor c.

Thereafter, this factor is used to convert the load sequence into a time sequence of local linear-elastic equivalent stress.

2.2 Estimation of local elastic–plastic stresses and strains

To determine the local elastic–plastic stresses and strains from the existing linear-elastic stresses, the uniaxial material deformation behavior must be known. This is described as a cyclic stress–strain curve according to the approach of Ramberg and Osgood [18], Eq. 3.

$$\varepsilon\text{ = }\frac\sigma {\text{E}}\text{ + }\left(\frac\sigma {\text{K}^\prime}\right)^\frac1{\text{n}^\prime}$$
(3)

The cyclic strain hardening coefficient K’ and the cyclic strain hardening exponent n’ can be determined experimentally in strain-controlled tests on unnotched material specimens or estimated from quasi-static material properties. For homogeneous non-welded steel components, the estimation is carried out in the FKM-guideline “nonlinear” from the tensile strength [10, 19, 20]. The scope of the estimation is limited for materials with tensile strengths up to Rm = 1200 MPa [10]. For components with inhomogeneous material properties, such as welded components, the tensile strength is not a suitable input parameter since it cannot be determined locally and finely resolved. Instead, hardness measurements are used. The estimation method used in [10] is modified to utilize the Vickers hardness HV1 input variable. For the steel material group, the Young’s modulus is assumed to be constant at E = 206 GPa.

For the described modification, a large database with test results of cyclic material properties and hardness measurements for the same steel materials is utilized. Details on the database and the development of the estimation method from the Vickers hardness can be found in [21]. The cyclic strain hardening exponent n’ is set to a constant value for steel, and the strain hardening coefficient K’ is dependent on the tensile strength or the hardness, as shown in Table 1.

Table 1 Parameters for estimating the cyclic stress–strain curve
Full size table

In this context, the load level HV1 is recommended for the hardness measurement of welds. This load level represents a good compromise between deviations due to local inhomogeneities of the material and a sufficiently high resolution to determine the different weld areas.

This reduces the effort of the measurement compared to measuring microhardness such as HV0.2 without losing information on the different weld areas.

After determining the cyclic deformation behavior of the material, the local stresses and local elastic–plastic strains can be determined using notch approximation methods: the extended Neuber’s rule [22] and the approximation method according to Seeger/Beste [23]. The comparison of different notch approximation methods was not part of the research for welded components. But different notch approximations were investigated during the development of the FKM-guideline “nonlinear.” In combination with Masing’s behavior [24] and the effects of material memory [25], the local stress–strain paths for the load-time sequence can be simulated. The Masing and Memory model is an essential theory module for the complete description of the local stress–strain path of metallic materials and base of the notch strain approach. Therefore, both effects are presented, even if the memory effects have to be considered only in the case of variable amplitude loading, which will not be further investigated in this paper.

The local elastic–plastic stresses can occur as an initial load curve according to Ramberg and Osgood or, in the case of load reversal, as a hysteresis load according to the doubled Ramberg–Osgood curve shown in Eq. 4 and Fig. 2a.

Fig. 2
figure 2

Local stress–strain path considering Masing behavior (a) and memory effects (b) cf. [10]

Full size image
$$\triangle\varepsilon=\frac{\triangle\sigma}{\text{E}}\text{ + }{2\;\cdot\left(\frac{\triangle\sigma}{\text{2K} ^\prime}\right)}^\frac1{\text{n}^\prime}$$
(4)

Considering Masing behavior and material memory, the closed hysteresis loops in the σ-ε-path are detected using the Rainflow Hysteresis Counting Method algorithm [25] (Fig. 2b).

These closed hysteresis loops are subsequently required for the damage parameter calculation.

2.3 Damage parameters and linear damage accumulation

A damage parameter is subsequently calculated for each closed hysteresis loop, allowing us to take into account different damaging influences. In the FKM-guideline “nonlinear,” two damage parameters can be chosen for the calculation. First, the damage parameter PRAM is a modification of the damage parameter according to Smith, Watson, and Topper [26], includes the mean stress sensitivity of the material using the factor k, and depends on the applied mean stress and alternating stress (Eq. 5).

$${\mathrm P}_{\mathrm{RAM}}=\left\{\begin{array}{lc}\sqrt{\left({\mathrm\sigma}_{\mathrm a}+\mathrm k\cdot{\mathrm\sigma}_{\mathrm m}\right)\cdot{\mathrm\varepsilon}_{\mathrm a}\cdot\mathrm E}&\mathrm{for}\;\left({\mathrm\sigma}_{\mathrm a}+\mathrm k\cdot{\mathrm\sigma}_{\mathrm m}\right)\geq0\\0&\mathrm{for}\;\left({\mathrm\sigma}_{\mathrm a}+\mathrm k\cdot{\mathrm\sigma}_{\mathrm m}\right)<0\end{array}\right.$$
(5)

According to [27], the factor k takes into account the mean stress sensitivity Mσ depending on the material via Eq. 6.

$$\text{k= }\left\{\begin{array}{cc}{\text{M}}_\sigma{\cdot}\left({\text{M}}_\sigma+\text{2}\right)&\text{for }\sigma_\text{m}{\geq0}\\\frac{{\text{M}}_\sigma}3{\cdot}\left(\frac{{\text{M}}_\sigma}3+\text{2}\right)&\text{for }\sigma_\text{m}<0\end{array}\right.$$
(6)

Second, the damage parameter PRAJ is derived from PJ according to Vormwald [28] and is based on a crack propagation model for short cracks. In the algorithm using the PRAJ, it is assumed that there is already a short crack with crack length a0 in the structure at the verification point, which can open and close under cyclic loading. This crack grows up to the technical crack with aend = 0.5 mm, which is defined as the failure criteria in the FKM-guideline “nonlinear.” Compared to PRAM, the use of PRAJ offers the advantage that load sequence effects due to crack closure may be considered in the damage accumulation. PRAJ only considers the part of the stress–strain hysteresis for which the crack is open (effective stress and strain ranges Δσeff und Δεeff), Eq. 7. The crack opening strain depends on the previous loading.

$${\mathrm P}_{\mathrm{RAJ}}=1.24\frac{\triangle{\mathrm\sigma}_{\mathrm{eff}}^2}{\mathrm E}+\frac{1.02}{\sqrt{\mathrm n'}}\cdot\triangle{\mathrm\sigma}_{\mathrm{eff}}\cdot\left(\triangle{\mathrm\varepsilon}_{\mathrm{eff}}-\frac{\triangle{\mathrm\sigma}_{\mathrm{eff}}}{\mathrm E}\right)$$
(7)

In Eq. 7, n’ is the cyclic strain hardening exponent, and E is the Young’s modulus.

For the description of the fatigue resistance of the component, first, the damage parameter Wöhler curve is estimated or determined experimentally. Subsequently, the support factor and surface roughness are taken into account to adapt the material Wöhler curve to the specific conditions of the component. Traditionally, the notch strain approach uses the strain Wöhler curve with the Coffin-Manson relationship, but Wächter has shown that the damage parameter Wöhler curve can also be used directly to describe the fatigue strength without reducing the accuracy [19].

The shape of the material damage parameter Wöhler curves depends on the damage parameter used. The damage parameter Wöhler curve for PRAM follows a trilinear approach, and that for PRAJ follows a bilinear approach in double logarithmic scale. The two support points at 1000 cycles and the fatigue limit and two slopes determine the PRAM Wöhler curve. For the PRAJ Wöhler curve, two support points at 1 cycle and the fatigue limit and one constant slope are used analogously. The fatigue limit of the damage parameter Wöhler curves for weld geometries modeled according to the specifications of the effective notch stress approach with rref = 1 mm is adjusted to the fatigue limit of the effective notch stress approach [1]. For this purpose, the fatigue limit of the effective notch stress approach according to the fatigue limit of FAT 200 [29] for equivalent von Mises stresses is used. For steel, the factors to estimate the material damage parameter Wöhler curves are shown in Fig. 3 and are described in Table 2; they were first published in [21, 30].

Fig. 3
figure 3

Comparison of the material damage parameter Wöhler curve for the damage parameters PRAM and PRAJ

Full size image
Table 2 Parameters for estimating the damage parameter Wöhler curves
Full size table

The development of the estimation method for the material damage parameter Wöhler curves was carried out with the same database of strain-controlled tests on unnotched material samples like the estimation method of the cyclic material properties. For this purpose, material samples were taken from the base material, heat-affected zone, and weld metal. The results obtained in the project were expanded with data from tests in the literature and first published as the modified FKM method [21]. However, this database only covers the low cycle fatigue and the high cycle fatigue up to \(5\cdot\text{10}^5\) cycles; the fatigue limit had to be adapted for welds in [30].

For the component, the damage parameter Wöhler curve is derived from the damage parameter Wöhler curve of the material. Influences from the construction of the component, such as the statistical and fracture mechanics support factors, which are related to the highly stressed surface and the stress gradient, and the surface roughness are taken into account. The statistical support factor is defined according to [31].

The fracture mechanics support factor and the factor considering the surface roughness are directly taken from the FKM-guideline “nonlinear,” in which the factors are defined with dependence on tensile strength.

For application to welds and the use of the Vickers hardness to describe the material strength, the relationship between the Vickers hardness and tensile strength from Eq. 8 is used. This approximation is based on the evaluation of [32].

$${\mathrm R}_{\mathrm m}=\left({3.3}\cdot\mathrm{HV}-16.7\right)\;\mathrm{MPa}$$
(8)

2.4 Safety concept

The calculation concept of the FKM-guideline “nonlinear” provides three safety factors: the factor f2.5%, the load safety factor γL, and the material safety factor γM. The factor f2.5% shifts the damage parameter Wöhler curves to a failure probability of Pf = 2.5%. When determining the factor f2.5%, a confidence interval with a probability of error α = 10% was also taken into account. The load safety factor γL can be used to secure the load assumption. The material safety factor γM considers the scatter of the fatigue resistance of the material and reduces the strength in the component damage parameter Wöhler curve to a lower level.

To compare calculated service lives with experimental values without considering the safety concept, the factors are set to f2.5% = γL = γM = 1.

3 Accuracy of the service life calculation with the notch strain approach

To check the accuracy of the introduced calculation algorithm, a database of welded specimen and components has been gathered with results from fatigue tests. In addition to tests that have been done specifically for this purpose [30], the database consists of test series from Baumgartner [33, 34] and Deinböck et al. [35]. In order for the test series to be used to verify the algorithms, the following information must be available: geometry information of the specimens and the weld, material information on the hardness distribution across the weld, and the number of cycles up to crack initiation. The tests on welded specimens and components are listed in Table 3.

Table 3 Database of fatigue tests on welded specimen
Full size table

For each test series, the critical weld seam is modeled according to the specifications of the effective notch stress concepts with rref = 1.0 mm, as listed in [1, 36]. Afterwards, a linear-elastic finite element calculation is performed. The extended Neuber’s rule [22] is used for the service life calculation with the damage parameter PRAM and the Seeger/Beste notch approximation method [23] for the calculation with the damage parameter PRAJ. For each model, the plastic notch factor Kp is additionally determined in an elastic-ideal-plastic finite element calculation. The plastic notch factor indicates how the load can be increased after reaching the yield strength at the most highly stressed point before plastic collapse of the component occurs. The factor Kp is used in the notch approximation with the extended Neuber’s rule and the Seeger/Beste notch approximation method. To determine the plastic notch factor, a finite element calculation with elastic-ideal-plastic material behavior is carried out. As an input parameter for the estimation of the cyclic stress–strain curve and the damage parameter Wöhler curve, the tensile strength of the base material and the Vickers hardness of the heat-affected zone are compared.

For the evaluation of the accuracy, two quality criteria are defined: the logarithmic mean m and the scatter range T of the ratio of experimental to calculated fatigue life, given in Eqs. 9 and 10. Both quantities become m = T = 1 for the optimal but unrealistic case of Ncalc = Nexp. A mean value of m < 1 tends to mean unsafe calculation results; a mean value of m > 1 tends to indicate a conservative calculation. The aim is to achieve an average calculation of the service life that is true to expectations, if all safety factors are set to 1.

$$\text{m}=10^{\frac1{\text{n}}{\cdot}\sum_\text{i=1}^\text{n}\text{log}\left(\frac{{\text{N}}_\text{exp}}{{\text{N}}_\text{calc}}\right)}$$
(9)
$$T=\frac {90 \% - quantile \left(\frac{N_{exp}}{N_{calc}}\right)}{10 \% - quantile \left(\frac{N_{exp}}{N_{calc}}\right)}$$
(10)

The calculated fatigue lives with the adapted calculation algorithms of the FKM-guideline “nonlinear” and the use of the tensile strength with deactivated safety concept are shown in Fig. 4. In comparison the calculated fatigue lives with the use of the Vickers hardness of the heat-affected zone can be taken from Fig. 5.

Fig. 4
figure 4

Calculated fatigue lives with tensile strength, deactivated safety concept and PRAM (a) or with PRAJ (b)

Full size image
Fig. 5
figure 5

Calculated fatigue lives with Vickers hardness, deactivated safety concept and PRAM (a) or with PRAJ (b)

Full size image

When considering the calculated service life with all safety factors deactivated, the average calculated service lives are m > 1, i.e., on the conservative side of the calculation. The approach therefore tends to lead to conservative results, even more for the calculation with PRAJ than for the calculation with PRAM. The scatter is smaller when calculated with PRAM than when calculated with PRAJ. This can also be observed with non-welded components [27] and is not due to the application of the adjusted calculation algorithms to the database with welded components.

The choice of the parameter describing the material strength also has an influence on the calculated service life. The use of the Vickers hardness is recommended for the service life calculation of welds, as this allows the user to take into account differences in strength along the cross-section of a weld seam. The tensile strength of the base material can be used if, as in the case of the investigated database, the weld metal has a similar strength to the base material and no significant change in strength is measured across the heat-affected zone.

The calculated results of the notch strain approach can be classified when compared with the effective notch stress approach. This comparison is only possible because the same weld geometry is used for both approaches. For the comparison of the calculated results of the notch strain approach for different hardnesses and the expected results when using the effective notch stress approach, the factor f2.5% for reducing the probability of failure to Pf = 2.5% is used. For the calculation with the PRAM, the factor is f2.5%,RAM = 0.64, for the use of the PRAJ f2.5%,RAJ = 0.30 valid. These factors are taken from the database for the estimation of cyclic material properties from the Vickers hardness [21] and were determined for the application of the FKM-guideline “nonlinear.”

Considering different hardnesses, the calculation for the notch strain approach is carried out with the adjusted algorithms of the FKM-guideline “nonlinear.” The results of the calculated service lives are then compared with the FAT 200 for the notch strain approach using equivalent stresses [29] and a failure probability of Pf,FAT = 2.3% (Fig. 6).

Fig. 6
figure 6

Comparison of calculated lifetimes calculated with the notch strain approach and PRAM (a) or calculated with PRAJ (b) and the effective notch stress approach

Full size image

Since the FAT 200 applies to a stress ratio of R = 0.5, but the FKM-guideline “nonlinear” applies to a stress ratio of R =  − 1, the FAT 200 according to [4] is converted to R =  − 1. For this purpose, the mean stress correction is used, taking into account the mean stress sensitivity Mσ. For the examples considered, the residual stresses are assumed to be low due to material and temperature treatments, and a mean stress sensitivity of Mσ = 0.15 [4] is used for the conversion. When considering the results, the failure criterion must be taken into account: The notch strain approach calculates service life until crack initiation; the FAT 200 applies to the failure criterion fracture.

Therefore, the service life determined with the adjusted calculation algorithms must be lower than the service life of the FAT 200.

The calculated results of the notch strain approach show a flatter slope than the results with the FAT 200. This is because crack propagation is predominant in notched components, especially in the area of low-cycle fatigue [15], resulting in steeper Wöhler curves. Due to the different failure criteria, technical crack initiation in the notch strain approach and fracture in the effective notch stress approach, the results for the calculation cannot be directly compared. Due to the concept, shorter service lives must be calculated for the notch strain concept, as shown in Figs. 5 and 6. By using the notch strain concept, crack initiation can be determined, and higher notch stresses can be taken into account.

The comparison shows that the service life up to crack initiation of the component can be determined using the notch strain approach with the adjusted algorithms of the FKM-guideline “nonlinear.” The results prove that the service life up to crack initiation can be calculated with the notch strain approach. Thus, it represents a good alternative to the existing effective notch stress approach [1], since all service life regimes can be covered at a similar effort.

4 Conclusion and outlook

The adapted calculation algorithms of the FKM-guideline “nonlinear” can be used for the analytical fatigue assessment of welded steel components. These adjustments are a proposal for a consistent procedure for applying the notch strain approach to welds, in which the calculated service life considers a safety concept. The hardness is taken into account when calculating the service life so that a reliable assessment is also possible for welds in which different weld areas have very different strength properties. By using the notch strain approach and applying the adjusted FKM-guideline “nonlinear,” welded and non-welded areas of a component can be designed with the same concept.

For the analytical fatigue assessment, the weld geometry of the effective notch stress concept and the hardness of the heat-affected zone are used. With finite element analyses, the transfer factor c, the highly stressed weld length, the stress gradient, and the plastic notch factor are determined. All other material properties can be estimated. The roughness is assumed if no further information is available. The verification is carried out up to the technical crack initiation and allows service lives from Ncalc > 10.

The adapted approach has thus far been applied to tests with constant load amplitudes on components with plate thicknesses of 5 mm ≤ t ≤ 12 mm and for steel components with low residual stresses. Verification by using thinner plates, tests with variable amplitude, welded aluminum components, and specimens with high residual stresses is pending.