FormalPara Key Summary Points

Why carry out this study?

Crystalline lens power (LP) plays an important role in the process of emmetropization; however, whether the cycloplegic ocular parameters could be used to calculate lens power still remains controversial

This study aimed to analyze the discrepancies between cycloplegic LP calculated using non-cycloplegic biometry and those using cycloplegic biometry, and to explore potential factors associated with the differences

What was learned from this study?

Significant difference was found between cycloplegic LP calculated using non-cycloplegic biometry and those using cycloplegic biometry (21.24 ± 1.58 D vs 21.43 ± 1.92 D, p = 0.001; paired t test). Calculations of cycloplegic LP in myopic eyes, especially those with low to moderate level of myopia, were particularly influenced by using cycloplegic biometry

Introduction

Myopia has emerged as a major threat to global public health over the past few decades. The problem is particularly acute in China, where the prevalence of myopia among individuals aged 14–25 years has been estimated to be 70–75% and increases with age [1,2,3]. Children with early-onset myopia are at risk of various complications that can lead to blindness, including myopic macular degeneration, retinal detachment, cataract, and glaucoma [4]. Therefore, myopia control is crucial to reducing the associated burden on individuals and society.

The foundation of myopia control lies in a full understanding of the process of eye growth and morphological changes in ocular components in the early stages of myopia development. A growing body of literature has demonstrated that cornea refractive power (CP), refractive crystalline lens power (LP), and axial length (AL) growth rate determine the final refractive status [5,6,7]. Throughout the early years of ocular development, although the AL continues to increase, with an increase of at least 3 mm till adulthood, which corresponds to a myopic shift in refraction of around 6–7 D (diopter), refraction is still clustered around mild hyperopia for a long time. Since the CP stabilizes after the second year of life [8], the loss of LP appears to be the major compensating factor against the elongation of AL for maintaining refraction stability. Clinical evidence suggests that when the acceleration of axial elongation outpaces LP reduction, myopia develops [9].

Although LP is considered a factor acting against AL increase during myopia development, the exact mechanism has not been extensively studied because of the difficulty of LP measurement. In contrast to the AL and corneal curvature radii, which can be measured simultaneously, LP can be calculated only with Bennett’s formula, which is based on the anterior chamber depth (ACD), lens thickness (LT), cornea power (CP), and spherical equivalent refraction (SER). Thus, the accuracy of LP depends on the accuracy of the ocular biometer measurements.

Though cycloplegia SER is considered to be more accurate to assess the refractive status in children, whether the cycloplegia ocular components data could be used to calculate the LP still remains controversial. Some large cohort studies have suggested that measurements under cycloplegia are recommended for biometric evaluations [10, 11]. Furthermore, recent large-scale studies focusing on LP did not clearly clarify whether the ocular biometry measurements were performed under cycloplegia or not [12]. (See Supplementary Table 1 for more details.)

The disagreement on whether biometry measurements should be performed under cycloplegia may result in inconsistent LP calculations, given that clinical studies have shown that cycloplegic agents may cause significant changes in the anterior ocular biometric components, including ACD, LT, and corneal curvature that are involved in LP calculation [13,14,15]. Thus, it is of clinical importance to carry out this large-scale hospital-based prospective study to analyze the difference in cycloplegic LP calculation using cycloplegic biometry and non-cycloplegic biometry.

Methods

Participants and Protocol

This study was approved by the Medical Ethics Committee of Zhongshan Ophthalmic Center, Sun Yat-sen University (approval no. 2021KYPJ185, approval date November 15, 2021) and registered on ClinicalTrials.gov. (NCT05247099, registration date January 6, 2022). Participants aged from 3 to 18 years were recruited at the Pediatric and Ophthalmology Departments of Zhongshan Ophthalmic Center, Sun Yat-sen University, Guangzhou, China, from January to March 2022. The prospective participants and their legal guardians were informed of the aims and methods of this cross-sectional study. Only children whose legal guardians provided written informed consent were enrolled.

The exclusion criteria were as follows: (1) astigmatism ≥ 1.5 D; (2) ocular diseases such as high intraocular pressure (IOP ≥ 20 mmHg), strabismus, keratoconus, microcornea, corneal infection, uveitis, glaucoma, congenital cataract, congenital lens dislocation, or other congenital ocular disorders; (3) previous use of orthokeratology lenses or low-concentration atropine; (4) allergy to compounds in tropicamide eye drops; (5) systemic diseases, such as diabetes and nephrotic syndrome; (6) premature birth; (7) history of ocular surgery or trauma causing alterations to the structure of the eyeball; and (8) poor cooperation during ocular examination.

All optometric and biometric measurements were performed by trained and experienced ophthalmologists (RX, RYL, and ZDL). The AL, ACD, LT, and the anterior corneal radii of curvature were measured using an IOLMaster 700 (Carl Zeiss Meditec AG, Jena, Germany). The quality control criteria conformed to the manufacturer’s recommendations. If the device indicated a low-quality inspection result, the operator repeated the measurement.

All measurements were performed in room light conditions (1000 lx). The patients underwent the first measurements before inducing cycloplegia. At the beginning of each measurement, the patients were asked to blink to ensure an even tear film coating on the ocular surface. Thereafter, cycloplegia was induced using tropicamide (0.5% tropicamide plus 0.5% phenylephrine hydrochloride). Two drops were applied to each eye three times at 10-min intervals. Ten minutes after the third application, the patients were double-checked by two experienced ophthalmologists to ensure adequate cycloplegic conditions: no light reflexes and a pupil diameter of more than 6 mm. Measurements were performed within 1 h of confirming full cycloplegia. After the final IOLMaster examination, each patient underwent mydriatic optometry by an experienced optometrist. Each eye was measured three times before and after inducing cycloplegia, and the mean value of each parameter was used in the analysis. CP and LP were calculated using Bennett’s method as previously described [7]. Anterior segment length (ASL) was defined as anterior chamber depth plus lens thickness. For each variable the outliers were checked and those at ± 2.00 standard deviations of the mean value were deleted.

Refractive status was divided into three categories according to international criteria [12, 16]: myopia (SER [spherical equivalent refraction] ≤  − 0.5 D), emmetropia (SER >  − 0.5 D and ≤ 0.75 D), and hyperopia (SER > 0.75 D). Myopia was further classified as low (SER >  − 3 D and ≤  − 0.5 D), medium (SER >  − 5 D and ≤  − 3 D), and high (SER ≤  − 5 D). In addition, LP calculated with non-cycloplegic data was defined as nLP, otherwise it was defined as cLP. Both calculations used cycloplegic refractive error, as non-cycloplegic error is affected by accommodative spasm.

Statistical Analysis

IBM SPSS Statistics (version 25.0; IBM Corp., Armonk, NY, USA) was used for the statistical analysis. Because Pearson’s coefficients showed strong correlations (r = 0.71–0.97) between the left and right eyes, only the data of the right eyes were used in the analysis. Continuous variables were expressed as means ± standard deviations. Multiple comparisons were performed using one-way analysis of variance (ANOVA). Differences in AL, ACD, LT, ASL, CP, AL/CR ratio, and LP before and after inducing cycloplegia were evaluated using paired t test. Correlations between ocular components were evaluated using Pearson’s correlation coefficients. Difference in ΔLP was analyzed in terms of refractive error, age and gender, respectively. The |ΔLP| was divided into two groups with 0.5 D as the boundary for analysis. Multiple linear regression analysis was performed to investigate the factors associated with ΔLP and absolute ΔLP (|ΔLP|). Values of p < 0.05 (two-tailed) were considered statistically significant.

Results

Of the 852 participants enrolled in this study, 31 were excluded because of low-quality measurements. Thus, 821 participants, including 419 boys (51.04%) and 402 girls (48.96%), were included in the final analysis. The mean age of the participants was 9.83 ± 2.97 years (range 3–18 years). The mean SER was − 1.06 ± 2.12 D (range − 11.38 to 8.38 D), and the mean best-corrected visual acuity was 0.014 ± 0.056 (range − 0.079 to 0.699) logMAR.

Differences in Non-cycloplegic and Cycloplegic Ocular Components

Table 1 shows the differences in ocular components measured before and after inducing cycloplegia. Overall, the ACD, LT, and ASL were significantly affected by cycloplegia agent (all p < 0.001; paired t test), respectively. ACD and ASL increased significantly from 3.30 ± 0.35 mm and 6.77 ± 0.32 mm to 3.42 ± 0.33 mm and 6.80 ± 0.33 mm (both p < 0.001, paired t test), respectively, while LT decreased from 3.45 ± 0.19 mm to 3.37 ± 0.15 mm (p < 0.001). Conversely, no statistically significant differences were documented in AL, CP, or AL/CR ratio before and after inducing cycloplegia (p = 0.917, p = 0.515, and p = 0.549, respectively).

Table 1 Sex-specific distribution of ocular components and refractive crystalline lens power
Full size table

Tables 2 and 3 show a comparison of the distribution of ocular components in the refractive status groups and subgroups. Eyes with myopia had longer AL (24.46 ± 0.81 mm), deeper ACD (3.35 ± 0.33 mm), greater AL/CR ratio (3.13 ± 0.15), and thinner LT (3.40 ± 0.17 mm) than those with hyperopia and emmetropia (p < 0.001; one-way ANOVA). As shown in Table 2, the three groups (myopia, emmetropia, and hyperopia group) had statistically significant differences in the changes in ASL before and after cycloplegia (p < 0.001, p < 0.001, p = 0.004, respectively; paired t test).

Table 2 Distribution of ocular parameters in different refractive groups
Full size table
Table 3 Distribution of ocular parameters in different myopia subgroups
Full size table

A comparison of ocular parameters among the low, medium, and high myopia subgroups is shown in Table 3. Among all ocular parameters, only AL and AL/CR ratio show significant differences among subgroups (both p < 0.001; one-way ANOVA). Statistically significant difference in the ASL was found in low and medium myopia subgroups (p < 0.001, p = 0.003, respectively; paired t test), but not in the high myopia group (p = 0.131).

Differences in LP Calculation Using Non-cycloplegic and Cycloplegic Biometry

The mean cLP was 21.43 ± 1.92 D and was significantly stronger than nLP with a mean value of 21.24 ± 1.85 D (p = 0.001; paired t test).

Significant difference of LP was observed in terms of gender and age groups. Girls’ cLP was slightly stronger than nLP (21.89 ± 1.88 D vs 21.64 ± 1.54 D; p = 0.003), as was boys’, but the change was smaller (21.01 ± 1.87 D vs 20.86 ± 1.54 D; p = 0.012). The mean nLP values and cLP in the age groups of 3–6, 7–10, 11–14, and 15–18 years listed in Table 4 suggested a dramatic decrease in LP until the age of 10 years. Moreover, in the groups of 7–10 and 11–14 years, significant changes were found between nLP and cLP (21.34 ± 1.49 D vs 21.45 ± 1.63 D, p = 0.008; 20.64 ± 1.35 vs 20.76 ± 1.55 D, p = 0.029; paired t test).

Table 4 Age-specific distribution of ocular parameters
Full size table

Table 2 shows distribution of nLP and cLP in the refractive status groups. In the myopia group, cLP was stronger than nLP (21.06 ± 1.69 D vs 20.91 ± 1.46 D; p < 0.001). In the emmetropia and hyperopia group, the difference was not statistically significant (21.55 ± 1.88 D vs 21.53 ± 1.57 D, p = 0.615; 22.89 ± 2.17 D vs 22.51 ± 1.50 D, p = 0.679). Furthermore, significant differences in nLP and cLP were observed in both low (p = 0.001; paired t test) and medium (p = 0.043) myopia subgroups (Table 3) but not in the high myopia subgroup (p = 0.335).

Associated Factors with the Discrepancy in LP Calculated with Non-cycloplegic and Cycloplegic Biometry

The mean ΔLP was 0.11 ± 0.87 D (range − 7.01 to 7.08 D), while the mean |ΔLP| was 0.43 ± 0.76 D (range 0–7.08 D). A total of 140 (19.75%, 140/852) participants had a more than 0.5-D change in |ΔLP|. Each parameter was not significantly different between participants with a change in |ΔLP| greater than or less than 0.5 D.

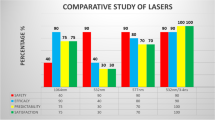
Boys had greater |ΔLP| than girls, but the difference was not statistically significant (0.45 ± 0.79 D vs 0.40 ± 0.72 D; p = 0.385; paired t test). Likewise, no statistically significant differences were observed between the age groups (p = 0.238; one-way ANOVA). The mean |ΔLP| values in the myopia, emmetropia, and hyperopia groups were 0.39 ± 0.70 D, 0.53 ± 0.86 D, and 0.52 ± 0.92 D, respectively (p = 0.114; one-way ANOVA) (Fig. 1).

Fig. 1
figure 1

The cycloplegic crystalline lens power decreases with axial elongation. a The relationship between axial length and lens power in noncycloplegic. b The relationship between axial length and lens power in cycloplegia

Full size image

Pearson’s correlation coefficients (Fig. 2) showed that ΔLP positively correlated with LP (r = 0.45, p < 0.001), while it negatively correlated with AL (r = − 0.16, p < 0.001) and AL/CR ratio (r = − 0.16, p < 0.001). Considering the strong correlations between AL/CR ratio, AL, and CP, the independent variables of gender, age, SER, the changes of AL, ASL, and CP were included in the multiple regression analysis. As shown in Table 5, ΔLP was significantly associated with age (β = − 0.010, [95% CI − 0.007 to − 0.001], p < 0.001), SER (β = 0.026, [95% CI 0.010 to 0.019], p < 0.001), ΔAL (β = −1.084, [95% CI − 1.827 to − 1.799], p < 0.001), ΔASL (β = 0.184, [95% CI 0.212 to 0.230], p < 0.001), and ΔCP (β = − 0.836, [95% CI − 1.093 to − 1.072], p < 0.001).

Fig. 2
figure 2

Pearson correlation between age, spherical equivalent refraction, and ocular parameters

Full size image
Table 5 Multiple linear regression models for associations of change of refractive lens power after cycloplegia with changes of ocular parameters
Full size table

|ΔLP| positively correlated with ACD (r = 0.13, p = 0.001), ASL (r = 0.16, p < 0.001), and LP (r = 0.12, p = 0.002), but did not significantly correlate with age (p = 0.312), SER (p = 0.162), AL (p = 0.178), CP (p = 0.799), or AL/CR ratio (p = 0.102). When the independent variables of gender, age, SER, the changes of AL, ASL, and CP were included in the multiple regression analysis, |ΔLP| was significantly associated with ΔASL (β = 0.172, [95% CI 0.112–0.300], p < 0.001).

Discussion

This study was the first to analyze the difference in cycloplegic LP calculation using non-cycloplegic biometry and cycloplegic biometry in a large cohort of participants aged 3–18 years with a wide refraction range (− 11.38 to 8.38 D). Our results demonstrated that using cycloplegic biometry could lead to a 0.43 ± 0.76 D (range 0–7.08 D) difference in LP calculation and nearly one-fifth of the participants exhibited a difference of more than 0.5 D in LP calculated using cycloplegic biometry. Moreover, subjects with low to moderate level of myopia were more likely to have a discrepancy in LP calculation when using cycloplegic biometry.

Cycloplegic refraction is well recommended in young children [17], whereas there is no consensus on whether the ocular components be measured before or after cycloplegia. In clinical practice, ocular biometry could be performed during the intervals of applying cycloplegic drops to save time. Moreover, some large cohort studies have suggested that measurements under cycloplegia are recommended for biometric evaluations [10, 11]. Whether the cycloplegic biometry could be applied for the LP calculation remained unknown. Our study firstly observed that cycloplegia may be associated with an increase in LP regardless of refractive status, with a maximum change of 7 D. Moreover, nearly one-fifth of the participants exhibited a change of more than 0.5 D under cycloplegia. Thus, the question that arises is whether a difference of 0.5 D is important for assessing ocular development. In a cross-sectional study of 1133 pre-school children between the ages of 3 to and 6 years, an AL increase of 0.44 mm accompanied by an SER reduction of 0.26 D and an LP reduction of 1.87 D was documented [18]. Usually, a 1-mm increase in AL corresponded to an SER change of 3 D, suggesting that the SER was supposed to decrease by 1.32 D. Since CP is stable, it seems plausible the actual limitation of refraction change is due to an LP reduction, which indicates a 0.5-D change in LP might offset a 0.25-D clinically significant reduction in SER. Another study [19] also reported that an LP decrease of around 0.5 D per year could compensate for a clinically significant change of 0.43 D in SER among school-aged children. Thus, the LP calculation error of more than 0.5 D may affect the understanding of the compensation effect of LP during refraction development.

It is plausible that under cycloplegia, significant changes occur in the ocular parameters used in Bennett’s formula. In this study, a significant increase in ACD along with reduction in LT was observed after inducing cycloplegia. These findings are in line with previous reports. Palamar et al. [10] found a post-cycloplegia ACD increase of around 0.2 mm. Gao et al. [20] reported a significant reduction in LT under cycloplegia among 135 children. The effect of cycloplegia on these two parameters may be explained by the Helmholtz theory [21], according to which the relaxation of the ciliary body increases the zonular tension around the lens equator, resulting in a decrease in LT, and the lens moves backward.

In this study, a comparison among different refractive groups also produced an interesting finding. Our results showed that calculations of cycloplegic LP in myopic eyes, especially those with low to medium level of myopia, were particularly influenced by using cycloplegic biometry.

However, in highly myopic eyes and hyperopic eyes, no significant changes were observed in ocular biometric measurements or LP calculation when introducing cycloplegia biometry. Cycloplegia has more effect on the lens thickness and position in hyperopic eyes than myopic eyes after it paralyzes accommodation, since hyperopic eyes accommodate during normal distance reading and viewing [22, 23]. Consistent with this theory, we found that cycloplegia induced a 0.05, 0.04, and 0.03-mm increase in ASL for the hyperopic, emmetropic, and myopic eyes, respectively. However, in addition to increasing ASL, we found that the cycloplegia also resulted in a 0.16, 0.12, and 0.06-mm decrease of LT for the hyperopic, emmetropic, and myopic eyes, respectively. In accordance with Bennett’s method, we suspect that the loss of LT compensates the change of ASL in hyperopic eyes and attributed it to the unremarkable effect in LP. Notably, in highly myopic eyes, no significant changes were observed in ocular biometric measurements after inducing cycloplegia. It remains unknown why people with high myopia have a weak response to cycloplegia; future in vivo studies on structural and functional change in ciliary body and zonule fibers may be helpful to explore the mechanism.

In this study, measurements of ocular parameters under cycloplegia did not alter the typical pattern of LP loss with age. In the SCES study [12], LP decreased by 1.93 D between the ages of 6 and 10 years, while after the age of 10 years, the reduction rate decreased significantly, and LP loss almost plateaued. Guo et al. [18] found that LP decreased from 25.56 to 23.69 D between the ages of 3 and 6 years. In line with these studies, we found that the mean LP declined dramatically, from 23.26 to 21.34 D (0.27 D per year), between the ages of 3 and 10 years, but after the age of 10, the reduction rate tended to decrease, with a mean drop of 0.02 D per year. It has been suggested that the lens keeps thinning and flattening, from birth until approximately the age of 10 years. Interestingly, in this study, all age groups except the group of 7–14 years exhibited a slight increase in LP under cycloplegia. The reason might be the higher prevalence of mild to moderate myopia at those ages. In Guo et al. [18] and the SCES study [12], LP was approximately 1 D greater in girls than in boys. Our data also support a gender-related difference. Girls had greater LP irrespective of age or refractive status, and cycloplegia had little influence on this patten.

As in previous studies [24, 25], no statistical differences in AL or CP before and after inducing cycloplegia were found in this study. It is known that CP remains stable after the age of 3 [26], and our results confirm that cycloplegia has a minimal effect on the corneal curvature radii. Regarding the AL, it is still debated whether it increases after inducing cycloplegia. Some studies have reported significant increases [12, 18], whereas Gao et al. [20] found a decrease in myopic pediatric eyes under cycloplegia and suggested that it was likely caused by cornea flattening.

In general, we identified a positive correlation of the ΔLP with LP and negative correlation with AL. Logically, the absolute value of ΔLP is more suitable for reflecting the influence on LP. Therefore, we analyzes the Pearson’s correlation coefficients and found that |ΔLP| was positively correlated with ACD, ASL, and LP, respectively, which may indicate that eyes with deeper ACD, deeper ASL, or stronger LP were more likely to be affected. This matter warrants further large cohort research.

This study has several limitations. First, as it was conducted in a single center, selection bias could not be avoided. Moreover, since the prevalence of myopia in China is relatively high, myopia may have been slightly dominant in the entire cohort, and the results may not be generalizable to the general population. Second, since Bennett’s formula is the most used method for calculating LP, the results may not fully correspond to reality, although studies have shown good agreement between LP calculated using this formula and phakometric data [27, 28].

In conclusion, this study highlights substantial gaps in our knowledge of the accuracy of LP calculation using cycloplegic biometry, and our results showed that it could lead to great differences in the calculation of the LP in pediatric populations, especially in young subjects with low and moderate levels of myopic. Therefore, the findings might facilitate the routine approach of future studies on refraction in school-age children.

Conclusions

Our results indicated that using cycloplegic biometry could lead to an overestimation in LP for low and moderate myopic eyes. This finding is likely to facilitate the routine approach of refractive development research.