Introduction

Integro-differential equations (IDEs) and their delay types (IDDEs) govern many physical phenomena emerging in mathematics, mechanics, engineering, biology, economics, electrodynamics and oscillating magnetic field [1,2,3,4,5,6,7,8]. These varieties encourage many researchers in all over the world to give more attention than ever before. Because the sophisticated phenomena can be easily described with the aid of IDDEs. As these phenomena are evolved, finding the physical behavior of IDDEs becomes far more difficult. For example, state-dependent Riccati equation modeling vehicle state estimation [9], state-dependent delay Volterra equations considered in viscoelasticity theory [10] and the system of state-dependent delay differential equation describing forest growth [11] can be found in the literature. Thus, a difficult task appears while interpreting the physical responses of these complex structures, analytically. Therefore, several numerical methods have recently been focused and established more on IDEs and their various types. To this end, Kürkçü et al. [12, 13] have solved IDEs and IDEs of difference type by means of Dickson matrix-collocation method. Reutskiy [14] has utilized the backward substitution method for solving the neutral Volterra–Fredholm IDEs. Chen ve Wang [15] have dealt with the neutral functional–differential equation with proportional delays using the variational iteration method. Bellen and Zennaro [4] have investigated the convergence and numerical solution of state-dependent delay differential equations. Gökmen et al. [16] have proposed Taylor polynomial method for solving the Volterra-type functional integral equations. Gülsu et al. [17] have used Chebyshev polynomial for delay differential equations. Savaşaneril and Sezer [18, 19] have employed Taylor and Taylor–Lucas polynomial method for searching the solution of Fredholm IDEs and pantograph-type delay differential equations, respectively. Maleknejad and Mahmoidi [20] have obtained the Taylor and block–pulse numerical solutions of Fredholm integral equation. Rohaninasa et al. [21] have established Legendre collocation method to solve Volterra–Fredholm IDEs. Yüzbaşı [22] have approached the numerical solutions of pantograph-type Volterra IDES with the aid of Laguerre polynomial. Gümgüm at al. [23] have obtained the Lucas polynomial solutions of functional IDEs involving variable delays.

All above studies motivate us to develop a numerical method and deal with the highly stiff problems, such as the integro-differential delay equations with state-dependent bounds in this paper. In the literature, there is no study maintaining the numerical solution of such equations. By way of this study, we can investigate their physical responses numerically, evaluating the obtained values in tables and figures. This paper is organized as follows: “Fundamental properties of Mott polynomial” section mentions some properties of the Mott polynomials. “Constructing method of solution via matrix relations” section establishes new matrix relations and method solution. “Mott-residual error estimation” section gives Mott-residual error estimation as an algorithmic sense. “Numerical examples” section includes stiff numerical examples solved with the aid of the present method. “Conclusions” section presents the discussions about the present method and its efficiency by taking into account the results in “Numerical examples” section. The functional integro-differential delay equations with state-dependent bounds are of the form

$$\begin{aligned}&\sum \limits _{r = 0}^{m_1}{P_{r}}\left( t \right) y^{(r)}\left( t - \sigma _{r} \right) \nonumber \\&\quad = g\left( t \right) + \sum \limits _{q = 0}^{{m_2}} \lambda _q \int \limits _{c_{q}y\left( t \right) }^{d_{q}y\left( t \right) } { {K_q}\left( {t,s} \right) {y\left( s - \tau _{q} \right) }\hbox {d}s},\,\,\,\nonumber \\&\qquad a \le t,s \le b, \end{aligned}$$
(1)

subject to the initial conditions

$$\begin{aligned} \sum \limits _{k = 0}^{{m_1} - 1} {{y^{(k)}}\left( a \right) } = {\psi _k}, \end{aligned}$$
(2)

where y(t), \({P_{r}}\left( t \right)\), g(t) and \(K_q\left( {t,s} \right)\) are analytic functions on [a, b]; \(\sigma _{r}\) and \(\tau _{q}\) are real constant delays \(\left( \sigma _{r},\,\tau _{q} \ge 0 \right)\); \(\lambda _q\), \({c_{q}}\), \({d_{q}}\)\(\left( c_{q}<d_{q}\right)\) and \(\psi _k\) are proper constants.

Our aim in this study is to efficiently obtain an accurate approximate solution of Eq. (1) by developing the Mott matrix-collocation method, which was previously introduced in [24]. Besides, the parameter-\(\beta\) in the generalized Mott polynomial is used as a control parameter in the numerical approximations. Hence, we can control the obtained solutions in terms of their more consistent structures. The approximate solution comes out to be in the form (see [24])

$$\begin{aligned} y\left( t \right) \cong {y_N}\left( t \right) = \sum \limits _{n = 0}^N {{y_n}{S_n}\left( {t,\beta } \right) }, \end{aligned}$$
(3)

where \(y_{n}\), \(n = 0,1, \ldots ,N\) are unknown Mott coefficients to be calculated by the method and \({S_n}\left( {t,\beta } \right)\) is the generalized Mott polynomial [25]. Chebyshev–Lobatto collocation points used in the matrix systems are defined to be (see [23])

$$\begin{aligned} {t_i} = \frac{a+b}{2}+\frac{a-b}{2}\hbox {cos}\left( \frac{\pi i}{N}\right) \end{aligned}$$
(4)

where \(i = 0,1, \ldots ,N\) and \(a = {t_0}< {t_1}< \cdots < {t_N} = b\).

Fundamental properties of Mott polynomial

In this section, we briefly describe some fundamental properties of Mott polynomial, which is used as a basis of the matrix-collocation method. In 1932, Mott [26] originally introduced the polynomial while monitoring the roaming behaviors of electrons for a problem in the theory of electrons. After this exploration, Erdèlyi et al. [27] established the explicit formula of the polynomial \({S_n}\left( t \right)\) as follows:

$$\begin{aligned} \begin{aligned} {S_n}\left( t \right)&= {\left( { - \frac{t}{2}} \right) ^n}\left( {n - 1} \right) !\sum \limits _{l = 0}^{\left\lfloor {n/2} \right\rfloor } {\frac{{{t^{ - 2l}}}}{{l!\left( {n - l} \right) !\left( {n - 2l - 1} \right) !}}} \\&= {\left( {n!} \right) ^{ - 1}}{\left( { - \frac{t}{2}} \right) ^n}{}_3{F_0}\left( { - n,\frac{1}{2} - \frac{n}{2},1 - \frac{n}{2}; - 4{t^{ - 2}}} \right) , \end{aligned} \end{aligned}$$

where \({}_3{F_0}\) is a generalized hypergeometric function.

In 1984, Roman [28] presented both an associated Sheffer sequence and a generating function for the polynomial as follows:

$$\begin{aligned} f\left( t \right) = \frac{{ - 2t}}{{1 - {t^2}}}\,\,\, \text {and}\,\,\, \sum \limits _{k = 0}^\infty {\frac{{{S_k}\left( t \right) }}{{k!}}} {s^k} = \exp \left( {\frac{{t\sqrt{1 - {s^2}} - t}}{s}} \right) , \end{aligned}$$

where \({S_0}\left( t \right) = 1\), \({S_1}\left( t \right) = - \frac{t}{2}\), \({S_2}\left( t \right) = \frac{{{t^2}}}{4}\), \({S_3}\left( t \right) = - \frac{{3t}}{4} - \frac{{{t^3}}}{8}\) and \({S_4}\left( t \right) = \frac{{{t^2}}}{2} + \frac{{{t^4}}}{{16}}\).

On the other hand, a triangle coefficient matrix of the polynomial can be found in A137378 of OEIS [29]. In 2014, Kruchinin [25] converted the polynomial to a generalized form with a parameter-\(\beta\):

$$\begin{aligned} {S_n}\left( {t,\beta } \right) & = \sum \limits _{p = 1}^n {\sum \limits _{q = 0}^p {{{\left( { - 1} \right) }^{p - q + \left( {n + p} \right) /2}}\frac{{n!\left( {1 + {{\left( { - 1} \right) }^{n + p}}} \right) }}{{2p!}}} } \left( {\begin{array}{*{20}{c}} p \\ q \end{array}} \right) \\&\left( {\begin{array}{*{20}{c}} {\beta q} \\ {\left( {n + p} \right) /2} \end{array}} \right) {t^p}, \,\,\, n > 0, \end{aligned}$$

where the Mott polynomial is obtained for \(\beta = 0.5\). For further properties of the polynomial, the reader can refer to [25,26,27,28].

Constructing method of solution via matrix relations

In this section, the fundamental matrix relations are presented to construct method of solution. Let us first state the solution form (3) in the matrix relation [24]

$$\begin{aligned} y\left( t \right) = {{\varvec{S}}}\left( {t,\beta } \right) {{\varvec{Y}}} \,\,\text {and}\,\, {y^{\left( r \right) }}\left( t \right) = {{{\varvec{S}}}^{\left( r \right) }}\left( {t,\beta } \right) {{\varvec{Y}}}, \end{aligned}$$
(5)

where

$$\begin{aligned} &{{\varvec{S}}}\left( {t,\beta } \right)= \left[ {\begin{array}{*{20}{c}} {{S_0}\left( {t,\beta } \right) }&{{S_1}\left( {t,\beta } \right) }&\cdots&{{S_N}\left( {t,\beta } \right) } \end{array}} \right] ,\\ &{{{\varvec{S}}}^{\left( r \right) }}\left( {t,\beta } \right)= \left[ {\begin{array}{*{20}{c}} {S_0^{\left( r \right) }\left( {t,\beta } \right) }&{S_1^{\left( r \right) }\left( {t,\beta } \right) }&\cdots&{S_N^{\left( r \right) }\left( {t,\beta } \right) } \end{array}} \right] \,\,\text {and}\,\, \\ & {{\varvec{Y}}}= \left[ {\begin{array}{*{20}{c}} {y_0}&{y_1}&\cdots&{y_N} \end{array}} \right] ^\mathrm{T}. \end{aligned}$$

Now, inserting \(t\rightarrow t - \sigma _r\) into the matrix relation (5), then we get

$$\begin{aligned} {y^{\left( r \right) }}\left( {t - \sigma _r } \right) = {{\varvec{S}}}^{\left( r \right) }\left( {t - \sigma _r,\beta } \right) {{\varvec{Y}}}, \end{aligned}$$
(6)

where

$$\begin{aligned} {{{\varvec{S}}}^{\left( r \right) }}\left( {t - \sigma _r,\beta } \right) = \left[ {\begin{array}{*{20}{c}} {S_0^{\left( r \right) }\left( {t - \sigma _r,\beta } \right) }&{S_1^{\left( r \right) }\left( {t - \sigma _r,\beta } \right) }&\cdots&{S_N^{\left( r \right) }\left( {t - \sigma _r,\beta } \right) } \end{array}} \right] . \end{aligned}$$

Similarly, it holds that

$$\begin{aligned} y\left( {s - \tau _q } \right) = {{\varvec{S}}}\left( {s - \tau _q,\beta } \right) {{\varvec{Y}}}, \end{aligned}$$
(7)

By the matrix relation (6), the left hand side of Eq. (1) is of the matrix relation form

$$\begin{aligned} \sum \limits _{r = 0}^{m_{1}} {{P_{r}}\left( t \right) {y^{(r)}}\left( {t - \sigma _r } \right) }= \sum \limits _{r = 0}^{m_{1}} {{{{\varvec{P}}}_{r}}\left( t \right) {{\varvec{S}}}^{\left( r \right) }\left( {t - \sigma _r,\beta } \right) {{\varvec{Y}}}} . \end{aligned}$$
(8)

Now, the matrix relation of integral part of Eq. (1) is given. First, the kernel function \(K_{q}(t,s)\) can be written in the truncated Taylor series form [16, 18],

$$\begin{aligned} {K_q}\left( {t,s} \right) = \sum \limits _{m = 0}^N {\sum \limits _{n = 0}^N {{k_{mn}}{t^m}{s^n}} } \Rightarrow {K_q}\left( {t,s} \right) = {{\varvec{X}}}\left( t \right) {{\varvec{K}}}_q{{{\varvec{X}}}^\mathrm{T}}\left( s\right) , \end{aligned}$$
(9)

where

$$\begin{aligned} {{\varvec{K}}}_q = \left[ {k_{mn}^q} \right] ,\,\, k_{mn}^q = \frac{1}{{i!j!}}\frac{{{\partial ^{i + j}}{K_q}\left( {0,0} \right) }}{{\partial {t^i}\partial {s^j}}},\,\, i,j = 0,1, \ldots ,N, \end{aligned}$$

and

$$\begin{aligned} {{\varvec{X}}}\left( {t} \right) = \left[ {\begin{array}{*{20}{c}} {1}&{t}&\cdots&{t^N} \end{array}} \right] . \end{aligned}$$

Then, it holds from the matrix relations (7) and (9) that

$$\begin{aligned}&\sum \limits _{q = 0}^{{m_2}} \lambda _q \int \limits _{c_{q}y\left( t \right) }^{d_{q}y\left( t \right) } { {K_q}\left( {t,s} \right) {y\left( s - \tau _{q} \right) }} \hbox {d}s\nonumber \\&\quad =\sum \limits _{q = 0}^{m_2} \lambda _q { {{\varvec{X}}}\left( t \right) {{\varvec{K}}}_q{{{\varvec{R}}}_q (t)}{{\varvec{Y}}}}, \end{aligned}$$
(10)

where

$$\begin{aligned} {{\varvec{R}}}_q (t) & = \int \limits _{c_{q}y\left( t \right) }^{d_{q}y\left( t \right) } {{{{\varvec{X}}}^\mathrm{T}}\left( s \right) {{\varvec{S}}}\left( s - \tau _q,\beta \right) \hbox {d}s} = \left[ {r_{ij}^q (t)} \right] ,\\&\qquad i,j = 0,1, \ldots ,N. \end{aligned}$$

Recalling the matrix relations (8) and (10) and collocation points (4), we thus write the combined matrix relation as

$$\begin{aligned}&\sum \limits _{r = 0}^{m_{1}} {{{{\varvec{P}}}_{r}}\left( t_i \right) {{\varvec{S}}}^{\left( r \right) }\left( {t_i - \sigma _r,\beta } \right) {{\varvec{Y}}}}\nonumber \\&\quad =g(t_i)+\sum \limits _{q = 0}^{m_2} \lambda _q { {{\varvec{X}}}\left( t_i \right) {{\varvec{K}}}_q{{{\varvec{R}}}_q (t_i)}{{\varvec{Y}}}}. \end{aligned}$$
(11)

More briefly, we can construct the matrix relation (11) as the fundamental matrix equation

$$\begin{aligned} \left( \sum \limits _{r = 0}^{m_{1}} {{{\varvec{P}}}_{r}}{{\varvec{S}}}^{\left( r \right) }\left( {\beta } \right) -\sum \limits _{q = 0}^{m_2} \lambda _q \overline{{{\varvec{X}}}}\,\, \overline{{{\varvec{K}}}_q}\,\,\overline{{{\varvec{R}}}_q }\right) {{\varvec{Y}}}={{\varvec{G}}}, \end{aligned}$$
(12)

where

$$\begin{aligned} {{\varvec{S}}}^{(r)}(\beta ) & = \left[ \begin{array}{c} {{{\varvec{S}}}^{(r)} \left( t_{0}-\sigma _r,\beta \right) } \\ {{{\varvec{S}}}^{(r)} \left( t_{1}-\sigma _r,\beta \right) } \\ {\vdots } \\ {{{\varvec{S}}}^{(r)} \left( t_{N}-\sigma _r,\beta \right) } \end{array}\right] \\ & = \left[ \begin{array}{cccc} {S_0^{\left( r \right) }\left( {t_0 - \sigma _r,\beta } \right) } &{} {S_1^{\left( r \right) }\left( {t_0 - \sigma _r,\beta } \right) } &{} {\cdots } &{} {S_N^{\left( r \right) }\left( {t_0 - \sigma _r,\beta } \right) } \\ {S_0^{\left( r \right) }\left( {t_1 - \sigma _r,\beta } \right) } &{} {S_1^{\left( r \right) }\left( {t_1 - \sigma _r,\beta } \right) } &{} {\cdots } &{} {S_N^{\left( r \right) }\left( {t_1 - \sigma _r,\beta } \right) } \\ {\vdots } &{} {\vdots } &{} {\ddots } &{} {\vdots } \\ {S_0^{\left( r \right) }\left( {t_N - \sigma _r,\beta } \right) } &{} {S_1^{\left( r \right) }\left( {t_N - \sigma _r,\beta } \right) } &{} {\cdots } &{} {S_N^{\left( r \right) }\left( {t_N - \sigma _r,\beta } \right) } \end{array}\right] ,\\ \overline{{{\varvec{X}}}} & = {\left[ {\begin{array}{*{20}{c}} {{{\varvec{X}}}\left( {{t_0}} \right) }&{}0&{} \cdots &{}0\\ 0&{}{{{\varvec{X}}}\left( {{t_1}} \right) }&{} \cdots &{}0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{}0&{}{{{\varvec{X}}}\left( {{t_N}} \right) } \end{array}} \right] _{\left( {N + 1} \right) \times {{\left( {N + 1} \right) }^2}}}, \,\, \\ {{\varvec{G}}} & = {\left[ {\begin{array}{*{20}{c}} {g\left( {{t_0}} \right) }&{g\left( {{t_1}} \right) }&\cdots&{g\left( {{t_N}} \right) } \end{array}} \right] ^\mathrm{T}},\\ \overline{{{\varvec{K}}}_q} & = {\left[ {\begin{array}{*{20}{c}} {{{\varvec{K}}}_q}&{}0&{} \cdots &{}0\\ 0&{}{{{\varvec{K}}}_q}&{} \cdots &{}0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0&{}0&{}0&{}{{{\varvec{K}}}_q} \end{array}} \right] _{{{\left( {N + 1} \right) }^2} \times {{\left( {N + 1} \right) }^2}}},\,\, \\ \overline{{{\varvec{R}}}_q} & = {\left[ {\begin{array}{*{20}{c}} {{{\varvec{R}}}_q\left( {{t_0}} \right) }\\ {{{\varvec{R}}}_q\left( {{t_1}} \right) }\\ \vdots \\ {{{\varvec{R}}}_q\left( {{t_N}} \right) } \end{array}} \right] _{{{\left( {N + 1} \right) }^2} \times \left( {N + 1} \right) }}. \end{aligned}$$

Using the matrix relation (5), we similarly state the matrix relation of the initial conditions (2) as the following:

$$\begin{aligned} \sum \limits _{k = 0}^{{m_1} - 1} {{{\varvec{S}}}^{(k)}\left( a,\beta \right) } {{\varvec{Y}}} = {\psi _k}. \end{aligned}$$
(13)

By the matrix equation (12), we are now ready to constitute the method of solution

$$\begin{aligned} \underbrace{\left( \sum \limits _{r = 0}^{m_{1}} {{{\varvec{P}}}_{r}}{{\varvec{S}}}^{\left( r \right) }\left( {\beta } \right) -\sum \limits _{q = 0}^{m_2} \lambda _q \overline{{{\varvec{X}}}}\,\,\,\overline{{{\varvec{K}}}_q} \,\,\,\overline{{{\varvec{R}}}_q }\right) }_{{\varvec{W}}}{{\varvec{Y}}} = {{\varvec{G}}}. \end{aligned}$$
(14)

Then, it follows that

$$\begin{aligned} {{\varvec{W}}}{{\varvec{Y}}}={{\varvec{G}}} \,\,\,\text {or}\,\,\, \left[ {{\varvec{W}}};\, {{\varvec{G}}}\right] . \end{aligned}$$

On the other hand, we can construct the matrix relation of Eq. (13) as

$$\begin{aligned} {{\varvec{U}}}_{k} {{\varvec{Y}}}=\psi _k \Rightarrow \left[ {{\varvec{U}}}_{k}\,\, ;\,\, \psi _k \right] ,\,\, k = 0,1, \ldots {m_1} - 1, \end{aligned}$$
(15)

where

$$\begin{aligned} {{{\varvec{U}}}_k} \equiv \left[ {\begin{array}{*{20}{c}} {{u_{k0}}}&{{u_{k1}}}&\cdots&{{u_{kN}}} \end{array}} \right] . \end{aligned}$$

Replacing the row(s) of the matrix relation (15) by the last \(m_1\) row(s) in \({{\varvec{W}}}\), we then obtain the augmented matrix

$$\begin{aligned} \left[ {\widetilde{{{{\varvec{W}}}}}\,\,;\,\,{\widetilde{{{\varvec{G}}}}}} \right] = \left[ {\begin{array}{*{20}{c}} {{w_{00}}}&{}{{w_{01}}}&{} \cdots &{}{{w_{0N}}}&{};&{}{g\left( {{t_0}} \right) }\\ {{w_{10}}}&{}{{w_{11}}}&{} \cdots &{}{{w_{1N}}}&{};&{}{g\left( {{t_1}} \right) }\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{}{ \vdots ;}&{} \vdots \\ {{w_{N - {m_1},0}}}&{}{{w_{N - {m_1},1}}}&{} \cdots &{}{{w_{N - {m_1},N}}}&{};&{}{g\left( {{t_{N - {m_1}}}} \right) }\\ {{u_{00}}}&{}{{u_{01}}}&{} \cdots &{}{{u_{0N}}}&{};&{}{{\psi _0}}\\ {{u_{10}}}&{}{{u_{11}}}&{} \cdots &{}{{u_{1N}}}&{};&{}{{\psi _1}}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{}{ \vdots ;}&{} \vdots \\ {{u_{{m_1} - 1,0}}}&{}{{u_{{m_1} - 1,1}}}&{} \cdots &{}{{u_{{m_1} - 1,N}}}&{};&{}{{\psi _{{m_1} - 1}}} \end{array}} \right] . \end{aligned}$$
(16)

We solve the augmented matrix (16) only if rank\(\tilde{{{\varvec{W}}}}\!=\!\text {rank}\left[ {{\tilde{{{\varvec{W}}}}}\,\,;\,\,{\tilde{{{\varvec{G}}}}}} \right] \!=\!N+1\). We can state \({{\varvec{Y}}} \!=\! {\left( {{\tilde{{{\varvec{W}}}}}} \right) ^{ - 1}}{\tilde{{{\varvec{G}}}}}\). Thus, the Mott coefficients appearing in the form (3) are obtained, and then, they are substituted into the form (3); we finally reach the Mott polynomial solution with the parameter-\(\beta\).

Mott-residual error estimation

The residual error analysis has successfully been employed in [7, 8, 12, 13, 16, 22, 30]. For this motivation, we introduce the Mott-residual error estimation technique including the Mott polynomial and a residual function to improve the Mott polynomial solution (3) of Eq. (1). Algorithmic procedure of this technique can be described for the present method as

  1. Step 1:

    \({R_N}(t) \leftarrow \sum \nolimits _{r = 0}^{m_1}{P_{r}}\left( t \right) y_N^{(r)}\left( t - \sigma _{r} \right) -\sum \nolimits _{q = 0}^{{m_2}} \lambda _q \int \limits _{c_{q}y_N\left( t \right) }^{d_{q}y_N\left( t \right) } { {K_q}\left( {t,s} \right) {y_N\left( s - \tau _{q} \right) }\hbox {d}s}-g\left( t \right) ,\)

  2. Step 2:

    \({{e_N}(t)} \leftarrow {y(t)} - {{y_N}(t)} = - {R_N}(t),\)

  3. Step 3:

    \(0 \leftarrow \sum \nolimits _{k = 0}^{{m_1} - 1} { e_N^{(k)}\left( a \right) },\)

  4. Step 4:

    Solve the error problem consisting of Steps 2 and 3,

  5. Step 5:

    \({e_{N,M}}(t) \leftarrow \sum \nolimits _{n = 0}^M {y_n^*{S_n}\left( {t,\beta } \right) } \,,\,\mathrm{{ }}\left( {M > N} \right)\), where \({S_n}\left( {t,\beta } \right)\) is the Mott polynomial and \({e_{N,M}}(t)\) is a Mott-estimated error function,

  6. Step 6:

    \({y_{N,M}}(t) \leftarrow {y_N}(t) + {e_{N,M}}(t)\), where \({y_{N,M}}(t)\) is a corrected Mott polynomial solution.

Thus, we improve the Mott polynomial solution and it is worth specifying that the corrected error function is of the form \({E_{N,M}}(t) = y(t) - {y_{N,M}}(t)\).

Numerical examples

In this section, we apply the present method to solve some stiff problems concerned with Eq. (1). To do this, we develop a computer program routine on Mathematica 11. The obtained solutions and numerical values are elucidated in figures and tables.

Example 1

Consider the second-order FIDE with state-dependent bounds and multi-delays

$$\begin{aligned}&y''\left( {t} \right) - ty'\left( {t - 1} \right) + t^2y\left( {t-0.6} \right) \\&\quad =g\left( t \right) - \int \limits _{2(t^2+1)}^{3(t^2+1)} (t^2+s^2) y\left( s-0.5 \right) \hbox {d}s\\&\qquad + \int \limits _{0}^{t^2+ 1} ( {t^2}{s^2} )y\left( s-0.1 \right) \hbox {d}s \end{aligned}$$

subject to the initial conditions \(y\left( 0 \right) = 1\), \(y'\left( 0 \right) = 0\), and \(t,s \in [0,1]\). Here, the constant delays are \(\left\{ \left\{ \sigma _0=0.6,\,\sigma _1=1\right\} ,\,\left\{ \tau _0=0.5,\, \tau _1=0.1\right\} \right\}\) and

$$\begin{aligned} \begin{aligned} g\left( t \right) =&-31.8667 + 2 t - 174.987 t^2- 1.2 t^3 - 360.69 t^4 \\&-\, 378.707 t^6 -198.947 t^8 - 41.25 t^{10} + t^{12}/5. \end{aligned} \end{aligned}$$

By the fundamental matrix equation (14), we construct the fundamental matrix equation as

$$\begin{aligned}&\left( {{{\varvec{P}}}_{0}}{{\varvec{S}}}^{(0)}\left( {\beta } \right) + {{{\varvec{P}}}_{1}}{{\varvec{S}}}^{(1)}\left( {\beta } \right) + {{{\varvec{P}}}_{2}}{{\varvec{S}}}^{(2)}\left( {\beta } \right) \right. \\&\qquad \left. +\,\lambda _0 \overline{{{\varvec{X}}}}\,\,\,\overline{{{\varvec{K}}}_0} \,\,\,\overline{{{\varvec{R}}}_0 }-\lambda _1 \overline{{{\varvec{X}}}}\,\,\,\overline{{{\varvec{K}}}_1} \,\,\,\overline{{{\varvec{R}}}_1 }\right) {{\varvec{Y}}} = {{\varvec{G}}}, \end{aligned}$$

After applying the described procedure to the equation above, we easily get the augmented matrix

$$\begin{aligned} \left[ \tilde{{{{\varvec{W}}}}}\,\,;\,\,\tilde{{{{\varvec{G}}}}} \right] = \left[ {\begin{array}{*{20}{c}} -\,6.33&{}\quad 13.0833\beta &{}\quad { -\,25.533\beta ^2}&{};&{}-\,31.87\\ 1&{}0&{}0&{};&{}{ 1}\\ 0&{}-\,\beta &{}0&{};&{}0 \end{array}} \right] . \end{aligned}$$

Solving this matrix system, we get

$$\begin{aligned} {{\varvec{Y}}} = \left[ {\begin{array}{*{20}{c}} {1}\,\,&{0}\,\,&{1/\beta ^2} \end{array}} \right] ^\mathrm{T}. \end{aligned}$$

and it holds from Eq. (3) that

$$\begin{aligned} y\left( t \right) =t^2+1, \end{aligned}$$

which is the exact solution.

Table 1 Comparison of the absolute errors of Example 2 with \(\sigma _2=\tau _0=0.01\) for \(\beta =1.5\)
Full size table
Table 2 Comparison of \(L_\infty\) errors \((N=12\), \(\beta =1.5)\) with respect to the delays \(\sigma _2\) and \(\tau _0\) for Example 2
Full size table
Fig. 1
figure 1

Comparison of the Mott polynomial with the control parameter \(\beta =1.5\) and exact solutions in terms of N on [0, 1] for Example 2 with \(\sigma _2=\tau _0=0.5\)

Full size image
Fig. 2
figure 2

Oscillatory behavior of the Mott polynomial \((\beta =1.5)\) and exact solutions on [0, 10] for Example 2 with \(\sigma _2=\tau _0=0.5\)

Full size image
Fig. 3
figure 3

Logarithmic scaled plot of \(L_\infty\) error with respect to \(\beta\) for Example 2 with \(L=1\) and \(\sigma _2=\tau _0=0.5\)

Full size image

Example 2

Consider the fourth-order IDDE with state-dependent bounds and variable coefficients

$$\begin{aligned}&y^{(iv)}\left( t \right) +\sin (t)y''\left( {t -\sigma _2} \right) -\cos (t) y\left( t \right) =g(t)\\&\qquad +\, \int \limits _{\cos (t)}^{2\cos (t)} {\exp (t+s)y\left( {s -\tau _0} \right) \hbox {d}s}, \end{aligned}$$

subject to the initial conditions \(y\left( 0 \right) = 1\), \(y'\left( 0 \right) = 0\), \(y''\left( 0 \right) = -1\), \(y'''\left( 0 \right) = 0\), and \(t,s \in [0,L]\). Here, the exact solution is \(y\left( t \right) = \cos \left( t \right)\) and for \(\sigma _2=\tau _0=0\),

$$\begin{aligned} g(t) & = \cos (t)\left[ 1 - \cos (t) -\sin (t)\right] \\&+\,2.71828^{(t +\cos (t)}[0.5\cos (\cos (t))\\&+\, 0.5\sin (\cos (t)) + 2.71828^{\cos (t)}\left( -0.5 \cos (2\cos (t))\right. \\&\left. -\, 0.5 \sin (2 \cos (t))\right) ]. \end{aligned}$$

Similarly, g(t) can be calculated via the exact solution for various values of \(\{\sigma _2,\,\tau _0\}\).

Taking different truncation limit N and \(L=\{1,\,10\}\), we solve the problem by using both the present method and Taylor collocation method [16, 18] to compare the obtained results. We later employ the Mott-residual error estimation to improve the solution. It is important to state that we investigate the effects of \(\beta\) and the delays on the Mott polynomial solutions. Therefore, the following discussion is made:

  • Table 1 shows the absolute errors for fixed \(\sigma _2=\tau _0=0.01\) and \(\beta =1.5\). Also in there, the better numerical results are obtained in comparison with Taylor collocation method [16, 18].

  • When \(L=\{1,\,10\},\) the oscillatory behaviors of the solutions coincide properly with the exact solution in Figs. 1 and 2 , respectively.

  • \(L_\infty\) errors obtained with \(N=12\), \(\beta =1.5\) are investigated with respect to different delays \(\sigma _2\) and \(\tau _0\) in Table 2. The best approximation stands for \(8.92e{-}10\) when \(\sigma _2=\tau _0=1.\)

  • Similarly, the behavior of \(L_\infty\) errors obtained with the fixed \(N=12\) and \(\sigma _2=\tau _0=0.5\) is demonstrated with respect to \(\beta\) in the logarithmic scaled plot shown in Fig. 3.

Table 3 Comparison of the absolute errors between the Mott polynomial and Mathematica solutions \((\beta =1)\) for Example 3 with \(\varepsilon =0.1\) and \(\sigma _1=0\)
Full size table
Fig. 4
figure 4

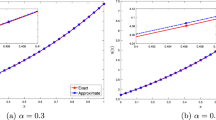
Oscillatory behavior of the Mott polynomial \((\beta =1.5)\) and exact solutions with respect to \(\sigma _1\) in [0, 15] for Example 3 with \(\varepsilon =0.1\), \(F=2\), and \(\omega =2\)

Full size image
Fig. 5
figure 5

Oscillatory behavior the Mott polynomial \((\beta =1.5)\) and exact solutions with respect to \(\sigma _1\) in [0, 15] for Example 3 with \(\varepsilon =0.45\), \(F=2\) and \(\omega =2\)

Full size image
Fig. 6
figure 6

Phase plane behavior of the Mott polynomial \((\beta =1.5)\) and exact solutions in phase plane for Example 3 with \(\varepsilon =0.1\), \(F=2\), \(\omega =2\) and \(L=15\)

Full size image
Fig. 7
figure 7

Phase plane behavior of the Mott polynomial \((\beta =1.5)\) and exact solutions in phase plane for Example 3 with \(\varepsilon =0.45\), \(F=2\), \(\omega =2\) and \(L=15\)

Full size image
Fig. 8
figure 8

Logarithmic scaled plot of \(L_\infty\) error with respect to \(\beta\) for Example 3 with \(L=1\), \(\varepsilon =0.1\), \(\sigma _1=0\), \(F=2\) and \(\omega =2\)

Full size image

Example 3

Consider the second-order external forced oscillatory differential equation exposing to single time-delayed effect

$$\begin{aligned} y''\left( t \right) + 2\varepsilon y'\left( {t - \sigma _1} \right) + y\left( t \right) =F\cos (\omega t),\,\, t \in [0,L], \end{aligned}$$

subject to the initial conditions \(y\left( 0 \right) = 0\) and \(y'\left( 0 \right) = 1\). A under-damped parameter \(|\varepsilon |<1\), an external force F, a non-resonance excitation \(\omega \ne 1\) [5]. Here, \(L=\{1, 15\}\) and also the exact solution of the problem is unknown, but it can be approached numerically with the aid of Mathematica as

$$\begin{aligned}&\text {NDSolve}[y''[t] + 2\varepsilon y'[t-\sigma _1] \\&\qquad +\, y[t] == 2 \hbox {Cos}[2t], y[0] == 0, y'[0] == 1, \\&\quad y[t], \{t,0,L\}][[1, 1, 2]]. \end{aligned}$$

Previously, Kalmar–Nagy and Balachandran [5] have studied the linear oscillator differential equation with external forcing, under-damped system and non-resonance excitation. They have determined the steady-state response and magnification factor. In this example, by exposing the linear oscillator equation [5] to the delayed effect \(\sigma _1\), let us seek the numerical solutions for different N, M, \(\sigma _1\), \(\varepsilon\), \(\beta\), and the fixed \(F=\omega =2\). Thus,

  • By increasing N and M, we demonstrate the absolute errors for \(\sigma _1=0\) and \(\beta =1\) in Table 3. This indicates that N and M enable us to enhance the accuracy of the method.

  • Figs. 4 and 5 illustrate the oscillatory response of both the Mott polynomial \(y_{25}(t)\) and Mathematica solutions for \(L=15\), \(\sigma _1={0, 0.5}\) and \(\varepsilon =\{0.1, \,0.45\}\). Figures 6 and 7 also illustrate these solutions in the phase plane.

  • The decreasing \(L_\infty\) error diagram obtained with \(N=12\) is demonstrated with respect to the control parameter \(\beta\) in Fig. 8.

In addition, we draw the attention to the fact that both \(\varepsilon\) and \(\sigma _1\) have a different effect on the Mott polynomial solution.

Conclusions

An efficient numerical method based on the generalized Mott polynomial, Chebyshev–Lobatto collocation points and the matrix structures has been proposed to solve stiff IDDEs with state-dependent bounds, which are introduced for the first time with this paper. Thanks to the simplicity of the present method, the obtained solutions have been accurately approximated to the exact and Mathematica solutions. Controlling the optimum value of the parameter-\(\beta\) in the solutions is of importance as can be seen in Figs. 3 and 8. Therefore, this parameter plays a specific role in numerical approximations. The Mott-residual error estimation has effectively improved the obtained solutions as seen from Tables 1 and 3 . The effects of the delays have been monitored differently. So, we here want to state from Table 2, Figs. 4 and 5 that the delays change the behavior of the problems in a physical sense. By investigating all results, as N is increased, the accuracy of the method increases. Thus, we conclude that the present method could be very applicable and reliable for solving other well-known phenomena, such as partial differential and fractional differential equations after making some required modifications on the proposed method.