Abstract
Numerical analysis of stochastic delay differential equations has been widely developed but frequently for the cases where the delay term has a simple feature. In this paper, we aim to study a more general case of delay term which has not been much discussed so far. We mean the case where the delay term takes random values. For this purpose, a new continuous split-step scheme is introduced to approximate the solution and then convergence in the mean-square sense is investigated. Moreover, given a test equation, the mean-square asymptotic stability of the scheme is presented. Numerical examples are provided to further illustrate the obtained theoretical results.
Similar content being viewed by others
1 Introduction
In many physical phenomena with random nature, the state future of a system not only depends on the current state but also depends on the whole past history of the system over a finite time interval, and certainly the mathematical modelling actually describing the system leads to a stochastic delay differential equation (SDDE) and not a stochastic ordinary differential equation (SODE). In this paper, an autonomous d-dimensional Itô stochastic delay differential equation is considered
where r is a positive constant and τ is called lag process. The drift and diffusion coefficients \(a, b^{j}: \mathbb{R}^{d} \rightarrow \mathbb{R}^{d}\) for \(j = 1,\ldots, m\) are Borel-measurable functions and \(\eta , \eta \in \mathbb{R}^{d}\), is named initial process. Obviously, the inaccessibility of the closed-form of the solutions or their distributions of these mathematical modelings, which arise in diverse areas of applications, reveal the significance of addressing numerical methods, because they play an important role to educe a realistic view of the solution behaviour of such equations. In recent years, some authors have dealt with the numerical analysis of SDDEs whose time lag is a discrete, see, e.g. [3, 12, 16]. But the delay function might be dynamically changed and even disturbed under an ambient noise. If the delay function depends only on time, then it is called time-dependent, see, e.g. [1, 6, 8, 22]. But if, in addition to the time, it depends on the solution process, then it is named state-dependent. As far as the author knows, only a few numerical schemes for SDDEs which contain the third type of lag function have been proposed, see, e.g. [13, 14]. The authors [13, 14] considered the continuous-time \(\operatorname{GARCH}(1,1)\) model for stochastic volatility involving state-dependent delayed response and applied the Euler–Maruyama discrete-time approximation in the strong convergence sense to simulate. On the other hand, there exist some papers which extend some types of stochastic functional (evolution, fractional, neutral) differential equations with state-dependent delay and study some theoretical aspects particularly the existence and uniqueness of (mild) solution and controllability results, see, e.g. [2, 19, 31, 32]. In the following, a new interpolation, whose computational costs are not too high, is presented. The main contribution of this paper is to investigate the numerical solution of Eq. (1.1), under sufficient conditions which will be mentioned later, with three cases of lag process as follows:
-
(L1)
τ is a constant,
-
(L2)
τ is time-dependent as \(\tau (t)\),
-
(L3)
τ is state-dependent as \(\tau (t, X(t))\).
Note that in case (L2), τ can be a continuous-time random process or a deterministic function. Here, we just consider the deterministic case. Since the main task in all integration formulas for SDDEs is to provide an interpolation at non-mesh points, a new split-step scheme will be properly extended over the whole interval \([t_{0}, T]\). The authors in [28] studied the strong convergence and the mean-square stability of the split-step backward Euler method to linear SDDEs with constant lag and took the stepsize as a multiplier of that. This type of stepsize selection by a semi-implicit split-step θ-Milstein method was developed in [7], too. But Wang et al. in [22] proposed a new improved split-step backward Euler method for SDDEs with time-dependent delay where a piecewise linear interpolation is used to approximate the solution at the delayed points. Also, in contrast to [7, 28], in [22], the restriction of stepsize is removed and the unconditional stability property is extended as well. In our proposed method, this restriction on stepsize is dropped, too. As more papers, we could mention [11, 17] which investigate the behaviour of the split-type methods for stochastic differential equations and [26] which studies the strong convergence of the split-step θ-method for a class of neutral stochastic delay differential equations.
As we know, the (numerical) stability concept is a powerful tool in measuring the sensitivity of the (difference) equation for any confusion. For instance, the disturbances, which occur during mathematical modelling, or round off errors made in the implementation of the numerical method may lead to fundamental changes. Undoubtedly, reviewing the numerical stability of stochastic differential equations is an inspiration to that of SDDEs. Among the most prominent papers which scrutinise the numerical stability for stochastic differential equations, the readers can refer to [9, 20] for a review. Mao in [18] developed pth moment and almost sure exponential stability of stochastic functional differential equations by means of the Razumikhin-type theorems. Also, [25] examined almost sure exponential stability of the Euler–Maruyama scheme for such equations. Furthermore, the authors in [4] employed the Halanay-type theory as the main tool to analyse pth exponential stability of the solution and the Euler-type method. In this work, we study the mean-square stability of SDDE (1.1) and also that of the proposed scheme. Note that the case of state-dependent delay is almost new. Some papers help us to accomplish our aim; see [18, 27, 30]. Also, the stability for such a class of SDDEs under weaker conditions like one-sided Lipschitz and locally Lipschitz, which has been studied in the case of SDE or SDDE with discrete or time-dependent delay [5, 10, 24, 29, 30], could be extended in the future. This paper consists of two parts. The first deals with convergence and the second with stability, both of which are examined in the mean-square sense.
This paper is organised as follows. Section 2 is concerned with the notations, assumptions and a numerical scheme for the underlying problem. In Sect. 3, the convergence of the scheme in the mean-square sense is derived. In Sect. 4, we define the stability concept for the problem and numerical solution, too. Moreover, the mean-square stability of the scheme is established. Ultimately, some test problems are indicated in Sect. 5.
2 Results formulation
Let \((\varOmega , {\mathcal{F}}, {\{\mathcal{F}_{t}\}}_{t \geq t_{0}}, {P})\) be a complete probability space with the filtration \({\{ \mathcal{F}_{t}\}}_{t \geq t_{0}}\) satisfying the usual conditions. Moreover, \(W =(W_{t})_{t \geq t_{0}}\) is an m-dimensional Brownian motion on the probability space. Let \(D = C([t_{0} - r, t_{0}], \mathbb {R}^{d})\) be the Banach space of all continuous functions from \([t_{0} - r, t_{0}]\) to \(\mathbb {R}^{d}\). Also, we use the \(\mathcal{L}^{p}( \varOmega , D)\) to be the space of all \(\mathcal{F}_{t_{0}}\)-measurable and integrable initial processes \(\eta : \varOmega \rightarrow D\) which can be equipped with the following seminorm:
where the supremum norm \(\|\cdot\|^{p}_{D}\) for \(p \geq 1\) is defined as
where \(|\cdot|\) is the Euclidian norm in \(\mathbb{R}^{k}\) for \(k \geq 1\). In this sequel, we make the necessary assumptions on the problem as follows.
Assumption 1
The functions \(a: (\mathbb{R}^{d} )^{2} \rightarrow \mathbb{R}^{d}\) and \(b: (\mathbb{R}^{d} )^{2} \rightarrow \mathbb{R}^{d\times m}\) are globally Lipschitz continuous, i.e. there is a positive constant \(K_{1}\) such that
for all \(X_{1}, X_{2}, Y_{1}, Y_{2} \in \mathbb{R}^{d}\).
Assumption 2
In case (L2), let \(\tau : [t_{0}, T] \rightarrow (0, r]\) be of Lipschitz continuous as
where \(K_{2}\) is a positive constant. In case (L3), let \(\tau : [t_{0}, T] \times \mathbb{R}^{d} \rightarrow (0, r]\) be of Lipschitz continuous, i.e. there exist two positive constants \(K_{2}\) and \(K_{3}\) such that
for all \(t, s \in [t_{0}, T]\) and \(X, X_{1}, X_{2} \in \mathbb{R}^{d}\). Note that in each of the two cases above, the fact that τ is positive guarantees the measurability and then the existence of the Itô integral.
Assumption 3
Given two adapted integrable stochastic processes \(\rho _{1}, \rho _{2} : \varOmega \times [t_{0} - r, T] \rightarrow [t_{0} - r, t_{0}]\), we have
where \(K_{4}\) is a positive constant.
Theorem 2.1
Suppose that \(\|\eta \|_{{\mathcal{L}^{2}}(D)} < \infty \), under Assumptions 1–3, SDDE (1.1) has a unique strong solution X such that
where \(\bar{D} = C([t_{0} - r, T], \mathbb{R}^{d})\) is the Banach space of all continuous sample paths with values in \(\mathbb{R}^{d}\) and H is a positive constant. Moreover, there exists a positive constant \(K_{5}\) such that for every \(t, s \in [t_{0}, T]\) we have
where \(\rho _{1}\), \(\rho _{2}\): \(\varOmega \times [t_{0}, T]\) → \([t_{0} ,T]\) are two adapted integrable stochastic processes.
The proof of the theorem above is deferred to the Appendix.
2.1 Underlying scheme
We now focus on the main intent, namely developing a new continuous split-step scheme based on the Euler–Maruyama to SDDE (1.1). To do this, consider a non-equidistant discretization of the interval \(I = [t_{0}, T]\) as follows:
the approximation \(\widetilde{X}(t)\) for SDDE (1.1) is defined recursively through the underlying scheme
where if \(t_{k} - \tau _{k} \leq t_{0}\), then
otherwise if \(t_{k} - \tau _{k} \in [t_{i}, t_{i+1})\), then
where \(\Delta t_{k} = t_{k+1} - t_{k}\) and \(\Delta W_{k} = W(t_{k+1}) - W(t_{k})\) are independent Gaussian distributed random variables with mean zero and variance \(t_{k+1} - t_{k}\) which can be made by a pseudo random generation. Note that \(\tau _{k}\) in (2.3)–(2.4) is equal to τ and \(\tau (t_{k})\) in cases (L1) and (L2), respectively, and in case (L3), \(\tau _{k} = \tau (t_{k}, \widetilde{X}(t_{k}))\). One can simulate the value \(W(t_{k} - \tau _{k}) - W(t_{i})\) by means of the Brownian bridges to remain on the correct Brownian paths [15]. We can extend the following continuous approximation for whole \([t_{0}, T]\):
where \(t \in [t_{i}, t_{i+1})\) for \(i=0,\ldots,N-1\). Furthermore, \(\widetilde{Z}(t_{i})\) is obtained similar to (2.3)–(2.4). We can present a continuous version of the approximation solution as follows:
where 1 denotes the indicator function.
Proposition 2.2
Consider the approximation processes \({X}^{*}\), Z̃ and X̃ which are computed by (2.2), (2.3) and (2.4). Assume that \(a(0,0) =0\) and \(b(0,0) = 0\), then there exists a positive constant H̄ such that
where D̄ was specified in Theorem 2.1.
In the sequel, for the simplicity, we take H̄ such that it is equal to H in Theorem 2.1. Under these conditions, we establish the strong convergence of scheme (2.5)–(2.6) over \([t_{0}, T]\) in the next section.
3 Convergence
Having been motivated to analyse the behaviour of scheme (2.5)–(2.6), we naturally concentrate on the convergence concept. To this end, the mean-square convergence is invoked by a theorem as follows.
Theorem 3.1
Suppose that Assumptions 1–3 hold and \(\|\eta \|_{ {\mathcal{L}^{2}}(D)} < \infty \). Moreover, we assume that \(a(0,0) = 0\) and \(b(0,0) = 0\). If we apply scheme (2.5)–(2.6) to SDDE (1.1), then
where \(e(t) = X(t) - \widetilde{X}(t)\) and \(h = \smash{\max_{i =0,\ldots, N - 1}}\Delta _{t_{i}}\). Moreover, γ is equal to \(1/2\) in cases (L1) and (L2) and to \({1/4}\) in case (L3).
Proof
Note that proving of case (L1) is similar to that of (L2), so we leave it to the reader and we start proving with (L2). Let \(t \in [t_{n}, t_{n+1})\). We can write
where based on (2.5) and (2.6), \(X^{*}(s) = X^{*}(t _{i})\) and \(\widetilde{Z}(s) = \widetilde{Z}(t_{i})\) when \(s \in [t _{i}, t_{i+1})\), \(i = 0,\ldots, n\). So
By Hölder’s and Doob’s martingale inequalities, we derive
By Assumption 1, we have
We can write
where \(M = 4K_{1}(T-t_{0} + 4)\) and for \(s \in [t_{i}, t_{i+1})\)
and in case (L2)
and in case (L3)
where \(\widetilde{Z}(t_{i}) = \widetilde{X}(t_{i} - \tau (t_{i}, \widetilde{X}(t_{i})))\). We can write \(A_{1i}\), \(A_{2i}\), \(A_{3i}\) and \(A_{4i}\) instead of \(A_{1}\), \(A_{2}\), \(A_{3}\) and \(A_{4}\) to be more precise. But the second subscripts have been removed for the sake of simplicity. We now present the necessary upper bounds for these functions. Definitely
Due to the Hölder continuity property of the Brownian motion as well as Assumption 1 and relation (2.7), we have
where
Note that \(H =\bar{H}\). We now try to obtain the necessary error bounds for \(A_{3}(s)\) and \(A_{4}(s)\). We first consider case (L2). If both values \(s - \tau (s)\) and \(t_{i} - \tau (t_{i})\) are less or larger than \(t_{0}\), under Assumption 3, Theorem 2.1 and due to being Lipschitz of τ in Assumption 2, we see that
If \(s - \tau (s)\) or \(t_{i} - \tau (t_{i})\) is less than \(t_{0}\) and the other is larger than \(t_{0}\), then under the intermediate value theorem there exists a point \(t^{*} \in [t_{i}, s] \subset [t_{i}, t_{i+1}]\) such that \(t^{*} - \tau (t^{*}) = t_{0}\). So we get
Similar to the previous argument discussed in obtaining (3.4), we get
Besides, we find that \(\widetilde{Z}(t_{i})\) approximates the solution at \(t_{i} - \tau (t_{i})\) by (2.3)–(2.4). So we can write \(A_{4}(s) = \mathbf{E}|e(t_{i} - \tau (t_{i}))|^{2}\) and then we have
Applying Gronwall’s lemma yields
where \(C = \frac{M}{2} (2(K_{4}+ K_{5})(1 + K_{2})+ K_{6} ) e ^{2M(T - t_{0})}\). Due to the arbitrariness of n, we can write
since \(\sum_{i=0}^{N-1}{\Delta t_{i}}= T - t_{0}\), the desired result is obtained. We now turn to case (L3) where τ is the function of \(X(t)\). To this end, we break down \(A_{3}(s)\) into four terms as follows:
where
with
Assumption 3, Assumption 2 and Theorem 2.1 yield that
by considering the dominant terms, we achieve
Similarly, an upper bound for \(A_{34}(s)\) using Theorem 2.1, Assumption 2 and Assumption 3 is obtained as
To obtain an upper bound for \(A_{32}\) and \(A_{33}\), we suppose that there exists \(t^{*}\), \(t_{i} < t^{*} < s\), such that
We can write
In a similar manner which was employed in finding the upper bound of \(A_{31}(s)\), we see that
and
Then we have
Since \(\widetilde{Z}(t_{i}) = \widetilde{X}(t_{i} - \tau (t_{i}, \widetilde{X}(t_{i})))\), the function \(A_{4}\) becomes
Therefore by (3.1), (3.2), (3.3), (3.5) and (3.6)
The application of Gronwall’s lemma results in
we can write
where \(C_{1} = \frac{10(T-t_{0})}{3} M(K_{4} + K_{5})K_{3}\sqrt{K _{5}}e^{2M(T-t_{0})}\). In view of \((\mathbf{E}(A))^{2} \leq \mathbf{E}(A^{2})\), by Jensen’s inequality, we can write
We now set
where \(C_{2} = \frac{9C_{1}}{10 \sqrt{K_{5}}}\). By recurrence, one sees that
We define
By (3.10), firstly,
and secondly,
Since \(C_{2} > 0\) and \(A \geq 0\), so from (3.11) we get
By (3.13) and (3.14), we observe that \((B - C_{1}h^{1/2})^{2} \leq {C_{2}}^{2}{B}\) and
For this quadratic inequality, we obtain two quantities for B as follows:
Obviously, relation (3.15) is satisfied for \(B \in [B_{1}, B_{2}]\). By the Taylor expansion of function \(\sqrt{{C_{2}}^{4} + 4C_{1} {C_{2}}^{2}h^{1/2}}\) about point \({C_{2}}^{4}\), we achieve
where \(\xi _{1}, \xi _{2} \in ({C_{2}}^{4}, {C_{2}}^{4} + 4C_{1}{C_{2}} ^{2}h^{1/2} )\). By (3.12), \(A^{2} \leq B\) for all \(B \in [B_{1}, B_{2}]\) and also \(B_{1}\) is the sharpest bound. Note that if \(h \rightarrow 0\), then \(B_{1} \rightarrow 0\), and so \(A^{2} \rightarrow 0\). Hence, by definition A in (3.9), \(\mathbf{E} ( \sup_{t_{0} \leq v \leq t} |e(v)| ) \rightarrow 0\), and we get \(\mathbf{E} (\sup_{t_{0} \leq v \leq t} |e(v)|^{2} ) \rightarrow 0\) by (3.7). Henceforth, the convergence of the scheme is visible. In order to determine a sharp bound for \(A^{2}\), we are interested in a quantity which is as small as possible. So \(B_{1}\) reveals the convergence rate. Because \(A = \mathcal{O}(h^{1/2})\) and consequently by (3.9) and (3.7), we obtain
Since there is no restriction on t, the desired result follows immediately. □
Let us now mention two important remarks in line with Theorem 3.1.
Remark 3.2
([21])
As we know, there exist no two seminorms which can be generally majorized by a multiplier of each other. So there is no ambiguity if \(\|\cdot\|_{{\mathcal{L}^{1}}}\) and \(\|\cdot\|_{{\mathcal{L}^{2}}}\) are proportional to different powers of h in Theorem 3.1.
Remark 3.3
Note that as the scheme proceeds on the partition \({\varLambda }_{1}\) to integrate the solution at the mesh points, where \({\varLambda }_{1} = \{t_{0}, t_{1},\ldots, t_{N} =T\}\) is a partition which covers all discrete points, some points, which we can say are hidden, are brought up. For instance, \(t_{k} \in \varLambda _{1}\) corresponds to \(t_{k} - \tau _{k}\) and the approximation \(\widetilde{Z}_{k}\). We can rename \(t_{k} - \tau _{k}\) by \(t_{m}\) and make partition \(\varLambda _{2}\) by means of these points. Besides, here, the underlying scheme and the interpolation, which approximate the stochastic process on \(\varLambda _{1}\) and \(\varLambda _{2}\), respectively, are the same. So, practically, the proposed approximation computes the solution at the points in \({\varLambda }_{1}\) and \({\varLambda }_{2}\).
4 Stability
The main objective in the numerical stability literature is to examine whether the numerical solution mimics the behaviour of the exact process or not. In particular, it is important to know the reaction of the scheme when n tends to infinity whilst the exact process becomes trivial as large as t becomes very large. In fact, the impact of rounding errors, which are not inevitable, on the numerical results in the long term case is analysed. In this section, the asymptotic mean-square stability, corresponding to SDDE (1.1) and also a linear test equation, will be challenged.
Definition 4.1
The exact solution (strong solution) of SDDE (1.1) denoted by X is named asymptotically mean-square stable if
In the sequel, we present a theorem which deals with the mean-square stability of SDDE (1.1) and the proof sketch is given in the Appendix.
Theorem 4.2
Given SDDE (1.1) which satisfies Assumptions 1–3, assume that there exist a positive constant λ and non-negative constants \(\alpha _{0}\), \(\alpha _{1}\), \(\beta _{0}\) and \(\beta _{1}\) such that
for all \(x, \bar{x}, y \in \mathbb{R}^{d}\). If
then the zero solution is mean-square stable.
Definition 4.3
Let X̃ be the numerical solution of SDDE (1.1). If there exists \({\bar{h}}(a, b, c, d) > 0\) such that the maximum stepsize lies in \((0, {\bar{h}}(a, b, c, d))\), then the scheme is called asymptotically mean-square stable if
Theorem 4.4
Given SDDE (1.1), let Assumptions 1–3 hold and \(\|\eta \|_{{\mathcal{L}^{2}}(D)} < \infty \). Assume that there exist two positive constants \(\lambda _{1}\) and \(\lambda _{2}\) and non-negative constants \(\beta _{0}\) and \(\beta _{1}\) such that
for all \(x, y \in \mathbb{R}^{d}\). Assume that \(a(0,0) =0\) and \(b(0,0) = 0\). If \(2\lambda _{1}>2\lambda _{2}+\beta _{0} +\beta _{1}\), \(\beta _{0}\lambda _{2} +\beta _{1}\lambda _{1} \neq 0\) and \({\Delta t _{k}} \in (0, \frac{2\lambda _{1}-2\lambda _{2}-\beta _{0} -\beta _{1}}{2( \beta _{0}\lambda _{2}+ \beta _{1}\lambda _{1})})\), then scheme (2.2)–(2.4) is asymptotically mean-square stable.
Proof
From (2.2), we can write
by (4.1), we get
Henceforth, we get
Again, from (2.2), we have
By applying the expectation and using (4.1) and (4.2), we get
where \(\widetilde{X}(t_{m_{k}}) = \widetilde{Z}(t_{k})\) by \(t_{m_{k}} = t_{k} - \tau _{k}\). Hence, we can write
To have mean-square stability, we set \(\frac{(1+2\lambda _{2}{\Delta t _{k}})(1 + \beta _{0} \Delta t_{k}) }{1+2\lambda _{1}{\Delta t_{k}}} + \beta _{1} {\Delta t_{k}} <1\), and so we obtain \({\Delta t_{k}} \in (0, \frac{2\lambda _{1}-2\lambda _{2}-\beta _{0} -\beta _{1}}{2(\beta _{0} \lambda _{2}+ \beta _{1}\lambda _{1})})\) by assumption that \(2\lambda _{1}>2\lambda _{2}+\beta _{0} +\beta _{1}\) and \(\beta _{0}\lambda _{2} + \beta _{1}\lambda _{1} \neq 0\). □
As it is customary, we consider a linear scalar test equation with state-dependent delay:
where \(a, b, c, d \in \mathbb{R}\) and \(\tau = \tau (t, X(t))\). Let \(\|\eta \|_{{\mathcal{L}^{2}}(D)} < \infty \). Such test problems in the case of discrete delay and time-dependent delay can be found in [23, 28]. The following corollary states what condition results in asymptotic mean-square stability for (4.3).
Corollary 4.5
If the following condition is satisfied
then SDDE (4.3) is mean-square stable.
Proof
By Theorem 4.2 and setting \(\lambda = -a\), \(\alpha _{0} = |a|\), \(\alpha _{1} = |b|\), \(\beta _{0} = 2|c|^{2}\), \(\beta _{1} = 2 |d|^{2}\), the desired result is achieved. □
Now we turn our attention to the proposed method (2.2)–(2.4). Clearly, applying this scheme to the given equation (4.3) is indicated as
Remember that the scheme has been applied on \({\varLambda }_{1}\), which is a non-uniform partition as \({\varLambda }_{1} =\{t_{0}, t_{1},\ldots,t_{N}=T \}\), with \(\Delta _{t_{k}} = t_{k+1} - t_{k}\) and \(\Delta W_{k} = W _{k+1} - W_{k}\). Based on what was discussed in Remark 3.3, we have an approximation on \({\varLambda }_{1} \cup {\varLambda }_{2}\). This survey paves the way to analyse the stability of the scheme. In the following, the sufficient conditions to mean-square stability of scheme (4.5) will be determined.
Theorem 4.6
Under condition (4.4), the numerical scheme (4.5) applied to linear SDDE (4.3) is asymptotic mean-square stable by some limitations on the stepsize.
Proof
As we know, practically, the scheme proceeds along the partition \({\varLambda }_{1} \cup {\varLambda }_{2}\). Thus, we can write
Now, by applying the expectation, we have
By replacing \(2|\widetilde{X}_{k}||\widetilde{Z}_{k}|\) to \(| \widetilde{X}_{k}|^{2} + |\widetilde{Z}_{k}|^{2}\), we obtain
we can rearrange the relation above as follows:
Note that based on what was discussed on the mesh points, \(t_{k} - \tau _{k} \in \varLambda _{2}\), and so we can replace \(\widetilde{Z}_{k}\) with \(\widetilde{X}_{m}\) in which \(t_{m} = t_{k} - \tau _{k}\). Hence
where
Obviously, in order to have the desired result, we have to impose
that is, \({\Delta _{t_{k}}}\) must be selected such that M will be bounded by 1. Relation (4.6) yields that
and then
we now come up with a quadratic equation which can be invoked as
with
We define
Here, we first consider
and compute the discriminant Δ for that. Obviously, \(A(a, b, c, d) \geq 0\) and by Theorem 4.5 we have
It follows that \(\Delta \geq 0\) with
If \(A(a, b, c, d) > 0\), then the discriminant Δ is positive, and we have two distinct roots \(h_{1}(a, b, c, d)\) and \(h_{2}(a,b,c,d)\). Furthermore, given the relation between the roots of a polynomial and its coefficients, we get
It is profitably viewed that \(h_{1}(a, b, c, d)\) and \(h_{2}(a,b,c,d)\) have different signs. Without any loss of generality, we assume that \(h_{1}(a, b, c, d) < h_{2}(a,b,c,d)\), then (4.7) is satisfied for all \(\Delta _{t_{k}} \in (h_{1}(a, b, c, d), h_{2}(a,b,c,d))\). Hence, if the stepsize is taken in the interval \((0, h_{2}(a,b,c,d))\), then the stability of the scheme will be guaranteed. If \(A(a, b, c, d) = 0\), then \(B(a,b,c,d) = b^{2} - a^{2}\) and by Theorem 4.5, \(b^{2} < a^{2}\), and so \(B(a,b,c,d)<0\). In this case, for all stepsizes, relation (4.7) is satisfied, and so unconditional stability arises. So we can say if \(\Delta _{t_{k}} \in (0, \bar{h})\) for all k, where \(\bar{h} = \infty \) or \(\bar{h} = h_{2}(a,b,c,d)\), scheme (4.5) is asymptotic mean-square stable. □
Remark 4.7
We can prove Theorem 4.6 using Theorem 4.4 by setting \(\lambda _{1} = -a -\frac{|b|}{2}\), \(\lambda _{2} = \frac{|b|}{2}\), \(\beta _{0} = |c|^{2}+|c||d|\) and \(\beta _{1} = |d|^{2}+|c||d|\). By (4.4), we have \(2\lambda _{1}>2\lambda _{2}+ \beta _{0} +\beta _{1}\) and \(\beta _{0} \lambda _{2} + \beta _{1}\lambda _{1} \neq 0\). By Theorem 4.4, if we take the stepsize in \((0, h ^{*} )\), \(h^{*}= \frac{-2a-2|b|-(|c|+|d|)^{2}}{|b|(|c|^{2}+|cd|)+(|d|^{2}+|cd|)(-2a-|b|)}\), then scheme (4.5) is mean-square stable. Thus, if \(\Delta _{t_{k}} \in (0, {\tilde{h}})\) for all k, then scheme (4.5) is mean-square stable where \({\tilde{h}} = \max (h ^{*}, \bar{h})\). Note that h̄ was obtained in the proof of Theorem 4.6.
5 Simulation experiments
In this section, we seek the accuracy and efficiency of the numerical scheme for some test problems. As we know, stochastic models in addition to the deterministic aspect possess a probabilistic one. Accordingly, the noise process must be properly simulated in order to obtain an efficient numerical scheme. In this work, the Wiener process models the noise, and one must be careful when generating the Brownian motion and take an approach such that the correct paths of that are followed. Particularly, due to the delay nature, some points become evident during the implementation of the scheme which do not belong to the partition but have to be simulated. For this aim, given the Markov property of the Wiener process, one can utilise a linear interpolation to simulate \(W_{t}\) if the values \(W_{t_{1}}\) and \(W_{t_{2}}\), \(t_{1} < t < t_{2}\), are known. We call \(\Delta W_{t_{i}}\), \(\Delta W_{t_{i}} = W_{t_{i+1}} - W_{t_{i}}\), to be the Brownian increment and \(\Delta t_{i}\), \(\Delta t_{i} = t_{i+1} - t_{i}\), to be time one. Besides, one very challenging point in the study of stochastic delay differential equations is the non-availability of the exact solution of the most test problems. So one has to obtain the exact one by discretising the equation on a fine mesh. Note that, because of the computational and round off errors, too delicate partition is not necessarily the right choice. Thus, we must be cautious in choosing the right mesh. We begin with a discrete delay.
Example 5.1
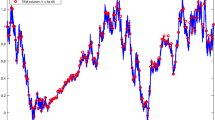
Here \(\tau = 1\) and in the determining the parameters, the numerical stability condition has been taken into account, see relation (4.4), and such condition will also be considered in the two next examples. Since delay is constant, for every \(t_{i}\), \(t_{i}- 1\) point situates in a subinterval far from current interval, and accordingly the overlapping does not exist. We postpone this discussion to the next example. Consequently, the relevant programmes are easily accomplished, which leads us to Table 1, Fig. 1 and Fig. 5.
As a second problem, we consider the time-dependent case with a delay function \((1 + t^{2})^{-1}\) decreasing versus time.
Example 5.2
By virtue of the fact that \((1 + t^{2})^{-1}\) decreases in t, it is expected that the implementation of the scheme with a slight difference is similar to (L1). Here, unlike the constant delay, we face overlapping. We use the word overlapping if during the implementation of the scheme, there exists a point \(t_{i+1}\) such that \(t_{i+1} - \tau _{i+1} \in [t_{i}, t_{i+1})\) separates the latter interval into \([t_{i}, t_{i+1} - \tau _{i+1} )\) and \([t_{i+1} - \tau _{i+1}, t_{i+1})\). In this case, by approximating the process at \(t_{i+1} - \tau _{i+1}\), because of the fact that the scheme is one-step, recomputation of \(\widetilde{X}(t_{i+1})\) is required. So the generation of each path is more time-consuming than that of the previous one. Furthermore, stepsize 2−12 will be selected to create a partition in order to simulate the exact solution in these two examples.
Example 5.3
where \(\tau (t, X(t))= \frac{|X(t)|}{c+|X(t)|}\), and let c be a positive constant.
Here, according to the dependence of the delay term on the noise process, the simulation is not analogous to the two previous ones. Notice that for every point \(t_{i}\), in addition to \(\widetilde{X} _{i}\), the amount \(\widetilde{Z}_{i}\) has to be computed, namely approximation of the process at \(t_{i} - \tau _{i}\), and if we denote this point by \({t}_{mi}\), then the value \(\widetilde{Z}_{mi}\) has to be computed. If we set \(t_{ki} = {t}_{mi} - \tau _{mi}\), then an important question is whether the quantity \(\widetilde{Z}_{ki}\) has to be computed or not. Since in the two first cases of delay term we have \({t}_{mj} > {t}_{mi} > t_{ki}\) for every j such that \(j > i\), so we do not need the approximation \(\widetilde{Z}_{ki}\). Note that τ is a decreasing function in Example 5.2. Hence, in order to avoid nesting calculations, we can use α for the value of the \(\widetilde{Z}_{ki}\), requiring α to be constant. But in the state-dependent case, as we evidently observed in our running, unlike the two first cases, going back to the past is not necessarily consecutive. Hence, we might use \(\widetilde{Z}_{ki}\) during the next computations, and so it has to be modified. Assume that nesting calculations have to be required at the points \(t_{ki_{1}} < t_{ki_{2}}<\cdots<t _{ki_{l}} <t_{ki}\), and naturally they have to be stopped after a finite period. For this, we rectify \(\widetilde{Z}_{ki_{1}}\) by averaging every \(\widetilde{Z}_{j}\) where \(\widetilde{Z}_{j} \neq \alpha \) for \(j < ki_{1}\). By the way, the overlapping problem exists here, too. Thus, as mentioned in the previous example, we must carefully execute the scheme. Considering the case of state-dependent delay which includes more computation errors, too many small stepsizes may lead us to a wrong direction. So our proposed partition is made by the stepsize 2−11. Needless to say, time and computing costs are considerably higher than those of the two previous cases.
5.1 Comment on results
The rate of strong convergence for Example 5.1 with \(T = 1\). The logarithm of \(\epsilon _{T}\) is denoted by the green line with asterisk which is parallel with the dashed red line by slope \(\frac{1}{2}\)
After having finished implementing the numerical scheme for the three examples above, we now hint at some tips in line with the obtained numerical results. To simplify the notation, let \(X^{e}\) and \(X^{a}\) stand for the exact and numerical solutions, respectively. The numerical implementations have been made with various input stepsizes up to the end of the interval and the exact one by a small stepsize as previously mentioned for N discretized Brownian paths. Then, in order to visualise error \(\epsilon _{T} = \mathbf{E}{|X^{e}(T) - X^{a}(T)|}\) inspiring confidence to the scheme, practically, we utilise the sample mean of the individual paths as \(\frac{1}{N} \sum_{i=1}^{N} |{X_{i}} ^{e}(T) - {X_{i}}^{a}(T)|\) provided N is sufficiently large. Here, \(N = 10\text{,}000\). All four Tables 1, 2, 3 and 4 reveal the reasonable behaviour of the computational error to the shrinkaging of the stepsize. Apparently, the smaller stepsize results in improving the approximation, which indicates the significant response of the scheme. In order to indicate the speed of convergence of the scheme, we draw the logarithm of global computational error versus that of the stepsize. In doing so, the command loglog in Matlab, which is interpreted as the logarithm function, has been applied and it provides us with Figs. 1, 2, 3 and 4. We observe that the obtained curves are parallel to the functions \(x^{\frac{1}{2}}\) and \(x^{\frac{1}{4}}\), which is in agreement with the theoretical results. Remember that we must pay particular attention to (4.4) in order to preserve the numerical stability. The parameters of the given problem are \(T= 20\) and \(\Delta t_{i} = 0.2\). Note that Figs. 5, 6, 7 and 8 present the mean of normed approximation over N realisations as \(\frac{1}{N} \sum_{i=1}^{N} |X^{a} _{i}(t_{n})|^{2}\), which establishes the stability. Regarding the trends, one can see that the summation converges to zero as \(t_{n}\) becomes larger. By means of these results, we conclude that scheme (2.2)–(2.4) is a well-developed scheme for problem (1.1).
The rate of strong convergence for Example 5.2 with \(T = 1\). The logarithm of \(\epsilon _{T}\) is denoted by the green line with asterisk which is parallel with the dashed red line by slope \(\frac{1}{2}\)
The rate of strong convergence for Example 5.3 with \(T=1\), \(c = 0.01\). The logarithm of \(\epsilon _{T}\) is denoted by the green line with asterisk which is parallel with the dashed red line by slope \(\frac{1}{4}\)
The rate of strong convergence for Example 5.3 with \(T = 1\), \(c = 1\). The logarithm of \(\epsilon _{T}\) is denoted by the green line with asterisk which is parallel with the dashed red line by slope \(\frac{1}{4}\)
The average of numerical solution over 10,000 discretized Brownian paths with \(h = 0.2\) and \(T = 20\) for Example 5.1
The average of numerical solution over 10,000 discretized Brownian paths with \(h = 0.2\) and \(T = 20\) for Example 5.2
The average of numerical solution over 10,000 discretized Brownian paths with \(h = 0.2\), \(T = 20\) and \(c = 0.01\) for Example 5.3
The average of numerical solution over 10,000 discretized Brownian paths with \(h = 0.2\), \(T = 20\) and \(c = 1\) for Example 5.3
6 Conclusion
In this paper, emphasising the numeric, the stochastic differential equations with a variety of delay terms were interrogated. A new continuous split-step scheme based on the Euler–Maruyama, with a non-uniform partition and free-limitation stepsize, was introduced and the convergence in the \(\mathcal{L}^{2}\) sense was stabilised. As expected, because of using an interpolation which is the same as the underlying scheme, the rate of mean-square convergence takes the amount \(1/2\) in the two first delay terms and it does \(1/4\) in the last one. The asymptotic mean-square stability of the scheme was probed. The stability and convergence concepts, as the two basic desirable properties, satisfied the efficiency of the scheme. More general test equations under weaker conditions and also the other senses of stability such as almost sure asymptotic (exponential) stability in the state-dependent case, can be inquired in the future.
References
Akhtari, B., Babolian, E., Neuenkirch, A.: An Euler scheme for stochastic delay differential equations on unbounded domains: pathwise convergence. Discrete Contin. Dyn. Syst., Ser. B 20(1), 23–38 (2015)
Arthi, G., Park, J.H., Jung, H.Y.: Existence and controllability results for second-order impulsive stochastic evolution systems with state-dependent delay. Appl. Math. Comput. 248, 328–341 (2014)
Baker, C.T.H., Buckwar, E.: Numerical analysis of explicit one-step methods for stochastic delay differential equations. LMS J. Comput. Math. 3, 315–335 (2000)
Baker, C.T.H., Buckwar, E.: Exponential stability in p-th mean of solutions, and of convergent Euler-type solutions, of stochastic delay differential equations. Comput. Appl. Math. 184, 404–427 (2005)
Chen, L., Wu, F.: Almost sure exponential stability of the backward Euler–Maruyama scheme for stochastic delay differential equations with monotone-type condition. J. Comput. Appl. Math. 282, 44–53 (2015)
Fan, Z., Liu, M.Z., Cao, W.R.: Existence and uniqueness of the solutions and convergence of semi-implicit Euler methods for stochastic pantograph equations. J. Math. Anal. Appl. 325(2), 1142–1159 (2007)
Guo, Q., Tao, X., Xie, W.: A split-step θ-Milstein method for linear stochastic delay differential equations. J. Inf. Comput. Sci. 10(5), 1261–1273 (2013)
Gyöngy, I., Sabanis, S.: A note on Euler approximations for stochastic differential equations with delay. Appl. Math. Optim. 68(3), 391–412 (2013)
Higham, D.J.: Mean-square and asymptotic stability of the stochastic theta method. SIAM J. Numer. Anal. 38(3), 753–769 (2000)
Higham, D.J., Mao, X., Stuart, A.M.: Strong convergence of Euler-type methods for nonlinear stochastic differential equations. SIAM J. Numer. Anal. 40(3), 1041–1063 (2002)
Higham, D.J., Mao, X., Stuart, A.M.: Exponential mean-square stability of numerical solutions to stochastic differential equations. LMS J. Comput. Math. 6, 297–313 (2003)
Hofmann, N., Müller-Gronbach, T.: A modified Milstein scheme for approximation of stochastic delay differential equations with constant time lag. Comput. Appl. Math. 197, 89–121 (2006)
Kazmerchuk, Y.I.: Pricing of derivatives in security markets with delayed response. Ph.D. thesis, University of York, Toronto, Canada (2005)
Kazmerchuk, Y.I., Wu, J.H.: Stochastic state-dependent delay differential equations with applications in finance. Funct. Differ. Equ. 11(1–2), 77–86 (2004)
Kloeden, P.E., Platen, E.: Numerical Solution of Stochastic Differential Equations. Springer, Berlin (1992)
Küchler, U., Platen, E.: Strong discrete time approximation of stochastic differential equations with time delay. Math. Comput. Simul. 54(1–3), 189–205 (2000)
Lu, Y., Song, M., Liu, M.: Convergence rate and stability and of the split-step theta method for stochastic differential equations with piecewise continuous arguments. Discrete Contin. Dyn. Syst., Ser. B 24(2), 695–717 (2019)
Mao, X.: Razumikhin-type theorems on exponential stability of stochastic functional differential equations. Stoch. Process. Appl. 65(2), 233–250 (1996)
Parthasarathy, C., Mallika Arjunan, M.: Controllability results for first order impulsive stochastic functional differential systems with state-dependent delay. J. Math. Comput. Sci. 3(1), 15–40 (2013)
Saito, Y., Mitsui, T.: Stability analysis of numerical schemes for stochastic differential equations. SIAM J. Numer. Anal. 33(6), 2254–2267 (1996)
Schikhof, W.H., Perez-Garcia, C., Kakol, J.: p-Adic Functional Analysis: Proceedings of the Fourth International Conference. Dekker, New York (1997)
Wang, X., Gan, S.: The improved split-step backward Euler method for stochastic differential delay equations. Int. J. Comput. Math. 88(11), 2359–2378 (2011)
Wang, Z., Zhang, C.: An analysis of stability of Milstein method for stochastic differential equations with delay. Comput. Math. Appl. 51(9–10), 1445–1452 (2006)
Wu, F., Mao, X.: Numerical solutions of neutral stochastic functional differential equations. SIAM J. Numer. Anal. 46(4), 1821–1841 (2008)
Wu, F., Mao, X., Kloeden, P.E.: Almost sure exponential stability of the Euler–Maruyama approximations for stochastic functional differential equations. Random Oper. Stoch. Equ. 19(2), 165–186 (2011)
Yan, Z., Xiao, A., Tang, X.: Strong convergence of the split-step theta method for neutral stochastic delay differential equations. Appl. Numer. Math. 120, 215–232 (2017)
Yuan, H., Shen, J., Song, C.: On mean square stability and dissipativity of split-step theta method for nonlinear neutral stochastic delay differential equations. Discrete Dyn. Nat. Soc. 2016(3–4), 1–8 (2016)
Zhang, H., Gan, S., Hu, L.: The split-step backward Euler method for linear stochastic delay differential equations. Comput. Appl. Math. 225(2), 558–568 (2009)
Zong, X., Wu, F., Huang, C.: Theta schemes for SDDEs with non-globally Lipschitz continuous coefficients. J. Comput. Appl. Math. 278, 258–277 (2015)
Zong, X., Wu, F., Xu, G.: Convergence and stability of two classes of theta-Milstein schemes for stochastic differential equations. J. Comput. Appl. Math. 336, 8–29 (2018)
Zuomao, Y., Lu, F.: Existence and controllability of fractional stochastic neutral functional integro-differential systems with state-dependent delay in Fréchet spaces. J. Nonlinear Sci. Appl. 9, 603–616 (2016)
Zuomao, Y., Zhang, H.: Existence of solutions to impulsive fractional partial neutral stochastic integro-differential inclusions with state-dependent delay. Electron. J. Differ. Equ. 2013, 81 (2013)
Acknowledgements
Not applicable.
Availability of data and materials
Not applicable.
Author information
Authors and Affiliations
Contributions
There is one author that contributed to the work. The author read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that she has got no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs
Appendix: Proofs
In this section, we deal with proving Theorems 2.1 and 4.2. First, we start with a useful lemma.
Lemma A.1
Assume that \(X, Y : \varOmega \rightarrow \bar{D}\) are two stochastic processes with \(\bar{D} = C([t_{0} - r, T], \mathbb{R}^{d})\). Furthermore, X and Y are denoted by \(\eta _{X}\) and \(\eta _{Y}\) on \([t_{0} - r, t_{0}]\), respectively. Consider the function τ which has been defined in Assumption 2 and suppose that there exists a positive constant H such that
Then there exists a positive constant \(L^{*}\) such that, for all \(t \in [t_{0}, T]\),
where \({D} = C([t_{0} - r, t_{0}], \mathbb{R}^{d})\).
Proof
We divide \([t_{0}, T]\) into two sets as follows:
For all \(t \in I_{1}\), we can easily write
if \(t \in I_{2}\), then we define
We claim that \(L_{t}\) is bounded above. If we suppose that the claim is not true, then for every \(\alpha > 0\) there exists \(t_{\alpha } \in I_{2}\) such that \(L_{t_{\alpha }} > {\alpha }\) and
clearly, due to (A.1), \(\mathbf{E}|X(t_{\alpha }) - Y(t_{\alpha })|^{2} + \|\eta _{X} - \eta _{Y}\|^{2}_{{\mathcal{L}^{2}}(D)} \leq 4H^{2}\), and so the right-hand side of the expression above will tend to infinity as \(\alpha \rightarrow \infty \), i.e.
Also, by (A.1) again, for all \(\alpha >0\),
These two last expressions reveal a contradiction. Therefore, the claim is true and we can set
Finally, we obtain
where \(t \in I_{2}\). By setting \(L^{*} = \max \{\bar{L}, 1\}\), the desired result is obtained. □
In the sequel, we define a unique strong solution for SDDE (1.1) in the third case.
Definition A.2
The stochastic process X is called a strong solution of SDDE (1.1) in case (L3) if the following properties are satisfied:
-
1.
\(X(t)\) is continuous and adapted to \(\mathcal{F}_{t}\) for all \(t \in [t_{0}, T]\);
-
2.
For all \(t \geq 0\), with probability one we have
$$ \int _{t_{0}}^{t} \bigl\vert a \bigl(X(s), X\bigl(s - \tau \bigl(s, X(s)\bigr)\bigr) \bigr) \bigr\vert \,ds + \int _{t_{0}}^{t} \bigl\vert b \bigl(X(s), X\bigl(s - \tau \bigl(s, X(s)\bigr)\bigr) \bigr) \bigr\vert ^{2} \,ds < \infty ; $$ -
3.
For all \(t_{0} \leq t \leq T\), as almost surely
$$\begin{aligned} X(t) =& \eta (t_{0}) + \int _{t_{0}}^{t}a \bigl(X(s), X\bigl(s - \tau \bigl(s, X(s)\bigr)\bigr) \bigr) \,ds \\ &{}+ \int _{t_{0}}^{t}b \bigl(X(s), X\bigl(s - \tau \bigl(s,X(s)\bigr)\bigr) \bigr) \,dW(s), \end{aligned}$$and if we set \(\bar{t} = t - \tau (t, X(t))\) and \(\bar{t} \leq t_{0}\), then \(X(\bar{t}) = \eta (\bar{t})\).
If \({P} \{X(t) = \bar{X}(t), t_{0} \leq t \leq T \} = 1\) for all stochastic processes X̄ satisfying the three conditions above, then we say the solution satisfies the uniqueness.
Now we deal with the proving of Theorem 2.1. Since there exist some texts which deal with the existence and uniqueness for cases (L1) and (L2), so we just consider the third case.
Proof of Theorem 2.1
First, supposing that the equation has a strong solution X, we show that \(\|X\|_{\mathcal{L}^{2}(\bar{D})} <\infty \), and then X is unique in the strong sense. Finally, we deal with the existence of the solution. Note that, for every \(t \in [t_{0}, T]\), by Hölder’s and Doob’s martingale inequalities, we derive
where the relation \((a + b + c)^{3} \leq 3a^{3} + 3b^{3} + 3c^{3}\) has been used. By Assumption 1 and remembering that \(a(0, 0) = 0\) and \(b(0, 0) =0\), we have
We know \(\|\eta \|_{{\mathcal{L}^{2}}(D)} < \infty \). Hence
By Gronwall’s inequality, we get
where \(k = 3 \mathbf{E}|\eta (t_{0})|^{2} +2(3 (t - t_{0}) + 12)K _{1}(t-t_{0}){\|\eta \|^{2}}_{{\mathcal{L}^{2}}(D)}\). So
By setting \(H^{2} = {\|\eta \|^{2}}_{{\mathcal{L}^{2}}(D)} + k e^{4K _{1}(3 (T- t_{0}) + 12)(T - t_{0})}\), the exact solution is bounded in \(\mathcal{L}^{2}\) as
Note that \(H>0\). In order to prove the Hölder type of the exact solution, we suppose that, for every positive constant \(\alpha > 0\), there exist \(t_{\alpha }\), \(s_{\alpha } \in [t_{0}, T]\) such that
if \(\alpha \rightarrow \infty \), then \(\mathbf{E}|X(\rho (t_{\alpha })) - X(\rho (s_{\alpha }))|^{2} \rightarrow \infty \). Note that \(\rho _{1}(t_{\alpha })\) and \(\rho _{2}(s_{\alpha })\) are the two bounded random variables taking values in \([t_{0}, T]\). In addition, from (A.4) we have \(\mathbf{E}|X(\rho _{1}(t_{\alpha })) - X(\rho _{2}(s_{\alpha }))|^{2} \leq 2H^{2}\). So it is a contradiction, and then there exists a positive constant, like \(K_{5}\), such that (2.1) holds.
Now we firstly prove the uniqueness and secondly the existence. Suppose that X and Y are the two strong solutions of the equation with \(Y(s) = X(s) =\eta (s)\) for all \(s \in [t_{0}-r, t_{0}]\). Note that, for all \(t \in (t_{0}, T]\),
by Assumption 1, Hölder’s and Doob’s inequalities
where (A.2) has been employed. Note that \(\eta _{X} = \eta _{Y}\). Finally, by Gronwall’s inequality, we have
So, for all \(t \in [t_{0}, T]\), \(X(t) = Y(t)\) with probability one, and then the proof of uniqueness is finished. Now we turn to the existence. To do this, the classical fixed-point approach, which is also called Picard iteration, is applied. Remember that τ is a bounded continuous process taking values in \((0, r]\). In the sequel, we define sequence \(\{X^{n}(t)\}_{t \in [t_{0}-r, T]}\) as
and
and
and in this way, for all \(n \geq 2\), we define
Note that since \(\eta (t) \in \mathcal{F}_{t}\), \(X^{1}(t) \in \mathcal{F}_{t}\) and so \(X^{2}(t) \in \mathcal{F}_{t}\), too. By induction \(X^{n}(t) \in \mathcal{F}_{t}\) for all n. Moreover, due to the continuity of η, \(X^{1}\) is continuous, and in the same manner, \(X^{n}\) is continuous for all n. Besides, due to \(\|\eta \|_{ {\mathcal{L}^{2}}(D)} < \infty \), by Assumption 1, Hölder’s and Doob’s inequalities
for all \(t \geq t_{0}\) and n. We can write
for every \(k \geq 1\). By Gronwall’s lemma, we get
with \(\bar{H} = 3 (1 +6 ((T - t_{0}) + 4)K_{1}(T-t_{0}) ){\| \eta \|^{2}}_{{\mathcal{L}^{2}}(D)}e^{12 ((T - t_{0}) + 4)K_{1}(T-t _{0})}\). Now we show that the sequence \(X^{n}(t)\) is convergent. Corresponding to (A.6) and by Assumption 1, Hölder’s and Doob’s inequalities
with \(b = (T - t_{0}) + 4\) and \(M = 4{\|\eta \|^{2}}_{{\mathcal{L} ^{2}}(D)}\). By relations (A.6), (A.7) and (A.2) and Hölder’s and Doob’s inequalities and also Assumption 1
By (A.10), we can write
remember that \(X^{2}(t_{0}) = X^{1}(t_{0}) = \eta (t_{0})\). Similarly
Analogously, one can see that, for all \(n\geq 1\),
Hence, by Chebyshev’s inequality, we get
where \(d = 2bK_{1}(1+L^{*})(T- t_{0})\). It is clear that \(\sum_{n=0} ^{\infty } \frac{d^{n}}{n!} < \infty \), and so by the Borel–Cantelli lemma, for almost all \(\omega \in \varOmega \), there exists \(n_{0} = n _{0}(\omega )\), which is a positive integer such that
Hence, for all \(t \in [t_{0}, T]\),
since \(|X^{i+1}(t) - X^{i}(t)| < \frac{1}{(\sqrt{2})^{i}}\) and \(\sum_{i=1}^{n}\frac{1}{(\sqrt{2})^{i}}\) is convergent, so by a sufficient condition presented by K. Weierstrass, \(X^{n}(t)\) converges uniformly. We set \(X(t) = \lim_{n \rightarrow \infty }X^{n}(t)\). By (A.12), we can find that \(X^{n}(t)\) is a Cauchy sequence. So, for every \(\varepsilon >0\), there exists \(n_{0}(\varepsilon ) \in \mathbb{N}\) such that, for all \(n \geq n_{0}(\varepsilon )\), we have
so by (A.9), \(\mathbf{E} (\sup_{t_{0} \leq u \leq t}|X(u)|^{2} ) \leq \bar{H}\). Notice that item 2 in Definition A.2 is satisfied and, obviously, X is continuous and adapted. Now we must examine whether \(X(t)\) is satisfied in problem (1.1). By Assumptions 1 and 2, one can see that \(\tau (t, X^{n}(t))\), \(a (X^{n}(s), X^{n}(s-\tau (s, X^{n}(s))) )\) and \(b (X^{n}(s), X^{n}(s-\tau (s, X^{n}(s))) )\) converge pointwise to \(\tau (t, X(t))\), \(a (X(s), X(s-\tau (s, X(s))) )\) and \(b (X(s), X(s- \tau (s, X(s))) )\), respectively. By Assumption 1 and relation (A.9), we apply the dominated convergence theorem, and so
where the convergence occurs in probability. Hence
with probability one tending to
□
We now deal with the proof of Theorem 4.2. The proof in the two first cases, where τ is discrete or time-dependent, is found in [18], and so just the last one has to be accomplished. To this end, we generalise the Razumikhin-type theorems for the case in which the delay has a random nature. However, our proofs are very close to the non-random case. We provide our main result by three theorems.
Theorem A.3
Consider SDDE (1.1) with state-dependent delay satisfying Assumptions 1–3. Suppose that there exists a function \(V :[t_{0}-r, \infty ) \times \mathbb{R}^{d} \rightarrow \mathbb{R} ^{+}\) which is continuous once differentiable with respect to the first variable and twice to the second one. Besides
where \(c_{1}, c_{2}, p >0\), and there exists positive constant \(\lambda _{1}\) such that, for all \(t \geq 0\),
whenever we have
where \(\lambda _{0}>1\). Also, η is a stochastic process which was defined in Sect. 2. Furthermore, θ is a random variable taking values in \([-r, 0]\). Notice that operator \(\mathcal{L} : C^{1,2}([t _{0} - r, \infty ) \times \mathbb{R}^{d}, \mathbb{R}^{+}) \rightarrow \mathbb{R}\) is given as
Then
with \(K = \frac{c_{2}}{c_{1}} \mathbf{E}\|\eta \|^{p}\) and \(\gamma = \min (\lambda _{1}, \frac{\log (\lambda _{0})}{r})\).
Proof
We define
where \(\bar{\gamma } = \gamma - \epsilon \) for ϵ as an arbitrary positive constant and also θ is a random variable taking values in \([-r,0]\). We suppose that the maximum occurs in θ̄, that is,
Note that \(U(t) \geq 0\). We claim that \(U(t) < U(t_{0})\). For this aim, we show that U is a decreasing function. Clearly, for all random variables \(\theta \in [-r, 0]\),
Here, we review two cases \(\bar{\theta } = 0\) and \(\bar{\theta } \neq 0\). If \(\bar{\theta } = 0\) almost surely, then by (A.17)
for all random variables \(\theta \in [-r, 0]\). By relations (A.13) and (A.19), we have \(c_{1} \mathbf{E} (e^{\bar{\gamma }(t+ \theta )}|X(t+\theta )|^{p} ) \leq \mathbf{E} (e^{\bar{\gamma } t}V(t , X(t)) )\). If \(U(t)\), namely \(\mathbf{E} (e^{\bar{ \gamma } t}V(t , X(t)) )\), is equal to zero, then almost surely
for all random variables \(\theta \in [-r, 0]\). We assert that \(U(t + h) = 0\) for every sufficiently small h. If \(U(t + h) > 0\), then there exists a random variable \(\theta ^{*}\) such that
it is clear that \(\mathbf{E} (e^{\bar{\gamma }( t+h +{\theta }^{*})}V(t+h + {\theta }^{*} , X(t+h + {\theta }^{*})) )>0\). Due to the continuity of \(\mathbf{E} ( e^{\bar{\gamma }\cdot}V(\cdot, X(\cdot)) )\) and since h is a very small quantity, we have \(\mathbf{E} (e^{\bar{\gamma }( t+{\theta }^{*})}V(t + {\theta }^{*} , X(t+ {\theta }^{*})) ) > 0\). Moreover, by relation (A.13), \(X(t+{\theta }^{*})\neq 0\) almost surely and it is a contradiction with (A.20). So the assertion is true, i.e. \(U(t+h) = 0\) and \(U(t+h) \leq U(t)\). We now turn to the case \(U(t)>0\), that is, \(\mathbf{E} (e^{\bar{\gamma } t}V(t , X(t))) > 0\). By (A.19), we have
it is obvious that
by setting \(\lambda _{0} = e^{\bar{\gamma }r}\) and \(\eta (t_{0}+\theta ) = X(t + \theta )\), relation (A.15) is satisfied. Accordingly, by (A.14), we achieve
where \(\eta (t_{0}) = X(t)\). So we can write
for every \(h > 0\). So
We claim that \(U(t + h) = \mathbf{E} (e^{\bar{\gamma }(t + h)}V(t + h, X(t + h)) )\) for every sufficiently small \(h>0\). It means that the maximum in (A.17) takes place in \({\theta }^{*} = 0\) almost surely. Assume that it does not hold, then \(U(t + h) = \mathbf{E} (e^{\bar{ \gamma }(t + h+{\theta }^{*})}V(t + h + {\theta }^{*}, X(t + h + {\theta }^{*})) )\) with \(P\{{\theta }^{*} < 0\} > 0\), and so, for all random variables \(\theta \in [-r, 0]\),
Due to the continuity of \(\mathbf{E} ( e^{\bar{\gamma }\cdot}V(\cdot, X(\cdot )) )\), we obtain
and especially for \(\theta = 0\) almost surely
but it disaffirms (A.19). So the claim is satisfied, and by (A.21) we get \(U(t+h) \leq U(t)\). We now turn to the case \(P\{\bar{\theta } < 0\} > 0\). We claim that \(U(t+h) \leq U(t)\) for every sufficiently small \(h >0\). If
Due to the continuity of \(\mathbf{E} ( e^{\bar{\gamma }\cdot}V(\cdot, X(\cdot)) )\), we obtain
We observe that (A.22) contradicts (A.18), and so the claim is satisfied. Based on what was discussed above, we arrive at \(U(t+h) \leq U(t)\) for every sufficiently small h. Now we define Dini-derivatives \(D^{+} U(t)\) as
Considering \(D^{+} U(t) \leq 0\), the function U is non-increasing, see Lemma 5 in [4]. So \(U(t) \leq U(t_{0})\). Putting everything together, we get
since \(|e^{\bar{\gamma }\theta }| \leq 1\) and by (A.13), we obtain
Consequently,
□
Below, we present more simple conditions to check the stability in the two theorems.
Theorem A.4
Assume that Assumptions 1–3 are fulfilled. Consider the function V defined in Theorem A.3 holding condition (A.13). Moreover, for all \(t \geq 0\) and \(x, y \in \mathbb{R} ^{d}\),
where λ and λ̄ are positive constants. Remember that τ is the lag function. If \(\lambda > q\bar{\lambda }\) for all \(q \in (1, \lambda /\bar{\lambda })\), then the zero solution of SDDE (1.1) with state-dependent delay is pth moment exponentially stable.
Proof
The proof starts with reviewing the condition in the previous theorem. Just checking relation (A.14) is required. In relation (A.23) we set \(x= \eta (t_{0})\) and \(y = \eta ( -\tau (t, \eta (t_{0})))\), so
We can call the left-hand side (A.24) by \(\mathcal{L}(V( t, \eta ))\), and so
If we suppose that
then
so the proof is complete. □
Finally, next theorem concludes our aim.
Theorem A.5
Consider SDDE (1.1) with state-dependent delay which satisfies Assumptions 1–3. Assume that there exist a positive constant λ and non-negative constants \(\alpha _{0}\), \(\alpha _{1}\), \(\beta _{0}\) and \(\beta _{1}\) such that
for all \(x, \bar{x}, y \in \mathbb{R}^{d}\). If
then the zero solution is pth moment exponentially stable.
Proof
The theorem is a special case of Corollary 3.2 in [18] which is easily established by Theorem A.4 and it is therefore omitted. □
Proof of Theorem 4.5
By Theorem A.5 and setting \(p = 2\), the mean-square stability is achieved. □
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Akhtari, B. Numerical solution of stochastic state-dependent delay differential equations: convergence and stability. Adv Differ Equ 2019, 396 (2019). https://doi.org/10.1186/s13662-019-2323-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2323-x