The annihilating graph of a ring

Abstract

Let A be a commutative ring with unity. The annihilating graph of A, denoted by ${{\mathbb {G}}}(A)$, is a graph whose vertices are all non-trivial ideals of A and two distinct vertices I and J are adjacent if and only if ${\rm Ann}(I){\rm Ann}(J)=0$. For every commutative ring A, we study the diameter and the girth of ${\mathbb {G}}(A)$. Also, we prove that if ${\mathbb {G}}(A)$ is a triangle-free graph, then ${\mathbb {G}}(A)$ is a bipartite graph. Among other results, we show that if ${\mathbb {G}}(A)$ is a tree, then ${\mathbb {G}}(A)$ is a star or a double star graph. Moreover, we prove that the annihilating graph of a commutative ring cannot be a cycle. Let n be a positive integer number. We classify all integer numbers n for which ${\mathbb {G}}({{\mathbb {Z}}}_n)$ is a complete or a planar graph. Finally, we compute the domination number of ${\mathbb {G}}({\mathbb {Z}}_n)$.

Introduction

There are many papers on assigning a graph to algebraic structures, for instance see [2,3,4,5,6, 8, 9]. Throughout this paper, all graphs are simple with no loops and multiple edges and A is a commutative ring with non-zero identity. We denote by $\mathbb {I}(A)^{*}$ and ${\rm Max}(A)$, the set of all non-trivial ideals of A and the set of all maximal ideals of A, respectively. A ring having just one maximal ideal is called a local ring and a ring having only finitely many maximal ideals is said to be a semilocal ring. For every ideal I of A, we denote by ${\rm Ann}(I)$, the set of elements $a\in A$ such that $aI=0$.

Let G be a graph with vertex set V(G). If u is adjacent to v, then we write $u - v$. For $u,v\in V(G)$, we recall that a path between u and v is a sequence $u = x_{0} - \cdots - x_{n} = v$ of vertices of G such that for every i with $1 \le i \le n$, the vertices $x_{i-1}$ and $x_{i}$ are adjacent and $x_{i}\ne x_{j}$, where $i\ne j$. For every positive integer n, we denote the path of order n, by $P_n$. For $u,v\in V(G)$ with $u\ne v$, d(u, v) denotes the length of a shortest path between u and v. If there is no such path, then we define $d(u,v)=\infty$. The diameter of G is defined ${\rm diam}(G)={\rm sup}\{d(u,v)| u$ and v are vertices of $G\}$. For any $u\in V(G)$, the degree of u, ${\rm deg}(u)$, denotes the number of edges incident with u. The neighborhood of a vertex u is denoted by $N_G(u)$ or simply N(u). A graph G is k-regular if $d(v) = k$ for all $v \in V(G)$ ; a regular graph is one that is k-regular for some k. We denote the complete graph on n vertices by $K_n$. A bipartite graph is one whose vertex set can be partitioned into two subsets $V_1$ and $V_2$ so that each edge has one end in $V_1$ and one end in $V_2$. A complete bipartite graph is a bipartite graph with two partitions $V_1$ and $V_2$ in which every vertex in $V_1$ is joined to every vertex in $V_2$. The complete bipartite graph with two partitions of size m and n is denoted by $K_{m,n}$. A star graph with center v and n vertices is the complete bipartite graph with part sizes 1 and n such that ${\rm deg}(v)=n$. A double-star graph is a union of two star graphs with centers u and v such that u is adjacent to v. We use $C_{n}$ for the cycle of order n, where $n\ge 3$. If a graph G has a cycle, then the girth of G (notated ${\rm gr}(G)$) is defined as the length of a shortest cycle of G; otherwise ${\rm gr}(G)=\infty$. A triangle-free graph is a graph which contains no triangle. A clique of a graph is a complete subgraph and the number of vertices in a largest clique of graph G, denoted by $\omega (G)$, is called the clique number of G. Recall that a graph is said to be planar if it can be drawn in the plane so that its edges intersect only at their ends. A subdivision of a graph is any graph that can be obtained from the original graph by replacing edges by paths. Also, a dominating set is a subset S of V(G) such that every vertex of $V(G){\setminus} S$ is adjacent to at least one vertex in S. The number of vertices in a smallest dominating set denoted by $\gamma (G)$, is called the domination number of G.

Let A be a commutative ring with non-zero identity. The annihilating graph of A, denoted by ${\mathbb {G}}(A)$, is a graph with the vertex set $\mathbb {I}(A)^{*}$, and two distinct vertices $I,J\in{\mathbb {Z}}(A)^{*}$ are adjacent if and only if ${\rm Ann}(I){\rm Ann}(J)=0$. In this paper, we prove that if A is a ring, then ${\mathbb {G}}(A)$ is a connected graph, ${\rm diam}({\mathbb {G}}(A))\le 3$ and ${\rm gr}({\mathbb {G}}(A))\in \{3, 4, \infty \}$. Also, we prove that for every ring A, if ${\mathbb {G}}(A)$ is a triangle-free graph, then ${\mathbb {G}}(A)$ is a bipartite graph. Among other results, we show that if A is a ring and ${\mathbb {G}}(A)$ is a tree, then ${\mathbb {G}}(A)$ is a star or a double star graph. Moreover, we prove that the annihilating graph of a ring cannot be a cycle. Also, we obtained some results about ${\mathbb {G}}({\mathbb {Z}}_n)$. We show that ${\mathbb {G}}({\mathbb {Z}}_n)$ is a complete graph if and only if $n\in \{p_1^{2},p_1^{3},p_1p_2\}$. We also prove that ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph if and only if $n\in \{p_1,p_1^{2},\ldots ,p_1^{8},p_1p_2,p_1^{2}p_2,p_1^{3}p_2,p_1^{3}p_2^{2},p_1^{4}p_2,p_1^{2}p_2^{2}, p_1p_2p_3,p_1^{2}p_2p_3\}$. Finally, we determine the domination number of ${\mathbb {G}}({\mathbb {Z}}_n)$.

The annihilating graph of A

In this section, we study the diameter and the girth of the annihilating graph of a ring. Also, we classify all rings whose annihilating graphs are complete graph, tree or cycle.

We start with the following lemma.

Lemma 1

If A is a commutative ring, then $\gamma ({\mathbb {G}}(A))\le |{\rm Max}(A)|\le \omega ({\mathbb {G}}(A))$.

Proof

Suppose that ${{\mathfrak {m}}}_1,{\mathfrak {m}}_2$ are two distinct maximal ideals of A. Then we have ${\rm Ann}({\mathfrak {m}}_1){\rm Ann}({\mathfrak {m}}_2)\subseteq {\rm Ann}({\mathfrak {m}}_1)\cap {\rm Ann}({\mathfrak {m}}_2)\subseteq {\rm Ann}({\mathfrak {m}}_1+{\mathfrak {m}}_2)$. Since ${\mathfrak {m}}_1+{\mathfrak {m}}_2=A$, we conclude that ${\rm Ann}({\mathfrak {m}}_1+{\mathfrak {m}}_2)=0$ and so ${\mathfrak {m}}_1$ is adjacent to ${\mathfrak {m}}_2$. This implies that ${\rm Max}(A)$ is a clique in ${\mathbb {G}}(A)$. Now, suppose that $I\in{\mathbb {Z}}(A)^{*} {\setminus} {\rm Max}(A)$. Let ${\mathfrak {m}}$ be a maximal ideal containing ${\rm Ann}(I)$. Since ${\rm Ann}(I){\rm Ann}({\mathfrak {m}})\subseteq {\mathfrak {m}}{\rm Ann}({\mathfrak {m}})=0$, we deduce that I is adjacent to ${\mathfrak {m}}$. Hence ${\rm Max}(A)$ is a dominating set of ${\mathbb {G}}(A)$. $\square$

By the previous lemma, if the clique number of ${\mathbb {G}}(A)$ is finite, then A is a semilocal ring. Also, we have the following result.

Corollary 1

Let A be a ring. If every maximal ideal of A has finite degree, then ${\mathbb {G}}(A)$ is a finite graph.

Proof

Since ${\rm Max}(A)$ is a clique in ${\mathbb {G}}(A)$, so ${\rm Max}(A)$ is finite. Now, since ${\rm Max}(A)$ is a dominating set of ${\mathbb {G}}(A)$, the result holds. $\square$

Next, we study the diameter and the girth of ${\mathbb {G}}(A)$.

Theorem 1

Let A be a ring. Then ${\rm diam}({\mathbb {G}}(A))\le 3$. Moreover, if A is a local ring, then ${\rm diam}({\mathbb {G}}(A))\le 2$.

Proof

Assume that I and J are two non-trivial ideals of A. Suppose that ${\mathfrak {m}}_1$ and ${\mathfrak {m}}_2$ are maximal ideals such that ${\rm Ann}(I)\subseteq {\mathfrak {m}}_1$ and ${\rm Ann}(J)\subseteq {\mathfrak {m}}_2$. Since ${\rm Ann}(I){\rm Ann}({\mathfrak {m}}_1)\subseteq {\mathfrak {m}}_1{\rm Ann}({\mathfrak {m}}_1)=0$, we conclude that $I={\mathfrak {m}}_1$ or I is adjacent to ${\mathfrak {m}}_1$. Similarly, $J={\mathfrak {m}}_2$ or J is adjacent to ${\mathfrak {m}}_2$. Now, if ${\mathfrak {m}}_1={\mathfrak {m}}_2$, then $d(I,J)\le 2$. Otherwise, ${\mathfrak {m}}_1$ and ${\mathfrak {m}}_2$ are adjacent and so $d(I,J)\le 3$. Thus ${\rm diam}({\mathbb {G}}(A))\le 3$. (Note that if A has a non-trivial ideal I with ${\rm Ann}(I)=0$, then I is adjacent to all other vertices and hence ${\rm diam}({\mathbb {G}}(A))\le 2$.) Finally, assume that $(A,{\mathfrak {m}})$ is a local ring. By the proof of Lemma 1, ${\mathfrak {m}}$ is adjacent to all other vertices, so ${\rm diam}({\mathbb {G}}(A))\le 2$. $\square$

Theorem 2

Let A be a ring. Then ${\rm gr}({\mathbb {G}}(A))\in \{3, 4, \infty \}$. Moreover, if A is a local ring and ${\mathbb {G}}(A)$ contains a cycle, then ${\rm gr}({\mathbb {G}}(A))=3$.

Proof

Clearly, if A has at least three maximal ideals, then ${\rm gr}({\mathbb {G}}(A))=3$. So assume that A has exactly two maximal ideals and ${\mathbb {G}}(A)$ contains a cycle C. If C is a cycle of length at most 4, then we are done. Otherwise, C contains two adjacent vertices I and J which are not maximal ideals. Suppose that $I\subseteq {\mathfrak {m}}_1$ and $J\subseteq {\mathfrak {m}}_2$, where ${\mathfrak {m}}_1$ and ${\mathfrak {m}}_2$ are maximal ideals of A. Since ${\rm Ann}(I){\rm Ann}({\mathfrak {m}}_2)\subseteq {\rm Ann}(I)Ann(J)=0$, we deduce that I and ${\mathfrak {m}}_2$ are adjacent. Similarly, J and ${\mathfrak {m}}_1$ are adjacent. If ${\mathfrak {m}}_1={\mathfrak {m}}_2$, then ${\rm gr}({\mathbb {G}}(A))=3$. Otherwise, ${\rm gr}({\mathbb {G}}(A))\le 4$. The last part follows from the proof of Lemma 1. $\square$

The following theorem shows that triangle-free annihilating graphs are bipartite.

Theorem 3

Let A be a ring. If ${\mathbb {G}}(A)$ is a triangle-free graph, then ${\mathbb {G}}(A)$ is a bipartite graph.

Proof

Let ${\mathbb {G}}(A)$ be a triangle-free graph. Clearly A has at most two maximal ideals. If A is a local ring, then ${\mathbb {G}}(A)$ is a star and so ${\mathbb {G}}(A)$ is bipartite. Suppose that A contains exactly two distinct maximal ideals ${\mathfrak {m}}_1$ and ${\mathfrak {m}}_2$. One can easily see that ${\mathbb {G}}(A)$ is a bipartite graph with parts $N({\mathfrak {m}}_1)$ and $N({\mathfrak {m}}_2)$. $\square$

Theorem 4

Let A be a ring. If ${\mathbb {G}}(A)$ is a tree, then ${\mathbb {G}}(A)$ is a star or a double star graph.

Proof

Assume that ${\mathbb {G}}(A)$ is a tree. It is enough to show that if A has exactly two distinct maximal ideals ${\mathfrak {m}}_1$ and ${\mathfrak {m}}_2$, then ${\mathbb {G}}(A)$ is a double star graph. By the proof of Lemma 1, ${\mathfrak {m}}_1$ is adjacent to ${\mathfrak {m}}_2$ and every other vertex is adjacent to one of the ${\mathfrak {m}}_1$ and ${\mathfrak {m}}_2$. Now, since ${\mathbb {G}}(A)$ contains no cycles, ${\mathbb {G}}(A)$ is a double star graph. $\square$

By the previous theorem, we have the following immediate corollary.

Corollary 2

Let A be a ring. If ${\mathbb {G}}(A)\cong P_n$, then $n\le 4$.

Theorem 5

The annihilating graph of a ring cannot be a cycle.

Proof

By contrary suppose that ${\mathbb {G}}(A)\cong C_n$, for some $n\ge 3$. By Theorem 2, we conclude that $n\le 4$. First assume that ${\mathbb {G}}(A)\cong C_4$. So A has exactly four non-trivial ideals. By Theorem 2, we deduce that A is not a local ring. Hence by [6, Theorem 8.7], $A\cong F\times S$, where F is a field and S is a ring with exactly one non-trivial ideal. Let ${\mathfrak {m}}$ be the non-trivial ideal of S. Thus $\mathbb {I}(A)^{*}=\{0\times {\mathfrak {m}}, 0\times S, F\times 0, F\times {\mathfrak {m}}\}$. We have ${\rm Ann}(0\times {\mathfrak {m}})=F\times {\mathfrak {m}}$, ${\rm Ann}(F\times {\mathfrak {m}})=0\times {\mathfrak {m}}$, ${\rm Ann}( 0\times S)=F\times 0$ and ${\rm Ann}(F\times 0)=0\times S$. Therefore, ${\mathbb {G}}(A)$ is the path $0\times {\mathfrak {m}}- F\times {\mathfrak {m}} - 0\times S - F\times S$, a contradiction. Next assume that ${\mathbb {G}}(A)\cong C_3$. Since A has exactly three non-trivial ideals, by [6, Theorem 8.7], A is an Artinian local ring. Let $\mathbb {I}(A)^{*}=\{I, J, {\mathfrak {m}}\}$, where ${\mathfrak {m}}$ is the maximal ideal of A. Suppose that k is the smallest positive integer such that ${\mathfrak {m}}^ k=0$. So ${\rm Ann}({\mathfrak {m}})\ne 0$. With no loss of generality, we consider two cases. Note that the annihilating-ideal graph $\mathbb {AG}(A)$ of A is a graph whose vertex set is the set of all non-zero ideals of A with non-zero annihilator and two distinct vertices I and J are adjacent if and only if $IJ =0$, see [1].

Case 1

${\rm Ann}({\mathfrak {m}})={\mathfrak {m}}$. So ${\mathfrak {m}}^2=0$ and hence $IJ=I{\mathfrak {m}}=J{\mathfrak {m}}=0$. This implies that $\mathbb {AG}(A)\cong {\mathbb {G}}(A)\cong C_3$. By [1, Corollary 9], $\mathbb {AG}(A)$ cannot be a cycle, a contradiction.

Case 2

${\rm Ann}({\mathfrak {m}})=I$. Thus $I{\mathfrak {m}}=0$. So $IJ=0$ and ${\mathfrak {m}}={\rm Ann}(I)$. If ${\mathfrak {m}}J=0$, then $\mathbb {AG}(A)\cong {\mathbb {G}}(A)\cong C_3$, a contradiction. Therefore, ${\mathfrak {m}}J\ne 0$ and hence $\mathbb {AG}(A)\cong P_3$. Now, by [1, Theorem 11], we have $k=4$ and so $I={\mathfrak {m}}^3$ and $J={\mathfrak {m}}^2$. This implies that ${\rm Ann}(I)={\mathfrak {m}}$ and ${\rm Ann}(J)={\mathfrak {m}}^2$. Thus ${\mathbb {G}}(A)\cong P_3$, a contradiction. $\square$

Theorem 6

If ${\mathbb {G}}(A)$ is a regular graph of finite degree, then ${\mathbb {G}}(A)$ is a complete graph.

Proof

By Corollary 1, A has finitely many ideals. So A is an Artinian ring. First suppose that $(A,{\mathfrak {m}})$ is an Artinian local ring. Since ${\mathfrak {m}}$ is a vertex of ${\mathbb {G}}(A)$ which is adjacent to all other vertices, we deduce that ${\mathbb {G}}(A)$ is a complete graph. Now, by [6, Theorem 8.7], we may assume that $A\cong A_1\times \cdots \times A_n$, where $n\ge 2$ and $(A_i,\mathfrak {m_i})$ is an Artinian local ring for $i=1,\ldots ,n$. We have ${\rm Ann}(0\times A_2\times \cdots \times A_n)=A_1\times 0\times \cdots \times 0$, ${\rm Ann}(\mathfrak {m_1}\times A_2\times \cdots \times A_n)={\rm Ann}(\mathfrak {m_1})\times 0\times \cdots \times 0$, and ${\rm Ann}(A_1\times 0\times \cdots \times 0)=0\times A_2\times \cdots \times A_n$. Let $v_1=0\times A_2\times \cdots \times A_n$, $v_2=\mathfrak {m_1}\times A_2\times \cdots \times A_n$ and $v_3=A_1\times 0\times \cdots \times 0$. One can easily see that

$$\begin{aligned} N(v_1)=\{ A_1\times I_2\times \cdots \times I_n \ | \ I_i \ \hbox {is an ideal of} \ A_i \ \hbox {for} \ i=2,\ldots ,n \}{\setminus} \{A\}, \end{aligned}$$

and

$$\begin{aligned} N(v_2)=\{ I_1\times I_2\times \cdots \times I_n \ | \ I_i \ \hbox {is an ideal of} \ A_i \ \hbox {for} \ i=1,\ldots ,n \ \hbox {and} \ I_1\ne 0 \}{\setminus} \{A\}. \end{aligned}$$

Note that every non-trivial ideal of an Artinian ring A has a non-zero annihilator. Since ${\rm deg}(v_1)={\rm deg}(v_2)$, we conclude that $A_1$ has no proper ideal other than $0, \mathfrak {m_1}$. Thus

$$\begin{aligned} N(v_3)=\{ 0\times A_2\times \cdots \times A_n, \mathfrak {m_1}\times A_2\times \cdots \times A_n \}. \end{aligned}$$

Hence ${\rm deg}(v_3)\le 2$. If ${\mathbb {G}}(A)$ is a 2-regular graph, then ${\mathbb {G}}(A)$ is a cycle, a contradiction. Note that by Theorem 1, ${\mathbb {G}}(A)$ is a connected graph. Therefore, ${\mathbb {G}}(A)$ is a 1-regular graph. So ${\mathbb {G}}(A)\cong K_2$ is a complete graph. In this case, $A\cong F_1\times F_2$, where $F_1, F_2$ are fields.

Remark 1

Let A be a commutative ring and ${\mathfrak {m}}$ be a maximal ideal of A with non-zero annihilator. Since ${\mathfrak {m}}{\rm Ann}({\mathfrak {m}})=0$, we conclude that ${\mathfrak {m}}\subseteq {\rm Ann}(Ann({\mathfrak {m}}))$. Now, ${\rm Ann}({\mathfrak {m}})\ne 0$ implies that ${\rm Ann}({\rm Ann}({\mathfrak {m}}))={\mathfrak {m}}$.

Lemma 2

Let A be a local ring with non-zero maximal ideal ${\mathfrak {m}}$. If $I\in{\mathbb {Z}}(A)^{*}$ and ${\rm Ann}(I)={\rm Ann}({\mathfrak {m}})$, then I is adjacent to all other vertices of ${\mathbb {G}}(A)$.

Proof

Suppose that ${\rm Ann}(I)={\rm Ann}({\mathfrak {m}})$. Let J be a non-trivial ideal of A and $J\ne I$. Since ${\rm Ann}(J)\subseteq {\mathfrak {m}}$, we deduce that ${\rm Ann}(J){\rm Ann}(I)\subseteq {\mathfrak {m}}{\rm Ann}({\mathfrak {m}})=0$. Hence I and J are adjacent. The proof is complete. $\square$

Theorem 7

Let A be a local ring with non-zero maximal ideal ${\mathfrak {m}}$ such that ${\rm Ann}({\mathfrak {m}})\ne 0$. Then ${\mathbb {G}}(A)$ is a complete graph if and only if ${\rm Ann}(I)={\rm Ann}({\mathfrak {m}})$, for every ideal $I\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\rm Ann}({\mathfrak {m}})\}$.

Proof

Suppose that ${\mathbb {G}}(A)$ is a complete graph and let $I\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\rm Ann}({\mathfrak {m}})\}$. Since ${\rm Ann}({\mathfrak {m}})\ne 0, A$, we conclude that ${\rm Ann}({\mathfrak {m}})$ is a vertex of ${\mathbb {G}}(A)$ and hence is adjacent to I. Thus ${\rm Ann}(I){\rm Ann}(Ann({\mathfrak {m}}))=0$. By Remark 1, ${\rm Ann}({\rm Ann}({\mathfrak {m}}))={\mathfrak {m}}$. So ${\rm Ann}(I){\mathfrak {m}}=0$ which implies that ${\rm Ann}(I)\subseteq {\rm Ann}({\mathfrak {m}})$. In other hand, since $I\subseteq {\mathfrak {m}}$, we deduce that ${\rm Ann}({\mathfrak {m}})\subseteq {\rm Ann}(I)$. Therefore, ${\rm Ann}(I)={\rm Ann}({\mathfrak {m}})$. Conversely, suppose that ${\rm Ann}(I)={\rm Ann}({\mathfrak {m}})$, for every ideal $I\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\rm Ann}({\mathfrak {m}})\}$. Assume that $I, J\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\rm Ann}({\mathfrak {m}})\}$ and $I\ne J$. Since ${\rm Ann}(I)={\rm Ann}(J)=Ann({\mathfrak {m}})$, we conclude that ${\rm Ann}(I){\rm Ann}(J)=Ann({\mathfrak {m}}){\rm Ann}({\mathfrak {m}})\subseteq {\mathfrak {m}}{\rm Ann}({\mathfrak {m}})=0$. Hence I and J are adjacent. Now, since ${\rm Ann}({\rm Ann}({\mathfrak {m}})){\rm Ann}(I)={\mathfrak {m}}{\rm Ann}(I)={\mathfrak {m}}{\rm Ann}({\mathfrak {m}})=0$, then ${\rm Ann}({\mathfrak {m}})$ is adjacent to all other vertices. Thus ${\mathbb {G}}(A)$ is a complete graph. $\square$

Theorem 8

Let A be an Artinian local ring with non-zero maximal ideal ${\mathfrak {m}}$. Then ${\mathbb {G}}(A)$ is a complete graph if and only if either ${\mathfrak {m}}^2=0$ or ${\mathfrak {m}}^3=0$ and $IJ={\mathfrak {m}}^2$, for every ideal $I,J\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\mathfrak {m}}^2\}$.

Proof

First assume that ${\mathfrak {m}}^2=0$. Thus ${\mathfrak {m}}\subseteq {\rm Ann}({\mathfrak {m}})$ and hence ${\rm Ann}({\mathfrak {m}})={\mathfrak {m}}$. Let $I\in{\mathbb {Z}}(A)^{*}$. Since $I\subseteq {\mathfrak {m}}$, we deduce that ${\mathfrak {m}}={\rm Ann}({\mathfrak {m}})\subseteq {\rm Ann}(I)$. So ${\rm Ann}(I)={\mathfrak {m}}$. Now, Theorem 9 implies that ${\mathbb {G}}(A)$ is a complete graph. Next assume that ${\mathfrak {m}}^3=0$ and $IJ={\mathfrak {m}}^2$, for every ideal $I,J\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\mathfrak {m}}^2\}$. Note that ${\mathfrak {m}}^2\ne 0$. Hence ${\rm Ann}({\mathfrak {m}})\ne {\mathfrak {m}}$ and ${\rm Ann}({\mathfrak {m}}^2)={\mathfrak {m}}$. Since ${\rm Ann}({\mathfrak {m}}){\rm Ann}({\mathfrak {m}})\subseteq {\mathfrak {m}}{\rm Ann}({\mathfrak {m}})=0$, we conclude that ${\rm Ann}({\mathfrak {m}})={\mathfrak {m}}^2$. Let $I\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\mathfrak {m}}^2\}$. Since $I{\rm Ann}(I)=0\ne {\mathfrak {m}}^2$, we deduce that ${\rm Ann}(I)={\mathfrak {m}}^2={\rm Ann}({\mathfrak {m}})$. Thus by Theorem 9, ${\mathbb {G}}(A)$ is complete. Conversely, suppose that ${\mathbb {G}}(A)$ is a complete graph. Let k be the smallest positive integer such that ${\mathfrak {m}}^k=0$. If $k=2$, we are done. Assume that $k\ge 3$. So ${\rm Ann}({\mathfrak {m}})\ne {\mathfrak {m}}$. Since ${\mathfrak {m}}\subseteq {\rm Ann}({\mathfrak {m}}^{k-1})$, we conclude that ${\rm Ann}({\mathfrak {m}}^{k-1})={\mathfrak {m}}$. Now, by Theorem 9, ${\rm Ann}({\mathfrak {m}})={\mathfrak {m}}^{k-1}$. In other hand, since ${\mathfrak {m}}^{k-2}\subseteq {\rm Ann}({\mathfrak {m}}^2)$, then ${\rm Ann}({\mathfrak {m}}^2)\ne {\mathfrak {m}}^{k-1}={\rm Ann}({\mathfrak {m}})$. This implies that ${\mathfrak {m}}^2={\rm Ann}({\mathfrak {m}})={\mathfrak {m}}^{k-1}$. Therefore, $k=3$ and so we have ${\mathfrak {m}}^3=0$, ${\rm Ann}({\mathfrak {m}})={\mathfrak {m}}^2$, and ${\rm Ann}({\mathfrak {m}}^2)={\mathfrak {m}}$. Finally, suppose that $I,J\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\mathfrak {m}}^2\}$. Since ${\mathfrak {m}}IJ\subseteq {\mathfrak {m}}^3=0$, we deduce that $IJ=0$ or ${\rm Ann}(IJ)={\mathfrak {m}}$. If $IJ=0$, then $I\subseteq {\rm Ann}(J)={\mathfrak {m}}^2$ and hence ${\mathfrak {m}}={\rm Ann}({\mathfrak {m}}^2)\subseteq {\rm Ann}(I)={\mathfrak {m}}^2$, a contradiction. Thus ${\rm Ann}(IJ)={\mathfrak {m}}$ and so Theorem 7 implies that $IJ={\mathfrak {m}}^2$. The proof is complete. $\square$

We close this section by the following theorem which is a classification of rings whose annihilating graphs are complete.

Theorem 9

Let A be a commutative ring. If ${\mathbb {G}}(A)\cong K_n$, then one of the following holds:

• (i) $(A,{\mathfrak {m}})$ is an Artinian local ring with ${\mathfrak {m}}^2=0$.

• (ii) $(A,{\mathfrak {m}})$ is an Artinian local ring with ${\mathfrak {m}}^3=0$ and $IJ={\mathfrak {m}}^2$, for every ideal $I,J\in{\mathbb {Z}}(A)^{*}{\setminus} \{{\mathfrak {m}}^2\}$.

• (iii) $A\cong F_1\times F_2$, where $F_1, F_2$ are fields.

Proof

Suppose that ${\mathbb {G}}(A)\cong K_n$, for some positive integer n. So A is an Artinian ring. By Theorem 8, if A is a local ring, then the cases (ii) or (iii) occur. Otherwise, by the proof of Theorem 6, $A\cong F_1\times F_2$, where $F_1, F_2$ are fields. $\square$

The annihilating graph of ${\mathbb {Z}}_n$

In this section, we study the case that $A={\mathbb {Z}}_n$. Throughout this section, without loss of generality, we assume that $n=p_1^{\alpha _1}\cdots p_s^{\alpha _s}$, where $p_i$’s are distinct primes and $\alpha _i$’s are positive integers. It is easy to see that $\mathbb {I}({\mathbb {Z}}_n)=\{d{\mathbb {Z}}_n : d$ divides $n \}$ and $|\mathbb {I}({\mathbb {Z}}_n)^{*}|=\prod _{i=1}^{s}(\alpha _i+1)-2$. We denote the least common multiple and the greatest common divisor of integers a and b by [a, b] and (a, b), respectively. Also, we write a|b ($a\not \mid b$) if a divides b (a does not divide b). We begin with the following lemma.

Lemma 3

If $p_1^{\beta _1}\cdots p_s^{\beta _s}{\mathbb {Z}}_n \in{\mathbb {Z}}({\mathbb {Z}}_n)^{*}$, then ${\rm Ann}(p_1^{\beta _1}\cdots p_s^{\beta _s}{\mathbb {Z}}_n)=p_1^{\alpha _1-\beta _1} \cdots p_s^{\alpha _s-\beta _s} {\mathbb {Z}}_n$.

Proof

Let $d=p_1^{\beta _1}\cdots p_s^{\beta _s}$ and $d'=p_1^{\alpha _1-\beta _1} \cdots p_s^{\alpha _s-\beta _s}$. Clearly, $d{\mathbb {Z}}_n d'{\mathbb {Z}}_n = 0$ and so $d' {\mathbb {Z}}_n \subseteq {\rm Ann}(d{\mathbb {Z}}_n)$. Let $r\in {\rm Ann}(d{\mathbb {Z}}_n)$. Then n divides rd. Since $n=p_1^{\alpha _1}\cdots p_s^{\alpha _s}$ and $d= p_1^{\beta _1}\cdots p_s^{\beta _s}$, so $p_1^{\alpha _1-\beta _1} \cdots p_s^{\alpha _s-\beta _s}$ divides r. This implies that $r\in d'{\mathbb {Z}}_n$ and ${\rm Ann}(d{\mathbb {Z}})\subseteq d'{\mathbb {Z}}_n$. The proof is complete. $\square$

Remark 2

Let $d_1{\mathbb {Z}}_n, d_2 {\mathbb {Z}}_n \in{\mathbb {Z}}({\mathbb {Z}}_n)^{*}$ and let $d_1=p_1^{\beta _1}\cdots p_s^{\beta _s}$, $d_2=p_1^{\gamma _1}\cdots p_s^{\gamma _s}$. Then $d_1 {\mathbb {Z}}_n$ and $d_2 {\mathbb {Z}}_n$ are adjacent if and only if $p_1^{\alpha _1}\cdots p_s^{\alpha _s}$ divides $p_1^{2\alpha _1-(\beta _1+\gamma _1)}\cdots p_s^{2\alpha _s-(\beta _s+\gamma _s)}$ which implies that $\alpha _i\ge \beta _i+\gamma _i$, for $i=1,\ldots ,s$. Also, if $(d_1, d_2)=1$ then $d_1{\mathbb {Z}}_n$ and $d_2{\mathbb {Z}}_n$ are adjacent.

Lemma 4

If $d=p_1^{\beta _1}\cdots p_s^{\beta _s}$, then $\prod _{i=1}^{s}(\alpha _i-\beta _i+1)-2\le {\rm deg}(d{\mathbb {Z}}_n)\le \prod _{i=1}^{s}(\alpha _i-\beta _i+1)-1$.

Proof

If $p_1^{\gamma _1}\cdots p_s^{\gamma _s}{\mathbb {Z}}_n$ and $d{\mathbb {Z}}_n$ are adjacent, then by Remark 2, $0\le \gamma _i\le \alpha _i-\beta _i$. On the other hand, $p_1^{\gamma _1}\cdots p_s^{\gamma _s}\notin \{1,d\}$ which implies that ${\rm deg}(d{\mathbb {Z}}_n)\in \{\prod _{i=1}^{s}(\alpha _i-\beta _i+1)-2,\prod _{i=1}^{s}(\alpha _i-\beta _i+1)-1\}$. $\square$

Next, we study the girth of ${\mathbb {G}}({\mathbb {Z}}_n)$.

Theorem 10

Let n be a positive integer number. Then ${\rm gr}({\mathbb {G}}({\mathbb {Z}}_n))\in \{3, \infty \}$. Moreover, ${\mathbb {G}}({\mathbb {Z}}_n)$ is a tree if and only if $n\in \{p_1^2, p_1^3, p_1 p_2, p_1^2 p_2\}$.

Proof

If $s\geqslant 3$, then $p_1 {\mathbb {Z}}_n - p_2 {\mathbb {Z}}_n - p_3 {\mathbb {Z}}_n - p_1 {\mathbb {Z}}_n$ is a 3-cycle in ${\mathbb {G}}({\mathbb {Z}}_n)$. Therefore ${\rm gr}({\mathbb {G}}({\mathbb {Z}}_n))=3$. Now, consider two following cases:

Case 1

$s=1$. If $\alpha _1\geqslant 4$, then it is easy to see that $p_1 {\mathbb {Z}}_n - p_1^{2} {\mathbb {Z}}_n - p_1^{3} {\mathbb {Z}}_n - p_1 {\mathbb {Z}}_n$ is a triangle in ${\mathbb {G}}({\mathbb {Z}}_n)$ and so ${\rm gr}({\mathbb {G}}({\mathbb {Z}}_n))=3$. Also, it is clear that if $n=p_1^2$ or $n=p_1^3$, then ${\rm gr}({\mathbb {G}}({\mathbb {Z}}_n))=\infty$.

Case 2

$s=2$. If $\alpha _1\geqslant 3$, then $p_1{\mathbb {Z}}_n - p_2 {\mathbb {Z}}_n - p_1^2 {\mathbb {Z}}_n - p_1{\mathbb {Z}}_n$ is a 3-cycle in ${\mathbb {G}}({\mathbb {Z}}_n)$. This yields that ${\rm gr}({\mathbb {G}}({\mathbb {Z}}_n))=3$. Now, suppose that $\alpha _1,\alpha _2\in \{1, 2 \}$. Whit out lose of generality we may assume the following three subcases:

Subcase 1

$n=p_1 p_2$. Then ${\mathbb {G}}({\mathbb {Z}}_n)\cong K_2$ and ${\rm gr}({\mathbb {G}}({\mathbb {Z}}_n))=\infty$.

Subcase 2

$n=p_1^2 p_2$. Then ${\mathbb {G}}({\mathbb {Z}}_n)\cong P_4$ and so ${\rm gr}({\mathbb {G}}({\mathbb {Z}}_n))=\infty$. Note that, $p_1p_2 {\mathbb {Z}}_n - p_1 {\mathbb {Z}}_n - p_2 {\mathbb {Z}}_n - p_1^2 {\mathbb {Z}}_n$.

Subcase 3

$n=p_1^2 p_2^2$. Then $p_1 {\mathbb {Z}}_n - p_1 p_2 {\mathbb {Z}}_n - p_2 {\mathbb {Z}}_n - p_1 {\mathbb {Z}}_n$ is a triangle in ${\mathbb {G}}({\mathbb {Z}}_n)$. Hence ${\rm gr}({\mathbb {G}}({\mathbb {Z}}_n))=3$. $\square$

Now, we compute some numerical invariants of ${\mathbb {G}}({\mathbb {Z}}_n)$, namely domination number and clique number.

Theorem 11

If n is a positive integer number, then $\gamma ({\mathbb {G}}({\mathbb {Z}}_n))=s$.

Proof

We note that ${\rm Max}({\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n,\ldots ,p_s{\mathbb {Z}}_n\}$. Hence by Theorem 1, we find that $\gamma ({\mathbb {G}}({\mathbb {Z}}_n))\le s$. Next, we prove that $\gamma ({\mathbb {G}}({\mathbb {Z}}_n))\ge s$. Let D be a smallest dominating set for ${\mathbb {G}}({\mathbb {Z}}_n)$ and let $I_j=p_j^{\alpha _j-1}\prod _{i\ne j}p_i^{\alpha _i}{\mathbb {Z}}_n$, for $j=1,\ldots ,s$. We have $N(I_j)=\{p_j{\mathbb {Z}}_n\}$. This implies that $\{I_j,p_j{\mathbb {Z}}_n\}\cap D\ne \varnothing$, for every j, $1\le j\le s$. Therefore $|D|\ge s$ and so $\gamma ({\mathbb {G}}({\mathbb {Z}}_n))=s$. $\square$

Theorem 12

If $n=p^{\alpha }$, then $\omega (\mathbb {G}(\mathbb {Z}_n))=\left\{ \begin{array}{ll} \dfrac{\alpha }{2}, &{} {\text {if}} \, \alpha \, {\text {is even;}}\\ \dfrac{\alpha +1}{2}, &{} {\text {otherwise.}} \end{array} \right.$

Proof

First suppose that $\alpha$ is even. By Remark 2, $p^{r}{\mathbb {Z}}_n$ and $p^{r'}{\mathbb {Z}}_n$ are adjacent, where $1\le r,r'\le \alpha /2$. This yields that $A=\{p^{r}{\mathbb {Z}}_n: r=1,\ldots ,\alpha /2\}$ is a clique in ${\mathbb {G}}({\mathbb {Z}}_n)$. We claim that A is a maximum clique in ${\mathbb {G}}({\mathbb {Z}}_n)$. By contradiction, suppose that $\{p^{r_1}{\mathbb {Z}}_n,\ldots , p^{r_{\alpha /2+1}}{\mathbb {Z}}_n\}$ is a clique in ${\mathbb {G}}({\mathbb {Z}}_n)$. Clearly, $1\le r_i\le \alpha$, for $i=1,\ldots , \alpha /2+1$. With no loss of generality, we may assume that $r_1\ge \alpha /2+1$. By Remark 2, we conclude that ${\rm deg}(p^{r_1}{\mathbb {Z}}_n)\le \alpha /2$, a contradiction. Therefore $\{p^{r}{\mathbb {Z}}_n: r=1,\ldots ,\alpha /2\}$ is a maximum clique in ${\mathbb {G}}({\mathbb {Z}}_n)$ and $\omega ({\mathbb {G}}({\mathbb {Z}}_n))=\alpha /2$. Similarly, $\{p^{r}{\mathbb {Z}}_n: r=1,\ldots ,(\alpha +1)/2\}$ is a maximum clique in ${\mathbb {G}}({\mathbb {Z}}_n)$, where $\alpha$ is odd. This completes the proof. $\square$

Theorem 13

${\mathbb {G}}({\mathbb {Z}}_n)$ is a complete graph if and only if $n\in \{p_1^{2},p_1^{3},p_1p_2\}$.

Proof

One side is obvious. For the other side assume that ${\mathbb {G}}({\mathbb {Z}}_n)$ is a complete graph. By Theorem 9, we find that $s=1,2$. For the case $s=1$, we have ${\rm Max}({\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n\}$. Hence by Theorem 9, $\alpha _1=2,3$. Also, if $s=2$, then Theorem 9 implies that $\alpha _1=\alpha _2=1$. Therefore $n=p_1p_2$. $\square$

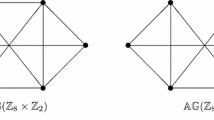
If $n=p_1^{3}p_2^{2}$ and $v_1=p_1p_2{\mathbb {Z}}_{n},v_2=p_1p_2^{2}{\mathbb {Z}}_{n},v_3=p_1{\mathbb {Z}}_{n},v_4=p_1^{2}p_2{\mathbb {Z}}_{n},v_5=p_1^{2}{\mathbb {Z}}_{n},v_6=p_2^{2}{\mathbb {Z}}_{n}, v_7=p_1^{2}p_2^{2}{\mathbb {Z}}_{n},v_8=p_1^{2}p_2^{2}{\mathbb {Z}}_{n},v_9=p_2{\mathbb {Z}}_{n},v_{10}=p_1^{3}p_2{\mathbb {Z}}_{n}$, then we have the following graph (Fig. 1):

Fig. 1

${\mathbb {G}}({\mathbb {Z}}_{p_1^{3}p_2^{2}})$

Also, if $n=p_1^{2}p_2p_3$ and $v_1=p_1{\mathbb {Z}}_{n},v_2=p_1p_2{\mathbb {Z}}_{n},v_3=p_1p_3{\mathbb {Z}}_{n},v_4=p_2{\mathbb {Z}}_{n},v_5=p_1^{2}{\mathbb {Z}}_{n},v_6=p_2p_3{\mathbb {Z}}_{n},v_7=p_3{\mathbb {Z}}_{n}, v_8=p_1p_2p_3{\mathbb {Z}}_{n},v_9=p_1^{2}p_2{\mathbb {Z}}_{n},v_{10}=p_1^{2}p_3{\mathbb {Z}}_{n}$, then we have the following graph (Fig. 2):

Fig. 2

${\mathbb {G}}({\mathbb {Z}}_{p_1^{2}p_2p_3})$

Now, we investigate the planarity of ${\mathbb {G}}({\mathbb {Z}}_{n})$. We will frequently need a celebrated theorem due to Kuratowski.

Proposition 1

[7, Theorem 10.30] A graph is planar if and only if it contains no subdivision of either $K_5$ or $K_{3,3}$.

Theorem 14

${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph if and only if $n\in \{p_1,p_1^{2},\ldots ,p_1^{8},p_1p_2,p_1^{2}p_2,p_1^{3}p_2,p_1^{3}p_2^{2},p_1^{4}p_2,p_1^{2}p_2^{2},$ $p_1p_2p_3,p_1^{2}p_2p_3\}$.

Proof

One side is obvious. For the other side assume that ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $s\ge 5$, then $\{p_1{\mathbb {Z}}_n,\ldots ,p_5{\mathbb {Z}}_n\}$ is a clique, a contradiction. Therefore $s\le 4$. Consider two following cases:

Case 1 $s=1$. If $\alpha _1\ge 9$, then $\{p_1{\mathbb {Z}}_n,p_1^{2}{\mathbb {Z}}_n,\ldots ,p_1^{5}{\mathbb {Z}}_n\}$ is a clique, a contradiction. Hence $\alpha _1\le 8$. It is clear that if $\alpha _1\le 5$, then $|V({\mathbb {G}}({\mathbb {Z}}_n))|\le 4$ and so ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $\alpha _1=6$, then $|V({\mathbb {G}}({\mathbb {Z}}_n))|=5$. On the other hand $p_1^{4}{\mathbb {Z}}_n$ and $p_1^{5}{\mathbb {Z}}_n$ are two non adjacent vertices. Now, by Theorem 1, we find that ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $\alpha _1=7$, then $|V({\mathbb {G}}({\mathbb {Z}}_n))|=6$. Also, $N(p_1^{6}{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n\}$. Therefore by Theorem 1, ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $\alpha _1=8$, then $|V({\mathbb {G}}({\mathbb {Z}}_n))|=7$. It is easy to see that $N(p_1^{7}{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n\}$, $N(p_1^{6}{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n, p_1^{2}{\mathbb {Z}}_n\}$ and $N(p_1^{5}{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n, p_1^{2}{\mathbb {Z}}_n,p_1^{3}{\mathbb {Z}}_n\}$. Hence ${\mathbb {G}}({\mathbb {Z}}_n)$ contains no subdivision of either $K_5$ or $K_{3,3}$. Therefore by Theorem 1, ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph.

Case 2 $2\le s\le 4$. If $\alpha _1,\alpha _2\ge 3$, then vertices of the set $\{p_1{\mathbb {Z}}_n,p_1^{2}{\mathbb {Z}}_n,p_1^{3}{\mathbb {Z}}_n\}$ are adjacent to the vertices of the set $\{p_2{\mathbb {Z}}_n,p_2^{2}{\mathbb {Z}}_n,p_2^{3}{\mathbb {Z}}_n\}$, and so $K_{3,3}$ is a subgraph of ${\mathbb {G}}({\mathbb {Z}}_n)$, a contradiction. Hence we may assume that $\alpha _2,\ldots ,\alpha _s\le 2$. If $\alpha _1\ge 5$, then two sets $\{p_1{\mathbb {Z}}_n,p_1^{2}{\mathbb {Z}}_n,p_1^{3}{\mathbb {Z}}_n\}$ and $\{p_2{\mathbb {Z}}_n,p_1p_2{\mathbb {Z}}_n,p_1^{2}p_2{\mathbb {Z}}_n\}$ imply that ${\mathbb {G}}({\mathbb {Z}}_n)$ contains $K_{3,3}$, a contradiction. Therefore $\alpha _1\le 4$. There are three following subcases:

Subcase 1 $s=2$. Since $\alpha _1\le 4$ and $\alpha _2\le 2$, $n\in \{p_1p_2,p_1^{2}p_2,p_1^{3}p_2,p_1^{4}p_2,p_1p_2^{2},p_1^{2}p_2^{2},p_1^{3}p_2^{2},p_1^{4}p_2^{2}\}$. With no loss of generality we may assume that $n\in \{p_1p_2,p_1^{2}p_2,p_1^{3}p_2,p_1^{4}p_2,p_1^{2}p_2^{2},p_1^{3}p_2^{2},p_1^{4}p_2^{2}\}$. It is clear that if $n\in \{p_1p_2,p_1^{2}p_2\}$, then $|V({\mathbb {G}}({\mathbb {Z}}_n))|\le 4$ and so ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $n=p_1^{3}p_2$, then $|V({\mathbb {G}}({\mathbb {Z}}_n))|=6$. Clearly, $N(p_1^{3}{\mathbb {Z}}_n)=\{p_2{\mathbb {Z}}_n\}$ and $N(p_1^{2}p_2{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n\}$. This implies that ${\mathbb {G}}({\mathbb {Z}}_n)$ contains no subdivision of either $K_5$ or $K_{3,3}$. Therefore by Theorem 1, ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $n=p_1^{4}p_2$, then $|V({\mathbb {G}}({\mathbb {Z}}_n))|=8$. Clearly, $N(p_1^{4}{\mathbb {Z}}_n)=\{p_2{\mathbb {Z}}_n\}$, $N(p_1^{3}p_2{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n\}$ and $N(p_1^{2}p_2{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n,p_1^{2}{\mathbb {Z}}_n\}$. Hence ${\mathbb {G}}({\mathbb {Z}}_n)$ contains no subdivision of either $K_5$ or $K_{3,3}$. Therefore by Theorem 1, ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $n=p_1^{2}p_2^{2}$, then $|V({\mathbb {G}}({\mathbb {Z}}_n))|=7$. Clearly, $N(p_1^{2}p_2{\mathbb {Z}}_n)=\{p_2{\mathbb {Z}}_n\}$, $N(p_1p_2^{2}{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n\}$ and $N(p_1p_2{\mathbb {Z}}_n)=\{p_1{\mathbb {Z}}_n,p_2{\mathbb {Z}}_n\}$. Hence ${\mathbb {G}}({\mathbb {Z}}_n)$ contains no subdivision of either $K_5$ or $K_{3,3}$. Therefore by Theorem 1, ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $n=n=p_1^{3}p_2^{2}$, then by Fig.1, we find that ${\mathbb {G}}({\mathbb {Z}}_n)$ is planar. If $n=p_1^{4}p_2^{2}$, then two sets $\{p_1{\mathbb {Z}}_n,p_1^{2}{\mathbb {Z}}_n,p_1^{3}{\mathbb {Z}}_n\}$ and $\{p_2{\mathbb {Z}}_n,p_2^{2}{\mathbb {Z}}_n,p_1p_2{\mathbb {Z}}_n\}$ imply that $K_{3,3}$ is a subgraph of ${\mathbb {G}}({\mathbb {Z}}_n)$, a contradiction.

Subcase 2 $s=3$. If $\alpha _1\ge 3$, then two sets $\{p_1{\mathbb {Z}}_n,p_1^{2}{\mathbb {Z}}_n,p_1^{3}{\mathbb {Z}}_n\}$ and $\{p_2{\mathbb {Z}}_n,p_3{\mathbb {Z}}_n,p_2p_3{\mathbb {Z}}_n\}$ imply that $K_{3,3}$ is a subgraph of ${\mathbb {G}}({\mathbb {Z}}_n)$, a contradiction. Hence $\alpha _1\le 2$ and $n\in \{p_1p_2p_3,p_1^{2}p_2p_3,p_1p_2^{2}p_3,p_1p_2p_3^{2},p_1^{2}p_2^{2}p_3,$ $p_1^{2}p_2p_3^{2},p_1p_2^{2}p_3^{2},p_1^{2}p_2^{2}p_3^{2}\}$. With no loss of generality we may assume that $n\in \{p_1p_2p_3,p_1^{2}p_2p_3,p_1^{2}p_2^{2}p_3,p_1^{2}p_2^{2}p_3^{2}\}$. If $n=p_1p_2p_3$, then ${\rm deg}(p_1p_2{\mathbb {Z}}_n)={\rm deg}(p_1p_3{\mathbb {Z}}_n)={\rm deg}(p_2p_3{\mathbb {Z}}_n)=1$ and ${\rm deg}(p_1{\mathbb {Z}}_n)={\rm deg}(p_2{\mathbb {Z}}_n)={\rm deg}(p_3{\mathbb {Z}}_n)=2$. This yields that ${\mathbb {G}}({\mathbb {Z}}_n)$ is a planar graph. If $n=p_1^{2}p_2p_3$, then by Fig.2, we conclude that ${\mathbb {G}}({\mathbb {Z}}_n)$ is planar. If $n\in \{p_1^{2}p_2^{2}p_3,p_1^{2}p_2^{2}p_3^{2}\}$, then two sets $\{p_1{\mathbb {Z}}_n,p_2{\mathbb {Z}}_n,p_1p_2{\mathbb {Z}}_n\}$ and $\{p_3{\mathbb {Z}}_n,p_2p_3{\mathbb {Z}}_n,p_1p_2p_3{\mathbb {Z}}_n\}$ imply that $K_{3,3}$ is a subgraph of ${\mathbb {G}}({\mathbb {Z}}_n)$, a contradiction.

Subcase 3 $s=4$. If $\alpha _2,\alpha _3\ge 2$, then $\{p_1{\mathbb {Z}}_n,p_1p_2{\mathbb {Z}}_n,p_1p_3{\mathbb {Z}}_n,p_1p_4{\mathbb {Z}}_n,p_1p_5{\mathbb {Z}}_n\}$ is a clique, a contradiction. Similarly, we conclude that at most one of the element of the set $\{\alpha _2,\alpha _3,\alpha _4\}$ can be more than 2. Therefore with no loss of generality we may assume that $\alpha _3=\alpha _4=1$. If $\alpha _1\ge 3$ and $\alpha _2=1$, then $\{p_1{\mathbb {Z}}_n,p_2{\mathbb {Z}}_n,p_3{\mathbb {Z}}_n,p_4{\mathbb {Z}}_n,p_1^{2}{\mathbb {Z}}_n\}$ is a clique, a contradiction. Otherwise, two sets $\{p_1{\mathbb {Z}}_n,p_2{\mathbb {Z}}_n,p_1p_2{\mathbb {Z}}_n\}$ and $\{p_3{\mathbb {Z}}_n,p_4{\mathbb {Z}}_n,p_3p_4{\mathbb {Z}}_n\}$ imply that $K_{3,3}$ is a subgraph of ${\mathbb {G}}({\mathbb {Z}}_n)$, a contradiction. $\square$