Introduction

The aim of this study is to present a high-order computational method for solving special cases of singular Volterra integral equations of the first and second kinds, namely Abel’s integral equations, defined by

$$\begin{aligned} f(x)=\int _0^x |x-t|^{-\alpha }y(t) \mathrm{d}t, \end{aligned}$$
(1)

and

$$\begin{aligned} y(x)=f(x)+\int _0^x |x-t|^{-\alpha }y(t) \mathrm{d}t, \end{aligned}$$
(2)
$$\begin{aligned} 0< \alpha <1,\quad 0 \le x \le T, \end{aligned}$$

where \(f(x)\in C[0,T]\) is the known function and y(x) is the unknown function that to be determined, and T is a positive constant.

Abel’s equation is one of the integral equations derived directly from a concrete problem of mechanics or physics (without passing through a differential equation). Historically, Abel’s problem is the first one that led to the study of integral equations. The generalized Abel’s integral equations on a finite segment appeared in the paper of Zeilon [15] for the first time.

A comprehensive reference on Abel-type equations, including an extensive list of applications, can be found in [8, 9].

The construction of high-order methods for the equations is, however, not an easy task because of the singularity in the weakly singular kernel. In fact, in this case, the solution y is generally not differentiable at the endpoints of the interval [3], and due to this, to the best of the authors’ knowledge, the best convergence rate ever achieved remains only at polynomial order. For example, if we set uniform meshes with \(n+1\) grid points and apply the spline method of order m, then the convergence rate is only \(O(n^{-2P})\) at most (see [4, 12]), and it cannot be improved by increasing m. One way of remedying this is to introduce graded meshes [13]. By doing so, the rate is improved to \(O(n^{-m})\), which now depends on m, but still at polynomial order. Rashit Ishik [10] used Bernstein series solution for solving linear integro-differential equations with weakly singular kernels. In [5] and [6], wavelets method was applied for solution of nonlinear fractional integro-differential equations in a large interval and systems of nonlinear singular fractional Volterra integro-differential equations. Authors of [11] applied fractional calculus for solving Abel integral equations. The expansions approach for solving cauchy integral equation of the first kind is discussed in [14].

In this paper, we use the Chebyshev polynomials operational matrices via Galerkin method for solving weakly singular integral equations. Our method consists of reducing the given weakly singular integral equation to a set of algebraic system by expanding the unknown function by Chebyshev polynomials of the first kind. Galerkin method is utilized to solve the obtained system.

The structure of this paper is arranged as follows. The main problem and brief history of some presented methods are expressed in Sect. 1. In Sect. 2, we present some necessary definitions and mathematical preliminaries of the fractional calculus theory in the sense of Riemann–Liouville. Section 3 is devoted to introducing Chebyshev polynomials, properties and some operational matrices of these functions. In Sect. 4, Chebyshev polynomials are applied as testing and weighting functions of Galerkin method for efficient solution of Eq. 1. In Sect. 5, we report our numerical founds and compare with other methods in solving these integral equations, and Sect. 6 contains our conclusion.

Some preliminaries in fractional calculus

In this section, we briefly present some definitions and results in fractional calculus for our subsequent discussion. The fractional calculus is the name for the theory of integrals and derivatives of arbitrary order, which unifies and generalizes the notions of integer-order differentiation and n-fold integration [7]. There are various definitions of fractional integration and differentiation, such as Grunwald–Letnikov, and Caputo and Riemann–Liouville’s definitions. In this study, fractional calculus in the sense of Riemann–Liouville is considered.

Definition 1

Let f be a real function on [a, b] and \(0<\alpha <1\). Then, the left and right Riemann–Liouville fractional integral operators of order \(\alpha\) for the function f are defined, respectively, as

$$\begin{aligned}&_{a}I_{x}^{\alpha }f(x)=\frac{1}{\Gamma (\alpha )} \int _{a}^{x}(x-t)^{\alpha -1}f(t)\mathrm{d}t,\\&_{x}I_{b}^{\alpha }f(x)=\frac{1}{\Gamma (\alpha )} \int _{x}^{b}(t-x)^{\alpha -1}f(t)\mathrm{d}t,\\&x \in [a,b],\quad \alpha >0. \end{aligned}$$

Definition 2

For \(f\in C[a,b]\), the left and right Riemann–Liouville fractional derivatives are defined, respectively, as

$$\begin{aligned}&_{a}D_{x}^{\alpha }f(x)=\frac{1}{\Gamma (1-\alpha )} \frac{\mathrm{d}}{\mathrm{d}t}\int _{a}^{x}(x-t)^{-\alpha }f(t)\mathrm{d}t,\\&_{x}D_{b}^{\alpha }f(x)=\frac{1}{\Gamma (1-\alpha )} \frac{\mathrm{d}}{\mathrm{d}t}\int _{x}^{b}(t-x)^{-\alpha }f(t)\mathrm{d}t. \end{aligned}$$

In this study, the left Riemann–Liouville fractional integral operator is utilized to transform singular integral equation to some algebraic system. Therefore, for abbreviation, the mentioned operator is denoted by \(I^{\alpha }\).

Theorem 1

The operator \(I^{\alpha }\) (stand for left and right Riemann–Liouville fractional integral operator) satisfies the following properties:

$$\begin{aligned}&(1) \quad I^{\alpha }\left( \sum _{i=o}^{n}\mu _{i}f_{i}(x)\right) =\sum _{i=0}^{n}\mu _{i} I^{\alpha }f_{i}(x),\\&(2) \quad I^{\alpha }x^{\beta }=\frac{\Gamma (\beta +1)}{\Gamma (\beta +\alpha +1)}x^{\alpha +\beta },\quad \beta >-1. \end{aligned}$$

Proof

We prove the proposition for left Riemann–Liouville fractional integral operator and the proof for right Riemann–Liouville fractional integral operator can be done similarly. For the part (1), we have

$$\begin{aligned} I^{\alpha }\left( \sum _{i=o}^{n}\mu _{i}f_{i}(x)\right)= & {} \frac{1}{\Gamma (\alpha )}\int _{a}^{x}(x-t)^{\alpha -1} \left( \sum _{i=o}^{n}\mu _{i}f_{i}(t)\right) \mathrm{d}t\\= & {} \frac{1}{\Gamma (\alpha )}\sum _{i=o}^{n}\mu _{i}\left( \int _{a}^{x}(x-t)^{\alpha -1}f_{i}(t)\mathrm{d}t\right) \\= & {} \sum _{i=o}^{n}\mu _{i} \frac{1}{\Gamma (\alpha )}\left( \int _{a}^{x}(x-t)^{\alpha -1}f_{i}(t)\mathrm{d}t\right) \\= & {} \sum _{i=0}^{n}\mu _{i} I^{\alpha }f_{i}(x). \end{aligned}$$

In addition, for part (2), we have

$$\begin{aligned} I^{\alpha }x^{\beta }=\frac{1}{\Gamma (\alpha )} \int _{a}^{x}(x-t)^{\alpha -1}t^{\beta }\mathrm{d}t, \end{aligned}$$

by changing the variable \(t=rx\), we get

$$\begin{aligned} I^{\alpha }x^{\beta }=\frac{1}{\Gamma (\alpha )}\int _{0}^{1} x^{\alpha -1}(1-r)^{\alpha -1}r^{\beta }x^{\beta }x\mathrm{d}r, \end{aligned}$$

now, using the formulae of the beta function, we have

$$\begin{aligned} I^{\alpha }x^{\beta }=\frac{x^{\alpha +\beta }}{\Gamma (\alpha )} \int _{0}^{1}(1-r)^{\alpha -1}r^{\beta }\mathrm{d}r=\frac{x^{\alpha +\beta }}{\Gamma (\alpha )}B(\alpha ,\beta +1). \end{aligned}$$

On the other hand, we know that the beta function can be written in terms of the Gamma function as follows:

$$\begin{aligned} B(a,b)=\frac{\Gamma (a)\Gamma (b)}{\Gamma (a+b)}, \end{aligned}$$

so we have

$$\begin{aligned} I^{\alpha }x^{\beta }=\frac{\Gamma (\beta +1)}{\Gamma (\alpha +\beta +1)} x^{\alpha +\beta }. \end{aligned}$$

\(\square\)

Chebyshev polynomials

In this section, a brief summary of orthogonal Chebyshev polynomials is expressed.

Definition 3

The nth degree of Chebyshev polynomials is defined by

$$\begin{aligned} T_{n}(t)=\cos (n\theta ), \quad 0 \le \theta \le \pi , \end{aligned}$$

where \(t=\cos (\theta )\). The roots of Chebyshev polynomial of degree \(n+1\) can be obtained by

$$\begin{aligned} t_{i}=\cos \left( \frac{(2i+1)\pi }{2n+1} \right) ,\quad i=0,\ldots ,n. \end{aligned}$$

In addition, the following successive relation holds for Chebyshev polynomials:

$$\begin{aligned} T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x), \end{aligned}$$

where

$$\begin{aligned} T_{0}(x)=1,\quad T_{1}(x)=x. \end{aligned}$$

Chebyshev polynomials are orthogonal with respect to the weight function \(w(x)=\frac{1}{\sqrt{1-x^{2}}}\) in the interval \([-1,1]\), that is

$$\begin{aligned} \int _{-1}^{1}\frac{T_{n}(x)T_{m}(x)}{\sqrt{1-x^{2}}}\mathrm{d}x=\left\{ \begin{array}{ll} 0\ ;&{}\quad m\ne n,\\ \frac{\pi }{2}\ ;&{}\quad m=n \ne 0\\ \pi \ ;&{}\quad m=n=0. \end{array}\right. \end{aligned}$$

Matrix form

We can represent Chebyshev polynomials in the matrix form. Put

$$\begin{aligned} \mathbf T (x)=\left( T_{0}(x), T_{1}(x),\ldots , T_{n}(x) \right) ^{T},\quad X=\left( 1, x,\ldots , x^{n}\right) ^{T}, \end{aligned}$$
(3)

then we can write

$$\begin{aligned} \mathbf T (x)=T X, \end{aligned}$$
(4)

where T is a \((n+1)\times (n+1)\) matrix defined by

$$\begin{aligned} T=\left( \begin{array}{llllllll} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad ...&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad ...&{}\quad 0\\ -1&{}\quad t_{21}&{}\quad 2&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad ...&{}\quad 0\\ 0&{}\quad t_{31} &{}\quad t_{32} &{}\quad 2^{2}&{}\quad 0&{}\quad 0&{}\quad ...&{}\quad 0\\ 1&{}\quad t_{41} &{}\quad t_{42} &{}\quad t_{43} &{}\quad 2^{3}&{}\quad 0&{}\quad ...&{}\quad 0\\ \vdots &{}\quad &{}\quad &{}\quad \vdots &{}\quad &{}\quad &{}\quad \ddots &{}\quad \\ \cos (\frac{n \pi }{2}) &{}\quad t_{n1} &{}\quad t_{n2} &{}\quad t_{n3} &{}\quad t_{n4} &{}\quad \cdots &{}\quad &{}\quad 2^{n-1} \\ \end{array}\right) , \end{aligned}$$
(5)

and the first element of each row is \(t_{i0}=\cos (\frac{i \pi }{2})\), \(i=0,\ldots ,n\). In addition, other elements are defined by \(t_{i,j}=sign (t_{i-1,j-1})(2\vert t_{i-1,j-1}\vert +\vert t_{i-2,j}\vert .\) The Chebyshev polynomials are defined in the \([-1,1]\), but the integration interval of Eqs. (1) and (2) is [0, T]. To transform the interval \([-1,1]\) to [0, T], we apply the \((n+1)\times (n+1)\) shift matrix R, which is defined by

$$\begin{aligned} R_{ij}=\left\{ \begin{array}{ll} \left( \begin{array}{c} i\\ j \end{array}\right) \gamma _{1}^{i-j}\gamma _{2}^{j}\ ;&{}\quad j=0,1,\ldots ,i,\quad i=0,1,\ldots ,n,\\ 0 ;&{} i<j, \end{array}\right. \end{aligned}$$
(6)

and \(\gamma _{1}=-1,\gamma _{2}=\frac{2}{T}.\) Thus, the shifted Chebyshev polynomial matrix is written as WX, where \(W=T R\).

Function approximation

A function \(y(x) \in L_{2}[0,T]\), can be expressed in terms of the shifted Chebyshev polynomials as [2]

$$\begin{aligned} y(x)=\sum _{j=0}^{\infty }c_{j}\varphi _{j}(x)\mathrm{d}x=C^{T}\cdot W \cdot X, \end{aligned}$$
(7)

where \(\varphi _{j}\) is the shifted Chebyshev polynomial of degree j. The coefficients \(c_{j}\) are given by

$$\begin{aligned} c_{0}=\frac{1}{\pi }\int _{0}^{T}\frac{f(x)\varphi _{0}(x)}{\sqrt{\frac{4x}{T}-\frac{4x^{2}}{T^{2}}}}\mathrm{d}x, \end{aligned}$$

and

$$\begin{aligned} c_{j}=\frac{2}{\pi }\int _{0}^{T}\frac{f(x)\varphi _{j}(x)}{\sqrt{\frac{4x}{T}-\frac{4x^{2}}{T^{2}}}}\mathrm{d}x,\quad j=1,2,\ldots . \end{aligned}$$

Operational matrix of fractional Integration

The fractional integral of Chebyshev polynomials can be defined by

$$\begin{aligned} I^{\alpha }(T X)=\left( A*T\right) X^{(\alpha )}, \end{aligned}$$
(8)

where

$$\begin{aligned} X^{(\alpha )}=x^{\alpha }\cdot X=\left[ x^{\alpha } \ x^{\alpha +1} \ \ldots \ x^{\alpha +n}\right] ^{T}, \end{aligned}$$

and \(*\) is point by point product and A is \((n+1)\times (n+1)\) lower triangular matrix defined by

$$\begin{aligned} A_{ij}=\left\{ \begin{array}{cc} \frac{\Gamma (j+1)}{\Gamma (\alpha +j+1)},\ &{}\quad i \ge j,\\ 0,\ &{}\quad i<j. \end{array}\right. \end{aligned}$$

In addition, for each function g(x), approximated by shifted Chebyshev functions (\(g(x)=D^{T}WX\)), the fractional integral can be written as

$$\begin{aligned} I^{\alpha }(g(x))=I^{\alpha }(D^{T}WX)=D^{T}\left( A*W\right) X^{(\alpha )}. \end{aligned}$$
(9)

Numerical implementation

In this section, the shifted Chebyshev polynomials are applied for solving singular integral Eqs. (1) and (2). For this purpose, initially, the singular integral equation is transformed to nonsingular integral equation, utilizing Riemann–Liouville calculus.

Putting \(-\alpha =\beta -1\) in the integral part of the Eqs. (1) and (2), we get

$$\begin{aligned} \int _{0}^{x}(x-t)^{-\alpha }y(t)\mathrm{d}t=\Gamma (\beta ) \left( \frac{1}{\Gamma (\beta )}\int _{0}^{x}(x-t)^{\beta -1}y(t)\mathrm{d}t\right) , \end{aligned}$$

by definition of Riemann–Liouville fractional integral operator, the current relation can be rewritten as

$$\begin{aligned} \int _{0}^{x}(x-t)^{-\alpha }y(t)\mathrm{d}t=\Gamma (\beta )I^{\beta }y(x). \end{aligned}$$
(10)

Now, the unknown function y(x) is approximated by shifted Chebyshev polynomials as

$$\begin{aligned} y(x)\simeq y_{n}(x)=C^{T}WX, \end{aligned}$$
(11)

where \(C^{T}\) is the unknown vector, that to be determined. In the following, we describe the method in detail for the first and second kinds.

The first kind

Consider the weakly singular Volterra integral equation of the first kind (1), according to Eq. (10), we have

$$\begin{aligned} f(x)=\Gamma (\beta )I^{\beta }y(x), \end{aligned}$$
(12)

substituting Eqs. (11) and (8) in (12), we can get

$$\begin{aligned} f(x)=\Gamma (\beta ) C^{T}(A*W)X^{\beta }. \end{aligned}$$
(13)

Therefore, singular integral equation (1) is transformed to the above algebraic system. For solving this system, Galerkin procedure is utilized via shifted Chebyshev polynomials. Put \(\Gamma (\beta ) (A*W)=\Lambda\) and suppose \(\varphi _{i}(x)\) be the shifted Chebyshev polynomial of degree i, which can be written as

$$\begin{aligned} \varphi _{i}(x)=W_{i}X,\quad i=0,1,\ldots ,n, \end{aligned}$$

where \(W_{i}\) is the ith row of the matrix W. Multiplying Eq. (13) by \(\varphi _{i}(x)\), we get

$$\begin{aligned} C^{T}\Lambda X^{\beta }W_{i}X=f(x)W_{i}X,\quad i=0,1,\ldots ,n. \end{aligned}$$
(14)

Putting

$$\begin{aligned} {\tilde{X}}=\left( \begin{array}{ccccc} 1 &{}\quad x &{}\quad x^{2} &{}\quad ...&{}\quad x^{n} \\ x &{}\quad x^{2} &{}\quad x^{3} &{}\quad ...&{}\quad x^{n+1} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ x^{n}&{}\quad x^{n+1} &{}\quad x^{n+2} &{}\quad ...&{}\quad x^{2n} \end{array}\right) , \end{aligned}$$
(15)

and

$$\begin{aligned} {\tilde{X}}^{\beta }=x^{\beta } {\tilde{X}}, \end{aligned}$$

we get

$$\begin{aligned} C^{T}\Lambda {\tilde{X}}^{\beta }W_{i}^{T}=f(x)W_{i}X, \quad i=0,1,\ldots ,n . \end{aligned}$$
(16)

by integrating current equations from 0 to T, we have

$$\begin{aligned} W_{i}P^{\beta }\Lambda ^{T}C=W_{i}P_{x}, \end{aligned}$$
(17)

where \(P_{x}\) and \(P^{\beta }\) are related integration operational matrix, defined by

$$\begin{aligned} P_{x}=\int _{0}^{T}X f(x)\mathrm{d}x, \quad (P_{x})_{i1}=\int _{0}^{T}x^{i} f(x)\mathrm{d}x, \end{aligned}$$
$$\begin{aligned} P^{\beta }=\int _{0}^{T}{\tilde{X}}^{\beta }\mathrm{d}x, \quad (P^{\beta })_{ij}=\frac{T^{i+j+\beta +1}}{i+j+\beta +1}, \end{aligned}$$
$$\begin{aligned} i=0,\ldots ,n,\quad j=0,\ldots , n. \end{aligned}$$

Considering Eq. (17) for \(i=0,\ldots ,n\), we get

$$\begin{aligned} WP^{\beta }\Lambda ^{T}C=WP_{x}, \end{aligned}$$
(18)

a system of \(n+1\) equations and \(n+1\) unknowns that can be solved easily.

The second kind

Similarly, for the second kind singular integral equation (2), we have

$$\begin{aligned} y(x)=f(x)+\int _{0}^{x}(x-t)^{-\alpha }y(t)\mathrm{d}t= f(x)+\Gamma (\beta ) I^{\beta }(C^{T}WX), \end{aligned}$$
(19)

so Eq. (19) can be written as

$$\begin{aligned} C^{T}WX-\Gamma (\beta ) C^{T}\left( A*W\right) X^{\beta }=f(x). \end{aligned}$$
(20)

Multiplying Eq. (20) by \(\varphi _{i}(x)\) and integrating from 0 to T, we can rewrite the current equation in the following form:

$$\begin{aligned} \left( WPW^{T}- WP^{\beta }\Lambda ^{T}\right) C=WPf(x), \end{aligned}$$
(21)

where

$$\begin{aligned} P=\int _{0}^{T}{\tilde{X}}\mathrm{d}x, \quad P_{ij}=\frac{T^{i+j+1}}{i+j+1}. \end{aligned}$$

Eq. (21) is a system of \(n+1\) equations and \(n+1\) unknowns that can be solved easily.

Illustrative examples

In this section, for showing the accuracy and efficiency of the described method, we present some examples. Moreover, the condition number of the operational matrices, defined by

$$\begin{aligned} cond(A)=\Vert A\Vert .\Vert A^{-1}\Vert , \end{aligned}$$
(22)

are given in corresponding tables. In Examples 1 and 2 singular Volterra integral equation of the second kind, and in examples 3 and 4, singular Volterra integral equation of the first kind is solved. As we know, numerically solving the first kind integral equations is so difficult, because their operational matrices have large condition numbers and in the other words are bad-conditioned, while, as seen in Tables 2 and 3, the maximum condition number of the problem is 64. The abbreviation c.n.m in the tables denotes the condition number of the operational matrices.

Example 1

Consider the following singular integral equation of the second kind:

$$\begin{aligned} y(x)+\int _{0}^{x}\frac{y(t)}{(x-t)^{1/2}}\mathrm{d}t=x^{2}+\frac{16}{15}x^{5/2}, \end{aligned}$$

with the exact solution \(y(x)=x^2\). The unknown coefficients for \(c_{i}\) are obtained through the method explained in Sect. 4 for \(N=4\).

$$\begin{aligned} c_{0}=\frac{3}{8},\quad c_{1}=\frac{1}{2} \quad c_{2}=\frac{1}{8} \quad c_{3}=0\quad c_{4}=0. \end{aligned}$$

The function y(x) is a polynomial of degree 2 and the least approximation level for Chebyshev polynomials, in this study, is \(N=4\). Therefore, the approximated solution through the presented method is the same as the exact solution, that is \(y_{4}(x)=x^{2}\).

Example 2

Consider the following singular integral equation:

$$\begin{aligned} y(x)-\int _{0}^{x}\frac{y(t)}{(x-t)^{1/2}}\mathrm{d}t=x^{3/2}-\frac{3}{8}\pi x^{2}, \end{aligned}$$

with the exact solution \(y(x)=x^{\frac{3}{2}}\). The solution for y(x) is obtained by the method in Sect. 4 for \(N=4, 8\) and 12. The unknown coefficients for \(c_{i}\) are obtained through the method explained in Sect. 4 for \(N=4\):

$$\begin{aligned} c_{0}=0.4242, \quad c_{1}=0.5097 \quad c_{2}=0.0724 \quad c_{3}=-0.0076 \quad c_{4}=0.0018, \end{aligned}$$

and the approximate solution for \(N=4\) is calculated as

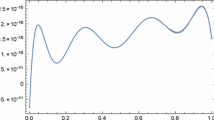
$$\begin{aligned} y_{4}(x)=0.2253 x^{4}+0.6927 x^{3}+1.2240 x^{2}+0.2477 x-0.0038. \end{aligned}$$

In Table 1, we have presented exact and approximated solutions of Example 2 in some arbitrary points. In addition, the last line of Table 1 shows the condition number of operational matrices. The errors of approximate solutions in the levels \(N=4, 8\), and 12 are shown in Fig. 1.

Fig. 1
figure 1

Graph of estimated solution of Example 2 for \(N=4,8\) and 12

Full size image
Table 1 Exact and approximate solutions of Example 2
Full size table

Example 3

Consider the following singular integral equation of the first kind:

$$\begin{aligned} \int _{0}^{x}\frac{y(t)}{(x-t)^{1/3}}\mathrm{d}t=x^{7/6}, \end{aligned}$$

with the exact solution \(y(x)=\frac{7\Gamma (1/6)}{18\Gamma (2/3)}\sqrt{\frac{x}{\pi }}\). The solution for y(x) is obtained by the method in Sect. 4 for \(N=4, 8\), and 12. The unknown coefficients for \(c_{i}\) are obtained through the method explained in Sect. 4 for \(N=4\):

$$\begin{aligned} c_{0}=0.5739, \quad c_{1}=0.3719 \quad c_{2}=-0.0768 \quad c_{3}=0.0218 \quad c_{4}=-0.0172, \end{aligned}$$

and the approximate solution for \(N=4\) is calculated as

$$\begin{aligned} y_{4}(x)=-2.1983 x^{4}+5.0939 x^{3}-4.4082 x^{2}+2.2999 x+0.0862. \end{aligned}$$

In Table 2, we present exact and approximate solutions of Example 3 in some arbitrary points and compare them by the results of [1] for \(n=20\). In addition, the last line of Table 2 shows the condition number of operational matrices. Figure 2 illustrates the error of approximate solutions in the levels \(N=4, 8\), and 12.

Fig. 2
figure 2

Graph of estimated solution of Example 3 for \(N=4,8\) and 12

Full size image
Table 2 Exact and approximate solutions of Example 3
Full size table

Example 4

Consider the following singular integral equation of the first kind:

$$\begin{aligned} \int _{0}^{x}\frac{y(t)}{(x-t)^{2/3}}\mathrm{d}t=\pi x, \end{aligned}$$

with the exact solution \(y(x)=\frac{3\sqrt{3}}{4}x^{2/3}\). The solution for y(x) is obtained through the method in Sect. 4 for \(N=4, 8\), and 12. The unknown coefficients for \(c_{i}\) are obtained through the method explained in Sect. 4 for \(N=4\).

$$\begin{aligned} c_{0}=07539, \quad c_{1}=0.5968 \quad c_{2}=-0.0738 \quad c_{3}=0.0212 \quad c_{4}=-0.0118, \end{aligned}$$

and the approximate solution for \(N=4\) is calculated as

$$\begin{aligned} y_{4}(x)=-1.5114 x^{4}+3.7014 x^{3}-3.4978 x^{2}+2.5439 x+0.0502. \end{aligned}$$

In Table 3, exact and approximated solutions of Example 4 in some arbitrary points are given. The condition number of operational matrices for \(N=4, 8\), and 12 are calculated by Eq. 22, and is shown in the last row of Table 3. Figure 3 is helpful in geometric understanding the errors of approximated solutions in the levels \(N=4, 8\), and 12.

Fig. 3
figure 3

Graph of estimated solution of Example 4 for \(N=4,8\) and 12

Full size image
Table 3 Exact and approximate solutions of Example 4
Full size table

Conclusions

In this study, a numerical approach based on Chebyshev polynomials operational matrices was developed to approximate the solution of the weakly singular Volterra integral equations of the first and second kinds. Applying fractional derivative of these polynomials, we have transformed the singular integral equations to some linear algebraic system. The numerical results obtained support the validity and efficiency of the proposed method. It is noteworthy that when the solution of equation is in power series form, the method evaluates the exact solution, such as Example 1. In addition, as can be seen, the operational matrices of first kind integral equations have relatively low condition numbers. Thus, the corresponding matrices are well posed.