Introduction

The study of systems governed by ordinary differential equation with period coefficients is of basic importance in many branches such as mathematics, physics, chemistry, biology, mechanics and finance, such systems are known as Floquet systems [1, 2]. The Floquet systems are defined with the n × n matrix function A as \(x'=A(t)x\), where the components in matrix A are continuous and periodic function with smallest positive period w, that is, \(A(t+w)=A(t)\) for all ts. Although the coefficient matrix in \(x'=A(t)x\) is periodic, in general solutions they are not considered as periodic. The idea of Floquet systems has been stated by Gaston Floquet in the early 1880s, and later he established his celebrated theorem on the structure of solutions of periodic differential equations [3]. In this paper, we first focus our attention on fractional Floquet system, and then we consider the stability analysis for this class system.

The fractional order calculus establishes the branch of mathematics dealing with differentiation and integration under an arbitrary order of the operation, that is the order can be any real or even complex number, not only the integer one. Although the history of fractional calculus is more than three centuries old, it only has received much attention and interest in the past 20 years; the reader may refer to [4–6] for the theory and applications of fractional calculus. The generalization of dynamical equations using fractional derivatives proved to be useful and more accurate in mathematical modeling related to many interdisciplinary areas. Applications of fractional order differential equations include: electrochemistry [7], porous media [8] and so on [9–11]. It is worth noting that recently much attention has been paid to the distributed-order differential equations and their applications in engineering fields that both integer-order systems and fractional order systems are special cases of distributed-order systems. The reader may refer to [12–14]. The analytic results on the existence and uniqueness of solutions to the fractional differential equations have been investigated by many authors [5, 6].

Preliminaries and notations

Basic definitions

We give some basic definitions and properties of the fractional calculus theory used in this work.

Definition 1

Let \(f:{\mathbb R} \rightarrow {\mathbb R}\), \(t\rightarrow f(t)\) denote a continuous (but not necessarily differentiable) function and let partition \(h>0\) in the interval [0, 1]. The Jumarie’Derivative is defined through the fractional difference [15]:

$$\begin{aligned} \Delta ^{\alpha } f(t)=(\mathrm{FW}-1)^{\alpha } f(t)=\sum _{k=0}^{\infty }(-1)^{k} \left( \begin{array}{c} {\alpha } \\ {k} \end{array}\right) f[t+(\alpha -k)h], \end{aligned}$$
(1)

where FW \(f(t)=f(t+h)\). Then the fractional derivative is defined as the following limit

$$\begin{aligned} f^{(\alpha )} (t)=D_{t}^{\alpha } f(t)=\frac{\mathrm{d}^{\alpha } f(t)}{\mathrm{d}t^{\alpha }} =\mathop {\lim }\limits _{h\rightarrow 0} \frac{\Delta ^{\alpha } [f(t)-f(0)]}{h^{\alpha }}. \end{aligned}$$
(2)

This definition is close to the standard definition of derivatives, and as a direct result, the αth derivative of a constant \(0\,<\, \alpha\, \le\, 1\) is zero.

Definition 2

The Riemann–Liouville fractional integral operator of order \(\alpha >0\) is defined as [16]:

$$\begin{aligned} I_{t}^{\alpha } f(t)=\frac{1}{\Gamma (\alpha )} \int _{0}^{t}(t-\varepsilon )^{\alpha -1} f(\varepsilon )\mathrm{d}\varepsilon ,\quad \alpha >0. \end{aligned}$$
(3)

Definition 3

The modified Riemann–Liouville derivative is defined as [16]:

$$\begin{aligned} D_{t}^{\alpha } f(t)=\left( f^{(\alpha -1)} (t)\right) '=\frac{1}{\Gamma (1-\alpha )} \frac{\mathrm{d}}{\mathrm{d}t} \int _{0}^{t}(t-\varepsilon )^{-\alpha } (f(\varepsilon )-f(0))\mathrm{d}\varepsilon ,\quad \quad 0<\alpha \le 1, \end{aligned}$$
(4)

and

$$\begin{aligned} D_{t}^{\alpha } f(t)=\left( f^{(\alpha -n)} (t)\right) ^{(n)} ,\quad n\le \alpha <n+1,\; \; n\ge 1. \end{aligned}$$

The proposed modified Riemann–Liouville derivative as shown in Eq. (4) is strictly equivalent to Eq. (2).

Definition 4

Fractional derivative of compounded functions is defined as [16]:

$$\begin{aligned} d^{\alpha } f \approx \Gamma (1+\alpha )\mathrm{d}f,\quad 0<\alpha < 1. \end{aligned}$$
(5)

Definition 5

The integral with respect to \((\mathrm{d}t)^{\alpha }\) is defined as the solution of fractional differential equation [17]:

$$\begin{aligned} \mathrm{d}y=f(t)(\mathrm{d}t)^{\alpha } ,\quad \quad t\ge 0,\quad y(0)=0,\quad \quad 0<\alpha \le 1. \end{aligned}$$
(6)

Lemma 1

Let f(t) denotes a continuous function then the solution of the Eq. (6) is defined as [17]:

$$\begin{aligned} y=\int _{0}^{t}f(\varepsilon )(\mathrm{d}\varepsilon )^{\alpha } =\alpha \int _{0}^{t}(t-\varepsilon )^{\alpha -1} f(\varepsilon )\mathrm{d}\varepsilon ,\quad \quad 0<\alpha \le 1. \end{aligned}$$
(7)

Definition 6

Function f(t) is αth differentiable then the following equalities holds:

$$\begin{aligned} f^{(\alpha )} (t)=\mathop {\lim }\limits _{h\rightarrow 0} \frac{\Delta ^{\alpha } f(t)}{h^{\alpha } } =\Gamma (1+\alpha )\mathop {\lim }\limits _{h\rightarrow 0} \frac{\Delta f(t)}{h^{\alpha } } ,\quad \quad \quad 0<\alpha \le 1. \end{aligned}$$
(8)

Mittag-Leffler function

The Mittag-Leffler function which plays a very important role in the fractional differential equations was in fact introduced by Mittag-Leffler in 1903 [18]. The Mittag-Leffler function \(E_{\alpha }(t)\) is defined by the power series:

$$\begin{aligned} E_{\alpha } (t)=\sum _{n=0}^{\infty }\frac{t^{n} }{\Gamma (n\alpha +1)} ,\quad \quad \quad \alpha >0, \end{aligned}$$
(9)

which

$$\begin{aligned} D_{t}^{\alpha } E_{\alpha } (\lambda t^{\alpha } )=\lambda E_{\alpha } (\lambda t^{\alpha } ). \end{aligned}$$
(10)

As further result of the above formula

$$\begin{aligned} E_{\alpha } (\lambda t^{\alpha } )E_{\alpha } (\lambda (\pm s)^{\alpha } )\approx E_{\alpha } (\lambda (t\pm s)^{\alpha } ),\quad \quad \lambda \in \mathbb {C}. \end{aligned}$$
(11)

The matrix extension of the mentioned Mittag-Liffler function for \(A\in M_{m}\) is defined as in the following representation:

$$\begin{aligned} E_{\alpha } (At^{\alpha } )=\sum _{n=0}^{\infty }\frac{A^{n} t^{\alpha n} }{\Gamma (n\alpha +1)} ,\quad \quad \quad \alpha >0. \end{aligned}$$
(12)

If \(A,B\in {\mathbb R}^{n\times n}\) and \(\alpha >0\), then it is easy to prove the following nice properties of Mittag-Leffler matrix \(E_{\alpha } (At^{\alpha })\):

  1. (i)

    \(E_{\alpha }^{-1} (At^{\alpha } )\approx E_{\alpha } (-At^{\alpha } ),\)

  2. (ii)

    If P is a non-singular matrix, then \(E_{\alpha } (P^{-1} AP)=P^{-1} E_{\alpha } (A)P\),

  3. (iii)

    \(E_{\alpha } ((A+B)t^{\alpha } )\approx E_{\alpha } (At^{\alpha } )E_{\alpha } (Bt^{\alpha } )\) if and only if \(AB=BA\),

  4. (iv)

    \(E_{\alpha }^{-1} (At^{\alpha } )\approx E_{\alpha } (A(-t)^{\alpha })\).

Corollary 1

[19] If the matrix A is diagonalizable, that is, there exists an invertible matrix T such that

$$\begin{aligned} \Lambda =T^{-1} AT=diag(\lambda _{1} ,\lambda _{2} ,\ldots ,\lambda _{n} ), \end{aligned}$$

then, we have

$$\begin{aligned} E_{\alpha } (At^{\alpha } )=T\; E_{\alpha } (\Lambda t^{\alpha } )T^{-1} =T\, \, diag(E_{\alpha } (\lambda _{1} t^{\alpha } ),E_{\alpha } (\lambda _{2} t^{\alpha } ),\ldots ,E_{\alpha } (\lambda _{n} t^{\alpha } ))T^{-1}. \end{aligned}$$

Next, suppose the matrix A is similar to a Jordan canonical form, that is there exists an invertible matrix T such that

$$\begin{aligned} J=T^{-1} AT=diag(J_{1} ,J_{2} ,\ldots ,J_{n} ), \end{aligned}$$

where j i, \(1\, \le \, i\, \le \, r\) has the following form

$$\begin{aligned} \left[ \begin{array}{ccccc} {\lambda _{i} } &{} {1} &{} {0} &{} {\ldots } &{} {0} \\ {0} &{} {\lambda _{i} } &{} {1} &{} {\ddots } &{} {\vdots } \\ {\vdots } &{} {0} &{} {\ddots } &{} {\ddots } &{} {0} \\ {0} &{} {\ddots } &{} {\ddots } &{} {\lambda i} &{} {1} \\ {0} &{} {0} &{} {\ldots } &{} {0} &{} {\lambda _{i} } \end{array}\right] _{n_{i} \times n_{i} } , \end{aligned}$$

and \(\sum _{i=1}^{r}n_{i} =n\). Obviously,

$$\begin{aligned} E_{\alpha } (At^{\alpha } )=Tdiag(E_{\alpha } (J_{1} t^{\alpha } ),E_{\alpha } (J_{2} t^{\alpha } ),\ldots ,E_{\alpha } (J_{r} t^{\alpha } ))T^{-1} , \end{aligned}$$

and

$$\begin{aligned} \begin{array}{l} {E_{\alpha } (J_{i} t^{\alpha } )=\sum\limits_{k=0}^{\infty }\frac{(J_{i} \, t^{\alpha } )^{k} }{\Gamma (\alpha k+1)} =\sum\limits_{k=0}^{\infty }\frac{(t^{\alpha } )^{k} }{\Gamma (\alpha k+1)} \left( \begin{array}{cccc} {\lambda _{i}^{k} } &{} {\mathcal {C}_{k}^{1} \lambda _{i}^{k-1} } &{} {\ldots } &{} {\mathcal {C}_{k}^{n_{i} -1} \lambda _{i}^{k-n_{i} +1} } \\ \\ {0} &{} {\lambda _{i}^{k} } &{} {\ddots } &{} {\vdots } \\ \\ {\vdots } &{} {\ddots } &{} {\ddots } &{} {\mathcal {C}_{k}^{1} \lambda _{i}^{k-1} } \\ \\ {0} &{} {\ldots } &{} {0} &{} {\lambda _{i}^{k} } \end{array}\right) } \\ \\ {\, \,\,\,\, \,\,\,\,\,\,\,\, \, \, \, \, \, \, \, \, \, \, \, \, \, =\left( \begin{array}{cccc} {\sum\limits_{k=0}^{\infty }\frac{(t^{\alpha } )^{k} }{\Gamma (\alpha k+1)} \lambda _{i}^{k} } \, \,&{}\,\, {\sum\limits_{k=0}^{\infty }\frac{(t^{\alpha } )^{k} }{\Gamma (\alpha k+1)} \mathcal {C}_{k}^{1} \lambda _{i}^{k-1} } \,\,&{}\, {\ldots } &{}\,\, {\sum\limits_{k=0}^{\infty }\frac{(t^{\alpha } )^{k} }{\Gamma (\alpha k+1)} \mathcal {C}_{k}^{n_{i} -1} \lambda _{i}^{k-n_{i} +1} } \\ \\ {0} &{} {\sum\limits_{k=0}^{\infty }\frac{(t^{\alpha } )^{k} }{\Gamma (\alpha k+1)} \lambda _{i}^{k} } &{} {\ddots } &{} {\vdots } \\ \\ {\vdots } &{} {\ddots } &{} {\ddots } &{} {\sum\limits_{k=0}^{\infty }\frac{(t^{\alpha } )^{k} }{\Gamma (\alpha k+1)} \mathcal {C}_{k}^{1} \lambda _{i}^{k-1} }\\ \\ {0} &{} {\ldots } &{} {0} &{} {\sum\limits_{k=0}^{\infty }\frac{(t^{\alpha } )^{k} }{\Gamma (\alpha k+1)} \lambda _{i}^{k} } \end{array}\right) } \\ \\ {\quad \quad \, \; \, \, \;\;\;\;\;=\left( \begin{array}{cccc} {E_{\alpha } (\lambda _{i} t^{\alpha } )} &{} {\frac{1}{1!} \frac{\partial }{\partial \lambda _{i} } E_{\alpha } (\lambda _{i} t^{\alpha } )} &{} {\ldots } &{} {\frac{1}{(n_{i} -1)!} \left( \frac{\partial }{\partial \lambda _{i} } \right) ^{n_{i} -1} E_{\alpha } (\lambda _{i} t^{\alpha } )} \\ \\ {0} &{} {E_{\alpha } (\lambda _{i} t^{\alpha } )} &{} {\ddots } &{} {\vdots } \\ \\ {\vdots } &{} {\ddots } &{} {\ddots } &{} {\frac{1}{1!} \frac{\partial }{\partial \lambda _{i} } E_{\alpha } (\lambda _{i} t^{\alpha } )} \\ \\ {0} &{} {\ldots } &{} {0} &{} {E_{\alpha } (\lambda _{i} t^{\alpha } )} \end{array}\right) ,\,} \end{array} \end{aligned}$$

where \(\mathcal {C}_{k}^{j}\), \(1\le j\le n_{i} -1,1\le i\le r\) are the binomial coefficients.

Fractional trigonometric functions and Mittag-Leffler logarithm function

The idea of the fractional trigonometric functions has been stated by Jumarie [20] asserting that these functions are not periodic. Now, we introduce new fractional trigonometric functions which are periodic with the period \(2\pi _{\alpha } \approx 2\pi\). Analogous with the trigonometric function, we can write

$$\begin{aligned} E_{\alpha } ((it)^{\alpha } ) = \cos _{\alpha } (t^{\alpha } )+i\sin _{\alpha } (t^{\alpha } ), \end{aligned}$$
(13)

and

$$\begin{aligned} E_{\alpha } ((-it)^{\alpha } ) = \cos _{\alpha } (t^{\alpha } )-i\sin _{\alpha } (t^{\alpha } ), \end{aligned}$$
(14)

with

$$\begin{aligned} \cos _{\alpha } (t^{\alpha } ) = \frac{E_{\alpha } ((it)^{\alpha } )+E_{\alpha } ((-it)^{\alpha } )}{2} ,\;\;\; \text {and } \;\;\;\sin _{\alpha } (t^{\alpha } )= \frac{E_{\alpha } ((it)^{\alpha } )-E_{\alpha } ((-it)^{\alpha } )}{2i}. \end{aligned}$$

These fractional functions have the period \(2\pi _{\alpha } \approx 2\pi\). Figure 1 shows \(\sin _{\alpha } (t^{\alpha } )\) for \(\alpha =1,\;0.95,\;0.9\) which is periodic with the period \(2\pi _{\alpha } \approx 2\pi\).

Some properties of the fractional trigonometric functions are presented as follows:

$$\begin{aligned} \sin _{\alpha }^{2} \theta ^{\alpha } +\cos _{\alpha }^{2} \theta ^{\alpha } \approx 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{aligned}$$
$$\begin{aligned} &\sin _{\alpha } (-t)^{\alpha } = -\sin _{\alpha } (t^{\alpha } ),\\ &\cos _{\alpha } (-t)^{\alpha } = \cos _{\alpha } (t^{\alpha } ),\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{aligned}$$
$$\begin{aligned} D_{t}^{\alpha } (\sin _{\alpha } (\omega ^{\alpha } t^{\alpha } ))=\omega ^{\alpha } (i)^{\alpha -1} \cos _{\alpha } (\omega ^{\alpha } t^{\alpha } ), D_{t}^{\alpha } (\cos _{\alpha } (\omega ^{\alpha } t^{\alpha } ))=\omega ^{\alpha } (i)^{\alpha +1} \sin _{\alpha } (\omega ^{\alpha } t^{\alpha } ). \end{aligned}$$
Fig. 1
figure 1

Plot of \(\sin _{\alpha } (t^{\alpha })\) with respect to t for \(\alpha =1,\;0.95,\;0.9\)

Full size image

The fractional functions \(\sin _{\alpha } (\omega ^{\alpha } t^{\alpha } )\) and \(\cos _{\alpha } (\omega ^{\alpha } t^{\alpha } )\) both are periodic functions with the period \((2\pi _{\alpha } /\omega )\).

In addition Eq. (11) provides the equalities

$$\begin{aligned} \cos _{\alpha } (t+s)^{\alpha } \approx \cos _{\alpha } (t^{\alpha } )\cos _{\alpha } (s^{\alpha } )-\sin _{\alpha } (t^{\alpha } )\sin _{\alpha } (s^{\alpha } ), \end{aligned}$$
(15)
$$\begin{aligned} \sin _{\alpha } (t+s)^{\alpha } \approx \cos _{\alpha } (t^{\alpha } )\sin _{\alpha } (s^{\alpha })+\cos _{\alpha } (s^{\alpha } )\sin _{\alpha } (t^{\alpha } ). \end{aligned}$$
(16)

There are similar formulas like for \(\cos _{\alpha } (t-s)^{\alpha }\)and \(\sin _{\alpha } (t-s)^{\alpha }.\)

Substituting \(\theta\) for both t and s in the addition formulas gives

$$\begin{aligned} \cos _{\alpha } 2\theta ^{\alpha } \approx \cos _{\alpha }^{2} \theta ^{\alpha } -\sin _{\alpha }^{2} \theta ^{\alpha },\;\;\;\;\;\;\; sin_{\alpha } 2\theta ^{\alpha } \approx 2\sin _{\alpha } \theta ^{\alpha } \cos _{\alpha } \theta ^{\alpha }. \end{aligned}$$

Additional formulas come from combining the equations

$$\begin{aligned} \sin _{\alpha }^{2} \theta ^{\alpha } +\cos _{\alpha }^{2} \theta ^{\alpha } \approx 1,\quad \cos _{\alpha } 2\theta ^{\alpha } \approx \cos _{\alpha }^{2} \theta ^{\alpha } -\sin _{\alpha }^{2} \theta ^{\alpha }, \end{aligned}$$

we add the two equations to get \(\cos _{\alpha } 2\theta ^{\alpha } \approx 2\cos _{\alpha }^{2} \theta ^{\alpha } -1\) and subtract the second from the first to get \(\cos _{\alpha } 2\theta ^{\alpha } \approx 1-2\sin _{\alpha }^{2} \theta ^{\alpha }\).

Definition 7

\(Ln_{\alpha } t\) denotes the inverse function of the \(E_{\alpha }(t)\), referred to as Mittag-Leffler logarithm, clearly \(E_{\alpha }(Ln_{\alpha }t)=t\) and the Mittag-Leffler logarithm function is defined as [20]:

$$\begin{aligned} \int _{0}^{t}\frac{d^{\alpha } \xi }{\xi } =\frac{1}{(1-\alpha )!} \int _{0}^{t}\frac{(d\xi )^{\alpha } }{\xi ^{\alpha } } =Ln_{\alpha } (t). \end{aligned}$$
(17)

Fractional linear system and its stability analysis

Here, we will consider the following linear fractional differential system with modified Riemann–Liouville fractional derivative

$$\begin{aligned} D_{t}^{\alpha } \,x=Ax, \end{aligned}$$
(18)

with initial value \(x(0)=x_{0} =(x_{10} ,x_{20} ,\ldots ,x_{no} )^{T}\), where \(x=(x_{1} ,x_{2},\ldots ,x_{n} )^{T}\), \(\alpha \in (0,1]\) and \(A\in {\mathbb R}^{n\times n}\). By implementation of the Laplace transform on the above system and using the initial condition, the general solution can be written as

$$\begin{aligned} x=x_{0} E_{\alpha } (At^{\alpha }). \end{aligned}$$
(19)

The stability of the equilibrium of system (18) was first defined and established by Matignon as follows [21].

Definition 8

The linear fractional differential system (18) is said to be

(i) stable if for any initial value \(x_{0}\), there exists a ε > 0 such that for all t ≥ 0,

(ii) asymptotically stable if at first it is stable and \(\mathop {\lim }\nolimits _{t\rightarrow \infty } \left\| x(t^{\alpha } )\right\| =0\).

Theorem 1

The linear fractional differential system (18) is asymptotically stable if all the eigenvalues of A satisfy

$$\begin{aligned} \left| \arg (\lambda (A))\right| >\frac{\alpha \pi }{2}. \end{aligned}$$
(20)

We can very easily prove Theorem 1 analogously using Proposition 3.1 in [21].

Now, we state the following important existence–uniqueness theorem for solutions of initial value problems (21).

Theorem 2

([22]) Let \(0<\alpha \le 1\), \((0,b)\subset {\mathbb R}\), U be an open connected set in \({\mathbb R}^{n+1}\), \(\Delta =(0,b)\times U\) and \((t_{0} ,x_{0} )\in \Delta\). If

$$\begin{aligned} A(t^{\alpha } )=\left[ \begin{array}{cccc} {a_{11} (t^{\alpha } )} &{} {a_{12} (t^{\alpha } )} &{} {\ldots } &{} {a_{1n} (t^{\alpha } )} \\ {a_{21} (t^{\alpha } )} &{} {a_{22} (t^{\alpha } )} &{} {\ldots } &{} {a_{2n} (t^{\alpha } )} \\ {\vdots } &{} {\vdots } &{} {\ddots } &{} {\vdots } \\ {a_{n1} (t^{\alpha } )} &{} {a_{n2} (t^{\alpha } )} &{} {\ldots } &{} {a_{nn} (t^{\alpha } )} \end{array}\right] \quad \mathrm{and}\quad B(t^{\alpha } )=\left[ \begin{array}{c} {b_{1} (t^{\alpha } )} \\ {\vdots } \\ {b_{n} (t^{\alpha } )} \end{array}\right] , \end{aligned}$$

are continuous matrices in \(\left[ 0,b\right]\), then equation

$$\begin{aligned} D_{t}^{\alpha } x=A(t^{\alpha } )x+B(t^{\alpha } ), \end{aligned}$$
(21)

has a unique solution \(x(t^{\alpha } )\), continuous in (0, b],  such that \(x(t_{0}^{\alpha } )=x_{0}.\)

Fractional Floquet system

In this Section, we will consider fractional order linear periodic differential equations involving modified Riemann–Liouville derivative that can be written in the form

$$\begin{aligned} D_{t}^{\alpha } \, x(t^{\alpha } )=f_{\alpha } (t^{\alpha } )x(t^{\alpha } ), \end{aligned}$$
(22)

where we assume that \(f_{\alpha } :(a,b)\rightarrow {\mathbb R}\) is continuous periodic function with smallest positive periodic \(w_{\alpha }\), that is, \(f_{\alpha } ((t+w_{\alpha } )^{\alpha } )\approx f_{\alpha } (t^{\alpha } )\).

Also, the solution of Eq. (22) obtained with respect to the Mittag-Leffler function is as

$$\begin{aligned} x({t}^{\alpha } )\approx C\;E_{\alpha }\left( \int _{0}^{t}f_{\alpha } (\tau ^{\alpha } )(d\tau )^{\alpha }\right) , \end{aligned}$$
(23)

where C is a constant.

Example 1

Consider the fractional order linear periodic differential equation

$$\begin{aligned} D_{t}^{\alpha } \, x(t^{\alpha } ) = \sin _{\alpha } (t^{\alpha } )x(t^{\alpha } ). \end{aligned}$$
(24)

Thus, by (23), \(x(t^{\alpha } )\approx C\, E_{\alpha } (\frac{1}{i^{\alpha +1} } \cos _{\alpha } (t^{\alpha } ))\), where for \(t\in {\mathbb R}\) is a general solution on \({\mathbb R}\) for (24).

Definition 9

We say x is a solution of (22) on an interval \(L\subset (0,b)\) if x is a continuously \(\alpha\)th differentiable function on L and for \(t\in L\), x satisfies (22).

In the rest of this section, we will generalize linear periodic systems to fractional periodic systems involving modified Riemann–Liouville derivative form

$$\begin{aligned} \begin{array}{l} {D_{t}^{\alpha } \, x_{1} =a_{\alpha _{11}} (t^{\alpha } )x_{1} +a_{\alpha _{12}} (t^{\alpha } )x_{2} +\cdots +a_{\alpha _{1n}} (t^{\alpha } )x_{n} ,} \\ {D_{t}^{\alpha } \, x_{2} =a_{\alpha _{21}} (t^{\alpha } )x_{1} +a_{\alpha _{22}} (t^{\alpha } )x_{2} +\cdots +a_{\alpha _{2n}} (t^{\alpha } )x_{n} ,} \\ {\quad \vdots \quad \quad \quad \quad \vdots \quad \quad \quad \quad \vdots \quad \quad \quad \quad \quad \vdots } \\ {D_{t}^{\alpha } \, x_{n} =a_{\alpha _{n1}} (t^{\alpha } )x_{1} +a_{\alpha _{n2}} (t^{\alpha } )x_{2} +\cdots +a_{\alpha _{nn}} (t^{\alpha } )x_{n} ,} \end{array} \end{aligned}$$
(25)

where \(a_{\alpha _{ij}} (t^{\alpha })\), \((i,\,j=1,2,\ldots ,n)\) are given continuous periodic functions with smallest positive periodic \(w_{\alpha }\) on an interval L.

This system can be transformed to a vector–matrix form as

$$\begin{aligned} D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x, \end{aligned}$$
(26)

where

$$\begin{aligned} x=\left[ \begin{array}{c} {x_{1} } \\ {\vdots } \\ {x_{n} } \end{array}\right] ,\quad D_{t}^{\alpha } \, x=\left[ \begin{array}{c} {D_{t}^{\alpha } \, x_{1} } \\ {\vdots } \\ {D_{t}^{\alpha } \, x_{n} } \end{array}\right] , \end{aligned}$$

and

$$\begin{aligned} A_{\alpha } (t^{\alpha } )=\left[ \begin{array}{cccc} {a_{\alpha _{11}} (t^{\alpha } )} &{} {a_{\alpha _{21}} (t^{\alpha } )} &{} {\ldots } &{} {a_{\alpha _{1n}} (t^{\alpha } )} \\ {a_{\alpha _{21}} (t^{\alpha } )} &{} {a_{\alpha _{22}} (t^{\alpha } )} &{} {\ldots } &{} {a_{\alpha _{2n}} (t^{\alpha } )} \\ {\vdots } &{} {\vdots } &{} {\ddots } &{} {\vdots } \\ {a_{\alpha _{n1}} (t^{\alpha } )} &{} {a_{\alpha _{n2}} (t^{\alpha } )} &{} {\ldots } &{} {a_{\alpha _{nn }} (t^{\alpha } )} \end{array}\right] , \end{aligned}$$

where the components in matrix \(A_{\alpha }\) are continuous and periodic functions with smallest positive period w α (saying \(A_{\alpha } ((t+w_{\alpha } )^{\alpha } )\approx A_{\alpha } (t^{\alpha } )\)).

Consider the matrix fractional differential equation

$$\begin{aligned} D_{t}^{\alpha } \, X=A_{\alpha } (t^{\alpha } )X, \end{aligned}$$
(27)

where

$$\begin{aligned} X=\left[ \begin{array}{cccc} {x_{11} } &{} {x_{12} } &{} {\ldots } &{} {x_{1n} } \\ {x_{21} } &{} {x_{22} } &{} {\ldots } &{} {x_{2n} } \\ {\vdots } &{} {\vdots } &{} {\ddots } &{} {\vdots } \\ {x_{n1} } &{} {x_{n2} } &{} {\ldots } &{} {x_{nn} } \end{array}\right] , \quad \text {and}\quad D_{t}^{\alpha } X=\left[ \begin{array}{cccc} {D_{t}^{\alpha } x_{11} } &{} {D_{t}^{\alpha } x_{12} } &{} {\ldots } &{} {D_{t}^{\alpha } x_{1n} } \\ {D_{t}^{\alpha } x_{21} } &{} {D_{t}^{\alpha } x_{22} } &{} {\ldots } &{} {D_{t}^{\alpha } x_{2n} } \\ {\vdots } &{} {\vdots } &{} {\ddots } &{} {\vdots } \\ {D_{t}^{\alpha } x_{n1} } &{} {D_{t}^{\alpha } x_{n2} } &{} {\ldots } &{} {D_{t}^{\alpha } x_{nn} } \end{array}\right] , \end{aligned}$$

are \(n\times n\) matrix variables and \(A_{\alpha }\) is an n × n continuous matrix function on L.

Theorem 3

(Existence–Uniqueness Theorem) If the entries of the square matrix \(A_{\alpha }\) are continuous on an interval L containing \(t_{0}\), then the initial value problem

$$\begin{aligned} D_{t}^{\alpha } \, X=A_{\alpha } (t^{\alpha } )X,\;\;\;\;\;\; X(t_{0} )=X_{0} \in \mathbb {R}^{n\times n}, \end{aligned}$$

has one and only one solution X on the whole interval L.

Proof

The proof is similar to that of Theorem 2.21 in [2]. \(\square\)

Definition 10

An n × n matrix fractional function \(\Phi _{\alpha }\), defined on an interval L, is called a fractional fundamental matrix of the linear system (3.5) if \(\Phi _{\alpha }\) is a solution of the fractional matrix equation (27) on L and \(\det \Phi _{\alpha } (t^{\alpha } )\ne 0\) on L.

Theorem 4

If \(\Phi _{\alpha }\) is a fractional fundamental matrix for \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\) , then, for an arbitrary n × n non-singular constant matrix C, \(\Psi _{\alpha } =\Phi _{\alpha } C\) is a general fractional fundamental matrix of \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\).

Proof

Since \(\Phi _{\alpha }\) is a fractional fundamental matrix solution to \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\) and setting \(\Psi _{\alpha } =\Phi _{\alpha } C\), we have

$$\begin{aligned} D_{t}^{\alpha } \Psi _{\alpha } (t^{\alpha } )&=D_{t}^{\alpha } \Phi _{\alpha } (t^{\alpha } )C=A_{\alpha } (t^{\alpha } )\Phi _{\alpha } (t^{\alpha } )C \\&=A_{\alpha } (t^{\alpha } )\Psi _{\alpha } (t^{\alpha } ),\end{aligned}$$

and also \(\Psi _{\alpha }\) is continuously \(\alpha\)th differentiable function on L. Thus, \(\Psi _{\alpha } =\Phi _{\alpha } C\) is a solution of the matrix fractional equation (3.6). Since \(\Phi _{\alpha }\) is a fractional fundamental matrix solution to (26), Definition 10 implies that \(\det [\Phi _{\alpha } (t^{\alpha } )] \ne 0\). As well, since, \(\det [C] \ne 0\). Hence,

$$\begin{aligned} \begin{array}{ll} {\det [\Psi _{\alpha } (t^{\alpha } )] = \det [\Phi _{\alpha } (t^{\alpha } )C]} \\ \quad \quad \quad\quad\;\;\;= \det [\Phi _{\alpha } (t^{\alpha } )]\det [C]\ne 0, \end{array} \end{aligned}$$

for \(t\in L\), and by Definition 10, \(\Psi _{\alpha } =\Phi _{\alpha } C\) is a fractional fundamental matrix of (27). \(\square\)

Theorem 5

If C is an n × n non-singular matrix, then there is a matrix B such that \(E_{\alpha } (B)=C\).

Proof

To avoid some tedious calculations, we prove this theorem for a 2 × 2 matrices. For the eigenvalues \(\mu _{1} ,\; \mu _{2}\ne \;0\) of nonsingular matrix C. We consider two special cases:

Case I Let

$$\begin{aligned} C=\left[ \begin{array}{cc} {\mu _{1} } &{} {0} \\ {0} &{} {\mu _{2} } \end{array}\right] , \end{aligned}$$

then, in this case we are looking for a diagonal matrix

$$\begin{aligned} B=\left[ \begin{array}{cc} {b_{1} } &{} {0} \\ {0} &{} {b_{2} } \end{array}\right] , \end{aligned}$$

so that \(E_{\alpha } (B)=C\). For this purpose, according to the definition of the Mittag-Leffler function, we pick \(b_{1}\) and \(b_{2}\) so that

$$\begin{aligned} E_{\alpha } (B)=\left[ \begin{array}{cc} {E_{\alpha } (b_{1} )} &{} {0} \\ {0} &{} {E_{\alpha } (b_{2} )} \end{array}\right] =\left[ \begin{array}{cc} {\mu _{1} } &{} {0} \\ {0} &{} {\mu _{2} } \end{array}\right] . \end{aligned}$$

Hence, the matrix B can be taken as

$$\begin{aligned} B=\left[ \begin{array}{cc} {\ln _{\alpha } (\mu _{1} )} &{} {0} \\ {0} &{} {\ln _{\alpha } (\mu _{2} )} \end{array}\right] . \end{aligned}$$

Case II Let

$$\begin{aligned} C=\left[ \begin{array}{cc} {\mu _{1} } &{} {1} \\ {0} &{} {\mu _{1} } \end{array}\right] , \end{aligned}$$

then, we seek a matrix B of the form

$$\begin{aligned} B=\left[ \begin{array}{cc} {a_{1} } &{} {a_{2} } \\ {0} &{} {a_{1} } \end{array}\right] , \end{aligned}$$

so that \(E_{\alpha } (B)=C\). We choose the parameters \(a_{1}\) and \(a_{2}\) so that

$$\begin{aligned} E_{\alpha } (B)=\left[ \begin{array}{cc} {E_{\alpha } (a_{1} )} &{} \;\;{a_{2} E_{\alpha } (a_{1} )} \\ {0} &{} {E_{\alpha } (a_{1} )} \end{array}\right] =\left[ \begin{array}{cc} {\mu _{1} } &{} {1} \\ {0} &{} {\mu _{1} } \end{array}\right] . \end{aligned}$$

Hence, in the view of the inverse function derivative, the matrix B can be taken as

$$\begin{aligned} B=\left[ \begin{array}{cc} {\ln _{\alpha } (\mu _{1} )} &{} {\frac{1}{\mu _{1} } } \\ {0} &{} {\ln _{\alpha } (\mu _{1} )} \end{array}\right] . \end{aligned}$$

Case III When \(C \in \mathbb {R}^{2\times 2}\) is an arbitrary matrix such that \(\det [C]\ne 0\). By the Corollary 1, there is a non-singular matrix P such that \(C=PJP^{-1}\), where

$$\begin{aligned} C=\left[ \begin{array}{cc} {\mu _{1} } &{} {0} \\ {0} &{} {\mu _{2} } \end{array}\right] ,\;\;\;\;\;or\;\;\;\;\; C=\left[ \begin{array}{cc} {\mu _{1} } &{} {1} \\ {0} &{} {\mu _{1} } \end{array}\right] . \end{aligned}$$

Now, by the previous two cases there is a matrix \(B_{1}\) so that \(E_{\alpha } (B_{1} )=J\).

If we set the matrix B as

$$\begin{aligned} B=PB_{1} P^{-1}, \end{aligned}$$

then, we see that

$$\begin{aligned} E_{\alpha } (B)=E_{\alpha } (PB_{1} P^{-1} )=PE_{\alpha } (B_{1} )P^{-1} =C. \end{aligned}$$

Similarly, for the higher order of n, the matrix B can be easily found. \(\square\)

Example 2

For example, consider

$$\begin{aligned} D_{t}^{\alpha } \, x=\left[ \begin{array}{cc} {1} &{} {1} \\ {0} &{}\;\;\;{\frac{\Gamma (\alpha +1)i^{\alpha -1} \cos _{\alpha } (t^{\alpha } )-\Gamma (\alpha +1)\sin _{\alpha } (t^{\alpha } )}{(2+\Gamma (\alpha +1)\sin _{\alpha } (t^{\alpha } )-\, \, \frac{\Gamma (\alpha +1)}{i^{\alpha +1} } \cos _{\alpha } (t^{\alpha } ))} } \end{array}\right] x. \end{aligned}$$

Here, we know that the solution is in general

$$\begin{aligned} x_{1} (t^{\alpha } )&\approx \mu E_{\alpha } (t^{\alpha } )+\beta (\frac{\Gamma (\alpha +1)}{i^{\alpha +1} } \cos _{\alpha } (t^{\alpha } )-2),\\ x_{2} (t^{\alpha } )&\approx \beta (2+\Gamma (\alpha +1)\sin _{\alpha } (t^{\alpha } )-\frac{\Gamma (\alpha +1)}{i^{\alpha +1} } \cos _{\alpha } (t^{\alpha } )), \end{aligned}$$

for \(t\in {\mathbb R}\), where \(\beta , \mu \in {\mathbb R}\) denote two constants. Using all the above definitions, the fractional fundamental matrix is

$$\begin{aligned} \begin{array}{l} {\Phi _{\alpha } (t^{\alpha } )\approx \left[ \begin{array}{cc} {\frac{\Gamma (\alpha +1)}{i^{\alpha +1} } \cos _{\alpha } (t^{\alpha } )-2} &{} {E_{\alpha } (t^{\alpha } )} \\ {2+\Gamma (\alpha +1)\sin _{\alpha } (t^{\alpha } )-\frac{\Gamma (\alpha +1)}{i^{\alpha +1} } \cos _{\alpha } (t^{\alpha } )} &{} {0} \end{array}\right] } \\ {\quad \quad \quad \; =\left[ \begin{array}{cc} {\frac{\Gamma (\alpha +1)}{i^{\alpha +1} } \cos _{\alpha } (t^{\alpha } )-2} &{} {1} \\ {2+\Gamma (\alpha +1)\sin _{\alpha } (t^{\alpha } )-\frac{\Gamma (\alpha +1)}{i^{\alpha +1} } \cos _{\alpha } (t^{\alpha } )}\;\;\;&{} {0} \end{array}\right] \left[ \begin{array}{cc} {1} &{} {0} \\ {0} &{}\;\; {E_{\alpha } (t^{\alpha } )} \end{array}\right] .} \end{array} \end{aligned}$$

Theorem 6

(Fractional Floquet’s Theorem) Every fractional fundamental matrix solution \(\Phi _{\alpha } (t^{\alpha } )\) of (26) has the form

$$\begin{aligned} \Phi _{\alpha } (t^{\alpha } )\approx P_{\alpha } (t^{\alpha } )E_{\alpha } (Bt^{\alpha } ), \end{aligned}$$
(28)

where \(P_{\alpha }(t^{\alpha })\), B are \(n\times n\) matrices, \(P_{\alpha } ((t+w_{\alpha } )^{\alpha } )\approx P_{\alpha } (t^{\alpha } )\) for all t and B is a constant.

Proof

Assume that \(\Phi _{\alpha } (t^{\alpha } )\) is a fractional fundamental matrix solution of (26). Then \(\Phi _{\alpha } ((t+w_{\alpha } )^{\alpha } )\) is also a fractional fundamental matrix solution, since \(A_{\alpha } (t^{\alpha } )\) is periodic of period \(w_{\alpha }\). Therefore, there is a nonsingular matrix C such that

$$\begin{aligned} \Phi _{\alpha } ((t+w_{\alpha } )^{\alpha } )=\Phi _{\alpha } (t^{\alpha } )C. \end{aligned}$$

From Theorem 5, there is a matrix B so that \(C=E_{\alpha } (w_{\alpha } B)\). For this matrix B, let \(P_{\alpha } (t^{\alpha } )\approx \Phi _{\alpha } (t^{\alpha } )E_{\alpha } (B(-t)^{\alpha } )\). Then

$$\begin{aligned} \begin{array}{l} {P_{\alpha } ((t+w_{\alpha } )^{\alpha } )\approx \Phi _{\alpha } ((t+w_{\alpha } )^{\alpha } )E_{\alpha } (B(-t-w_{\alpha } )^{\alpha } )} \\ {\quad \quad \quad \quad \quad \, \;\, \quad \approx \Phi _{\alpha } (t^{\alpha } )E_{\alpha } (B(w_{\alpha } )^{\alpha } )E_{\alpha } (B(-t-w_{\alpha } )^{\alpha } )\approx P_{\alpha } (t^{\alpha } ),} \end{array} \end{aligned}$$

and the theorem is proved. \(\square\)

Definition 11

The eigenvalues \(\mu _{1} ,\mu _{2} ,\ldots ,\mu _{n}\) of \(C=\Phi _{\alpha }^{-1} (0)\Phi _{\alpha } (w_{\alpha } )\) are called the multipliers of the fractional Floquet system \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\), where \(\Phi _{\alpha } (t^{\alpha } )\) is a fractional fundamental matrix of system \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\).

Example 3

Solving the following equation,

$$\begin{aligned} D_{t}^{\alpha } \, x=\sin _{\alpha }^{2} (t^{\alpha } )x, \end{aligned}$$
(29)

we get that

$$\begin{aligned}\Phi _{\alpha } (t^{\alpha } ) &\approx E_{\alpha } \left( \frac{1}{2} t^{\alpha } -\frac{\Gamma (\alpha +1)}{4i^{\alpha -1} } \sin _{\alpha } (2t^{\alpha } )\right) \\ &\approx E_{\alpha } (\frac{1}{2} t^{\alpha } )E_{\alpha }^{-1} \left( \frac{\Gamma (\alpha +1)}{4i^{\alpha -1} } \sin _{\alpha } (2t^{\alpha } )\right)\end{aligned}$$

so that

$$\begin{aligned} C=\Phi _{\alpha }^{-1} (0)\Phi _{\alpha } (\pi _{\alpha } )=E_{\alpha } \left( \frac{(\pi _{\alpha } )^{\alpha } }{2}\right) . \end{aligned}$$

As a result \(E_{\alpha } \left( \frac{(\pi _{\alpha } )^{\alpha } }{2} \right)\) is the multiplier for this fractional differential equation.

Theorem 7

Let \(\Phi _{\alpha } (t^{\alpha } )\approx P_{\alpha } (t^{\alpha } )E_{\alpha } (Bt^{\alpha } )\) be the fractional fundamental matrix in Theorem 6. Then, x is a solution of the fractional Floquet system \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\) if and only if the vector function y defined by \(y(t^{\alpha } )=P_{\alpha }^{-1} (t^{\alpha } )x(t^{\alpha } )\) be a solution of

$$\begin{aligned} D_{t}^{\alpha } \, y=By. \end{aligned}$$
(30)

Proof

Assume that x is a solution of the fractional Floquet system \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\). Then, for some vector \(x_{0} \in \mathbb {R}^{n\times 1}\) we have \(x(t^{\alpha } )=\Phi _{\alpha } (t^{\alpha } )x_{0}\).

Now, by setting \(y(t^{\alpha } )=P_{\alpha }^{-1} (t^{\alpha } )x(t^{\alpha } )\), we get

$$\begin{aligned} \begin{array}{l} {y(t^{\alpha } )=P_{\alpha }^{-1} (t^{\alpha } )\Phi _{\alpha } (t^{\alpha } )x_{0} \approx P_{\alpha }^{-1} (t^{\alpha } )P_{\alpha } (t^{\alpha } )E_{\alpha } (Bt^{\alpha } )x_{0} }\\ {\quad \;\; \quad =E_{\alpha } (Bt^{\alpha } )x_{0} ,} \end{array} \end{aligned}$$

which is a solution of (30).

Conversely, assume that y is a solution of system (30) and set \(x(t^{\alpha } )=P_{\alpha } (t^{\alpha } )y(t^{\alpha } )\). Since y is a solution of \(D_{t}^{\alpha } \, y=By\), there is a vector \(y_{0}\in \mathbb {R}^{n\times 1}\) such that \(y(t^{\alpha } )=E_{\alpha } (Bt^{\alpha } )y_{0}\).

It follows that

$$\begin{aligned} \begin{array}{l} {x(t^{\alpha } )=P_{\alpha } (t^{\alpha } )y(t^{\alpha } )=P_{\alpha } (t^{\alpha } )E_{\alpha } (Bt^{\alpha } )y_{0} } \\ {\quad \quad \; \; \approx \Phi _{\alpha } (t^{\alpha } )y_{0} ,} \end{array} \end{aligned}$$

which is a solution of the fractional Floquet system \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\). \(\square\)

Theorem 8

Two matrices A and B are called similar if there exists a nonsingular matrix A such that \(A=TBT^{-1}\) [23].

Theorem 9

A fractional Floquet system \(D_{t}^{\alpha } \, x =A_{\alpha } (t^{\alpha } )x\) with the multipliers \(\mu _{1} ,\mu _{2} ,\ldots ,\mu _{n}\) is

  1. (i)

    asymptotically stable on \([0,\infty )\) if all multipliers satisfy \(\left| \mu _{i} \right| <1,\; 1\le i\le n,\)

  2. (ii)

    unstable on \([0,\infty )\), when there is an \(i_{0} ,\; 1\le i_{0} \le n,\) such that \(\left| \mu _{i_{0} } \right| >1\).

Proof

Without loss of generality, we prove this theorem for \(2\times 2\) matrices \(A_{\alpha }\). Let \(\Phi _{\alpha } (t^{\alpha } )\approx P_{\alpha } (t^{\alpha } )E_{\alpha } (Bt^{\alpha } )\) and C be the same as in the Theorem 6. Therefore, the matrix B can be chosen such that \(E_{\alpha } (Bw^{\alpha } )=C\).

Suppose the matrix B is similar to a Jordan canonical form, i.e., there exists an invertible matrix M such that \(B=MJM^{-1}\). Now by letting \(\lambda _{1} ,\, \lambda _{2}\) as the eigenvalues of B, we see that for the matrix C we have

$$\begin{aligned} C=E_{\alpha } (Bw^{\alpha } )=E_{\alpha } (MJM^{-1} w^{\alpha } )=ME_{\alpha } (Jw^{\alpha } )M^{-1} =MHM^{-1} , \end{aligned}$$

where either

$$\begin{aligned} H=\left[ \begin{array}{cc} {E_{\alpha } (\lambda _{1} w^{\alpha } )} &{} {0} \\ {0} &{} {E_{\alpha } (\lambda _{2} w^{\alpha } )} \end{array}\right] ,\;\;\;\;\;or\;\;\;\;\;H=\left[ \begin{array}{cc} {E_{\alpha } (\lambda _{1} w^{\alpha } )} &{} \;\;\;{w^{\alpha } E_{\alpha } (\lambda _{1} w^{\alpha } )} \\ {0} &{} {E_{\alpha } (\lambda _{1} w^{\alpha } )} \end{array}\right] . \end{aligned}$$

Since the eigenvalues of H are the same as the eigenvalues of C, we take the multipliers \(\mu _{i}\) as \(\mu _{i} =E_{\alpha } (\lambda _{i} w^{\alpha } )\), \(i=1,2\). Since \(\left| \mu _{i} \right| =E_{\alpha } (Re(\lambda _{i} )w^{\alpha } )\), we have that

$$\begin{aligned} \left| \mu _{i} \right| <1\quad iff\quad Re(\lambda _{i} )\,<\,0, \end{aligned}$$
$$\begin{aligned} \left| \mu _{i} \right| >1\quad iff\quad Re(\lambda _{i} )>0. \end{aligned}$$

Since according to the Theorem 7, there is a one-to-one correspondence between solutions of the fractional Floquet system \(D_{t}^{\alpha } \, x=A_{\alpha } (t^{\alpha } )x\) and system (30).

For constant \(Q_{1} >0\), we have

$$\begin{aligned} \left\| x(t^{\alpha } )\right\| =\left\| P_{\alpha } (t^{\alpha } )y(t^{\alpha } )\right\| \le \left\| P_{\alpha } (t^{\alpha } )\right\| \left\| y(t^{\alpha } )\right\| \le Q_{1} \left\| y(t^{\alpha } )\right\| , \end{aligned}$$

and for constant \(Q_{2} >0\), we get

$$\begin{aligned} \left\| y(t^{\alpha } )\right\| =\left\| P_{\alpha }^{-1} (t^{\alpha } )x(t^{\alpha } )\right\| \le \left\| P_{\alpha }^{-1} (t^{\alpha } )\right\| \left\| x(t^{\alpha } )\right\| \le Q_{2} \left\| x(t^{\alpha } )\right\| . \end{aligned}$$

Finally by Theorem 1 the results can be derived. \(\square\)

Fig. 2
figure 2

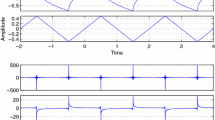
The numerical approximations of equation (3.8) when \(\alpha =1,\; 0.98,\; 0.95\)

Full size image

In Example 3, we saw that the multiplier of the fractional differential equation (29) is \(\mu =E_{\alpha } (\frac{(\pi _{\alpha } )^{\alpha } }{2} )\). When \(0<\alpha \le 1\), then the solution fractional differential equation (29) is unstable, since we always have \(\left| \mu \right| >1\). Figure 2 indicates that equation (29) with parameters \(\alpha =1,\; 0.98,\; 0.95\) is unstable.

Example 4

We can show \(\Phi _{\alpha } (t^{\alpha } )\) in the form

$$\begin{aligned} \Phi _{\alpha } (t^{\alpha } )\approx \left[ \begin{array}{cc} {E_{\alpha } (-t^{\alpha } )} &{} {0} \\ {\frac{1}{i^{\alpha -1}}E_{\alpha } (-t^{\alpha } )\sin _{\alpha } (t^{\alpha } )} \;\;\;&{} {E_{\alpha } (-t^{\alpha } )} \end{array}\right] , \end{aligned}$$

is a fractional fundamental matrix for the fractional Floquet system

$$\begin{aligned} \left[ \begin{array}{cc} {D_{t}^{\alpha } \, x} \\ {D_{t}^{\alpha } \, y} \end{array}\right] =\left[ \begin{array}{cc} {-1} &{} \;\;\;{0} \\ {\cos _{\alpha } (t^{\alpha } )}\;\;\; &{}{-1} \end{array}\right] \left[ \begin{array}{cc} {x} \\ {y} \end{array}\right] . \end{aligned}$$
(31)

Since

$$\begin{aligned} C=\Phi _{\alpha }^{-1}(0)\Phi _{\alpha }(2\pi _{\alpha })=\left[ \begin{array}{cc} {E _{\alpha }(-(2\pi _{\alpha })^{\alpha })} &{} {0} \\ {0}\;\;\; &{}{E _{\alpha }(-(2\pi _{\alpha })^{\alpha })} \end{array}\right] , \end{aligned}$$

the multipliers are \(\mu _{1}=\mu _{2}=E _{\alpha }(-(2\pi _{\alpha })^{\alpha })\). When \(0<\alpha \le 1\), then the solution system (31) is asymptotically stable, as we always have \(\left| \mu _{i} \right| <1\) for \(i=1,2\). Figure 3 indicates that the solution fractional Floquet system (3.10) with parameters \(\alpha =1,\; 0.98,\; 0.95\) is asymptotically stable.

Fig. 3
figure 3

The numerical approximations of fractional Floquet system (31) when \(\alpha =1,\; 0.98,\; 0.95\)

Full size image

Conclusion

In the present article, we have recalled some properties of the Mittag-Leffler function and Mittag-Leffler logarithm function as described in [20]. Then we have presented fractional trigonometric function and the fractional Floquet system based on the modified Riemann–Liouville derivation. Since, the study of stability for the fractional Floquet system is very important, the asymptotical stability for such systems has been investigated. We have shown the fractional Floquet system is asymptotically stable if all multipliers have real parts between -1 and 1. Finding the stability of nonlinear periodic fractional systems and delay linear periodic fractional systems can be an interesting topic for future research work.