Introduction

In recent years, electric propulsion is being used successfully in space missions and the Hall thruster is one of the most promising devices [1,2,3] for small satellites because of its high thrust density and efficiency. To improve the efficiency of the Hall thruster, we require a detailed knowledge of physical processes occurring in the plasma of a thruster. Several physical phenomena are associated with the plasma fluctuations. One of the major problems of Hall thrusters is the discharge current oscillation, which has an adverse effect on the power processing unit (PPU) when its oscillations lie in the range 10–100 kHz frequency.

Plasma resistivity has been found to induce resistive instabilities corresponding to lower hybrid waves and Alfven waves, as well as the resistive instabilities associated with the axial ion flows. Tsikata et al. [4] have observed spectra with a single peak of positive frequency, for the case of the k vector in the direction of the jet axis. Lazurenko et al. [5] have used electrostatic probes and antennas to measure the fluctuations in a Hall thruster plasma. Nejoh group has done appreciable work concerning collisional sheath structure and fluctuations in Hall thruster plasmas including charging near the ion engine [6,7,8,9,10]. Barral et al. [11] have studied low-frequency oscillations under the effect of ionization in a Hall thruster. Chesta et al. [12] have theoretically obtained the growth rate and frequencies of predominantly axial and azimuthally propagating plasma disturbances. They also identified the persistence of a low-frequency instability associated with the ionization process. High-frequency (HF) instability in the range of 5–10 MHz has also been reported experimentally by Litvak et al. [13]. Since the plasma in Hall thrusters is far from equilibrium and is placed in a rather strong magnetic field, both features create conditions for plasma instabilities to occur. These instabilities influence the performance of the thruster; therefore, the instabilities in the Hall thrusters have been the topic of most significance to the researchers [14,15,16,17,18,19,20,21]. It is found that in the previous studies, dust particles have been neglected by the researchers, which become important plasma species in the Hall thrusters due to the erosion of the wall of the chamber and sputtering [22, 23]. In general, it is found that current carried by the highly mobile electrons plays the important role in dust charging, and as a result, the dust particles are negatively charged in the plasma [24,25,26,27,28,29]. The negatively charged dust particles will hinder the movement of ions and, hence, alter the thrust and efficiency of the thruster. Moreover, these particles will collect large number of electrons that will lower the ionization in the plasma. In view of all these points, we focus on the resistive instability which is caused due to the resistive coupling of electrons flow with the oscillations in the presence of collisions.

Dusty plasma model and theoretical calculations

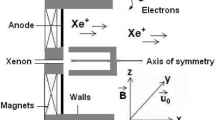
In the present model, we consider a Hall thruster channel with plasma consisting of ions, electrons and negatively charged dust particles of same size. External magnetic field \( \vec{B}_{{}} = B_{{}} \hat{z} \) is assumed, such that electrons are magnetized (cyclotron frequency \( \varOmega = \frac{eB}{{m_{e} }} \)), while ions and dust particles are unmagnetized. The axial electric field \( \vec{E} \) (along x-axis) causes the electrons to have an \( \vec{E} \) × \( \vec{B} \) drift in the azimuthal direction (y-axis). The movement of other species is restricted along x-axis. We take into account the motion of all the species, i.e., dust (density \( n_{d} \), mass \( m_{d} \), velocity \( \vec{\upsilon }_{d} \), temperature \( T_{d} \), charge − \( Z_{d} \)\( e \)), ions (density \( n_{i} \), mass \( m_{i} \), velocity \( \vec{\upsilon }_{i} \), temperature \( T_{i} \)), and electrons (density \( n_{e} \), mass \( m_{e} \), velocity \( \vec{\upsilon }_{e} \), and temperature \( T_{e} \)) for the excitation of waves and instability. In view of strongly tilted waves, we consider an additional axial component of wave number, \( k_{x} \) with the same magnitude as that of azimuthal wave number, i.e., \( k_{x} = k_{y} \) = \( k_{xy} \). We can say that the wave propagates at an angle θ = tan−1 \( k_{x} \)/\( k_{y} \) = 45° with the axis of the thruster. The basic fluid equations for all species read:

$$ \frac{{\partial n_{i} }}{\partial t} + \vec{\nabla } \cdot (\vec{\upsilon }_{i} n_{i} ) = 0, $$
(1)
$$ m_{i} n_{i} \left[ {\frac{{\partial \vec{\upsilon }_{i} }}{\partial t} + (\vec{\upsilon }_{i} \cdot \vec{\nabla })\vec{\upsilon }_{i} } \right] = en_{i} \vec{E} - \vec{\nabla }p_{i} , $$
(2)
$$ \frac{{\partial n_{e} }}{\partial t} + \vec{\nabla } \cdot \left( {\vec{\upsilon }_{e} n_{e} } \right) = 0, $$
(3)
$$ m_{e} n_{e} \left[ {\frac{{\partial \vec{\upsilon }_{e} }}{\partial t} + (\vec{\upsilon }_{e} \cdot \vec{\nabla })\vec{\upsilon }_{e} } \right] = - en_{e} (\vec{E} + \vec{\upsilon }_{e} \times \vec{B}) - \vec{\nabla }p_{e} - m_{e} n_{e} v\vec{\upsilon }_{e} , $$
(4)
$$ \frac{{\partial n_{d} }}{\partial t} + \vec{\nabla } \cdot (\vec{\upsilon }_{d} n_{d} ) = 0, $$
(5)
$$ m_{d} n_{d} \left[ {\frac{{\partial \vec{\upsilon }_{d} }}{\partial t} + (\vec{\upsilon }_{d} \cdot \vec{\nabla })\vec{\upsilon }_{d} } \right] = - eZ_{d} n_{d} \vec{E} - \vec{\nabla }p_{d} , $$
(6)
$$ \varepsilon_{0} \nabla^{2} \phi_{1} = e(n_{e1} - n_{i1} + Z_{d} n_{d1} ). $$
(7)

In view of the fact that the ions are unmagnetized and accelerated along the axial direction of the chamber, we consider their drift only in the x-direction (\( \vec{\upsilon }_{i0} \) = \( \upsilon_{i0} \) \( \hat{x} \)). Dust particles being heavier and unmagnetized have their motion (drift) in the x-direction (\( \vec{\upsilon }_{d0} \) = \( \upsilon_{d0} \) \( \hat{x} \)). However, electrons’ \( \vec{E} \) × \( \vec{B} \) drift is only in the y-direction (\( \vec{\upsilon }_{e0} \) = \( \upsilon_{e0} \) \( \hat{y} \)). Under this situation, we write the linearized form of Eqs. (1–6).

The oscillations of the first-order quantities \( n_{i1} \), \( n_{e1} \), \( n_{d1} \), \( \vec{\upsilon }_{i1} \), \( \vec{\upsilon }_{e1} \), \( \vec{\upsilon }_{d1} \), and \( \vec{E}_{1} \) are taken as ~ \( e^{{i(\omega t - k_{x} x - k_{y} y)}} \) together with \( \omega \) as the frequency of oscillations. In view of large density gradient scale length \( L \) or the weak inhomogeneity, we use the condition \( \upsilon_{i} < < \omega L \). The usual mode analysis yields the expressions for the perturbed quantities. Hence, from the equation of continuity and the equation of motion of ions, we then obtain:

$$ n_{i1} = \frac{{ek^{2} n_{i0} \phi_{1} }}{{m_{i} \left[ {(\omega - k_{xy} \upsilon_{i0} )^{2} - k^{2} V_{{{\text{th}}i}}^{2} } \right]}}. $$
(8)

Similarly, we get for the electrons:

$$ n_{e1} = \frac{{en_{e0} \hat{\omega }k^{2} \phi_{1} }}{{m_{e} \left[ {\varOmega^{2} (\omega - k_{xy} \upsilon_{e0} ) + \hat{\omega }k^{2} V_{{{\text{th}}e}}^{2} } \right]}}, $$
(9)

where \( \hat{\omega } = \omega - k_{xy} \upsilon_{e0} - i\nu \).

Finally, the dust density oscillations are obtained as follows:

$$ n_{d1} = - \frac{{ek^{2} Z_{d} n_{d0} \phi_{1} }}{{m_{d} \left[ {(\omega - k_{xy} \upsilon_{d0} )^{2} - k^{2} V_{{{\text{th}}d}}^{2} } \right]}}. $$
(10)

We define the plasma frequencies as \( \omega_{pe} = \sqrt {\frac{{e^{2} n_{e0} }}{{m_{e} \varepsilon_{0} }}} \), \( \omega_{pi} = \sqrt {\frac{{e^{2} n_{i0} }}{{m_{i} \varepsilon_{0} }}} \), and \( \omega_{pd} = \sqrt {\frac{{Z_{d}^{2} e^{2} n_{d0} }}{{m_{d} \varepsilon_{0} }}} , \) and use the linearized form of Poisson’s equation to get:

$$ - k^{2} \phi_{1} = \frac{{\omega_{pe}^{2} \hat{\omega }k^{2} \phi_{1} }}{{\varOmega^{2} (\omega - k_{xy} \upsilon_{e0} ) + \hat{\omega }k^{2} V_{{{\text{th}}e}}^{2} }} - \frac{{\omega_{pi}^{2} k^{2} \phi_{1} }}{{(\omega - k_{xy} \upsilon_{i0} )^{2} - k^{2} V_{{{\text{th}}i}}^{2} }} - \frac{{\omega_{pd}^{2} k^{2} \phi_{1} }}{{(\omega - k_{xy} \upsilon_{d0} )^{2} - k^{2} V_{{{\text{th}}d}}^{2} }}. $$
(11)

Here, \( V_{{{\text{th}}j}} \) is the thermal speed of the plasma species, given by \( V_{{{\text{th}}j}} = \sqrt {T_{j} /m_{j} } \) together with j = i, e and d for the ions, electrons, and dust, respectively.

Equation (11) yields the following dispersion equation in polynomial form, as \( \phi_{1} \) ≠ 0:

$$ \omega^{5} (\omega_{pe}^{2} + \varOmega^{2} + k^{2} V_{{{\text{th}}e}}^{2} ) - \omega^{4} f_{1} + \omega^{3} f_{2} - \omega^{2} f_{3} + \omega f_{4} - f_{5} = 0. $$
(12)

Here

$$ f_{1} = \omega_{pe}^{2} (2k_{xy} \upsilon_{i0} + 2k_{xy} \upsilon_{d0} + g_{4} ) + 2k_{xy} (\upsilon_{i0} + \upsilon_{d0} )\left\{ {\varOmega^{2} + k^{2} V_{{{\text{th}}e}}^{2} } \right\} + g_{3} , $$
$$ f_{2} = \left[ \begin{aligned} \omega_{pe}^{2} (g_{1} + g_{2} + 2k_{xy} \upsilon_{i0} g_{4} + 2k_{xy} \upsilon_{d0} g_{4} + 4k_{xy}^{2} \upsilon_{i0} \upsilon_{d0} ) + 2k_{xy} g_{3} (\upsilon_{i0} + \upsilon_{d0} ) \hfill \\ + (\varOmega^{2} + k^{2} V_{{{\text{th}}e}}^{2} )\left\{ {4k_{xy}^{2} \upsilon_{i0} \upsilon_{d0} - \omega_{pi}^{2} - \omega_{pd}^{2} + g_{1} + g_{2} } \right\} \hfill \\ \end{aligned} \right], $$
$$ f_{3} = \left[ \begin{aligned} \omega_{pe}^{2} (g_{1} g_{4} + g_{2} g_{4} + 2k_{xy} \upsilon_{i0} g_{2} + 2k_{xy} \upsilon_{d0} g_{1} + 4k_{xy}^{2} \upsilon_{i0} \upsilon_{d0} g_{4} ) + g_{3} (4k_{xy}^{2} \upsilon_{i0} \upsilon_{d0} - \omega_{pi}^{2} + g_{1} + g_{2} ) \hfill \\ + 2k_{xy} (\varOmega^{2} + k^{2} V_{{{\text{th}}e}}^{2} )\left\{ {\upsilon_{d0} g_{1} + \upsilon_{i0} g_{2} - \omega_{pi}^{2} \upsilon_{d0} } \right\} - 2\omega_{pd}^{2} k_{xy} \upsilon_{i0} (\varOmega^{2} + k^{2} V_{{{\text{th}}e}}^{2} ) - \omega_{pd}^{2} g_{3} \hfill \\ \end{aligned} \right], $$
$$ f_{4} = \left[ \begin{aligned} \omega_{pe}^{2} (g_{1} g_{2} + 2k_{xy} \upsilon_{i0} g_{2} g_{4} + 2k_{xy} \upsilon_{d0} g_{1} g_{4} ) + 2k_{xy} g_{3} (\upsilon_{d0} g_{1} + \upsilon_{i0} g_{2} - \upsilon_{d0} \omega_{pi}^{2} ) \hfill \\ + g_{2} (\varOmega^{2} + k^{2} V_{{{\text{th}}e}}^{2} )\left\{ {g_{1} - \omega_{pi}^{2} } \right\} - \omega_{pd}^{2} (\varOmega^{2} g_{1} + k^{2} V_{{{\text{th}}e}}^{2} g_{1} + 2k_{xy} \upsilon_{i0} g_{3} ) \hfill \\ \end{aligned} \right], $$
$$ f_{5} = (\omega_{pe}^{2} g_{1} g_{2} g_{4} - \omega_{pi}^{2} g_{2} g_{3} - \omega_{pd}^{2} g_{1} g_{3} + g_{1} g_{2} g_{3} ), $$

together with

$$ g_{1} = k_{xy}^{2} \upsilon_{i0}^{2} - k_{xy}^{2} V_{{{\text{th}}i}}^{2} , $$
$$ g_{2} = k_{xy}^{2} \upsilon_{d0}^{2} - k_{xy}^{2} V_{{{\text{th}}d}}^{2} , $$
$$ g_{3} = k_{xy} \upsilon_{e0} (\varOmega^{2} + k^{2} V_{{{\text{th}}e}}^{2} ) + ivk^{2} V_{{{\text{th}}e}}^{2} , $$
$$ g_{4} = (k_{xy} \upsilon_{e0} + iv). $$

This equation governs the electrostatic waves in the Hall thruster’s channel.

Approximated growth rate: analytical calculations

As per Refs. [15, 17, 20], we can make use of the condition \( \omega < < \left| {k_{xy} \upsilon_{e0} } \right| \). The use of the other condition \( \omega < < \left| {k_{xy} \upsilon_{i0} } \right| \) for the low-frequency waves is also justified in view of the strongly tilted azimuthal wave, where a strong axial component of the wave vector, i.e., \( k_{x} \), is developed and the wave numbers \( k_{x} \) and \( k_{y} \) can attain values up to 104 and the velocity of the ions is also about 104 in the Hall thruster plasma. Hence, both these conditions yield the following from Eq. (11):

$$ (\omega - k_{xy} \upsilon_{d0} )^{2} = \frac{{\left[ {\omega_{pe}^{2} g_{1} (k_{xy} \upsilon_{e0} + iv) + k_{xy} \upsilon_{e0} g_{22} (g_{1} - \omega_{pi}^{2} )} \right]k^{2} V_{{{\text{th}}d}}^{2} + \omega_{pd}^{2} k_{xy} \upsilon_{e0} g_{1} g_{22} }}{{k_{xy} \upsilon_{e0} \left[ {\omega_{pe}^{2} g_{1} \left( {1 + \frac{iv}{{k_{xy} \upsilon_{e0} }}} \right) + g_{22} (g_{1} - \omega_{pi}^{2} )} \right]}}. $$
(13)

or

$$ (\omega - k_{xy} \upsilon_{d0} )^{2} = \frac{{g_{33} \left[ {1 + \left\{ {\frac{{ivg_{1} k^{2} V_{{{\text{th}}d}}^{2} }}{{k_{xy} \upsilon_{e0} g_{33} }}} \right\}} \right]}}{{g_{44} \left[ {1 + \left\{ {\frac{{ivg_{1} }}{{k_{xy} \upsilon_{e0} g_{44} }}} \right\}} \right]}}. $$
(14)

Since the last terms in the square brackets of the numerator and denominator in the right-hand side of (14) are small, we can approximate Eq. (14) as follows:

$$ \omega - k_{xy} \upsilon_{d0} = \pm \sqrt {\frac{{g_{33} }}{{g_{44} }}} \left[ {\left( {1 + \frac{{ivg_{1} k^{2} V_{{{\text{th}}d}}^{2} }}{{2k_{xy} \upsilon_{e0} g_{33} }}} \right)\left( {1 - \frac{{ivg_{1} }}{{2k_{xy} \upsilon_{e0} g_{44} }}} \right)} \right]. $$
(15)

Here, \( g_{33} = \left( {\frac{{\omega_{pd} }}{{\omega_{pe} }}} \right)^{2} g_{1} g_{22} + k^{2} V_{{{\text{th}}d}}^{2} g_{44} \), \( g_{44} = g_{1} + g_{22} \left[ {\frac{{g_{1} }}{{\omega_{pe}^{2} }} - \frac{{\omega_{pi}^{2} }}{{\omega_{pe}^{2} }}} \right] \) together with \( g_{22} = \varOmega^{2} + k^{2} V_{{{\text{th}}e}}^{2} + \left( {\frac{{ivk^{2} V_{{{\text{th}}e}}^{2} }}{{k_{xy} \upsilon_{e0} }}} \right) \).

Finally, the growth rate \( \gamma \) of the resistive instability is evaluated from the above equation. From here on, we normalize the growth rate to the ion plasma frequency, so that the dimensionless ratio \( \gamma \) \( \equiv {{\text{Im} (\omega )} \mathord{\left/ {\vphantom {{\text{Im} (\omega )} {\omega_{pi} }}} \right. \kern-0pt} {\omega_{pi} }} \) is given by the following:

$$ \gamma \approx \frac{v}{{2k_{xy} \upsilon_{e0} }}\sqrt {\frac{{g_{33} }}{{g_{44} }}} \left[ {g_{1} \left( {\frac{1}{{g_{44} }} - \frac{{k^{2} V_{{{\text{th}}d}}^{2} }}{{g_{33} }}} \right)} \right]. $$
(16)

The above relation (16) reveals that the source of the present resistive instability is the electron collisions. Although the collision rate does not change with the temperatures of the plasma species, the growth rate \( \gamma \) of the instability is modified due to the finite temperatures \( T_{i} \), \( T_{d} \), and \( T_{e} \).

Results: based on numerical calculations of Eq. (12)

To analyze the results, we solve Eq. (12) numerically with the parameters generally realized in the Hall thrusters [14,15,16,17, 20, 21, 30,31,32,33]. This way which we find five roots of Eq. (12) out of which two belong to the instabilities along with the other two for the damped waves. The magnitude of the growth rate of one of the instabilities is very less (about 3 orders less than the growth rate of the resistive instability studied in the article), and hence, that is not considered. The fifth root belongs to the damped wave, which is also not of importance. Hence, we plot the growth rate of only one of the resistive instabilities in Figs. 1 and 2 that show the effect of dust charge, dust density, and magnetic field on the growth.

Fig. 1
figure 1

Variation of growth rate \( \gamma \) with the dust charge \( Z_{d} \) for different dust density in the plasma having Xe ions (M = 131 amu), when \( B = 0.015 \) T, \( T_{e} = 25 \) eV, \( T_{i} = 1 \) eV, \( T_{d} = 0.03 \) eV, \( n_{i0} = 10^{18} \)/m3, \( n_{d0} = 10^{14} \)/m3, \( n_{e0} = n_{i0} - Z_{d} n_{d0} \), \( \upsilon_{e0} = 10^{6} \) m/s, \( \upsilon_{i0} = 10^{4} \) m/s, \( \upsilon_{d0} = 10 \) m/s, \( k_{x} = \) \( k_{y} = 1000 \)/m, \( m_{d} \) = \( 10^{ - 17} \) kg, \( d = 6.0 \) cm, and \( v = 10^{6} \)/s

Full size image
Fig. 2
figure 2

Variation of growth rate \( \gamma \) with the dust density \( n_{d0} \) for different magnetic fields in the plasma having Xe ions (M = 131 amu) and \( Z_{d} \) = 500, and all other parameters are the same as Fig. 1

Full size image

In Fig. 1, we show the dependence of the growth rate on the dust charge number with different density of the dust contamination. It is observed that the charge of the dust influences the growth very significantly; the same is the case for the higher density of the dust particles. It means that the present resistive instability grows faster when the channel of the thruster is contaminated more with larger dust density having large negative charge. The increase of the growth rate with the dust charge is an expected result, because the increase of the charges on the dust particles results in the rise of potential and an enhancement in the distorting force which unsettles the equilibrium of the plasma in the thruster channel [34]. Although the magnetic field affects only the motion of the electrons, this is important to examine the behavior of the growth rate in view of the coupling of \( \vec{E} \) × \( \vec{B} \) drift of the electrons with the oscillations. On the other hand, if the dust particles attain positive charge, then the perturbed dust density is obtained as \( n_{d1} = \frac{{ek^{2} Z_{d} n_{d0} \phi_{1} }}{{m_{d} \left[ {(\omega - k_{xy} \upsilon_{d0} )^{2} - k^{2} V_{{{\text{th}}d}}^{2} } \right]}} \) [in place of Eq. (10)] and the quasineutrality condition reads \( n_{e0} = n_{i0} + Z_{d} n_{d0} \). For this situation, the variation of the growth rate shown in Fig. 1 reveals that the growth rate of the instability behaves oppositely with the charge of the dust. This is due to the different Coulomb’s force existing between the dust particles and other species of the plasma.

The most striking results in Fig. 1 are that there is a sudden increase of the growth rate when the charge (negative) of the dust is around 900 or more. This can be understood as follows. As per charge neutrality condition \( n_{i0} = n_{e0} + Z_{d} n_{d0} \), the density of the electrons goes down with the increase of the dust charge, and around Zd = 900 or more and \( n_{d0} = 9 \times 10^{14} \)/m3, almost all the electrons are attached to the dust particles reducing drastically the electrons density, i.e., ne0 → 0. Under this situation, enormously large Coulomb’s force affects the dynamics of the plasma oscillations and leads to more unstable situation; and hence, a sudden increase in the growth rate is realized.

Figure 2 shows the impact of dust density with increasing magnetic field on the growth rate. The growth rate amounts to higher magnitude in the case of higher magnetic field. In addition, the effect of dust density on the growth rate of instability is also significant when stronger magnetic field is applied. The increase of the growth rate with the dust density is due to the reduced grain distance with the increase of the dust density in the plasma which increases the inter grain repulsion due to Coulomb force between the dust particles and results in a stronger distorting force that unsettles the equilibrium [34].

Conclusions

In the present paper, we have examined strongly tilted the resistive instability under the effect of dust in Hall thruster plasma. In the channel plasma, due to the coupling of electron drift with the oscillations in the presence of collisions, azimuthally propagating wave of wave vector \( k_{y} \) grows. In such types of instabilities, an axial component of wave vector \( k_{x} \) also generates. In the present model, we considered the case of strongly tilted wave, i.e., when \( k_{x} \) = \( k_{y} \). It was found that the instability grows faster when this component is developed. The main focus was on the impact of dust on the growth of this instability in the plasma. The magnitude of growth rate in the presence of dust is much lower than in its absence in the plasma and the growth rate behaves oppositely with the charge of the dust for the different cases of the positively and negatively charged dust particles.