Introduction and motivation

Gamma rays are produced in a nuclear explosion, which interact with air molecules through a process called Compton effect, and electrons are scattered at high energies that ionize the atmosphere, hence, generating a powerful electrical field. A large-scale electromagnetic pulse (EMP) effect can be produced by a single nuclear explosion exploded high in the atmosphere. This effect is known as High Altitude EMP (HEMP) effect, which is harmless to people as it radiates outward, but can overload computer circuitry and damage it much more swiftly with effects similar to a lightning strike. A similar but smaller scale EMP effect can be created through explosion by nonnuclear devices having powerful batteries or reactive chemicals. This method is called high power microwave (HPM) effect. Due to generation of intense microwaves, these effects are also very damaging to electronics, but within a much smaller area. Depending upon the amount of energy that is coupled to the target, the microwave weapon systems have the ability to produce graduated effects in the target electronics [1]. Actually the electronic components, especially the integrated circuits, microelectronics, and components found in modern electronic systems, are very sensitive to the microwave emissions [2–4].

The HPM sources have been investigated by several researchers [2, 5, 6] as potential weapons for a variety of battle, damage, and terrorist applications in view of very short pulse (about 100 ps) released by an electromagnetic weapon and the damage they can cause. On the other hand, beams of ions and electrons are created in an explosion-generated plasma (EGP), which is a source of free energy. This energy can be transferred to waves generated by the oscillations of plasma species in the explosion. Then, these waves can evolve into different types of instabilities including explosive instabilities [7–10]. The explosive instabilities are of practical importance, as these seem to offer a mechanism for rapid dissipation of coherent wave energy into thermal motion and, hence, may be effective for plasma heating [7, 8]. The simplest wave coupling process that can exhibit explosive character is the coupling of three waves with fixed phases [11–13]. The phenomenon of a wave triplet was first described by Cairns [14] using the kinetic equation, in which all the three waves grow simultaneously. Considering a relativistic ion beam and a nonisothermal plasma, Fainshtein and Chernova [15] have investigated high-frequency instabilities and the high power electromagnetic radiation generation from the development of an explosive. Relativistic plasmas have also been explored for the instabilities and nonlinear waves that retain their shapes during propagation [16–21].

In the plasma generated by an explosion, the electrons may not follow the Boltzmann distribution and, hence, their finite mass needs to be taken into account. Moreover, the relativistic effects of plasma species should be included to realize the exact behavior of the waves or instabilities. Hence, in this article, we consider the relativistic effects of the electrons and ions. Also, we take into account the dust particles which are always present in most of such plasmas and whose charge may fluctuate due to currents flowing into the dust and emissions taking place [22, 23]. Further, we consider the temperature of electrons (T e) to be higher than that of the ions (T i) and dust particles (T d), i.e., \( T_{\text{e}} \gg T_{i} \gg T_{\text{d}} \), in view of a strongly nonisothermal plasma [24–27].

Basic fluid equations and dispersion equation

We consider that the plasma consists of electrons (density n e, mass m), ions (density n i , mass M), and dust particles (density n d, mass m d) having uniform mass and charge (Z d e). If the unperturbed density of these species is \( n_{j 0} \), where j refers to e for electrons, i for ions, and d for dust particles, then the quasineutrality condition reads \( n_{\text{e0}} = n_{\text{i0}} + \alpha Z_{\text{d}} n_{\text{d0}} \), where \( \alpha \) is +1 for the positively charged dust particles and −1 for the negatively charged dust particles. If \( \vec{\upsilon }_{\text{i}} \) (\( \vec{u}_{\text{e}} \)) is the ion (electron) fluid velocity along with their unperturbed values as \( \upsilon_{0} \) and \( u_{0} \), then the one-dimensional continuity and momentum equations for the ion, electron and dust fluids can be written as:

$$ \frac{\partial }{\partial t}(\gamma_{i} n_{i} ) + \frac{\partial }{\partial x}(\gamma_{i} n_{i} \upsilon_{i} ) = 0 , $$
(1)
$$ \frac{\partial }{\partial t}(\gamma_{\text{e}} n_{\text{e}} ) + \frac{\partial }{\partial x}(\gamma_{\text{e}} n_{\text{e}} u_{\text{e}} ) = 0 , $$
(2)
$$ \frac{{\partial {\text{n}}_{\text{d}} }}{\partial t} + \frac{\partial }{\partial x}(n_{\text{d}} \upsilon_{\text{d}} ) = 0 , $$
(3)
$$ \frac{\partial }{\partial t}\left( {\gamma_{\text{e}} u_{\text{e}} } \right) + u_{\text{e}} \frac{\partial }{\partial x}\left( {\gamma_{\text{e}} u_{\text{e}} } \right) + \frac{M}{{{\text{mn}}_{\text{e}} }}\frac{{\partial {\text{n}}_{\text{e}} }}{\partial x} - \frac{M}{m}\frac{\partial \varphi }{\partial x} = 0 , $$
(4)
$$ \frac{\partial }{\partial t}\left( {\gamma_{i} \upsilon_{i} } \right) + \upsilon_{i} \frac{\partial }{\partial x}\left( {\gamma_{i} \upsilon_{i} } \right) + \frac{\sigma }{{n_{i} }}\frac{{\partial {\text{n}}_{i} }}{\partial x} + \frac{\partial \varphi }{{\partial {\text{x}}}} = 0 , $$
(5)
$$ \frac{{\partial \upsilon_{\text{d}} }}{\partial t} + \upsilon_{\text{d}} \frac{{\partial \upsilon_{\text{d}} }}{\partial x} + \delta \frac{M}{{n_{{{\text{d}}0}} m_{\text{d}} }}\frac{{\partial n_{\text{d}} }}{\partial x} + \frac{\alpha M}{{m_{\text{d}} }}\frac{\partial \varphi }{\partial x} = 0 . $$
(6)

Here \(\upsilon_{\text{d}}\) is the dust fluid velocity along with its unperturbed value as \(\upsilon_{\text{d0}}\).

The system of equations can be closed with the following Poisson’s equation:

$$ \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} - n_{\text{e}} + n_{i} + \alpha n_{\text{d}} Z_{\text{d}} = 0 $$
(7)

In the above equations, the densities are normalized by a background density \( n_{0} \), potential \( \varphi \) by \( T_{\text{e}} /e \), time t by the inverse of frequency \( \omega_{\text{pi}} = \sqrt {e^{2} n_{0} /\varepsilon_{0} M} \), space x by the Debye length \( \lambda_{\text{De}} = \sqrt {\varepsilon_{0} T_{\text{e}} /e^{2} n_{0} } \), and velocities \( \upsilon_{\text{i}}, u_{\text{i}} \) and \( \upsilon_{\text{d}}\) by the ion acoustic speed C s = \( \sqrt {T_{\text{e}} /M} \). The ion- (dust-)-to-electron temperature ratio \( T_{i} /T_{\text{e}} \)(\( T_{\text{d}} /T_{\text{e}} \)) is taken as \( \sigma (\delta ) \). Also \( \gamma_{e} = \left( {1 - \frac{{u_{0}^{2} }}{{c^{2} }}} \right)^{{ - \frac{1}{2}}} \) and \( \gamma_{i} = \left( {1 - \frac{{\upsilon_{0}^{2} }}{{c^{2} }}} \right)^{{ - \frac{1}{2}}} \) are the relativistic factors for the electrons and ions, respectively.

We consider the variation of perturbed quantities as \( \psi_{1} \) ~\( \exp (i\omega t - ikx) \), where \( \psi_{1} \equiv n_{i1} , \) \( n_{e1} \), \( n_{d1} \), \( \vec{\upsilon }_{i1} \), \( \vec{u}_{e1} \), \( \vec{\upsilon }_{d1} \), \( \vec{\varphi }_{1} \), \( \omega \) is the frequency of oscillations and \( k \) is the wave number. Then, such variations are used in the basic fluid equations while employing the normal mode analysis. This way linear analysis yields:

$$ n_{i1} = \frac{{k^{2} n_{i0} \varphi_{1} }}{{\gamma_{i} (\omega - k\upsilon_{0} )^{2} - \sigma k^{2} }},\,\, n_{e1} = \frac{{k^{2} \varphi_{1} }}{{\gamma_{e} \frac{m}{M}(\omega - ku_{0} )^{2} - k^{2} }},\,\, n_{d1} = \frac{{k^{2} \alpha Z_{d} n_{d0} \varphi_{1} }}{{\frac{{m_{d} }}{M}(\omega - k\upsilon_{d0} )^{2} - k^{2} \delta }}. $$

The use of these expressions in the Poisson’s Eq. (7) gives rise to:

$$ \frac{{k^{2} \varphi_{1} }}{{\frac{m}{M}\gamma_{\text{e}} (\omega - ku_{0} )^{2} - k^{2} }} - \frac{{k^{2} n_{i0} \varphi_{1} }}{{\gamma_{i} (\omega - k\upsilon_{0} )^{2} - \sigma k^{2} }} - \frac{{k^{2} \alpha^{2} Z_{\text{d}}^{2} n_{{{\text{d}}0}} \varphi_{1} }}{{\frac{{m_{\text{d}} }}{M}(\omega - k\upsilon_{{{\text{d}}0}} )^{2} - k^{2} \delta }} + k^{2} \varphi_{1} = 0 $$
(8)

After simplifying the above equation, we get the following dispersion equation:

$$ \frac{{mm_{\text{d}} }}{{M^{2} }}\gamma_{\text{e}} \gamma_{i} \omega^{6} - b_{0} \omega^{5} + \omega^{4} b_{1} + \omega^{3} b_{2} + \omega^{2} b_{3} + \omega b_{4} + a_{1} a_{2} a_{3} + a_{2} a_{4} + a_{1} a_{4} (n_{i0} - a_{2} ) = 0 . $$
(9)

Here

$$ \begin{gathered} b_{0} = \frac{{m_{{\text{d}}} }}{M}\left( {a_{{11}} + \frac{{2m}}{M}\gamma _{i} \gamma _{{\text{e}}} k\upsilon _{{{\text{d}}0}} } \right){\mkern 1mu} ,\;b_{1} = a_{{14}} + \frac{{m_{{\text{d}}} }}{M}\left( {\gamma _{i} - \gamma _{{\text{e}}} \frac{{n_{{i0}} m}}{M}} \right) - a_{3} \frac{m}{M}\gamma _{i} \gamma _{{\text{e}}} {\mkern 1mu} ,\;b_{2} = a_{3} a_{{11}} - a_{{15}} + n_{{i0}} a_{8} - a_{5} , \hfill \\ {\mkern 1mu} b_{3} = a_{3} a_{{12}} - a_{{16}} + a_{6} + n_{{i0}} a_{9} ,\;{\mkern 1mu} b_{4} = a_{{17}} - a_{7} + a_{3} a_{{13}} + n_{{i0}} a_{{10}} {\mkern 1mu} ,a_{1} = k^{2} \left( {1 - \frac{m}{M}\gamma _{{\text{e}}} u_{0}^{2} } \right) \hfill \\ {\mkern 1mu} a_{2} = k^{2} (\gamma _{i} \upsilon _{0}^{2} - \sigma ),\;{\mkern 1mu} a_{3} = \alpha ^{2} Z_{{\text{d}}}^{2} n_{{{\text{d}}0}} ,\;{\mkern 1mu} a_{4} = k^{2} \left( {\frac{{m_{{\text{d}}} }}{M}\upsilon _{{{\text{d0}}}}^{2} - \delta } \right). \hfill \\ \end{gathered} $$

Together with \( a_{5} = \gamma_{i} \frac{{m_{\text{d}} }}{M}k(\upsilon_{0} + \upsilon_{\text{d0}} ) \), \( a_{6} = \gamma_{i} \left[ {\frac{{m_{\text{d}} }}{M}\left( {4k^{2} \upsilon_{0} \upsilon_{\text{d0}} + \frac{{a_{2} }}{{\gamma_{i} }}} \right) + a_{4} } \right] \), \( a_{7} = 2k\left( {\gamma_{i} \upsilon_{0} a_{4} + \frac{{m_{\text{d}} }}{M}a_{2} \upsilon_{\text{d0}} } \right) \), \( a_{8} = \frac{{2\gamma_{e} mm_{\text{d}} }}{{M^{2} }}k\left( {u_{0} + \upsilon_{\text{d0}} } \right) \), \( a_{9} = \frac{{m_{\text{d}} }}{M}\left( {a_{1} - \frac{4m}{M}\gamma_{\text{e}} k^{2} u_{0} \upsilon_{\text{d0}} } \right) - \gamma_{\text{e}} \frac{m}{M}a_{4} \), \( a_{10} = \frac{{2ku_{0} m}}{M}a_{4} \gamma_{\text{e}} - \frac{{2m_{\text{d}} }}{M}k\upsilon_{\text{d0}} a_{1} \), \( a_{11} = \frac{{2\gamma_{\text{e}} \gamma_{i} m}}{{M^{2} }}k(u_{0} + \upsilon_{0} ) \), \( a_{12} = \gamma_{i} \left( {a_{1} - \frac{4m}{M}\gamma_{\text{e}} k^{2} u_{0} \upsilon_{0} } \right) - \gamma_{\text{e}} \frac{m}{M}a_{2} \), \( a_{13} = 2k\left( {\frac{m}{M}\gamma_{\text{e}} a_{2} u_{0} - \gamma_{i} a_{1} \upsilon_{0} } \right) \),\( a_{14} = \gamma_{\text{e}} \gamma_{i} \frac{m}{M}a_{4} - \frac{{m_{\text{d}} }}{M}(a_{12} - 2ka_{11} \upsilon_{{{\text{d}}0}} ) \), \( a_{15} = \frac{{m_{\text{d}} }}{M}(a_{13} - 2a_{12} k\upsilon_{{{\text{d}}0}} ) + a_{4} a_{11} \), \( a_{16} = \frac{{m_{d} }}{M}(a_{1} a_{2} - 2a_{13} k\upsilon_{d0} ) + a_{4} a_{12} \), \( a_{17} = \frac{{2m_{\text{d}} }}{M}a_{1} a_{2} k\upsilon_{\text{d0}} - a_{4} a_{13} \).

Numerical solution to dispersion equation and the results

We solve Eq. (9) numerically by giving typical values to various parameters in view of the explosion-generated relativistic plasma (EGRP). Hence \( k = 1 \), \( n_{i0} = 1.1 \), \( M = 23.38 \times 10^{ - 27} \) kg, \( m_{\text{d}} = 10^{ - 20} \) kg, \( \upsilon_{\text{d0}} = 1 \), \( u_{0} = 4,000 \), \( \upsilon_{ 0} = 2,000 \), \( n_{\text{nd0}} = 0.001 \), \( Z_{\text{d}} = 100 \), \( T_{i} = 10 \) eV, \( T_{\text{d}} = 1 \) eV and \( T_{\text{e}} = 50 \) eV [28–32]. Our calculations reveal that two types of instabilities occur in the said plasma if the dust particles and relativistic effects are considered. Both types of the instabilities are high-frequency instabilities but carry growth rates of different magnitudes. In view of the magnitudes, the instability having higher growth rate \( \gamma_{1} \) is taken to correspond to the high-frequency higher growth rate instability, which we call as HFHGI, and the instability having lower growth rate \( \gamma_{2} \) is taken to correspond to the high-frequency lower growth rate instability, which we call as HFLGI. In addition to these instabilities, a propagating mode is also found to occur.

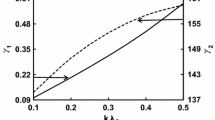
Figure 1 shows the variation of growth rates \( \gamma_{1} \) and \( \gamma_{2} \) along with their real frequencies \( \omega_{\text{R1}} \) and \( \omega_{\text{R2}} \) with normalized wave number \( k \). Here one obtains that the growth rates attain different peaks corresponding to different values of k. The peak corresponding to HFHGI appears towards higher side of k compared to the case of HFLGI. However, the growth rate \( \gamma_{2} \) is found to almost saturate for the longer values of \( k \). Since the free energy needs to be coupled with the wave to cause the wave to grow, it appears that the maximum energy transfer takes place to the oscillations of a particular wavelength only. Hence, in our case, the growth rate of HFHGI is a maximum at a particular value of k. However, another type of instability (HFLGI) may attain the maximum value at much larger value of k. This can be confirmed if we plot the graph for much larger values of k.

Fig. 1
figure 1

Variation of growth rates \( \gamma_{1} \) and \( \gamma_{2} \) along with their real frequencies \( \omega_{R1} \) and \( \omega_{R2} \) with normalized wave number \( k \), when \( n_{i0} = 1.1 \), \( M = 23.38 \times 10^{ - 27} \) kg, \( m_{\text{d}} = 10^{ - 20} \) kg, \( \upsilon_{\text{d0}} = 1 \), \( u_{0} = 4,000 \), \( \upsilon_{0} = 2,000 \), \( n_{\text{nd0}} = 0.001 \), \( Z_{\text{d}} = 100 \), \( T_{i} = 10 \) eV, \( T_{\text{d}} = 1 \) eV and \( T_{\text{e}} = 50 \) eV

Full size image

Another interesting result is that both these instabilities propagate at constant velocities. The HFHGI propagates faster than the HFLGI. Hence, it can also be said that the wave propagating at higher speed evolves into an instability having larger growth rate. This is the similar result as obtained recently in a nonrelativistic EGP [33]. Consistent to Ref. 33, the present plasma also supports a propagating mode which has a constant velocity (Fig. 2).

Fig. 2
figure 2

Variation of frequency \( \omega_{\text{PR}} \) of the propagating mode with normalized wave number, when the parameters are taken the same as in Fig. 1

Full size image

Figures 3 and 4 show the effect of relativistic speeds of electrons and ions on the growth rates \( \gamma_{1} \) and \( \gamma_{2} \) along with the real frequencies \( \omega_{\text{R1}} \) and \( \omega_{\text{R2}} \). Both types of the instabilities are observed to behave oppositely with the speeds v 0 and u 0. The growth rates \( \gamma_{1} \) and \( \gamma_{2} \) are reduced with the higher speed of the electrons, whereas these are enhanced for the higher speed of the ions. It means that the relativistic effects of the ions support the instability to grow, whereas due to the relativistic effect of the electrons the instabilities are suppressed. However, the propagation speed of the instabilities is enhanced in both the cases and this effect is linear in nature. Consistent to this observation in an EGRP, other investigators have also found the same effect of relativistic speeds of ions and electrons on the phase velocity of linear ion acoustic waves [16–21, 31].

Fig. 3
figure 3

Variation of growth rates \( \gamma_{1} \) and \( \gamma_{2} \) along with the real frequency \( \omega_{\text{R1}} \) corresponding to HFHGI with relativistic speed of electrons, when \( k = 1 \) and the other parameters are the same as in Fig. 1

Full size image
Fig. 4
figure 4

Variation of growth rates \( \gamma_{1} \) and \( \gamma_{2} \) along with the real frequency \( \omega_{\text{R2}} \) corresponding to HFLGI with relativistic speed of ions, when \( k = 1 \) and the other parameters are the same as in Fig. 1

Full size image

With respect to the contribution of dust particles to these instabilities, we focus on Fig. 5 and observe that the growths of the instabilities remain unaltered by the drift velocity of the dust particles. However, an interesting feature of the dust grain effect is that a new type of instability develops in the system when the dust drift velocity exceeds a critical value; for example, v d0 > 6 in the present case. But the magnitude of the growth rate of this instability is 4 order less than the ones of HFHGI and HFLGI. On the other hand, the propagation speed of this new type of instability does not show linear dependence on the dust grain drift velocity.

Fig. 5
figure 5

Weak dependence of growth rates\( \gamma_{1} \) and \( \gamma_{2} \) on dust drift velocity, when \( k = 1 \) and other parameters are the same as given in Fig. 1

Full size image

Since this instability is the low-frequency instability, it means that this is related to the wave generated by the oscillations of the dust particles. Since the free energy needs to be coupled with the wave for its growth, it is plausible that the free energy is coupled with such oscillations when the dust particles attain certain value of the drift velocity. Hence, we get a critical value of the drift velocity of the dust particles for the evolution of this new type of the instability.

In Fig. 6, we study the effect of electron temperature on the growth rates \( \gamma_{1} \) and \( \gamma_{2} \). Here, the electron temperature is found to reduce the growth rates of both the instabilities. This result is contrary to the observation made in an explosion-generated nonrelativistic plasma [33]. Hence, it appears that due to the relativistic effect of the ions and electrons, the thermal motions of the electrons start suppressing the growth of the instabilities. On the other hand, Keidar and Beilis [34] had also observed similar effect of the electron temperature on the growth rate of dissipative instability.

Fig. 6
figure 6

Variation of growth rates \( \gamma_{1} \) and \( \gamma_{2} \) with electron temperature, when \( k = 1 \) and the other parameters are the same as in Fig. 1

Full size image

The present calculations are for the realistic situation where a relativistic plasma is generated in an explosion. Hence, we have included the relativistic effects of the speeds of the ions and electrons. However, in view of heavy mass of the dust particles, this is justified to consider them as nonrelativistic but to drift with a finite speed. Our earlier article [33] depicts an approximate situation, where we considered only the initial drifts of the plasma species. In view of the nonrelativistic situation, we had also neglected the temperature of the dust species. However, the finite dust temperature is taken into account in the current calculations. Moreover, the instabilities talked about here correspond to the family of two-stream instabilities since there is a difference in the speeds of all the plasma species.

Finally, we mention that we did more calculations to examine the possibility of wave triplets in the present relativistic plasma. These calculations reveal that the wave triplet can evolve in the plasma only when the dust particles attain negative drift velocity. Since this is not physically acceptable, it can be said that the wave triplets are not possible in an EGRP. In support of this statement, we also understood that the waves are not found to grow for the negative values of k. It means that the possibility of negative energy wave is also ruled out in the plasma where the ions and electrons attain relativistic speeds.

Conclusions

We have investigated high-frequency instabilities in an EGRP under the effect of relativistic speeds of the ions and electrons. The dust particles were also taken into account with their initial nonrelativistic drifts. It was observed that two types of the instabilities generally evolve in such systems. However, a third type of instability appears in the system when the dust particles’ drift velocity exceeds a critical value. The electron temperature was found to suppress the instabilities, whereas the ion temperature does not affect their growths. Both the instabilities were observed to be constant velocity waves. Consistent to the case of explosion-generated nonrelativistic plasma, the present plasma also supports a wave, which does not grow under the relativistic effects of the ions and electrons.