Introduction

An extensive review of the literature identified more than 300 completed bridges (i.e. pedestrian and motorway bridges combined) constructed worldwide using UHPFRC in one or more components (Binard 2017; Voo et al. 2018). In brief, UHPFRC is an ultra-high strength cementitious material that contains a high quantity of cement and silica fume, low quantity of water, incorporates large amounts of fibres and exhibits remarkable characteristics such as high fracture energy, low permeability, limited shrinkage and increased corrosion resistance (Buttignol et al. 2017; El-Tawil et al. 2018). Although UHPFRC precast segmental bridges (PSBs) have been widely used in many countries (Voo and Foster 2016; Hafezolghorani and Voo 2018; Chen et al. 2016), there is relatively scant information available on the shear behaviour and design of such bridges, especially related to the joints between the segments. One of the most used techniques in the PSBs is in their construction using dry keyed joints as the speed of erection and the lack of reliance on weather conditions make this technique more suitable than using epoxy joints (Issa and Abdalla 2007; Bu and Wu 2018). However, the shear load capacity of the joints in PSBs increases by applying epoxy layer across the segments joints (Shamass et al. 2016; Zhou et al. 2005). Rombach (2004), Shamass et al. (2015) and Han et al. (2017) investigated the behaviour of reinforced concrete (RC) multiple-keyed dry joints both numerically and experimentally. Zhou et al. (2005) performed a series of experimental tests and analysed the behaviour of RC single and three-keyed dry joints. A finite-element study investigated the shear strength of RC dry joints of concrete panels to be used in PSBs with external prestressing under combined shear and flexure (Turmo et al. 2006). Hu and Xie (2016) investigated and simulated the bending and twisting working conditions between the shear keys and segments where ultimately, some structural strengthen suggestions on RC shear keys were offered. Nowadays, use of unreinforced small epoxy keys distributed across the precast concrete segmental box girder bridges is a common practice among countries with cold weather. A numerical finite element model analysis using Abaqus program was performed to simulate the shear-off failure of unreinforced RC keyed epoxy joints (Shamass et al. 2016). In this study, damaged plasticity model was used to simulate the concrete material and epoxy layer was modelled as linear elastic material. Initial numerical investigations and experimental tests (Voo et al. 2014; Shin 2017; Jang et al. 2017) indicated that shear strength capacity of UHPFRC keyed dry joints increased with the increase in confining stress and with an increasing number of shear keys. Voo et al. (2014) conducted six-keyed dry joints under push-of setup up to failure and investigated the effects of number of shear keys and amount of confining pressure on the shear capacity on the full-scale specimens. They proposed a shear deign provision approach to estimate the ultimate shear capacity of these jonits, however more test data are needed to validate the accuracy of the proposed approach.

In most previous studies like those presented above, the existing numerical models and empirical formulas from different researchers and design standard codes for calculating the shear capacity of keyed dry and epoxy joints were only dedicated to RC precast segmental bridges [Eqs. (1)–(6)] which lead to different and uncertain values.

Kaneko et al. (1993) proposed shear design provision models to estimate ultimate shear capacity (\(V_{\text{u}}\)) of keyed dry joints with normal strength concrete (20 MPa ≤ \(f_{\text{ck}}\) ≤ 50 MPa) and high strength concrete (50 MPa < \(f_{\text{ck}}\) ≤ 90 MPa) as follows:

$$V_{\text{u}} = A_{\text{k}} \frac{{f_{\text{ck}}^{2/3} }}{100}\left( {7\sigma_{\text{n}} + 33} \right) + 0.6A_{\text{sm}} \sigma_{\text{n}} \left( {f_{\text{ck}} \le 50 \;{\text{MPa}}} \right)$$
(1)
$$V_{\text{u}} = A_{\text{k}} \frac{{\ln \left( {1 + \frac{{f_{\text{ck}} }}{10}} \right)}}{100}\left( {49\sigma_{\text{n}} + 233} \right) + 0.6A_{\text{sm}} \sigma_{\text{n}} \left( {f_{\text{ck}} > 50 \;{\text{MPa}}} \right)$$
(2)

where, \(A_{\text{k}}\), \(f_{\text{ck}}\), \(\sigma_{\text{n}}\) and \(A_{\text{sm}}\) are the area of all the shear keys at the failure plane, characteristic compressive cylinder strength of concrete, confining pressure applied across the joint and smooth area of the joint.

Spanish Standard ATEP (1996) recommends a formula which is reliant upon the sum area of the joint surface as given below:

$$V_{\text{u}} = A_{\text{k}} \left( {1.14\sigma_{\text{n}} + 1.8\sqrt {f_{\text{ck}} } } \right) + 0.6A_{\text{sm}} \sigma_{\text{n}}$$
(3)

AASHTO (1999) suggested a formula to be included as part of the American design code, which separates the shear strength conveyed by the keys from the strength given by the smooth surfaces in contact as presented in Eq. (4).

$$V_{\text{u}} = A_{\text{k}} \sqrt {f_{\text{ck}} } \left( {0.2048\sigma_{\text{n}} + 0.9961 } \right) + 0.6A_{\text{sm}} \sigma_{\text{n}}$$
(4)

Rombach and Specker (Rombach and Specker 2004) analysed the behaviour of multiple-keyed joints by an FE model and proposed the following formula:

$$V_{\text{u}} = 0.14A_{\text{k}} f_{\text{cm}} + 0.65\left( {A_{\text{sm}} + A_{\text{k}} } \right)\sigma_{\text{n}}$$
(5)

where \(f_{\text{cm}}\) is mean value compressive cylinder strength of concrete.

Turmo et al. (2006) recommended a novel formula for inclusion in the Eurocode predicated on the AASHTO formula as:

$$V_{\text{u}} = A_{\text{k}} \sqrt {f_{\text{cd}} } \left( {0.1863\sigma_{\text{n}} + 0.9064 } \right) + 0.45A_{\text{sm}} \sigma_{\text{n}}$$
(6)

where, \(f_{\text{cd}} = \alpha_{\text{cc}} f_{\text{ck}} /\gamma_{\text{c}}\) is design compressive strength. \(\alpha_{\text{cc}} = 1\) and \(\gamma_{c} = 1.5\) are long term effects coefficient and partial safety factor of concrete according to Eurocode 2 (BS 1992).

Hence, there is no numerical model, enough experiments, and practical code provisions to calculate the shear capacity of the UHPFRC dry and especially epoxy joints. To address this issue, this paper presents a numerical analysis model using Abaqus FE code to analyze full-scale UHPFRC joint models with different variable parameters (i.e. number of shear keys, confining stress, and types of joints). Furthermore, to validate the FE models, two full-scale UHPFRC keyed joint specimens were tested under direct shear test and the numerical and experimental results compared together.

Proposed numerical model for UHPFRC shear joints

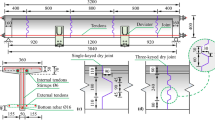
In this study, FE computer program code Abaqus (2011) was used to simulate the 3D UHPFRC keyed joint models under increasing direct shear loading as illustrated in Fig. 1. A 3D mesh type “reduced-integration 8-noded linear brick, hourglass control” (C3D8R) with element size of 25 mm was chosen for male and female components of the shear joint models to ensure the compatibility of mesh topology [see Fig. 1a, c]. Prestressing strands were modelledas a 2-node linear 3D truss elements (T3D2) with mesh element size of 12 mm as shown in Fig. 1a. In Abaqus program code, there are three different constitutive models in order to simulate concrete material(i.e. concrete damaged plasticity (CDP), smeared crack (SC) and brittle model). In this study, the CDP model was chosen which is a suitable method to accurately simulate the inelastic behaviour of concrete in compression and tension (Hafezolghorani et al. 2017). In this study, the uniaxial compressive stress–strain relation, effective parameters called damages in compression and tension and initial parameters were chosen according to the previous studies in the literature (Shamass et al. 2015; Mansur and Ong 1991). In contact modeling, the interaction of the male to female models without epoxy was chosen as surface to surface with frictionless interaction property, while for the numerical models with epoxy, the effect of epoxy was considered through friction coefficient of 0.3 (Mihu et al. 2017). As shown in Fig. 1a, surface to surface interaction was selected for the contact between the prestressing strands and the UHPFRC male and female components and the effects of confining pressure were applied to the shear joint models using predefined field stress in X-direction (Sigma11).

Fig. 1
figure 1

Dimensions and details of the proposed FE keyed joints

Full size image

Parametric study and validation of the proposed numerical model

In this study, a parametric study was performed to investigate the effects of various number of keys (single, three and five keys), type of joints (dry and epoxy) and amount of confining stress (10 MPa and 20 MPa) on the shear capacity of the full-scale keyed joint models as listed in Table 1. In this table, the joint models were designated as D or E JX-Y, where D or E are the models without or with epoxy across the joint, respectively, X represents the number of shear keys and Y indicates the average confining pressure applied to the joints through prestressing strands. For instance, joint model EJ5-20 is five-keyed epoxy joint with confining pressure level of 20 MPa. In general, a total of twelve UHPFRC full-scale FE shear keyed joint models were analysed by considering all the geometries, boundaries, interactions and constraints as shown in Fig. 1. In Table 1, \(A_{\text{k}}\) and \(A_{\text{sm}}\) are total shear key area and smooth contact surface of the failure plane, respectively.

Table 1 Summary of the FE models
Full size table

In the current research, in order to verify the proposed FE model, two full-scale UHPFRC five-keyed dry and epoxy joints subjected to confining pressure level of 20 kN (i.e. DJ5-20 and EJ5-20) were casted and tested under direct shear load as shown in Fig. 2.

Fig. 2
figure 2

Preparation and test setup of the experimental UHPFRC specimens DJ5-20 and EJ5-20

Full size image

The keyed joint specimens were cast through employing the male and female match–cast method. The first stage of the casting procedure of the UHPFRC shear keyed joint specimens started with the female components, then demoulded following 24 h. The second stage consisted of casting the male components and during casting, initial curing was performed before standard heat curing. Within 30 min of casting, the exposed surface of the male and female components as well as the test control samples were sprayed with a curing compound.

Later, all UHPFRC specimens underwent heat treatment of 90 °C and 100% humidity for 48 h as recommended by the French Standard for UHPFRC (2016). The purpose of standard heat curing was to achieve densifying in the hardened state of UHPFRC, accelerate all long-term creep and shrinkage thus leading to a stable geometrical structure and improving the overall durability and strength of the composite material. For the epoxy joint specimen EJ5-20, after applying the epoxy resin on the male component (Fig. 2a), 5-ton concrete block were positioned on top to densely compress the male and female components together.

Confining pressures of 20 MPa was applied to the dry and epoxy joints using 8 numbers of 15.2 mm diameter prestressing strands. In this experiment, two LVDTs were used to measure slip between male and female components of the UHPFRC joint specimens as presented in Fig. 2b. As shown in Fig. 2c, load cell and hydraulic jack with capacity of 500 kN (112,000 lb) were utilised to apply the direct shear load with a stroke rate of 0.005 mm/s during test.

The test results of the concrete mechanical properties according to the French Standard for UHPFRC (2016) is indicated in Table 2. A total of six 100 × 100 × 100 mm cubes an six 100 × 100 × 500 mm prisms were tested at 28 days to calculate mean cube compressive strength (\(f_{{{\text{cm}},{\text{cu}}}}\)), tensile limit of elasticity (\(f_{{{\text{ctm}},{\text{el}}}}\)) and post-cracking tensile strength (\(f_{\text{ctfm}}\)) of the UHPFRC. The characteristic yield strength (\(f_{\text{pk}}\)), elastic modulus (\(E_{\text{p}}\)), and Poisson’s ratio (\(\nu\)) of prestressing strands were taken as 1860 MPa, 195 GPa and 0.3, respectively. Similar material properties was used during analyzing of the FE joint models.

Table 2 Test results on material properties of UHPFRC
Full size table

As shown in Figs. 3a and 4a, it can be seen that the male key zones were detached from keyed joint specimens DJ5-20 and EJ5-20 once reaching the ultimate shear capacity (\(V_{{{\text{j}},{\text{u}}, {\text{Exp}}}}\)).

Fig. 3
figure 3

Comparison of the experimental and FE results for DJ5-20

Full size image
Fig. 4
figure 4

Comparison of the experimental and FE results for EJ5-20

Full size image

From the experimental observations, the initial cracks at key zones of the joint specimens were initially occurredon the bottom of the male key zones at shear loads about 2300 kN and 2700 kN in DJ5-20 and EJ5-20, respectively due to the concentration of the shear stress. At this stage, the existence of steel fibres in the UHPFRC keyed joints improved the shear stress transmission which were almost perpendicular to the crack growth direction. This scenario proves the theories of inelastic behaviour and very high ductility of UHPFRC which leads to an un-brittle failure mechanism. By increasing the direct shear load during the experimental tests, the ultimate shear capacity loads of 3216 kN and 3495 kN were recorded for DJ5-20 and EJ5-20, respectively. Furthermore, as shown in Fig. 5, 2.71 mm and 2.60 mm slips were measured at the ultimate shear capacities between the male and female components ofDJ5-20 and EJ5-20, respectively. From these results, it can be seen that epoxy joint has improved the ultimate shear capacity by 8% and reduced the corresponding slip between male and female components by 4%.From the shear load–displacement curves (Fig. 5a, b), after the ultimate shear load stage, a sudden slip of the middle part occurred which led the specimens to experience sudden drops of load (shear off stage). Once the specimens were completely sheared off, gradual ascending patterns were observed in the shear force–displacement curves, which are attributed by the friction between the two male and female UHPFRC surfaces.

Fig. 5
figure 5

Shear load–displacement curves from experimental and FE results for DJ5-20 and EJ5-20

Full size image

Similarly, from the FE models DJ5-20 and EJ5-20, the results demonstrated that the maximum tension and compression damages occurred at the key zone area as shown in Figs. 3b, c and 4b, c. This would arises due to the concentration of stress distributed along the shear failure plane during applying direct shear load (see Figs. 3d, 4d). From Fig. 5, the FE graphs indicate a sign of reduction in linear elasticity after initial damages in tension and compression and then propagated in an upward direction until failure (shear-off) of the male and female components (\(V_{{{\text{j}},{\text{u}}, {\text{FEM}}}}\)).It can be seen from the FE models (see Figs. 3c, 4c) that less compressive damage occurred on the UHPFRC joint models due to the high compressive strength of the UHPFRC (\(f_{{{\text{cm}},{\text{cu}}}}\) = 170.4 MPa). As shown in Figs. 3b and 4b, more damage was observed due to the tension that occurred at the centre part of the key zone.

Following the shear-off stage, the specimens and FE models continued resisting the applied shear force through the existence of friction between contacted surfaces.

The shear load–displacement curves obtained from experimental and numerical results for specimens DJ5-20 and EJ5-20 are illustrated in Fig. 5a, b, respectively. A comparison between experimental results and numerical responses is carried out in Table 3. From this table, the ultimate shear loads (\(V_{{{\text{j}},{\text{u}}, {\text{FEM}}}}\)) obtained numerically from both the joint models DJ5-20 and EJ5-20 match well with the ultimate shear loads (\(V_{{{\text{j}},{\text{u}}, {\text{Exp}}}}\)) obtained from experimental study. A maximum difference of 0.8% is observed between FE and experimental results of the five-keyed dry joint (DJ5-20).Moreover, a maximum difference of 5.4% is observed in terms of slip between male and female components of the five-keyed epoxy joint (EJ5-20) at ultimate from the experimental and numerical results. Hence, the excellent agreement between simulation and experimental results demonstrates the reliability of the proposed numerical model for UHPFRC keyed dry or epoxy joints.

Table 3 Comparison of experimental and numerical results
Full size table

Figure 6a–c shows the numerical shear load–displacement curves of the single-keyed, three-keyed and five-keyed joint models, respectively under direct shear load considering two variables, types of joint (dry or epoxy) and amount of confining pressure (10 MPa and 20 MPa). As expected and presented in Table 4, it can be seen that the ultimate shear loads (\(V_{{{\text{j}},{\text{u}},{\text{FEM}}}}\)) are higher at the keyed epoxy joint models with larger confining pressure. As shown in Fig. 6a–c, the ultimate shear capacities of EJ1-20, EJ3-20 and EJ5-20 improved by 45.6%, 34%, and 13.5%, respectively compared to DJ1-10, DJ3-10 and DJ5-10. Hence, by increasing the number of shear keys, the effects of epoxy and confining pressure on the ultimate shear load will decrease.

Fig. 6
figure 6

Numerical shear load–displacement curves for UHPFRC keyed joint models

Full size image
Table 4 Results of parametric study on various keyed joint models
Full size table

The ultimate shear load (\(V_{\text{j,u,FEM}}\)) and the corresponding displacement (\({\text{Dis}}_{{{\text{j}},{\text{u}},{\text{FEM}}}}\)) from analysis of the five-keyed dry joint model DJ5-10 are 3045 kN and 1.87 mm, respectively as presented in Fig. 6c. While, the ultimate shear load and the corresponding displacement from analysis of the five-keyed epoxy joint model EJ5-20 are 3521 kN and 2.74 mm, respectively. In overall, by considering all parameters (i.e. number of shear keys, confining stress, and types of joints), the ultimate shear capacity of EJ5-20 improved remarkably by 64% compared to DJ1-10 as shown in Table 4. Also, at ultimate shear capacity, slip between male and female components(\({\text{Dis}}_{{{\text{j}},{\text{u}},{\text{FEM}}}}\)) of EJ5-20 increased up to 99% compared with DJ1-10, which indicates a higher energy dissipation capacity (area below shear load–displacement curve) of the keyed epoxy joint models with more shear keys and larger confining pressure before shearing-off failure.

Comparison of existing provisions with experimental and FEM results for keyed dry joint models

The application of the existing formulations proposed by the various authors leads to significantly different values for the ultimate shear capacity (\(V_{{{\text{j}},{\text{u}},{\text{Exist}}}}\)) of the dry keyed joint as presented in Table 5. Besides, based on an extensive review of the literature, there is no design provision model available to estimate the ultimate shear capacity of the UHPFRC epoxy keyed joints. In this paper, a brief overview of the existing shear joint strength found in the literature was already explained. Some of these formulas have a theoretical basis while others are empirically derived from experimental studies. As illustrated in Table 5, all five existing joint design provision models as given in Eqs. (1)–(6) were used to compare against the experimental results of the full-scale UHPFRC five-keyed dry joint DJ5-20 since all these design provisions are formulated based on dry keyed joints. From this table, minimum and maximum differences of 13% and 87% were observed between results of Kaneko et al. (1993) and ASSHTO (1999) provision models with experimental data in terms of ultimate shear load capacities, respectively.

Table 5 Comparison of existing provision models withexperimental data for DJ5-20
Full size table

Furthermore, the five existing joint design provision models were used to compare against the numerical dry shear keyed joint results since all these design provisions are formulated based on dry shear keyed joints. The mean Exist/FEM ratios, standard deviation (SD) and coefficient of variations (COV) of the all the keyed dry joint models used in this study are presented in Table 6. From this table, results obtained from design provisions by Kaneko et al. (1993) and Turmo et al. (2006) are close to the results that obtained from the proposed numerical model in this research. Mean Exist/FEM ratios of 1.01 and 1.09 exhibit good correlation between results from these two design provisions with the proposed FEM results. However, AASTHO (1999) provision is not providing a reasonable correlation with FEM data which led to the worst mean Exist/FEM ratio of 1.46 and the highest inconsistency of results with a COV of 17.6%. A maximum difference of 87% is observed between results of ASSHTO and FEM for five-keyed dry joint model (DJ5-20)under confining pressure of 20 kN.

Table 6 Comparison of existing provisions with the proposed FEM results
Full size table

As shown in Fig. 7, the safe zone comparison graph clearly shows that the majority of the ultimate shear capacities calculated through the existing design provisions (AASHTO 1999; ATEP 1996; Rombach and Specker 2004) are in the unsafe zone which leads to an unsafe correlation with the numerical results of the UHPFRC keyed dry joints. However, the ultimate shear capacities calculated using design provisions Kaneko et al. (1993) and Turmo et al. (2006) are mostly located in the safe zone and provide good correlation with FEM results. However, this comparison study indicated that new design provision models should be developed to estimate the shear capacity of UHPFRC dry and epoxy joints.

Fig. 7
figure 7

Safe zone comparison of the existing provisions to the FEM results

Full size image

Conclusion

In order to accurately investigate the shear behavior of the joints in UHPFRC precast segmental bridges, a numerical analysis model based on finite-element (FE) code was established in this study. To validate the proposed numerical model, two full-scale UHPFRC five-keyed dry and epoxy joints were fabricated and tested experimentally under direct shear load. Maximum differences of 0.8% and 5.4% were observed between the ultimate shear loads and corresponding slips, respectively from comparison of FE and experimental observations. The excellent agreement between the numerical results and experimental data demonstrated the reliability of the present model. Moreover, a parametric study was carried out to evaluate the effects of the number of shear keys, confining stress, and types of joints on the shear capacity of the UHPFRC keyed joint models.Results from the developed numerical models showed that the capacity of the UHPFRC key joints increased with increasing horizontal pressure applied across the joint (confining stress), number of shear keys and the epoxy layers applied on joints. Considering all the parameters, the ultimate shear capacity improved remarkably up to 64%.However, by increasing the number of shear keys, the effects of epoxy and confining pressure on the ultimate shear load was reduced. Finally, the FE data and experimental results were compared with the results from five existing shear design provisions available in literature for RC keyed dry joints.Findings indicated that existing shear design models lead to unsafe and inconsistent results on UHPFRC dry keyed joints. All the five provisions tend to over-estimate the Vj,u under higher confining stress. AASHTO (1999) design provision led to the worst mean Exist/FEM of 1.46 and COV of 17.6%.The simulations outlined in this study were limited to the response of the UHPFRC shear joints and nonlinear analysis of complete UHPFRC precast segmental bridges is recommended for the future studies. Moreover, it is recommended to develop a new constitutive model for UHPFRC considering the effect of steel fiber orientation in future FE studies of shear keyed joints.