Thermocapillary flow of thin Cu-water nanoliquid film during spin coating process

Abstract

Unsteady flow of thin Cu-water nanoliquid film over a horizontal rotating disk is studied numerically using finite difference technique under the assumption of planar interface. It is also assumed that the disk is cooling axisymmetrically from below. The effects of the nanolayer thickness and nanoparticle radius are considered for investigation. It is found that the film thinning rate decreases with increase of the nanoparticle volume fraction. It is also found that thickness of liquid decreases with increase of the thermocapillary parameter. The results show that the rate of film thinning is more for the thermal conductivity model of Yu and Choi [47] compared to the model of Maxwell [46]. It is observed that the film thinning rate increases with increase of nanolayer thickness but it decreases with the nanoparticle radius. A curve $R=R_c(z,t)$ in $R-z$ plane is delineated along which temperature gradient $T_z$ is zero and positive or negative according to $R<R_c$ or $R >R_c$ respectively. Furthermore, it is shown that the region for $T_z>0$ enlarges with increase of the nanoparticle volume fraction and the nanolayer thickness.

Introduction

The process of development of thin liquid film over a horizontal rotating disk by the action of the centrifugal force is known as spin coating in the literature. This technique is widely used in micro-electronics industry to manufacture the integrated circuits, magnetic and optical disks for data storage, colour television screens and optical mirrors etc. The hydrodynamic flow of a thin liquid film on a rotating disk was first modelled by Emslie et al. [1]. They analyzed the flow of Newtonian liquid by assuming the balance between the centrifugal driving force with the viscous resisting force and neglecting the influence of the other body forces. This pioneering work has been widely employed in the subsequent investigations on spin coating. For example, Acrivos et al. [2], Jenekhe and Schuldt [3] extended the analysis of Emslie [1] to study the flow of a power-law liquid on a rotating disk. Whereas Charpin et al. [4] investigated the axisymmetric spin coating of power law and Ellis fluids. The effect of solvent evaporation in spin coating process was first included by Myerhofer [5]. Y. Mouhamad et al. [6] studied the effects of concentration dependent viscosity and solvent evaporation on the development of thin polymer film during spin coating process. Middleman [7] studied the effect of induced air-flow on the thinning of a liquid film over the rotating disk. Ma and Hwang [8] considered the combined effects of centrifugation, surface roughness and air shear on the flow of a thin spinning liquid film. The hydrodynamic approximations used in these above models are typically those employed by Emslie et al. [1]. The full Navier–Stoke equations for unsteady film development was first considered by Higgins [9] to study the flow problem from the initial stage of film development through the match asymptotic analysis. Later, Rehg and Higgins [10] obtained the numerical solution of transient film flow on a rotating disk for large value of Reynolds number and different spin-up protocols. Dandapat and Ray [11, 12] investigated the effects of heating/cooling on thin liquid film development over a rotating disk in presence of the thermocapillarity at the free surface and found that the film thins faster due to thermocapillary effect for the cooling of the disk. Dandapat [13] studied numerically the development of thin liquid film under the assumption of non-uniform rotation of the disk. Usha and Ravindran [14] explored the development of a heat conducting fluid film over a rotating disk which cooled axisymmetric from below. Wu [15] studied both numerically and theoretically the effects of the thermocapillarity and thermoviscosity on spin coating when a radial temperature difference is applied to the disk surface. In addition he has considered the effects of the external air shearing and disjoining pressure. Recently, Cregan and O’Brien [16] obtained the extended asymptotic solution to the spin-coating model in presence of the small evaporation from the free surface. Matsumoto et al. [17] and Kitamura [18] first considered the nonuniform film development on the center of the wetted surface of a disk. Dandapat et al [19] investigated the effect of non-uniform heating of the disk on the development of a thin liquid film. Recently, Dandapat and Maity [20] studied the combined effects of external air flow and evaporation on the film development over a rotating annular disk. Quinn and Cetegen [21] analyzed the heat transfer from a horizontal heated rotating disk to a thin water liquid film flowing over it. In this study, they performed the several experiments to determine Nusselt numbers on the disk both with and without evaporation from the surface of the liquid film. Lin and Chen [22] investigated the stability of a thin incompressible viscoelastic fluid during spin coating using the long-wave perturbation method. Prieling and Steiner [23] considered the unsteady flow of thin liquid film over a rotating disk at the large Ekman numbers using the integral boundary layer method. McIntyre and Brush [24] explored the axisymmetric model for the spin-coating of two immiscible vertically stratified Newtonian thin liquid films using the lubrication theory. Dandapat and Singh [25] studied the unsteady two-layer liquid film flow on a horizontal rotating disk using asymptotic method for small values of Reynolds number. They showed that the viscous force dominates over centrifugal force, and the upper layer film thins faster than the lower layer at large time. Later, they  [26] also investigated the unsteady flow of thin two-layer liquid film on a non-uniform rotating disk in presence of uniform transverse magnetic field and found that the thinning rate for both the layers slowdown with increase of transverse magnetic field. Recently, Sahoo et al.  [27] demonstrated the axisymmetric flow of two-layer Newtonian liquid film over a rotating disk with the effects of surface/interfacial tension and contact line evolution.

It is to be mentioned here that, all the above investigations are primarily concerned about the flow of a clear liquid film or polymeric solution of coating material. Recently, heat transfer within nanoliquids has attracted researchers due to many possible applications in industries. Nanoliquids are described the liquids in which nanometer-sized particles suspended in conventional heat transfer base liquids. Conventional heat transfer liquids include water, oil and ethylene glycol. Nanoliquids exhibit enhancement of the thermal conductivity and heat transfer coefficient compared to the base liquids. For this reason nanoliquids are useful in many heat transfer processes including microelectronic chips cooling, fuel cells, pharmaceutical processes and hybrid powered engines, etc. Choi [28] first studied the enhancement of thermal conductivity by nanofluids. Subsequently, Choi et al. [29] showed that the addition of a small amount (less than 1% by volume) of nanoparticles to conventional heat transfer liquids increase the thermal conductivity of the fluid up to approximately two times. The earliest observations of thermal conductivity enhancement in liquid were reported by Masuda et al.[30], Xuan and Li [31], Eastman et al. [32]. Basic properties of nanofluids and related studies are briefly discussed in Das et al [33] and the review articles by Buongiorno [34], Wang and mazumdar [35], Kakac and Pramuanjaroenkij [36]. Recently, Ahmad et al. [37] studied the heat transfer in MHD three-dimensional flow of magnetic nanofluid (ferrofluid) over a bidirectional exponentially stretching sheet. Ibanez et al. [38] investigated effects of hydrodynamic slip, magnetic field, suction/injection, thermal radiation, entropy generation on the flow of a viscous electrically conducting nanofluid through a microchannel. Ferdows et al. [39, 40] studied numerically the Magnetohydrodynamic (MHD), mixed convective boundary layer flow of a nanofluid over stretching sheet. Beg et al. [41] analyzed the mixed convective hydromagnetic boundary layer flow of nanofluid over an unsteady exponentially stretching sheet in presence of porous media. Maity et al. [42] explored the study of thin nanoliquid film development over an unsteady stretching sheet. Maity [43] considered the development of thin nanoliquid film over an unsteady stretching sheet in presence of the thermal radiation.

To the best of our knowledge, no theoretical study of thin nanoliquid film development due to spinning of a horizontal disk has been reported in the literature. In this present article, we are interested to study the flow and development of a thin nanoliquid film over a rotating disk. The thermophysical properties like density, viscosity, heat capacity and thermal conductivity of the nanoliquid are assumed to be the function of the nanopartical volume faction. The thermal conductivity of the nanoliquid is modelled base on the effective medium theory. We have also assumed that the initially deposited liquid film over the rotating disk is planar and remain planar throughout film thinning process.

The rest of this paper is organized as follows. In Sect. 2, the problem formulation is done using suitable similarity transformation on the governing equations and the corresponding boundary conditions. These transformed equations are then expressed in suitable dimensionless form. The resulting set of partial differential equations in one space coordinate and time is solved numerically using finite-difference technique in Sect. 3. The results and discussion and concluding remarks are presented in Sects. 4 and 5, respectively.

Mathematical formulation

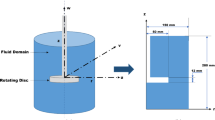
Consider an incompressible, viscous Cu-water nanoliquid film of uniform thickness $h_{0}$ on the surface of a horizontal rotating disk whose radius is quite large compared with the thickness of the film. At this stage of the nanoliquids development, the enormous increase of thermal conductivity is not known precisely, but researchers proposed two different models of nanoliquids to resolve this issue. The first model considers the effects of the Brownian motion and thermophoresis (see, Das et al [33], Buongiorno [34]) in the energy equation. Whereas other model is based on the effective medium theory like the Maxwell-Garnett theory for the electrical conductivity and dielectric constant of the medium. In this study, the later model is followed, i.e., the thermophysical properties of the nanoliquid such as density, viscosity, heat capacity and thermal conductivity are expressed in terms of the properties and relative functions of its components, namely liquid and the suspended nanoparticles. The nanoliquid is assumed to be non-volatile and thin so that evaporation and bouncy effect can be neglected. It is also assumed that the base fluid water and nanoparticles are in thermal equilibrium and no slip occurs between them. We consider the cylindrical polar coordinate system $(r,\theta ,z)$ with the origin is fixed at the center of the disk and the z axis is pointed vertically upwards coinciding with the axis of the rotation of the disk (see Fig. 1).

Fig. 1

Schematic diagram of the flow problem

Initially the system is at room temperature $T_0$. Simultaneously, the disk starts to rotate with angular velocity $\Omega$ about its axis at time $t=0$. Let (u, v, w) and T are the velocity components along $(r,\theta ,z)$ directions and temperature of the nanoliquid respectively. For the axisymmetric motion, the governing equations are

$$\begin{aligned} u_{r}+\frac{u}{r}+w_{z}=0, \end{aligned}$$

(1)

$$\begin{aligned} \rho _{nf}\left[ u_{t}+uu_{r}+wu_{z}-\frac{v^{2}}{r}\right] =-p_{r} +\mu _{nf}\left[ u_{rr}+(u/r)_{r}+u_{zz}\right] , \end{aligned}$$

(2)

$$\begin{aligned} \rho _{nf}\left[ v_{t}+uv_{r}+wv_{z}+\frac{uv}{r}\right] =\mu _{nf}\left[ v_{rr}+(v/r)_r+v_{zz}\right] , \end{aligned}$$

(3)

$$\begin{aligned} \rho _{nf}\left[ w_{t}+uw_{r}+ww_{z}\right] =-p_{z}+\mu _{nf}\left[ w_{rr}+\frac{1}{r}w_r+w_{zz}\right] , \end{aligned}$$

(4)

$$\begin{aligned} (\rho C_p)_{nf}[T_t+uT_r+wT_z]=k_{nf}\left[ T_{rr}+\frac{T_r}{r}+T_{zz}\right] , \end{aligned}$$

(5)

where p, $\rho _{nf}$, $\mu _{nf}$, $(\rho C_p)_{nf}$ and $k_{nf}$ are the pressure, density, dynamic viscosity, heat capacity and thermal conductivity of the nanoliquid, respectively. Equation (1) represents the equation of continuity and Eqs. (2)–(4) are the Navier-Stokes equations. Equation (5) represents the energy conservation equation.

The effective physical properties like density, viscosity, and heat capacitance of the nanoliquid are defined as follows: (Ahmad et al. [37], Ibanez et al. [38], Maity et al. [42], Maity [43], Narayana and Sibanda [44], Oztop and Abu-Nada [45])

$$\begin{aligned} \rho _{nf}=(1-\phi )\rho _f+\phi \rho _s, \end{aligned}$$

(6)

$$\begin{aligned} \mu _{nf}=\frac{\mu _f}{(1-\phi )^{5/2}}, \end{aligned}$$

(7)

$$\begin{aligned} (\rho C_p)_{nf}=(1-\phi )(\rho C_p)_f+\phi (\rho C_p)_s, \end{aligned}$$

(8)

here suffixes f and s stand for the properties of the base fluid and nanoparticle respectively and $\phi$ is the nanoparticle volume fraction.

There are many models proposed for estimating the effective thermal conductivity of nanofluids. In this investigation, we have considered two different models to estimate the effective thermal conductivity of the nanoliquid and namely, these are Maxwell [46] model and Yu and Choi [47] model. Based on the Maxwell’s work [46], the effective thermal conductivity of solid particles suspended in the based liquid for low volume fraction of spherical particles is given by

$$\begin{aligned} \frac{k_{nf}}{k_f}=\frac{k_s+2k_f-2\phi (k_f-k_s)}{k_s+2k_f+\phi (k_f-k_s)}, \end{aligned}$$

(9)

where $k_f$ is the thermal conductivity of the host medium (base liquid), $k_s$ is the thermal conductivity of the nanoparticles.

Yu and Choi [47] modified Maxwell [46] model with the assumption that the base fluid molecules closed to the solid surface of the monosized spherical particles from a solid like structures. Hence the nanolayer works as a thermal bridge between the bulk liquid and the solid nanoparticles, and this will enhance the effective thermal conductivity of the nanoliquids. They have assumed that the particle volume concentration in the base fluid to be very low such that there is no overlap of these equivalent particles. Based on the assumptions Yu and Choi [47] modified the Maxwell equation (9) into

$$\begin{aligned} \frac{k_{nf}}{k_f}=\frac{k_s+2k_s+2\phi (k_s-k_f)(1+\beta )^3}{k_s+2k_f-\phi (k_s-k_f)(1+\beta )^3}, \end{aligned}$$

(10)

where $\beta =\frac{h_n}{r_a}$ is the ratio between the nanolayer thickness $h_n$ and the original nanoparticle radius $r_a$. Here, $h_n$ and $r_a$ are assumed to be constants.

The thermophysical properties like density $\rho$, heat capacity at constant pressure $C_p$ and thermal conductivity k of the base liquid water and Cu nanoparticles are given in Table 1.

Table 1 Thermo-physical properties of water and Cu nanoparticles  (Narayana and Sibanda [44], Oztop and Abu-Nada [45])

The boundary conditions associated with the problem are

On the surface of the disk at $z=0$,

$$\begin{aligned} u=0,\,\, v=r\Omega ,\,\, w=0, \,\,T=T_0-\frac{r^2}{2}T_1, \end{aligned}$$

(11)

where $T_0$ and $T_1$ are the positive constant.

At the free surface $z=h(t)$,

$$\begin{aligned} -p+2\mu _{nf} w_{z}=0, \end{aligned}$$

(12)

$$\begin{aligned} \mu _{nf}(w_{r}+u_{z})=\frac{\partial \sigma }{\partial T}T_r, \end{aligned}$$

(13)

$$\begin{aligned} \mu _{nf} v_z=\frac{\partial \sigma }{\partial T}T_z, \end{aligned}$$

(14)

$$\begin{aligned} T_z+L(T-T_g)=0, \end{aligned}$$

(15)

$$\begin{aligned} \frac{dh}{dt}=w. \end{aligned}$$

(16)

Here, L and $T_g$ denote the heat transfer coefficient at the free surface and the temperature in the gas phase, respectively. Equation (12) represents the vanishing of the normal stress at the free surface. Equations (13) and (14) represent that the shear stress balanced with the thermal stress at the free surface. $\sigma$ is the surface tension which varies linearly with the temperature as $\sigma =\sigma _0[1-\gamma (T-T_0)]$ (see  [11]). For most of the liquids, surface tension decreases with temperature, i.e. $\gamma$ is a positive constant. $\sigma _0$ is the surface tension at initial time. Equation (15) represents Newton’s law of cooling. Equation (16) represents the kinematic condition at the free surface.

The initial conditions at $t=0$ are given by

$$\begin{aligned} u=v=w=0, \,\,T=T_0,\,\, h(0)=h_{0}. \end{aligned}$$

(17)

Now, we introduce the following similarity variables ( see, Rehg and Higgins [10], Dandapat and Ray [11], Usha and Ravindran [14])

$$\begin{aligned} u(r,z,t)=rF(z,t),v(r,z,t)=rG(z,t), w(r,z,t)=W(z,t) \end{aligned}$$

(18)

$$\begin{aligned} p=-\frac{r^2}{2} A(z,t)+B(z,t), \end{aligned}$$

(19)

$$\begin{aligned} T(r,z,t)=T_0-\frac{r^2}{2}M(z,t)-N(z,t), \end{aligned}$$

(20)

where the functions M(z, t) and N(z, t) appearing in Eq. (20) are clearly compatible with the temperature boundary condition given in (11). It is assumed that the Eq. (20) holds for large but finite value of r so that T(r, z, t) can never tend to $\infty$ or $-\infty$. Substituting (18)–(20) into the governing set of Eqs. (1)–(5) and equating the like order terms of r from both sides, we get

$$\begin{aligned} 2F+W_{z}=0, \end{aligned}$$

(21)

$$\begin{aligned} \rho _{nf}[F_{t}+F^{2}-G^{2}+WF_{z}]=A+\mu _{nf} F_{zz}, \end{aligned}$$

(22)

$$\begin{aligned} \rho _{nf}[G_{t}+2FG+WG_{z}]=\mu _{nf} G_{zz}, \end{aligned}$$

(23)

$$\begin{aligned} \rho _{nf}[W_{t}+WW_{z}]=\mu _{nf} W_{zz}- B_{z}, \end{aligned}$$

(24)

$$\begin{aligned} A_{z}=0, \end{aligned}$$

(25)

$$\begin{aligned} (\rho C_p)_{nf}[M_t+2FM+WM_z]=k_{nf}M_{zz}, \end{aligned}$$

(26)

$$\begin{aligned} (\rho C_p)_{nf}[N_t+WN_z]=k_{nf}[N_{zz}+2M], \end{aligned}$$

(27)

Using the same similarity transformation to the boundary conditions (11)–(16) and initial condition (17), we get:

at $z=0$,

$$\begin{aligned} F=0,\,\, G=\Omega ,\,\, W=0,\,\,M=T_1, \,\,N=0, \end{aligned}$$

(28)

at $z=h(t)$,

$$\begin{aligned} A=0,~~~~~ B=2\mu _{nf}W_z, \end{aligned}$$

(29)

$$\begin{aligned} F_z=\left( \frac{\gamma \sigma _0}{\mu _{nf}}\right) M, \end{aligned}$$

(30)

$$\begin{aligned} G_z=0,~~M_z=0, N_z=0, \end{aligned}$$

(31)

$$\begin{aligned} M_ z+L M=0,~~~N_z+L(N+T_g-T_0)=0, \end{aligned}$$

(32)

$$\begin{aligned} \frac{dh}{dt}=w, \end{aligned}$$

(33)

at $t=0$,

$$\begin{aligned} F=0,\,\, G=0,\,\, W=0,\,\, h=h_0,\,\, M=0,\,\, N=0. \end{aligned}$$

(34)

For consistency with the Eqs. (31) and (32) we have assumed $L=0$.

Integrating Eq. (25) using the boundary condition (29), we get $A=0$. B(z, t) can be found by integrating Eq. (24) with respect to z from z to $z=h(t)$, thus we can calculate the pressure from Eq. (19).

The following dimensionless variables

$$\begin{aligned} \hat{t}=\frac{t}{t_c}, \hat{z}=\frac{z}{h_0}, \hat{H}=\frac{h}{h_0}, \hat{F}=\frac{h_0F}{U_0}, \hat{G}=\frac{G}{\Omega }, \hat{W}=\frac{W}{U_0}, \hat{M}=\frac{h_0^2 M}{\triangle T}, \hat{N}=\frac{N}{\triangle T} \end{aligned}$$

(35)

are introduced into the Eqs. (21)–(23) and (26)–(27). The hat over the variable in Eq. (35) denotes the dimensionless quantities. Here, $t_c=\nu _{f}/h_0^2 \Omega ^2$ is the characteristic time scale at which the viscous and centrifugal forces balance each other, $U_0=\frac{h_0}{t_c}$ is the characteristic velocity and $\triangle T= h_0^2 T_1$.

The final set of dimensionless equations after dropping the hat over the dependent variables are

$$\begin{aligned} 2F+W_z=0, \end{aligned}$$

(36)

$$\begin{aligned} \mathrm{Re} \phi _1(F_t+F^{2}+WF_z)=F_{zz}+G^{2}, \end{aligned}$$

(37)

$$\begin{aligned} \mathrm{Re} \phi _1(G_t-W_zG+WG_z)=G_{zz}, \end{aligned}$$

(38)

$$\begin{aligned} \mathrm{Re Pr} \phi _2(M_t-W_zM+WM_z)=\frac{k_{nf}}{k_f}M_{zz}, \end{aligned}$$

(39)

$$\begin{aligned} \mathrm{Re Pr} \phi _2(N_t+WN_z)=\frac{k_{nf}}{k_f}(2M+N_{zz}), \end{aligned}$$

(40)

where $\mathrm{Re}=\frac{U_0 h_0}{\nu _f}$ , $\mathrm{Pr}=\frac{\nu _f(\rho C_P)_f}{k_f}$ are the Reynolds number and Prandtl number respectively. The constants $\phi _1$ and $\phi _2$ that depend on the nanoparticle volume fraction are respectively given by $\phi _1=(1-\phi )^{2.5}\left[ (1-\phi )+\phi \left\{ \frac{\rho _s}{\rho _f} \right\} \right]$, $\phi _2=\left[ (1-\phi )+\phi \left\{ \frac{(\rho C_P)_s}{(\rho C_P)_f} \right\} \right] .$

The corresponding dimensionless boundary conditions are:

at $z=0$;

$$\begin{aligned} F=0,\,\, G=1, \,\, W=0, \,\, M=1, \,\, N=0, \end{aligned}$$

(41)

at $z=H(t)$;

$$\begin{aligned} F_z=\alpha (1-\phi )^{2.5} M,~~G_z=0,~~~ M_z=0,~~~ N_z=0,~~~ \frac{dH}{dt}=W, \end{aligned}$$

(42)

where $\alpha =\frac{\gamma \sigma _0 \triangle T}{\Omega h_0 \mu _f}$ is the thermocapillary parameter.

The dimensionless form of the initial conditions at $t=0$ are

$$\begin{aligned} F=G=W=0,\,\, M=N=0,\,\, H=1. \end{aligned}$$

(43)

Equations (36)–(40), boundary conditions (41)–(42) and initial conditions (43) reduce to the equations obtained by Dandapat and Ray [11] in case of the pure liquid film (i.e., $\phi =0$).

Numerical solution

The coupled nonlinear system of partial differential Eqs. (36)–(40) with boundary and initial conditions can be solved efficiently by the finite difference method. As the film thickness continuously decreases with time, the conventional finite difference method can not be used directly in this problem. For this reason, the time dependent physical domain has to be transformed to a fixed computational domain [0, 1] such that the film height will always remain fixed into the computational domain. It is to be mentioned here that the fine grid distribution is needed for large velocity gradient near the surface of the disk when the Reynolds number is large. It is to be pointed out that the said transformation will be useful for the fine as well as uniform grid distribution. Following Robert [48], we used the transformation (44) which shift the physical domain [0, h(t)] into the fixed computational domain [0, 1].

$$\begin{aligned} \eta (t)=1-a_{1}\ln \left( \frac{a_{2}H(t)-z}{b_{2}H(t)+z}\right) , \quad 1<c<\infty . \end{aligned}$$

(44)

where $a_{1} = [\ln (a_{2}/b_{2})]^{-1}$, $a_{2} = c+1$ and $b_{2} = c - 1$. The parameter c controls the grid spacing in the physical domain and the small values of c cluster grid points at the surface where large values make the grid spacing uniform throughout the liquid film. The Crank-Nicholson scheme is used to solve the transformed non-linear system of Eqs. (36)–(40) after approximating the non-linear terms according to the Newton’s linearization technique (Fletcher [49]). Computation is carried out in each time level with following linear tridiagonal system of algebraic equations.

$$\begin{aligned} P_1 F^{n+1}_{j-1}+ Q_1 F^{n+1}_{j} + R_1 F^{n+1}_{j+1} = (S_1)^{n}_{j}, \end{aligned}$$

(45)

$$\begin{aligned} P_1 G^{n+1}_{j-1}+ Q_1 G^{n+1}_{j} + R_1 G^{n+1}_{j+1} = (S_2)^{n}_{j}, \end{aligned}$$

(46)

$$\begin{aligned} P_2 M^{n+1}_{j-1}+ Q_2 M^{n+1}_{j} + R_2 M^{n+1}_{j+1} = (S_3)^{n}_{j}, \end{aligned}$$

(47)

$$\begin{aligned} P_2 N^{n+1}_{j-1}+ Q_2 N^{n+1}_{j} + R_2 N^{n+1}_{j+1} = (S_4)^{n}_{j}, \end{aligned}$$

(48)

where

$$\begin{aligned} \left. \begin{array}{llll} \displaystyle P_1 = \frac{B_1 - A_1}{4\triangle \eta } - \frac{C}{2 (\triangle \eta )^2},\\ \displaystyle Q_1 = \frac{1}{\triangle t} + \frac{C}{(\triangle \eta )^2}+ 2 F^{n}_{j},\\ \displaystyle R_1 = \frac{A_1 - B_1}{4 \triangle \eta } - \frac{C}{2 (\triangle \eta )^2},\end{array}\right\} \end{aligned}$$

(49)

$$\begin{aligned} (S_1)^{n}_{j}&= F^{n}_{j-1} \left[ \frac{A_1 - B_1}{4 \triangle \eta }+ \frac{C}{2 (\triangle \eta )^2}\right] + F^{n}_{j} \left[ \frac{1}{\delta t}+ F^{n}_{j} - \frac{C}{(\triangle \eta )^2}\right] \\ \nonumber&\quad + F^{n}_{j+1}\left[ \frac{B_1 - A_1}{4 \triangle \eta }+ \frac{C}{2 (\triangle \eta )^2}\right] +\frac{1}{\mathrm{Re} \phi _1}(G^{n}_j)^2, \end{aligned}$$

(50)

$$\begin{aligned} (S_2)^{n}_{j} = G^{n}_{j-1} \left[ \frac{A_1 - B_1}{4 \triangle \eta }+ \frac{C}{2 (\triangle \eta )^2}\right] + G^{n}_{j} \left[ \frac{1}{\delta t} - \frac{C}{(\triangle \eta )^2}\right] + G^{n}_{j+1}\left[ \frac{B_1 - A_1}{4 \triangle \eta }+ \frac{C}{2 (\triangle \eta )^2}\right] , \end{aligned}$$

(51)

$$\begin{aligned} \left. \begin{array}{llll} \displaystyle P_2 = \frac{D - A_1}{4\triangle \eta } - \frac{E}{2 (\triangle \eta )^2},\\ \displaystyle Q_2 = \frac{1}{\triangle t} + \frac{E}{(\triangle \eta )^2}, \\ \displaystyle R_2 = \frac{A_1 - D}{4 \triangle \eta } - \frac{E}{2 (\triangle \eta )^2}, \end{array}\right\} \end{aligned}$$

(52)

$$\begin{aligned} (S_3)^{n}_{j}& = M^{n}_{j-1} \left[ \frac{A_1 - D}{4 \triangle \eta }+ \frac{E}{2 (\triangle \eta )^2}\right] \\ & \quad + M^{n}_{j} \left[ \frac{1}{\delta t}-2F^{n}_{j} - \frac{E}{(\triangle \eta )^2}\right] + M^{n}_{j+1}\left[ \frac{D - A_1}{4 \triangle \eta }+ \frac{E}{2 (\triangle \eta )^2}\right] , \end{aligned}$$

(53)

$$\begin{aligned} (S_4)^{n}_{j}&= N^{n}_{j-1} \left[ \frac{A_1 - D}{4 \triangle \eta }+ \frac{E}{2 (\triangle \eta )^2}\right] + N^{n}_{j} \left[ \frac{1}{\delta t} - \frac{E}{(\triangle \eta )^2}\right] \\ \nonumber&\quad +N^{n}_{j+1}\left[ \frac{D - A_1}{4 \triangle \eta }+ \frac{E}{2 (\triangle \eta )^2}\right] +\frac{1}{\mathrm{Re Pr} \phi _2}\left( \frac{k_{nf}}{k_f}\right) M_j^n, \end{aligned}$$

(54)

$$\begin{aligned} A_1 = \frac{a_{1}(a_2 + b_2)\left(H^nW^{n}_{j} - z_{j} \left(\frac{dH}{dt}\right)^{n}\right)}{(a_2H^n -z_{j})(b_{2}H^n + z_{j})}, \end{aligned}$$

(55)

$$\begin{aligned} B_1 = \frac{1}{\mathrm{Re} \phi _1}\frac{a_1 (a_2 +b_2)H^n [(b_2 - a_2) H^n + 2 z_{j}]}{ (a_2H^n -z_{j})^2 (b_{2}H^n + z_{j})^2}, \end{aligned}$$

(56)

$$\begin{aligned} C = \frac{1}{\mathrm{Re} \phi _1} \left[ \frac{a_1 (a_2 +b_2)H^n }{(a_2H^n -z_{j})(b_{2}H^n + z_{j}) }\right] ^2, \end{aligned}$$

(57)

$$\begin{aligned} D=\frac{1}{\mathrm{Re Pr} \phi _2}\left( \frac{k_{nf}}{k_f}\right) \frac{a_1 (a_2 +b_2)H^n [(b_2 - a_2) H^n + 2 z_{j}]}{ (a_2H^n -z_{j})^2 (b_{2}H^n + z_{j})^2}, \end{aligned}$$

(58)

$$\begin{aligned} E=\frac{1}{\mathrm{Re Pr} \phi _2}\left( \frac{k_{nf}}{k_f}\right) \left[ \frac{a_1 (a_2 +b_2)H^n }{(a_2H^n -z_{j})(b_{2}H^n + z_{j}) }\right] ^2. \end{aligned}$$

(59)

The values of F, G, M and N are computed in each time level from the tri-diagonal system of linear Eqs. (45)–(48). Then W is obtained from the finite difference representation of the equation of continuity using values of F at that time level. Once W is determined, its value at the free surface is then substituted into the kinematic condition (Eq. 42) to obtain the film thickness H.

The unknowns F, G, W, M, N and H are calculated until the following convergence criterium is satisfied:

$$\begin{aligned} \frac{\sum _{j}|Q_j^{n+1}-Q_j^{n}|}{\sum _j|Q_j^{n+1}|}\le \epsilon , \end{aligned}$$

(60)

where $Q=(F, G, W, M, N, H)$, n represents the iteration number and $\epsilon$ is the convergence criterium. In this study the convergence criterion is set for $\epsilon =10^{-6}$.

To explore the grid accuracy of presented results, we have carried the simulation for film thickness with respect to time for 41, 51, 71 grids in vertical direction with $Re=0.1$, $Pr=6.2$, $\alpha =0.5$, $\phi =0.05$ (see, Fig. 2). Here, the Fig. 2 explored that outcomes are same in all the cases. The rest of the computation are carried out on 51 grid points in the vertical direction with $c=10^4$ (equivalent to a uniform grid distribution in the physical domain), this gives the uniform grid distribution in computational domain.

Fig. 2

Variation h with time t for different number of grids when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\alpha =0.5$ and $\phi =0.05$

The time step has been calculated by

$$\begin{aligned} \delta t \le 0.25 \times \delta \eta ^2. \end{aligned}$$

(61)

The above condition comes from the Courant-Friedrichs-Lewy (CFL) condition of numerical stability. The domain of $\delta t$ is chosen smaller than the stability domain for linear equations due coupled nonlinear system. To cheek the accuracy of this numerical scheme, we have plotted the present numerical solution under the condition of pure liquid (i.e. for $\phi =0$) with the analytical solution obtained by Dandapat and Ray  [11] in Fig. 3. It is clear from this figure that both the solutions agrees well.

Fig. 3

Comparison of the present numerical solution in case of pure liquid film i.e., $\phi =0$ with the analytical solution by Dandapat and Roy [11] for $\mathrm{Re}=0.1$, $\mathrm{Pr}=0.5$, $\alpha =0.5$

Results and discussion

In this article, we have obtained the numerical solution of thin nanoliquid film development over a rotating disk under the assumption of uniform planar interface. Thermophysical properties of the nanoliquid such as density, heat capacity and thermal conductivity are expressed in terms of the properties and relative fractions of its components, namely, base liquid and the suspended nanoparticles. The value of Prandtl number $Pr\approx 6.8$ for the base liquid water is obtained using the definition of Prandtl number and thermophysical properties of water (see, Table 1) along with $\mu _f=1\times 10^{-3}$ Pa s at $20^\mathrm{\circ }C$. The results presented in Figs. 4, 5, 6, 7, 8, 9, 10, 11, 12 are based on the thermal conductivity model predicted by the Maxwell [46] and in rest of the figures we have considered the effective thermal conductivity model given by Yu and Choi [47]. Figure 4 shows variation of the film thickness H with time t for different values of the nanoparticle volume fraction $\phi$. It is clear from the figure that the rate of film thinning decreases with the increasing values of $\phi$. A close scrutiny of the Eq. (7) shows that the increasing values of nanoparticle volume fraction $\phi$ contribute the enhancement of nanoliquid viscosity. As a result the increasing viscosity produces the considerable drag to the motion of the liquid film and it opposes the film thinning process. The effect of the thermocapillary parameter $\alpha$ on the film thinning process is explored in Fig. 5. It is evident from the figure that the thickness of the nanoliquid film decreases with increase of the tharmocapillary parameter $\alpha$. Thermocapillarity is the thermally induced surface-tension gradient along the horizontal interface between the passive gas and the liquid film. This surface-tension gradient generates an interfacial flow through viscous drag. Since, the disk is cooled along the radial direction the temperature at the center of the disk is maximum and it decreases along the radial direction. Thus, the surface tension is minimum at the origin and increases along the radial direction of the disk. So, the surface tension gradient is positive along the radial direction. As a result, the thermocapillary flow is induced at the free surface from lower to higher surface tension zone or in other words, thermocapillary flow takes place at the free surface toward the radial direction of the disk resulting in decrease of the film thickness. Figure 6 depicts the variation of the radial velocity components F with respect to time t at free surface $z=H$ for different values of nanoparticle volume fraction $\phi$. It is observed from this figure that the radial velocity F decreases with increase of the nanoparticle volume fraction. We know that the increase of the particle volume fraction $\phi$ contributes the enhancement of the nanoliquid viscosity as a result slowdowns the motion of the liquid film. Figure 7 represents the variation of the azimuthal velocity components G with t for different values of nanoparticle volume fraction $\phi$ at the free surface. It is observed from this figure that the values of G decreases with increase of the nanoparticle volume fraction $\phi$. Figure 8 shows the variation of the axial velocity with time at free surface. It is clear from the figure that, the magnitude of the axial velocity increases initially but it decreases gradually with the spinning time. It is also clear from the Fig. 8 that the magnitude of W decreases with increase of the nanoparticle volume fraction $\phi$.

Fig. 4

Variation of film thickness H with time t for different values of $\phi$ when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\alpha =1.0$

Fig. 5

Variation of film thickness H with time t for different values of $\alpha$ when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\phi =0.1$

Fig. 6

Variation of radial velocity component F with time t for different values of $\phi$ at the free surface $z=H$ when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\alpha =1$

Fig. 7

Variation of azimuthal velocity component G with time t for different values of $\phi$ at the free surface $z=H$ when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\alpha =1$

Fig. 8

Variation of axial velocity W with time t for different values of $\phi$ at the free surface $z=H$ when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\alpha =1$

Fig. 9

Variation of a M with z and b N with z for different values of $\phi$ when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\alpha =1$ and $t=2.0$

Fig. 10

Variation of a $M_{z}$ with z and b $N_{z}$ with z for different values of $\phi$ when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\alpha =1$ and $t=2.0$

Fig. 11

Variation of $T_{z}$ with respect to R for different values of $\phi$ at $z=0.2H(t)$ when $\mathrm{Re}=0.1$, $\mathrm{Pr}=6.8$, $\alpha =1$ and $t=2.0$

Fig. 12

Variation of $R_c$ with $\eta$ for different values of $\phi$ and t when $\mathrm{Re}=0.8$, $\mathrm{Pr}=6.8$, $\alpha =0.5$

The non-dimensional temperature distribution in the film due to the cooling of the disk is obtained from the Eq. (20) as

$$\begin{aligned} T=\frac{R^2}{2} M(z,t)+N(z,t), \end{aligned}$$

(62)

where $R=(r/h_0)$.

Figure 9a, b represents the variation of M and N with respect to z for different values of the nanoparticle volume fraction $\phi$. It is observed from the figure that the values of M and N increase with $\phi$ at a particular film height. It is also noted from the figure that the overall values of M decreases while N increases with the film height. Upon differentiating Eq. (62) with respect to z one can obtain the temperature gradient within the film as,

$$\begin{aligned} T_z=\frac{R^2}{2} M_z+N_z. \end{aligned}$$

(63)

In the Fig. 10a, b we have plotted the variation of $M_{z}$ and $N_{z}$ for different values of the nanoparticle volume fraction $\phi$. It is evident from the figure that $M_{z}<0$ and $N_{z}>0$ for all $z \ne H$ but the magnitude of $M_{z}$ and $N_{z}$ decrease with increase of z. Therefore, one expected from the Eq. (63) that the temperature gradient $T_{z}$ may becomes zero at different film height depending on the values of R. Thus, it indicates that $T_z$ changes it sign at a value of $R=R_c$ (say) at which $T_{z}=0$. Figure 11 represents the variation of $T_{z}$ with respect to R for different values of nanoparticle volume fraction $\phi$. It is observed from the figure that $T_{z}>0$ for $R<R_c$ and $T_{z}<0$ for $R>R_c$ i.e., the heat flows from the disk to the film or from the film to the disk according as $R<R_c$ or $R>R_c$. It is also clear from the figure that the region for $T_{z}>0$ increases with the increasing values of $\phi$. This is due to the fact that, the addition of nanoparticles in water has increased the liquid thermal conductivity greatly resulting in enhancement of heat transfer rate. Figure 12 depicts the variation of $R_c$ with z for different values of nanoparticle volume fraction $\phi$ and time t. It is clear from Fig. 12 that $R_c$ increases with the increasing values of $\phi$ and t, i.e., the region for $T_z>0$ enhances with increase of $\phi$ and t. In the present investigation the axisymmetric cooling of the Cu-water nanoliquid on a rotating disk is considered, the profile for $R_c$ with respect to z is similar to the result presented by Dandapat and Ray [12] in case of pure liquid film.

The effects of the nanolayer thickness and particle diameter on the effective thermal conductivity of the nanoliquid are shown in the Fig. 13. It is evident from the figure that, the effective thermal conductivity improved remarkably when the nanolayer impact is considered. It is also observed from the Fig. 13 that the effective thermal conductivity enhances with increase of nanolayer thickness but decreases with increase of particle diameter and this agrees with the results presented by Yu and Choi [47]. The influence of the nanolayer thickness and particle diameter on the film thinning are presented in Fig. 14 for a fixed value of $\phi =0.1$. It is evident from the Fig. 14 that the rate of film thinning increases with the increase of the nanolayer thickness and decreases with the increase of the nanoparticle diameter. One can witness with the fact that the rate of film thinning is more for the thermal conductivity model by Yu and Choi [47] compared to the model of Maxwell [46]. Figure 15 shows the variation of the temperature gradient $T_z$ with R for different values of the nanolayer thickness and particle radius for a fixed values of $\phi$ and t. It is evident from the figure that the region for $T_z>0$ enhances with the increase of the nanolayer thickness but decreases with the increase of the nano-particle diameter. In other words, the region for $T_z>0$ increases with the increase of the nanoliquid thermal conductivity. Figure 16 represents the variation of $R_c$ with z for different values of nanolayer thickness $h_n$ and particle radius $r_a$ for the fixed values of $\phi$ and t.

Fig. 13

Comparison of the thermal conductivity models represented by Maxwell [46] and Yu and Choi [47]

Fig. 14

Variation of film thickness H with time t for different thermal conductivity models when $Re=0.1$, $Pr=6.8$, $\phi =0.1$, $\alpha =1.0$

Fig. 15

Variation of $T_{z}$ with respect to R for different values of nanolayer thickness $h_n$ and particle radius $r_a$ at $z=0.2H(t)$ when $Re=0.1$, $Pr=6.8$, $\alpha =1$, $\phi =0.05$ and $t=2.0$

Fig. 16

Variation of $R_c$ with z for different values of nanolayer thickness $h_n$ and particle radius $r_a$ when $Re=0.8$, $Pr=6.8$, $\alpha =0.5$, $\phi =0.05$ and $t=2.0$

Conclusions

We have investigated the flow and heat transfer within a thin nanoliquid film containing the Cu nanoparticles on an rotating disk and the disk is assumed to be cooled axisymmetrically from below. The effective thermal conductivity of nanoliquid is estimated using the models of Maxwell [46] and Yu and Choi [47]. The coupled nonlinear system of equations are solved numerically by Crank-Nicholson scheme and the numerical result is verified with the analytical solution obtained by Dandapat et al. [11] for pure liquid film. The following observations have been made from the present investigation in presence of Cu nanoparticles.

• (i) The film thickness enhances with the increase of the nanoparticle volume fraction.

• (ii) The thermocapillary parameter has strong influence on thinning of the nanoliquid film.

• (iii) The rate of film thinning increases with increase of nanolayer thickness but it decreases with increase of the nano-particle diameters.

• (iv) There exists a curve within the film that demarcating the region of heat transfer. One side of this curve, heat is transported from the film to the disk while in other side, heat is transported from the disk to the film.

• (v) The region of the heat flows from film to the disk enhances with the increase of the nanoparticle volume fraction and nanolayer thickness, whereas decreases with the nano-particle diameter.