Abstract
The functor that takes a ring to its category of modules has an adjoint if one remembers the forgetful functor to abelian groups: the endomorphism ring of linear natural transformations. This uses the self-enrichment of the category of abelian groups. If one considers enrichments into symmetric sequences or even bisymmetric sequences, one can produce an endomorphism operad or an endomorphism properad. In this note, we show that more generally, given a category  enriched in a monoidal category
enriched in a monoidal category  , the functor that associates to a monoid in
, the functor that associates to a monoid in  its category of representations in
its category of representations in  is adjoint to the functor that computes the endomorphism monoid of any functor with domain
is adjoint to the functor that computes the endomorphism monoid of any functor with domain  . After describing the first results of the theory we give several examples of applications.
. After describing the first results of the theory we give several examples of applications.
Similar content being viewed by others
1 Introduction
The functor that takes a ring R to its category of modules has an adjoint, provided that in addition to \(R\text {-}{\mathsf {mod}}\), one remembers the forgetful functor \(R\text {-}{\mathsf {mod}} \rightarrow {{\mathsf {A}}}{{\mathsf {b}}}\).
The adjoint sends a functor \(F : {\mathcal {D}}\rightarrow {{\mathsf {A}}}{{\mathsf {b}}}\) to its endomorphism ring of natural transformations. This fact is familiar to people working on duality results à la Tannaka.
of natural transformations. This fact is familiar to people working on duality results à la Tannaka.
If instead of using the self-enrichment \(\langle -, - \rangle : {{\mathsf {A}}}{{\mathsf {b}}}{}^{\text {op}}\times {{\mathsf {A}}}{{\mathsf {b}}}\rightarrow {{\mathsf {A}}}{{\mathsf {b}}}\), one uses an enrichment into symmetric sequences or bisymmetric sequences, then  can be promoted to an endomorphism operad or an endomorphism properad. This is summarized in the table:
can be promoted to an endomorphism operad or an endomorphism properad. This is summarized in the table:
| enrichment |
|---|---|
endomorphism ring | \(\langle X,Y\rangle \) |
endomorphism operad | \(\langle X^{\otimes n},Y\rangle \) |
endomorphism properad | \(\langle X^{\otimes p},Y^{\otimes q}\rangle \) |
In this note we study the general case, replacing \({{\mathsf {A}}}{{\mathsf {b}}}\) by a category  enriched in a monoidal category
enriched in a monoidal category  . First we review representations of monoids in the context of an enriched category. Then we describe the endomorphism monoid of a functor whose target is an enriched category and show that this construction is adjoint to the representations functor.
. First we review representations of monoids in the context of an enriched category. Then we describe the endomorphism monoid of a functor whose target is an enriched category and show that this construction is adjoint to the representations functor.
After describing the adjunction between monoids in  and functors with target
and functors with target  , we shall study the basic properties of this adjunction, in particular in the case where the enrichment is also tensored.
, we shall study the basic properties of this adjunction, in particular in the case where the enrichment is also tensored.
In two brief appendices, we provide quick definitions of terms in enriched category theory that we need and give a few examples of contexts in which this setup holds.
The sequel, Endomorphism operads of functors [1], contains some explicit computations.
After seeing the definitions of the functors  and \({\mathsf {Rep}}\) and their adjunction, the reader is encouraged to take a look at the appendix [§ B]. Some of the examples there might be surprising.
and \({\mathsf {Rep}}\) and their adjunction, the reader is encouraged to take a look at the appendix [§ B]. Some of the examples there might be surprising.
2 Monoids and their representations
Let us fix a a bicomplete monoidal category  and a category
and a category  enriched in
enriched in  :
:

For convenience, we shall assume given a locally large universe enlargement  [§ A.1]. Because
[§ A.1]. Because  is fully faithful and monoidal, one has a fully faithful embedding of categories of monoids
is fully faithful and monoidal, one has a fully faithful embedding of categories of monoids

In order to distinguish between the two, we shall say that a monoid in  is large.
is large.
Remark 1
(Endomorphism monoid of an object) Thanks to the  -enrichment of
-enrichment of  , every object
, every object  has a natural endomorphism monoid [X, X].
has a natural endomorphism monoid [X, X].
Definition 1
(Representations of monoids) Let M be a monoid. Its category of representations in 
is the large category
-
whose objects are \((X,\alpha )\) where X is an object of
 and \(\alpha :M\rightarrow [X,X]\) is a map of monoids and
and \(\alpha :M\rightarrow [X,X]\) is a map of monoids and -
whose morphisms \((X,\alpha )\rightarrow (Y,\beta )\) are maps \(f:X\rightarrow Y\) such that the following diagram commutes:
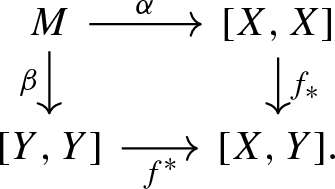
The category of representations of M has an evident forgetful functor

that is both faithful and conservative. The assignment \(M \mapsto M\text {-}{\mathsf {rep}}\) is moreover functorial: given a morphism of monoids \(\psi : M \rightarrow N\), one has a commutative diagram

Denoting by \(\widehat{{\mathsf {Cat}}}\) the very large category of large categories, one gets a representation functor

Remark 2
(Representations of large monoids) Since we have required  to be locally large, the definition of the category of representations \(M\text {-}{\mathsf {rep}}\) also makes sense for M a large monoid. Then, the large category
to be locally large, the definition of the category of representations \(M\text {-}{\mathsf {rep}}\) also makes sense for M a large monoid. Then, the large category  having been fixed, the representations functor extends to the category of large monoids:
having been fixed, the representations functor extends to the category of large monoids:

Indeed, let M be a large monoid. The cardinality of the objects of \(M\text {-}{\mathsf {rep}}\) is bounded by

Since  is large and
is large and  is locally large, we deduce that \(M\text {-}{\mathsf {rep}}\) has a large set of objects. Given two representations X and Y of a monoid M, one has
is locally large, we deduce that \(M\text {-}{\mathsf {rep}}\) has a large set of objects. Given two representations X and Y of a monoid M, one has

Hence, since  has large sets of morphisms, so does \(M\text {-}{\mathsf {rep}}\).
has large sets of morphisms, so does \(M\text {-}{\mathsf {rep}}\).
3 The endomorphism monoid of a functor
In this section we show that the representation functor \(M \mapsto M\text {-}{\mathsf {rep}}\) has a right adjoint

It takes as inputs large categories \({\mathcal {D}}\) over  and outputs the endomorphism monoid
and outputs the endomorphism monoid of the functor
of the functor  .
.
Remark 3
(Enriched natural transformations) Given a large category \({\mathcal {D}}\), the category of functors  is naturally enriched in
is naturally enriched in  as follows. Given two functors
as follows. Given two functors  , the
, the  -natural transformations from F to G are presented by the object of
-natural transformations from F to G are presented by the object of  given by
given by

where, following Yoneda’s original notation [2, § 4],  denotes the cointegration (or end) of a functor
denotes the cointegration (or end) of a functor  .
.
Definition 2
The endomorphism monoid of a functor  is
is

the (large) monoid of  -natural transformations of F.
-natural transformations of F.
Remark 4
(Functoriality of  ) As is the case in any 2-categorical setting,
) As is the case in any 2-categorical setting,  -natural transformations are compatible with ‘horizontal composition’ or ‘whiskering’:
-natural transformations are compatible with ‘horizontal composition’ or ‘whiskering’:

Thus, the construction  is functorial in the sense that given
is functorial in the sense that given

one gets a morphism of large monoids

Theorem 1
The functor  is right adjoint to
is right adjoint to 

There are a number of examples where this setup gives interesting endomorphism monoids and interesting adjunctions [§ B].
Proof
Observe that a functor from \({\mathcal {D}}\) to \(M\text {-}{\mathsf {rep}}\) over  consists of:
consists of:
-
at the object level, a monoid map \(M\xrightarrow {\psi _X} [F(X),F(X)]\) for each object X of \({\mathcal {D}}\), and
-
at the morphism level, no data, since the value on morphisms is determined by being over
 and the functor from \(M\text {-}{\mathsf {rep}}\) to
and the functor from \(M\text {-}{\mathsf {rep}}\) to  is faithful.
is faithful.
However, to be a functor, the collection \(\psi _X\) must satisfy a condition so that for each map f in \(\text {Hom}_{{\mathcal {D}}}(X, Y)\), the map F(f) is an M-representation map between F(X) and F(Y). This is precisely the condition for the maps \(\psi _X\) to assemble to a map  . Compatibility with the M-representation structures for each object X implies that \(\psi \) is a morphism of large monoids. \(\square \)
. Compatibility with the M-representation structures for each object X implies that \(\psi \) is a morphism of large monoids. \(\square \)
Example 1
Let  be an object of
be an object of  . Then the equalizer formula for the cointegral computing
. Then the equalizer formula for the cointegral computing  collapses to [X, X]. So in this case
collapses to [X, X]. So in this case  recovers the ordinary endomorphism object [X, X].
recovers the ordinary endomorphism object [X, X].
Example 2
Let  be a morphism of
be a morphism of  , with domain X and codomain Y. Again the cointegral has a simple description via the equalizer formula; it is the pullback of [X, X] and [Y, Y] over [X, Y].
, with domain X and codomain Y. Again the cointegral has a simple description via the equalizer formula; it is the pullback of [X, X] and [Y, Y] over [X, Y].

This is sometimes called the endomorphism monoid of f [3, 13.10].
Remark 5
(Generalized enrichments) We have taken as our fundamental input an enrichment of the category  in the monoidal category
in the monoidal category  . A generalization of this framework is to consider instead a lax functor
. A generalization of this framework is to consider instead a lax functor

where  is the bicategory whose objects are monoids in
is the bicategory whose objects are monoids in  , whose morphisms are pointed bimodules, and whose 2-morphisms are maps of bimodules.
, whose morphisms are pointed bimodules, and whose 2-morphisms are maps of bimodules.
Let us present an example of such a generalized enrichment that does not fit directly in our framework. Let  be a large category, seen as naturally enriched in large sets. There is a lax functor
be a large category, seen as naturally enriched in large sets. There is a lax functor

given on objects by
which sends a map \(f : X \rightarrow Y\) to
and which sends the composite of two maps f and g to
Using the same ideas, one can see how to produce a generalized enrichment out of a  -enriched category
-enriched category  via
via
The cointegral defining the endomorphism monoid of a functor F has a natural extension to the generalized framework.
The generalized enrichment of our example yields the following adjunction

Of course one could—indirectly—obtain the adjunction between representations and automorphism groups by first taking the monoid of endomorphisms and then restricting to groups.
4 Small endomorphism monoids
When the domain category \({\mathcal {D}}\) of F is small, the endomorphism monoid  is obviously small. We shall show that this is still the case when \({\mathcal {D}}\) is large under appropriate accessibility conditions.
is obviously small. We shall show that this is still the case when \({\mathcal {D}}\) is large under appropriate accessibility conditions.
Lemma 1
(Accessible reduction) Assume that the category  is accessibly enriched [7], \({\mathcal {D}}\) is an accessible category and
is accessibly enriched [7], \({\mathcal {D}}\) is an accessible category and  is an accessible functor.
is an accessible functor.
Let \(\kappa \) be a small cardinal big enough so that \({\mathcal {D}}\) is \(\kappa \)-accessible and so that both F and \(X \mapsto [X,Y]\) commute with \(\kappa \)-filtered colimits. Let us denote by \(F^\kappa \) the restriction of F to the full subcategory \({\mathcal {D}}^\kappa \subset {\mathcal {D}}\) of \(\kappa \)-compact objects of \({\mathcal {D}}\). Then the canonical map

is an isomorphism. In particular  is a (small) monoid.
is a (small) monoid.
Proof
Using the universal property of the cointegrals, it is enough to show the existence of compatible maps

for every \(X \in {\mathcal {D}}\), such that for every \(\kappa \)-compact \(X^\kappa \), the map \(\varphi _{X^\kappa }\) is equal to the projection map  .
.
Since every \(X \in {\mathcal {D}}\) is canonically the \(\kappa \)-filtered colimit \(X ={{\,\mathrm{colim}\,}}_{X^\kappa \rightarrow X} X^\kappa \) of the \(\kappa \)-compact objects over it,
Every map \(g : X^\kappa \rightarrow X\) induces a morphism

and given \(h : \underline{X}^\kappa \rightarrow X^\kappa \), one can draw a commutative diagram

where the commutation of the first square is guaranteed by the universal property of  . This shows that we get a well-defined morphism \(\varphi _X\) for every \(X \in {\mathcal {D}}\).
. This shows that we get a well-defined morphism \(\varphi _X\) for every \(X \in {\mathcal {D}}\).
By construction of \(\varphi _X\), the following diagram commutes

hence when g is the identity of a \(\kappa \)-compact object \(X^\kappa \), we get \(\pi _{X^\kappa } = \varphi _{X^\kappa }\) as promised.
Let \(f : X \rightarrow Y\) be a morphism in \({\mathcal {D}}\). We need to check the commutativity of the induced square

By accessibility again, one may check the equality \(f^*\varphi _Y = f_*\varphi _X\) after projection \(g^*: [F(X), F(Y)] \rightarrow [F(X^\kappa ),F(Y)]\) for every \(g : X^\kappa \rightarrow X\). Then by the commutativity of the diagrams

and

we may conclude the desired result.
Remark 6
(Accessibility of the category of representations) In view of the previous reduction lemma, one may wonder whether  is an accessible functor between accessible categories whenever
is an accessible functor between accessible categories whenever  is accessibly enriched.
is accessibly enriched.
This appears to be an intricate question in general: it is still unknown whether the category of bigebras over some well-known props are actually accessible. In the particular case where  is accessibly tensored (or cotensored), this question receives a positive answer. We shall give more details about this case in the next section.
is accessibly tensored (or cotensored), this question receives a positive answer. We shall give more details about this case in the next section.
Cogebras over a dg-operad over a field give an example of an accessibly enriched context [B.1.3] that is neither tensored, nor cotensored, in which \(P\text {-}{\mathsf {cog}}\) is accessible for any dg-operad P [4].
5 The case of tensored enrichment
In the case where  is tensored over
is tensored over  , the additional structure allows one to say more about the adjunction between representations and endomorphisms, particularly when the tensor structure is well-behaved.
, the additional structure allows one to say more about the adjunction between representations and endomorphisms, particularly when the tensor structure is well-behaved.
5.1 The adjunction in the accessibly tensored case
In the case where forgetful functors are accessible, we no longer need to have jumps in sizes and we get a refined adjunction with the category of small monoids.
Proposition 1
(Accessibly tensored case) Assume that  is accessibly tensored over
is accessibly tensored over  . Then there is an adjunction
. Then there is an adjunction

in which \({\mathsf {Acc}}\) is the very large category of large accessible categories and accessible functors.
For this one restricts the adjunction  using accessible reduction [1] and the following lemmas.
using accessible reduction [1] and the following lemmas.
Lemma 2
If  is accessibly tensored, then every monoid M induces an accessible monad \({\widetilde{M}}\) on
is accessibly tensored, then every monoid M induces an accessible monad \({\widetilde{M}}\) on  whose category of modules is canonically equivalent to \(M\text {-}{\mathsf {rep}}\) as an object of
whose category of modules is canonically equivalent to \(M\text {-}{\mathsf {rep}}\) as an object of 
As a consequence, the category of representations \(M\text {-}{\mathsf {rep}}\) is accessible and the forgetful functor

is accessible.
Proof
Because the functor \(M \mapsto (M \otimes -)\) is monoidal [4], each monoid M induces an accessible monad \({\widetilde{M}}\) with underlying functor \(X \mapsto M \otimes X\). As a consequence its category of modules is accessible and the forgetful functor

is accessible.
We now claim that there is a canonical equivalence of categories above 
compatible with the forgetful functors. Let \((X,\alpha )\) be a representation of M. Then the monoid morphism \(\alpha : M \rightarrow [X, X]\) is equivalent by adjunction to an \({\widetilde{M}}\)-module structure \({\widetilde{\alpha }} : M \otimes X \rightarrow X\). Let \((Y, \beta )\) be another representation of M, then \(f : X \rightarrow Y\) is a morphism of representations if

commutes. By adjunction the top right part of the diagram is equivalent to \(M\otimes X \rightarrow X \rightarrow Y\) and the bottom left is equivalent to \(M \otimes X \rightarrow M \otimes Y \rightarrow Y\) so that the commutativity of the above square is equivalent to the commutativity of

Hence \(f : X \rightarrow Y\) is a morphism of M-representations if and only if it is a morphism of \({\widetilde{M}}\)-modules. \(\square \)
Lemma 3
Let  be an accessible functor with accessible domain. Then the counit of the adjunction
be an accessible functor with accessible domain. Then the counit of the adjunction  applied to F
applied to F

is given by an accessible functor.
Proof
The top map of the diagram if accessible because the two other maps are accessible [2] and the forgetful functor  is conservative. \(\square \)
is conservative. \(\square \)
Remark 7
In the accessibly tensored case, the representation functor factors through the category of accessible monads on  . Using an adapted version of a result of Janelidze and Kelly [5], one can show that the adjunction
. Using an adapted version of a result of Janelidze and Kelly [5], one can show that the adjunction  factors as a composite of adjunctions
factors as a composite of adjunctions

5.2 Faithfulness of \({\mathsf {Rep}}\)
The question of reconstructing a monoid M out of its category \(M\text {-}{\mathsf {rep}}\) of representations is an old one, in the Tannakian context for example [B.2.1]. Such a result cannot be obtained in general without additional hypotheses. Instead one can look at the opportunity of recovering M as a submonoid of  .
.
This is the question of faithfulness of the \({\mathsf {Rep}}\) functor which is of independent interest. As an example, one can view Joyal’s results on analytic monads [6] as saying in particular that the representation functor is faithful in the case where  is the category of sets operadically enriched in symmetric sequences.
is the category of sets operadically enriched in symmetric sequences.
The representation functor \(M \mapsto M\text {-}{\mathsf {rep}}\) is a priori not faithful. A trivial example of this takes  to be the empty category. A nontrivial example of independent interest is given by looking at the functor \(P \mapsto P\text {-}{\mathsf {cog}}\) mapping a dg-operad to its category of cogebras. Indeed, one can show that there exists a non-zero dg-operad without nontrivial cogebras [7]:
to be the empty category. A nontrivial example of independent interest is given by looking at the functor \(P \mapsto P\text {-}{\mathsf {cog}}\) mapping a dg-operad to its category of cogebras. Indeed, one can show that there exists a non-zero dg-operad without nontrivial cogebras [7]:
However, when  is tensored, we get a criterion to check whether the representation functor is faithful.
is tensored, we get a criterion to check whether the representation functor is faithful.
Proposition 2
(Faithfulness of representations) Assume that  is faithfully tensored over
is faithfully tensored over  , then the representations functor
, then the representations functor

is faithful. Equivalently, for every monoid M, the unit map

is a monomorphism.
Proof
Let \(\phi , \psi : M \rightrightarrows N\) be two morphisms of monoids such that

If \(\phi _{!}\) denotes the (partially defined) left adjoint to \({\text {U}}_{\phi }\) and \(\psi _{!}\) the (partially defined) left adjoint to \({\text {U}}_{\psi }\), then one has \(\phi _{!} = \psi _{!}\). Let X be an object of  , because
, because  is tensored over
is tensored over  , the monoid M acts on \(M \otimes X\) and \(M \otimes X\) is then the free representation of M induced on X. The same goes for \(N \otimes X\). As a consequence, one has
, the monoid M acts on \(M \otimes X\) and \(M \otimes X\) is then the free representation of M induced on X. The same goes for \(N \otimes X\). As a consequence, one has
Using the units of the adjunctions, one then gets that

Since this is true for every X, we get \(\phi = \psi \). \(\square \)
Change history
06 March 2020
The first equation under section “Remark 3” was processed and published incorrectly. The correct equation should read as follows:
References
Drummond-Cole, G.C., Hirsh, J., Lejay, D.: Endomorphism operads of functors. ArXiv e-prints arXiv:1906.09006 [math.CT] (2019)
Yoneda, N.: On Ext and exact sequences. J. Fac. Sci. (Imperial University of Tokyo) 8, 507–576 (1960)
Yau, D.: Colored operads, Graduate Studies in Mathematics, vol. 170. American Mathematical Society, Providence (2016)
Grignou, B.L., Lejay, D.: Homotopy theory of linear cogebras. ArXiv e-prints arXiv:1803.01376 [math.AT] (2018)
Janelidze, G., Kelly, G.M.: A note on actions of a monoidal category. Theory Appl. Categ. 9, 61–91 (2001)
Joyal, A.: Foncteurs analytiques et espèces de structures. In: Combinatoire énumérative, pp. 126–159. Springer, Berlin (1986). https://doi.org/10.1007/BFb0072514
Grignou, B.L., Lejay, D.: Operads without cogebras, ArXiv e-prints arXiv:1902.02551 [math.AT] (2019)
Kelly, G.M.: Basic Concepts of Enriched Category Theory, London Mathematical Society Lecture Note Series, vol. 64. Cambridge University Press, Cambridge (1982)
Ross, S.: Quantum Groups: A Path to Current Algebra, Australian Mathematical Society Lecture Series, vol. 19. Cambridge University Press, Cambridge (2007)
Arone, G., Ching, M.: Operads and chain rules for the calculus of functors, vol. 338 of Astérisque. Société Mathématique de France (2011)
Vallette, B.: Koszul duality for PROPs. Comptes Rendus Mathematique 338(12), 909–914 (2004)
Gan, W.L.: Koszul duality for dioperads. Math. Res. Lett. 10(1), 109–124 (2003)
Yau, D., Johnson, M.: A Foundation for PROPs, Algebras, and Modules. American Mathematical Society, Providence (2015)
Joyal, A., Ross, S.: An Introduction to Tannaka duality and quantum groups. In: Lecture Notes in Mathematics, pp. 413–492. Springer, Berlin (1991)
Anel, M., Joyal, A.: Sweedler Theory for (co)algebras and the bar-cobar constructions. ArXiv e-prints arXiv:1309.6952 [math.CT] (2013)
Montgomery, S.: Hopf Algebras and Their Actions on Rings. American Mathematical Society, Providence (1993)
Acknowledgements
The authors would like to thank Rune Haugseng, Theo Johnson-Freyd, Johan Leray, Emily Riehl, and Claudia Scheimbauer for useful discussions, as well as Greg Arone and Birgit Richter for pointing us to relevant literature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jiri Rosicky.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Gabriel C. Drummond-Cole and Damien Lejay were supported by IBS-R003-D1.
The original version of this article was revised to correct the table under “Introduction” section and an equation under “Remark 3” section.
Appendices
Terminology of enriched categories
We let the reader turn to Kelly [8] for a detailed exposition on categories enriched in a monoidal category  . In order to not be bothered by size issues, we fix once and for all three infinite inaccessible cardinals L < XL < XXL and use the dictionary
. In order to not be bothered by size issues, we fix once and for all three infinite inaccessible cardinals L < XL < XXL and use the dictionary
We now assume that  is large (has large sets of objects and morphisms) and has all small limits and colimits. In what follows we consider a large
is large (has large sets of objects and morphisms) and has all small limits and colimits. In what follows we consider a large  -enriched category
-enriched category

and assume that  is large.
is large.
1.1 Enlargement of the universe
For convenience (when computing over large diagrams), we shall enlarge  : we choose a very large monoidal category
: we choose a very large monoidal category  with a full monoidal embedding
with a full monoidal embedding

The enlarged universe can be chosen to be locally large, have all large limits and colimits and the embedding can be assumed to commute with small limits and colimits. This is discussed for example by Kelly [8, §2.6] (albeit in the closed symmetric setting).
The  -category
-category  can now without effort be seen as a
can now without effort be seen as a  -category
-category

1.2 Properties of enrichments
Definition 3
(Closed monoidal category) One says that  is closed when the functor \(Y \mapsto Y \otimes X\) has a right adjoint \(Z \mapsto X^Z\) for each object X in
is closed when the functor \(Y \mapsto Y \otimes X\) has a right adjoint \(Z \mapsto X^Z\) for each object X in  .
.
Definition 4
(Tensored) One says that  is tensored over
is tensored over  whenever
whenever  is closed and for every
is closed and for every  and
and  , the functor
, the functor
is  -representable by an object denoted
-representable by an object denoted  . In that case, since
. In that case, since  is closed the induced functor
is closed the induced functor

is naturally endowed with a monoidal structure.
Definition 5
(Faithfully tensored) We shall say that  is faithfully tensored over
is faithfully tensored over  if it is tensored and the functor
if it is tensored and the functor

is faithful.
Definition 6
(Accessibly tensored) We shall say that  is accessibly tensored over
is accessibly tensored over  if it is tensored, both
if it is tensored, both  and
and  are accessible and for every
are accessible and for every  , the functor
, the functor

is accessible.
Definition 7
(Accessibly enriched) When  and
and  are both accessible, we shall say that
are both accessible, we shall say that  is accessibly enriched if there exists a small cardinal \(\kappa \) such that for every
is accessibly enriched if there exists a small cardinal \(\kappa \) such that for every  , the functor
, the functor

commutes with \(\kappa \)-cofiltered limits.
Remark 8
One can check that if  is accessibly tensored, it is then accessibly enriched.
is accessibly tensored, it is then accessibly enriched.
Examples of contexts of application
In this appendix, we give several application contexts for the adjunction

In each context, the terminology is specific, both for monoids and for their categories of representations.
1.1 Using a closed symmetric monoidal category
In the next examples, we fix a presentable closed symmetric monoidal category  and denote its internal hom by \(\langle - ,- \rangle \). We then consider several enrichments for
and denote its internal hom by \(\langle - ,- \rangle \). We then consider several enrichments for  .
.
Potential examples of such closed symmetric monoidal categories include the category of sets, vector spaces or coassociative cogebras (more generally cogebras over Hopf operads). It also includes the categories of sheaves valued in those categories.
1.1.1 Self enrichment
This one is the most obvious, since the monoidal structure of  is closed, it is self-enriched via
is closed, it is self-enriched via
In this context, the general idea of the adjunction  was well-known to people doing reconstruction theorems à la Tannaka. It appears for example in Street’s Quantum groups: a path to current algebra [9, Ch. 16].
was well-known to people doing reconstruction theorems à la Tannaka. It appears for example in Street’s Quantum groups: a path to current algebra [9, Ch. 16].
1.1.2 Operadic enrichment
Let us denote by  the category of symmetric sequences: sequences of objects M(n) of
the category of symmetric sequences: sequences of objects M(n) of  endowed with right \(\mathbf{S }_{n}\)-actions for every natural n. The category
endowed with right \(\mathbf{S }_{n}\)-actions for every natural n. The category  is accessibly tensored over the category of symmetric sequences via the formula
is accessibly tensored over the category of symmetric sequences via the formula
This induces a monoidal structure on symmetric sequences
Where \(\circledast \) denotes the convolution of symmetric sequences. The associated enrichment is given by
Monoids in symmetric sequences are called operads

Given an operad P, its category of representations is called the category of P-algebras. One thus gets an adjunction

1.1.3 The other (cogebraic) operadic enrichment
This time we let  be the category of symmetric sequences with left actions of the symmetric groups. It admits a monoidal structure given by
be the category of symmetric sequences with left actions of the symmetric groups. It admits a monoidal structure given by
and the associated enrichment is
Since left and right actions of symmetric groups are equivalent, one has an equivalence of categories

In this case, the category of representations of an operad P is its category of cogebras. Conversely, the functor  associates to a functor F, seen as an object of the functor category, its coendomorphism operad.
associates to a functor F, seen as an object of the functor category, its coendomorphism operad.
In general, the category of P-cogebras may not be presentable, although (for example) it is presentable if the ground category is dg-vector spaces [4]. Thus, one has the adjunction

This example arises naturally in applications and appeared, for example, in unpublished work by May, who considered it well-known.
In one application, the singular chains functor from topological spaces to chain complexes factors through the category of \({\mathsf {E}}_\infty \)-cogebras in chain complexes.
The following stable improvement of this example was pointed out to us by Arone: the coendomorphism operad of the suspension functor from pointed spaces to spectra can be shown to be weakly equivalent to the commutative operad [10].
1.1.4 Propic enrichments
Going further, one can enrich  in the category of bisymmetric sequences
in the category of bisymmetric sequences  using
using
There are several monoidal structures on bisymmetric sequences compatible with these enrichment objects, depending on the classes of graphs involved in the definition of the monoidal structure. One can allow connected graphs, in which case the monoids are properads [11, 2.1], or allow only simply connected graphs, in which case the monoids are dioperads [12, 4.2]. Similar but more exotic examples are also possible [13].
1.2 Examples with exogenous enrichments
1.2.1 Representations of topological monoids
The following example is taken from the duality between topological groups and their categories of representations due to Tannaka [14]. The category of finite dimensional vector spaces is canonically enriched in topological spaces. Since this category is small, one gets an adjunction

where  associates to any functor \(F : {\mathcal {D}}\rightarrow {\mathsf {Vect}}_{\text {fd}}\) its topological monoid of endomorphisms.
associates to any functor \(F : {\mathcal {D}}\rightarrow {\mathsf {Vect}}_{\text {fd}}\) its topological monoid of endomorphisms.
1.2.2 Bigebras
Let \({\varvec{K}}\) be a field. The category of associative \({\varvec{K}}\)-algebras is naturally cotensored over \({\varvec{K}}\)-cogebras: given a cogebra V and an algebra \({\varLambda }\), convolution gives \(\text {Hom}_{{\varvec{K}}}(V, {\varLambda })\) a structure of associative algebra. This cotensorization comes with an enrichment and a tensorization [15].
Monoid objects in cogebras are bigebras. Given a bigebra H, it is an exercise to verify that the category of representations \(H\text {-}{\mathsf {rep}}\) is naturally isomorphic to the category of H-module algebras studied by Hopf theorists [16, 4.1.1] equipped with the functor to algebras forgetting the H-module structure. We thus obtain an adjunction

where for an accessible functor \(F :{\mathcal {D}}\rightarrow {\mathsf {Alg}}\), the endomorphism bigebra  is universal among bigebras acting compatibly on the objects of \({\mathcal {D}}\).
is universal among bigebras acting compatibly on the objects of \({\mathcal {D}}\).
Rights and permissions
About this article
Cite this article
Drummond-Cole, G.C., Hirsh, J. & Lejay, D. Representations are adjoint to endomorphisms. J. Homotopy Relat. Struct. 15, 377–393 (2020). https://doi.org/10.1007/s40062-019-00252-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-019-00252-1




 and
and 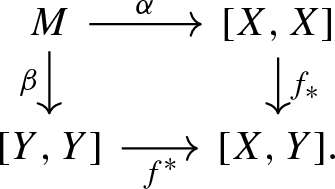
 and the functor from
and the functor from  is faithful.
is faithful.