Abstract
Fix a symbol \(\underline{a}\) in the mod-\(\ell \) Milnor K-theory of a field k, and a norm variety X for \(\underline{a}\). We show that the ideal generated by \(\underline{a}\) is the kernel of the K-theory map induced by \(k\subset k(X)\) and give generators for the annihilator of the ideal. When \(\ell =2\), this was done by Orlov, Vishik and Voevodsky.
Similar content being viewed by others
1 Introduction
Let \(\ell \) be a prime and k a field containing \(1/\ell \). Given units \(a_1,\ldots ,a_n\in k^\times \) we can form the Steinberg symbol \(\underline{a}= \{a_1,\ldots ,a_n\}\) in \(K^M_n(k)\); we wish to study the ideal \((\underline{a})\) generated by \(\underline{a}\) in \(K^M_n(k)/\ell \). What is the quotient ring \((K^M_*(k)/\ell )/(\underline{a})\), and what is the annihilator ideal \({{\mathrm{ann}}}(\underline{a})\), so that \((\underline{a}) = (K^M_*(k)/\ell )/{{\mathrm{ann}}}(\underline{a})\)?
Here is the main result of this paper; it was proven for \(\ell =2\) by Orlov, Vishik and Voevodsky in [12, 2.1].
Theorem 1.1
Suppose that \(\mathrm {char}\,k = 0\), and let X be a norm variety for a nontrivial symbol \(\underline{a}\) in \(K^M_n(k)/\ell \). Then:
-
(a)
the kernel of
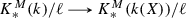 is the ideal of \(K^M_*(k)/\ell \) generated by \(\underline{a}\);
is the ideal of \(K^M_*(k)/\ell \) generated by \(\underline{a}\); -
(b)
the annihilator of \(\underline{a}\) is the ideal of \(K^M_*(k)/\ell \) generated by the norms
$$\begin{aligned} \{ N(\alpha ) \in K^M_*(k)/\ell \,|\, \alpha \in K^M_*(k(x)),\ x \text { a closed point in }X \}. \end{aligned}$$
Theorem 1.1 uses the notion of a norm variety; see Definition 3.1 below. The existence of norm varieties is due to Rost; the terminology comes from [13] and [6, 1.18].
Examples 1.2
Theorem 1.1(a) implies that  is an injection when \(i<n\), that the kernel of
is an injection when \(i<n\), that the kernel of  is exactly the cyclic subgroup generated by \(\underline{a}\) and that the kernel of
is exactly the cyclic subgroup generated by \(\underline{a}\) and that the kernel of  is the subgroup \(\underline{a}\cup k^\times \).
is the subgroup \(\underline{a}\cup k^\times \).
The group of units b in \(k^\times /k^{\times \ell }\) such that \(\{ a_1,\dots ,a_n,b\}=0\) in \(K^M_{n+1}(k)/\ell \) forms the degree 1 part of the ideal \({{\mathrm{ann}}}(\underline{a})\). This group, described in Theorem 1.1(b) was originally described by Voevodsky. If \(H_{p,q}(X)\) is the motivic homology of a norm variety for \(\underline{a}\), X, and k has no extensions of degree \(\ell \), Voevodsky proved in [13, A.1 and 2.9] that the pushforward  induces an exact sequence
induces an exact sequence

Here \(\overline{H}_{p,q}(X)\) denotes the coequalizer of the two projections \(H_{p,q}(X\times X)\rightrightarrows H_{p,q}(X)\). Thus the degree 1 part of \({{\mathrm{ann}}}(\underline{a})\) is \(\overline{H}_{-1,-1}(X)\): \(\{\underline{a},b\}=0\) if and only if \(b\in \overline{H}_{-1,-1}(X)\).
When \(n=1\), write \(\underline{a}=(a)\) for \(a\in k^\times \), and set \(E=k(\root \ell \of {a})\). Then \(X={{\mathrm{Spec}}}(E)\) is a norm variety for \(\underline{a}\). For simplicity, suppose that k contains an \(\ell \)th root of unity, \(\zeta \). The degree 2 part of \((\underline{a})\) is the group of symbols \(a\cup b\); under the isomorphism \(H_{\mathrm {et}}^2(k,\mathbb {Z}/\ell )\cong {}_\ell \!{{\mathrm{Br}}}(k)\), \(a\cup b\) is identified with the class of the cyclic algebra \(A_\zeta (a,b)\) in the Brauer group. Theorem 1.1 describes the group of units b for which \(A_\zeta (a,b)\) is a matrix algebra, and the class of division algebras (or classes \([A]\in {}_\ell \!{{\mathrm{Br}}}(k)\)) which are equivalent to cyclic algebras. In this case, Kummer theory gives the answer: the group of units is the image \(N(E^\times )\) of the norm map  , and the class of division algebras equivalent to cyclic algebras is the class of algebras split by E. (See [20, 6.4.8].) In fact, we have the classical exact sequence
, and the class of division algebras equivalent to cyclic algebras is the class of algebras split by E. (See [20, 6.4.8].) In fact, we have the classical exact sequence

When \(n=1\), Theorem 1.1 states that for every unit a not in \(k^{\times \ell }\) there are exact sequences

when \(i=1\) this is exactly (1.2b). This follows from Voevodsky’s Galois computations [6, 3.2 and 3.6] (cf. [14, 5.2 and 6.11]) and the fact that \(\ell \cdot K^M_i(k)\subseteq N(K^M_i(E))\).
Theorem 1.1 follows from the more technical Theorem 1.3. We note that the analysis in [12] did not need to worry about roots of unity, as any field of characteristic 0 contains the square roots of unity, and Pfister quadrics always have points of degree 2. For an odd prime \(\ell \), the existence of a norm variety with points of degree \(\ell \) is established in [13, 1.21] modulo the Norm Principle, proven in [5, 0.3]; see Chapter 10 of [6].
Theorem 1.3
Let \(\mathrm {char}\,k = 0\). Suppose that X is a norm variety for a symbol \(\underline{a}\) in \(K^M_n(k)/\ell \) containing a point x with \([k(x):k]=\ell \). Write \(q = n+i\) and let \(\widetilde{K}^M_{q}(k(X))/\ell \) denote the equalizer of the maps  ; \(\mathfrak {X}\) denotes the 0-coskeleton of X (see Definition 3.3).
; \(\mathfrak {X}\) denotes the 0-coskeleton of X (see Definition 3.3).
-
(a)
If \(\mu _\ell \subset k^\times \), there is an exact sequence for all i:

-
(b)
If \(\mu _\ell \not \subset k^\times \), set \(e=[k(\zeta ):k]\) and \(X'=X\times _{k_1}k(\zeta )\), where \(k_1=k(\zeta )\cap k(X)\). If \(\mathfrak {X}'\) denotes the 0-coskeleton of \(X'\) over \(k(\zeta )\), then for all i there is an exact sequence:

The map \(\iota \) is induced by the homomorphism
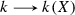 , and \(G = {{\mathrm{Gal}}}(k'/k_1)\).
, and \(G = {{\mathrm{Gal}}}(k'/k_1)\).
The sequences (1.2a), (1.2b) and (1.2c) begin with an injection. This is often, but not always, the case.
Question 1.4
In the situation of Theorem 1.3(a) with \(\mu _\ell \subset k^\times \), when is \(\pi _*\) an injection?
For \(i=0\), the map \(\pi _*\) is an injection: \(\overline{H}_{0,0}(X)=\mathbb {Z}\), and its image in \(K_0(k)=\mathbb {Z}\) is \(\ell \mathbb {Z}\). (This observation goes back to [9, 8.7.2].) This calculation shows that the mod-\(\ell \) reduction  of \(\pi _*\) is not always an injection.
of \(\pi _*\) is not always an injection.
The map \(\pi _*\) is an injection for \(i=1\) by Eq. (1.2a), and for \(n=1\) by Lemma 2.5 below. However, if k does not contain the \(\ell ^{th}\) roots of unity, \(\pi _*\) need not be an injection even for \(i=n=1\), as the classical Hilbert Theorem 90 can fail; see Example 2.6 below.
Theorem 1.1(b) could be strengthened to only look at norms of elements in \(K^M_1(k)=k^\times \) if we knew that the answer to the following question was affirmative:
Question 1.5
If E / F is a Galois extension of prime degree, is \(K^M_{n+1}(E)\) always generated by symbols \(\{a_1,\ldots ,a_n,b\}\) with \(a_i\in F^\times \) and \(b\in E^\times \)?
It suffices to check the case \(n=1\): is \(K^M_2(E)\) is always generated by symbols \(\{a,b\}\) with \(a\in F^\times \) and \(b\in E^\times \)?
If \(\ell =2\), \(\ell =3\) or k is \(\ell \)-special, this is the case; \(K^M_2 k(x)\) is generated by symbols \(\{a,b\}\) with \(a\in k^\times \) and \(b\in k(x)^\times \); see [8, Lemma 2], [1, p. 388]. By Becher [2, 1.1], \(K^M_n k(x)\) is also generated by symbols \(\{\alpha ,\beta \}\) with \(\alpha \in K^M_{n-m}(k)\), \(\beta \in K^M_m(k)\) if \(\ell <2^{m+1}\).
The restriction to prime degree is necessary in Question 1.5. Becher has pointed out in [2, 3.1] that if \(E=k(x,y)\) and \(F=k(x^\ell ,y^\ell )\) then \(\{x,y\}\) cannot be written in this form, as the tame symbol  shows. In this case, \([E:F]=\ell ^2\).
shows. In this case, \([E:F]=\ell ^2\).
Remark 1.6
Although most of our results work over perfect fields of arbitrary characteristic, the assumption that k has characteristic 0 is needed in two places.
-
1.
To prove that norm varieties exist for symbols of length n. This would go through for any perfect field of positive characteristic (by induction on n) if we could prove that for symbols of length \(n-1\) over k, a norm variety Y exists which satisfies the Norm Principle (see [5, 0.3] or [6, 10.17]). The inductive step is given in [6, 10.21].
-
2.
We also need characteristic 0 to show that the symmetric characteristic class \(s_d(X)\) of a norm variety is nonzero modulo \(\ell ^2\). The proof in characteristic 0 is due to Rost (unpublished), and given in Proposition 10.13 of [6], and depends upon the Connor–Floyd theory of equivariant cobordisms on complex G-manifolds (as given by Theorem 8.16 in loc. cit.) It is possible that a proof in characteristic \(p>0\) could be given along the lines of [13, 5.2], if we assume resolution of singularities.
We will therefore state as many of our results in as much generality as possible, only restricting to characteristic zero when absolutely necessary.
Remark 1.7
After writing this paper, we discovered that many of our results are in Yagita’s paper [21] and in the Merkurjev–Suslin paper [10] when \(\mu _\ell \subset k^\times \). (Compare [21, Thm. 10.3] to our 1.3a and [10, 2.1] to our 1.1 and 1.3.) The basic technique in these papers, and in ours, is the same: generalize the ideas in [12], using Rost’s norm varieties for \(\ell >2\). Yagita’s proof is somewhat sketchy as it predated a clear understanding of norm varieties. Merkurjev and Suslin prove Theorem 1.1(b) when \(\mu _\ell \subset k^\times \), but their result does not discuss \(K_n^M(k)\) in the absence of roots of unity. Since neither of these results directly addresses the ring structure of \(K^M_*(k)/\ell \), nor do they contain the final term \(H^{q+1,q-1}\) in our Theorem 0.3, we feel that our exposition should be added to the public record.
Notation and conventions
We fix a prime \(\ell \) and an \(\ell \)th root of unity \(\zeta \). We write \(H^{p,q}(Y,\mathbb {Z}/\ell )\) for \(H^p_{\text {nis}}(Y,\mathbb {Z}/\ell (q))\).
2 Borel–Moore homology
The first term in Theorem 1.3 uses the motivic homology group \(H_{-i,-i}(X)\) of a smooth projective variety X (with coefficients in \(\mathbb {Z}\)). However, it is more useful to think of it as the Borel–Moore homology group \(H^{BM}_{-i,-i}(X)\), which is covariant for proper maps between smooth varieties, and contravariant for finite flat maps; see [4, p. 185] or [11, 16.13]. We define \(H^{BM}_{-i,-i}(X)\) to be \(H^{BM}_{-i,-i}(X,\mathbb {Z})\) if \(\mathrm {char}\,k = 0\), and \(H^{BM}_{-i,-i}(X,\mathbb {Z}[1/p])\) if \(\mathrm {char}\,k = p\!>\!0\).
Let X be smooth and projective. We then have \(H_{-i,-i}(X)=H^{BM}_{-i,-i}(X)\), and more generally \(H_{p,q}(X,\mathbb {Z})=H^{BM}_{p,q}(X,\mathbb {Z})\), because the natural map from \(M(X)=\mathbb {Z}_{\mathrm {tr}}(X)\) to \(M^c(X)\) in \(\mathbf {DM}\) is an isomorphism for smooth projective X. Recall from [11, 2.8] that \(\mathbb {Z}_{\mathrm {tr}}(X)\) denotes the sheaf with transfers represented by X, and Voevodsky’s triangulated category \(\mathbf {DM}\) is a localization of the derived category of sheaves with transfers; see for example [11, p. 110]. The motivic homology groups \(H_{p,q}(X,\mathbb {Z})\) of X are defined to be \(\mathrm {Hom}_{\mathbf {DM}}(\mathbb {Z}(q)[p],M(X))\), while the Borel–Moore homology groups \(H^{BM}_{p,q}(X,\mathbb {Z})\) are defined to be \(\mathrm {Hom}_{\mathbf {DM}}(\mathbb {Z}(q)[p],M^c(X))\); see [4, p. 185] or [11, 14.17, 16.20].
The case \(i=1\) of the following result was proven in [13].
Proposition 2.1
Let X be a smooth variety over a perfect field k; write \(X^{(0)}\) for the closed points of X and \(X^{(1)}\) for the dimension 1 points of X. If \(i\ge 0\), \(H^{BM}_{-i,-i}(X)\) is the abelian group generated by symbols \([x,\alpha ]\), where x is a closed point of X and \(\alpha \in K^M_i(k(x))\), modulo the relations
-
(i)
\([x,\alpha ][x,\alpha ']=[x,\alpha +\alpha ']\) and
-
(ii)
the image of the tame symbol
 is zero for every dimension 1 point y of X.
is zero for every dimension 1 point y of X.
That is, we have an exact sequence

In addition, \(H^{BM}_{-i,-i}(X)\) is isomorphic to \(H^{2d+i,d+i}(X,\mathbb {Z})\).
Proof
Let A denote the abelian group with generators \([x,\alpha ]\) and relations (i) and (ii), described in the Proposition, and set \(d=\dim (X)\). We first show that A is isomorphic to \(H^d(X,\mathscr {H}^{d+i})\), where \(\mathscr {H}^q\) denotes the Zariski sheaf associated to the presheaf \(H^{q,d+i}(-,\mathbb {Z})\). For each q, \(\mathscr {H}^{q}\) is a homotopy invariant Zariski sheaf, by [11, 24.1]. As such, it has a canonical flasque “Gersten” resolution on each smooth X (given in [11, 24.11]), whose \(c^{th}\) term is the coproduct over codimension c points z of X of the skyscraper sheaves \(H^{q-c,d+i-c}(k(z))\). Taking \(q=d+i\), and recalling that \(K^M_i\cong H^{i,i}\) on fields, we see that the stalks of the skyscraper sheaves in the \((d-1)^{st}\) and \(d^{th}\) terms are groups \(K^M_{i+1}(k(y))\) and \(K^M_i(k(x))\). Moreover, the map  is the tame symbol if \(x\in \overline{\{ y\}}\), and zero otherwise. As \(H^d(X,\mathscr {H}^{d+i})\) is obtained by taking global sections and then cohomology, it is isomorphic to A.
is the tame symbol if \(x\in \overline{\{ y\}}\), and zero otherwise. As \(H^d(X,\mathscr {H}^{d+i})\) is obtained by taking global sections and then cohomology, it is isomorphic to A.
Next, we show that A is isomorphic to \(H^{2d+i,d+i}(X,\mathbb {Z})\). To this end, consider the hypercohomology spectral sequence \(E_2^{p,q}=H^{p}(X,\mathscr {H}^q) \Rightarrow H^{p+q,d+i}(X,\mathbb {Z})\). Since \(H^{q,d+i}(k(z))=0\) for \(q>d+i\), the spectral sequence is zero unless \(p\le d\) and \(q\le d+i\). From this we deduce that \(H^{2d+i,d+i}(X,\mathbb {Z}) \cong H^d(X,\mathscr {H}^{d+i})\cong A\).
Finally, we show that \(H^{BM}_{-i,-i}(X)\) is isomorphic to \(H^{2d+i,d+i}(X,\mathbb {Z})\). Suppose first that \(i=0\). Then the presentation describes \(CH_0(X)\cong H^{2d,d}(X,\mathbb {Z})\), and by [17] we also have \(H_{0,0}^{BM}(X)=CH_0(X)\). Thus we may assume that \(i>0\).
If \(\text {char}(k)=0\), the proof is finished by the duality calculation, which uses Motivic Duality with \(d=\dim (X)\) (see [11, 16.24] or [4, 7.1]):
Now suppose that k is a perfect field of \(\text {char}(k)=p>0\). As we show below in Lemma 2.2, \(K^M_i(k(x))\) and \(K_{i+1}^M(k(y)\)) are uniquely p-divisible for \(i\ge 1\) (when x is closed in X and \(\text {trdeg}_k k(y)=1\)). Thus A must also be uniquely p-divisible. Since \(H^{2d+i,d+i}(X,\mathbb {Z})\cong \!A\), the duality calculation above goes through with \(\mathbb {Z}\) replaced by \(\mathbb {Z}[1/p]\), using the characteristic p version of Motivic Duality (see [7, 5.5.14]) and we have \(H^{BM}_{-i,-i}(X,\mathbb {Z}[1/p])\cong \! H^{2d+i,d+i}(X,\mathbb {Z}[1/p])\cong \! H^{2d+i,d+i}(X,\mathbb {Z})\). \(\square \)
Lemma 2.2
(Izhboldin) Let E be a field of transcendence degree t over a perfect field k of characteristic p. Then \(K^M_{m}(E)\) is uniquely p-divisible for \(m>t\).
Proof
For any field E of characteristic p, the group \(K^M_m(E)\) has no p-torsion by Izhboldin’s Theorem ([20, III.7.8]), and the d\(\log \) map  is an injection with image \(\nu (m)\); see [20, III.7.7.2]. Since k is perfect, \(\Omega ^1_k=0\) and \(\Omega ^1_E\) is t-dimensional, so if \(m>t\) then \(\Omega ^m_E=0\) and hence \(K^M_m(E)/p=0\).\(\square \)
is an injection with image \(\nu (m)\); see [20, III.7.7.2]. Since k is perfect, \(\Omega ^1_k=0\) and \(\Omega ^1_E\) is t-dimensional, so if \(m>t\) then \(\Omega ^m_E=0\) and hence \(K^M_m(E)/p=0\).\(\square \)
Example 2.3
-
(i)
\(H_{-i,-i}({{\mathrm{Spec}}}E)=K^M_i(E)\) for every field E over k, as is evident from the presentation in Proposition 2.1.
-
(ii)
If E is a finite extension of k, the proper pushforward from \(K^M_i(E)=H_{-i,-i}({{\mathrm{Spec}}}E)\) to \(K^M_i(k)=H_{-i,-i}({{\mathrm{Spec}}}k)\) is just the norm map \(N_{E/k}\); see [20, III. 7.5.3].
-
(iii)
If
 is proper, and \(x\in X\) is closed, the restriction of the pushforward
is proper, and \(x\in X\) is closed, the restriction of the pushforward 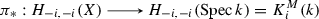
to \(K^M_i(k(x))\) sends \([x,\alpha ]\) to the norm \(N_{k(x)/k}(\alpha )\). This follows from (ii) by functoriality of \(H_{-i,-i}\) for the composite
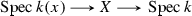 , \(x\in X\) closed. From the presentation in Proposition 2.1, the map \(N_{X/k}\) is completely determined by the formula \(\pi _*[x,\alpha ]=N_{k(x)/k}(\alpha )\). In particular, the image of \(\pi _*\) is the subgroup of \(K^M_i(k)\) generated by the norms \(N_{k(x)/k}(\alpha )\) of \(\alpha \in k(x)^\times \) as x ranges over the closed points of X.
, \(x\in X\) closed. From the presentation in Proposition 2.1, the map \(N_{X/k}\) is completely determined by the formula \(\pi _*[x,\alpha ]=N_{k(x)/k}(\alpha )\). In particular, the image of \(\pi _*\) is the subgroup of \(K^M_i(k)\) generated by the norms \(N_{k(x)/k}(\alpha )\) of \(\alpha \in k(x)^\times \) as x ranges over the closed points of X.
Lemma 2.4
Suppose that \(\mu _\ell \subset k\). Let \(E = k(\root \ell \of {a})\) and write \(X = {{\mathrm{Spec}}}(E)\), \(G = {{\mathrm{Gal}}}(E/k)\). Then \(X \times X \cong \coprod _G X\).
Proof
Since E is a Galois extension, \(E\otimes E \cong \prod _G E\); thus \(X \times X \cong {{\mathrm{Spec}}}(E\otimes E) \cong \coprod _G X\). \(\square \)
Lemma 2.5
Suppose that \(\mu _\ell \subset k\) and \(a\in k^\times \), and set \(E=k(\root \ell \of {a})\), \(X={{\mathrm{Spec}}}(E)\). Then \(\overline{H}_{-i,-i}(X)\cong K^M_i(E)_{{{\mathrm{Gal}}}(E/k)}\), and  is an injection.
is an injection.
Proof
Note that E / k is Galois with group G, so \(X\times X\cong \coprod _GX\) by Lemma 2.4 and \(\overline{H}_{-i,-i}(X)\cong (K^M_iE)_G\) by Example 2.3(i). In this case, \((K^M_iE)_G\) is a subgroup of \(K^M_i(k)\) by (1.2c).\(\square \)
Example 2.6
If E / k is not Galois,  need not be an injection, even for \(n=1\). One way to think of this is to realize that the classical Hilbert 90 asserts exactness of
need not be an injection, even for \(n=1\). One way to think of this is to realize that the classical Hilbert 90 asserts exactness of  , and Hilbert 90 requires E / k to be Galois [19, 6.4.7]. A concrete example is given by \(\ell =3\), \(k=\mathbb {Q}\), and \(E=\mathbb {Q}(\root 3 \of {2})\). In this case, \({{\mathrm{Spec}}}(E)\times {{\mathrm{Spec}}}(E)\cong {{\mathrm{Spec}}}(E\times F)\), where \(F=E(\root 3 \of {1})\), and the coequalizer \(\overline{H}_{-1,-1}({{\mathrm{Spec}}}(E))\) of \((E\times F)^\times \rightrightarrows E^\times \) does not inject into \(\mathbb {Q}^\times \). This shows that \(\pi _*\) in Theorem 1.3(a) is not always an injection.
, and Hilbert 90 requires E / k to be Galois [19, 6.4.7]. A concrete example is given by \(\ell =3\), \(k=\mathbb {Q}\), and \(E=\mathbb {Q}(\root 3 \of {2})\). In this case, \({{\mathrm{Spec}}}(E)\times {{\mathrm{Spec}}}(E)\cong {{\mathrm{Spec}}}(E\times F)\), where \(F=E(\root 3 \of {1})\), and the coequalizer \(\overline{H}_{-1,-1}({{\mathrm{Spec}}}(E))\) of \((E\times F)^\times \rightrightarrows E^\times \) does not inject into \(\mathbb {Q}^\times \). This shows that \(\pi _*\) in Theorem 1.3(a) is not always an injection.
3 Norm varieties
Let \(\underline{a}=(a_1,\ldots ,a_n)\) be a sequence of units in a field k of characteristic not equal to \(\ell \).
Definition 3.1
A field F over k is said to be a splitting field for \(\underline{a}\) if \(\underline{a}\) vanishes in \(K_n^M(F)/\ell \). We say that a variety X is a splitting variety for \(\underline{a}\) if k(X) is a splitting field for \(\underline{a}\), i.e., if \(\underline{a}\) vanishes in \(K_n^M(k(X))/\ell \).
Let X be a splitting variety for \(\underline{a}\). We say that X is an \(\ell \)-generic splitting variety for \(\underline{a}\) if any splitting field F has a finite extension E of degree prime to \(\ell \) with \(X(E)\ne \emptyset \).
A norm variety for \(\underline{a}\) is a smooth projective variety X of dimension \(d=\ell ^{n-1}-1\) which is an \(\ell \)-generic splitting variety for \(\underline{a}\). When \(\text {char}(k)=0\), a norm variety for \(\underline{a}\) always exists (see [6, 10.16]).
For example, \(E=k(\root \ell \of {a}_1)\) is a splitting field for \(\underline{a}=(a_1,\ldots ,a_n)\). Since a norm variety X is \(\ell \)-generic, there is a finite field extension \(E'/E\) of degree prime to \(\ell \) and an \(E'\)-point of X. The following result, due to Rost, is proven in Chapter 10 of [6].
Theorem 3.2
If \(\underline{a}\) is a nonzero symbol over k and \(\text {char}(k)=0\), then there exists a norm variety X for \(\underline{a}\) having a closed point x with \([k(x):k]=\ell \).
We will frequently use the following fact, proven in [13, 1.21] (see [6, 10.13]): if k has characteristic 0 and \(n\ge 2\), the symmetric characteristic class \(s_d(X)\) of a norm variety X is nonzero modulo \(\ell ^2\) (i.e., X is a \(\nu _{n-1}\)-variety).
Definition 3.3
Given a norm variety X, let \(\mathfrak {X}\) denote its 0-coskeleton, i.e., the simplicial scheme  with the projections
with the projections  as face maps and the diagonal inclusions as degeneracies.
as face maps and the diagonal inclusions as degeneracies.
For simplicity, we write \(\mathbb {L}\) for \(\mathbb {Z}_{(\ell )}(1)[2]\), R for \(\mathbb {Z}_{(\ell )}\), and \(R_{\mathrm {tr}}(\mathfrak {X})\) for \(\mathbb {Z}_{tr}(\mathfrak {X})_{(\ell )}\). We also regard X as a Chow motive. Recall [11, 20.1] that Chow motives form a full subcategory of \(\mathbf {DM}\), and that an idempotent element \(e\in CH^{\dim X}(X\times X)\) gives rise to a summand (X, e) of X in this category. Switching factors in \(X\times X\) yields the transpose idempotent \(e^t\) and a summand \((X,e^t)\).
Theorem 3.4
Let X be a norm variety for \(\underline{a}\) such that \(s_d(X)\) is nonzero modulo \(\ell ^2\). Then there is a Chow motive \(M=(X,e)\) with coefficients \(\mathbb {Z}_{(\ell )}\), such that
-
(i)
\(M=(X,e)\) is a symmetric Chow motive, i.e., \((X,e)=(X,e^t)\);
-
(ii)
The projection
 factors as
factors as 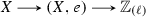 , i.e., is zero on \((X,1-e)\);
, i.e., is zero on \((X,1-e)\); -
(iii)
There is a motive D related to the structure map
 and its twisted dual \(y^D\) by two distinguished triangles in \(\mathbf {DM}\), where \(b=d/(\ell -1)\):
and its twisted dual \(y^D\) by two distinguished triangles in \(\mathbf {DM}\), where \(b=d/(\ell -1)\):  (3.4a)
(3.4a) (3.4b)
(3.4b)
Proof
This is proven carefully in [6, Ch. 5]; the construction is due to Voevodsky [16, pp. 422–428] and appears in Section 1 of [18]. Specifically, \(\underline{a}\) determines a motive A by (5.1), Definition 5.5 and 5.13.1 of [6]; by definition, \(M=S^{\ell -1}(A)\) and \(D=S^{\ell -2}(A)\), where \(S^m(A)\) is the mth symmetric product of A. Part (i) follows from 5.19; part (ii) follows from 5.9; and part (iii) follows from 5.7 of loc. cit. \(\square \)
Although many of our techniques require the field k to contain the \(\ell \)th roots of unity, we can sometimes remove this restriction using the following observation. Given a norm variety X over a field k, let \(k_1\) denote the largest subfield of \(k(\zeta )\) contained in k(X). Then X is also a norm variety for \(\underline{a}\) over \(k_1\).
Lemma 3.5
Given a nonzero symbol \(\underline{a}\in K^M_*(k)/\ell \), let X be a norm variety for \(\underline{a}\) over k. Then every component \(X'\) of \(X_{k(\zeta )}\) is a norm variety for \(\underline{a}\) over \(k(\zeta )\).
Proof
Clearly, \(X'\) is a splitting variety for \(\underline{a}\) of the right dimension. Given a splitting field F of \(\underline{a}\) over \(k(\zeta )\), there is a prime-to-\(\ell \) extension E of F such that \(k(\zeta )\subset E\) and such that there exists a map  over k. By basechange, there is a map
over k. By basechange, there is a map  over \(k(\zeta )\). As \(k(\zeta )\subset E\), \(E\otimes _kk(\zeta )\) is a \({{\mathrm{Gal}}}(k(\zeta )/k)\)-indexed product of copies of E. Since \({{\mathrm{Gal}}}(k(\zeta )/k)\) acts transitively on the components of \(X_{k(\zeta )}\), each component \(X'\) of \(X_{k(\zeta )}\) has an E-point. Thus \(X'\) is a norm variety over \(k(\zeta )\).\(\square \)
over \(k(\zeta )\). As \(k(\zeta )\subset E\), \(E\otimes _kk(\zeta )\) is a \({{\mathrm{Gal}}}(k(\zeta )/k)\)-indexed product of copies of E. Since \({{\mathrm{Gal}}}(k(\zeta )/k)\) acts transitively on the components of \(X_{k(\zeta )}\), each component \(X'\) of \(X_{k(\zeta )}\) has an E-point. Thus \(X'\) is a norm variety over \(k(\zeta )\).\(\square \)
Remark 3.6
\(X_{k(\zeta )}\) is a \({{\mathrm{Gal}}}(k_1/k)\)-indexed coproduct of copies of \(X'=X\times _{k_1}{{\mathrm{Spec}}}\,k(\zeta )\).
4 Reducing to Theorem 1.3 over fields containing \(\ell \)-th roots
We are now ready to prove Theorem 1.1 assuming Theorem 1.3. Fix a field k of characteristic 0, a symbol \(\underline{a}\) and a norm variety X for \(\underline{a}\). We first observe that, given Example 2.3(ii), the statement of Theorem 1.1 is equivalent to the exactness of the sequence

As observed in Example 1.2, Theorem 1.1 for \(n=1\) follows from (1.2c) when \(\mu _\ell \subset k^\times \).
Proposition 4.2
Suppose that Theorem 1.3 holds over k. Then so does Theorem 1.1.
Proof
As the equalizer \(\tilde{K}^M_{i+n}(k(X))/\ell \) is a subgroup of \(K^M_{i+n}(k(X))/\ell \), Theorem 1.3 implies that there is an exact sequence

(If \(\mu \subset k^\times \) then \(e=1\)). Exactness of (4.1) is immediate.\(\square \)
Thus we have reduced the proof of Theorem 1.1 to Theorem 1.3. We will now show that proving Theorem 1.3 over fields containing \(\ell \)th roots of unity suffices.
Proposition 4.3
Suppose that Theorem 1.3 holds for all fields of characteristic 0 which contain \(\ell \)th roots of unity. Then Theorem 1.3 holds for all fields of characteristic 0.
Proof
Let k be any field of characteristic 0 not containing an \(\ell ^{th}\) root of unity, \(\zeta \). Set \(q = n+i\), \(k'=k(\zeta )\), \(k_1=k'\cap k(X)\), \(e=[k':k]\) and \(G = {{\mathrm{Gal}}}(k'/k_1)\), as in the statement of Theorem 1.3(b). By Lemma 3.5 and Remark 3.6, the component \(X'=X\times _{k_1}{{\mathrm{Spec}}}(k')\) of \(X_{k'}\) is a norm variety for \(\underline{a}\) over \(k'\). The action of G on \(k'\) induces actions of G on \(X'\) and its 0-skeleton \(\mathfrak {X}'\), and induces the last map in Theorem 1.3(b):

Since e is prime to \(\ell \), inverting e in the exact sequence of Theorem 1.3 for \(k'\) yields the exact sequence forming the bottom row of the following diagram, in which the downward arrows are base change maps and the upward arrows are the norm maps.

As each K-group is covariantly functorial, the diagram with the downward set of arrows commutes; the diagram with the upward set of arrows commutes by naturality and the projection formula [20, III.7.5.2]. The downward map  , followed by the norm map, is multiplication by \(e=[k':k]\). A diagram chase now shows that the top row of the diagram is exact.\(\square \)
, followed by the norm map, is multiplication by \(e=[k':k]\). A diagram chase now shows that the top row of the diagram is exact.\(\square \)
Remark 4.4
The map j is also injective in the above diagram. To see this, note that (by the projection formula) the norm  induces a map \(\tilde{N}\) from \(\tilde{K}^M_q(k(X'))/\ell \) to \(\tilde{K}^M_q(k(X))/\ell \), and the composition \(\tilde{N}\,j\) is multiplication by \([k':k_1]\), not e. Note that \(\tilde{N}\) does not commute with the norm
induces a map \(\tilde{N}\) from \(\tilde{K}^M_q(k(X'))/\ell \) to \(\tilde{K}^M_q(k(X))/\ell \), and the composition \(\tilde{N}\,j\) is multiplication by \([k':k_1]\), not e. Note that \(\tilde{N}\) does not commute with the norm  unless \(k=k_1\).
unless \(k=k_1\).
5 The exact sequence
In this section and the next, we assume that our field k contains an \(\ell \)th root of unity, \(\zeta \). As before, we fix a symbol \(\underline{a}\) and a norm variety X for \(\underline{a}\), writing \(\mathfrak {X}\) for the 0-coskeleton of X.
Given a complex \(\mathcal {F}^{\mathbf {\scriptscriptstyle \bullet }}\) of étale sheaves, let \(\mathcal {H}^q=\mathcal {H}_{\text {nis}}^q(\mathcal {F}^{\mathbf {\scriptscriptstyle \bullet }})\) denote the Nisnevich sheaf associated to the presheaf \(H_{\mathrm {et}}^q(-,\mathcal {F}^{\mathbf {\scriptscriptstyle \bullet }})\). If \(\mathcal {F}\) is a locally constant étale sheaf (such as \(\mu _\ell ^{\otimes i}\)), \(\mathcal {H}^q(\mathcal {F})\) is a Nisnevich sheaf with transfers, by [11, 6.11, 6.21 and 13.1].
Lemma 5.1
If \(\mathcal {F}\) is a sheaf, \(H^0(\mathfrak {X},\mathcal {H}^q)\) is the equalizer of  .
.
Proof
This is the definition of \(H^0\) on a simplicial scheme; see [3, 5.2.2]. Alternatively, it follows from the spectral sequence \(E_1^{p,q}=H^q(X^{p+1},\mathcal {F})\Rightarrow H^{p+q}(\mathfrak {X},\mathcal {F})\) for the cohomology of a sheaf on a simplicial scheme. \(\square \)
Remark 5.2
The Nisnevich sheaves \(\mathcal {H}^q(\mu _\ell ^{\otimes q})\) are homotopy invariant sheaves with transfers, by [11, 24.1]. By [11, 11.1], if X is smooth then \(H^0(X,\mathcal {H}^q(\mu _\ell ^{\otimes q}))\)—and hence \(H^0(\mathfrak {X},\mathcal {H}^q(\mu _\ell ^{\otimes q}))\)—injects into \(\mathcal {H}^q(\mu _\ell ^{\otimes q})({{\mathrm{Spec}}}k(X))=H_{\mathrm {et}}^q(k(X),\mu _\ell ^{\otimes q})\cong K^M_q(k(X))/\ell \).
Proposition 5.3
If \(\mu _\ell \subset k^\times \), there is a distinguished triangle in \(\mathbf {DM}\) for each \(q\ge 0\):

Proof
For any Nisnevich complex C and any q we have a distinguished triangle

Now let C be the total direct image \(R\pi _*\mu _\ell ^{\otimes q}\), where  , so \(H_{\text {nis}}^*(X,C)=H_{\mathrm {et}}^*(X,\mu _\ell ^{\otimes q})\). Since \(\mu _\ell \subset k^\times \), multiplication by \(\zeta \) induces an isomorphism \(\mu _\ell ^{\otimes q-1}\cong \mu _\ell ^{\otimes q}\). Thus we have an isomorphism
, so \(H_{\text {nis}}^*(X,C)=H_{\mathrm {et}}^*(X,\mu _\ell ^{\otimes q})\). Since \(\mu _\ell \subset k^\times \), multiplication by \(\zeta \) induces an isomorphism \(\mu _\ell ^{\otimes q-1}\cong \mu _\ell ^{\otimes q}\). Thus we have an isomorphism  . In this case, the triangle reads:
. In this case, the triangle reads:

By the Beilinson–Lichtenbaum conjecture (which has now been proven; see [16, 6.17] or [6, Thm. B]), \(\mathbb {Z}/\ell (q)\cong \tau ^{\le q}C\) and \(\mathbb {Z}/\ell (q-1)\cong \tau ^{\le q-1}R\pi _*\mu _\ell ^{\otimes q-1}\cong \tau ^{\le q-1}C\). Combining these facts yields the distinguished triangle in question.\(\square \)
Let \(\tilde{\mathfrak {X}}\) denote the simplicial cone of  . As a consequence of the Beilinson–Lichtenbaum conjectures, Voevodsky observed that
. As a consequence of the Beilinson–Lichtenbaum conjectures, Voevodsky observed that
Lemma 5.4
If X is smooth, the map  is an isomorphism if \(p\le q\) and an injection if \(p=q+1\). That is, \(H^{p,q}(\tilde{\mathfrak {X}},\mathbb {Z}/\ell )=0\) if \(p\le q+1\).
is an isomorphism if \(p\le q\) and an injection if \(p=q+1\). That is, \(H^{p,q}(\tilde{\mathfrak {X}},\mathbb {Z}/\ell )=0\) if \(p\le q+1\).
Proof
See [14, 6.9 and 7.3] or [6, 1.37].\(\square \)
Proposition 5.5
If \(\mu _\ell \subset k^\times \), there is a natural five-term exact sequence:

Proof
Apply \(H^q(\mathfrak {X},-)\) to the distinguished triangle in Proposition 5.3. Using the fact that \(H^q(\mathfrak {X},C[j])=H^{q+j}(\mathfrak {X},C)\) and writing \(\mathcal {H}^q\) for \(\mathcal {H}^q(\mu _\ell ^{\otimes q})\), we get

The first term (\(H^{-1}\)) is 0 because the coefficients are a sheaf. By Lemma 5.4 with \(p=q\), the third term is \(H^{q,q}(k,\mathbb {Z}/\ell )=K^M_q(k)/\ell \) [11, Theorem 5.1].\(\square \)
Corollary 5.6
Theorem 1.3 holds for \(n=1\).
Proof
By Proposition 4.3, we may assume \(\zeta \in k\) so that \(X={{\mathrm{Spec}}}(E)\), \(E=k(\root \ell \of {a})\) and \(X\times X=\coprod _GX\) (by Lemma 2.4), where \(G={{\mathrm{Gal}}}(E/k)\). By Lemma 5.1 with \(\mathcal {F}\) being \(\mu _\ell ^{\otimes q}\), \(H^0(\mathfrak {X},\mathcal {H}^q)\) is the equalizer of  , i.e., \(H^q(X,\mu _\ell ^{\otimes q})^G\). Since \(H^q(X,\mu _\ell ^{\otimes q})\) is \(K^M_q(E)/\ell \), we have \(H^0(\mathfrak {X},\mathcal {H}^q) \cong (K^M_q(E)/\ell )^G\). Proposition 5.5 yields exactness of
, i.e., \(H^q(X,\mu _\ell ^{\otimes q})^G\). Since \(H^q(X,\mu _\ell ^{\otimes q})\) is \(K^M_q(E)/\ell \), we have \(H^0(\mathfrak {X},\mathcal {H}^q) \cong (K^M_q(E)/\ell )^G\). Proposition 5.5 yields exactness of

Now combine this with the exact sequence (1.2c), using Lemma 2.5 to identify \(\overline{H}_{-i,-i}(X)\).\(\square \)
Our next goal, achieved in Corollary 5.8, is to connect the first map in Proposition 5.5 to the cup product with \(\underline{a}\). We assume that \(n\ge 2\), so that \(d=\dim (X)>0\) and \(s_d(X)\) is defined.
Proposition 5.7
Let X be a norm variety for \(\underline{a}\) such that \(s_d(X)\not \equiv 0\pmod {\ell ^2}\). For \(i\ge 0\), there is a four-term exact sequence

Suppose in addition that X has a point of degree \(\ell \). Then the following sequence is exact:

Proof
Let M, D and \(\mathbb {L}\) be as in Theorem 3.4. Since \(H^{p,q}(M[1]) = H^{p-1,q}(M)\), applying \(H^{i+2d+1,i+d}(-,\mathbb {Z}_{(\ell )})\) to the distinguished triangle in (3.4b) gives us the exact sequence

where for brevity we have written \(H^{p,q}(\mathfrak {X}\otimes \mathbb {L}^d)\) for \(\mathrm {Hom}_{\mathbf {DM}}(R_{\mathrm {tr}}(\mathfrak {X})\otimes \mathbb {L}^d,\mathbb {Z}_{(\ell )}(q)[p])\). We will show that this may be rewritten as the 4-term sequence of the proposition.
Because M is a direct summand of X, \(H^{p,q}(M,\mathbb {Z}_{(\ell )})\) is a summand of \(H^{p,q}(X,\mathbb {Z}_{(\ell )})\), which vanishes whenever \(p-q>\dim (X)\); see [11, 3.6]. Hence the last term \(H^{i+2d+1,i+d}(M,\mathbb {Z}_{(\ell )})\) vanishes. Similarly, the first term, \(H^{i+2d,i+d}(M,\mathbb {Z}_{(\ell )})\), is a summand of \(H^{i+2d,i+d}(X,\mathbb {Z}_{(\ell )})\), which we showed to be isomorphic to \(H_{-i,-i}(X,\mathbb {Z}_{(\ell )})\) if \(i\ge 0\), in the proof of Proposition 2.1. Therefore we may replace the first term by \(H_{-i,-i}(X,\mathbb {Z}_{(\ell )})\). Since  factors through \(\mathfrak {X}\), the map
factors through \(\mathfrak {X}\), the map  factors through the coequalizer \(\overline{H}_{-i,-i}(X,\mathbb {Z}_{(\ell )})\) of the two projections from \(H_{-i,-i}(X\times X,\mathbb {Z}_{(\ell )})\). We also know that
factors through the coequalizer \(\overline{H}_{-i,-i}(X,\mathbb {Z}_{(\ell )})\) of the two projections from \(H_{-i,-i}(X\times X,\mathbb {Z}_{(\ell )})\). We also know that
where the last two isomorphisms follow from Lemma 5.4 and the Nestorenko–Suslin–Totaro Theorem [11, 5.1]. Thus we have constructed an exact sequence

When X has a point x of degree \(\ell \) over k, every element \(\alpha \) of \(K^M_i(k)\) has \(\ell \,\alpha =\pi _*([x,\alpha ])\), so the cokernel of  has exponent \(\ell \), and is the same as the cokernel of
has exponent \(\ell \), and is the same as the cokernel of  . Thus we can replace the first two terms of the exact sequence with these to get the desired sequence.\(\square \)
. Thus we can replace the first two terms of the exact sequence with these to get the desired sequence.\(\square \)
Corollary 5.8
If \(\mu _\ell \subset k^\times \), there are maps 
 for all i so that
for all i so that  (the cup product with \(\underline{a}\)) factors as
(the cup product with \(\underline{a}\)) factors as

Proof
Set \(q=n+i\). For each closed point x of X, the diagram

commutes by the projection formula [20, III.7.5.2]. Thus the map  is zero, since by Proposition 2.1 it is induced by the maps
is zero, since by Proposition 2.1 it is induced by the maps

By Proposition 5.7, the cup product factors through the quotient \(H^{i+2d+1,i+d}(D,\mathbb {Z}_{(\ell )})\) of \(K^M_i(k)/\ell \). It remains to show that the image \(\underline{a}K^M_i(k)\) of the cup product lands in the subgroup \(H^{q,q-1}(\mathfrak {X},\mathbb {Z}/\ell )\) of \(K^M_q(k)/\ell \). Since \(H^0(X,\mathcal {H}^q(\mu _\ell ^{\otimes q}))\) is a subgroup of \(K^M_{q}(k(X))/\ell \) (by Remark 5.2), it suffices by Proposition 5.5 to show that \(\underline{a}K^M_i(k)\) vanishes in \(K^M_{q}(k(X))/\ell \). This is so because k(X) splits \(\underline{a}\).\(\square \)
In Corollary 5.12, we will show that the map \(\alpha _i\) is an isomorphism. The inverse of \(\alpha _i\) will be constructed using the cohomology operations \(Q_i\) constructed in [15, p. 51]. Each \(Q_i\) has bidegree \((2\ell ^i-1,\ell ^i-1)\); see loc. cit. or [6, 13.3] for a summary of their properties. Thus the composite \(Q=Q_{n-1}Q_{n-2}\cdots Q_0\) has bidegree \((2b\ell -n+2,b\ell -n+1)\), where \(b=d/(\ell -1) = \ell ^{n-2} + \cdots + \ell + 1\).
Definition 5.9
Define the \(\mathbb {Z}\)-graded ring \(\mathbb {H}^*(k)\) by
In particular, \(\mathbb {H}^0(k)\cong K^M_*(k)/\ell \). The cohomology operation Q maps \(\mathbb {H}^i(Y)\) to \(\mathbb {H}^{i+b\ell +1}(Y)\). Note that \(\mathbb {H}^i(\tilde{\mathfrak {X}})=0\) for \(i\le 1\), by Lemma 5.4.
Now the operations \(Q_j\) vanish on each \(K^M_p(k)/\ell =H^{p,p}(k,\mathbb {Z}/\ell )\), because \(H^{p,q}(k,\mathbb {Z}/\ell )=0\) for \(p>q\). Since the \(Q_j\) are derivations for \(\ell \) odd ([6, 13.10]), this means that \(\mathbb {H}^*(Y)\) is a graded \(K^M_*(k)/\ell \)-module for each Y, and each  -module homomorphism. Thus
-module homomorphism. Thus  is also a \(K^M_*(k)/\ell \)-module homomorphism.
is also a \(K^M_*(k)/\ell \)-module homomorphism.
Lemma 5.10
Let X be a norm variety over a field of characteristic 0, and let \(\mathfrak {X}\) be its 0-coskeleton. Then the map  is an injection.
is an injection.
Proof
Since \(H^{p,q}({{\mathrm{Spec}}}k,\mathbb {Z}/\ell ) = 0\) for \(p>q\), we have \(\mathbb {H}^i({{\mathrm{Spec}}}k)=0\) for \(i>0\). This yields isomorphisms  for all \(i>0\). In particular, \(\mathbb {H}^1(\mathfrak {X}) \cong \mathbb {H}^2(\tilde{\mathfrak {X}})\). Thus it suffices to show that Q is injective on \(\mathbb {H}^2(\tilde{\mathfrak {X}})\). Setting \(a(j)={2+\frac{\ell ^j-1}{\ell -1}}\), \(Q_{j-1}\cdots Q_0\) maps \(\mathbb {H}^2(\tilde{\mathfrak {X}})\) to \(\mathbb {H}^{a(j)}(\tilde{\mathfrak {X}})\). In particular it suffices to show that \(Q_j\) is injective on \(\mathbb {H}^{a(j)}(\tilde{\mathfrak {X}})\) for all \(0\le j\le n-1\). Because X is a norm variety, we know from [14, 3.2] (or [6, 10.14]) and [6, 13.20] that the Margolis sequence is exact for each \(Q_j\), \(j<n\):
for all \(i>0\). In particular, \(\mathbb {H}^1(\mathfrak {X}) \cong \mathbb {H}^2(\tilde{\mathfrak {X}})\). Thus it suffices to show that Q is injective on \(\mathbb {H}^2(\tilde{\mathfrak {X}})\). Setting \(a(j)={2+\frac{\ell ^j-1}{\ell -1}}\), \(Q_{j-1}\cdots Q_0\) maps \(\mathbb {H}^2(\tilde{\mathfrak {X}})\) to \(\mathbb {H}^{a(j)}(\tilde{\mathfrak {X}})\). In particular it suffices to show that \(Q_j\) is injective on \(\mathbb {H}^{a(j)}(\tilde{\mathfrak {X}})\) for all \(0\le j\le n-1\). Because X is a norm variety, we know from [14, 3.2] (or [6, 10.14]) and [6, 13.20] that the Margolis sequence is exact for each \(Q_j\), \(j<n\):

By Lemma 5.4, the left term is zero because \(a(j)-\ell ^j\le 1\). The result follows.\(\square \)
Since X is a splitting variety, \(\underline{a}\) vanishes in \(K^M_n(k(X))/\ell \). By Remark 5.2, \(\underline{a}\) vanishes in \(H^0(X,\mathcal {H}^n(\mu _\ell ^{\otimes n}))\). It follows from Proposition 5.5 (or [16, 6.5]) that there is a unique element \(\delta \) in \(H^{n,n-1}(\mathfrak {X},\mathbb {Z}/\ell )\) whose image in \(K^M_n(k)/\ell \) is \(\underline{a}\).
In the following proposition, \(\zeta \) is the map defined in Proposition 5.5, \(\alpha \) is the direct sum of the maps \(\alpha _i\) defined in Corollary 5.8, and the maps \(r^*\), \(s^*\) are given in Theorem 3.4.
Proposition 5.11
If \(s_d(X)\not \equiv 0\pmod {\ell ^2}\), the following diagram commutes up to sign, and the top composite is multiplication by \(\underline{a}\).

Proof
Note that all maps in the diagram are (right) module maps over the ring \(K^M_*(k)/\ell \cong \mathbb {H}^0(\mathfrak {X})\). This is clear for multiplication by \(\delta \), and we have already seen that the cohomology operation Q is also a \(\mathbb {H}^0(\mathfrak {X})\)-module map. Finally, the maps \(r^*\) and \(s^*\) are also \(\mathbb {H}^0(\mathfrak {X})\)-module maps, since they come from morphisms in \(\mathbf {DM}\); see (3.4a) and (3.4b).
The top row sends \(x\in \mathbb {H}^0(\mathfrak {X})\) to \(\zeta (\delta \cup x)=\underline{a}\cup x\); since \(\zeta \) is an injection (by Proposition 5.5), and \(\underline{a}\cup x=\zeta \circ \alpha ^*r^*(x)\) (by Corollary 5.8), the upper triangle commutes: \(\delta \cup x=\alpha ^*r^*(x)\).
We will show that \(s^*r^*(1) = (-1)^{n-1} Q(\delta )\). By linearity for \(\mathbb {H}^0(\mathfrak {X})\), it will follow that \(s^*r^*(x)=(-1)^{n-1} Q(\delta \cup x)\) for all \(x\in \mathbb {H}^0(\mathfrak {X})\). Since \(r^*\) is surjective by Proposition 5.7, the result will follow.
We need to recall the definition of \(\phi _V(\mu )\) from [16, p. 413] and [6, 5.10]. Given an element \(\mu \) in \(H^{2b+1,b}(\mathfrak {X},\mathbb {Z}/\ell )\), form the triangle  and set \(S=S^{\ell -2}A\). Since \(H^{2b\ell +2,b\ell }(\mathfrak {X},\mathbb {Z}/\ell ) \cong \mathrm {Hom}_{\mathbf {DM}}(R_{\mathrm {tr}}(\mathfrak {X}), R_{\mathrm {tr}}(\mathfrak {X})(b\ell )[b\ell +2])\), to define \(\phi _V(\mu )\) it suffices to assign it a map
and set \(S=S^{\ell -2}A\). Since \(H^{2b\ell +2,b\ell }(\mathfrak {X},\mathbb {Z}/\ell ) \cong \mathrm {Hom}_{\mathbf {DM}}(R_{\mathrm {tr}}(\mathfrak {X}), R_{\mathrm {tr}}(\mathfrak {X})(b\ell )[b\ell +2])\), to define \(\phi _V(\mu )\) it suffices to assign it a map  . We define \(\phi _V(\mu )\) to be represented by the composition
. We define \(\phi _V(\mu )\) to be represented by the composition

When \(\mu =Q_{n-2}\cdots Q_0(\delta )\), we get the distinguished triangles (3.4a) and (3.4b) with \(D=S\). Thus the composition \(s^*\circ r^*\) in the above diagram is multiplication by the element \(\phi _V(\mu )\). By [16, Thm. 3.8] (cf. [6, Cor. 6.33]), \(\phi _V\) agrees with \(Q_0 P^b\), where \(P^b\) is the reduced power operation. In addition, since \(\mu \) is annihilated by the \(Q_i\) with \(i\le n-2\) we have
see [16, p. 427] or [6, 5.14]. This shows that the bottom right triangle commutes in the above diagram.\(\square \)
Remark
In the proof of Proposition 5.11, we have cited Definition 5.10, Corollary 6.33 and Lemma 5.14 from the book [6]. These are slightly improved versions of Lemma 3.2 and (5.2), Theorem 3.8 and Lemma 5.13 in Voevodsky’s paper [16]. Note that [16, 5.13] is missing several minus signs.
Corollary 5.12
In Proposition 5.11, Q and \(\alpha \) are isomorphisms, and the maps \(r^*\) and \(\delta \cup -\) are surjections.
Proof
From Proposition 5.7, we see that \(r^*\) is surjective. By [6, 4.16], \(s^*\) is an isomorphism (because \(d+1>d\)), and Q is an injection by Lemma 5.10. The results follows from a diagram chase.\(\square \)
Note that \(H^{q,q-1}(\mathfrak {X})=0\) for \(q<n\), because by Corollary 5.12 this is a quotient of \(H^{q-n,q-n}(\mathfrak {X})\). Recall that \(\widetilde{K}^M_q(k(x))/\ell \) is the equalizer of the two maps
The following result was proved for \(n=1\) in Corollary 5.6, and will be proved for \(n\ge 2\) in the next section.
Proposition 5.13
\(H^0(\mathfrak {X}, \mathcal {H}^q(\mu _\ell ^{\otimes q})) \cong \tilde{K}^M_q(k(X))/\ell .\)
We are now ready to prove Theorem 1.3 when \(n\ge 2\).
Proof of Theorem 1.3
Putting Proposition 5.5 for \(q=n+i\) and Proposition 5.7 together, we get that the rows are exact in the following diagram, where \(H^{p,q}(-)\) denotes \(H^{p,q}(-,\mathbb {Z}/\ell )\).

From Corollary 5.12 we can conclude that the five-term sequence indicated by the dotted arrow is exact:

6 The fourth term
Let \(\iota _1,\iota _2\) be the two inclusions  induced by the projections
induced by the projections  . To finish the proof of Theorem 1.3, we need to prove Proposition 5.13 for \(n\ge 2\).
. To finish the proof of Theorem 1.3, we need to prove Proposition 5.13 for \(n\ge 2\).
Lemma 6.1
Fix \(n\ge 2\). Let \(E_i\) be the equalizer of the morphisms \(p_i\) and \(p'_i\) in the following diagram. Then in the commutative diagram

the first row and all of the columns are exact.
Proof
Exactness of the first row (i.e., that \(H^0(\mathfrak {X},\mathcal {H}^q)\) is the equalizer) is immediate from Lemma 5.1. The two right-hand columns are exact, as they are obtained from the Gersten resolutions for \(\mathcal {H}^q\). The homomorphisms which are known to be injective are denoted  . By an elementary diagram chase, the left-hand column is also exact. \(\square \)
. By an elementary diagram chase, the left-hand column is also exact. \(\square \)
In order to prove Proposition 5.13 it thus suffices to show that \(E_1 \cong 0\) in Lemma 6.1.
Lemma 6.2
If \(n\ge 2\), \(E_1 = \ker p_1 = \ker p_1'.\)
Proof
Since \(n>1\), we have \(\dim X = \ell ^{n-1}-1 \ge 1\). For any point \(x\in X^{(1)}\) the summand indexed by x is mapped by \(p_1\) and \(p_1'\) to the summands indexed by the generic points of \(x\times X\) and \(X\times x\), respectively. Since these points (and hence the summands) are distinct, the images of \(p_1\) and \(p_1'\) intersect in 0. It follows that their equalizer is \(\ker (p_1)=\ker (p_1')\), as asserted. \(\square \)
Proposition 6.3
If X is a smooth variety of dimension \(\ge 1\), then \(p_1\) is injective.
Proof
For each \(x\in X^{(1)}\), let \(y_x\) denote a generic point of \(x\times X\); since X is smooth, \(x\times X\) is reduced. We will show that the composition of \(p_1\) with the projection \(\pi _x\) onto \(K^M_{q-1}(k(y_x))/\ell \),

is an injection on the x-summand; since \(\pi _x p_1\) is zero on all the other summands of the left term, it will follow that \(p_1\) is an injection.
Fix x and write F for k(X); as X is smooth, the function field of \(x\times X\) is a finite product of fields. Choosing an affine neighborhood \({{\mathrm{Spec}}}R\) of x, x is given by a height 1 prime ideal \(\mathfrak {p}\) of R: \(k(x)={{\mathrm{frac}}}(R/\mathfrak {p})\) and \(F={{\mathrm{frac}}}(R)\). Note that \(k(x)\otimes R\) is a regular ring because X is smooth over k. The kernel \(\mathfrak {m}\) of the multiplication map

is a maximal ideal of \(k(x)\otimes R\), and the localization \(R'=(k(x)\otimes R)_{\mathfrak {m}}\) at \(\mathfrak {m}\) is a regular local ring with residue field k(x) and fraction field \(k(y_x)\). Choose a regular sequence \(r_1,\ldots ,r_d\) generating the maximal ideal of \(R'\); by iterated use of [20, III.7.3], there is a specialization map

which is a left inverse to the component  of \(p_1\).\(\square \)
of \(p_1\).\(\square \)
Proposition 5.13 now follows for \(n\ge 2\), since norm varieties are smooth by definition. This completes the proof of Theorem 1.3.
References
Bass, H., Tate, J.: The Milnor ring of a global field. In: Algebraic \(K\)-theory II, Lecture Notes in Math., vol. 342, pp. 349–446. Springer-Verlag (1973)
Becher, K.J.: Milnor \(K\)-groups and finite field extensions. \(K\)-theory 27, 245–252 (2002)
Deligne, P.: Théorie de Hodge III. Publ. Math. Inst. Hautes Ét. Sci. 44, 5–77 (1974)
Friedlander, E.M., Voevodsky, V.: Bivariant Cycle Cohomology. In: Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, vol. 143, pp. 138–187. Princeton University Press, Princeton (2000)
Haesemeyer, C., Weibel, C.: Norm Varieties and the chain lemma (after Markus Rost). In: Abel Symposium, pp. 95–130. Springer Berlin Heidelberg (2009)
Haesemeyer, C., Weibel, C.: The norm residue theorem in motivic cohomology. http://www.math.rutgers.edu/~weibel/BK.pdf
Kelly, S.: Triangulated categories of motives in positive characteristic (Ph.D. thesis) (2013). arXiv:1305.5349
Merkurjev, A.: Brauer groups of fields. Commun. Algebra 11, 2611–2624 (1983)
Merkurjev, A., Suslin, A.: \(K\)-cohomology of Severi-Brauer varieties and the norm residue homomorphism. Izv. Akad. Nauk SSSR Ser. Mat. 46(5), 1011–1046, 1135–1136 (1982)
Merkurjev, A., Suslin, A.: Motivic cohomology of the simplicial motive of a Rost variety. J. Pure Appl. Algebra 214, 2017–2026 (2010)
Mazza, C., Voevodsky, V., Weibel, C.: Lecture notes on motivic cohomology. In: Clay Mathematics Monographs, vol. 2. American Mathematical Society, Providence, Clay Mathematics Institute, Cambridge (2006)
Orlov, D., Vishik, A., Voevodsky, V.: An exact sequence for \(K^M_\ast /2\) with applications to quadratic forms. Ann. Math. (2) 165(1), 1–13 (2007)
Suslin, A., Joukhovitski, S.: Norm varieties. J. Pure Appl. Algebra 206(1–2), 245–276 (2006)
Voevodsky, V.: Motivic cohomology with \(\mathbf{Z}/2\)-coefficients. Publ. Math. Inst. Hautes Études Sci. 98, 59–104 (2003)
Voevodsky, V.: Reduced power operations in motivic cohomology. Publ. Math. Inst. Hautes Études Sci. (98), 1–57 (2003)
Voevodsky, V.: On motivic cohomology with \(\mathbf{Z}/l \)-coefficients. Ann. Math. 174, 401–438 (2011)
Voevodsky, V.: Motivic cohomology groups are isomorphic to higher Chow groups in any characteristic. Int. Math. Res. Not. 7, 351–355 (2002)
Weibel, C.: The norm residue isomorphism theorem. J. Topol. 2, 346–372 (2009)
Weibel, C.: An introduction to homological algebra. Cambridge Univ Press, Cambridge (1994)
Weibel, C.: The \(K\)-book, AMS Grad. Studies in Math. vol. 145 (2013)
Yagita, N.: Algebraic \(BP\)-theory and norm varieties. Hokkaido Math J. 41, 275–316 (2012)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jonathan Rosenberg.
Weibel was supported by NSA and NSF grants, and by the IAS Fund for Math. Zakharevich was supported by an NSF MSRFP, the University of Chicago and by the IAS Fund for Math.
Rights and permissions
About this article
Cite this article
Weibel, C., Zakharevich, I. Principal ideals in mod-\(\ell \) Milnor K-theory. J. Homotopy Relat. Struct. 12, 1033–1049 (2017). https://doi.org/10.1007/s40062-017-0176-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40062-017-0176-0



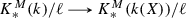 is the ideal of
is the ideal of 

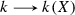 , and
, and  is zero for every dimension 1 point y of X.
is zero for every dimension 1 point y of X. is proper, and
is proper, and 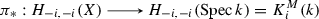
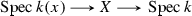 ,
,  factors as
factors as 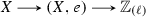 , i.e., is zero on
, i.e., is zero on  and its twisted dual
and its twisted dual 
