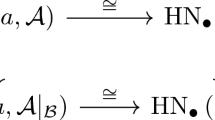1 Introduction

In [4], we defined for every generalized homology theory \({{\mathcal {H}}}_*\), another homology theory \(\widehat{{\mathcal {H}}}_*\) taking values in a certain abelian category \({{\mathscr {D}}}\). This homology \(\widehat{{\mathcal {H}}}_*\) is related to the generalized homology with values in a Moore spectrum M by a universal coefficient exact sequence, using a tensor product and its derived functors in the category \({{\mathscr {D}}}\).

In this paper, besides the proofs of results announced in [4], we give a similar construction for every generalized cohomology theory and a convenient universal coefficient sequence. We also give a wide study of homological algebra of the category \({{\mathscr {D}}}\) which is of independent interest.

Let A be a \({\mathbb {Z}}\)-module and \(n\ge 2\) be an integer. A Moore space M(A, n) is a simply connected CW-complex X such that \(H_n(X)\simeq A\) and \(\widetilde{ H_i}(X)=0\) for \(i\not =n\). The homotopy type of M(A, n) is uniquely determined by the pair (A, n) (see [6]). The sequence \(\{M(A, n)\}_n\) leads to a spectrum which will be denoted by M(A). This spectrum has the property that \(H_i(M(A))=0\) if \(i\not =0\). So a Moore spectrum is defined as a spectrum M such that one has \(H_n(M)=0\) for \(n\not =0\).

The category of \({\mathbb {Z}}\)-modules is denoted by \({\mathcal Mod}\). Observe that the construction associating to a module A the Moore spectrum M(A) is not functorial. In fact, if A and B are two objects of \({\mathcal Mod}\), the homotopy classes [M(A), M(B)] of maps between the associated Moore spectra is not isomorphic to \(\mathrm{Hom}(A,B)\), unlike what is happening in the case of Eilenberg–MacLane spectra. Actually we have a natural exact sequence (see [2]):

(1.1)

Moreover this exact sequence doesn’t split in general, which does prove that the correspondance \(A\mapsto M(A)\) is not functorial.

Let \(M=M(A)\) be a Moore spectrum. For any homology theory \({{\mathcal {H}}}_*\) we may define a homology theory \({{\mathcal {H}}}'_*\) by:

$$\begin{aligned}{{\mathcal {H}}}'_*(X,Y)={{\mathcal {H}}}_*(X\wedge M,Y\wedge M)\end{aligned}$$

for every pair (X, Y) in the category of pairs of topological spaces \({\mathcal T}op_2\). This new homology theory is functorial in M but not in A and will be denoted by \({{\mathcal {H}}}_*^M\) or \({{\mathcal {H}}}_*(-,M)\).

By using a projective resolution of A, we get the universal coefficient exact sequence:

(1.2)

By doing the same thing for cohomology theories, we may define for any cohomology theory \({{\mathcal {H}}}^*\) a cohomology theory \({{\mathcal {H}}}_M^*\) by:

$$\begin{aligned}{{\mathcal {H}}}_M^*(X,Y)={{\mathcal {H}}}^*(X\wedge M,Y\wedge M)\end{aligned}$$

and we have the universal coefficient exact sequence:

(1.3)

Notice that if \({{\mathcal {H}}}_*\) is defined by a spectrum E, then \({{\mathcal {H}}}_*^M\) is obtained from \({{\mathcal {H}}}_*\) by replacing E with \(E\wedge M\). But that’s not the case for cohomology theories.

As well as \({{\mathcal {H}}}_*^M\), the construction of \({{\mathcal {H}}}_M^*\) is functorial in M but not in \(A=H_0(M)\). Let \({\mathscr {M}}\) denote the category whose objects are Moore spectra and whose morphisms are homotopy classes of spectra maps.

The category \({\mathscr {M}}\) is linear but not abelian. We identify it with a subcategory of the abelian category \({{\mathscr {D}}}\) of [4] the definition of which is recalled below:

Definition 1.1

Let \({{\mathscr {D}}}\) be the category of diagrams in the category \({\mathcal {M}od}\)

(1.4)

such that \(2\alpha =2\beta =\beta \alpha =0\) and \(\alpha \beta =2\).

Remark 1.2

We have two forgetful functors \(F_0\) and \(F_1\) from \({{\mathscr {D}}}\) to \({\mathcal Mod}\) by assigning to the diagram (1.4) the modules A and B respectively. These are exact functors.

Proposition 1.3

The category \({{\mathscr {D}}}\) is abelian and has enough projectives and enough injectives. Moreover, \({{\mathscr {D}}}\) has a tensor product \(\ \otimes _{{\mathscr {D}}}\mathbin : {{\mathscr {D}}}\otimes {{\mathscr {D}}}\longrightarrow {\mathcal Mod}\) which is right exact.

The derived functors of the tensor product are denoted by \(\mathrm{Tor}^{{\mathscr {D}}}_{*} \); the derived functors of \(\mathrm{Hom}_{{\mathscr {D}}}\) are denoted by \(\mathrm{Ext}_{{\mathscr {D}}}^{*}\).

Definition 1.4

The full subcategory of \({{\mathscr {D}}}\) whose objects are diagrams which are exact couples, will be denoted by \({{\mathscr {D}}}_e\). The objects of \({{\mathscr {D}}}_e\) are then called exact objects of \({{\mathscr {D}}}\).

Proposition 1.5

There is an equivalence between the category \({\mathscr {M}}\) and the subcategory \({{\mathscr {D}}}_e\) of \({{\mathscr {D}}}\).

Consider a generalized homology theory \({{\mathcal {H}}}_*\) (or a generalized cohomology theory \({{\mathcal {H}}}^*\)). If M is a Moore spectrum corresponding to a diagram \(D\in {{\mathscr {D}}}_e\), we have a homology (or cohomology) theory with coefficient defined by:

$$\begin{aligned} {{\mathcal {H}}}_*^D(X,Y)={{\mathcal {H}}}_*^M(X,Y)={{\mathcal {H}}}_*(X\wedge M,Y\wedge M) \end{aligned}$$

or:

$$\begin{aligned} {{\mathcal {H}}}^*_D(X,Y)={{\mathcal {H}}}^*_M(X,Y)={{\mathcal {H}}}^*(X\wedge M,Y\wedge M). \end{aligned}$$

The main result of this paper, proved in Sect. 4, gives exact sequences which connect the functors \({{\mathcal {H}}}_*^{D}\) and \({{\mathcal {H}}}_{D}^*\) respectively to the functors \(\otimes _{{\mathscr {D}}}\) and \(\mathrm{Hom}_{{\mathscr {D}}}\), and their derived functors.

Theorem 1.6

For every homology (or cohomology) theory \({{\mathcal {H}}}\) with values in \({\mathcal Mod}\), there is a homology (or cohomology) theory \(\widehat{{\mathcal {H}}}\) with values in \({{\mathscr {D}}}\) satisfying the following properties:

$$\begin{aligned} F_0\circ \widehat{{\mathcal {H}}}={{\mathcal {H}}} \end{aligned}$$

and for every pair \((X,Y)\in {\mathcal Top}_2\) and every exact diagram \(D\in {{\mathscr {D}}}\), there are exact sequences, natural on (X, Y) and on D:

(1.5)
(1.6)

Remark 1.7

It can be shown that for every exact object D, \(\mathrm{Tor}^{{{\mathscr {D}}}}_{i} (\cdot \mathbin , D)=0\) and \(\mathrm{Ext}_{{{\mathscr {D}}}}^{i} (\cdot \mathbin , D)=0\), for \(i\ge 2\).

The exact sequences (1.2) and (1.5) are related, but different in general. It is the same for the two exact sequences (1.3) and (1.6). The examples, studied in the last section, of the stable homotopy and the real K-theory, show that the new exact sequences (1.5) and (1.6) can be more interesting.

2 General properties of the category \({{\mathscr {D}}}\)

2.1 \({\mathscr {C}}\)-module structure on the objects of \({{\mathscr {D}}}\)

For simplicity of notation, an object D of \({{\mathscr {D}}}\) will be denoted

(2.1)

We set \(D^0=F_0(D)=A\) and \(D^1=F_1(D)=B\).

Let \({\mathscr {C}}\) be the \({\mathbb {Z}}\)-linear category having two objects 0 and 1, and whose morphisms are given by \(\mathrm{Hom}(0,0)={{\mathbb {Z}}}\), \(\mathrm{Hom}(1,1)={{\mathbb {Z}}}/4\), \(\mathrm{Hom}(0,1)={{\mathbb {Z}}}/2\cdot \alpha \), \(\mathrm{Hom}(1,0)={{\mathbb {Z}}}/2\cdot \beta \) and satisfying:

$$\begin{aligned} 2\alpha =0,\qquad 2\beta =0,\qquad \beta \circ \alpha =0,\qquad \alpha \circ \beta =2. \end{aligned}$$

The category \({{\mathscr {D}}}\) is then identified with the category of covariant functors from \({\mathscr {C}}\) to \({\mathcal Mod}\). Then, each object of \({{\mathscr {D}}}\) is naturally endowed with a left \({\mathscr {C}}\)-module structure and \({{\mathscr {D}}}\) can be seen as the category \({\mathscr {C}}\)-\({\mathcal Mod}\) of left \({\mathscr {C}}\)-modules.

There is a unique isomorphism of category \(\rho \): \({\mathscr {C}}\longrightarrow {\mathscr {C}}^{op}\) which exchanges \(\alpha \) and \(\beta \). Due to \(\rho \), a right \({\mathscr {C}}\)-module structure can be assigned to each left \({\mathscr {C}}\)-module structure on the object of \({{\mathscr {D}}}\).

2.2 Tensor product in the category \({{\mathscr {D}}}\)

Due to the \({\mathscr {C}}\)-module structure on the objects of \({{\mathscr {D}}}\) and the category isomorphism \(\rho \), we can define a tensor product of \({\mathscr {C}}\)-modules, denoted by \(\otimes _{{\mathscr {D}}}\), and taking values in \({\mathcal Mod}\).

Definition 2.1

Let D and \(D'\) be two objects of \({{\mathscr {D}}}\), given respectively by:

the tensor product \(D\otimes _{{\mathscr {D}}}^{} D'\) is defined by the pushout diagram:

Let S and P be the exact objects given respectively by:

The next result can be easily shown:

Proposition 2.2

If D is an object of \({{\mathscr {D}}}\), then

$$\begin{aligned}&D\otimes _{{\mathscr {D}}}^{} S=D^0,\qquad D\otimes _{{\mathscr {D}}}^{} P= D^1,\\&\mathrm{Hom}_{{\mathscr {D}}}(S, D)=D^0,\quad \mathrm{Hom}_{{\mathscr {D}}}(P, D)=D^1\quad \mathrm{and}\quad \\&\quad \mathrm{Hom}_{{\mathscr {D}}}(D, P)= \mathrm{Hom}(D^1, {{\mathbb {Z}}}/4). \end{aligned}$$

2.3 Subcategory of exact objects and category equivalence

Let us fix respectively two Moore spectra \(\Sigma \) and \(\Pi \) of type \(M({\mathbb {Z}})\) and \(M({\mathbb {Z}}/2)\). Then, there is a cofibration sequence:

(2.2)

where \(\theta \) is of degree 0 and \(\delta \) of degree \(-1\). If \(\lambda \) denotes the composition of \(\delta \) by the Hopf map from \(\Sigma \) to \(\Sigma \) (which is of degree \(+1\)), then we get the Moore spectra diagram, called \(\Delta \):

(2.3)

verifying \(2\theta =0\), \(2\lambda =0\), \(\lambda \theta =0\) and \(\theta \lambda =2\).

For every Moore spectrum M, the diagram (2.3) induces by functoriality a diagram \(D_M=\mathrm{Hom}_{\mathscr {M}}(\Delta ,M)\):

(2.4)

Here is another way to define the diagram \(D_{M}\): consider the unique functor \(\Phi \) from the category \(\mathscr {C}\) to \(\mathscr {M}\) assigning \(\Sigma \) to the object 0 and \(\Pi \) to the object 1, and assigning to the morphisms \(\alpha \) and \(\beta \) the morphisms \(\theta \) and \(\lambda \). If M is a Moore spectrum, then \(\mathrm{Hom}_{\mathscr {M}}(\Phi (-),M)\) is a contravariant functor from \(\mathscr {C}\) to \(\mathcal Mod\) or a covariant functor from \({\mathscr {C}}^{op}\) to \(\mathcal Mod\). Now using the isomorphism \(\rho : {\mathscr {C}}\longrightarrow {\mathscr {C}}^{op}\) of sect. 2.1 we get a functor from \({\mathscr {C}}\) to \({\mathcal Mod}\), which define an object of the category \({{\mathscr {D}}}\). This object is exactly the diagram \(D_{M}\).

The following statement makes the Proposition 1.5 more precise:

Proposition 2.3

The diagram \(D_{M}\) defined by (2.4) is exact. Moreover, the functor \(\Phi \) from \({\mathscr {M}}\) to \({{\mathscr {D}}}_e\), assigning to a Moore spectrum M the diagram \(D_M\), is an equivalence of categories.

A key result used in the proof is the fact that the group \([\Pi ,\Pi ]\) is cyclic of order 4 (see [2, 7]).

Comment The Propositon 2.3 has to be compared with the theorem 1.6.7 in the book Homotopy Type and Homology by Baues [1]. The category \(\varvec{\mathcal {G}}\) appearing in this theorem is essentially equivalent to the category \({{\mathscr {D}}}_e\) defined in (1.4).

Remark 2.4

By means of this category equivalence, we note indifferently the Moore spectrum M and the exact diagram \(D_M\). In particular we identify \(\Sigma \) and \(\Pi \) with S and P respectively.

3 Homological algebra in \({{\mathscr {D}}}\)

3.1 Projectives, injectives and resolutions in \({{\mathscr {D}}}\)

Let D be an object of \({{\mathscr {D}}}\) given by the following diagram

This can be seen as a \({\mathbb {Z}}/3\)-graded differential complex where B is indexed by 0, and A by 2 and then 1, following the direction of the arrows. The homology of this complex is denoted by \(H_*(D)\), with \(*\in {\mathbb {Z}}/3\).

Remark 3.1

Let D be an object of \({{\mathscr {D}}}\).

(i):

\(H_*(D)=0 \Leftrightarrow D\) is exact.

(ii):

Since \(\mathrm{Hom}_{{\mathscr {D}}}(S,D)=D^0 \) and \(\mathrm{Hom}_{{\mathscr {D}}}(P,D)=D^1\), we can deduce that S and P are projectives.

The next result characterizes the projectives of \({{\mathscr {D}}}\).

Proposition 3.2

Let L be an object of \({{\mathscr {D}}}\).

  1. (i)

    If L is projective then L is exact.

  2. (ii)

    L is projective if and only if L is a direct sum of copies of S and copies of P.

Proof

Let L be a object in \({{\mathscr {D}}}\). Because of Proposition 2.2, there is an object \(X\in {{\mathscr {D}}}\), which is a direct sum of copies of S and P, and a surjection \(\lambda :X\rightarrow L\). Suppose L is projective.

(i) In this case \(\lambda \) has a section \(\mu \), and in homology we get:

$$\begin{aligned} 1=\lambda _*\circ \mu _*. \end{aligned}$$

But \(H_*(X)\) is trivial and the identity on \(H_*(L)\) factorizes through 0. Then \(H_*(L)\) is also trivial and L is exact.

(ii) Since \(L^0\) is a direct summand of \(X^0\), \(L^0\) is the direct sum of a free \({\mathbb {Z}}\)-module and a \({\mathbb {Z}}/2\)-module. Therefore \(\lambda \) can be chosen in such a way that \(\lambda ^0: X^0\rightarrow L^0\) is an isomorphism. Using five lemma one checks that \(\lambda ^1:X^1\rightarrow L^1\) is also an isomorphism. Therefore \(\lambda \) is an isomorphism.

Remark 3.3

What precedes shows that the abelian category \({{\mathscr {D}}}\) has enough projectives.

Now, we give a characterization of injectives in \({{\mathscr {D}}}\).

Lemma 3.4

A sum of copies of P is injective in \({{\mathscr {D}}}\).

Proof

Let D be an object of \({{\mathscr {D}}}\) and \(D'=\oplus P\). Then \(\mathrm{Hom}_{{\mathscr {D}}}(D,D')=\mathrm{Hom}(D^1,D'^1)\) and \(D'^1=\oplus {\mathbb {Z}}/4\). But free \({\mathbb {Z}}/4\)-modules are injective in the category of \({\mathbb {Z}}/4\)-modules, then \(D'\) is injective in \({{\mathscr {D}}}\).

Lemma 3.5

Let A be an injective \({\mathbb {Z}}\)-module and \(J=M(A)\). Then J is injective in \({{\mathscr {D}}}\).

Proof

Let

be the object J. Since A is an injective \({\mathbb {Z}}\)-module, A is divisible and \(\alpha :A\rightarrow A'\) is trivial. Then \(A'\) is the 2-torsion part of A and we have for every \(D\in {{\mathscr {D}}}\):

$$\begin{aligned} \mathrm{Hom}_{{\mathscr {D}}}(D,J)=\mathrm{Hom}(D^0,A) \end{aligned}$$
(3.1)

Since A is injective, this functor is exact and J is injective in \({{\mathscr {D}}}\).

Remark 3.6

Using the above lemma we deduce that \(M({{\mathbb {Z}}/{p^\infty }})\) (p is any prime number) and \(M({{\mathbb {Q}}})\) are injectives.

To characterize completely the injectives in \({{\mathscr {D}}}\), we need to define new objects \(Q_i\), \(i=0,1,2\) in \({{\mathscr {D}}}\), given respectively by the following diagrams

Remark 3.7

The diagram (2.3) induces a long exact sequence in \({{\mathscr {D}}}\):

(3.2)

and the objects \(Q_i\), \(i=0,1,2\), appear to be the images of the maps of (3.2). Therefore there are related by the following exact sequences:

An easy computation proves that, for each i, the homology of \(Q_{-i}\) is concentrated in degree i and that \(H_i(Q_{-i})\) is isomorphic to \({\mathbb {Z}}/2\). The generator of \(H_i(Q_{-i})\) will be denoted by \(e_i\).

Lemma 3.8

Let D be a diagram in \({{\mathscr {D}}}\) and \(u\in H_i(D)\). There exists a morphism \(\lambda \mathbin : Q_{-i}\longrightarrow D\) such that \(\lambda _*(e_i)=u\). Moreover if \(\lambda \) and \(\lambda '\) are two morphisms satisfying this property, the difference \(\lambda -\lambda '\) factorizes through a projective object.

Proof

Let D be an object of \({{\mathscr {D}}}\) given by:

and let \(u\in H_i(D)\). Suppose \(i=0\); the element u is represented by an element \(u'\in B\) such that \(\beta (u')=0\) and then \(2u'=0\). So, there exists a unique morphism \(\lambda :Q_0\longrightarrow D\) sending the unique nonzero element to \(u'\).

Suppose now \( i=2\). The element u is represented by an element \(u'\in A\) such that \(2u'=0\). In this case, there is a unique morphism \(\lambda : Q_1\longrightarrow D\) sending the generator of \((Q_1)^0\) to \(u'\) and the generator of \((Q_1)^1\) to \(\alpha (u')\).

Finally, suppose \(i=1\). The element u is represented by \(u'\in A\) such that \(\alpha (u')=0\). Then, there exists a unique morphism \(\lambda : Q_2\longrightarrow D\) sending the generator of \((Q_2)^0\) on \(u'\).

In all cases, the morphism \(\lambda \) takes the generator of \(H_i(Q_{-i})\) to u.

The morphism \(\lambda \) is determined by the cycle \(u'\) representing the class u. If \(u'\) is the boundary of an element v, the map \(\lambda \) factorizes through S or P via the map \(\xi _i\) defined in Remark 3.7.

Proposition 3.9

Let I be an injective of \({{\mathscr {D}}}\). Then I is an exact object and \(I= M(J)\oplus I'\) where J is an injective \({\mathbb {Z}}\)-module and \(I'\) is a direct sum of copies of P.

Proof

Let I be an injective in \({{\mathscr {D}}}\) and \(u\in H_i(I)\). Due to Lemma 3.8, there exists \(\lambda \mathbin : Q_{-i}\longrightarrow I\) realizing u when taking \(H_i\). But each \(Q_{-i}\) can be injected in S or P, as indicated in Remark 3.7, then \(\lambda \) factors through S or P, which are exact objects, so, necessarily \(\lambda _*=0\) on \(H_i\) and then \(u=0\).

Let I be the diagram

Let J be the injective hull of A and M(J) be the corresponding Moore spectrum. By Lemma 3.5, M(J) is injective in \({{\mathscr {D}}}\). Due to (3.1), the inclusion \(A\rightarrow J\) induces a morphism \(\mu : D\rightarrow M(J)\). Since \(\mu \) is injective on A, its kernel K is of the following form

Then, K is a sum of copies of \(Q_0\). Because \(Q_0\) injects in P, we get an injective morphism f from K to a sum \(I'\) of copies of P. And since \(I'\) is injective, f extends to D by a morphism \(g:D\rightarrow I'\). The morphism \(\mu \oplus g\) is injective from D to \(M(J)\oplus I'\) which is injective object of \({{\mathscr {D}}}\).

In the next result, we give a characterisation of exact objects in \({{\mathscr {D}}}\).

Proposition 3.10

Let D be an object of \({{\mathscr {D}}}\). Then

  1. (i)

    D is an exact object if and only if D has a projective resolution \( 0\longrightarrow L' \longrightarrow L \longrightarrow D\longrightarrow 0\) with L and \(L'\) projectives.

  2. (ii)

    D is an exact object if and only if D has an injective resolution \(0 \longrightarrow D \longrightarrow I \longrightarrow I' \longrightarrow 0\) with I and \(I'\) injectives.

Remark 3.11

The objects \(Q_i\) have the following 3-periodic projective resolutions:

$$\begin{aligned}&\cdots \longrightarrow S\longrightarrow S\longrightarrow P \longrightarrow S\longrightarrow S\longrightarrow P\longrightarrow Q_0\\&\cdots \longrightarrow P\longrightarrow S\longrightarrow S \longrightarrow P\longrightarrow S\longrightarrow S\longrightarrow Q_1\\&\cdots \longrightarrow S\longrightarrow P\longrightarrow S \longrightarrow S\longrightarrow P\longrightarrow S\longrightarrow Q_2 \end{aligned}$$

They are the only non-exact objects which can be injected in S or P.

Using the above resolutions, we can verify that every non-exact object has a stably 3-periodic projective resolution.

We can also deduce that \({{\mathscr {D}}}\) has enough injectives and then prove the Proposition 1.3.

3.2 The derived functors \(\mathrm{Tor}_*^{{\mathscr {D}}}(-\mathbin ,-)\) and \(\mathrm{Ext}_{{\mathscr {D}}}^*(-\mathbin ,-)\)

Lemma 3.12

For each object \(D\in {{\mathscr {D}}}\), there exists free \({\mathbb {Z}}\)-modules \(E_i\), \(i\in {\mathbb {Z}}/3\) and a morphism

$$\begin{aligned} \varphi :\bigoplus _i E_i\otimes Q_{-i}\longrightarrow D \end{aligned}$$

inducing an isomorphism on the modules \(H_*\). Moreover, for all i,

$$\begin{aligned} E_i\otimes {\mathbb {Z}}/2\simeq H_{i}(D). \end{aligned}$$

Proof

Let \(D\in {{\mathscr {D}}}\) and let \(B_i=\{e_{ij}\}_j\) be a basis of \(H_i(D)\) for \(i\in {\mathbb {Z}}/3\). Each vector \(e_{ij}\) induces a map \(\lambda _{ij}:Q_{-i}\longrightarrow D\). We choose a family \(B'_i=\{e'_{ij}\}_j\) in bijection with the basis \(B_i\), and note \(E_i\) the free \({\mathbb {Z}}\)-module generated by \(B_i'\). Then we define \(\varphi \) by \(e'_{ij}\otimes x\mapsto \lambda _{ij}(x)\).

Notice that the morphism \(\varphi \) is not canonical, and that the construction is not functorial on \({{\mathscr {D}}}\).

To avoid the functoriality problem, we consider the category \(\widetilde{{\mathscr {D}}}\) defined as a quotient of \({{\mathscr {D}}}\) as follows: two morphisms of \({{\mathscr {D}}}\) are equivalent if they have the same source and the same target and their difference factorizes through a projective object. This relation is compatible with the composition and the quotient \(\widetilde{{\mathscr {D}}}\) of \({{\mathscr {D}}}\) is a category.

Notice that every functor on \({{\mathscr {D}}}\) which is trivial on projective objects factorizes through this quotient category.

The next result gives the functoriality in the previous lemma:

Lemma 3.13

Let D and \(D'\) be two objects of \({{\mathscr {D}}}\), and \(\varphi \) (respectively \(\varphi '\)) a morphism \(\oplus _i E_i\otimes Q_{-i} \longrightarrow D\) (respectively \(\oplus _i E'_i\otimes Q_{-i} \longrightarrow D'\)) inducing an isomorphism in homology. Let f be a morphism from D to \(D'\) and \(g=\oplus _i g_i\) a map from \(\oplus E_i\) to \(\oplus E'_i\) such that for each i, the mod 2-reduction of \(g_i:E_i\longrightarrow E'_i \) is the map \(f_*:H_i(D)\longrightarrow H_i(D')\). Then, the following diagram is commutative in \(\widetilde{{\mathscr {D}}}\)

Proof

Consider a basis \(\{u_k\}\) of \(\oplus E_i\). For a given k, if \(u_k \in E_i\), then, there are two maps from \(u_k\otimes Q_{-i}\) to \(D'\) obtained by the two possibilities of composition in the diagram. Due to Lemma 3.8, the difference between these two maps factors through a projective \(L_k\). Then, the difference between the two maps from \(\oplus E_i\otimes Q_{-i}\) to \(D'\) factors by the direct sum of all the \(L_k\), so that the diagram commutes in the quotient category.

The remaining of this section is devoted to determining the groups \(\mathrm{Tor}_{{\mathscr {D}}}^*(D,D')\) and \(\mathrm{Ext}^*_{{\mathscr {D}}}(D,D')\), for any two objects D and \(D'\) of \({{\mathscr {D}}}\). It’s easy to verify the next lemma.

Lemma 3.14

Let D and \(D'\) be two objects of \({{\mathscr {D}}}\). For all \(k>0\),

  1. (i)

    \(\mathrm{Tor}_k^{{\mathscr {D}}}(D,D')\) is functorial on D and \(D'\), in the category \(\widetilde{{\mathscr {D}}}\).

  2. (ii)

    \(\mathrm{Ext}_{{\mathscr {D}}}^k(D,D')\) is functorial on \(D \,in \in \widetilde{{\mathscr {D}}}\) and on \(D' \,in {{\mathscr {D}}}\).

  3. (iii)

    \(\mathrm{Tor}_k^{{\mathscr {D}}}(Q_i,D)=H_{i+k}(D)\) and \( \mathrm{Ext}_{{\mathscr {D}}}^k(Q_i,D)=H_{-k-i}(D)\).

Theorem 3.15

If D and \(D'\) are two objects of \({{\mathscr {D}}}\), then

  1. (i)

    for each \(k>0\), there exists a morphism, natural on D and \(D'\)

    $$\begin{aligned} \bigoplus _{i+j\equiv k}^{} H_{i}(D)\otimes H_{j}(D')\longrightarrow \mathrm{Tor}_k^{{\mathscr {D}}}(D,D'). \end{aligned}$$

    Moreover, this morphism is a bijection if \(k\ge 2\) and an injection if \(k=1\).

  2. (ii)

    for each \(k>0\), there exists a morphism, natural on D and \(D'\)

    $$\begin{aligned} \mathrm{Ext}^k_{{\mathscr {D}}}(D,D')\longrightarrow \bigoplus _{i-j\equiv k} \mathrm{Hom}(H_i(D),H_j(D')). \end{aligned}$$

    Moreover, this morphism is a bijection if \(k\ge 2\) and a surjection if \(k=1\).

Proof

Let \(D\in {{\mathscr {D}}}\). By Lemma 3.12, there exists \({\mathbb {Z}}\)-modules \(E_i\), for \(i\in {\mathbb {Z}}/3\), and a morphism \(\varphi :\oplus _i E_i\otimes Q_{-i}\longrightarrow D\) inducing isomorphisms on the modules \(H_*\). We can then find two projective objects L and \(L'\), and an exact sequence:

$$\begin{aligned} 0 \longrightarrow L' \longrightarrow L\oplus \oplus _i E_i\otimes Q_{-i} \longrightarrow D \longrightarrow 0 \end{aligned}$$

Applying the functor \(\mathrm{Tor}_k^{{\mathscr {D}}}(-,D')\) (respectively \(\mathrm{Ext}_k^{{\mathscr {D}}}(-,D')\) ) gives the desired result.

Remark 3.16

The functoriality in the first assertion of the previous theorem is in the category \(\widetilde{{\mathscr {D}}}\). Since \(\mathrm{Ext}^*_{{\mathscr {D}}}(D,D')\) is functorial for \(D\in \widetilde{{\mathscr {D}}}\) and \(D'\in {{\mathscr {D}}}\), the same functoriality property remains for the second assertion and then we deduce a functoriality for D and \(D'\) in \({{\mathscr {D}}}\).

4 New universal coefficient exact sequences

4.1 Proof of Theorem  1.6

Let \({{\mathcal {H}}}_*\) be a generalized homology theory. Using the Moore spectra diagram (2.3), for each degree n and each pair (X, Y) in \( {\mathcal Top}_2\), we get an object of \({{\mathscr {D}}}\) denoted by \(\widehat{{\mathcal {H}}}_n(X, Y)\):

(4.1)

Similarly, if \({{\mathcal {H}}}^*\) is a generalized cohomology theory and (X, Y) a pair, we have the following diagram

(4.2)

which is an object of \({{\mathscr {D}}}\) and will be denoted by \(\widehat{{\mathcal {H}}}^*(X,Y)\).

Let L be a projective of \({{\mathscr {D}}}\). The characterization of the projective objects, together with the Proposition 2.2, allow to easily express the functors \({{\mathcal {H}}}^L_*\) and \({{\mathcal {H}}}^*_L\) using respectively the two objects \(\widehat{{\mathcal {H}}}_*(X, Y)\) and \(\widehat{{\mathcal {H}}}^*(X,Y)\).

Lemma 4.1

If L is a projective of \({{\mathscr {D}}}\), then, there are isomorphisms:

$$\begin{aligned} {{\mathcal {H}}}^L_*(X,Y)\simeq \widehat{{\mathcal {H}}}_*(X,Y)\otimes _{{\mathscr {D}}} L \quad and \quad {{\mathcal {H}}}_L^*(X,Y) \simeq \mathrm{Hom}_{{\mathscr {D}}}(L,\widehat{{\mathcal {H}}}^*(X,Y)). \end{aligned}$$

If D is an exact object of \({{\mathscr {D}}}\), there is a projective resolution:

$$\begin{aligned} 0 \longrightarrow L' \longrightarrow L \longrightarrow D\longrightarrow 0. \end{aligned}$$

Then, we obtain the exact sequence:

$$\begin{aligned} \longrightarrow {{\mathcal {H}}}^{L'}_{i}(X,Y) \longrightarrow {{\mathcal {H}}}^L_i(X,Y) \longrightarrow {{\mathcal {H}}}^D_i(X,Y) \longrightarrow {{\mathcal {H}}}^{L'}_{i-1}(X,Y) \longrightarrow {{\mathcal {H}}}^L_{i-1}(X,Y) \end{aligned}$$

that is:

$$\begin{aligned}\rightarrow & {} \widehat{{\mathcal {H}}}_i(X,Y)\otimes L' \rightarrow \widehat{{\mathcal {H}}}_i(X,Y)\otimes L \rightarrow {{\mathcal {H}}}^D_i(X,Y) \rightarrow \widehat{{\mathcal {H}}}_{i-1}(X,Y)\otimes L\\\rightarrow & {} \widehat{{\mathcal {H}}}_{i-1}(X,Y)\otimes L \end{aligned}$$

and then:

$$\begin{aligned} 0 \longrightarrow \widehat{{\mathcal {H}}}_i(X,Y)\otimes D \longrightarrow {{\mathcal {H}}}^D_i(X,Y) \longrightarrow \mathrm{Tor}^{{\mathscr {D}}}_1(\widehat{{\mathcal {H}}}_{i-1}(X,Y),D) \longrightarrow 0 \end{aligned}$$

This gives the exact sequence (1.5).

The projective resolution of D gives also the long exact sequence:

$$\begin{aligned} \longleftarrow {{\mathcal {H}}}_{L'}^{i}(X,Y) \longleftarrow {{\mathcal {H}}}_{L}^{i}(X,Y) \longleftarrow {{\mathcal {H}}}_D^i(X,Y) \longleftarrow {{\mathcal {H}}}_{L'}^{i-1}(X,Y) \longleftarrow {{\mathcal {H}}}_{L}^{i-1}(X,Y) \end{aligned}$$

Since L and \(L'\) are projectives, and using the second isomorphism of the previous lemma, we deduce the exact sequence (1.6):

$$\begin{aligned} 0 \longleftarrow \mathrm{Hom}_{{\mathscr {D}}}(D,\widehat{{\mathcal {H}}}^i(X,Y)) \longleftarrow {{\mathcal {H}}}_D^i(X,Y) \longleftarrow \mathrm{Ext}_{{\mathscr {D}}}^1(D,\widehat{{\mathcal {H}}}^{i-1}(X,Y)) \longleftarrow 0 \end{aligned}$$

4.2 Relations between the new and the classical universal coefficient exact sequences

Let be an exact object of \({{\mathscr {D}}}\) and \({{\mathcal {H}}}_*\) a generalized homology theory. For every topological spaces pair (X, Y), we have the commutative square:

Filling by the horizontal map cokernels, we obtain the following diagram allowing to compare the two exact sequences:

Similarly, if \({{\mathcal {H}}}^*\) is a generalized cohomology theory, we have the commutative diagram:

Filling by the horizontal map kernels, we get the following diagram which can be used to compare the classical and the new exact sequences:

4.3 Differences between the classical and new exact sequences

The two pairs of exact sequences are pairwise different. In fact, in the homology case, applying the exact sequences to the stable homotopy theory shows that the new exact sequence is more precise than the classical one. Using the first stable homotopy groups of the sphere (given, among others, in [3]) and those of the projective plane (see [7]), we find:

$$\begin{aligned} \widehat{\pi }_{0}^S=S\quad \widehat{\pi }_{1}^S=Q_1\quad \widehat{\pi }_{2}^S=P\quad \widehat{\pi }_{3}^S=M({{{\mathbb {Z}}}/24})\quad \widehat{\pi }_{4}^S=Q_0, \end{aligned}$$

where \(\widehat{\pi }_*\) denotes \(\widehat{\pi }_*(pt)\).

If is an exact object of \({{\mathscr {D}}}\), applying the two exact sequences (1.2) et (1.5) for \(i=3\), we get:

(4.3)
(4.4)

This shows that the second exact sequence allows to deduce \({\pi }_{3}^S(D)\simeq M({{{\mathbb {Z}}}/24})\otimes _{{\mathscr {D}}} D\).

In the cohomology case, the real K-theory illustrates the interest of the new exact sequence. In fact, using the real K-theory of the projective plane, given in [5], we find the following diagrams, where \(\widehat{{KO}}^{*}\) denotes \(\widehat{{KO}}^{*}(pt)\):

$$\begin{aligned}&\widehat{{KO}}^{\,0}=S\quad \widehat{{KO}}^{\,1}=Q_0\quad \widehat{{KO}}^{\,2}=\widehat{{KO}}^{\,3}=0\quad \widehat{{KO}}^{\,4}=Q_2\\&\widehat{{KO}}^{\,5}=Q_0\quad \widehat{{KO}}^{\,6}=Q_1\quad \widehat{{KO}}^{\,7}=P. \end{aligned}$$

Applying the two exact sequences (1.3) and (1.6), for \(i=0\), \(D=P\) and \(X= \mathrm{pt}\), we get the two different sequences:

(4.5)
(4.6)

The same method gives \(KO^0(D)\) for every Moore spectrum D. In fact, \(\mathrm{Ext}^1_{{\mathscr {D}}}(D, P)=0\) since P is injective, and then, the exact sequence (1.6) induces the isomorphism \(KO^0(D)\simeq \mathrm{Hom}_{{\mathscr {D}}}(D, S)=D^0\).

Remark 4.2

Using the diagrams \(\widehat{{KO}}^{*}\) and the exact sequence (1.6), we can compute real K-theory of Moore spaces.