Rich phenomenology of the solutions in a fractional Duffing equation

Abstract

In this paper, we characterize the chaos in the Duffing equation with negative linear stiffness and a fractional damping term given by a Caputo fractional derivative of order $\alpha$ ranging from 0 to 2. We use two different numerical methods to compute the solutions, one of them new. We discriminate between regular and chaotic solutions by means of the attractor in the phase space and the values of the Lyapunov Characteristic Exponents. For this, we have extended a linear approximation method to this equation. The system is very rich with distinct behaviours. In the limits $\alpha$ to 0 or $\alpha$ to 2, the system tends to basically the same undamped system with a behaviour clearly different from the classical Duffing equation.

1 Introduction

The classical theory of dynamical systems has long been a way to understand how various phenomena evolve over time. Natural and engineered systems may exhibit complex and nonlocal behaviours that cannot be accurately described solely by integer-order derivatives. Systems in different fields (such as electrochemistry, chemistry, biology, physics, and viscoelasticity) can be successfully described by fractional differential equations (see, for instance, [23] and references therein). These equations extend the concept of ordinary differential equations to include fractional derivatives that have the property of capturing memory effects and long-range dependencies.

Duffing equation is a paradigmatic model among systems of nonlinear dynamics that exhibit chaos [7, 13, 14, 17, 32, 38]. It can be used to present a diversity of physical systems. It can be consider as a benchmark for studying chaos in a low-dimensional dynamical system. It has been extended to the fractional case. Depending on which fractional derivative is used (Riemann-Liouville, Caputo, Grünwald-Letnikov, etc.) and what integer order it replaces, different systems are obtained which are not in principal equivalent [5, 16, 26, 27, 33, 37, 39].

In the study we present in this paper we have chosen a fractional Duffing equation with specific regularity conditions, that ensure the existence and unicity of solutions [19], replacing the first-order derivative in the Duffing equation by a Caputo fractional derivative of order $\alpha$ ranging within the two intervals (0, 1) and (1, 2). This system has the particularity of corresponding to feasible physical systems.

In previous works, some of us started to study the effects of chaos in this very same fractional equation. We presented a way to estimate the Lyapunov Characteristic Exponents (LCEs), in order to establish the chaoticity or regularity of the solutions [21] and the onset of chaos as a function of the parameters. We also analyzed the controlling effect of anharmonic external perturbations and the existence of geometric resonances that suppress the chaotic behaviour [19]. The present work is a continuation of these. Specifically, in [21], we pointed out a complexity of the behaviour of the solutions for a certain range of the fractional order of derivation that needed further clarification and in this present work we carry out a more thorough study.

Once the fractional model is set, a numerical method has to be used to approximate it and, in practice, one ends studying a discrete system, close to the continuous one. This supposes that not only the choices related to the fractional derivatives but, also, the choice of a numerical technique may be relevant. Different methods may been considered (see, for instance, [6, 34]).

In our case, we use a numerical scheme based on the conservative Strauss-Vázquez method (SV method) [20], to approximate the non-fractional terms, and the Odibat representation [28, 29] for the fractional derivative. This method improves the one we used in our previous studies.

Besides, these studies were limited to the case with a fractional derivative of order $\alpha \in (0,1)$ and in this present work we extend to include also the range $\alpha \in (1,2)$.

Equations with fractional derivatives present a computational challenge due to the non-locality. It is thus worth to use different numerical methods and contrast the agreement of their results. In our case, we use this new method (SV + Odibat method) and the one used in our previous work. Since that method was only valid in the range $0<\alpha <1$, we have suitably extended it to the range $1<\alpha <2$.

The extension to values of $\alpha \in (1,2)$ is also motivated by the fact that as $\alpha \rightarrow 2^-$, the fractional model becomes closer to a limit system where no damping and no saddle point exist. And that system can be seen as equivalent, at least for some range of the parameters, to the one obtained in the opposite limit, when $\alpha \rightarrow 0^+$. In this way, the fractional equations can be seen as an interpolation between the Duffing equation (limit $\alpha =1$) and an undamped, forced system.

The chaotic behaviour in the limit systems is due to the perturbation caused by the external forcing on a Hamiltonian. In these limit cases, chaos is present in the central region of the phase space independently of the parameter’s values with a chaotic region tending to fill a two-dimensional area of the phase space. This is quite different to the phenomenology of Duffing equation where the chaos is directly related to the perturbation of the stable and unstable manifolds around the saddle point. In this work, we study the behaviour of the fractional system near these limits.

Understanding chaotic behaviour is a complex task and different methods and approaches have been used to study its properties. See for instance [4, 18, 35, 36, 40] and, more recently, [8]. In our work we estimate the LCEs by means of two different techniques: the fiduciary orbit and a linearization. This second method cannot be applied in the range (1, 2) as is done for (0, 1) and the extension requires some adaptations, using several tools that differ from the previous technique.

With all these tools, we have sampled the different behaviours exhibited by the solutions of the fractional system, which appear to have a rich phenomenology: transition between regular and chaotic regimes inside the solution, bifurcation in time, and intermittency.

We also study the appearance of chaos by estimating its threshold and examining how the system parameters influence this threshold.

This paper is structured as follows: in Section 2 we present the fractional Duffing equation we consider. Section 2.1 presents the numerical methods used, Section 2.2 the analytic construction of the LCEs in the range $\alpha \in (0,1)$. In Section 2.3, this is extended to the range $\alpha \in (1,2)$. The corresponding numerical results are presented in Section 3. In Section 4, we examine the underlying models for the limiting cases when $\alpha$ goes to $0^+$ and when $\alpha$ goes to $2^-$. In Section 5 we present our conclusions and we discuss the results obtained.

2 Fractional Duffing’s equation

We design by “classical” (as opposed to “fractional”) the Duffing equation given by:

$$\begin{aligned} \ddot{x}+\gamma \dot{x}-x+x^{3}=f_{0}\cos (\omega t). \end{aligned}$$

(2.1)

The standard initial value problem is:

$$\begin{aligned} {x(0)}=x_0, \quad \dot{x}(0)=v_0, \end{aligned}$$

(2.2)

where $x_0$ and $v_0$ are real constants. The dots in (2.1) and (2.2) denote the derivation with respect to time. The parameters $\gamma$, $f_{0}$, $\omega$ correspond, respectively, to: the amplitude of the damping, the amplitude of the periodic driving force and its angular frequency. As is well known [14] this corresponds to a Hamiltonian system, given by

$$\begin{aligned} H(x,\dot{x}) = \frac{1}{2} \dot{x} ^2 -\frac{1}{2} x^2 + \frac{1}{4} x^4, \end{aligned}$$

(2.3)

perturbed by a dissipation and an external periodic forcing.

As an alternative to this classical model, we consider the fractional Duffing equation corresponding to the same forced Hamiltonian but, now, with a fractional-order damping:

$$\begin{aligned} \ddot{x}+\gamma (_{t_0}^{C}D_{t}^{\alpha }x)(t)-x+x^{3}=f_{0}\cos (\omega t), \end{aligned}$$

(2.4)

where $(_{t_0}^{C}D_{t}^{\alpha }x)(t)$ is the Caputo fractional derivative of order $\alpha$ with lower limit $t_0$. Its general expression, for $0\le n-1<\alpha <n,\quad n \in \mathbb {N}$ is:

$$\begin{aligned} (_{t_{0}}^{C}D_{t}^{\alpha }x)(t)=\frac{1}{\varGamma (n-\alpha )} \int \limits _{t_{0}}^{t}\frac{x^{(n)}(\tau )}{(t-\tau )^{\alpha +1-n}}d\tau ,\quad t>t_{0}, \end{aligned}$$

(2.5)

where $x^{(n)}$ is the derivative of x of order n and $\varGamma$ is Euler Gamma function. It is important to stress that this is not merely a mathematical model, since it can be viewed as the same mechanical or electromechanical device represented by Duffing equation but immersed in a viscoelastic medium. Compared to other fractional Duffing models, this equation has the advantage of a regular solution (at least $C^2$) whose existence can be ensured [19]. Modeling with the Caputo fractional derivative [23] has the advantage that initial value problems involve only derivatives of integer order. In our case, a standard initial value problem such as equation (2.4) with initial conditions (2.2) is suitable to ensure existence and unicity of the solution [21]. In this sense, we consider the space of the initial data as the phase space for this model. Since we choose $t=0$ as our initial time, this fixes the value $t_0$ as 0 in (2.5), and we represent that derivative by $D^\alpha _tx(t)$, in order to simplify the notation.

We will consider two separate cases: $0<\alpha < 1$ (ceiling of $\alpha$ equal 1: $\lceil \alpha \rceil =1$) and $1< \alpha < 2$ ($\lceil \alpha \rceil =2$). Besides, we will study the limit cases $\alpha =0$ and $\alpha =2$. For $\alpha =1$, the equation becomes the classical Duffing equation (2.1).

2.1 Numerical methods

To compute the solutions of the system, we have chosen two numerical methods that differently approximate the fractional derivative. A combined SV + Diethelm method and a combined SV + Odibat method. In both cases, an SV approach is used to represent the non-fractional terms, while the Caputo derivative is represented by either Diethelm [11] or Odibat approximation [28]. The two numerical methods are outlined below.

2.1.1 SV + Diethelm method for $\lceil \alpha \rceil =1$ and $\lceil \alpha \rceil =2$

In the case $\lceil \alpha \rceil =1$ we have used the same method as in [21]. It is limited to values of $\alpha \in (0,1)$ and has a truncation error $\mathcal {O}(\triangle t^{2-\alpha })$. We consider a discrete time-mesh of step-size $\triangle t$, with $t_n=t_0+n\triangle t$, and represent by $x_n$ the numerical approximation to the solution x at time $t_n$. Diethelm’s representation of the Caputo fractional derivative is given by [11]:

$$\begin{aligned} D_{t }^{\alpha }x(t_n)=\frac{1}{\triangle t^{\alpha }\varGamma (2-\alpha )} \sum \limits _{k=0}^{n}c_{k,n}\left( x_{n-k}-x_0\right) +\mathcal {O}(\triangle t^{2-\alpha }), \end{aligned}$$

(2.6)

where the coefficients $c_{k,n}$ are:

$$\begin{aligned} \left\{ \begin{array}{l} c_{0,n}=1,\quad k=0, \\ c_{k,n}=(k+1)^{1-\alpha }-2k^{1-\alpha }+(k-1)^{1-\alpha }, \quad 0<k<n, \\ c_{n,n}=(1-\alpha )n^{-\alpha }-n^{1-\alpha }+(n-1)^{1-\alpha }, \quad k=n. \end{array} \right. \end{aligned}$$

(2.7)

Since the term for $k=n$ in the sum is zero, we obtain:

$$\begin{aligned} D_{t }^{\alpha }x=\frac{1}{h^{\alpha }\varGamma (2-\alpha )}\left( x_n-x_0+ \sum \limits _{k=1}^{n-1}c_{k,n}\left( x_{n-k}-x_0\right) \right) . \end{aligned}$$

(2.8)

After substituting (2.8) in equation (2.4), the expression of the numerical method is:

$$\begin{aligned}{} & {} \frac{x_{n+1}-2x_n+x_{n-1}}{\triangle t^2} + \frac{\gamma }{\triangle t^{\alpha }\varGamma (2-\alpha )} \left( x_n-x_0+ \sum \limits _{k=1}^{n-1}c_{k,n}\left( x_{n-k}-x_0\right) \right) \nonumber \\{} & {} \quad -\frac{x_{n+1}+x_{n-1}}{2}+ \frac{x_{n+1}^3+x_{n+1}^2x_{n-1}+x_{n+1}x_{n-1}^2+x_{n-1}^3}{4}\nonumber \\{} & {} \quad = f_0\frac{\cos (\omega t_{n+1})+\cos (\omega t_{n-1})}{2}. \end{aligned}$$

(2.9)

This procedure is not self-starting since we must, initially, know both $x_0$ and $x_1$. The initial value $x_0$ is directly derived from the initial data (2.2). The other is computed, for instance, using a Taylor expansion of x(t) around $t_0 = 0$, particularized at $t=t_1=\triangle t$, with truncation error $\mathcal {O}(\triangle t^{4})$:

$$\begin{aligned} x(t_1)=x_1=x_0+\triangle t v_0+\frac{\triangle t^2}{2!}\ddot{x}_0+\frac{\triangle t^3}{3!}\dddot{x}_{0}. \end{aligned}$$

(2.10)

To determine $\dddot{x}_0$ we may assume that the initial data satisfy the equation. Differentiating equation (2.4) at time zero we obtain:

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{x}_{0}=x_0-x_0^3+f_0,\\ \dddot{x}_{0}=v_0-3x_0^2v_0. \end{array} \right. \end{aligned}$$

(2.11)

The details of this can be found in [19].

Diethelm’s approximation (2.8) is limited to the case $\lceil \alpha \rceil =1$ and we extend it to the case $\lceil \alpha \rceil =2$ transforming Eq.(2.4) into a system such that all fractional derivatives involved have orders that fall within the specified range (0, 1) [1, 10]. Using the property of the Caputo derivatives [23]:

$$\begin{aligned} D^{\alpha }=D^{\beta +1}=D^\beta D^1,\quad \alpha =1+\beta , \end{aligned}$$

(2.12)

we introduce an auxiliary variable, $v=D^1x$, and we have:

$$\begin{aligned} \left\{ \begin{array}{l} D^1x=v, \\ D^2x=-\gamma D^\beta v+x-x^{3}+f_{0}\cos (\omega t), \end{array} \right. \end{aligned}$$

(2.13)

with initial values

$$\begin{aligned} x(0)=x_0,\quad v(0)=v_0. \end{aligned}$$

(2.14)

Now, $\beta =\alpha -1\in (0,1)$, and we may apply the previous approach, with the benefit that the coefficients are the same as before. The numerical scheme that corresponds to the second equation of system (2.13) is:

$$\begin{aligned} \frac{x_{n+1}-2x_n+x_{n-1}}{\triangle t^2}= & {} - \frac{\gamma }{\triangle t^{\beta }\varGamma {(2-\beta )}} \left( v_n-x_0+ \sum \limits _{k=1}^{n-1}c_{k,n}\left( v_{n-k}-v_0\right) \right) \nonumber \\{} & {} +\frac{x_{n+1}+x_{n-1}}{2}\nonumber \\{} & {} - \frac{x_{n+1}^3+x_{n+1}^2x_{n-1}+x_{n+1}x_{n-1}^2+x_{n-1}^3}{4}\nonumber \\{} & {} +f_0\frac{\cos (\omega t_{n+1})+\cos (\omega t_{n-1})}{2}. \end{aligned}$$

(2.15)

The discretization of the first equation is quite relevant and may give rise to an unstable method. For instance:

$$\begin{aligned} \frac{x_{n+1}-x_{n-1}}{2\triangle t}=\frac{v_{n+1}+v_{n-1}}{2}, \end{aligned}$$

(2.16)

has a behaviour similar to that of the leap-frog method for partial differential equations and shows a splitting of the solution among alternating values that is unstable. A stable representation is obtained using the backwards finite difference of order 2:

$$\begin{aligned} v_n=\frac{3x_{n}-4x_{n-1}+x_{n-2}}{2\triangle t}, \end{aligned}$$

(2.17)

which has a local truncation error $\mathcal {O}(\triangle t^2)$.

To start the method we need now, besides $x_0$ and $v_0$, both $x_1$ and $v_1$. For the first one we use (2.10) and (2.11) as before, for the latter one we use a similar construction:

$$\begin{aligned} v_1=v_0+\triangle \dot{v}_{0}+\frac{\triangle t^2}{2!}\ddot{v}_{0}+\frac{\triangle t^3}{3!}\dddot{v}_{0}. \end{aligned}$$

(2.18)

We obtain $\ddot{v}_{0}$ and $\dddot{v}_{0}$ differentiating the second equation of system (2.13) at time zero, assuming, again, that the solution satisfies the equation at the initial time:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{v}_{0}=x_0-x_0^3+f_0,\\ \ddot{v}_{0}=v_0-3x_0^2v_0,\\ \dddot{v}_{0}=(1-3x_0^2)\dot{v}_{0}-6x_0v_0^2-\omega ^2f_0. \end{array} \right. \end{aligned}$$

(2.19)

2.1.2 SV + Odibat method for $\lceil \alpha \rceil =1$ and $\lceil \alpha \rceil =2$

In the previous Section  2.1.1, we used Diethelm’s approach to estimate the fractional derivative in (2.4). This method has a $\mathcal {O}(\triangle t^{2-\alpha })$ truncation error. In this Section to represent the fractional derivative we use the alternative technique of Odibat [28], which has a truncation error $\mathcal {O}(\triangle t^2)$. As a result, our new combined SV + Odibat numerical method has truncation error $\mathcal {O}(\triangle t^2)$. To check the consistency of our simulations, we have employed both numerical methods and compared the results. The discrete equation for this method is:

$$\begin{aligned}{} & {} \frac{x_{n+1}-2x_n+x_{n-1}}{\triangle t^2}+\gamma (D^\alpha _{t}x_n)-\frac{x_{n+1}+x_{n-1}}{2}\nonumber \\{} & {} \quad +\frac{x_{n+1}^3+x_{n+1}^2x_{n-1}+x_{n+1}x_{n-1}^2+x_{n-1}^3}{4} =f_0\frac{\cos (\omega t_{n+1})+\cos (\omega t_{n-1})}{2}.\nonumber \\ \end{aligned}$$

(2.20)

For $\lceil \alpha \rceil =1$, Odibat approximation of Caputo fractional derivative $D^\alpha _{t}x_n$ [28] for the discrete case is given by:

$$\begin{aligned} D^\alpha _{t}x_n= & {} \displaystyle \frac{\triangle t^{1-\alpha }}{\varGamma (3-\alpha )}\frac{x_{n+1}-x_{n-1}}{2\triangle t}\nonumber \\ {}{} & {} +\displaystyle \frac{\triangle t^{1-\alpha }}{\varGamma (3-\alpha )}\nonumber \\ {}{} & {} \times \left( C_{n,0}(\alpha ,1)\dot{x}_{0} +\sum \limits _{j=1}^{n-1}C_{n,j}(\alpha ,1)\frac{x_{j+1}-x_{j-1}}{2\triangle t} \right) . \end{aligned}$$

(2.21)

We substitute (2.21) in (2.20) to find:

$$\begin{aligned}{} & {} \displaystyle \frac{x_{n+1}-2x_n+x_{n-1}}{\triangle t^2}-\frac{x_{n+1}+x_{n-1}}{2}\nonumber \\{} & {} \quad + \frac{\gamma \triangle t^{1-\alpha }}{\varGamma (3-\alpha )} \left( C_{n,0}(\alpha ,1)\dot{x}_{0} + \displaystyle \sum \limits _{j=1}^{n-1}C_{n,j}\displaystyle (\alpha ,1)\frac{x_{j+1}-x_{j-1}}{2\triangle t}+\frac{x_{n+1}-x_{n-1}}{2\triangle t} \right) \nonumber \\{} & {} \quad +\frac{x_{n+1}^3+x_{n+1}^2x_{n-1}+x_{n+1}x_{n-1}^2+x_{n-1}^3}{4}=f_0\frac{\cos (\omega t_{n+1})+\cos (\omega t_{n-1})}{2}, \nonumber \\ \end{aligned}$$

(2.22)

with coefficients $C_{n,j}(\alpha ,1)$:

$$\begin{aligned} \left\{ \begin{array}{l} C_{n,0}(\alpha ,1)= \displaystyle (n-1)^{2-\alpha }-(n-2+\alpha )n^{1-\alpha },\\ C_{n,j}(\alpha ,1)= \displaystyle (n-j)^{2-\alpha }\left[ \Big ( 1-\frac{1}{n-j} \Big )^{2-\alpha }-2+\Big ( 1-\frac{1}{n-j}\Big )^{2-\alpha }\right] , \\ \displaystyle j=1,\ldots ,n-1. \end{array} \right. \end{aligned}$$

(2.23)

For $\lceil \alpha \rceil =2$, the Odibat representation of the fractional derivative $D^\alpha _{t}x_n$ at time $t_n$ is now [28]:

$$\begin{aligned} D^\alpha _{t} x_n= & {} \displaystyle \frac{\triangle t^{2-\alpha }}{\varGamma (4-\alpha )}\frac{x_{n+1}-2x_n+x_{n-1}}{\triangle t^2}\nonumber \\{} & {} +\frac{\triangle t^{2-\alpha }}{\varGamma (4-\alpha )} \begin{array}{c}\left( C_{n,0}(\alpha ,2)\ddot{x}_{0} +\sum \limits _{j=1}^{n-1}C_{n,j}(\alpha ,2)\displaystyle \frac{x_{j+1}-2x_j+x_{j-1}}{\triangle t^2} \right) \end{array}. \nonumber \\ \end{aligned}$$

(2.24)

We substitute (2.24) in (2.20) to find:

$$\begin{aligned}{} & {} \displaystyle \frac{x_{n+1}-2x_n+x_{n-1}}{\triangle t^2} -\frac{x_{n+1}+x_{n-1}}{2} +\displaystyle \frac{\gamma \triangle t^{2-\alpha }}{\varGamma (4-\alpha )}\frac{x_{n+1}-2x_n+x_{n-1}}{\triangle t^2} \nonumber \\{} & {} \quad +\displaystyle \frac{\gamma \triangle t^{2-\alpha }}{\varGamma (4-\alpha )} \begin{array}{c}\left( C_{n,0}(\alpha ,2)\ddot{x}_{0} + \displaystyle \sum \limits _{j=1}^{n-1}C_{n,j}(\alpha ,2)\frac{x_{j+1}-2x_j+x_{j-1}}{\triangle t^2} \right) \end{array}\nonumber \\{} & {} \quad + \displaystyle \frac{x_{n+1}^3+x_{n+1}^2x_{n-1}+x_{n+1}x_{n-1}^2+x_{n-1}^3}{4}=f_0\frac{\cos (\omega t_{n+1})+\cos (\omega t_{n-1})}{2}. \nonumber \\ \end{aligned}$$

(2.25)

The coefficients correspond in this case to:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle C_{n,0}(\alpha ,2)= \displaystyle (n-1)^{3-\alpha }-(n-3+\alpha )n^{2-\alpha }\\ \displaystyle C_{n,j}(\alpha ,2)= \displaystyle (n-j)^{3-\alpha }\Big [\Big ( 1-\frac{1}{n-j} \Big )^{3-\alpha }-2+\Big ( 1-\frac{1}{n-j}\Big )^{3-\alpha }\Big ],\\ j=1,\ldots ,n-1. \end{array} \right. \end{aligned}$$

(2.26)

2.2 LCEs for the fractional Duffing equation, case $\lceil \alpha \rceil =1$

The Lyapunov Characteristic Exponents measure the expansion or contraction of the phase space locally around a given orbit. They are a quantitative and qualitative tool that characterizes the chaoticity of bounded solutions.

The basic approaches to estimate them are the fiduciary orbit technique [2, 9], that gives the maximum LCE, and the linearization technique [3] that allows to estimate all the LCEs, and not just the largest one, using the Jacobian matrix of the linearized system.

For a dynamical system, once the matrix $M\big (x(t)\big )$ is found from the evolution equation [15]:

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{dM}{ \displaystyle dt}=JM,\\ M\big (x_0\big )=I, \end{array}\right. \end{aligned}$$

(2.27)

the LCEs are given by the logarithm of the eigenvalues of the following matrix [15]:

$$\begin{aligned} \varLambda _x:=\lim _{t \rightarrow \infty }\left[ M\big (x(t)\big )^{tr}M\big (x(t)\big )\right] ^{1/2t}. \end{aligned}$$

(2.28)

We estimate these values at each time step and consider their asymptotic behaviour as time increases. We consider the solution regular when $\lambda _{\max }$ is negative; whereas, if it is positive, the solution is chaotic.

We present, here, an adaptation of the linearization technique to compute all the LCEs [21]. We analyze the linearized system for this case and build an effective Jacobian matrix.

To simplify the notation, we introduce the potential U:

$$\begin{aligned} U(x)=-\frac{1}{2} x^2+\frac{1}{4} x^4. \end{aligned}$$

(2.29)

With this, we express our equation as:

$$\begin{aligned} \ddot{x} +\gamma D^{\alpha }_t x +U'(x)= f_0 \cos (\omega t). \end{aligned}$$

(2.30)

To compute the LCEs, we need to model the behaviour of two close solutions. Let be a reference solution (x, v) of (2.30), with $v = \dot{x}$, and let us consider some other solution (y, u), $u=\dot{y}$, close to the previous one. The difference between both solutions is governed by the system:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}-\dot{y} = v-u,\\ \dot{v}-\dot{u} = -U'(x)+U'(y)-\gamma D^{\alpha }_{t}(x-y),\quad 0<\alpha <1. \end{array}\right. \end{aligned}$$

(2.31)

After linearization, and posing $\delta =x-y$ and $\eta =v-u$, we obtain:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\delta } = \eta ,\\ \dot{\eta } = -U''(x)\delta -\gamma D^{\alpha }_{t}\delta . \end{array}\right. \end{aligned}$$

(2.32)

We substitute now the Caputo fractional derivative to obtain:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\delta } = \displaystyle \eta ,\\ \dot{\eta }= \displaystyle -U''(x)\delta - \frac{\gamma }{\varGamma (1-\alpha )} \int \limits _{0}^{t}\frac{\eta (\tau )}{(t-\tau )^{\alpha }}d\tau ,\quad 0<\alpha <1. \end{array}\right. \end{aligned}$$

(2.33)

We suppose both solutions to be very close, such that the linearization gives a valid approximation, but, also, they may be considered to be identical (up to the numerical precision we are going to use) for a given range of time $[0,t_1]$ and that they only differ effectively after that specific time $t_1$. Due to a continuity argument, functions with small variations, such as the difference between close solutions, will have a small fractional derivative and, thus, we may consider that the integral in (2.33) provides a small contribution. Thus, in good approximation, we have:

$$\begin{aligned} \int \limits _{0}^{t}\frac{\eta (\tau )}{(t-\tau )^{\alpha }}d\tau \approx \int \limits _{t_1}^{t}\frac{\eta (\tau )}{(t-\tau )^{\alpha }}d\tau ,\quad 0<\alpha <1, \end{aligned}$$

(2.34)

and, with this, we estimate:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\delta } = \displaystyle \eta ,\\ \dot{\eta }= \displaystyle -U''(x)\delta - \frac{\gamma }{\varGamma (1-\alpha )} \int \limits _{t_1}^{t}\frac{\eta (\tau )}{(t-\tau )^{\alpha }}d\tau ,\quad 0<\alpha <1. \end{array}\right. \end{aligned}$$

(2.35)

Let us consider the Taylor expansion of $\eta (\tau )$ around t:

$$\begin{aligned} {\eta (\tau )}= \eta (t)+(\tau -t)\dot{\eta }(t)+ \frac{(\tau -t)^2}{2} \ddot{\eta }(t)+\mathcal {O}((\tau -t)^3). \end{aligned}$$

(2.36)

After substitution in (2.35) and integration in $\tau$, the linearized system becomes:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\delta } = \displaystyle \eta ,\\ \dot{\eta }= \displaystyle \frac{-U''(x)}{C}\delta -\gamma \frac{\triangle t^{1-\alpha }}{C\varGamma (2-\alpha )}\eta , \end{array}\right. \end{aligned}$$

(2.37)

with $\triangle t= t-t_1$, discarding higher order terms.

The coefficient C is:

$$\begin{aligned} C= \displaystyle 1-\frac{\gamma \triangle t^{2-\alpha }(1-\alpha )}{\varGamma (3-\alpha )},\quad 0<\alpha <1. \end{aligned}$$

(2.38)

The corresponding Jacobian matrix for system (2.37), $J_1$, is:

$$\begin{aligned} J_1 = \displaystyle \left( {\begin{array}{ccc} 0 &{} 1 \\ \frac{-U''(x)}{C} &{} -\gamma \frac{ \triangle t^{1-\alpha }}{C\varGamma (2-\alpha )} \end{array} } \right) . \end{aligned}$$

(2.39)

We consider it to be the effective Jacobian matrix for the linearized fractional system and we have used it to estimate the two LCEs of the system, $\lambda _1$ and $\lambda _2$. Whenever the trace of the Jacobian matrix is constant, as in this case, we have that it is equal to the sum of all LCEs:

$$\begin{aligned} \lambda _1+\lambda _2 =\text {trace}(J_1)=-\gamma \frac{ \triangle t^{1-\alpha }}{C\varGamma (2-\alpha )},\quad 0<\alpha <1. \end{aligned}$$

(2.40)

We have checked the numeric conservation of the sum of the LCEs in our simulations computing the relative error of the sum of the estimates for both LCEs with respect to the trace of $J_1$.

To estimate the dimension of the strange attractor in the chaotic regime in the plane xv, we use the Lyapunov (or Kaplan–Yorke) dimension [24] that corresponds in our case to:

$$\begin{aligned} D_L=1+\frac{\lambda _1}{\vert \lambda _{2}\vert }, \end{aligned}$$

(2.41)

where $\lambda _1>0$ and $\lambda _2<0$.

2.3 LCEs for the fractional Duffing equation, case $\lceil \alpha \rceil =2$

We extend now the linear approximation to the case $\alpha \in (1,2)$, similarly to the previous case. The Caputo fractional derivative of $\delta$ changes, and is now:

$$\begin{aligned} D_{t}^\alpha \delta (t)= & {} \frac{1}{\varGamma (2-\alpha )}\int _{0}^t \frac{{\delta ''}(\tau )}{(t-\tau )^{\alpha -1}}\, d\tau , \quad 1<\alpha <2. \end{aligned}$$

(2.42)

We substitute (2.42) in (2.32) and use ${\delta ''}(\tau )={\eta '}(\tau )$ to obtain:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\delta } = \displaystyle \eta ,\\ \dot{\eta }= \displaystyle -U''(x)\delta - \frac{\gamma }{\varGamma (2-\alpha )} \int \limits _{0}^{t}\frac{{\eta '}(\tau )}{(t-\tau )^{\alpha -1}}d\tau ,\quad 1<\alpha <2. \end{array}\right. \end{aligned}$$

(2.43)

Considering the same assumptions as in the precedent case, we substitute $t=t_1+\triangle t$ in (2.43):

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \dot{\delta } = \displaystyle \eta ,\\ \displaystyle \dot{\eta }= \displaystyle -U''(x)\delta - \frac{\gamma }{\varGamma (2-\alpha )} \int \limits _{t_1}^{t_1+\triangle t}\frac{{\eta '}(\tau )}{(t-\tau )^{\alpha -1}}d\tau ,\quad 1<\alpha <2. \end{array}\right. \end{aligned}$$

(2.44)

Using the Taylor expansion to approximate ${\eta '}(\tau )$ around t for time step $\triangle t$ small enough, we have:

$$\begin{aligned} \dot{\eta }= & {} -U''(x)\delta -\frac{\gamma }{\varGamma (2-\alpha )} \dot{\eta }(t) \int \limits _{t_1}^{t_1+\triangle t}(t_1+\triangle t-\tau )^{1-\alpha }d\tau \nonumber \\{} & {} +\frac{\gamma }{\varGamma (2-\alpha )}\ddot{\eta }(t)\int \limits _{t_1}^{t_1+\triangle t}(t_1+\triangle t-\tau )^{2-\alpha }d\tau +\cdots \end{aligned}$$

(2.45)

After the integration, we obtain:

$$\begin{aligned} \dot{\eta }= -U''(x)\delta -\frac{\gamma \triangle t^{2-\alpha }}{\varGamma (3-\alpha )}\dot{\eta }(t)+\frac{ \gamma (2-\alpha )\triangle t^{3-\alpha }}{\varGamma {(4-\alpha )}}\ddot{\eta }(t)+\mathcal {O}(\triangle t^{4-\alpha }). \end{aligned}$$

(2.46)

The main difference with the previous case comes from the fact that we cannot “close” the equations since we cannot express $\ddot{\eta }$ as a function of the other variables. To solve this we resort to approximate the second order derivative by finite differences. Given the truncation error in our approximation of $\dot{\eta }$, a suitable approximation for $\ddot{\eta }$ is given by the three points finite difference:

$$\begin{aligned} \ddot{\eta }(t)= & {} \frac{\eta (t)-2\eta (t-\triangle t)+\eta (t-2\triangle t)}{\triangle {t^2}}+\mathcal {O}(\triangle t). \end{aligned}$$

(2.47)

As both solutions can be considered identical (up to numerical precision) over an interval of time $t\in [0,t_1)$, $\eta$ is zero for all times in this interval, and we have:

$$\begin{aligned} \eta (t-n \triangle t)=0,\quad \forall \quad n\ge 2. \end{aligned}$$

(2.48)

Using this assumption, the finite difference of $\ddot{\eta }$ (2.47) becomes:

$$\begin{aligned} \ddot{\eta }(t)= & {} \frac{\eta (t)-2\eta (t-\triangle t)}{\triangle {t^2}}+\mathcal {O}(\triangle t). \end{aligned}$$

(2.49)

In order to express $\ddot{\eta }$ as a function of $\eta$ and $\dot{\eta }$, we need now to express $\eta (t-\triangle t)$ as a function of those variables. Once again we use a finite difference with a suitable truncation error. In this case a four-point formula:

$$\begin{aligned} \dot{\eta }(t)= & {} \frac{-2\eta ({t-3\triangle t})+9\eta (t-2\triangle t)-18\eta (t-\triangle t)+11\eta (t)}{6\triangle t}+\mathcal {O}(\triangle t^3)\nonumber \\= & {} \frac{-18\eta (t-\triangle t)+11\eta (t)}{6\triangle t}+\mathcal {O}(\triangle t^3), \end{aligned}$$

(2.50)

that gives us:

$$\begin{aligned} \eta (t-\triangle t)= & {} \frac{11}{18}\eta (t)-\frac{\triangle t}{3}\dot{\eta }(t)+ \mathcal {O}(\triangle t^4). \end{aligned}$$

(2.51)

With all this have:

$$\begin{aligned} \ddot{\eta }(t)= & {} \frac{\eta (t)-2\eta (t-\triangle t)}{\triangle {t^2}}+\mathcal {O}(\triangle t) \nonumber \\= & {} \frac{1}{\triangle t^2}\eta (t)-\frac{2}{\triangle t^2}\left[ \frac{11}{18}\eta (t)-\frac{\triangle t}{3}\dot{\eta }(t)+ \mathcal {O}(\triangle t^4) \right] +\mathcal {O}(\triangle t) \nonumber \\= & {} \frac{-2}{9\triangle t^2}\eta (t)+\frac{2}{3\triangle t} \dot{\eta }(t)+\mathcal {O}(\triangle t), \end{aligned}$$

(2.52)

and, substituting into (2.46), we finally obtain:

$$\begin{aligned} \dot{\eta }= & {} -U''(x)\delta (t)-\frac{\gamma \triangle t^{2-\alpha }}{\varGamma (3-\alpha )}\dot{\eta }(t)+ \frac{2\gamma (2-\alpha )\triangle t^{2-\alpha }}{3\varGamma (4-\alpha )}\dot{\eta }(t) \nonumber \\{} & {} -\frac{2\gamma (2-\alpha )\triangle t^{1-\alpha }}{9\varGamma (4-\alpha )}{\eta }(t)+\mathcal {O}(\triangle t^{4-\alpha }). \end{aligned}$$

(2.53)

In order to use the same framework of the previous case, we rewrite (2.44) as:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{\delta } = \displaystyle \eta ,\\ \dot{\eta }=\displaystyle \frac{-U''(x)}{C}\delta +\frac{B}{C}\eta ,\quad 1<\alpha <2 ,\end{array}\right. \end{aligned}$$

(2.54)

where the coefficients C and B are, in this case:

$$\begin{aligned} \left\{ \begin{array}{l} C=1+ \displaystyle \frac{\gamma (5-\alpha )\varDelta t^{2-\alpha }}{3\varGamma (4-\alpha )},\\ B= \displaystyle -\frac{2\gamma (2-\alpha )\triangle t^{1-\alpha }}{9\varGamma (4-\alpha )} .\end{array}\right. \end{aligned}$$

(2.55)

The corresponding effective Jacobian matrix for system (2.54), $J_2$, is:

$$\begin{aligned} J_2 =\displaystyle \left( {\begin{array}{cc} 0 &{} 1 \\ \frac{-U''(x)}{C} &{} \frac{B}{C} \end{array} } \right) . \end{aligned}$$

(2.56)

As the trace of the Jacobian matrix is constant in this case too, we have that it is equal to the sum of the two LCEs:

$$\begin{aligned} \lambda _1+\lambda _2 =\text {trace}(J_2)=\frac{B}{C},\quad 1<\alpha <2. \end{aligned}$$

(2.57)

To show the validity of the approximations that we have assumed to obtain $J_1$ (2.39) and $J_2$ (2.56), we have computed the LCEs by the effective Jacobian matrices and compared the maximum value with the results of the fiduciary orbit technique [9]. The results are presented in Section 3 and show a very good agreement.

3 Numerical results

We have solved numerically the fractional equations for two cases ($0<\alpha <1$) and ($1<\alpha <2$) using both methods presented in Section 2.1. From the numerical solutions we have estimated the LCEs with the Jacobian matrices (2.39) and (2.56), as well as the maximum one by the fiduciary orbit technique.

Throughout all computations the results obtained by the two numerical methods agree up to the corresponding truncation errors. In some specific chaotic cases this gives rise to some qualitative discrepancies which are due to the extreme sensibility to the initial conditions. It will be commented at some point below in Section 3.1.

We have also solved the two non-fractional limit cases corresponding to $\alpha =0$, $\alpha =2$ using the Strauss-Vázquez numerical method [20]. When comparisons were necessary, we have solved the “classical” Duffing equation with the same numerical method presented in [19].

3.1 Phenomenology of solutions

As is done in the classical Duffing equation, to visualize the results we have represented the orbits in the xv-plane, that we consider to be our phase space, and the stroboscopic map of period $T=2\pi /w$ in time, that gives the solution at time multiples of that period, which is the period of the external forcing. In some cases we present only the x-component of both the solution and of the stroboscopic map. When necessary, we have also presented either the solutions or their stroboscopic maps in a (false) 3D projection, to clearly see the evolution in time.

In the classical Duffing equation there is, basically, a competition between the amplitude of the external forcing $f_0$ and the coefficient of the dissipation $\gamma$. Melnikov method marks the boundary that separates the regular regime from the chaotic one [14]: chaos may appear only for values of the parameters such that

$$\begin{aligned} \frac{f_0}{\gamma } > \frac{4}{3}\frac{\cosh (\pi \omega /2)}{\sqrt{2}\pi \omega }\,. \end{aligned}$$

(3.1)

In the fractional model we may look for different values of the parameters to see if a similar threshold exists. The numerical simulations are intended to investigate the effect of the amplitude $f_0$ and the order of the fractional derivative $\alpha$, with the frequency $\omega$ and the damping coefficient $\gamma$ taking constant values, $\omega =1$ and $\gamma =0.25$, respectively.

The system is very rich, it can exhibit very different behaviours. In our study, we have considered different values for $f_0$ and $\alpha$ to present these distinct types of behaviours. We enumerate in what follows the main features.

Fig. 1

Phase space and stroboscopic map for a regular solution that tends towards a T-periodic curve with $\alpha =0.5$, $f_0=0.1$, $x_0=v_0=0$

Fig. 2

Phase space and stroboscopic map of a regular solution that tends towards a 3T-periodic curve with $\alpha =0.8$, $f_0=2$, $x_0=v_0=0$

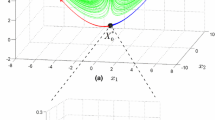
• 1. There are regular solutions, where the curves in the phase plane appear to tend rapidly to a closed curve. When the stroboscopic map is plotted, we see that the points tend to a fixed point (period T) or a discrete set of a few fixed points (higher periodicity with multiples of T). Although the fractional equation cannot have periodic solutions [19, 25, 30], the attractor in the regular case appears to be a periodic curve which is not a solution. This is a clear difference with classical case where the attracting periodic curve is also a solution. For instance, we show in Fig. 1 a regular solution that tends towards a T-periodic curve, with the points in the stroboscopic map tending towards a unique fixed point in the phase plane.

  In Fig. 2, we present a regular solution that tends towards a 3T-periodic curve. We see clearly how the three sets of points in the stroboscopic map tend to three fixed points as time increases.

  It is interesting to note that the regular attractor is not, in general, unique. For fixed values of all the parameters, depending on the initial conditions the solutions can exhibit diverse behaviours and converge towards distinct closed curves. This phenomenon underscores the system’s sensitivity to its starting state and the importance of considering a wide range of initial conditions when studying the dynamics. Consequently, even small deviations in the initial conditions can lead to significantly different outcomes.

  This sensitivity to the initial conditions, that is to be expected in a chaotic regime, is here present in the case of regular solutions. In Fig. 3 we show four regular attractors, with some different periodicities, for fixed values of the parameters but different initial conditions.

• 2. There are chaotic solutions, clearly identified by presenting a quick convergence to a strange attractor in the stroboscopic map, similar to the one obtained in the classical model for the same values of the parameters. We present several examples of the strange attractor in Fig. 4 for different values of $\alpha$ and $f_0$.

  As we mentioned before, solutions with the same parameters have the potential to converge towards distinct attractors. This happens also when chaotic solutions are present. For some values of the parameters, and depending on the initial conditions, there is a coexistence of regular solutions that tend to different regular attractors and chaotic solutions that tend to a unique strange attractor. We illustrate this in Fig. 5, where we only show the x-component of the solution, the behaviour of v being similar.

• 3. There is, though, a range of regular solutions that present a long chaotic transient: for some time, quite long in some cases, the stroboscopic map shows a “cloud” of points that resembles a strange attractor but after that the solution clearly tends towards a periodic curve. In Fig. 6(a), we illustrate this with a solution that, after a very long transient tends to a closed curve of period 8T in the phase plane. In Fig. 6(b), we present the stroboscopic map pf the solution restricted to the chaotic transient, and in Fig. 6(c) we present the stoboscopic map of the solutino in the regular regime, with the points tending towards to a limit set of 8 points.

  For a clearer view of this behaviour in Fig. 6(d), we present the evolution of the points in false 3D projection adding, thus, the time evolution.

  This behaviour also appears to be very sensitive to the initial conditions: two solutions starting from close initial data may present transients of very different lengths as shown in Fig. 7 for $\alpha =0.25$, $f_0=0.229$.

  We notice a chaotic transient for the initial conditions $x_0=0.001$, $v_0=0.0098$ (red points) but once we add the small quantity $\epsilon =(2\pi /700)^8$ to the previous initial conditions as a perturbation the transient is extended in the order of $10^5$ time steps (black points).

  The chaotic transient can even present an intermittent behaviour, with a chaotic regime alternating several times with a regular one, and eventually reaching a regular phase that can be different to the previous regular ones. We illustrate this in Fig. 8.

• 4. We have just mentioned above the case of solutions presenting a chaotic transient that regularize, afterwards, somehow switching from approaching a chaotic attractor to finally tending towards a regular one. Similarly, we have observed solutions switching from regular attractors: solutions that start close to a regular, periodic, curve but after some time evolve towards a different one. The stroboscopic map in such cases shows what resembles a bifurcation in time. We illustrate this with two examples in Figs. 9 and 10.

  This switching between two regular attractors can occur through a chaotic-like transition. We illustrate this in Fig. 11, where the solution starts near a T-periodic curve to finally approach a 3T curve.

  Finally, the transition can also be from a regular attractor to a chaotic one, as shown in Fig. 12. This last case is, somehow, the reverse situation of the long chaotic transient described in the previous point.

• 5. Last, but not least, we have found intermittent behaviours in some chaotic solutions: The system exhibits a periodic-like pattern during extended time intervals but with distinct lengths interrupted by chaotic bursts, their occurrence being seemingly random. Each burst has a distinct and finite duration before disappearing, leading to the initiation of a new laminar phase. This pattern repeats itself in a cyclic manner [31]. In some cases, the regular-like phases of the solution oscillate around just one of the centers $(\pm 1,0)$ of the underlying classical Hamiltonian system as in Fig. 13.

  In other cases, the regular-like phases that can be around any of the two centers, passing from one to the other, occasionally, as in Fig. 14.

  We have also found cases where the regular-like phases of the solution oscillate around both centers of the underlying classical Hamiltonian system. We present such a case in Fig. 15.

Fig. 3

Multiplicity of limit cycles in the regular regime: for different initial conditions, we find four different limit cycles of different periodicities: T: red and blue curve, 4T: green and pink curve, with the same set of parameters: $\alpha =0.6$, $f_0=0.2409$

Fig. 4

Strange attractors of the fractional Duffing equation for several values of $\alpha$

Fig. 5

Time series for chaotic and regular solutions for $\alpha =0.1$, $f_0 = 0.16$ for two different initial conditions. In (b) the solution tends to a regular attractor after a chaotic transient

Fig. 6

The solution becomes regular after a long chaotic transient and tends towards a closed curve of period 8T ( and a limit set of 8 points in the stroboscopic map), $\alpha =0.3$, $f_0=3$, $x_0=1.23$, $v_0=1.21$

Fig. 7

Stroboscopic map of different chaotic transients for $\alpha =0.25$, $f_0=0.229$ shows that two solutions with nearby initial conditions, display transients of different lengths

Fig. 8

Stroboscopic map with intermittent chaotic transient for $\alpha =1.1$, $f_0=0.25$

Fig. 9

Phase space and Stroboscopic map of the transition from a T-periodic attractor to a 2T attractor, $\alpha =1.1$, $f_0=0.2$, $x_0=0$, $v_0=0.5$

Fig. 10

Phase space and Stroboscopic map of the transition from a 2T-periodic attractor to a 4T attractor, $\alpha =1.2$, $f_0=0.19$, $x_0=0.5$, $v_0=0.5$

Fig. 11

Phase space and Stroboscopic map of the transition from a T-periodic attractor to a 3T attractor via a chaotic-like transition for $\alpha =1.1$, $f_0=0.2$, $x_0=0.5$, $v_0=0.5$

Fig. 12

Switching from regular attractor to a chaotic one, for $\alpha =1.1$, $f_0=0.4$, $x_0= 1.05$, $v_0=1.06$

Fig. 13

Intermittency with oscillations around one center $(-1,0)$, for $\alpha =1.25$,      $f_0=0.2271$, $x_0=0.00101$, $v_0=0.002$

Fig. 14

Intermittency with oscillations around any of the two centers $(\pm 1,0)$, for $\alpha =1.35$, $f_0=0.2119$, $x_0=v_0=0$

Fig. 15

Intermittency with oscillations around the two centers, $\alpha =0.1$, $f_0=0.778,x_0=1$, $v_2=0$

From all our computations we have obtained a numerical estimation of the threshold separating the regular regime from that where chaotic solutions are found, depending on the values of $\alpha$ and $f_0$, keeping $\gamma$ fixed. In Fig. 16, we present the resulting curve of $\alpha$ versus $f_0/\gamma$. This curve separates the two states of solution, chaotic and regular, where, in the region above it, the solution may exhibit chaotic behaviour, whereas below the curve, the solution is regular.

Fig. 16

Numerical threshold for chaos: above the curve the solution can be chaotic and below it, the solution is regular

In the classical Duffing equation, the analytic value of the threshold of chaos given by (3.1) appears for ${f_0}/{\gamma }\approx 0.75$ [14]. Numerically, the value of the threshold appears to be at ${f_0}/{\gamma }=1.06$, which satisfies the Melnikov criteria but is significant above. In the fractional case we recover the numerical value of the threshold of the classical case for the values of $\alpha$ near 1, as shown in Fig. 16.

3.2 LCEs

As we mentioned before, we have estimated the maximum LCE with two different techniques: the linearization using the approximated Jacobi matrix and the fiduciary orbit method. The linearization method gives us the two exponents $\lambda _1$ and $\lambda _2$ ($\lambda _1\ge \lambda _2$), and the fiduciary orbit approach gives an independent estimation of $\lambda _1$, that we denote by $\lambda _{\max }$.

In the study made in [21] a small quantitative gap was observed between the estimation of the values of the maximum LCE obtained by the two methods.

In the present study, we succeeded in reducing this gap, due to our numerical method SV + Odibat method being more accurate.

We discriminate regular and chaotic solutions by means of the LCEs, considering the solutions to be regular if both exponents $\lambda _1$ and $\lambda _2$ are negative or zero, and chaotic if the maximum one is positive. We illustrate this in Fig. 17 for regular and chaotic solutions with $\alpha$ below 1 and in Fig. 18 for $1<\alpha \le 2$.

Fig. 17

Estimation of LCEs shows the agreement between $\lambda _1$ and $\lambda _{\max }$ for both behaviours: chaotic and regular solution for $\alpha =0.5$, $x_0=0.8$, $v_0=0$

Fig. 18

Estimation of Lyapunov Characteristic Exponents (LCEs) illustrates the consistency between $\lambda _1$, and $\lambda _{\max }$ for both behaviours: chaotic and regular solutions, for for $\alpha =1.1$, $x_0=v_0=0$

The agreement between the exponent $\lambda _1$ derived through the linearization method and $\lambda _{\max }$ which is approximated with a totally different method (the fiduciary orbit method), supports the good estimation of the Jacobian matrix in both cases.

Besides, as an indication of possible computing errors, we have checked the conservation laws (2.40), (2.57) and found always a good agreement. We calculate the relative error of the sum of the LCEs with respect to the trace of $J_1$ and $J_2$ for different time-steps:

$$\begin{aligned} \Big \vert \frac{\vert \lambda _1+\lambda _2-\text {trace}(J)\vert }{ \text {trace}(J)}\Big \vert , \end{aligned}$$

where we found it smaller than $5\cdot 10^{-5}$.

In cases of intermittent behaviour the LCEs agree with the chaoticity of solutions. In cases where a long regular phase finally ends in a chaotic behaviour, the exponents may tend to zero but grow afterwards when the chaos is present, as in Fig. 19.

Fig. 19

Estimation of the LCEs for a solution with a long regular phase, $\alpha =1.1$, $f_0=0.4$, $x_0= 1.05$, $v_0=1.06$

For regular solutions with a long chaotic initial transient, the LCEs are computed only after this transient. The LCEs tend to negative values as time increases.

Having estimated both Lyapunov exponents we can compute the Lyapunov dimension $D_L$ given by (2.41). In Fig. 20, we present $D_L$ as a function of $\alpha$ for the threshold values in Fig. 16.

Fig. 20

Estimates of the Lyapunov dimension $D_L$ versus $\alpha$

4 Limiting cases

The fractional equation has three non fractional limiting cases. They correspond to the three integer values of $\alpha$ in the considered range: $\alpha =0$, 1 and 2. Since the dependence on $\alpha$ is continuous, the behaviour of the fractional model tends to that of the limiting cases as $\alpha$ tends to an integer.

The central case, $\alpha =1$, corresponds to the classical Duffing equation. The other two values correspond, basically, to the same model.

To understand the solution of the fractional equation (2.4) in the limits and show its behaviours, we need to compare it with the classical case of the non-fractional equation (undamped forced duffing equation) where there is no dissipation in the system and $\gamma$ is no longer a damping parameter. It merges with the coefficient of the linear stiffness as $\alpha \rightarrow 0^+$ or with the coefficient of the second derivative as $\alpha \rightarrow 2^-$, see (4.3) below.

4.1 Non-fractional equation: undamped forced Duffing equation

In the limit $\alpha \rightarrow 0^+$, the fractional derivative gives the identity operator [23], and we have the equation:

$$\begin{aligned} \ddot{x} +(\gamma - 1) x + x^3 = f_0 \cos (\omega t). \end{aligned}$$

(4.1)

In the limit $\alpha \rightarrow 2^-$, the fractional derivative corresponds to the second order derivative [23], giving the following:

$$\begin{aligned} (1+\gamma ) \ddot{x} - x +x^3 = f_0 \cos (\omega t). \end{aligned}$$

(4.2)

Provided $\gamma -1<0$, both equations correspond to a conservative system perturbed by a periodic driving force and the difference is solely in the value of some of the coefficients. Thus, the fractional model ends up, in both these extreme limits, modeling the same qualitative system. Let us present its general features.

Let be the general undamped Duffing equation:

$$\begin{aligned} m\ddot{x}-ax+x^{3}=f_0\cos (\omega t), \end{aligned}$$

(4.3)

with m and a are two positive constants. It corresponds to a Hamiltonian system perturbed by an external forcing. The unperturbed Hamiltonian function is

$$\begin{aligned} H(x,y)=\frac{m}{2} \dot{x}^{2}-\frac{a}{2}x^{2}+\frac{x^{4}}{4}. \end{aligned}$$

(4.4)

The unforced system has three critical points: two centers, located at $(+\sqrt{a},0)$ and $(-\sqrt{a},0)$, and a saddle point at the origin. The unstable equilibrium point (0, 0) is connected to itself by two homoclinic orbits [14]. This is, basically, the same Hamiltonian (2.3) on which the classical Duffing equation is built.

The presence of the forcing term introduces a period that competes with the internal periods of the unperturbed Hamiltonian system. This mechanism allows chaotic solutions to exist. Nevertheless, it is possible to show [12] that solutions in the plane xv are bounded between regular curves such that for large initial values the chaotic behaviour is suppressed.

The regular and the chaotic regions of the phase space can be visualized using the stroboscopic map with the period of the external force, $T=2\pi /\omega$. For the numerical simulations, we use the Strauss-Vázquez approach [22]:

$$\begin{aligned} m\left( \frac{x_{n+1}-2x_{n}+x_{n-1}}{\triangle t^2}\right) +\frac{U(x_{n+1})-U(x_{n-1})}{x_{n+1}-x_{n-1}} =f_0\frac{\cos (\omega t_{n+1})+\cos (\omega t_{n-1})}{2}, \end{aligned}$$

(4.5)

where $U(x)=-\frac{a}{2}x^2+\frac{1}{4}x^4$ is the potential. This method gives an exact discrete counterpart of the variation law of the Hamiltonian (4.4).

We illustrate the behaviour of the system with some different cases, depending on the values of the parameters. We have fixed $\omega =1$. In all the simulations we observe a bounded central chaotic region with some possible internal structure, basically regularity islands. Outside of this central region the system is always regular. In Fig. 21 we present two examples.

It is important to note that the chaos in the solutions of Equation (4.3) is quite different from that exhibited by the classical Duffing’s equation. This is mainly due to the fact that no dissipation is present.

The trace of the Jacobian matrix of the system is now always zero and the Lyapunov exponents have the same value with opposed signs. If we extend the Lyapunov dimension as defined by (2.41) to the undamped limit cases, the value for chaotic solutions is always 2. These features are closer to that of chaos in Hamiltonian systems.

The boundedness of the chaotic part, and of the solutions in general, can be seen in Fig. 21 where we show the central chaotic region that corresponds to small initial data and the regular behaviour of solutions with large initial data, for two different settings of the parameters and several initial values.

Fig. 21

Stroboscopic maps for Equation (4.3). Different colors correspond to different initial conditions

4.2 Fractional Duffing equation near the limits

Let us illustrate now the behaviour of the fractional system for values of $\alpha$ close to the limit cases. We have considered the typical regime ($\gamma -1 <0$) where both m and a are positive. We discard the case where ($\gamma -1 >0$) which is featureless, since the system has a single critical point (center) at the origin (0, 0). We present some solutions for different combinations of parameters and compare them with the classical case mentioned in Subsection 4.1, above.

• In Fig. 22 for $f_0=0.13$, $\gamma =0.01$ , $\omega =1$:

  The similarity to the classical case, when choosing the same parameters and the same initial conditions as in Fig. 21(a), is striking. For large initial conditions all solutions are regular.

• In Fig. 23 for $f_0=0.03$, $\gamma =0.25$, $\omega =1$:

  Although the similarity with the classical case is not as striking as previously, it is clear that the structure is the same.

• In Fig. 24 for $f_0=0.1,\gamma =0.25 , x_0=0.25, v_0=0.2, \omega =1$:

Fig. 22

Stroboscopic maps for both limits with $f_0=0.13$, $\gamma =0.01$, $\omega =1$ shows the similarity to the classical case (Fig. 21(a))

Fig. 23

Stroboscopic maps for $\alpha$ near to 1 and 2 for $f_0=0.03$, $\gamma =0.25$, $\omega =1$

Fig. 24

Stroboscopic maps showing the chaotic region of both limit cases: $f_0=0.1$

We have computed the Lyapunov Dimension which is close to 2 near both limits as shown in Fig. 20.

$\alpha \rightarrow 1$: The fractional derivative corresponds in this limit to the first order derivative [23] and we obtain the classical Duffing equation (2.1).

The strange attractor obtained as $\alpha \rightarrow 1$ with values above or below 1 tends to the classical one.

Although the system is not symmetric with respect to $\alpha$, this does not affect the behaviour of the fractional system as it tends to any of the three classical limits.

5 Conclusions

In this paper, we study Duffing’s equation with fractional damping term and linear stiffness using the Caputo fractional derivative. We have explored the equation in the range from $\alpha =0$ to $\alpha =2$. We have used two numerical methods, from two different approaches, that give consistent results.

The system appears to be very sensitive to the values of the parameters and of the initial conditions, especially in the region near the threshold that sepparates the regular and the chaotic regimes. Small variations in any of the values can give rise to solutions with different behaviours, even in the case of regular solutions, with multiple regular attractors, given a fixed set of parameter values. The classical equation may present three attractors that correspond to periodic solutions around one of the two centers of the undisturbed Hamiltonian, or around both of them. In the fractional case we have found that the number of regular attractors that coexist is not limited to three and several different closed curves may be found. We understand that the relaxation of the dissipation and the long memory that the fractional derivative introduces allow more periodic attractors to be stable.

For $\alpha$ near 1 and above, the transition from regular to chaotic solutions is marked by intermittencies.

We have estimated both Lyapunov Characteristic Exponents. They were in good agreement with the maximum LCE, simulated using the fiduciary orbit technique.

In both limits, $\alpha \rightarrow 0$ and $\alpha \rightarrow 2$, the system behaves similarly and tends to the classical case where no dissipation is present. In this sense, there is a closed transition that interpolates between these limits and the classical Duffing equation that corresponds to the intermediate limit $\alpha =1$.

Although the limit cases can be obtained, somehow, in the classical model by just diminishing the values of the dissipation coefficient $\gamma$, the behaviour is different to what we observe in the fractional model.

Although the behaviour of the system is similar in both extreme limits, the intermediate behaviour is different on both sides of $\alpha =1$.

Further studies are underway. Preliminary results indicate that the system presents different types of intermittency. The non-unicity of the regular attractors suggests to study the bifurcation diagrams of the transition from regular to chaotic regimes. As an analytical tool for these studies, an extension of the Melnikov method to this fractional case is under consideration.