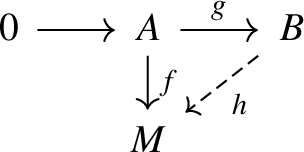Nonnil-FP-injective and nonnil-FP-projective dimensions and nonnil-semihereditary rings

Abstract

In this paper, we introduce the concept of nonnil-FP-injective dimension for both modules and rings. We explore the characterization of strongly $\phi$-rings that have a nonnil-FP-injective dimension of at most one. We demonstrate that, for a nonnil-coherent, strongly $\phi$-ring R, the nonnil-FP-injective dimension of R corresponds to the supremum of the $\phi$-projective dimensions of specific families of R-modules. We also define self-nonnil-injective rings as $\phi$-rings that act as nonnil semi-injective modules over themselves and establish the equivalence between a strongly $\phi$-ring R being $\phi$-von Neumann regular and R being both nonnil-coherent and self-nonnil semi-injective. Furthermore, we extend the notion of semihereditary rings to $\phi$-rings, coining the term ‘nonnil-semihereditary’ to describe rings where every finitely generated nonnil ideal is u-$\phi$-projective. We provide several characterizations of nonnil-semihereditary rings through various conceptual lenses. Our study also includes an investigation of the transfer of the nonnil-semihereditary property in trivial ring extensions. Additionally, we define the nonnil-FP-projective dimension for modules and rings, showing that for any strongly $\phi$-ring, a nonnil-FP-projective dimension of zero is indicative of the ring being nonnil-Noetherian. We also ascertain that, for a strongly $\phi$-ring R, its nonnil-FP-projective dimension is the supremum of the NFP-projective dimensions across different families of R-modules. Lastly, we provide numerous examples to illustrate our results.

1 0. Introduction and preliminaries

All rings considered in this paper are assumed to be commutative with non-zero identity and prime nilradical. We use ${\text {Nil}}(R)$ to denote the set of nilpotent elements of R and Z(R) the set of zero-divisors of R. Now we recall terminologies and notations that will be used throughout the paper.

1.1 $\phi$-ring, strongly $\phi$-ring, and $\phi$-torsion theory

A ring R with ${\text {Nil}}(R)$ being divided prime (i.e., ${\text {Nil}}(R) \subset x R$ for all $x \in R \setminus {\text {Nil}}(R)$) is called a $\phi$-ring. Let $\mathcal {H}$ (resp., $\overline{\mathcal {H}}$) be the set of all $\phi$-rings (resp., the set of all $\phi$-rings with non-maximal nilradical). A ring R is called a strongly $\phi$-ring if $R \in \mathcal {H}$ and $Z(R)={\text {Nil}}(R)$. Let $\overline{\mathcal {H}}^{ZN}$ be the set of all strongly $\phi$-rings in $\overline{\mathcal {H}}$. Let R be a ring and M be an R-module. Define

$$\begin{aligned} \phi \text {-}{\text {tor}}(M):=\{x \in M \mid sx=0 ~\text{ for } \text{ some }~ s \in R \setminus {\text {Nil}}(R)\}. \end{aligned}$$

If $\phi$-${\text {tor}}(M)=M$, then M is called a $\phi$-torsion module, and if $\phi$-${\text {tor}}(M)=0$, then M is called a $\phi$-torsion free module. A submodule N of an R-module M is said to be a $\phi$-submodule if M/N is $\phi$-torsion. It is worth noting that in the language of torsion theory, the class $\mathfrak {T}$ of all $\phi$-torsion modules is a (hereditary) torsion class, equivalently $\mathfrak {T}$ is closed under (submodules,) direct sums, epimorphic images, and extensions. An ideal I of R is said to be nonnil if $I \nsubseteq {\text {Nil}}(R)$. An R-module M is said to be $\phi$-uniformly torsion (u-$\phi$-torsion for short) if $sM=0$ for some $s\in R\setminus {\text {Nil}}(R)$. An R-module M is said to be $\phi$-divisible if $M=s M$ for all $s \in R \setminus {\text {Nil}}(R)$.

1.2 FP-injectivity and FP-projectivity

Maddox [29] studied the absolutely pure modules. It is well-known that an absolutely pure module is precisely FP-injective. An R-module M is said to be absolutely pure if every short exact sequence $0\rightarrow M\rightarrow N\rightarrow P\rightarrow 0$ is pure. Next, Stenström [33] studied the consequences of extending the notion of injective modules to that of FP-injective modules. He gave the basic properties of FP-injectivity in an arbitrary ring and the FP-injective dimension of a module. Recall that the FP-injective dimension of an R-module N (denoted by ${\hbox {FP-id}}_RN$) is the least non-negative integer n for which ${\text {Ext}}_R^{n+1}(M,N)=0$ for every finitely presented module M, and if no such an integer exists, set ${\hbox {FP-id}}_RN=\infty$. Next, he studied this notion in coherent rings, and then characterized the coherent rings which are self-FP-injective, that is the coherent rings R which are FP-injective modules over itself. He established in [33, Proposition 4.2] that a coherent ring is self-FP-injective if and only if each injective module is flat. He also established that a self-FP-injective coherent ring which is perfect is a quasi Frobenuis ring [33, Theorem 4.4]. According to [10], Ding and Mao studied the FP-projective dimension of a module and the FP-projective dimension of a ring. An R-module M is said to be FP-projective if ${\text {Ext}}_R^1(M,N)=0$ for any FP-injective module N. The FP-projective dimension of a module M (denoted by ${\hbox {FP-pd}}_RM)$ is the least non-negative integer n such that ${\text {Ext}}_R^{n+1}(M,N)=0$ for any FP-injective module N, and set ${\hbox {FP-pd}}_RM=\infty$ if no such n exists. They also defined the FP-projective dimension of a ring R as

$$\begin{aligned} {\text {FP-gl.dim}}(R):=\sup \left\{ {\hbox {FP-pd}}_RM\mid M\text { is a finitely generated }R\hbox {-module}\right\} . \end{aligned}$$

The FP-projective dimension has a nice properties when the ring in question is a Noetherian ring. In fact, it is shown in [10, Proposition 2.6] that a ring R is Noetherian if and only if its FP-projective dimension is zero. Therefore, the FP projection dimension measures how far the ring is from being Noetherian.

1.3 Generalizations of coherent rings and modules

Among the many recent generalizations of the concept of the coherent ring in the literature, we can find them as follows. Due to Bacem and Ali [26], a $\phi$-ring R is called $\phi$-coherent if $R/{\text {Nil}}(R)$ is a coherent domain [26, Corollary 3.1]. An ideal of a ring R is said to be nonnil if $I \nsubseteq {\text {Nil}}(R)$. A $\phi$-ring R is said to be nonnil-coherent if every finitely generated nonnil ideal is finitely presented, which is equivalent to saying that R is $\phi$-coherent and (0 : r) is a finitely generated ideal of R for each $r\in R\setminus {\text {Nil}}(R)$, where $(0:r)=\{x \in R \mid rx =0\}$ [32, Proposition 1.3]. If R is a strongly $\phi$-ring and $\phi$-coherent, then R is a nonnil-coherent [26, Remark 2.1]. Recently, El Haddaoui, Kim and Mahdou extended the nonnil coherence of $\phi$-rings to modules over $\phi$-rings. If R is a $\phi$-ring and M is an R-module, then M is said to be nonnil-coherent if M is finitely generated and every finitely generated $\phi$-submodule is finitely presented [11, Definition 2.1]. It is also shown in [11, Theorem 2.1] that a $\phi$-ring R is nonnil-coherent if and only if every finitely generated $\phi$-submodule of a finitely generated free module is finitely presented.

From [32, Definition 1.7], an R-module N is said to be nonnil-FP-injective if ${\text {Ext}}_R^1(M,N)=0$ for every finitely presented $\phi$-torsion module M. By [12, Definition 3], an R-module N is said to be nonnil semi-injective or $\phi$-FP-injective if ${\text {Ext}}_R^1(R/I,N)=0$ for every finitely generated nonnil ideal I of R. It is easy to see that every nonnil-FP-injective module is nonnil semi-injective. It is shown in [12, Proposition 2.3] that the converse holds if R is nonnil-coherent.

1.4 $\phi$-Prüfer rings, $\phi$-Bézout rings, and $\phi$-von Neumann regular rings

In [4], Badawi introduced and studied a new class of $\phi$-rings which are said to be nonnil-Noetherian. A $\phi$-ring R is said to be nonnil-Noetherian if $R/{\text {Nil}}(R)$ is a Noetherian domain [4, Theorem 1.2], which is equivalent to saying that every nonnil ideal of R is finitely generated. Anderson and Badawi [3] introduced two classes of $\phi$-rings which are called $\phi$-Prüfer and $\phi$-Bézout rings. A $\phi$-ring R is said to be $\phi$-chained if $R/{\text {Nil}}(R)$ is a valuation domain [3, Theorem 2.7]. A $\phi$-ring R is said to be $\phi$-Prüfer if $R/{\text {Nil}}(R)$ is a Prüfer domain [3, Theorem 2.6]. Every $\phi$-chained ring is $\phi$-Prüfer [3, Corollary 2.8]. A $\phi$-ring R is $\phi$-Prüfer if and only if $R_\mathfrak {p}$ is $\phi$-chained for every prime ideal $\mathfrak {p}$ of R, if and only if $R_\mathfrak {m}$ is $\phi$-chained for every maximal ideal $\mathfrak {m}$ of R [3, Theorem 2.9]. All $\phi$-Prüfer rings are Prüfer [3, Theorem 2.14], and if in addition $Z(R)={\text {Nil}}(R)$, then all Prüfer rings are $\phi$-Prüfer [3, Theorem 2.16]. A $\phi$-ring R is said to be $\phi$-Bézout if $R/{\text {Nil}}(R)$ is a Bézout domain [3, Theorem 3.3]. In [35], Tang, Wang and Zhao introduced the class of $\phi$-rings which are called $\phi$-von Neumann regular rings. An R-module M is said to be $\phi$ -flat if for every R-monomorphism $f: A \rightarrow B$ with ${\text {Coker}}(f)$ $\phi$-torsion, $f \otimes 1: A \otimes _{R} M \rightarrow B \otimes _{R} M$ is also monomorphism [35, Definition 3.1]. A $\phi$-ring R is said to be a $\phi$-von Neumann regular ring if its Krull dimension is 0, which equivalent to saying that every R-module is $\phi$-flat.

1.5 $\phi$-(weak) global dimension of a ring

El Haddaoui and Mahdou [14] introduced and defined the $\phi$-(weak) global dimension of rings with prime nilradical. An R-module P is said to be u-$\phi$-projective if ${\text {Ext}}_R^1(P,N)=0$ for each u-$\phi$-torsion R-module N [14, Definition 3.1]. The $\phi$-projective dimension of M over R, denoted by $\phi$-${\text {pd}}_{R} M$, is said to have at most $n\ge 1$ (where $n\in \mathbb {N})$ if either $M=0$ or $M\ne 0$ which is not u-$\phi$-projective and which satisfies ${\text {Ext}}_R^{n+1}(M,N)=0$ for every u-$\phi$-torsion module N. If n is the least non-negative integer for which ${\text {Ext}}_R^{n+1}(M,N)=0$ for every u-$\phi$-torsion module N, then we set $\phi$-${\text {pd}}_RM=n$. If no such n exists, set $\phi$-${\text {pd}}_{R} M=\infty$. An R-module E is said to be nonnil-injective if ${\text {Ext}}_R^1(R/I,E)=0$ for all nonnil ideals of R [40]. The $\phi$-injective dimension of M over R, denoted by $\phi$-${\text {id}}_{R} M$, is said to have at most $n\ge 1$ (where $n\in \mathbb {N})$ if either $M=0$ or $M\ne 0$ which is not nonnil-injective and which satisfies ${\text {Ext}}_R^{n+1}(R/I,M)=0$ for every nonnil ideal I of R. If n is the least non-negative integer for which ${\text {Ext}}_R^{n+1}(R/I,M)=0$ for every nonnil ideal I of R, then we set $\phi$-${\text {id}}_RM=n$. If no such n exists, set $\phi$-${\text {id}}_{R} M=\infty$. For a ring R, we define the $\phi$-global dimension of a ring as the supremum of $\phi$-${\text {pd}}_{R} (R/I)$, where I is a nonnil ideal of R such that R/I is not u-$\phi$-projective; if no such nonnil ideal exists, then the $\phi$-global dimension of R is zero. If R is a ring of $Z(R)={\text {Nil}}(R)$, then its $\phi$-global dimension is the supremum of $\phi$-${\text {pd}}_R(R/I)$, where I is a nonnil ideal of R or as the supremum of $\phi$-${\text {id}}_{R}N$, where N is a u-$\phi$-torsion R-module. Similarly, the $\phi$-flat dimension of M over R, denoted by $\phi$-${\text {fd}}_{R} M$, is said to have at most $n\ge 1$ (where $n\in \mathbb {N})$ if either $M=0$ or $M\ne 0$ which is not $\phi$-flat and which satisfies ${\text {Tor}}_{n+1}^R(M,N)=0$ for every u-$\phi$-torsion module N. If n is the least non-negative integer for which ${\text {Tor}}_{n+1}^R(M,N)=0$ for every u-$\phi$-torsion module N, then we set $\phi$-${\text {fd}}_RM=n$. If no such n exists, set $\phi$-${\text {fd}}_{R} M=\infty$. Let R be a ring of $Z(R)={\text {Nil}}(R)$. Define

$$\begin{aligned} \begin{aligned} \phi {\text {-w.gl.dim}}(R)&=\sup \left\{ \phi {\text {-fd}}_{R} M \mid M \ is \ \phi {\text {-torsion}}\right\} \\&=\sup \left\{ \phi {\text {-fd}}_{R} R/I \mid I ~\text{ is } \text{ a } \text{ finitely } \text{ generated } \text{ nonnil } \text{ ideal } \text{ of }~ R\right\} , \end{aligned} \end{aligned}$$

which is called the $\phi$-weak global dimension of R [14, Definition 5.7]. More generally, the $\phi$-weak global dimension of a ring R as the supremum of $\phi$-${\text {fd}}_{R}(R/I)$, where I is a nonnil ideal of R such that R/I is not $\phi$-flat; if no such nonnil ideal exists, then the $\phi$-weak global dimension of R equals to zero. More precisely, the $\phi$-weak global dimension of a ring R is either zero (i.e., if never nonnil ideal is proper) or the least non-negative integer n for which ${\text {Tor}}_{n+1}^R(R/I,N)=0$ for every nonnil ideal I of R such that R/I is not $\phi$-flat and every u-$\phi$-torsion module N.

1.6 Amalgamated duplication

To provide examples, we will use the amalgamated duplication of a ring R along an R-submodule E of the total ring of quotients T(R), introduced by D’Anna and Fontana and denoted by $R \bowtie E$ (see [9]), is the following sub-ring of $R \times T(R)$ (endowed with the usual component-wise operations):

$$\begin{aligned} R \bowtie E:= \{(r, r + e) \mid r \in R~ \text{ and }~ e \in E\}. \end{aligned}$$

1.7 Summary of results

This paper consists of five sections including an introduction.

In Sect. 1, we extend the FP-injective dimension (studied in [33]) to the rings with prime nilradical. We define the nonnil-FP-injective dimension of an R-module N and the nonnil-FP-injective dimension of a ring R, denoted by ${\hbox {NFP-id}}_R N$ and ${\hbox {NFP-i.gl.dim}}(R)$, respectively. Next, in Theorem 1.5, we characterize the strongly $\phi$-rings R of ${\hbox {NFP-i.gl.dim}}(R)\le 1$. Then it is shown in Corollary 1.6 that over a nonnil-coherent strongly $\phi$-ring R, ${\hbox {NFP-i.gl.dim}}(R)$ is the supremum of the $\phi$-projective dimension of certain families.

In Sect. 2, we define the self-nonnil-injective rings as $\phi$-rings which are nonnil semi-injective modules over themselves. We establish in Theorem 2.7 that a strongly $\phi$-ring R is a $\phi$-von Neumann regular ring if and only if R is nonnil-coherent and self-nonnil semi-injective.

In Sect. 3, we generalize the notion of semihereditary rings to the class of $\phi$-rings, in particular, to $\overline{\mathcal {H}}$. A ring R is said to be nonnil-semihereditary if every finitely generated nonnil ideal of R is u-$\phi$-projective. Then several characterizations of nonnil-semihereditary rings are given in terms of various notions. Next, we study the transfer of being nonnil-semihereditary in the trivial ring extensions. Finally, we end this section by providing an example of a $\phi$-Prüfer ring that is not nonnil-semihereditary.

In Sect. 4, we define the nonnil-FP-projective dimension of an R-module N and the nonnil-FP-projective dimension of a ring R (denoted by ${\hbox {NFP-pd}}_RN$ and ${\hbox {NFP-p.gl.dim}}(R)$, respectively). We next establish in Theorem 4.4 that for any strongly $\phi$-ring R: ${\hbox {NFP-p.gl.dim}}(R)=0$ if and only if R is nonnil-Noetherian, and we will show in Corollary 4.2 that for a strongly $\phi$-ring R, ${\hbox {NFP-p.gl.dim}}(R)$ is the supremum of the NFP-projective dimensions of various family of R-modules.

For any undefined terminology and notation the reader is referred to [7, 17, 18, 23, 34, 36].

2 Nonnil-FP-injective dimension

We start this section by recalling the definition of the nonnil-FP-injective module.

Definition 1.1

[32, Definition 1.7] An R-module N is said to be a nonnil-FP-injective module if ${\text {Ext}}_R^1(M,N)=0$ for every finitely presented $\phi$-torsion R-module M.

Proposition 1.1

Let R be a ring. Then every nonnil-FP-injective module is divisible.

Proof

The proof of this proposition is similar to that of [14, Theorem 2.8]. $\square$

Recall from [13] that an exact sequence $0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ is said to be nonnil-pure if for every finitely presented $\phi$-torsion module F, we obtain the following exact sequence $0\rightarrow F\otimes _RA\rightarrow F\otimes _RB\rightarrow F\otimes _RC\rightarrow 0$. In particular, every pure exact sequence is nonnil-pure. A submodule A of B is said to be nonnil-pure if the exact sequence $0\rightarrow A\rightarrow B\rightarrow B/A\rightarrow 0$ is nonnil-pure.

The concept of nonnil-FP-injectivity is closely related to that of nonnil-pure exact sequences.

Theorem 1.2

[13, Theorem 2.27] The following are equivalent for an R-module M.

• (1) M is nonnil-FP-injective.

• (2) If G is a finitely generated $\phi$-submodule of a finitely generated free module F, then every homomorphism $G \rightarrow M$ can be extended to $F \rightarrow M$.

• (3) Every exact sequence $0 \rightarrow M \rightarrow M^{\prime } \rightarrow M^{\prime \prime } \rightarrow 0$ is nonnil-pure.

• (4) There exists a nonnil-pure exact sequence $0 \rightarrow M \rightarrow M^{\prime } \rightarrow M^{\prime \prime } \rightarrow 0$ with $M^{\prime }$ nonnil-FP-injective.

• (5) Given any diagram of R-modules and homomorphisms

  

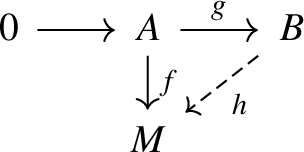
  with the above row exact and ${\text {Coker}}(g)$ a finitely presented $\phi$-torsion module, there is a homomorphism $h: B \rightarrow M$ making this diagram commute (i.e., $hg=f$).

• (6) Every exact sequence $0 \rightarrow M {\mathop {\rightarrow }\limits ^{f}}B \rightarrow C \rightarrow 0$ is split for any finitely presented $\phi$-torsion R-module C.

• (7) If $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$ is an exact sequence such that C is finitely presented $\phi$-torsion, then the sequence

  $$\begin{aligned} 0 \rightarrow {\text {Hom}}_{R}(C, M) \rightarrow {\text {Hom}}_{R}(B, M) \rightarrow {\text {Hom}}_{R}(A, M) \rightarrow 0 \end{aligned}$$

  is also exact.

Definition 1.2

Let M be an R-module. Then the nonnil-FP-injective dimension of M, denoted ${\hbox {NFP-id}}_R M$, is said to have at most $n\in \mathbb {N^*}$, if either $M=0$ or $M\ne 0$ which is not nonnil-FP-injective and which satisfies ${\text {Ext}}_R^{n+1}(F,M)=0$ for every finitely presented $\phi$-torsion R-module F. If n is the least non-negative integer for which ${\text {Ext}}_R^{n+1}(F,M)=0$ for every finitely presented $\phi$-torsion R-module F, then ${\hbox {NFP-id}}_RM=n$; if no such integer exists, then ${\hbox {NFP-id}}_R M=\infty$. For a ring R, we set its global nonnil-FP-injective dimension (${\hbox {NFP-p.gl.dim}}(R)$ for short) as follows:

$$\begin{aligned} {\hbox {NFP-p.gl.dim}}(R)=\sup \left\{ {\hbox {NFP-id}}_RN\mid N\text { is a u-}\phi \hbox {-torsion module}\right\} . \end{aligned}$$

Remark 1.1

(1) Let M be an R-module. It is easy to establish that M is a nonnil-FP-injective module if and only if ${\hbox {NFP-id}}_RM=0$.

(2) By Definition 1.2, the global nonnil-FP-injective dimension of a ring R is either zero (i.e., every finitely presented u-$\phi$-torsion module is nonnil-FP-injective) or the supremum of all ${\hbox {NFP-id}}_R N$, where N is a nonzero u-$\phi$-torsion and not a nonnil-FP-injective module.

(3) If R is a ring such that ${\text {Nil}}(R)=Z(R)$, then for every R-module N, we get ${\hbox {NFP-id}}_RN \le n$ if and only if ${\text {Ext}}_R^{n+1}(F,N)=0$ for every finitely presented $\phi$-torsion R-module F. In fact, if $N=0$, then the above equivalence holds. If $N\ne 0$, then N can not be nonnil-FP-injective. Deny, $N=0$ by Proposition 1.1 above, a desired contradiction. Therefore, the above equivalence holds by Definition 1.2.

Note that if an R-module M is u-$\phi$-torsion, then so is $M^+:={\text {Hom}}_\mathbb {Z}(M,\mathbb {Q}/\mathbb {Z})$ [14, Corollary 3.2].

Theorem 1.3

Let R be a ring of $Z(R)={\text {Nil}}(R)$ and $\mathfrak {F}$ denote the set of all finitely presented $\phi$-torsion R-modules. Then

$$\begin{aligned} \phi \text {-}{\text {w.gl.dim}}(R)\le {\hbox {NFP-i.gl.dim}}(R)\le \sup _{F\in \mathfrak {F}}\phi \text {-}{\text {pd}}_R F. \end{aligned}$$

In particular, R is a $\phi$-von Neumann regular ring if and only if ${\hbox {NFP-i.gl.dim}}(R)=0$.

Proof

Set $n:=\sup _{F\in \mathfrak {F}}\phi \text {-}{\text {pd}}_R F$. We claim that ${\hbox {NFP-i.gl.dim}}(R)\le n$. Let N be a u-$\phi$-torsion module and let $F\in \mathfrak {F}$. Then $\phi$-${\text {pd}}_RF\le n$, and so ${\text {Ext}}_R^{n+1}(F,N)=0$. Thus NFP-${\text {id}}_RN\le n$, and so ${\hbox {NFP-i.gl.dim}}(R)\le \sup _{F\in \mathfrak {F}}\phi \text {-}{\text {pd}}_R F$. Now, set $p:={\hbox {NFP-i.gl.dim}}(R)$ and we claim that $\phi \text {-}{\text {w.gl.dim}}(R)\le p$. Let $F\in \mathfrak {F}$ and N be a u-$\phi$-torsion module. Then $N^+$ is a u-$\phi$-torsion module. Thus ${\text {Tor}}_{p+1}^R(F,N)^+ \cong {\text {Ext}}_R^{p+1}(F,N^+) =0$ since ${\hbox {NFP-i.gl.dim}}(R)=p$. Consequently ${\text {Tor}}_{p+1}^R(F,N)=0$, and so $\phi \text {-}{\text {w.gl.dim}}(R)\le p$. $\square$

Theorem 1.4

Let R be a ring and M be a nonzero and non-nonnil-FP-injective module. Then the following assertions are equivalent:

• (1) ${\hbox {NFP-id}}_RM\leqslant n$.

• (2) ${\text {Ext}}_R^{n+1}(F, M)=0$ for any finitely presented $\phi$-torsion module F.

• (3) If the sequence $0 \rightarrow M \rightarrow E_{0} \rightarrow \cdots \rightarrow E_{n} \rightarrow 0$ is exact with $E_{0}, \ldots , E_{n-1}$ injective, then $E_{n}$ is nonnil-FP-injective.

  If R is a nonnil-coherent ring, then the above statements are equivalent to:

• (4) ${\text {Ext}}_R^{n+1}(R / I, M)=0$ for any finitely generated nonnil ideal I of R,

Proof

$(1)\Leftrightarrow (2)$ This follows immediately from Definition 1.2.

$(2)\Leftrightarrow (3)$ This follows from the isomorphism ${\text {Ext}}_R^{n+1}(F,M)\cong {\text {Ext}}_R^1(F,E_n)$.

Assume that R is nonnil-coherent. Then:

$(2)\Rightarrow (4)$ This is straightforward.

$(4)\Rightarrow (2)$ We use induction on the number of generators of F. Assume that F is finitely presented $\phi$-torsion by m generators and let $F^{\prime }$ be the submodule generated by one of these generators. Since R is nonnil-coherent, both $F^{\prime }$ and $F / F^{\prime }$ are finitely presented $\phi$-torsion by less than m generators. So we obtain an exact sequence ${\text {Ext}}_R^{n+1}\left( F / F^{\prime }, M\right) \rightarrow {\text {Ext}}_R^{n+1}(F, M) \rightarrow {\text {Ext}}_R^{n+1}\left( F^{\prime }, M\right) ,$ where both end terms are zero by induction. Hence ${\text {Ext}}_R^{n+1}(F,M)=0$. $\square$

Definition 1.3

[12, Definition 3] Let R be a ring and M be an R-module. Then M is said to be nonnil semi-injective or $\phi$-FP-injective if ${\text {Ext}}_R^1(R/I,M)=0$ for any finitely generated nonnil ideal I of R.

Remark 1.2

It is easy to see that every nonnil-FP-injective module is nonnil semi-injective. It is shown in [12, Proposition 2.3] that over any nonnil-coherent ring R, an R-module is nonnil-FP-injective if and only if it is nonnil semi-injective.

Recall that an R-module is said to be n-presented if M has an n-presentation (that is an exact sequence $F_n\rightarrow F_{n-1}\rightarrow \cdots \rightarrow F_{0}\rightarrow M\rightarrow 0$, where each $F_i$ is a finitely generated free R-module). In addition, if M is a $\phi$-torsion R-module, then M is said to be $\phi$-n-presented and the above exact sequence is called a $\phi$-n-presentation of M.

Definition 1.4

[12, Definition 2] Let R be a ring and $n,d\in \mathbb {N}$. An R-module N is said to be $\phi$-(n, d)-injective or nonnil (n, d)-injective if ${\text {Ext}}_R^{d+1}(R/I,N)=0$ for any nonnil ideal I such that R/I is a $\phi$-n-presented R-module.

The following theorem characterizes the nonnil-coherent ring R with nonnil-FP-injective dimension at most $n\in \mathbb {N}$.

Theorem 1.5

The following are equivalent for a nonnil-coherent strongly $\phi$-ring R.

• (1) ${\hbox {NFP-i.gl.dim}}(R)\le n$.

• (2) ${\hbox {NFP-id}}_RN\le n$ for any u-$\phi$-torsion R-module N.

• (3) $\phi$-${\text {pd}}_RF\le n$ for any finitely presented $\phi$-torsion R-module F.

• (4) $\phi$-${\text {pd}}_R R/I\le n$ for any finitely generated nonnil ideal I of R.

• (5) Every u-$\phi$-torsion module is $\phi$-(1, n)-injective.

Proof

$(1)\Leftrightarrow (2)$ This follows immediately from Definition 1.2.

$(2)\Rightarrow (3)$ Let F be a finitely presented $\phi$-torsion R-module. Then for every u-$\phi$-torsion module N we have ${\text {Ext}}_R^{n+1}(F,N)=0$, which implies that $\phi$-${\text {pd}}_RF\le n$.

$(3)\Rightarrow (4)$ This is straightforward.

$(4)\Rightarrow (2)$ This is similar to the proof of $(4)\Rightarrow (2)$ in Theorem 1.4.

$(4)\Leftrightarrow (5)$ This is obvious. $\square$

Corollary 1.6

Let R be a nonnil-coherent strongly $\phi$-ring R. Then:

$$\begin{aligned} \begin{aligned} {\hbox {NFP-i.gl.dim}}(R)&:=\sup \left\{ \phi \text {-}{\text {pd}}_RF\mid \ F~ \text {is finitely presented }\phi \hbox {-torsion}\right\} \\&=\sup \left\{ \phi \text {-}{\text {pd}}_R R/I\mid \ I~ \text {is a finitely generated nonnil ideal}\right\} \end{aligned} \end{aligned}$$

Proof

This follows immediately from Theorem 1.5. $\square$

3 Nonnil-self injective rings and nonnil semi-injective modules

We start the section by the following definition.

Definition 2.1

Let R be a ring and consider the following exact sequence of R-modules:

$$\begin{aligned} 0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0. \end{aligned}$$

(1)

The sequence (1) is said to be $\phi$-strongly pure exact if for every finitely generated nonnil ideal I of R, we get the following exact sequence $0\rightarrow {\text {Hom}}_R(R/I,A)\rightarrow {\text {Hom}}_R(R/I,B)\rightarrow {\text {Hom}}_R(R/I,C)\rightarrow 0$. In particular, every nonnil-pure exact sequence is $\phi$-strongly pure. A submodule A of B is said to be $\phi$-strongly pure if the exact sequence $0\rightarrow A\rightarrow B\rightarrow B/A\rightarrow 0$ is $\phi$-strongly pure. In particular, every nonnil-pure submodule is a $\phi$-strongly pure submodule.

The following is our first characterization of nonnil semi-injectivity of modules.

Theorem 2.1

The following are equivalent for an R-module M.

• (1) M is nonnil semi-injective,

• (2) If I is a finitely generated nonnil ideal of R, then every homomorphism $I \rightarrow M$ can be extended to $R \rightarrow M$.

• (3) Every exact sequence $0 \rightarrow M \rightarrow M^{\prime } \rightarrow M^{\prime \prime } \rightarrow 0$ is $\phi$-strongly pure.

• (4) There exists a $\phi$-strongly pure exact sequence $0 \rightarrow M \rightarrow M^{\prime } \rightarrow M^{\prime \prime } \rightarrow 0$ with $M^{\prime }$ nonnil semi-injective.

Proof

The proof is similar of that of [13, Theorem 2.27]. $\square$

Remark 2.1

Following the work of [31], we establish by similar way that the self-nonnil-semi-injectivity of R-modules is a hereditary property if we assume that $Z(R)={\text {Nil}}(R)$.

Definition 2.2

A $\phi$-ring R is said to be nonnil-self-injective if R is a nonnil-injective module over itself.

Recall from [31] that if R is a strongly $\phi$-ring, then the nonnil-injectivity is a hereditary property. The following theorem establishes that the $\phi$-von Neumann regular rings and the nonnil-self-injective rings are the same.

Theorem 2.2

Let $R\in \mathcal {H}$ and set $\overline{R}:=R/{\text {Nil}}(R)$. Then the following conditions are equivalent:

• (1) R is a $\phi$-von Neumann regular ring.

• (2) R is a nonnil-self-injective strongly $\phi$-ring R.

• (3) ${\text {Nil}}(R)$ and $R/{\text {Nil}}(R)$ are nonnil-injective R-modules.

• (4) ${\text {Nil}}(R)$ is a nonnil-injective ideal of R and $R/{\text {Nil}}(R)$ is a self-injective ring.

• (5) $R/{\text {Nil}}(R)$ is a self-injective ring.

• (6) Every u-$\phi$-torsion R-module M is $\overline{R}$-flat.

• (7) ${\text {Tor}}_1^{\overline{R}}(M,X)\cong {\text {Nil}}(R){\text {Tor}}_1^{\overline{R}}(M,X)$ for every u-$\phi$-torsion R-module M and every $\overline{R}$-module X.

• (8) ${\text {Tor}}_1^{\overline{R}}(M,X)\cong {\text {Nil}}(R){\text {Tor}}_1^{\overline{R}}(M,X)$ for every u-$\phi$-torsion R-module M and every finitely generated $\overline{R}$-module X.

• (9) ${\text {Tor}}_1^{\overline{R}}(M,X)\cong {\text {Nil}}(R){\text {Tor}}_1^{\overline{R}}(M,X)$ for every u-$\phi$-torsion R-module M and every finitely presented $\overline{R}$-module X.

• (10) ${\text {Tor}}_1^{\overline{R}}(M,R/I)\cong {\text {Nil}}(R){\text {Tor}}_1^{\overline{R}}(M,R/I)$ for every u-$\phi$-torsion R-module M and every nonnil ideal I of R.

• (11) ${\text {Tor}}_1^{\overline{R}}(M,R/I)\cong {\text {Nil}}(R){\text {Tor}}_1^{\overline{R}}(M,R/I)$ for every u-$\phi$-torsion R-module M and every finitely generated nonnil ideal I of R.

• (12) Every u-$\phi$-torsion R-module is an injective $\overline{R}$-module.

• (13) R is a total quotient ring such that $Z(R)={\text {Nil}}(R)$.

To prove Theorem 2.2, we need the following lemmas.

Lemma 2.3

If $R\in \mathcal {H}$, then $R/{\text {Nil}}(R)$ is a u-$\phi$-projective R-module.

Proof

Assuming that $R\in \mathcal {H}$, we claim that ${\text {Ext}}_R^1(R/{\text {Nil}}(R),X)=0$ for any u-$\phi$-torsion R-module X. Let X be a u-$\phi$-torsion R-module. We first establish that ${\text {Hom}}_R({\text {Nil}}(R),X)=0$. Let $\gamma \in {\text {Hom}}_R({\text {Nil}}(R),X)$. Since X is a u-$\phi$-torsion R-module, $sX=0$ for some $s\in R{\setminus } {\text {Nil}}(R)$. Since $R\in \mathcal {H}$, it follows that ${\text {Nil}}(R)$ is a $\phi$-divisible R-module, and so ${\text {Nil}}(R)=s{\text {Nil}}(R)$. Then for every $n\in {\text {Nil}}(R)$, we can write $n=sn'$ for some $n'\in {\text {Nil}}(R)$ and so, $\gamma (n)=s\gamma (n')\in sM=0$. It follows that ${\text {Hom}}_R({\text {Nil}}(R),X)=0$. But from the short exact sequence $0\rightarrow {\text {Nil}}(R)\rightarrow R\rightarrow R/{\text {Nil}}(R)\rightarrow 0$, we get $0={\text {Hom}}_R({\text {Nil}}(R),X)\rightarrow {\text {Ext}}_R^1(R/{\text {Nil}}(R),X)\rightarrow 0$. Therefore, $R/{\text {Nil}}(R)$ is a u-$\phi$-projective R-module. $\square$

Lemma 2.4

Let R and T be rings, M be an R-T-bi-module, A be a u-$\phi$-torsion R-module and X be a u-$\phi$-torsion T-module. If M is both a $\phi$-flat R-module and a u-$\phi$-projective T-module, then

$$\begin{aligned} {\text {Ext}}_T^1(A\otimes _RM,X)\cong {\text {Ext}}_R^1(A,{\text {Hom}}_T(M,X)). \end{aligned}$$

Proof

Let $0\rightarrow X\rightarrow E\rightarrow G\rightarrow 0$ be an exact sequence of T-modules, where E is an injective T-module. Since M is a u-$\phi$-projective T-module, we get the following short exact sequence $0\rightarrow {\text {Hom}}_T(M,X)\rightarrow {\text {Hom}}_T(M,E)\rightarrow {\text {Hom}}_T(M,G)\rightarrow 0$. But [14, Theorem 5.8] implies that ${\text {Hom}}_{T}(M,E)$ is a nonnil-injective R-module. So we get the exact sequence ${\text {Hom}}_{R}(A,{\text {Hom}}_{T}(M,E))\rightarrow {\text {Hom}}_{R}(A,{\text {Hom}}_{T}(M,G))\rightarrow {\text {Ext}}_{R}^1(A,{\text {Hom}}_{T}(M,X))\rightarrow 0$. By [36, Theorem 2.2.16 (Adjoint Isomorphism Theorem)], we get the following commutative diagram with exact rows

Therefore, we get the desired isomorphism ${\text {Ext}}_T^1(A\otimes _RM,X)\cong {\text {Ext}}_R^1(A,{\text {Hom}}_T(M,X)).$

$\square$

Lemma 2.5

Let R be a $\phi$-ring. Then we get the following isomorphism

$$\begin{aligned} {\text {Ext}}_R^1(A,X)\cong {\text {Ext}}_{\overline{R}}^1(A,X) \end{aligned}$$

for every u-$\phi$-torsion $\overline{R}$-module X and every u-$\phi$-torsion R-module A. In particular, a u-$\phi$-torsion R-module X is a nonnil-injective R-module if and only if X is an injective $\overline{R}$-module.

Proof

By combining Lemmas 2.3 and 2.4 and by setting $\overline{R}=M$, we get the following isomorphism ${\text {Ext}}_R^1(A,X)\cong {\text {Ext}}_{\overline{R}}^1(A,X)$ for every u-$\phi$-torsion $\overline{R}$-module X and every u-$\phi$-torsion R-module A, since $A\otimes _RM\cong A$. Now, assume that X is a u-$\phi$-torsion R-module. Then it is easy to see that M is a u-$\phi$-torsion $\overline{R}$-module, and so for every nonnil ideal I of R (setting $\overline{I}:=I/{\text {Nil}}(R)$), we have

$$\begin{aligned} \begin{aligned} X \text { is a nonnil-injective } R\text {-module}&\Longleftrightarrow {\text {Ext}}_R^1(R/I,X)=0\\&\Longleftrightarrow {\text {Ext}}_{\overline{R}}^1(R/I,X)=0\\&\Longleftrightarrow {\text {Ext}}_{\overline{R}}^1(\overline{R}/\overline{I},X)=0\\&\Longleftrightarrow X \text { is an injective } \overline{R}\text {-module}. \end{aligned} \end{aligned}$$

$\square$

Proof of Theorem 2.2

$(1)\Rightarrow (2)$ This follows from [14, Corollary 5.34].

$(2)\Rightarrow (3)$ Assume that R is a nonnil-self-injective strongly $\phi$-ring. Then ${\text {Nil}}(R)$ is a nonnil-injective ideal. In fact, it is easy to see that $R/{\text {Nil}}(R)$ is a $\phi$-torsion free R-module, and so for any nonnil ideal I of R, we get ${\text {Hom}}_R(R/I,R/{\text {Nil}}(R))=0$ by [35, Theorem 2.3]. Using the sequence $0\rightarrow {\text {Nil}}(R)\rightarrow R\rightarrow R/{\text {Nil}}(R)\rightarrow 0$, we get ${\text {Ext}}_R^1(R/I,{\text {Nil}}(R))=0$ since R is nonnil-self-injective. Thus ${\text {Nil}}(R)$ is a nonnil-injective ideal. Since ${\text {Ext}}_R^1(R/I,R/{\text {Nil}}(R))\cong {\text {Ext}}_R^2(R/I,{\text {Nil}}(R))$, it follows that ${\text {Ext}}_R^1(R/I,R/{\text {Nil}}(R))=0$, and so $R/{\text {Nil}}(R)$ is a nonnil-injective R-module.

$(3)\Leftrightarrow (4)$ This follows from [38, Proposition 1.4].

$(4)\Rightarrow (1)$ Let $s\in R \setminus {\text {Nil}}(R)$. Since $R/{\text {Nil}}(R)$ is a nonnil-injective R-module, it is divisible R-module by [14, Theorem 2.8]. So there exists $r\in R$ such that $1+{\text {Nil}}(R)=sr+{\text {Nil}}(R)$, and hence $sr\in 1+{\text {Nil}}(R)\subseteq U(R)$, the set of units of R. Thus $R{\setminus } {\text {Nil}}(R)\subseteq U(R)$. Therefore, R is a local $\phi$-ring with maximal ideal ${\text {Nil}}(R)$. Hence R is a $\phi$-von Neumann regular ring by [14, Theorem 5.14].

$(5)\Leftrightarrow (1)$ This follows immediately from [14, Corollary 5.15] and [35, Theorem 4.1] since $R/{\text {Nil}}(R)$ is a field because it is both an integral domain and a self-injective ring.

$(6)\Rightarrow (7)\Rightarrow (8)\Rightarrow (10)\Rightarrow (11)$ & $(8)\Rightarrow (9)\Rightarrow (11)$ These are obvious.

$(11)\Rightarrow (6)$ Since $R\in \mathcal {H}$, it follows that ${\text {Nil}}(R)$ is a $\phi$-divisible ideal of R, and so M can be considered as an $\overline{R}$-module. In addition, we have the natural isomorphism $\overline{R}\otimes M\cong M$. If I is an ideal of R containing ${\text {Nil}}(R)$, then we set $\overline{I}:=I/{\text {Nil}}(R)$, so $\overline{R}/\overline{I}\cong R/I$. Following [14, Theorem 5.9], by setting $A=T=\overline{R}$ and $X=R/I$ where I is a finitely generated nonnil ideal of R, we get the following isomorphism ${\text {Tor}}_1^{\overline{R}}(\overline{R}\otimes _R M,R/I)\cong {\text {Tor}}_1^{\overline{R}}(M,R/I)\cong \overline{R}\otimes _R {\text {Tor}}_1^{\overline{R}}(M,R/I)=0$. That is equivalent to ${\text {Tor}}_1^{\overline{R}}(M,R/I)\cong {\text {Nil}}(R){\text {Tor}}_1^{\overline{R}}(M,R/I)$.

$(1)\Rightarrow (12)$ If R is a $\phi$-von Neumann regular ring, then $\overline{R}$ is a field by [35, Theorem 4.1], and so every u-$\phi$-torsion R-module is an injective $\overline{R}$-module.

$(12)\Rightarrow (1)$ Let M be a u-$\phi$-torsion R-module and I be a nonnil ideal of R. Then ${\text {Ext}}_R^1(R/I,M)=0$ by Lemma 2.5 above. It follows that R/I is a u-$\phi$-projective R-module, i.e., $\phi$-${\text {gl.dim}}(R)=0$, and so R is a $\phi$-von Neumann regular ring by [14, Theorem 5.29 & Corollary 5.33].

$(6)\Rightarrow (1)$ Let I be a nonnil ideal of R. Then $\overline{R}/\overline{I}$ is a flat $\overline{R}$-module, and so ${\text {w.gl.dim}}(\overline{R})=0$. It follows that $\overline{R}$ is a semisimple domain, i.e., $\overline{R}$ is a field. Therefore, R is a $\phi$-von Neumann regular ring by [35, Theorem 4.1].

$(1)\Rightarrow (6)$ This is straightforward since every u-$\phi$-torsion R-module over a $\phi$-von Neumann regular ring is zero.

$(1)\Leftrightarrow (13)$ This follows immediately from [14, Theorem 5.14 & Corollary 5.15]. $\square$

Corollary 2.6

If $(R,{\text {Nil}}(R))$ is a non-reduced local $\phi$-ring, then $R\bowtie {\text {Nil}}(R)$ is a nonnil-self injective ring that is not self-injective.

Proof

From [8, Corollary 2.5], it is clear that $R\bowtie {\text {Nil}}(R)$ is never a nonnil-self-injective ring since ${\text {Nil}}(R)$ is not generated by an idempotent element. It is easy to establish that $\frac{R\bowtie {\text {Nil}}(R)}{{\text {Nil}}(R\bowtie {\text {Nil}}(R))}\cong \frac{R\bowtie {\text {Nil}}(R)}{{\text {Nil}}(R)\bowtie {\text {Nil}}(R)}\cong \frac{R}{{\text {Nil}}(R)}$, which is a $\phi$-von Neumann regular ring by [14, Theorem 5.14]. Hence R is a nonnil-self-injective ring by Theorem 2.2. $\square$

Definition 2.3

A ring R is said to be self-nonnil semi-injective if R is a nonnil semi-injective module over itself.

Next, the following theorem characterizes the $\phi$-von Neumann regular rings.

Theorem 2.7

The following are equivalent for a nonnil-coherent ring R.

• (1) R is a $\phi$-von Neumann regular ring.

• (2) R is self-nonnil semi-injective strongly $\phi$-ring.

• (3) Every nonnil semi-injective module is $\phi$-flat.

• (4) Every injective module is $\phi$-flat.

• (5) Every R-module can be embedded in a $\phi$-flat module.

• (6) An R-module is $\phi$-flat if and only if it is nonnil semi-injective.

Before proving Theorem 2.7, we establish the following lemma, which is an analog of [33, Lemma 4.1].

Lemma 2.8

Let R be a self-nonnil semi-injective and nonnil-coherent strongly $\phi$-ring. Then every $\phi$-flat module is nonnil semi-injective.

Proof

Let M be a $\phi$-flat module and consider an exact sequence $0\rightarrow K\rightarrow F\rightarrow M\rightarrow 0$, where F is free. Then F is a nonnil semi-injective module. Indeed, let I be a finitely generated nonnil ideal of R and set $F\cong \bigoplus _J R$ for some index set J. Using [36, Theorem 3.9.2 (1)], we get ${\text {Ext}}_R^1(R/I,F)\cong \bigoplus _J{\text {Ext}}_R^1(R/I,R)$, and so ${\text {Ext}}_R^1(R/I,F)=0$ since R is assumed to be self-nonnil semi-injective. Thus F is nonnil semi-injective. Since M is $\phi$-flat, the sequence $0\rightarrow K\rightarrow F\rightarrow M\rightarrow 0$ is $\phi$-strongly pure, and so K is nonnil semi-injective by Theorem 2.1. Then for any finitely generated nonnil ideal I of R, we get the following exact sequence $0\rightarrow {\text {Ext}}_R^1(R/I,M)\rightarrow {\text {Ext}}_R^2(R/I,K)=0$. Hence ${\text {Ext}}_R^1(R/I,M)=0$ by Remark 2.1. Therefore, M is nonnil semi-injective. $\square$

Proof of Theorem 2.7

$(1)\Rightarrow (2)$ This is straightforward.

$(2)\Rightarrow (3)$ Let E be a nonnil semi-injective module. Then $E^+$ is a $\phi$-flat module by [12, Corollary 3.13], and so $E^+$ is a nonnil semi-injective module by Lemma 2.8. Therefore, by duality formula (i.e., the isomorphism ${\text {Tor}}_1^R(R/I,E)^+\cong {\text {Ext}}_R^1(R/I,E^+)$, where I is a finitely generated nonnil ideal of R), we get ${\text {Tor}}_1^R(R/I,E)=0$. Therefore, E is a $\phi$-flat module by [35, Theorem 3.2].

$(3)\Rightarrow (4)$ This is straightforward since every injective module is nonnil semi-injective.

$(4)\Rightarrow (5)$ This is clair since every R-module can be embedded in an injective module.

$(5)\Leftrightarrow (1)$ This follows from [32, Theorem 2.5].

$(1) \& (2)\Rightarrow (6)$ It is easy to see that every nonnil semi-injective module is $\phi$-flat since R is a $\phi$-von Neumann regular ring. By (2) and Lemma 2.8, every $\phi$-flat module is nonnil semi-injective.

$(6)\Rightarrow (3)$ This is obvious. $\square$

Corollary 2.9

The following are equivalent for a nonnil-coherent ring R.

• (1) R is a von Neumann regular ring,

• (2) Every nonnil-FP-injective module is $\phi$-flat.

Proof

This follows immediately from Theorem 2.7 and [12, Proposition 2.3]. $\square$

4 Nonnil-semihereditary rings

In this section, we introduce and study a new generalization of the semihereditary ring. A ring R is said to be semihereditary if every finitely generated ideal is projective. Recall from [26] that an R-module P is said to be uniformly $\phi$-projective (u-$\phi$-projective for short) if ${\text {Ext}}_R^1(P,N)=0$ for every u-$\phi$-torsion module N [14, Definition 3.1].

Definition 3.1

A ring $R\in \mathcal {H}$ is said to be nonnil-semihereditary if every finitely generated nonnil ideal of R is u-$\phi$-projective.

It is shown that in [14, Theorem 5.11] that every u-$\phi$-projective module is $\phi$-flat.

Example 3.1

It is easy to see that every $\phi$-von Neumann regular ring is nonnil-semihereditary.

The following theorem is a first characterization of nonnil-semihereditary rings.

Theorem 3.1

The following are equivalent for a ring $R\in \overline{\mathcal {H}}$.

• (1) R is nonnil-semihereditary.

• (2) R is a nonnil-coherent ring such that every finitely generated nonnil ideal of R is projective.

Before proving Theorem 3.1, we need the following lemmas:

Lemma 3.2

Let $R\in \overline{\mathcal {H}}$. If M is a finitely presented $\phi$-flat module, then M is projective.

Proof

Let M be a finitely presented $\phi$-flat module. By [35, Theorem 3.5], we can assume that R is a local $\phi$-ring with unique maximal ideal $\mathfrak {m}\ne {\text {Nil}}(R)$ (see [36, Exercise 1.35]). From [35, Theorem 3.2], we get ${\text {Tor}}_1^R(M,R/\mathfrak {m})=0$, and so M is free by [36, Theorem 3.4.12]. Therefore, M is locally free and finitely presented, i.e., a projective module. $\square$

For a ring R and an R-module M, denote by $R \propto M$ the trivial extension of R by M.

Remark 3.1

Lemma 3.2 is not true if $R\in \mathcal {H}$, i.e., if R is a local $\phi$-ring with maximal ideal ${\text {Nil}}(R)$. In fact, from [14, Example 5.4], in the ring $R=\mathbb {Z}/2\mathbb {Z}\propto \mathbb {Z}/2\mathbb {Z}$, the R-module $R/{\text {Nil}}(R)\cong \mathbb {Z}/2\mathbb {Z}$ is finitely presented $\phi$-flat, but not projective.

Lemma 3.3

Let $R\in \overline{\mathcal {H}}$ and I be a finitely generated nonnil ideal of R. Then R/I is $\phi$-flat if and only if $I=R$.

Proof

First, we establish that the $\phi$-rings are connected. In fact, if there exists a nontrivial idempotent e in a $\phi$-ring R, then $e(1-e)\in {\text {Nil}}(R)$ implies that either $e\in {\text {Nil}}(R)$ or $1-e\in {\text {Nil}}(R)$. But if $e\in {\text {Nil}}(R)$, then $e=0$, which impossible. Then $1-e\in {\text {Nil}}(R)$, and so $e\in U(R)$, which is also impossible. Then R is connected. On the other hand, we have from [14, Corollary 5.36] that R/I is a projective R-module, and so I is generated by an idempotent by [1, Exercise (10.24)]. Then R/I is $\phi$-flat if and only if $I=R$. $\square$

Proof of Theorem 3.1

$(1) \Rightarrow (2)$ Suppose R is a nonnil-semihereditary ring and let I be a finitely generated nonnil ideal of R. We may assume that I is proper. By Lemma 3.3, R/I can not be $\phi$-flat, and so $\phi$-${\text {w.gl.dim}}(R)\le 1$. Suppose on the contrary that ${\text {Nil}}(R)\subsetneq Z(R)$. Then there exists $s\in Z(R)\setminus {\text {Nil}}(R)$. But R is a $\phi$-ring, which implies that R is a connected ring, and so R/sR can not be a $\phi$-flat R-module by [14, Theorem 5.13 & Corollary 5.36]. Then $\left\langle s\right\rangle$ is a $\phi$-flat ideal. By [14, Theorem 5.4], the short exact sequence $0\rightarrow (0:s)\rightarrow R\rightarrow \left\langle s\right\rangle \rightarrow 0$ is $\phi$-pure, which implies that the R-homomorphism given by $\varphi :\ (0:s)\otimes _R\frac{R}{\left\langle s\right\rangle }\rightarrow \frac{R}{\left\langle s\right\rangle }$ is an R-monomorphism. But its kernel equals to $\frac{\left\langle s\right\rangle }{s(0:s)}$. Then $\left\langle s\right\rangle =s(0:s)$, in particular, $s=rs$ for some $r\in (0:s)$, and so $s=0$, a contradiction. Consequently, we proved that every $\phi$-ring of $\phi$-$w.gl.dim(R)\le 1$ is a strongly $\phi$-ring, i.e., $Z(R)={\text {Nil}}(R)$. Thus R is a $\phi$-Pr$\ddot{\hbox {f}}$er ring by [14, Corollary 5.23], in particular, R is a nonnil-coherent ring. Hence I is a finitely presented ideal. But I is a $\phi$-flat ideal by [14, Theorem 5.11]. Therefore, I is projective by Lemma 3.2.

$(2) \Rightarrow (1)$ This is straightforward. $\square$

Corollary 3.4

Every nonnil-semihereditary ring is a nonnil-coherent ring.

Proof

If Nil(R) is a maximal ideal, then R is a $\phi$-von Neumann regular ring by [14, Theorem 5.14], and so R is a nonnil-coherent ring. If $R\in \overline{\mathcal {H}}$, then it follows from the proof of Theorem 3.1 that R is a nonnil-coherent ring. $\square$

Corollary 3.5

The following are equivalent for a ring $R\in \mathcal {H}$.

• (1) R is nonnil-semihereditary.

• (2) R is a $\phi$-Pr$\ddot{\hbox {f}}$er strongly $\phi$-ring.

Proof

$(1)\Rightarrow (2)$ This follows immediately from the proof of Theorem 3.1.

$(2)\Rightarrow (1)$ Assume that R is a $\phi$-Pr$\ddot{\hbox {f}}$er strongly $\phi$-ring. Then R is a nonnil-coherent ring by [26, Remark 2.1]. Let I be a finitely generated nonnil ideal of R. Then I is u-$\phi$-projective by [14, Theorem 5.41]. Consequently, R is a nonnil-semihereditary ring. $\square$

The following is an analog of a well-known result for the semihereditary ring. [36, Theorem 3.7.9].

Theorem 3.6

If $R\in \overline{\mathcal {H}}$ is a nonnil-semihereditary ring, then every finitely generated $\phi$-submodule M of a free module is a direct sum of a finite number of finitely generated nonnil ideals of R.

Before proving Theorem 3.6, we need the following:

Lemma 3.7

Consider the following commutative diagram of R-modules with exact rows:

where $\beta$,$\gamma$, i and $i'$ are the natural inclusions. If B is a $\phi$-submodule of $B'$, then C is a $\phi$-submodule of $C'$ and A is a $\phi$-submodule of $A'$.

Proof

Assume that B is a $\phi$-submodule of $B'$. Then we claim that C is a $\phi$-submodule of $C'$. Let $x'\in C'$. Then $p(y')=x'$ for some $y'\in B'$. Since B is a $\phi$-submodule of $B'$, it follows that $sy'\in B$ for some $s\in R\setminus {\text {Nil}}(R)$, and so $sp(y')=sx'\in C$. Hence C is a $\phi$-submodule of $C'$. Let $x\in A'$. Then there exists $s\in R\setminus {\text {Nil}}(R)$ such that $sx\in B$. Since $i'$ is the natural inclusion, we can set $A'=\ker (p)$, and so $sx\in \ker (p)\cap B\subset A$. Hence A is a $\phi$-submodule of $A'$. $\square$

Proof of Theorem 3.6

Let M be a finitely generated $\phi$-submodule of a free module F. We can set $F:=R^{(n)}$ and let $p:F\rightarrow R$ be the n-th projection, and set $I:=p(M)$. Then we get the following commutative diagram of exact rows:

By Lemma 3.7, we get that I is a $\phi$-submodule of R, that is, a nonnil ideal of R. Thus I is projective by Theorem 3.1. Hence $M\cong N\oplus I$. Using again Lemma 3.7, we get that N is a finitely generated $\phi$-submodule of $R^{(n-1)}$, and so the assertion can be proved by using induction on n. $\square$

Recall that the $\phi$-weak global dimension of a ring R is the least non-negative integer n for which ${\text {Tor}}_{n+1}^R(R/I,N)=0$ for every nonnil ideal I of R and every u-$\phi$-torsion module N [14, Remark 5.11].

Next, the following result is the $\phi$-torsion theoretical analog of the well-known theorem for the semihereditary ring [36, Theorem 3.7.10].

Theorem 3.8

The following are equivalent for a ring $R\in \overline{\mathcal {H}}$.

• (1) R is nonnil-semihereditary.

• (2) R is nonnil-coherent and every finitely generated nonnil ideal is u-$\phi$-projective.

• (3) Every finitely generated nonnil ideal of R is projective.

• (4) R is nonnil-coherent and every finitely generated nonnil ideal of R is flat,

• (5) R is nonnil-coherent and $\phi$-${\text {w.gl.dim}}(R)=1$.

• (6) Every finitely generated $\phi$-submodule of a finitely generated free module is projective,

• (7) R is nonnil-coherent and every u-$\phi$-torsion module is $\phi$-(1,1)-injective.

• (8) R is a nonnil-coherent strongly $\phi$-ring and ${\hbox {NFP-i.gl.dim}}(R)=1$.

Proof

$(6)\Rightarrow (1)$ This is straightforward.

$(1)\Leftrightarrow (2)$ This follows by Definition 3.1.

$(2)\Leftrightarrow (3)$ This follows by Theorem 3.1.

$(3)\Rightarrow (4)$ Let I be a finitely generated nonnil ideal of R. Then I is finitely presented since it is projective, and so R is a nonnil-coherent ring. It is easy to see that I is flat.

$(4)\Rightarrow (3)$ Let I be a finitely generated nonnil ideal of R. Then I is a finitely presented ideal since R is assumed nonnil-coherent, and so I is projective since it is flat.

$(1)\Rightarrow (6)$ Let M be a finitely generated $\phi$-submodule of a finitely generated free. Then M is a direct sum of finite number of finitely generated nonnil ideals. So M is projective by Theorem 3.1.

$(4)\Rightarrow (5)$ It follows from [14, Theorem 5.26] that $\phi$-${\text {w.gl.dim}}(R)\le 1$. But if $\phi$-${\text {w.gl.dim}}(R)=0$, then $R\not \in \overline{\mathcal {H}}$, a contradiction. Then $\phi$-${\text {w.gl.dim}}(R)=1$.

$(5)\Rightarrow (4)$ Let I be a finitely generated nonnil ideal of R. Since R is nonnil-coherent, I is a finitely presented nonnil ideal. By [14, Theorem 5.26 and Corollary 5.36], I is a $\phi$-flat ideal, and so I is projective.

$(7)\Leftrightarrow (8)$ This follows from Theorems 1.3 and 1.5.

$(1)\Leftrightarrow (8)$ This follows immediately from Corollary 1.6. $\square$

Recall from [12] that a $\phi$-ring is said to be $\phi$-(n, d), where $n,d\in \mathbb {N}$, if every $\phi$-n-presented module has a $\phi$-projective dimension at most d. It is shown in [12, Theorem 2.21] that every strongly $\phi$-ring which is a $\phi$-(1, 1)-ring is a $\phi$-Prüfer ring.

Theorem 3.9

Let $R\in \overline{\mathcal {H}}$ be a nonnil-coherent ring. Then R is a $\phi$-(1, 1)-ring if and only if R is a nonnil-semihereditary ring.

Proof

Let I be a finitely generated nonnil ideal of R, then either $I=R$ or $I\ne R$. If $I=R$, then I is projective. Now, if $I\ne R$, then R/I is never u-$\phi$-projective by Lemma 3.3, and so $\phi$-${\text {pd}}_R(R/I) = 1$. Thus I is u-$\phi$-projective, and so I is projective since R is assumed to be nonnil-coherent. Hence R is nonnil-semihereditary.

Conversely, let M be a finitely presented $\phi$-torsion R-module. Then $M\cong F/N$, where F is a finitely generated free R-module and N is a finitely generated $\phi$-submodule of F. By Theorem 3.8, N is projective, and so $\phi$-${\text {pd}}_RM\le 1$. Thus R is a $\phi$-(1,1)-ring. $\square$

Recall from [36, Theorem 3.7.12] that every semihereditary ring is closed under localization, and thus so is every Prüfer domain. We show that this result holds in the context of nonnil-semihereditary rings.

Theorem 3.10

Let $R\in \overline{\mathcal {H}}$ and S be a multiplicative subset of R. If R is a nonnil-semihereditary ring, then so is $S^{-1}R$.

Proof

First, it is easy to establish that $S^{-1}R\in \overline{\mathcal {H}}$. Let J be a finitely generated nonnil ideal of $S^{-1}R$. Then it is easy to see that there exists a finitely generated nonnil ideal I of R such that $S^{-1}I=J$. By Theorem 3.1, we get that J is $(S^{-1}R)$-projective since I is projective. Therefore $S^{-1}R$ is a nonnil-semihereditary ring by Theorem 3.1. Using [26, Exercise 1.16], we establish immediately that $S^{-1}R$ is a strongly $\phi$-ring if R so is. $\square$

Recall from [3, Theorem 3.2] that a $\phi$-ring R is said to be $\phi$-Bézout if every finitely generated nonnil ideal of R is principal. Also recall from [14, Definition 2.7] that a $\phi$-ring R is called a $\phi$-principal ideal ring if every nonnil ideal is principal. Therefore every $\phi$-principal ideal ring is $\phi$-Bézout.

Proposition 3.11

Let $R\in \overline{\mathcal {H}}^{ZN}$. If R is a $\phi$-Bézout ring, then R is nonnil-semihereditary.

Proof

Let J be a finitely generated nonnil ideal of R. Then there exists $a\in R{\setminus } {\text {Nil}}(R)$ such that $J=aR$. It is easy to verify that J is free since $Z(R)={\text {Nil}}(R)$, and so R is nonnil-semihereditary by Theorem 3.1. $\square$

Recall from [3, Theorem 2.7] that a $\phi$-ring is said to be a $\phi$-CR ring if $R/{\text {Nil}}(R)$ is a valuation domain. The following is an analog of the well-known result [36, Theorem 3.7.12].

Theorem 3.12

Let $R\in \overline{\mathcal {H}}^{ZN}$. Then R is a $\phi$-CR ring if and only if R is both nonnil-semihereditary and local.

Proof

This follows from Theorem 3.5 and [14, Theorem 5.44]. $\square$

Recall from [14, Definition 4.6] that a $\phi$-ring is said to be $\phi$-hereditary if every nonnil ideal is u-$\phi$-projective. It is known that a ring R is a Noetherian ring, then R is semihereditary if and only if R is hereditary. The next result establishes the relationship between the $\phi$-hereditary nonnil-Noetherian rings and the nonnil-semihereditary rings.

Proposition 3.13

Let $R\in \overline{\mathcal {H}}$. Assume that R is a nonnil-Noetherian ring. Then the following are equivalent.

• (1) R is nonnil-semihereditary.

• (2) R is $\phi$-hereditary.

Proof

This is straightforward. $\square$

Theorem 3.14

Let $R\in \overline{\mathcal {H}}$ be a nonnil-semihereditary ring and M be a finitely presented $\phi$-torsion module. Then for every direct system of R-modules $\left\{ N_i\right\} _{i\in I}$, ${\text {Ext}}_R^1(M,\varinjlim N_i)\cong \varinjlim {\text {Ext}}_R^1(M,N_i)$ and ${\text {Ext}}_R^n(M,\varinjlim N_i)=0$ for every $n\ge 2$.

Proof

Let M be a finitely presented $\phi$-torsion R-module and consider the following short exact sequence $0\rightarrow N\rightarrow F\rightarrow M\rightarrow 0$, where F is a finitely generated free R-module. Since R is nonnil-semihereditary, N is a finitely generated projective R-module by Theorem 3.8. Consider the following commutative diagram of R-modules with exact rows:

By [36, Theorem 3.9.4 (1)], the two left vertical arrows are isomorphisms, and so we have ${\text {Ext}}_R^1(M,\varinjlim N_i)\cong \varinjlim {\text {Ext}}_R^1(M,N_i)$. Since N is projective, we have ${\text {Ext}}_R^n(M,\varinjlim N_i)=0$ for every $n\ge 2$. $\square$

Corollary 3.15

Let $R\in \overline{\mathcal {H}}$ be a nonnil-semihereditary ring and $\left\{ N_i\right\} _{i\in I}$ be a direct system of nonnil semi-injective R-modules. Then $\varinjlim N_i$ is nonnil semi-injective.

Proof

This follows immediately from Theorem 3.14. $\square$

Theorem 3.16

Let $R\in \overline{\mathcal {H}}$ be both a nonnil-Noetherian ring and a nonnil-semihereditary ring, E be an injective module, and N be a submodule of E. Then E/N is nonnil-injective.

Proof

Let I be a nonnil ideal of R. Then ${\text {pd}}_RR/I\le 1$ by Theorem 3.1, and so for the following short exact sequence $0\rightarrow N\rightarrow E\rightarrow E/N\rightarrow 0$, we get $0={\text {Ext}}_R^1(R/I,E)\rightarrow {\text {Ext}}_R^1(R/I,E/N)\rightarrow {\text {Ext}}_R^2(R/I,E/N)=0$. Hence E/N is nonnil-injective. $\square$

Now, we study the transfer of being nonnil-semihereditary rings in the trivial ring extensions. From [15, Corollary 2.4], a trivial ring extension $R\propto M$ is a $\phi$-ring if and only if R is a $\phi$-ring and M is a $\phi$-divisible module. It is easy to establish that $R\propto M\in \overline{\mathcal {H}}$ if and only if $R\in \overline{\mathcal {H}}$ and M is $\phi$-divisible. If M is an R-module, then we set $Z_R(M):=\left\{ r\in R\mid ~\text{ there } \text{ exists }~ x\in M{\setminus }\left\{ 0\right\} ~\text{ such } \text{ that }~ rx=0\right\}$.

Theorem 3.17

Let $R\in \overline{\mathcal {H}}$ and M be a $\phi$-divisible R-module. If R is a nonnil-semihereditary ring and $Z_R(M)=0$, then $R\propto M$ is nonnil-semihereditary.

Before proving Theorem 3.17, we need the following:

Lemma 3.18

Let $R\in \overline{\mathcal {H}}$ and M be a $\phi$-divisible R-module such that $Z_R(M)=0$. If I is a projective ideal of R, then $I\propto M$ is a projective ideal of $R\propto M$.

Proof

Define

$$\begin{aligned} \varphi : \left. \begin{array}{rcl} R &{} \longrightarrow &{} R\propto M \\ r &{} \longmapsto &{} (r,0) \\ \end{array} \right. \end{aligned}$$

It is easy to see that $\varphi$ is a ring homomorphism. Let I be a projective ideal of R. Then we get $I\otimes _R(R\propto M)$ is a projective $(R\propto M)$-module. We claim that $I\propto M\cong I\otimes _R(R\propto M)$. Define

$$\begin{aligned} \sigma _I: \left. \begin{array}{rcl} I\otimes _{R}(R\propto M) &{} \longrightarrow &{} I(R\propto M)\\ a\otimes (r,u) &{} \longmapsto &{} a(r,u) \\ \end{array} \right. \end{aligned}$$

It is easy to see that $\sigma _I$ is a surjective R-homomorphism, and so $\sigma _I$ is a well-defined map. It is easy to verify that $\sigma _I$ is a surjective $(R\propto M)$-homomorphism. If $a\otimes (r,u)\in \ker (\sigma _I)$, then $(ar,au)=(0,0)$, and so we can write $a\otimes (r,u)=ar\otimes (1,0)+a\otimes (0,u)= a\otimes (0,u)$. If $u=0$, then $a\otimes (r,u)=0$. Assume that $u\ne 0$. Then $a\in Z_R(M)=0$, and so $a\otimes (r,u)=0$, i.e., $\sigma _I$ is an injective map. Hence $I\otimes _{R}(R\propto M)\cong I(R\propto M)$. From [14, Lemma 6.2], we get $I(R\propto M)=I\propto M$. Therefore $(I\propto M)\cong I\otimes _R(R\propto M)$ is a projective $(R\propto M)$-module. $\square$

Proof of Theorem 3.17

Assume that R is a nonnil-semihereditary ring and $Z_R(M)=0$. Let J be a finitely generated nonnil ideal of $R\propto M$. Then from [11, Lemma 4.2], there exists a unique finitely generated nonnil ideal I of R such that $J=I\propto M$. By Theorem 3.1, I must be projective, and so J is a projective ideal of $R\propto M$ by Lemma 3.18. Thus $R\propto M$ is nonnil-semihereditary by Theorem 3.1. $\square$

Recall from [21, Theorem 2.2] that every ring R of ${\text {w.gl.dim}}(R)\le 1$ is reduced. It follows from [2, Theorem 3.2 (3)] that ${\text {Nil}}(R\propto M)={\text {Nil}}(R)\propto M$, and so a trivial ring extension $R\propto M$ is reduced if and only if R is reduced and $M=0$.

Corollary 3.19

Let R be a Prüfer domain, but not a field, with quotient field Q. Then $A=R\propto Q$ is a nonnil-semihereditary ring which is not semihereditary.

Proof

The ring $A=R\propto Q$ satisfies the conditions of Theorem 3.17, and so A is a nonnil-semihereditary ring but not semihereditary since $Q\ne 0$. $\square$

Next we give some examples of nonnil-semihereditary rings.

Example 3.2

• (1) The ring $\mathbb {Z}\propto \mathbb {Q}$ is nonnil-semihereditary.

• (2) Let K be a field. Then the ring $A=K\left[ X\right] \propto qf(K\left[ X\right] )$ is nonnil-semihereditary.

• (3) The ring $(\mathbb {Z}+X\mathbb {Q}\left[ \left[ X\right] \right] )\propto qf(\mathbb {Q}\left[ \left[ X\right] \right] )$ is a nonnil-semihereditary ring.

It is known that every nonnil-semihereditary ring is $\phi$-Prüfer. What about the converse? (See Corollary 3.5). The following example responds to this question.

Example 3.3

The ring $R=\mathbb {Z}\propto \mathbb {Q}/\mathbb {Z}$ is $\phi$-Prüfer which is ‘in fact, it is easy to see that $R/{\text {Nil}}(R)$ is a Prüfer domain, and so R is $\phi$-Prüfer but $Z(R)\ne {\text {Nil}}(R)$. By Corollary 3.5, R is not a nonnil-semihereditary ring.

Our next goal is to generalize the following result.

Theorem 3.20

[28, Proposition 2.2] Let R be a Prüfer ring and P be a prime ideal of R. If P is either regular or maximal with respect to containing only zero divisors, then R/P is a Prüfer domain.

So, our first main result of this work is stated as follows.

Theorem 3.21

Let R be a Prüfer ring with a regular primary ideal Q. If $R/Q\in \mathcal {H}$, then R/Q is a nonnil-semihereditary ring such that either $\sqrt{Q}$ is a maximal ideal of R or $\sqrt{Q}$ is not maximal such that for every finitely generated ideal J strictly containing $\sqrt{Q}$, we get J/Q is a projective ideal of R/Q.

Proof

Let R be a Prüfer ring with a regular primary ideal Q of R such that $R/Q\in \mathcal {H}$. First, we claim that $R/\sqrt{Q}$ is a Prüfer domain. If $\sqrt{Q}$ is a maximal ideal of R, then it is straightforward to see that $R/\sqrt{Q}$ is a Prüfer domain. Now, assume that $\sqrt{Q}$ is not a maximal ideal of R. Let $\overline{I_i}:=I_i/\sqrt{Q}$ ($1\le i\le 3$) be nonzero ideals of $R/\sqrt{Q}$. Since Q is regular in R, $I_1$, $I_2$, and $I_3$ are regular ideals of R, and so we obtained that $I_1(I_2\cap I_3)=I_1I_2\cap I_1I_3$ by [22, Theorem 13 (6)] since R is assumed a Prüfer ring. Passing to the quotient, we get that $\overline{I_1}(\overline{I_2\cap I_3})=\overline{I_1}\ \overline{I_2}\cap \overline{I_1}\ \overline{I_3}$. It follows from [6, Theorem 1.1 (12)] that $R/\sqrt{Q}$ is a Prüfer domain. But R/Q is a $\phi$-ring and $Z(R/Q)={\text {Nil}}(R/Q)$ since Q is assumed primary in R, and so R/Q is a nonnil-semihereditary ring by Theorem 3.5. By [3, Theorem 2.6], R is a $\phi$-Prüfer ring since $R/\sqrt{Q}$ is a Prüfer domain. It follows from [3, Theorem 2.14] that R/Q is a Prüfer ring. On the other hand, we get that $\phi$-${\text {w.gl.dim}}(R/Q)\le 1$ by [14, Corollary 5.27]. If $\phi$-${\text {w.gl.dim}}(R/Q)=0$, then R/Q is a $\phi$-von Neumann regular ring by [14, Theorem 5.29], and so $\sqrt{Q}$ is a maximal ideal of R by [14, Theorem 5.14]. If $\phi$-${\text {w.gl.dim}}(R)=1$, then R/Q is a $\phi$-Prüfer ring such that $\sqrt{Q}$ is not a maximal ideal of R, i.e., ${\text {Nil}}(R/Q)$ is not a maximal ideal. Hence, if J is an ideal of R strictly containing $\sqrt{Q}$, then J/Q is a finitely generated nonnil ideal of R/Q, and so J/Q is a u-$\phi$-projective ideal of R/Q by [14, Theorem 5.41]. But R/Q is a nonnil-coherent ring by [26, Remark 2.1], so J/Q is a finitely presented ideal of R/Q. It follows from [14, Corollary 5.36] that J/Q is a projective ideal of R/Q. $\square$

By Theorem 3.21, it is easy to find the result of Theorem 3.20 above.

Corollary 3.22

Let R be a Prüfer ring with regular prime ideal Q. Then R/Q is a Prüfer domain.

Proof

If Q is a prime ideal of R, then R/Q is an integral domain, and so $R/Q\in \mathcal {H}$. It follows from Theorem 3.21 that R/Q is a Prüfer domain. $\square$

Corollary 3.23

Let $(R,\mathfrak {m})$ be a local Prüfer ring and Q be a regular primary ideal of R that is not $\mathfrak {m}$-primary. If $R/Q\in \mathcal {H}$, then R/Q is a Bézout ring such that for every finitely generated ideal I of R strictly containing $\sqrt{Q}$, we get that $(Q:I)=Q$.

Proof

Assume that $(R,\mathfrak {m})$ be a local Prüfer ring and Q be a regular primary ideal of R that is not $\mathfrak {m}$-primary. If $R/Q\in \mathcal {H}$, then $(R/Q,\mathfrak {m}/Q)$ is a local ring such that ${\text {Nil}}(R/Q)$ is not a maximal ideal of R/Q since Q is not an $\mathfrak {m}$-primary ideal of R. Following the proof of Theorem 3.21, R/Q is a $\phi$-Prüfer ring which is a strongly $\phi$-ring, and by [14, Corollary 5.42], we get that R/Q is a $\phi$-Bézout ring. According to [3, Proposition 3.7], we deduce that R/Q is a Bézout ring. Let I be a finitely generated ideal of R strictly containing $\sqrt{Q}$. Then $I/Q=\left\langle a+Q\right\rangle$ for some $a\in I$ since R/Q is a Bézout ring. By Theorem 3.21 and [36, Theorem 2.5.24], we get that J/Q is a free ideal of R/Q, which implies that $(Q:I)=Q$.

$\square$

Corollary 3.24

Let $(R,\mathfrak {m})$ be a local Prüfer ring and $\mathfrak {p}\subsetneq \mathfrak {m}$ be a regular prime ideal of R. Then $R/\mathfrak {p}$ is a Bézout domain and for every finitely generated ideal I of R such that $\mathfrak {p}\subsetneq I$, we get that $(\mathfrak {p}:I)=\mathfrak {p}$.

Proof

This is straightforward by Corollary 3.23. $\square$

Corollary 3.25

Let $(R,\mathfrak {m})$ be a local Prüfer ring and Q be a regular primary ideal of R that is not $\mathfrak {m}$-primary. Assume that $\overline{R}:=R/Q\in \mathcal {H}$ and let M be a finitely generated $\overline{R}$-submodule of a finitely generated free $\overline{R}$-module F. If for every $x\in F$ there exists $s\in R{\setminus }\sqrt{Q}$ such that $\overline{s}x\in M$, then M is a free $\overline{R}$-module.

Proof

Assume that $(R,\mathfrak {m})$ be a local Prüfer ring and Q be a regular primary ideal of R that is not $\mathfrak {m}$-primary. If $R/Q\in \mathcal {H}$, then $(R/Q,\mathfrak {m}/Q)$ is a local ring such that ${\text {Nil}}(R/Q)$ is not a maximal ideal of R/Q since Q is not an $\mathfrak {m}$-primary ideal of R. By the proof of Theorem 3.21, R/Q is a $\phi$-Prüfer ring that is a strongly $\phi$-ring. Assume that M is a finitely generated $\overline{R}$-submodule of a finitely generated free $\overline{R}$-module F such that the condition in the statement holds. Then M is a $\phi$-submodule of F. By [14, Corollary 5.43], we deduce that M is a free $\overline{R}$-module. $\square$

Let M be an R-module, the torsion submodule of M, denoted by ${\text {tor}}(M)$ and defined as follows

$$\begin{aligned} {\text {tor}}(M):=\left\{ x\in M\mid ~\text{ there } \text{ exists }~ s\in R\setminus Z(R)~\text{ such } \text{ that }~sx=0\right\} . \end{aligned}$$

Next, our goal is to introduce Theorem 3.33, which is an extension of the well-known behavior [30, Theorem 2], stated as follows.

Theorem 3.26

[30, Theorem 2] Let R be an integral domain. Then R is a Prüfer ring if and only if ${\text {tor}}(M)$ is a pure submodule of M for every finitely generated R-module M.

The above theorem is a generalization of the following theorem due to I. Kaplansky [25].

Theorem 3.27

[25] Let R be an integral domain. Then R is a Prüfer ring if and only if ${\text {tor}}(M)$ is a direct summand of M for every finitely generated R-module M.

We will study some characterizations of $\phi$-flatness for this purpose.

Theorem 3.28

Let $R \in \mathcal {H}$ and F be an R-module. Then F is $\phi$-flat if and only if any equation $\sum _{i=1}^n r_i x_i=0$ for each $r_i \in R$ such that at least one $r_i \in R\setminus {\text {Nil}}(R)$ and each $x_i \in F$, implies that there exist $\left\{ u_1, u_2, \ldots , u_m\right\} \subset F$ and $\left\{ a_{i, j}\right\} _{1 \le i \le n, 1 \le j \le m} \subset R$ such that $\sum _{i=1}^n r_i a_{i, j}=0$ and $x_i=\sum _{j=1}^m a_{i, j} u_j$.

Before establishing Theorem 3.28 above, we need the following Lemma 3.29.

Lemma 3.29

[34, Proposition 8.8, p. 30] Let $\left( y_i\right) _I$ be a set of generators for M and $\left( x_i\right) _I$ be a set of elements of L with almost all $x_i=0$. Then $\sum x_i \otimes y_i=0$ in $L \otimes _R M$ if and only if there exist a finite set $\left( u_j\right) _J$ of elements of L and a set $\left( a_{j i}\right) _{J \times I}$ of elements of R such that:

• (i) $a_{j i}=0$ for almost all (j, i),

• (ii) $\sum _I a_{j i} y_i=0$ for each $j \in J$

• (iii) $x_i=\sum _J u_j a_{j i}$ for each $i \in I$.

Proof of Theorem 3.28

Assume that F is a $\phi$-flat R-module such that $\sum _{i=1}^{n}r_ix_i=0$. If $I:=\left\langle r_1,r_2,\ldots ,r_n\right\rangle$, then I is a nonnil ideal of R, and so the R-homomorphism $\sigma : I\otimes _R F\rightarrow F$ given by $\sigma (r\otimes x)=rx$ is an R-monomorphism for every $(r,x)\in R\otimes F$ by [35, Theorem 3.2]. So, we get $\sum _{i=1}^nr_i\otimes x_i=0$ in $I\otimes F$. Then there exist $\left\{ u_1,u_2,\ldots , u_m\right\} \subset F$ and $\left\{ a_{i,j}\right\} _{1\le i\le n, 1\le j\le m}\subset R$ such that $\sum _{i=1}^nr_ia_{i,j}=0$ and $x_i=\sum _{j=1}^ma_{i,j}u_j$ by Lemma 3.29 above.

Conversely, assume that F satisfies the condition in the statement. Let I be a nonnil ideal of R. We claim that the R-homomorphism $\sigma : I\otimes _R F\rightarrow F$ given by $\sigma (r\otimes x)=rx$ is an R-monomorphism for every $(r,x)\in R\otimes F$. If $\sum b_i \otimes x_i \in I \otimes F$ goes to zero in F, then $\sum b_i x_i=0$. Without loss of generality, we assume that at least one of $b_i$ in the above sum is a non-nilpotent element since ${\text {Nil}}(R)$ is a $\phi$-divisible ideal of R. Then, by hypothesis, there exist $u_j$ and $a_{i j}$ according to the condition. This gives immediately $\sum _i b_i \otimes x_i=\sum _{i, j} b_i \otimes a_{i j} u_j=\sum _{i, j} b_i a_{i j} \otimes u_j=\sum _i 0 \otimes u_j=0$. The map $I \otimes F \rightarrow F$ is thus a monomorphism, and F is $\phi$-flat by [35, Theorem 3.2]. $\square$

Definition 3.2

Let R be a ring.

• (1) An $m \times n$-matrix $(a_{i,j})$ of elements in R is said to be a $\phi$-$(m\times n)$-matrix or a $\phi$-matrix if the ${\text {Coker}}(\alpha : R^m\rightarrow R^n)$ is a $\phi$-torsion R-module, where $\alpha :\left( x_i\right) \mapsto \left( \sum _i a_{i j} x_i\right)$.

• (2) A set $\left\{ u_1,u_2,\ldots ,u_m\right\}$ of a free R-module F with basis $\left\{ x_i\right\} _{i\in I}$ is said to be a $\phi$-set if its representative matrix in the basis $\left\{ x_i\right\} _{i\in I}$ is a $\phi$-matrix.

The following Theorem 3.30 establishes the relationship between the $\phi$-flatness and the $\phi$-purity in terms of relations.

Theorem 3.30

A submodule $M^{\prime }$ of M is $\phi$-pure in M if and only if it satisfies: if $y_1, \ldots , y_n$ are elements in $M^{\prime },\left( a_{i j}\right)$ is a $\phi$-$(m \times n)$-matrix of elements in R and the system of equations

$$\begin{aligned} \sum _{i=1}^m X_i a_{i j}=y_j \quad (j=1, \ldots , n), \end{aligned}$$

(2)

has a solution $\left( x_1, \ldots , x_m\right)$ in M, then it has a solution in $M^{\prime }$.

Proof

We assume that the condition is satisfied, and we want to show that for every finitely presented $\phi$-torsion R-module F, we get $0\rightarrow M^{\prime } \otimes F \rightarrow M \otimes F$ is an exact sequence. Let the exact sequence

$$\begin{aligned} R^m {\mathop {\longrightarrow }\limits ^{\alpha }} R^n \rightarrow F \rightarrow 0, \end{aligned}$$

where $\alpha$ is represented by a matrix $\left( a_{i j}\right)$ by the rule $\alpha :\left( x_i\right) \mapsto \left( \sum _i a_{i j} x_i\right)$. So $\left( a_{i j}\right)$ is a $\phi$-$(m\times n)$-matrix in R. This results in a commutative diagram where the two left vertical arrows are monomorphisms.

Applying [34, Lemma 11.3, p. 38] to the above diagram, an element $\left( x_1, \ldots , x_m\right) \in M^m \cong M \otimes R^m$ maps to $u=\sum _i x_i \otimes \left( a_{i j}\right) \in M \otimes R^n$, which also is the image of $\left( y_1, \ldots , y_n\right) \in M^{\prime n}$ just when $\sum _i x_i a_{i j}=y_j$. The existence of a solution $\left( z_1, \ldots , z_m\right)$ in $M^{\prime }$ of this system means that u is the image of an element in $M^{\prime } \otimes R^m=M^{\prime m}$, so [34, Lemma 11.3, p. 38] can be used to show that $M^{\prime } \otimes F \rightarrow M \otimes F$ is a monomorphism.

Conversely, assume that $M^{\prime }$ is $\phi$-pure in M and that the system (2) has a solution in M. The matrix $\left( a_{i j}\right)$ determines a homomorphism $\alpha : R^m \rightarrow R^n$, and one puts $L=R^n / {\text {Im}} \alpha$ which is a $\phi$-torsion R-module. One can now follow the previous argument backwards to get the existence of a solution in $M^{\prime }$. $\square$

Corollary 3.31

Let M be a $\phi$-flat module and $0 \rightarrow K \rightarrow F \rightarrow M \rightarrow 0$ be an exact sequence with F free. For any finite set $u_1, \ldots , u_m$ of elements of K which is a $\phi$-set in F, there exists a homomorphism $\varphi : F \rightarrow K$ such that $\varphi \left( u_j\right) =u_j$ for $j=1, \ldots , n$.

Proof

We can write

$$\begin{aligned} u_j=\sum _{i=1}^m x_i a_{i j}, \quad j=1, \ldots , n, \end{aligned}$$

(3)

where $\{x_1, \ldots , x_n\}$ is part of a basis for the free module F. Since M is $\phi$-flat, the given exact sequence is $\phi$-pure, so the system (3) has a solution $z_1, \ldots , z_m$ in K by Theorem 3.30 since $a_{i,j}$ is a $\phi$-matrix. We can define $\varphi : F \rightarrow K$ so that $\varphi \left( x_i\right) =z_i$, and then get

$$\begin{aligned} \varphi \left( u_j\right) =\varphi \left( \sum _i x_i a_{i j}\right) =\sum _i z_i a_{i j}=u_j. \end{aligned}$$

$\square$

Corollary 3.32

Let K be a finitely generated $\phi$-pure submodule of a finitely generated free module F. If K is generated by a $\phi$-set in F, then K is a direct summand of F.

Proof

Set $M:=F/K$. Then M is finitely presented and $\phi$-flat. Let the exact sequence $0 \rightarrow K \rightarrow F \rightarrow M \rightarrow 0$. Then K has a finite number of generators $u_1, \ldots , u_m$. If $\varphi : F \rightarrow K$ maps $u_j$ to $u_j$ according to Corollary 3.31, then $\varphi$ splits the sequence, and hence K is a direct summand of F. $\square$

Our second main result in this section is the following Theorem 3.33, which is an extension of the well-known behavior [30, Theorem 2].

Theorem 3.33

The following are equivalent for a strongly $\phi$-ring R.

• (1) R is a nonnil-semihereditary ring.

• (2) $\phi$-${\text {tor}}(M)={\text {tor}}(M)$ is a pure submodule of M for every finitely generated R-module M.

Proof

Assume that R is a nonnil-semihereditary ring and let M be a finitely generated R-module. First, it is easy to see that $\phi$-${\text {tor}}(M)$ is a u-$\phi$-torsion R-module since M is a finitely generated R-module, and so $(\phi$-${\text {tor}}(M))^+$ is a u-$\phi$-torsion R-module by [14, Corollary 3.2]. On the other hand, it is easy to see that $M/\phi \text{- }{\text {tor}}(M)$ is a $\phi$-torsion free R-module, and so $M/\phi \text{- }{\text {tor}}(M)$ is a $\phi$-flat R-module by [37, Theorem 3.3] and [39, Theorem 4.3]. Then $(M/\phi \text{- }{\text {tor}}(M))^+$ is a nonnil-injective R-module by [14, Theorem 5.8], and so the short exact sequence $0\rightarrow (M/\phi \text{- }{\text {tor}}(M))^+\rightarrow M^+\rightarrow (\phi$-${\text {tor}}(M))^+\rightarrow 0$ is split by [14, Theorem 2.1]. It follows from [19, Theorem 3.1] that the short exact sequence $0\rightarrow \phi \text{- }{\text {tor}}(M)\rightarrow M\rightarrow M/\phi \text{- }{\text {tor}}(M)\rightarrow 0$ is pure. Therefore, $\phi$-${\text {tor}}(M)$ is a pure submodule of M.

Conversely, assume that $\phi$-${\text {tor}}(M)$ is a pure submodule of M for every finitely generated R-module M. If ${\text {Nil}}(R)$ is a maximal ideal of R, then R is a $\phi$-von Neumann regular ring, and so R is a nonnil-semihereditary ring. Now, assume that ${\text {Nil}}(R)$ is not maximal and let $I=\left\langle a_1,a_2,\ldots ,a_n\right\rangle$ be a finitely generated nonnil ideal of R. Since $R\in \mathcal {H}$, we can assume that all $a_i\in R{\setminus } {\text {Nil}}(R)$. Our aim is to establish that I is a projective ideal of R by Theorem 3.1. Set

$$\begin{aligned} M:=\frac{R^n}{\left\langle a_1(a_1,a_2,\ldots ,a_n)\right\rangle }. \end{aligned}$$

It is easy to see that $\overline{\left( a_1,a_2,\ldots ,a_n\right) }\in \phi$-${\text {tor}}(M)$, and we get the following equality

$$\begin{aligned} \overline{\left( a_1,a_2,\ldots ,a_n\right) }=\sum _{i=1}^na_i\overline{e_i}, \end{aligned}$$

(4)

where $\left\{ e_i\right\} _{1\le i\le n}$ is the canonical basis of $R^n$. But (4) implies the following equality

$$\begin{aligned} \overline{\left( a_1,a_2,\ldots ,a_n\right) }=(\overline{e_1}, \overline{e_2},\ldots ,\overline{e_n}) (a_1, a_2, \ldots , a_n)^t, \end{aligned}$$

where $A^t$ denotes the transpose of a matrix A. The matrix $(a_1, a_2, \ldots , a_n)^t$ induces the following map $\varphi : R^n\longrightarrow R$ given by $(x_1,x_2,\ldots ,x_n)\mapsto \sum _{i=1}^na_ix_i$. In addition, for every $z\in R$, we get $a_1z=\varphi (z,0,\ldots ,0)\in \text{ Im }\,(\varphi )$. Then ${\text {Coker}}(\varphi )$ is a $\phi$-torsion R-module. Since $\phi$-${\text {tor}}(M)$ is a $\phi$-pure submodule of M, by Theorem 3.30 there exists $\left\{ p_{i,j}\right\} _{1\le j\le n}\subset R$ such that $\overline{(p_{i,1},p_{i,2},\ldots , p_{i,n})}\in \phi$-${\text {tor}}(M)$ such that $\overline{\left( a_1,a_2,\ldots ,a_n\right) }=\sum _{i=1}^na_i\overline{(p_{i,1},p_{i,2}\ldots , p_{i,n})}$. In particular, we get

$$\begin{aligned} a_1=\sum _{i=1}^na_ip_{i,1}+ra_1a_1\text { (where }r\in R). \end{aligned}$$

(5)

But there exist $\left\{ r_i\right\} _{1\le i\le n}\subset R{\setminus } {\text {Nil}}(R)$ and $\left\{ s_i\right\} _{1\le i\le n}\subset R$ such that for every $(i,j)\in \{1, 2, \ldots , n\}\times \{1, 2, \ldots , n\}$, we get

$$\begin{aligned} r_ip_{i,j}=s_ia_1a_j. \end{aligned}$$

(6)

Replacing $p_{i,j}=\frac{s_ia_1a_j}{r_i}\in R$ in (5), we get

$$\begin{aligned} 1=(r+\frac{s_1a_1}{r_1})a_1+\sum _{i=2}^n\frac{s_1a_1}{r_1}a_i. \end{aligned}$$

(7)

So (7) implies that I is an invertible ideal of R, and so I is projective by [21, Theorem 3.9], as desired. Therefore, R is a nonnil-semihereditary ring by Theorem 3.1. $\square$

We can easily find [30, Theorem 2] using Theorem 3.33.

Corollary 3.34

The following are equivalent for an integral domain R.

• (1) R is a Prüfer domain.

• (2) ${\text {tor}}(M)$ is a pure submodule of M for every finitely generated R-module M.

Proof

This follows immediately from Theorem 3.33. $\square$

The following Corollary 3.35 characterizes when an injective module over a nonnil-semihereditary ring R is a $\phi$-flat R-module.

Corollary 3.35

Let R be a nonnil-semihereditary ring and E be a finitely generated injective module. Then E is a $\phi$-flat R-module if and only if its $\phi$-torsion submodule $(\phi$-${\text {tor}}(E))$ is finitely generated.

Proof

Assume that E is a $\phi$-flat module. By [39, Theorem 4.3] E is a $\phi$-torsion free R-module, and so $\phi$-${\text {tor}}(E)$ is a finitely generated R-module.

Conversely, assume that $\phi$-${\text {tor}}(E)$ is a finitely generated R-module. By Theorem 3.33 the short exact sequence $0\rightarrow \phi \text{- }{\text {tor}}(E)\rightarrow E\rightarrow E/\phi \text{- }{\text {tor}}(E)\rightarrow 0$ is pure, and so for every R-module M, we get the short exact sequence $0\rightarrow {\text {Hom}}_R(M,\phi \text{- }{\text {tor}}(E))\rightarrow {\text {Hom}}_R(M,E)\rightarrow {\text {Hom}}_R(M,E/\phi \text{- }{\text {tor}}(E))\rightarrow 0$. But E is injective, and so we get the commutative diagram with exact rows:

Therefore, ${\text {Ext}}_R^1(M,\phi \text{- }{\text {tor}}(E))=0$, i.e., $\phi$-${\text {tor}}(E)$ is an injective module, and so $\phi$-${\text {tor}}(E)$ is a divisible R-module. But $\phi$-${\text {tor}}(E)$ is a finitely generated R-module, and so it is a u-$\phi$-torsion R-module. Since $Z(R)={\text {Nil}}(R)$, we get that $\phi$-${\text {tor}}(E)=0$. It follows from [39, Theorem 4.3] that E is a $\phi$-flat R-module. $\square$

5 Nonnil-FP-projective dimension

In this section, we introduce and study a new generalization of FP-projectivity of modules.

Definition 4.1

Let R be a ring. An R-module M is said to be nonnil-FP-projective if ${\text {Ext}}_R^1(M,N)=0$ for every nonnil-FP-injective module N.

Definition 4.2

Let M be an R-module. Then the nonnil-FP-projective dimension of an R-module M, denoted by ${\hbox {NFP-pd}}_RM$, is defined as the least integer $n \geqslant 0$ such that ${\text {Ext}}_R^{n+1}(M, N)=0$ for every nonnil-FP-injective module N. Define the nonnil-FP-projective global dimension of a ring R by

$$\begin{aligned} {\hbox {NFP-p.gl.dim}}(R):=\sup \left\{ {\hbox {NFP-pd}}_R M \mid M~\text {is a}~\phi \text {-torsion}~R\text {-module}\right\} . \end{aligned}$$

Remark 4.1

As in the classical case, an R-module M is nonnil-FP-projective if and only if ${\hbox {NFP-pd}}_RM=0$.

Theorem 4.1

The following are equivalent for a nonnil-coherent strongly $\phi$-ring R.

• (1) ${\hbox {NFP-pd}}_{R} M\le n$ for any finitely generated $\phi$-torsion module M.

• (2) ${\hbox {NFP-pd}}_{R} M\le n$ for any finitely generated $\phi$-torsion module M.

• (3) ${\hbox {NFP-pd}}_{R} R/I\le n$ for any nonnil ideal I of R.

• (4) $\phi$-${\text {id}}_RF\le n$ for any nonnil-FP-injective module F.

Proof

$(1)\Rightarrow (2)\Rightarrow (3)$ These are straightforward.

$(3)\Rightarrow (4)$ Let F be a nonnil-FP-injective module and I be a nonnil ideal of R. By hypothesis, we get ${\text {Ext}}_R^{n+1}(R/I,F)=0$, and so $\phi$-${\text {id}}_RF\le n$.

$(4)\Rightarrow (1)$ Let M be a finitely generated $\phi$-torsion R-module. Since $Z(R)={\text {Nil}}(R)$ and $\phi$-${\text {id}}_RF\le n$, it follows that ${\text {Ext}}_R^{n+1}(M,F)=0$, and so ${\hbox {NFP-pd}}_{R} M\le n$. $\square$

The following corollary is a consequence of Theorem 4.1.

Corollary 4.2

Let R be a nonnil-coherent strongly $\phi$-ring. Then

$$\begin{aligned} \begin{aligned} {\hbox {NFP-p.gl.dim}}(R)&=\sup \left\{ {\hbox {NFP-pd}}_{R} M \mid M ~\text {is a f.g. (u-)}\phi \text {-torsion}~\ R\text {-module}\right\} \\&=\sup \left\{ {\hbox {NFP-pd}}_{R} M \mid M ~\text {is a}~\phi \text {-torsion cyclic}~\ R\text {-module}\right\} \\&=\sup \left\{ {\hbox {NFP-pd}}_{R} R/I \mid I ~\text{ is } \text{ a } \text{ nonnil } \text{ ideal } \text{ of }~R)\right\} \\&=\sup \left\{ \phi \text {-}{\text {id}}_RF \mid F~\text {is a nonnil-FP-injective } R\text {-module}\right\} . \end{aligned} \end{aligned}$$

Corollary 4.3

The following are equivalent for a nonnil-coherent strongly $\phi$-ring R.

• (1) ${\hbox {NFP-p.gl.dim}}(R)\le 1$.

• (2) For every nonnil-FP-injective submodule N of an injective module E, we get E/N is nonnil-injective.

Proof

$(1)\Rightarrow (2)$ Assume that ${\hbox {NFP-p.gl.dim}}(R)\le 1$ and let N be a nonnil-FP-injective submodule of an injective module E. Then $\phi$-${\text {id}}_RN\le 1$ by Corollary 4.2, and so E/N is nonnil-injective by [14, Theorem 2.6].

$(2)\Rightarrow (1)$ Let N be a nonnil-FP-injective module. Then N is a submodule of its injective hull E(N). Therefore E(N)/N is nonnil-injective. Hence $\phi$-${\text {id}}_RN\le 1$. Consequently ${\hbox {NFP-p.gl.dim}}(R)\le 1$ by Corollary 4.2. $\square$

It is shown in [12, Proposition 2.3] that for a nonnil-coherent ring R, an R-module M is nonnil-FP-injective if and only if ${\text {Ext}}_R^1(R/I,M)=0$ for every finitely generated nonnil ideal I of R.

Theorem 4.4

The following are equivalent for a strongly $\phi$-ring R.

• (1) ${\hbox {NFP-p.gl.dim}}(R)=0$.

• (2) R is nonnil-Noetherian.

• (3) Every finitely generated $\phi$-torsion R-module is finitely presented.

• (4) Every cyclic $\phi$-torsion R-module is finitely presented.

• (5) Every nonnil-FP-injective R-module is nonnil-injective.

Proof

$(2)\Rightarrow (3)$ and $(3)\Rightarrow (4)$ These follow from [11, Theorem 3.13].

$(4)\Rightarrow (2)$ This is straightforward.

$(2)\Rightarrow (5)$ This follows immediately from [12, Proposition 2.3].

$(5)\Rightarrow (1)$ This is straightforward by Corollary 4.2.

$(1)\Rightarrow (2)$ Let I be a nonnil ideal of R and N be an FP-injective module. By Corollary 4.2, we have ${\text {Ext}}_R^1(R/I,N)=0$ since N is nonnil-FP-injective. Therefore R/I is finitely presented by [16]. Hence R is nonnil-Noetherian. $\square$

Corollary 4.5

Let R be a nonnil-Noetherian strongly $\phi$-ring and M be a finitely generated R-module. If M is nonnil-FP-injective, then M is a nonnil-FP-projective module.

Proof

This is obvious by Corollary 4.2 and Theorem 4.4. $\square$

Corollary 4.6

Let R be a nonnil-Noetherian strongly $\phi$-ring and M be an R-module. Then:

• (1) M is nonnil-injective if and only if $M^{++}$ is nonnil-injective.

• (2) M is nonnil-injective if and only if $M^+$ is $\phi$-flat.

Proof

(1) By Theorem 4.4, M is nonnil-injective if and only if M is a nonnil-FP-injective R-module. By [26, Remark 2.1], we deduce that R is a nonnil-coherent ring, and so M is a nonnil-FP-injective if and only if $M^{++}$ is a nonnil-FP-injective by [12, Corollary 3.13] and Remark 1.2. Using Theorem 4.4, we deduce that M is a nonnil-injective module if and only if so is $M^{++}$.

(2) This follows immediately by (1), Remark 1.2, and [12, Corollary 3.13]. $\square$

Corollary 4.7

Let R be a Noetherian domain and M be an R-module. Then:

• (1) M is injective if and only if $M^{++}$ is injective.

• (2) M is injective if and only if $M^+$ is flat.

Proof

This follows immediately from Corollary 4.6, [35, Theorem 3.2], and [14, Theorem 2.2]. $\square$