Algebraic structures in the set of sequences of independent random variables

Abstract

The space whose subsets we analyse with respect to lineability is $L_0(\Omega ,P)^{\mathbb {N}}$ consisting of random variables sequences on probability space $(\Omega ,P)$ with atomless probability measure P. We study lineability and algebrability of $L_0(\Omega ,P)^{\mathbb {N}}$-subsets of independent random variables with additional properties connected with various types of convergence, laws of large numbers, and Markov and Kolgomorov conditions.

1 Introduction

The last 20 years brought numerous papers devoted to the existence of large and rich algebraic structures inside subsets of linear spaces, function algebras and their Cartesian products. The topic has gained such popularity that the monograph devoted to it has been released [2] and a few surveys appeared [5, 3]. Recently the subject has obtained its place in Mathematical Subject Classification— 46B87. The custom name for problems in this area are lineability or algebrability problems. A large number of sets in function and sequence spaces naturally arising in many branches of mathematics were studied from this perspective. Probability, however, is rather scarcely represented in lineability theory. Only three of the papers on lineability published so far address probability theory—[6, 4] and [8]. The first of them [6] was published in RACSAM in 2017. The main feature distinguishing the probability theory from the measure theory is the independence or some kind of dependence for random variables. The other are theorems typical for probability theory, like Borel-Cantelli Lemma, the Laws of Large Numbers and so-called Markov and Kolmogorov conditions related to them, Central Limit Theorem, etc. In the mentioned papers independence or martingale dependence was assumed or obtained in [6, Theorem 5] (pairwise independence), [4, Theorem 10 and Theorem 11] (martingales), [4, Theorem 13] and [8, Theorem 2.11] (independence).

In present paper we have set the following goals. Firstly, to select the assumptions on the probability spaces so that there is no need to define spaces for particular theorems. This is discussed in Sect. 3. Secondly, to consider exclusively sequences of independent random variables. The space whose subsets we analyse with respect to lineability is the space $L_0(\Omega ,P)^{\mathbb {N}}$, i.e. the space of sequences of random variables on probability space $(\Omega ,P)$ with atomless probability measure P.

Throughout the paper [8] the Authors considered the following condition on probability space: $(\Omega ,{\mathcal {F}})$ is not isomorphic to $([N],2^{[N]})$ for any N, where $[N]=\{0,1,\dots ,N-1\}$. This condition says that probability space contains infinitely many events. Let us compare that condition to the following: in $(\Omega ,{\mathcal {F}},P)$ there is a sequence of independent events with probabilities in (0, 1). Clearly, the latter condition implies that $(\Omega ,{\mathcal {F}})$ cannot be isomorphic to finite probability spaces. However, there are infinite probability spaces which do not contain any proper pair of events (that is both with probabilities in (0, 1)) which are independent, see [7]. In our results we will construct sequences of independent random variables, which is possible in non-atomic probability space. Any probabilistic measure can be written as a sum of two measures: an atomic and an atomless. Our results hold true if the atomless part of a probabilistic measure is non-void. However, we decided to assume that probabilistic spaces are atomless to make our results more clear for the first reading.

The paper is organized as follows. In Sect. 2 we remain the basic definitions and facts concerning lineability, algebrability, and that of probability theory. In Sect.  3 we analyse the properties of probability spaces with atomless measures. These properties are likely to be known to the probability experts, however we were not able to find them in a single source. In Sect. 4 we consider various kinds of probability convergence. In Theorem  11 we consider the sequences of independent random variables convergent in probability but not almost everywhere. In Theorem 12 we consider the ones for which the Cesaro means are divergent in probability. In Theorem  13 we consider uniformly bounded sequences convergent in probability but not almost surely. Our theorems generalize known ones or are essentially different of them —compare Theorem 11 with [8, Theorem 2.2] and [6, Theorem 1], and Theorem 12 with [8, Theorem  2.11 and Theorem 2.15]. The inspiration, particularly for the last part of the paper come from the Stoyanov monograph [10]. Without the knowledge of these examples the paper would not have appeared in the present shape. Section 5 is devoted to the Laws of Large Numbers. In this part we frequently use the fact that the zero random variable is independent with respect to any other, even to itself. This and the use of almost disjoint families of subsets of ${\mathbb {N}}$ allows us to construct the necessary ${\mathfrak {c}}$-dimensional linear spaces consisting of sequences of independent random variables. The following diagram summarize the most of the results from Sect. 5.

2 Preliminaries

2.1 Lineability and algebrability

Definition 1

Let $\kappa$ be a cardinal number.

• (1) Let ${\mathcal {L}}$ be a vector space and $A \subseteq {\mathcal {L}}$. We say that A is $\kappa$-lineable if $A \cup \{0\}$ contains a $\kappa$-dimensional subspace of ${\mathcal {L}}$.

• (2) Let ${\mathcal {L}}$ be a commutative algebra and $A \subseteq {\mathcal {L}}$. We say that A is $\kappa$-algebrable if $A \cup \{0\}$ contains a $\kappa$-generated subalgebra B of ${\mathcal {L}}$ (i.e. the minimal cardinality of the system of generators of B is $\kappa$).

• (3) Let ${\mathcal {L}}$ be a commutative algebra and $A \subseteq {\mathcal {L}}$. We say that A is strongly $\kappa$-algebrable if $A \cup \{0\}$ contains a $\kappa$-generated subalgebra B that is isomorphic to a free algebra.

Proposition 2

$X=\left\{ x_{\alpha }: \alpha <\kappa \right\}$ is the set of free generators of some free algebra if and only if the set ${\tilde{X}}$ of elements of the form $x_{\alpha _{1}}^{k_{1}} x_{\alpha _{2}}^{k_{2}} \cdots x_{\alpha _{n}}^{k_{n}}$ is linearly independent; equivalently for any $k \in {\mathbb {N}}$, any nonzero polynomial P in k variables without a constant term and any distinct $x_{\alpha _{1}}, \ldots , x_{\alpha _{k}} \in X$, we have that $P\left( x_{\alpha _{1}}, \ldots , x_{\alpha _{k}}\right)$ is nonzero.

2.2 Borel–Cantelli lemma and various kinds of convergence

Let X be a random variable on a probability space $(\Omega ,{\mathcal {F}},P)$. By EX and VarX we denote the expected value of X and variation of X, respectively.

Lemma 3

[Borel–Cantelli] Let $(A_n)$ be a sequence of events in the probability space $(\Omega ,{\mathcal {F}},P)$. Let $\limsup A_n=\bigcap _{n=1}^\infty \bigcup _{k=n}^\infty A_k$ be a set of those $\omega \in \Omega$ which belong to infinitely many $A_n$’s. Then

• (a) if $\sum _{n=1}^\infty P(A_n)<\infty$, then $P(\limsup A_n)=0$;

• (b) if $\sum _{n=1}^\infty P(A_n)=\infty$ and $A_1,A_2,\dots$ are independent, then $P(\limsup A_n)=1$.

Let $(X_n)$ be a sequence of random variables on $(\Omega ,{\mathcal {F}},P)$. Then

• (p-w) $X_n\rightarrow X$ means that $(X_n)$ converges point-wise to X on $\Omega$,

• (a.s.) $X_n{\mathop {\longrightarrow }\limits ^{as}}X$ means that $(X_n)$ converges to X almost surely,

• (prob) $X_n{\mathop {\longrightarrow }\limits ^{P}}X$ means that $(X_n)$ converges to X in probability,

• (dist) $X_n{\mathop {\longrightarrow }\limits ^{d}}X$ means that $(X_n)$ converges to X in distribution.

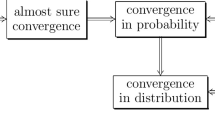
The following implications are well-known: (p-w)$\implies$(a.s.)$\implies$(prob)$\implies$(dist)

2.3 Laws of large numbers

Let $(X_n)$ be a sequence of random variables defined on the probability space $(\Omega ,{\mathcal {F}},P)$. Let $S_n=X_1+\dots +X_n$. The sequence $(X_n)$ satisfies the strong law of large numbers (or SLLN) if

$$\begin{aligned} \frac{1}{n}S_n-\frac{1}{n}E S_n{\mathop {\longrightarrow }\limits ^{as}} 0. \end{aligned}$$

The sequence $(X_n)$ satisfies the weak law of large numbers (or WLLN) if

$$\begin{aligned} \frac{1}{n}S_n-\frac{1}{n}E S_n{\mathop {\longrightarrow }\limits ^{P}} 0 \end{aligned}$$

that is

$$\begin{aligned} \lim _{n\rightarrow \infty }P\left( \left| \frac{1}{n}S_n-\frac{1}{n}E S_n\right| \ge \varepsilon \right) =0 \end{aligned}$$

for every positive $\varepsilon$.

Theorem 4

[Markov] Suppose that $(X_n)$ is a sequence of random variables such that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n^2}Var(X_1+\dots +X_n)=0. \end{aligned}$$

(1)

Then $(X_n)$ satisfies the WLLN.

We will refer to condition (1) as the Markov condition.

Theorem 5

[Kolmogorov] Let $(X_n)$ be a sequence of independent random variables. If

$$\begin{aligned} \sum _{n=1}^\infty \frac{Var X_n}{n^2}<\infty , \end{aligned}$$

(2)

then $(X_n)$ satisfies SLLN.

We will refer to condition (2) as the Kolmogorov condition.

Note that the Kolmogorov condition implies the Markov condition for independent random variables. Indeed, suppose that $\sum _{n=1}^\infty \frac{Var X_n}{n^2}<\infty$. Let $\varepsilon >0$. There is N such that $\sum _{n=N+1}^\infty \frac{Var X_n}{n^2}<\varepsilon /2$. Let $n_0>N$ be such that

$$\begin{aligned} \frac{Var X_1+\dots +Var X_N}{m^2}<\frac{\varepsilon }{2} \end{aligned}$$

for every $m>n_0$. Then

$$\begin{aligned} \frac{Var X_1+\dots +Var X_m}{m^2}= & {} \frac{Var X_1+\dots +Var X_N}{m^2}+\frac{Var X_{N+1}+\dots +Var X_m}{m^2} \\< & {} \frac{\varepsilon }{2}+\frac{Var X_{N+1}}{(N+1)^2}+\dots +\frac{Var X_m}{m^2}<\frac{\varepsilon }{2}+\frac{\varepsilon }{2}=\varepsilon . \end{aligned}$$

Thus $\lim _{n\rightarrow \infty }\frac{1}{n^2}Var( X_1+\dots +X_n)=0$.

Note that the proved implication is a statement about real sequences and has no probabilistic nature. The following diagram briefly summarizes relations between considered notions.

None of the above arrows, or implications, can be reversed.

2.4 Almost disjoint families

A family ${\mathcal {A}}$ of infinite subsets of ${\mathbb {N}}$ is called almost disjoint if any two distinct members of ${\mathcal {A}}$ have a finite intersection. It is well-known that there is an almost disjoint family of cardinality continuum. A family ${\mathcal {I}}$ of subsets of ${\mathbb {N}}$ is called ideal, provided that it is closed under taking subsets and finite unions, and does not contain ${\mathbb {N}}$. A particular example, which will be of our interest, is a so-called summable ideal. Let $(a_n)$ be a sequence of non-negative reals with $\sum _{n=1}^\infty a_n=\infty$. Then ${\mathcal {I}}_{(a_n)}:=\{S\subseteq {\mathbb {N}}:\sum _{n\in S}a_n<\infty \}$ is called a summable ideal. A family ${\mathcal {A}}$ is called ${\mathcal {I}}_{(a_n)}$-almost disjoint if it is almost disjoint and $A\notin {\mathcal {I}}_{(a_n)}$ for every $A\in {\mathcal {A}}$.

Lemma 6

Suppose that a series of positive real numbers $\sum _{n=1}^\infty a_n$ is divergent. Then there exists an ${\mathcal {I}}_{(a_n)}$-almost disjoint family of cardinality continuum.

Proof

Let $\{A_\alpha :\alpha <{\mathfrak {c}}\}$ be an almost disjoint family. Since the series $\sum _{n=1}^\infty a_n$ is divergent, we find indices $n_1<n_2<\dots$ such that

$$\begin{aligned} \sum _{k=n_i}^{n_{i+1}-1}a_k\ge 1. \end{aligned}$$

Sets of the form $B_\alpha :=\bigcup _{i\in A_\alpha }\{n_i,n_{i}+1,\dots ,n_{i+1}-1\}$ constitute the desired family. $\square$

3 Atomless probability measure

We say that a measure $\mu$ on $(\Omega ,{\mathcal {F}})$ is atomless if for any $\mu$-measurable set A with $\mu (A)>0$ there is a $\mu$-measurable set B with $0<\mu (B)<\mu (A)$. All considered subsets of $\Omega$ are in ${\mathcal {F}}$.

Lemma 7

Let $\mu$ be an atomless probability measure and let A be $\mu$-measurable. Then for any $0<t<\mu (A)$ there is $B\subseteq A$ with $\mu (B)= t$.

Proof

Firstly let us observe that for any $0<t<\mu (A)$ there is $B\subseteq A$ with $\mu (B)\le t$. Since $\mu$ is atomless, there is $C\subseteq A$ with $0<\mu (C)<\mu (A)$. Let $B_0=C$ if $\mu (C)\le \mu (A\setminus C)$, and $B_0=C\setminus A$ otherwise. Then $\mu (B_0)\le \frac{1}{2}\mu (A)$. Proceeding inductively we find a sequence $(B_n)$ with $B_{i+1}\subseteq B_i$ and $0<\mu (B_i)\le \frac{1}{2^{i+1}}\mu (A)$. Thus there is i with $0<\mu (B_i)\le t$.

Now, we are ready to prove the assertion. By a transfinite induction we define $B_\alpha \subseteq A$ such that $B_{\alpha +1}\subseteq A\setminus \bigcup _{\beta \le \alpha }B_\beta$ and $0<\mu (B_{\alpha +1})\le t-\sum _{\beta \le \alpha }\mu (B_\beta )$. Clearly after countably many steps, say after $\eta <\omega _1$ many, the construction stops. Then $\sum _{\beta \le \eta }\mu (B_\beta )=t$ and $B_\alpha$’s are pairwise disjoint. Therefore putting $B=\bigcup _{\beta \le \eta }B_\beta$ we have $\mu (B)=t$. $\square$

Lemma 8

Let $\mu$ be an atomless probability measure. Let $n_i\ge 2$ for $i\in {\mathbb {N}}$. Assume that $(p^i_j)_{i\in {\mathbb {N}}, j\le n_i}$ are such that

• (1) $0<p_j^i<1$

• (2) $\sum _{j\le n_i}p^i_j=1$.

Then there exists $(A^i_j)_{i\in {\mathbb {N}}, j\le n_i}$ such that

• (i) $\mu (A^i_j)=p^i_j$

• (ii) $A_1^i, A_2^i,\dots , A_{n_i}^i$ are pairwise disjoint

• (iii) The $\sigma$-fields ${\mathcal {F}}_i:=\sigma (\{A_j^i:j\le n_i\})$ are independent.

Proof

Using Lemma 7 we find pairwise disjoint $A^1_1,A^1_2,\dots , A^1_{n_1}$ with $\mu (A^1_j)=p^1_j$. Now, assume that for every $i\le k$ we have already defined $A^i_j$’s fulfilling (i)–(iii). Let $j\le n_{k+1}$. Fix $j_1\le n_1,j_2\le n_2,\dots ,j_k\le n_k$. By the inductive assumption $A^1_{j_1}\cap A^2_{j_2}\cap \dots \cap A^k_{j_k}=p^1_{j_1}p^2_{j_2}\cdots p^k_{j_k}$. Using Lemma 7 again we find $C_{j_1j_2\dots j_kj}\subseteq A^1_{j_1}\cap A^2_{j_2}\cap \dots \cap A^k_{j_k}$ such that $\mu (C_{j_1j_2\dots j_kj})=p^1_{j_1}p^2_{j_2}\cdots p^k_{j_k}p^{k+1}_j$. Put

$$\begin{aligned} A^{k+1}_j:=\bigcup _{j_1\le n_1}\bigcup _{j_2\le n_2}\cdots \bigcup _{j_k\le n_k}C_{j_1j_2\dots j_kj}. \end{aligned}$$

Then $(A^i_j)_{i\le k+1,j\le n_i}$ fulfills (i)–(iii). $\square$

Lemma 9

Let $\mu$ be an atomless probability measure. Assume that $\{B_k^1:k\le K_1\},\dots ,\{B_k^t:k\le K_t\}$ and $\{A_i:i\le I\}$ are partitions of $\Omega$ into sets of positive $\mu$-measure and such that $\sigma (\{B_k^1:k\le K_1\}),\dots ,\sigma (\{B_k^t:k\le K_t\})$ and $\sigma (\{A_i:i\le I\})$ are independent $\sigma$-fields. Let $\{p^\ell _i:\ell =1,2,\dots ,n_i\}$, $i\le I$, be positive real numbers with $p^1_i+p^2_i+\dots +p^{n_i}_i=\mu (A_i)$. Then there exist $A^\ell _i\subseteq \Omega$, $i\le I$, $\ell =1,2,\dots ,n_i$ such that

• (i) $A^1_i,A^2_i,\dots ,A^{n_i}_i$ are pairwise disjoint and $\bigcup _{\ell =1}^{n_i} A^\ell _i=A_i$;

• (ii) $\mu (A_i^\ell )=p^\ell _i$ for every $i\le I$ and $\ell \le n_i$;

• (iii) $\sigma$-fields $\sigma (\{B_k^1:k\le K_1\}),\dots ,\sigma (\{B_k^t:k\le K_t\})$ and $\sigma (\{A_i^\ell :i\le I, \ell =1,2,\dots ,n_i\})$ are independent.

Proof

Fix $i\le I$. By the independence assumption

$$\begin{aligned} \mu (A_i\cap B_{k_1}\cap \dots \cap B_{k_t})=\mu (A_i)\mu (B_{k_1})\cdots \mu (B_{k_t}) \end{aligned}$$

for every ${\bar{k}}=(k_1,\dots ,k_t)\in \{1,\dots ,K_1\}\times \dots \times \{1,\dots ,K_t\}$. Using Lemma 7 we find $C_{i,{\bar{k}}}^1,C_{i,{\bar{k}}}^2,\dots ,C_{i,{\bar{k}}}^{n_i}$ such that

• $C_{i,{\bar{k}}}^1,C_{i,{\bar{k}}}^2,\dots ,C_{i,{\bar{k}}}^{n_i}$ are pairwise disjoint and $\bigcup _{\ell =1}^{n_i}C_{i,k}^\ell =A_i\cap B_k$;

• $\mu (C_{i,{\bar{k}}}^\ell )=p_i^\ell \mu (B_{k_1})\cdots \mu (B_{k_t}).$

Having this we define $A_i^\ell$ as a union $\bigcup _{{\bar{k}}} C_{i,{\bar{k}}}^\ell$. Note that

$$\begin{aligned} \mu (A_i^\ell )=\mu (\bigcup _{{\bar{k}}} C_{i,{\bar{k}}}^\ell )=\sum _{{\bar{k}}} \mu (C_{i,{\bar{k}}})=\sum _{{\bar{k}}} p_i^\ell \mu (B_{k_1})\cdots \mu (B_{k_t})=p_i^\ell . \end{aligned}$$

Clearly conditions (i)–(iii) are fulfilled. $\square$

Let us define partitions ${\mathcal {X}}_k$ of ${\mathbb {R}}$, $k=0,1,\dots$ as follows: ${\mathcal {X}}_0=\{(-\infty ,-1],(-1,0], (0,1],(1,\infty )\}$ and

$$\begin{aligned} {\mathcal {X}}_k=\left\{ \left( \frac{n}{2^k},\frac{n+1}{2^k}\right] :-k2^k\le n<k2^k\right\} \cup \{(-\infty ,-k],(k,\infty )\}. \end{aligned}$$

Then ${\mathcal {X}}_{k+1}$ arises from ${\mathcal {X}}_k$ by

• dividing each $(\frac{n}{2^k},\frac{n+1}{2^k}]$ into two dyadic sub-intervals $(\frac{2n}{2^{k+1}},\frac{2n+1}{2^{k+1}}]$ and $(\frac{2n+1}{2^{k+1}},\frac{2n+2}{2^{k+1}}]$;

• adding $2\cdot 2^{k+1}$ dyadic intervals $(\frac{n}{2^{k+1}},\frac{n+1}{2^{k+1}}]$ for $-(k+1)2^{k+1}\le n<-k2^{k+1}$ and $k2^{k+1}\le n<(k+1)2^{k+1}$;

• replacing $(-\infty ,-k]$ and $(k,\infty )$ by $(-\infty ,-(k+1)]$ and $(k+1,\infty )$.

Note that $\sigma ({\mathcal {X}}_0)\subseteq \sigma ({\mathcal {X}}_1)\subseteq \dots$ If X is a random variable, then by $\mu _X$ we denote its distribution.

Theorem 10

Let P be an atomless probability measure on $(\Omega ,{\mathcal {F}})$. Let $\mu _0,\mu _1,\dots$ be a sequence of distributions on ${\mathbb {R}}$. Then there are independent random variables $X_0,X_1,\dots$ defined on $(\Omega ,{\mathcal {F}})$ with $\mu _{X_i}=\mu _i$ for every $i\in {\mathbb {N}}$.

Proof

We will inductively define partitions ${\mathcal {Y}}^k_\ell$ of ${\mathbb {N}}$ and random variables $X^k_\ell$ such that

• (i) ${\mathcal {Y}}^k_\ell =\{A_{I,\ell }:I\in {\mathcal {X}}_k\}$, in other words partition ${\mathcal {Y}}^k_\ell$ is indexed by elements of partition ${\mathcal {X}}_k$;

• (ii) $\mu _\ell (I)=P(A_{I,\ell })$ for every $I\in {\mathcal {X}}_k$;

• (iii) If $I_1,\dots ,I_p\in {\mathcal {X}}_{k+1}$ are pairwise disjoint, $I=I_1\cup \dots \cup I_p$ and $I\in {\mathcal {X}}_k$, then $A_{I,\ell }=A_{I_1,\ell }\cup \dots \cup A_{I_p,\ell }$;

• (iv) Let $\omega \in \Omega$. If $\omega \in A_{I,\ell }$ where $I=(-\infty ,-k]$, then $X^k_\ell (\omega )=-k$; otherwise $X^k_\ell (\omega )=\inf I$ for $\omega \in A_{I,\ell }$;

• (v) For every $\ell _1<\ell _2<\dots <\ell _t$ and $k_1,k_2,\dots ,k_t$, $\sigma$-fields $\sigma ({\mathcal {Y}}^{k_1}_{\ell _1}),\sigma ({\mathcal {Y}}^{k_2}_{\ell _2}), \dots ,\sigma ({\mathcal {Y}}^{k_t}_{\ell _t})$ are independent.

Suppose that we have defined ${\mathcal {Y}}^k_\ell$ and $X^k_\ell$ for every $k,\ell \in {\mathbb {N}}$. Note that $(X^k_\ell )_{k=1}^\infty$ converges in measure to some $X_\ell$ with $\mu _{X_\ell }=\mu _\ell$. To show that $X_1,X_2,\dots$ are independent, it is enough to prove that

$$\begin{aligned} X^{-1}_1(I_1),X^{-1}_2(I_2),\dots ,X^{-1}_\ell (I_\ell ) \end{aligned}$$

are independent for every (left-open and right-closed) dyadic interval. Note that $I_i\in \sigma ({\mathcal {X}}_{k_i})$ for some $k_i$. Then $X_{i}^{-1}(I_i)=(X_i^{k_i})^{-1}(I_i)=A_{I_i,i}\in {\mathcal {Y}}^{k_i}_i$. So by (v) we obtain that $X_1,X_2,\dots$ are independent.

We will construct ${\mathcal {Y}}^k_\ell$ and $X^k_\ell$ fulfilling (i)–(v) by induction. In first step we construct ${\mathcal {Y}}^0_0$ and $X^0_0$ as follows. Using Lemma 8 we find a partition ${\mathcal {Y}}^0_0=\{A_{I,0}:I\in {\mathcal {X}}_0\}$ of $\Omega$ with $P(A_{I,0})=\mu _0(I)$. This gives us (i) and (ii). Put

$$\begin{aligned} X^0_0(\omega ) = {\left\{ \begin{array}{ll} -1 &{} \text {if} \quad \omega \in A_{(-\infty ,-1],0}\cup A_{(-1,0],0} \\ 0 &{} \text {if} \quad \omega \in A_{(0,1],0} \\ 1 &{} \text {if} \quad \omega \in A_{(1,\infty ),0}. \end{array}\right. } \end{aligned}$$

This just (iv). Conditions (iii) and (v) are also satisfied.

Now, assume that we have already constructed ${\mathcal {Y}}^k_\ell$ and $X^k_\ell$ for $k,\ell \le n$. In one step we construct ${\mathcal {Y}}^{n+1}_\ell$, $X^{n+1}_\ell$ for $\ell =0,1,\dots ,n$, and ${\mathcal {Y}}^k_{n+1}$, $X^k_{n+1}$ for $k=0,1,\dots ,n+1$. Using $2n+3$ times Lemma 9 we define ${\mathcal {Y}}^{n+1}_\ell$ and ${\mathcal {Y}}^k_{n+1}$ fulfilling (i), (ii), (iii) and (v). Then we define $X^{n+1}_\ell$ and $X^k_{n+1}$ using the formula given in (iv). $\square$

4 Various kinds of convergence

Let $(\Omega , {\mathcal {F}},P)$ be a measurable space. By $L_0(\Omega )$ we denote the space of all random variables. The following should be compared with [1, Theorem 7.1] where the Authors proved maximal dense lineability of random variables sequences defined on [0, 1] which tend to 0 in measure, but not almost everywhere. Note that strong algebrability and dense lineability are incomparable notions—none of them implies the other.

Theorem 11

Let P be an atomless probability measure on $(\Omega ,{\mathcal {F}})$. There exists a ${\mathfrak {c}}$-generated free algebra ${\mathcal {A}}\subseteq L_0(\Omega )^{\mathbb {N}}$ such that any $(X_n)\in {\mathcal {A}}\setminus \{{\textbf{0}}\}$ is a sequence of independent random variables such that

• (i) $X_n\xrightarrow {P}0$

• (ii) $\limsup _{n\rightarrow \infty }\vert X_n(\omega )\vert =\infty$ for every $\omega \in \Omega$.

• (iii) $\lim _{n\rightarrow \infty }E\vert X_n\vert =\infty$.

Proof

By Lemma 8 there are $(A^n_{j})_{n\in {\mathbb {N}}, j\le n+1}$ such that $P(A^n_j)=\frac{1}{n+1}$ and sigma fields $\sigma (\{A^n_{j}:j\le n+1\})$ are independent. Let $B_n=A^n_1$ for $n\in {\mathbb {N}}$. Since $B_n$ are independent and $\sum _{n=1}^\infty \frac{1}{n+1}=\infty$, by Borel-Cantelli lemma we obtain that $P(\limsup B_n)=1$. Then $C:=\Omega \setminus \limsup B_n$ has probability 0. Put $I_n:=C \cup B_n$. Then $P(I_n)=P(B_n)=\frac{1}{n+1}$ and every $\omega \in \Omega$ belongs to infinitely many $I_n$’s.

Let $U\subseteq {\mathbb {R}}$ be a set of cardinality ${\mathfrak {c}}$ linearly independent over ${\mathbb {Q}}$. For any $\alpha \in U$ and $n\in {\mathbb {N}}$ we define a random variable $X_n^{(\alpha )}:=e^{\alpha n}{\textbf{1}}_{I_n}$ where ${\textbf{1}}_{I_n}$ is a characteristic function of $I_n$. The sequence $(X_n^{(\alpha )})$ consists of independent random variables.

We will show that any non-trivial algebraic combination of elements from $\{(X_n^{(\alpha )}):\alpha \in U\}$ is either a null sequence or it is a sequence of independent random variables fulfilling (i) and (ii). Let $\left( k_{i l}: i \le m, l \le j\right)$ be a matrix of non-negative integers with non-zero and distinct rows, and assume that $c_{1}, \ldots , c_{m} \in {\mathbb {R}}$ do not vanish simultaneously. Consider the following algebraic combination of $X_n^{(\alpha _1)}, X_n^{(\alpha _2)},\dots ,X_n^{(\alpha _j)}$

$$\begin{aligned} Y_n=\sum _{i=1}^m c_i e^{\left( k_{i1} \alpha _{1}+\ldots +k_{ij} \alpha _{j}\right) n}{\textbf{1}}_{I_n}. \end{aligned}$$

(3)

Since the set U is linearly independent, the numbers $k_{11} \alpha _{1}+\ldots +k_{1 j} \alpha _{j}, \ldots , k_{m 1} \alpha _{1}+\ldots +k_{m j} \alpha _{j}$ are distinct. To simplify the notation, put $\gamma _{i}:=k_{i 1} \alpha _{1}+\ldots +k_{i j} \alpha _{j}$ for every $i=1, \ldots , m$. We may assume that $\gamma _1>\gamma _2>\dots >\gamma _m$. Then for any $n\in {\mathbb {N}}$ and $\omega \in I_n$,

$$\begin{aligned} Y_n(\omega )=\sum _{i=1}^m c_i e^{\gamma _in}=e^{\gamma _1n} \left( c_1+\sum _{i=2}^m c_i e^{(\gamma _i-\gamma _1)n}\right) . \end{aligned}$$

Thus $Y_n(\omega )\approx c_1e^{\gamma _1n}$ for every $\omega \in I_n$ for large enough n. By (3), we obtain $(Y_n)$ is a sequence of independent random variables. Since every $\omega \in \Omega$ belongs to infinitely many $I_n$’s and $\gamma _i>1$, then

$$\begin{aligned} \limsup _{n\rightarrow \infty }\vert Y_n(\omega )\vert =\infty . \end{aligned}$$

Again by (3), we obtain $P(Y_n\ne 0)\le \frac{1}{n+1}$, and therefore $Y_n\xrightarrow {P}0$. Since $E(Y_n)=\frac{e^{\gamma _1n}}{n}$, then $\lim _{n\rightarrow \infty } E(Y_n)=\infty$ $\square$

Theorem 12

Let $(\Omega ,{\mathcal {F}},P)$ be an atomless probability space. Then the set

$$\begin{aligned} \left\{ (X_n)\in L_0(\Omega )^{\mathbb {N}}:X_n\xrightarrow {P}0\text { but }\frac{X_1+\dots +X_n}{n}\text { does not converge in probability to }0\right\} \end{aligned}$$

is strongly ${\mathfrak {c}}$-algebrable.

Proof

Let $(A_n)$ be a sequence of independent events defined on $(\Omega ,{\mathcal {F}},P)$ such that $P(A_n)=\frac{1}{n+1}$. Let $U\subseteq (1,2)$ be linearly independent over ${\mathbb {Q}}$. Fix $\alpha \in U$. Put $X_n^{(\alpha )}=2^{\alpha n}{\textbf{1}}_{A_n}$. Let $\left( k_{i l}: i \le m, l \le j\right)$ be a matrix of non-negative integers with non-zero and distinct rows, and assume that $c_{1}, \ldots , c_{m} \in {\mathbb {R}}$ do not vanish simultaneously. Consider the following algebraic combination of $X_n^{(\alpha _1)}, X_n^{(\alpha _2)},\dots ,X_n^{(\alpha _j)}$

$$\begin{aligned} Y_n=\sum _{i=1}^m c_i 2^{(k_{i1} \alpha _{1}+\ldots +k_{ij} \alpha _{j})n}{\textbf{1}}_{A_n}. \end{aligned}$$

(4)

Since the set U is linearly independent, the numbers $k_{11} \alpha _{1}+\ldots +k_{1 j} \alpha _{j}, \ldots , k_{m 1} \alpha _{1}+\ldots +k_{m j} \alpha _{j}$ are distinct. As in the proof of Theorem 11 we put $\gamma _{i}:=k_{i 1} \alpha _{1}+\ldots +k_{i j} \alpha _{j}$ for every $i=1, \ldots , m$. We may assume that $\gamma _1>\gamma _2>\dots >\gamma _m$. Then for any $n\in {\mathbb {N}}$ and $\omega \in A_n$,

$$\begin{aligned} Y_n(\omega )=\sum _{i=1}^m c_i 2^{\gamma _in}=2^{\gamma _1n}\left( c_1+\sum _{i=2}^m c_i 2^{(\gamma _i-\gamma _1)n}\right) . \end{aligned}$$

There is $n_0$ such that for $n\ge n_0$,

• (a) $\vert Y_n\vert \ge \frac{1}{2}\vert c_1\vert 2^{\gamma _1n}>\frac{1}{2}\vert c_1\vert 2^{n}$ on $A_n$ and $Y_n=0$ on the complement $A_n^c$ of $A_n$;

• (b) $Y_n$ has the same sign as $c_1$, and therefore $\vert Y_{n_0}+\dots +Y_n\vert =\vert Y_{n_0}\vert +\dots +\vert Y_n\vert$

Let $k_0\ge n_0$ be such that $P(\vert Y_1\vert +\dots +\vert Y_{n_0-1}\vert <\frac{1}{4}\vert c_1\vert 2^{k_0})=1$. The aim of the following reasoning is to show that $P\left( \frac{\vert Y_1\vert +\dots +\vert Y_{2^k}\vert }{2^k}<\frac{\vert c_1\vert }{4}\right)$ tends to zero, and consequently $\frac{\vert Y_1\vert +\dots +\vert Y_{n}\vert }{n}$ does not converge in probability to zero.

For $k>k_0$ we have

$$\begin{aligned}{} & {} P\left( \frac{\vert Y_1+\dots +Y_{2^k}\vert }{2^k}<\frac{1}{4} \vert c_1\vert \right) \\{} & {} \quad = P\left( \vert Y_1+\dots +Y_{2^k}\vert<\frac{1}{4}\vert c_1\vert 2^k\right) \\{} & {} \quad \le P\left( \vert Y_{n_0}+\dots + Y_{2^k}\vert -\vert Y_1 +\dots +Y_{n_0-1}\vert<\frac{1}{4}\vert c_1\vert 2^k\right) \\{} & {} \quad =P\left( \vert Y_{n_0}+\dots + Y_{2^k}\vert<\frac{1}{4}\vert c_1\vert 2^k +\vert Y_1+\dots +Y_{n_0-1}\vert \right) \\{} & {} \quad =P\left( \vert Y_{n_0}\vert +\dots +\vert Y_{2^k}\vert<\frac{1}{4}\vert c_1\vert 2^k +\vert Y_1+\dots +Y_{n_0-1}\vert \right) \\{} & {} \quad \le P\left( \vert Y_{n_0}\vert +\dots +\vert Y_{2^k}\vert<\frac{1}{4}\vert c_1\vert 2^k +\vert Y_1\vert +\dots +\vert Y_{n_0-1}\vert \right) \\{} & {} \quad \le P\left( \vert Y_{n_0}\vert +\dots +\vert Y_{2^k}\vert <\frac{1}{2}\vert c_1\vert 2^k\right) . \end{aligned}$$

If $\omega \in A_n$ for some $n\ge k$, then $Y_n(\omega )\ge \frac{1}{2}\vert c_1\vert \cdot 2^n\ge \frac{1}{2}\vert c_1\vert \cdot 2^k$. Hence $\vert Y_{n_0}\vert +\dots +\vert Y_{2^k}\vert \ge \vert Y_n\vert \ge \frac{1}{2}\vert c_1\vert \cdot 2^k.$ Thus

$$\begin{aligned} P\left( \vert Y_{n_0}\vert +\dots +\vert Y_{2^k}\vert <\frac{1}{2}\vert c_1\vert 2^k\right) \le P(A_k^c\cap \dots \cap A_{2^k}^c)=P(A_k^c)\cdots P( A_{2^k}^c)\\ =\frac{2^k}{2^{k}+1}\cdot \frac{2^k-1}{2^k}\cdots \frac{k}{k+1}=\frac{k}{2^k+1}\rightarrow 0. \end{aligned}$$

Thus $\frac{Y_1+\dots +Y_n}{n}$ does not converge in probability to 0. Since $P(Y_n=0)=\frac{n}{n+1}$, then $Y_n\xrightarrow {P}0$. $\square$

Theorem 13

Let $(\Omega ,{\mathcal {F}},P)$ be an atomless probability space. Let ${\mathbb {U}}$ be a set of all sequences $(X_n)\in L_0(\Omega )^{\mathbb {N}}$ such that

• (i) $(X_n)$ is independent

• (ii) $X_n\xrightarrow {P}0$

• (iii) there is a constant $C>0$ with $\vert X_n\vert <C$ for every $n\in {\mathbb {N}}$

• (iv) $X_n\nrightarrow 0$ almost surely.

Then ${\mathbb {U}}$ is ${\mathfrak {c}}$-lineable.

Proof

Let $(A_n)$ be a sequence of independent events in $\Omega$ with $P(A_n)=\frac{1}{n}$. Let ${\mathcal {A}}=\{B_\alpha :\alpha <{\mathfrak {c}}\}$ be an ${\mathcal {I}}_{(1/n)}$-almost disjoint family. We define $(X_n^{(\alpha )})$ as follows:

$$\begin{aligned} X_n^{(\alpha )} = {\left\{ \begin{array}{ll} {\textbf{1}}_{A_n} &{} \text {if}\quad n\in B_\alpha \\ 0 &{} \text {if}\quad n\notin B_\alpha . \end{array}\right. } \end{aligned}$$

Let $c_1,\dots ,c_m\in {\mathbb {R}}\setminus \{0\}$ and $\alpha _1<\dots<\alpha _m<{\mathfrak {c}}$. Consider $Y_n=c_1X_n^{(\alpha _1)}+\dots +c_mX_n^{(\alpha _m)}$. Since $B:=B_{\alpha _1}\setminus (B_{\alpha _2}\cup \dots \cup B_{\alpha _m})$ is infinite and $c_1\ne 0$, by Borel–Cantelli lemma we obtain that $P(\limsup _{n\in B}A_n)=1$, and therefore $Y_n\nrightarrow 0$ a.s. for $n\in B$, which implies (iv). Clearly $(Y_n)$ is independent and $Y_n\xrightarrow {P}0$; thus (i) and (ii) holds. Note also that $\vert Y_n\vert \le \vert c_1\vert +\dots +\vert c_m\vert$ for every $n\in {\mathbb {N}}$ which gives (iii). Therefore $(Y_n)\in {\mathbb {U}}$, which shows that ${\mathbb {U}}$ is ${\mathfrak {c}}$-lineable. $\square$

It is well known that if $(\Omega ,{\mathcal {F}},P)$ is atomic probability space, then for any $(X_n)$ defined there, $X_n\xrightarrow {P}0$ is equivalent to $X_n\xrightarrow {a.s.}0$. This shows that Theorems 11, 12 and 13 do not hold for atomic spaces.

Problem 14

Is the set ${\mathbb {U}}$ defined in Theorem  13 strongly ${\mathfrak {c}}$-algebrable?

5 Laws of large numbers

Theorem 15

Let $(\Omega ,{\mathcal {F}},P)$ be an atomless probability space. Then the set

$$\begin{aligned} \{(X_n)\in L_0(\Omega )^{\mathbb {N}}:X_n\text { are independent and } (X_n)\text { satisfies Markov condition but not SLLN}\} \end{aligned}$$

is ${\mathfrak {c}}$-lineable.

Proof

Let $a_n=\frac{1}{(n+1)\log (n+1)}$. Note that $\sum _{n=1}^\infty a_n$ is divergent, so there is an almost disjoint family $\{B_\alpha \subseteq {\mathbb {N}}:\alpha <{\mathfrak {c}}\}$ such that $B_\alpha \notin {\mathcal {I}}_{(a_n)}$.

Using Lemma 8 for

$$\begin{aligned} p^n_1=p^n_2=\frac{1}{2(n+1)\log (n+1)}\;\;\;\text { and }\;\;\; p^n_3=1-\frac{1}{(n+1)\log (n+1)} \end{aligned}$$

we obtain sets $\{A^n_i:n\in {\mathbb {N}}, i=1,2,3\}$ such that $P(A^n_i)=p^n_i$ and $\sigma$-fields $\sigma (\{A^n_i:i=1,2,3\})$ are independent. For $n\in {\mathbb {N}}$ let $Z_n$ be a random variable given by

$$\begin{aligned} Z_n(\omega ) = {\left\{ \begin{array}{ll} -n &{} \text {if}\quad \omega \in A^n_1 \\ n &{} \text {if}\quad \omega \in A^n_2 \\ 0 &{} \text {if}\quad \omega \in A^n_3. \end{array}\right. } \end{aligned}$$

(Note that $Z_n$ can be defined shortly as $-n{\textbf{1}}_{A^n_1}+n{\textbf{1}}_{A^n_2}$.) Then $Z_n$ are independent such that

$$\begin{aligned} P(Z_n=n)= & {} P(Z_n=-n)=\frac{1}{2(n+1)\log (n+1)}\;\;\;\text { and }\\ P(Z_n=0)= & {} 1-\frac{1}{(n+1)\log (n+1)}. \end{aligned}$$

Now, for $\alpha <{\mathfrak {c}}$ and $n\in {\mathbb {N}}$ we define: $X^{(\alpha )}_n=Z_n$ for indexes n from $B_\alpha$, and $X^{(\alpha )}_n=0$ otherwise. Consider a linear subspace ${\mathcal {V}}$ of $L_0(\Omega )^{\mathbb {N}}$ spanned by $\{(X_n^{(\alpha )}):\alpha <{\mathfrak {c}}\}$. Let $(X_n)\in {\mathcal {V}}$ be a non-null sequence. Then there are $c_1,\dots ,c_m\in {\mathbb {R}}\setminus \{0\}$ and $\alpha _1<\dots<\alpha _m<{\mathfrak {c}}$ such that $X_n=\sum _{i=1}^m c_i X_n^{(\alpha _i)}$ for every $n\ge 1$. Note that $X_n$ are independent.

Observe that $X_n=Z_n\cdot \sum _{i=1}^mc_i{\textbf{1}}_{B_{\alpha _i}}(n)$. Thus

$$\begin{aligned} Var X_n=\left| \sum _{i=1}^mc_i{\textbf{1}}_{B_{\alpha _i}}(n)\right| ^2 Var Z_n\le \left( \sum _{i=1}^m\vert c_i\vert \right) ^2 Var Z_n. \end{aligned}$$

Since $X_n$ are independent, $Z_n$ are independent and $(Z_n)$ satisfies Markov condition (see [10]), that is $\frac{1}{n^2} Var(Z_1+\dots +Z_n)\rightarrow 0$,

$$\begin{aligned}{} & {} 0 \le \frac{1}{n^2}Var(X_1+\dots +X_n)=\frac{1}{n^2}\sum _{j=1}^n Var X_j\le \frac{1}{n^2}\sum _{j=1}^n\left( \sum _{i=1}^m\vert c_i\vert \right) ^2\\{} & {} Var Z_j=\frac{1}{n^2}\left( \sum _{i=1}^m\vert c_i\vert \right) ^2 Var(Z_1+\dots +Z_n)\rightarrow 0. \end{aligned}$$

Thus $(X_n)$ satisfies Markov condition, and consequently the weak law of large numbers.

Put $B:=B_{\alpha _1}\setminus \bigcup _{i=2}^m B_{\alpha _i}$. Then $B\notin {\mathcal {I}}_{(a_n)}$. Note that $n\in B$ implies that $X_n=c_1 X^{(\alpha _1)}_n=c_1 Z_n$, and therefore

$$\begin{aligned} P(\vert X_n\vert \ge \vert c_1\vert n)=P(\vert Z_n\vert \ge n) =\frac{1}{(n+1)\log (n+1)}=a_n. \end{aligned}$$

Since $B\notin {\mathcal {I}}_{(a_n)}$, then

$$\begin{aligned} \sum _{n\in B}P(\vert X_n\vert \ge \vert c_1\vert n)=\sum _{n\in B}a_n=\infty . \end{aligned}$$

By Borel–Cantelli lemma $P(\limsup \{\vert X_n\vert \ge \vert c_1\vert n\})=1$. Since $\frac{X_n}{n}=\frac{S_n}{n}-\frac{S_{n-1}}{n}$, then $\frac{S_n}{n}\nrightarrow 0$, where $S_n=X_1+\dots +X_n$. On the other hand $E X_n=0$, which implies $\frac{1}{n}E S_n=0$. That means that $(X_n)$ does not satisfy strong law of large numbers. $\square$

Theorem 16

Let P be an atomless probability measure on a measure space $(\Omega ,{\mathcal {F}})$. The set of all sequences $(X_n)\in L_0(\Omega )^{\mathbb {N}}$ of random variables satisfying the weak law of large numbers but neither the strong law of large numbers nor Markov condition is ${\mathfrak {c}}$-lineable.

Proof

By Theorem 10 there is a sequence $(Z_n)$ of independent random variables defined on $(\Omega ,{\mathcal {F}},P)$ whose distribution functions are absolutely continuous and their densities $f_n$ are given by the formula

$$\begin{aligned} f_n(x)=\frac{1}{\sqrt{2}\sigma _n}\exp \left( -\frac{\sqrt{2}\vert x\vert }{\sigma _n}\right) , \text { where }\sigma _n=\frac{2n^2}{(\log n)^2}. \end{aligned}$$

Then $E Z_n=0$ and $Var Z_n=\sigma _n^2$. Let $\{B_\alpha \subseteq {\mathbb {N}}:\alpha <{\mathfrak {c}}\}$ be an almost disjoint family. We define

$$\begin{aligned} X_n^{(\alpha )}(\omega ) = {\left\{ \begin{array}{ll} Z_n(\omega ) &{} \text {if}\quad n\in B_\alpha \\ 0 &{} \text {if}\quad n\notin B_\alpha . \end{array}\right. } \end{aligned}$$

Let $(X_n)$ be a non-zero sequence contained in a vector subspace of $(L_2(\Omega ))^{\mathbb {N}}$ spanned by $\{(X_n^{(\alpha )}):\alpha <{\mathfrak {c}}\}$. Then $X_n=\sum _{i=1}^m c_iX_n^{(\alpha _i)}$ for some $m\in {\mathbb {N}}$, $c_1,\dots ,c_m\in {\mathbb {R}}\setminus \{0\}$ and $\alpha _1<\dots<\alpha _m<{\mathfrak {c}}$.

Now, we will check that $(X_n)$ does not satisfy SLLN. Let $n\in B_{\alpha _1}\setminus \bigcup _{i>1}B_{\alpha _i}$. Then $X_n=c_1 X_n^{(\alpha _1)}=c_1 Z_n$ and

$$\begin{aligned} P(\vert X_n\vert \ge \vert c_1\vert n) =P(\vert Z_n\vert \ge n)=\exp \left( -\frac{\sqrt{2}(\log n)^2}{2n}\right) . \end{aligned}$$

The set $B_{\alpha _1}\setminus \bigcup _{i>1}B_{\alpha _i}$ is infinite and $\exp (-\frac{\sqrt{2}(\log n)^2}{2n})\rightarrow 1$. Therefore the series

$$\begin{aligned} \sum _{n\in B_{\alpha _1}\setminus \bigcup _{i>1}B_{\alpha _i}}P(\vert X_n\vert \ge \vert c_1\vert n)\text { is divergent.} \end{aligned}$$

Since $X_n$ are independent, then Borel-Cantelli lemma implies that $P(\limsup \{\vert X_n\vert \ge \vert c_1\vert n\})=1$. Consequently $(X_n)$ does not satisfy SLLN.

Now we show that the Markov condition does not hold for $(X_n)$. Since $X_n$ are independent, then

$$\begin{aligned} \frac{1}{n^2}Var(X_1+\dots +X_n) =\frac{1}{n^2}(VarX_1+\dots +VarX_n)\ge \frac{1}{n^2}Var X_n \end{aligned}$$

For $n\in B_{\alpha _1}\setminus \bigcup _{i>1}B_{\alpha _i}$

$$\begin{aligned} \frac{1}{n^2}Var X_n=\frac{c_1^2}{n^2}Var Z_n =\frac{c_1^2}{n^2}\sigma ^2_n=\frac{4c_1n^2}{(\log n)^4}. \end{aligned}$$

Since $\frac{4c_1n^2}{(\log n)^4}\rightarrow \infty$ and $B_{\alpha _1}\setminus \bigcup _{i>1}B_{\alpha _i}$ is infinite, $(X_n)$ does not fulfill the Markov condition.

Stoyanov proved in [10, Sect. 15.4] using Feller Theorem that $(Z_n)$ fulfills the weak law of large numbers. It can be easily shown that any linear combination of $(X_n^{(\alpha )})$’s satisfies the weak law of large numbers as well. $\square$

Recall that two sequences of random variables $\left\{ \xi _{n}\right\}$ and $\left\{ \eta _{n}\right\}$ are said to be equivalent in the sense of Khintchine if $\sum _{n=1}^{\infty } P\left[ \xi _{n} \ne \eta _{n}\right] <\infty$. According to [9, Theorem 1.2.4] two such sequences simultaneously satisfy or do not satisfy the SLLN.

Theorem 17

Let P be an atomless probability measure on a measure space $(\Omega ,{\mathcal {F}})$. The set

$$\begin{aligned} \{(X_n)\in L_0(\Omega )^{\mathbb {N}}:(X_n)\text { fulfills SLLN but not the Kolmogorov condition}\} \end{aligned}$$

is ${\mathfrak {c}}$-lineable.

Proof

Let $(Z_n)$ be a sequence of independent random variables defined on $\Omega$ such that $P(Z_n=1)=P(Z_n=-1)=\frac{1}{2}-\frac{1}{2^{n+1}}$ and $P(Z_n=2^n)=P(Z_n=-2^n)=\frac{1}{2^{n+1}}$. Then $E Z_n=0$ and $Var Z_n=1-\frac{1}{2^n}+2^n$. Let $\{B_\alpha :\alpha \in [0,1]\}$ be an almost disjoint family of subsets of ${\mathbb {N}}$. Put

$$\begin{aligned} X_n^{(\alpha )}(\omega ) = {\left\{ \begin{array}{ll} Z_n(\omega ) &{} \text {if}\quad n\in B_\alpha \\ 0 &{} \text {if}\quad n\notin B_\alpha . \end{array}\right. } \end{aligned}$$

Let $0\le \alpha _1<\alpha _2<\dots <\alpha _m\le 1$, and $c_1,c_2\dots ,c_m\in {\mathbb {R}}\setminus \{0\}$. Let $Y_n=\sum _{i=1}^mc_iX_n^{(\alpha _i)}$. Since $B:=B_{\alpha _1}\setminus (B_{\alpha _2}\cup \dots \cup B_{\alpha _m})$ is infinite and $Y_n=c_1 Z_n$ if $n\in B$, then $E Y_n=0$ for every n, and $Var Y_n=1-\frac{1}{2^{n}}+2^n$ for $n\in B$. Thus

$$\begin{aligned} \sum _{n=1}^\infty \frac{Var Y_n}{n^2}\ge \sum _{n\in B}\frac{2^n}{n^2}=\infty \end{aligned}$$

which means that $(Y_n)$ does not fulfill the Kolmogorov condition.

Let us define $({\hat{Z}}_n)$ as follows

$$\begin{aligned} {\hat{Z}}_n=\pm 1\iff Z_n=\pm 1 \text { and }{\hat{Z}}_n=0\iff \vert Z_n\vert =2^n. \end{aligned}$$

Then $({\hat{Z}}_n)$ and $(Z_n)$ are equivalent in the sense of Khintchine as $P({\hat{Z}}_n\ne Z_n)=\frac{1}{2^n}$. Morevoer $E {\hat{Z}}_n=0$ and $Var{\hat{Z}}_n=1-\frac{1}{2^n}$. Thus $({\hat{Z}}_n)$ satisfies the Kolmogorov condition. Put

$$\begin{aligned} {\hat{X}}_n^{(\alpha )}(\omega ) = {\left\{ \begin{array}{ll} {\hat{Z}}_n(\omega ) &{} \text {if}\quad n\in B_\alpha \\ 0 &{} \text {if}\quad n\notin B_\alpha \end{array}\right. } \end{aligned}$$

and ${\hat{Y}}_n=\sum _{i=1}^m c_i{\hat{X}}_n^{(\alpha _i)}$. Then $E{\hat{Y}}_n=0$ and

$$\begin{aligned} Var{\hat{Y}}_n=E({\hat{Y}}_n)^2\le \left( \sum _{n=1}^m \vert c_n\vert \right) ^2E({\hat{Z}}_n)^2=\left( \sum _{n=1}^m \vert c_n\vert \right) ^2Var{\hat{Z}}_n. \end{aligned}$$

Therefore

$$\begin{aligned} \sum _{n=1}^\infty \frac{Var{\hat{Y}}_n}{n^2}\le \left( \sum _{n=1}^m \vert c_n\vert \right) ^2\sum _{n=1}^\infty \frac{1}{n^2}<\infty . \end{aligned}$$

Thus $({\hat{Y}}_n)$ satisfies the Kolmogorov condition, and consequently $(Y_n)$ fulfills SLLN. $\square$

Let us recall here the big-O and the little-o notation. Having two sequences $(a_n)$ and $(b_n)$ of positive reals we write $a_n=O(b_n)$, if there is a constant $C>0$ such that $a_n\le Cb_n$ for every $n\in {\mathbb {N}}$; we write $a_n=o(b_n)$ if $\lim _{n\rightarrow \infty }a_n/b_n=0$. Although SLLN does not imply Kolmogorov condition, the latter cannot be improved in the sense that $\sum _{n=1}^\infty \frac{\sigma ^2_n}{n^2}<\infty$ would be replaced by $\sum _{n=1}^\infty a_n\sigma ^2_n<\infty$ for some sequence $(a_n)$ of positive reals with $a_n=o(1/n^2)$

Theorem 18

Let P be an atomless probability measure on a measure space $(\Omega ,{\mathcal {F}})$. Assume that $\sum _{n=1}^\infty \frac{\sigma ^2_n}{n^2}=\infty$. Then the set

$$\begin{aligned} \{(X_n)\in L_0(\Omega )^{\mathbb {N}}: E X_n=0,\; Var X_n=O(\sigma ^2_n)\text { and }(X_n)\text { does not obey the SLLN}\} \end{aligned}$$

is ${\mathfrak {c}}$-lineable.

Proof

Let ${\mathcal {I}}:={\mathcal {I}}_{(\sigma ^2_n/n^2)}=\{A\subseteq {\mathbb {N}}:\sum _{n\in A}\frac{\sigma ^2_n}{n^2}<\infty \}$. Let $\{B_\alpha :\alpha \in [0,1]\}$ be an ${\mathcal {I}}$-almost disjoint family. Let $A_n^i$ for $n\in {\mathbb {N}}$ and $i=1,2,3$ be such that

• (i) $P(A^1_n)=P(A^2_n)=\frac{\sigma ^2_n}{2n^2}$ and $P(A^3_n)=1-\frac{\sigma ^2_n}{n^2}$, if $\frac{\sigma ^2_n}{n^2}\le 1$

• (ii) $P(A^1_n)=P(A^2_n)=\frac{1}{2}$ and $P(A^3_n)=0$, if $\frac{\sigma ^2_n}{n^2}>1$

• (iii) the families $\{A^i_n:i=1,2,3\}$ are independent.

Let $\alpha \in [0,1]$. If $n\notin B_\alpha$, we put $X_n^{(\alpha )}\equiv 0$. If $n\in B_\alpha$ and $\frac{\sigma ^2_n}{n^2}\le 1$, we put

$$\begin{aligned} X_n^{(\alpha )}(\omega ) = {\left\{ \begin{array}{ll} -n &{} \text {if}\quad \omega \in A^1_n \\ n &{} \text {if}\quad \omega \in A^2_n \\ 0 &{} \text {if}\quad \omega \in A^3_n. \end{array}\right. } \end{aligned}$$

If $n\in B_\alpha$ and $\frac{\sigma ^2_n}{n^2}> 1$, we put

$$\begin{aligned} X_n^{(\alpha )}(\omega ) = {\left\{ \begin{array}{ll} -\sigma _n &{} \text {if}\quad \omega \in A^1_n \\ \sigma _n &{} \text {if}\quad \omega \in A^2_n. \end{array}\right. } \end{aligned}$$

Then $E X^{(\alpha )}_n=0$ for every $n\in {\mathbb {N}}$, $Var X_n=\sigma ^2_n$ iff $n\in B_\alpha$. Let $Y_n=\sum _{i=1}^mc_iX_n^{(\alpha _i)}$ be a linear combination of $X^{(\alpha _1)}_n,\dots , X^{(\alpha _m)}_n$ where $c_i\ne 0$, $0\le \alpha _1<\dots <\alpha _m\le 1$. Since $B:=B_{\alpha _1}\setminus \bigcup _{i=2}^m B_{\alpha _i}\notin {\mathcal {I}}$, then $Var Y_n=\vert c_1\vert \sigma ^2_n$ for $n\in B$. Since $B\notin {\mathcal {I}}$, then $\sum _{n=1}^\infty \frac{Var Y_n}{n^2}=\infty$. Moreover, for $n\in B$ and $\varepsilon \in (0,1)$:

$$\begin{aligned} P(\frac{\vert Y_n\vert }{n}\ge \varepsilon )=P(Y_n\ne 0)={\left\{ \begin{array}{ll} \frac{\sigma ^2_n}{n^n} &{} \text {if}\quad \frac{\sigma ^2_n}{n^2}\le 1 \\ 1 &{} \text {if}\quad \frac{\sigma ^2_n}{n^2}> 1. \end{array}\right. } \end{aligned}$$

Then $\sum _{n=1}^\infty P(\vert Y_n\vert >\varepsilon n)=\infty$ and by Borel-Cantelli lemma $\frac{Y_n}{n}\nrightarrow 0$ almost surely. Thus $(Y_n)$ does not obey the SLLN. $\square$

Lemma 19

Let $(b_n)\in \ell _1$. Suppose that $a_n=o(b_n)$. Then there exists $(x_n)$ such that $\sum _{n=1}^\infty a_nx_n<\infty$ and $\sum _{n=1}^\infty b_nx_n=\infty$.

Proof

Since $a_n=o(b_n)$, there is $c_n\rightarrow 0$ with $a_n=c_nb_n$. If $(c_n)\in \ell _1$, then we put $d_n=1$ for every $n\in {\mathbb {N}}$. Otherwise there is an infinite set $A\in {\mathcal {I}}_{(c_n)}$ and then we put

$$\begin{aligned} d_n={\left\{ \begin{array}{ll} 1 &{} \text {if}\quad n\in A \\ \frac{1}{n^2} &{} \text {if}\quad n\notin A. \end{array}\right. } \end{aligned}$$

Finally we define $x_n$ as $d_n/b_n$. Then

$$\begin{aligned} \sum _{n=1}^\infty a_nx_n=\sum _{n=1}^\infty c_nb_n\cdot \frac{d_n}{b_n}=\sum _{n=1}^\infty c_nd_n<\infty \end{aligned}$$

and

$$\begin{aligned} \sum _{n=1}^\infty b_nx_n=\sum _{n=1}^\infty b_n\cdot \frac{d_n}{b_n}=\sum _{n=1}^\infty d_n=\infty . \end{aligned}$$

$\square$

We say that a sequence $(X_n)$ of independent random variables fulfills $(a_n)$-Kolmogorov condition provided that $\sum _{n=1}^\infty a_n Var(X_n)<\infty$.

Corollary 20

Let P be an atomless probability measure on a measure space $(\Omega ,{\mathcal {F}})$. Let $a_n=o(\frac{1}{n^2})$. The set of all $(X_n)\in L_0(\Omega )^{\mathbb {N}}$ such that

• $EX_n=0$,

• $(X_n)$ fulfills $(a_n)$-Kolmogorov condition,

• $(X_n)$ does not obey the SLLN

is ${\mathfrak {c}}$-lineable.

Proof

Using Lemma 19 for $b_n=\frac{1}{n^2}$, we find $(x_n)$ such that $\sum _{n=1}^\infty a_nx_n<\infty$ and $\sum _{n=1}^\infty x_n/n^2=\infty$. Then using Theorem 18 for $\sigma _n^2=x_n$, we obtain that the set of all $(X_n)\in L_0(\Omega )^{\mathbb {N}}$ such that

• $E X_n=0$,

• $Var X_n=O(\sigma ^2_n)$,

• $(X_n)$ does not obey the SLLN

is ${\mathfrak {c}}$-lineable. The equality $Var X_n=O(\sigma ^2_n)$ means that there is a constant $C>0$ such that $Var X_n\le C\sigma ^2_n$. Thus

$$\begin{aligned} \sum _{n=1}^\infty a_n Var X_n\le C\sum _{n=1}^\infty a_n \sigma _n^2= C\sum _{n=1}^\infty a_n x_n<\infty . \end{aligned}$$

$\square$