Uniform approximations of the first symmetric elliptic integral in terms of elementary functions

Abstract

We consider the standard symmetric elliptic integral $R_F(x,y,z)$ for complex x, y, z. We derive convergent expansions of $R_F(x,y,z)$ in terms of elementary functions that hold uniformly for one of the three variables x, y or z in closed subsets (possibly unbounded) of $\mathbb {C}{\setminus }(-\infty ,0]$. The expansions are accompanied by error bounds. The accuracy of the expansions and their uniform features are illustrated by means of some numerical examples.

1 Introduction

The family of elliptic integrals are integrals of the form $\int R(x,y)dx$, where R(x, y) is a rational function of the two variables x and y, and $y^2$ is a polynomial of the third or fourth degree in x. These functions cannot, in general, be expressed in terms of elementary functions when the polynomial $y^2$ has not a repeated factor and R(x, y) contains some odd power of y. Nevertheless, Legendre showed that all the elliptic integrals can be written in terms of three standard integrals, the so called Legendre’s normal elliptic integrals [23] (see [29] for further details).

The three standard elliptic integrals and the three complete elliptic integrals (that are particular cases of the first ones) are special functions quite useful in several mathematical and physical problems. For example, the first complete elliptic integral plays an important role in the theory of iterated number sequences based on the arithmetic geometric mean [33, Sect. 12.1.2]. The three standard elliptic integrals are connected to the Theta functions and the Weierstrass’ elliptic function [33, Sect. 12.3]. They appear, in a natural way, in certain geometrical and statistical problems [18, 32]. The period of a simple pendulum in a constant gravitational field can be computed in terms of the first complete elliptic integral [33, Sect. 12.1.1]; the zeros of these integrals can be used to determine an upper bound for the number of limit cycles of certain hamiltonian systems [35]; elliptic integrals play also an important role in certain problems of electromagnetism [37]. The inverse of the first symmetric standard elliptic integral is just the electric capacity of a conductor with an ellipsoidal shape [31]. See [22] for further applications.

In [4, 12] and [33, Chap. 12] we may find a comprehensive list of properties of the standard elliptic integrals. However, Carlson showed that, for numerical purposes, symmetric standard elliptic integrals are more appropriate than Legendre’s normal elliptic integrals [7,8,9,10,11]. And Legendre’s normal elliptic integrals may be written in terms of symmetric standard elliptic integrals by means of simple formulas [33, Eq. 12.33]. In this paper we are interested on the first symmetric standard elliptic integral, that is defined as follows [12, Sect. 19.16, Eq. 19.16.1],

$$\begin{aligned} R_{F}(x,y,z):={1\over 2}\int _0^\infty {ds\over \sqrt{s+x}\sqrt{s+y}\sqrt{s+z}},\qquad x, y\in \mathbb {C}{\setminus }(-\infty ,0]; z>0, \end{aligned}$$

(1)

where, for simplicity in the exposition, we assume first that one of its variables, say z, is positive. In Sect. 4 we extend the results derived in the paper to complex values of z.

It is also reasonable to assume that the three variables are different, because otherwise this integral is an elementary function, for example $R_F(x,x,x)=1/\sqrt{x}$. The integral is normalized in the form $R_F(1,1,1)=1$, and is a homogeneous function of degree $-1/2$ in its three variables [12, Sect. 19.20, Eq. 19.20.1]. This means that

$$\begin{aligned} {\begin{matrix} F(x,y) &{} :=\sqrt{z}R_F(z(1+x),z(1+y),z) \\ \\ &{} ={1\over 2}\int _0^\infty {ds\over \sqrt{s+x+1}\sqrt{s+y+1}\sqrt{s+1}}, x, y\in \mathbb {C}{\setminus }(-\infty ,-1], \end{matrix}} \end{aligned}$$

(2)

is indeed a function of only two variables x and y. For convenience in the analysis, in the remaining of the paper we consider the function F(x, y) instead of $R_F(x,y,z)$. All the results that we are going to derive in this paper for F(x, y) can be translated to $R_F(x,y,z)$ by means of the connection formula

$$\begin{aligned} R_F(x,y,z)=\frac{1}{\sqrt{z}}F\left( \frac{x-z}{z},\frac{y-z}{z}\right) , x, y\in \mathbb {C}{\setminus }(-\infty ,0]; z>0. \end{aligned}$$

(3)

In this paper we are interested on the approximation of $R_F(x,y,z)$ in terms of elementary functions. Several attempts on this line can be found in the literature. Without the aim of being exhaustive, we summarize below the most relevant ones (to our knowledge). First of all, some results concerning approximations of elliptic integrals can be found for example in [4, 20]. Several bounds and inequalities may be found in [5, 14, 21, 30].

About asymptotic approximations, the first results were obtained by Carlson, Gustafson and Wong by using the method of regularization [38, Chap. 6, Sect. 7]. The first (and sometimes the second too) term of the asymptotic expansion of $R_{F}$ when one of its variables tends to zero or infinity, has been obtained by Gustafson [19]; these results were later improved by Carlson and Gustafson when one of the variables goes to the infinity [14].

About convergent expansions, some of the first results were derived by Carlson who, using Mellin transforms techniques, obtained a complete convergent expansions of $R_{F}$ [6]. This expansion has an attractively simple structure, but the explicit computation of the terms of the expansion is not straightforward (see [6, Sect. 5]). Later, Carlson and Gustafson solved this problem in [13], where they computed the coefficients of the expansion of $R_{F}(x,y,z)$ in terms of Legendre functions and their derivatives. More recently, although in the context of the theory of asymptotic expansions of integrals, new convergent expansions of $R_{F}(x,y,z)$ have been obtained in [17, 24, 25].

The expansions mentioned in the above paragraph are valid for real positive values of the three variables x, y, z; and the expansions are accurate when one of the variables is large compared to the other ones. They are not accurate (or they are not even convergent) when two variables are of the same order. Therefore, they cannot be used when we need an approximation uniformly valid for large and small values of one of the variables (and fixed values of the other two).

On the other hand, in [36] we can find an expansion of $R_F(x,y,z)$ (written in the Legendre form) that is uniformly convergent in one of the variables when the other two are restricted to a certain bounded domain. It is derived for real positive values of the variables, and error bounds are not given. In this paper we want to extend and generalize the expansion given in [36]. To this end we use the theory of uniform convergent expansions of integral transforms developed in [28], deriving a family of uniformly convergent expansions of F(x, y) in terms of elementary functions that are uniformly valid in one of its variables, regardless of the value of the other one. Moreover, we consider complex values of x and y and derive error bounds. Because of the symmetry of this function, without loss of generality, we consider y as the uniform variable.

As an illustration of the type of approximations that we are going to obtain in this paper (see Theorems 1 and 2 below), we derive, for example, the following approximations that are valid for $0\le x<1$, $\Re y > 0$:

$$\begin{aligned} F(x,y)=\frac{(x+4y) arcsh \sqrt{y}}{4 y^{3/2}}-\frac{x \sqrt{y+1}}{4 y}+\theta _1(x), \end{aligned}$$

(4)

with $\vert \theta _1(x)\vert \le 0.075x^2\le 0.075$.

$$\begin{aligned} {\begin{matrix} F(x,y)= &{} \frac{\left( 36 x^2 y+25 x^3+64 xy^2+256 y^3\right) arcsh \sqrt{y}}{256 y^{7/2}}\\ &{}-\frac{x \sqrt{y+1} \left( 40 x^2 y^2-50 x^2 y+75 x^2-72 xy^2+108 xy+192 y^2\right) }{768 y^3}+\theta _2(x), \end{matrix}} \end{aligned}$$

(5)

with $\vert \theta _2(x)\vert \le 0.031x^4\le 0.031$. In these formulas, F(x, 0) must be understood in the limite sense.

The paper is structured as follows. The next section contains some preliminary results that we need in the later analysis. In Sect. 3 we give the main results of the paper: convergent expansions of F(x, y) that are uniformly valid for $y\in \mathbb {C}{\setminus }(-\infty ,-1]$ with fixed $x\in \mathbb {C}{\setminus }(-\infty ,-1]$. Some numerical examples show the accuracy of these expansions in Sect. 4. Also, in Sect. 4 we show that the condition $z>0$ for $R_F(x,y,z)$ may be relaxed and consider $z\in \mathbb {C}{\setminus }(-\infty ,0]$ if we restrict the variables x and y to smaller sectors inside $\mathbb {C}{\setminus }(-\infty ,0]$. In all the paper, for any complex variable w, $\arg w\in (-\pi ,\pi ]$ denotes its main argument and square roots are assumed to take their principal value.

2 Preliminaries

Except the expansion derived in [36], all the other convergent and asymptotic expansions mentioned in the introduction section are directly derived from the integral definition (1) of the first symmetric standard elliptic integral $R_{F}(x,y,z)$. And they are derived using typical techniques of the theory of asymptotic expansions of integrals [26, 34, Chap 16], [38, Chaps. 3 and 6]. This is why the expansions are accurate (regardless they are convergent or only asymptotic) when one of the variables is large compared to the other two. In order to avoid this restriction, we invoke the new ideas introduced in [2, 3, 15, 16, 27], where new convergent expansions of several special functions are derived in terms of elementary functions, expansions that are uniformly valid for large and small values of a certain selected variable. Those ideas are summarized in [28]. Consider the integral transform of a function g(t) with kernel h(t, y) of the form:

$$\begin{aligned} \Phi (y):=\int _0^1 h(t,y)g(t)dt y\in \mathcal {D}\subset \mathbb {C}, \end{aligned}$$

(6)

where $\mathcal {D}$ is a certain unbounded region of the complex plane that contains the point $y=0$, and with the following assumptions for the functions h and g:

• (i) $\vert h(t,y)\vert \le H(t)$ for $y\in \mathcal {D}$ with H integrable on [0, 1],

• (ii) g(t) is analytic in a region $\Omega \subset \mathbb {C}$ that contains the open set $(0,1)\subset \Omega$,

• (iii) the moments of h, $M[h(\cdot ,y);k]:=\int _0^1 h(t,y)t^kdt$, are elementary functions of y.

It has been shown in [28] that, when we replace g(t) in (6) by its Taylor expansion at an appropriate point $w\in \Omega$ and interchange sum and integral in (6), we obtain an expansion of $\Phi (y)$ with the following three properties:

• (a) The expansion is uniform for $y\in \mathcal {D}$: for any order n of the approximations $\Phi _n(y)$, the absolute error $\vert \Phi (y)-\Phi _n(y)\vert \le M_n$ for any $y\in \mathcal {D}$ with $M_n$ independent of y.

• (b) The expansion is convergent.

• (c) The terms of the expansions are elementary functions of y.

It has been proved in [28] (and we may intuitively assume) that a key point to derive uniformly convergent expansions by interchanging sum and integral is that the integration interval in (6) is bounded. And vice-versa, the price to pay when we derive expansions by interchanging sum and integral in integrals defined on unbounded intervals is that, in general, we lose convergence.¹ And moreover, they are not uniform in the asymptotic variable, as the very construction of the asymptotic expansion requires either a large or a small value of the asymptotic variable.

Therefore, in order to derive uniformly convergent expansions of F(x, y) we first must find an integral representation of F(x, y) on a bounded interval. This is straightforward from (2) by introducing the change of variable $s\rightarrow t$ defined in the form $1+s=1/t$. We obtain

$$\begin{aligned} F(x,y)=\dfrac{1}{2}\int _0^1 \frac{dt}{\sqrt{t}\sqrt{1+x\,t}\sqrt{1+y\,t}}. \end{aligned}$$

(7)

Obviously, we can use the symmetry of $R_F(x,y,z)$ to derive other representations of the form (7) by permuting the variables x, y, z. The integral representation (7) is the starting point for our analysis based on the general idea introduced in [28] and summarized above. The main results of the paper are given in Theorems 1 and 2 in the next section. In the remaining of this section we give some preliminary results used in the proof of these theorems.

Lemma 1

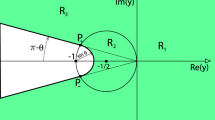
Let $\displaystyle {f(t,y):=\frac{1}{\sqrt{1+y\,t}}}$, with $t\in [0,1]$ and $y\in \mathbb {C}{\setminus }(-\infty ,-1]$. Then, for any fixed angle $\theta$, with $\pi /2\le \theta <\pi$, we define the extended sector $S(\theta ):=\lbrace y\in \mathbb {C}; \vert \arg (y)\vert \le \theta \rbrace \cup \left( \lbrace y\in \mathbb {C}; \vert \arg (y)\vert >\theta \rbrace \bigcap \lbrace y\in \mathbb {C}; \vert y+1\vert \ge \sin \theta \rbrace \bigcap \lbrace y\in \mathbb {C}; \vert y+1/2\vert \le 1/2\rbrace \right)$ (green region in Fig. 1). Then, for any $y\in S(\theta )$, f(t, y) is uniformly bounded in the form

$$\begin{aligned} \vert f(t,y)\vert \le \frac{1}{\sqrt{\sin \theta }}. \end{aligned}$$

(8)

Proof

The absolute maximum of the function $\vert f(t,y)\vert$ in the interval $t\in [0,1]$ depends on the value of $\Re (y)$. We divide the region $\mathbb {C}{\setminus }(-\infty ,-1]$ in three different regions $R_1$, $R_2$ and $R_3$, that are depicted in Fig. 1:

• When $y\in R_1:=\lbrace y\in \mathbb {C}; \Re (y)\ge 0\rbrace$, the maximum is attained at $t=0$ and its value is 1.

• When $y\in R_2:=\lbrace y\in \mathbb {C}; \Re (y)< -\vert y\vert ^2\rbrace$, the maximum is attained at $t=1$ and its value is $|1+ y|^{-1/2}$. The region $R_2$ is an open disk of center $y=-1/2$ and radius $r=1/2$.

• When $y\in R_3:=\lbrace y\in \mathbb {C};-\vert y\vert ^2\le \Re (y)<0\rbrace {\setminus }(-\infty ,-1]$, the maximum is attained at $t=-\Re (y)/\vert y\vert ^2$ and its value is $\vert \sin (\arg y)\vert ^{-1/2}$. The region $R_3$ is the left half complex plane $\Re (y)<0$, with both, the straight $(-\infty , -1]$, and the disk $R_2$, removed.

We fix an angle $\theta \in [\pi /2,\pi )$. The rays $\arg (y)=\pm \theta$ cut the boundary of the disk $R_2$ at the points $P_\pm =(-\cos ^2\theta ,\pm \sin \theta \cos \theta )$. At the portions of the rays $\arg (y)=\pm \theta$ that are inside the region $R_3$ (that is a portion of the boundary of $S(\theta )$) we have that

$$\begin{aligned} \vert f(t,y)\vert \le \dfrac{1}{\sqrt{\vert \sin (\arg y)\vert }}\le \frac{1}{\sqrt{\sin \theta }}. \end{aligned}$$

On the other hand, at the portion of the circle $\vert 1+y\vert =\sin \theta$ that is inside the disk $R_2$, that is, the remaining portion of the boundary of $S(\theta )$, we have that

$$\begin{aligned} \vert f(t,y)\vert \le \dfrac{1}{\sqrt{|1+ y|}}\le \frac{1}{\sqrt{\sin \theta }}, \end{aligned}$$

and the thesis of the lemma follows. $\square$

Fig. 1

The region $S(\theta )$ defined in Lemma 2.1 is the green area. Its boundary is the portion of the rays $\arg y=\pm \theta$ exterior to the open disk $R_2=D_{1/2}(-1/2)$, and also the portion of the circle $\vert y+1\vert =\sin \theta$ interior to $R_2$ (color figure online)

Lemma 2

For any $x\in \mathbb {C}{\setminus }(-\infty ,-1]$, define the multivalued function

$$\begin{aligned} w(x):=\frac{1}{2}\left\{ {\begin{matrix} 1&{} \quad \text {if}\quad \vert \arg (x+1)\vert<\pi /2, \\ 1+i\frac{u-\sqrt{u^2+v^2}}{v} &{}\quad \text {if}\quad 0<\vert \arg (x+1)\vert<\pi , \\ 0&{} \quad \text {if}\quad \vert x\vert <1, \end{matrix}} \right. \end{aligned}$$

(9)

with $u:=\Re (x+1)$, $v:=\Im (x+1)$. We have that

$$\begin{aligned} \vert x\,w(x) \vert<\vert 1+x\,w(x)\vert , \quad \vert x(1-w(x))\vert <\vert 1+x\,w(x) \vert . \end{aligned}$$

(10)

For $\arg (x+1)=\pi$, the two inequalities $\vert x\,w \vert <\vert 1+x\,w\vert$ and $\vert x(1-w)\vert <\vert 1+x\,w \vert$ cannot be simultaneously satisfied for any value of w.

Proof

We write $w(x)=w$ in order to simplify the notation. Divide the second inequality in (10) by $\vert x+1\vert$ to get the equivalent inequalities:

$$\begin{aligned} \left| x\,w \right|<\left| 1+x\,w \right| ,\quad \left| \frac{x}{x+1}(w-1)\right| <\left| 1+\frac{x}{x+1}(w-1)\right| . \end{aligned}$$

These two inequalities mean that the distance from both points, $x\,w$ and $\frac{x}{x+1}(w-1)$, to the point $-1$, must be larger than the distance to the point 0. This is equivalent to the following two inequalities:

$$\begin{aligned} \Re \left( x\,w \right)>-\frac{1}{2},\quad \Re \left( \frac{x}{x+1}(w-1)\right) >-\frac{1}{2}. \end{aligned}$$

Write $w=(a+1/2)+ib$ with $a\in \lbrace 0,-1/2\rbrace$, $b\in \mathbb {R}$, and define $\theta :=\arg (x+1)$ and $r:=\vert x+1\vert$. Then, the above two inequalities are equivalent to the following two ones:

$$\begin{aligned} {\begin{matrix} \left( \cos \theta -\frac{1}{r}\right) a-b\,\sin \theta +\frac{1}{2}\cos \theta &{}>0, \\ \left( r-\cos \theta \right) a-b\,\sin \theta +\frac{1}{2}\cos \theta &{} >0. \end{matrix}} \end{aligned}$$

(11)

For $\theta =\pi$ these inequalities read

$$\begin{aligned} \frac{1}{2(r+1)}<a<-\frac{r}{2(r+1)} \end{aligned}$$

and therefore, when $\arg (x+1)=\pi$, inequalities (11) do not hold for any $w\in \mathbb {C}$.

For $\vert \theta \vert <\pi /2$ the two inequalities (11) hold for $a=b=0$ ($w=1/2$, first line in (9)).

For $\theta \ne 0,\pi$, the two inequalities (11) hold for $a=0$ and $b<\cot (\theta )/2$ if $0<\theta <\pi$ and $b>\cot (\theta )/2$ if $-\pi<\theta <0$. In particular, for the value of w given in the second line of (9).

For $r<2\cos \theta$ the two inequalities (11) hold for $a=-1/2$ and $b=0$ ($w=0$). Inequality $r<2\cos \theta$ is equivalent to inequality $\vert x\vert <1$ (last line in (9)). $\square$

Lemma 3

For $y\in \mathbb {C}{\setminus }(-\infty ,-1]$, define

$$\begin{aligned} A_k(y):=\int _0^1\frac{t^{k-1/2}}{\sqrt{1+y t}}dt. \end{aligned}$$

(12)

Then,

$$\begin{aligned} A_k(y)=\frac{2}{\sqrt{\pi }}\frac{(-1)^k}{y^{k +1/2}}\frac{\Gamma (k+1/2)}{k!}\hbox {arcsh}(\sqrt{y}) - \sqrt{1+y} \sum _{j=1}^k \frac{(-y)^{-j}}{k-j+1}\frac{(1/2-k)_{j-1}}{(-k)_{j-1}}, \end{aligned}$$

(13)

where $(a)_m = a (a+1) (a+2) \cdot \ldots \cdot (a+m-1) = \frac{\Gamma (a+m)}{\Gamma (a)}$ denotes de Pochhammer’s symbol and empty sums must be understood as zero. The elementary functions $A_{k}(y)$ may also be computed by using the recurrence relation

$$\begin{aligned} A_k(y)= & {} \dfrac{2k-1}{2k\,y}\left( \dfrac{2\sqrt{1+y}}{2k-1}-A_{k-1}(y)\right) ,\qquad k=1,2,3,..., \end{aligned}$$

(14)

$$\begin{aligned} A_0(y)= & {} \dfrac{2}{\sqrt{y}}\hbox { arcsh}(\sqrt{y}). \end{aligned}$$

(15)

Proof

Write

$$\begin{aligned} A_{k+1}(y)= & {} \int _0^1\frac{t^{k+1/2}}{\sqrt{1+y t}}\,dt=\frac{1}{y}\int _0^1\frac{t^{k-1/2}(ty+1-1)}{\sqrt{1+y t}}\,dt\\= & {} \frac{1}{y}\int _0^1t^{k-1/2}\sqrt{1+y t}\,dt-\frac{1}{y}A_k(y). \end{aligned}$$

Integrating by parts the integral in the right hand side above we find

$$\begin{aligned} \int _0^1t^{k-1/2}\sqrt{1+y t}\,dt=\frac{\sqrt{1+y}}{n+1/2}-\frac{y}{2n+1}A_{k+1}(y). \end{aligned}$$

The recurrence in the first line of (14) follows after straightforward computations. The integral $A_0(y)$ is immediate. Recurrence (14)–(15) has a unique solution, and it may be checked that (13) is a solution of the recurrence.

3 Uniformly convergent expansions of F(x, y)

In order to apply the general theory introduced in [28] (and summarized in the Introduction), we first select the uniform variable, which, without loss of generality due to the symmetry of the function F(x, y), we choose to be y. Then, by comparing (6) and (7), we identify

$$\begin{aligned} h(t,y)=\frac{1}{\sqrt{t}\sqrt{1+y\,t}},\quad g(t)=\frac{1}{\sqrt{1+x\,t}}. \end{aligned}$$

The function g(t) is analytic in $\Omega =\lbrace t\in \mathbb {C}$; $1+x\,t\notin (-\infty ,0]\rbrace$. A possible point $t=w(x)\in \Omega$ for the Taylor expansion of g(t) is given in Lemma 2 and depends on $\arg (x+1)$. The point $t=w(x)$ indicated in Lemma 2 is not the unique possible election, but, as we will see in Theorem 1 below, it is the appropriate value to minimize the error of the approximation. In Theorem 2 we consider the case $w=0$. Although the election $w=0$ imposes a more demanding restriction on x ($\vert x\vert <1$) than other possible choices, we highlight this case because it gives the simplest possible expansion for F(x, y) and sharper error bounds.

Theorem 1

Fix an angle $\theta \in [\pi /2,\pi )$ and consider the region $S(\theta )\subset \mathbb {C}{\setminus }(-\infty ,-1]$ defined in Lemma 1. Then, for any $x\in \mathbb {C}{\setminus }(-\infty ,-1]$, $y\in S(\theta )$, and $n=1,2,3,...$,

$$\begin{aligned} F(x,y)= & {} \frac{1}{2 \sqrt{1+x\,w(x)}} \sum _{k=0}^{n-1} \frac{\left( 1/2\right) _k}{k!}\left( \frac{-x}{1+x\,w(x)}\right) ^k A_k\left( y;w(x)\right) +R_n(x,y), \end{aligned}$$

(16)

with w(x) given in the first or second line of formula (9) in Lemma 2,

$$\begin{aligned} A_k(y;w):=\sum _{j=0}^k\left( \begin{array}{c} k \\ j \end{array}\right) (-w)^{k-j} A_j(y), \end{aligned}$$

(17)

and $A_k(y)$ given Lemma 3. The remainder term is bounded in the form

$$\begin{aligned} |R_n(x,y)|\le \frac{1}{\sqrt{\sin \theta }}\frac{\left( 1/2\right) _n}{n!}\dfrac{|x\,w(x)|^n}{|x\,w(x) +1|^{n+1/2}} \, {}_2F_1\left( \left. \begin{array}{c} 1, n+\frac{1}{2}\\ \\ n+1 \end{array} \right| \frac{|x\,w(x)|}{|x\,w(x)+1|}\right) . \end{aligned}$$

(18)

Proof

Consider the Taylor expansion of $g(t)=\dfrac{1}{\sqrt{1+xt}}$ at $t=w\in \mathbb {C}$, with $w=w(x)$ defined in Lemma 2,

$$\begin{aligned} g(t)=\dfrac{1}{\sqrt{1+x\,w}}\sum _{k=0}^{n-1}\frac{(-x)^k \left( 1/2\right) _k}{k!}\,\left( \dfrac{t-w}{1+x\,w}\right) ^k+r_n(t;x), \end{aligned}$$

(19)

where the Taylor remainder is given by

$$\begin{aligned} r_n(t;x):= & {} \dfrac{1}{\sqrt{1+x\,w}}\sum _{k=n }^{\infty }\frac{(-x)^k \left( 1/2\right) _k }{k!}\,\left( \dfrac{t-w}{1+x\,w }\right) ^k\nonumber \\= & {} \dfrac{1}{\sqrt{1+x\,w }}\frac{\left( 1/2\right) _n (-x)^n}{n !} \left( \frac{t-w}{1+x\,w }\right) ^n \, {}_2F_1\left( \left. \begin{array}{c} 1, n +\frac{1}{2}\\ \\ n +1 \end{array} \right| \frac{x(w-t)}{1+x\,w }\right) .\nonumber \\ \end{aligned}$$

(20)

The value $w=w(x)$ given in Lemma 2 assures that inequalities (10) hold and then, $\vert t-w\vert <\vert w+1/x\vert$ for any $t\in [0,1]$. This means that the branch point $t=-1/x$ of g(t) is located outside the disk of convergence of (19): $\vert t-w\vert <\vert w+1/x\vert$, and expansion (19) is convergent for any $t\in [0,1]$.

Replacing $g(t)=(1+t\,x)^{-1/2}$ in the integrand in (7) by the right hand side of (19) and interchanging sum and integral, we obtain (16), with $A_k(y; w )$ given in (17) and

$$\begin{aligned} R_n(x,y):=\frac{1}{2}\int _0^1 \frac{r_n\left( t;x\right) }{\sqrt{t} \sqrt{1+y\,t}}\,dt. \end{aligned}$$

(21)

From (20) we have that

$$\begin{aligned} |r_n(t;x)|\le \dfrac{1}{\sqrt{|x\,w +1|}}\frac{\left( 1/2\right) _n}{n!} \left| \frac{x(t-w) }{x\,w +1}\right| ^n \, {}_2F_1\left( \left. \begin{array}{c} 1, n+\frac{1}{2}\\ \\ n+1 \end{array} \right| \left| \frac{x(t-w)}{x\,w +1}\right| \right) . \end{aligned}$$

From this bound and (8) in Lemma 1 we find

$$\begin{aligned} {\begin{matrix} |R_n(x,y)| &{}\le \frac{1}{\sqrt{\sin \theta }}\frac{\left( 1/2\right) _n}{2n!\sqrt{|1+x\,w|}} \\ &{}\quad \times \int _0^1 \left| \frac{x(t-w) }{1+x\,w}\right| ^n \, {}_2F_1\left( \left. \begin{array}{c} 1, n+\frac{1}{2}\\ \\ n+1 \end{array} \right| \left| \frac{x(t-w) }{1+xw}\right| \right) \,\frac{dt}{\sqrt{t}}. \end{matrix}} \end{aligned}$$

Using the series representation of the Gauss hypergeometric function and interchanging sum and integral we obtain

$$\begin{aligned} {\begin{matrix} |R_n(x,y)| &{}\le \frac{1}{\sqrt{\sin \theta }}\frac{\left( 1/2\right) _n}{2n!}\dfrac{1}{\sqrt{|1+xw|}} \\ &{}\quad \times \sum _{k=0}^\infty \dfrac{(n+1/2)_k}{(n+1)_k}\left| \frac{x}{1+w\,x}\right| ^{n+k}\int _0^1 \frac{|t-w|^{n+k}}{\sqrt{t}} \,dt. \end{matrix}} \end{aligned}$$

Using that $|t-w|\le \vert w\vert$ for $t\in [0,1]$ we find

$$\begin{aligned} |R_n(x,y)|\le & {} \frac{1}{\sqrt{\sin \theta }}\frac{\left( 1/2\right) _n}{n!}\dfrac{1}{\sqrt{|1+w \,x|}}\sum _{k=0}^\infty \dfrac{(n+1/2)_k|x\,w|^{n+k}}{(n+1)_k|1+w\,x|^{n+k}}. \end{aligned}$$

Equation (18) follows by using again the series representation of the Gauss hypergeometric function. $\square$

Observation 1

The convergence of expansion (16) only requires for the expansion point w in the proof of Theorem 1 to satisfy the inequalities (10). The value $w=w(x)$ given in Lemma 2 assures that inequalities (10) hold (indeed there may be more than one possible value for w as the function w(x) in (9) is multivalued). But moreover, the value $w=w(x)$ given in the second line of (9) in Lemma 2 for $0<\vert \arg (x+1)\vert <\pi$ and the value $w=1/2$ given in the first line for $\arg (x+1)=0$ minimize the value of the factor $\vert xw/(xw+1)\vert ^n$ in (18). For values of $\arg (x+1)$ close to zero, although the best choice w(x) is given in the second line of (9), its value is close to 1/2, and then $w=1/2$ is also a good choice.

Theorem 2

Fix an angle $\theta \in [\pi /2,\pi )$ and consider the region $S(\theta )\subset \mathbb {C}{\setminus }(-\infty ,-1]$ defined in Lemma 1. Then, for any $y\in S(\theta )$, $\vert x\vert <1$, and $n=1,2,3,...$,

$$\begin{aligned} F(x,y)= & {} \frac{1}{2} \sum _{k=0}^{n-1} \frac{\left( 1/2\right) _k}{k!}\left( -x\right) ^k A_k\left( y\right) +R_n(x,y), \end{aligned}$$

(22)

where the coefficients $A_k(y)$ are given in formula (13) in Lemma 3, and satisfy recurrence (14). The remainder term is bounded in the form

$$\begin{aligned} |R_n (x,y)|\le & {} \frac{1}{\sqrt{\sin \theta }}\frac{\left( 1/2\right) _n \left| x\right| ^n \, }{(2 n +1) n !}{}_3F_2\left( \left. \begin{array}{c} 1, n +\frac{1}{2}, n +\frac{1}{2}\\ \\ n +1 , n +\frac{3}{2}\end{array} \right| \left| x\right| \right) \nonumber \\\le & {} \frac{2}{\sqrt{\sin \theta }}\frac{\vert x\vert ^n\,\left( 1/2\right) _n }{(n-1)!(2n-1)}, \end{aligned}$$

(23)

where ${}_3F_2$ is a hypergeometric function. When $x\ge 0$ we have the sharper bound:

$$\begin{aligned} |R_n (x,y)|\le \frac{\left( 1/2\right) _n}{n!(2n+1)}\frac{x^n}{\sqrt{\sin \theta }}. \end{aligned}$$

(24)

When $x\ge 0$ and $\Re (y)>0$, we have the alternative bound:

$$\begin{aligned} |R_n (x,y)|\le \frac{\left( 1/2\right) _n}{n!(2n)}\frac{x^n}{\sqrt{\vert y\vert }}.\qquad \end{aligned}$$

(25)

Proof

Set $w=0$ in the proof of Theorem 1 and repeat that proof step by step to derive expansion (22) with

$$\begin{aligned} R_n(x,y):=\frac{1}{2}\int _0^1 \frac{r_n(t;x)}{\sqrt{t} \sqrt{1+y\,t}}\,dt, \end{aligned}$$

(26)

where now, $r_n(t;x)$ is the Taylor remainder in expansion (19) with $w=0$; expansion that is convergent for $\vert x\vert <1$ for any $t\in [0,1]$. We have that

$$\begin{aligned} r_n(t;x)=\sum _{k=n }^{\infty }\frac{(-x)^k t^k\left( 1/2\right) _k }{k!}. \end{aligned}$$

(27)

Replacing $r_n(t;x)$ in (26) by the above expansion and interchanging sum and integral we obtain

$$\begin{aligned} R_n(x,y)=\frac{1}{2 }\sum _{k=n}^\infty \frac{\left( 1/2\right) _k}{k!}\left( -x\right) ^k A_k\left( y\right) . \end{aligned}$$

Thus,

$$\begin{aligned} |R_n(x,y)|\le & {} \frac{1}{2}\sum _{k=n}^\infty \frac{\left( 1/2\right) _k}{k!}\left| x\right| ^k \left| A_k \left( y\right) \right| \le \frac{1}{\sqrt{\sin \theta }}\sum _{k=n}^\infty \frac{\left( 1/2\right) _k}{k! (2k+1)}\left| x\right| ^k\\= & {} \frac{1}{\sqrt{\sin \theta }}\frac{\left( 1/2\right) _n \left| x\right| ^n \, }{(2 n+1) n!}{}_3F_2\left( \left. \begin{array}{c} 1, n+\frac{1}{2}, n+\frac{1}{2}\\ \\ n+1 , n+\frac{3}{2}\end{array} \right| \left| x\right| \right) , \end{aligned}$$

and the first bound in (23) follows. In the second inequality above we have used the bound:

$$\begin{aligned} \left| A_k\left( y\right) \right| \le \int _0^1 \frac{t^{k-\frac{1}{2}}}{\sqrt{|1+y\,t|}} \,dt\le \frac{1}{\sqrt{\sin \theta }} \int _0^1 t^{k-\frac{1}{2}} \,dt=\dfrac{2}{2k+1}\frac{1}{\sqrt{\sin \theta }}. \end{aligned}$$

From the power series definition of the hypergeometric functions [1, Sect. 16.2, Eq. 16.2.1] we have

$$\begin{aligned} {}_3F_2\left( \left. \begin{array}{c} n+\frac{1}{2}, 1, n+\frac{1}{2}\\ \\ n+1 , n+\frac{3}{2}\end{array} \right| \left| x\right| \right) \le {}_3F_2\left( \left. \begin{array}{c} n+\frac{1}{2}, 1, n+\frac{1}{2}\\ \\ n+1 , n+\frac{3}{2}\end{array} \right| 1\right) . \end{aligned}$$

(28)

In [3] the authors have proved that, for $n>b-a$ and $a,b>0$,

$$\begin{aligned} {}_3F_2\left( \left. \begin{array}{c} n+1+a-b, 1, a +n\\ \\ n+1 , 1+a +n\end{array} \right| 1\right) \le \frac{n(a+n)}{(b-a)(n+a-b)}. \end{aligned}$$

Setting $a=1/2$ and $b=1$ in this formula we find

$$\begin{aligned} |R_n(x,y)|\le \frac{1}{\sqrt{\sin \theta }}\frac{\left| x\right| ^n\,\left( 1/2\right) _n }{n!}\frac{2n}{2n-1}, \end{aligned}$$

and the second inequality in (23) follows. When $x>0$, we have that the terms of the convergent series expansion (27) alternate sign and their modulus constitute a decreasing sequence. Then, applying the Leibniz criterion we find that $\vert r_n(t;x)\vert$ is bounded by the absolute value of the first neglected term in expansion (27):

$$\begin{aligned} \vert r_n(t;x)\vert \le \frac{(1/2)_n(x\,t)^n}{n!}. \end{aligned}$$

Using this bound in (26) and Lemma 1 we find (24). When $\Re y>0$ we may use this bound in (26) and also $\vert \sqrt{1+ty}\vert \ge \vert \sqrt{ty}\vert$, and we find (25). $\square$

Observation 2

All the bounds shown in Theorems 1 and 2, except bound (25), show that the expansions given in the Theorems 1 and 2 are uniformly valid for $y\in S(\theta )\subset \mathbb {C}{\setminus }(-\infty ,-1]$, with $S(\theta )$ defined in Lemma 1. On the other hand, they are not uniform in the variable x; error bounds (18) and (23) become worse when x approaches the boundary of the convergence region: $|x|\rightarrow \infty$ or $\vert \arg (x+1)\vert \rightarrow \pi$ in formula (18) and $\vert x\vert \rightarrow 1$ in formula (23). Although it is not a uniform bound, for $x,\Re y>0$, bound (25) is sharper than the other ones for large $\vert y\vert$.

Observation 3

Approximations (4) and (5) are the particular cases $n=2$ and $n=4$ of formula (22), with the error bound (24) setting $\theta =\pi /2$ (see Lemma 1 for $\Re y\ge 0$).

4 Final remarks and numerical experiments

Formula (2) is derived from (1) after the change of variable $s\rightarrow zs$ and under the assumption $z>0$. If, instead of $z>0$, we let $z\in \mathbb {C}{\setminus }(-\infty ,0]$ then, instead of the second inequality in (2) we obtain

$$\begin{aligned} R_{F}(x,y,z)={z\over 2}\int _0^{\infty e^{-i\arg z}}{ds\over \sqrt{z(s+x/z)}\sqrt{z(s+y/z)}\sqrt{z(s+1)}}. \end{aligned}$$

When $\arg (-u/z)$ $\notin [0,-\arg z]$, $u=x,y$, we may invoke Cauchy’s residue theorem to rotate the integration contour $[0,\infty e^{-i\arg z})$ to the contour $[0,\infty )$. We have that $\arg (-u/z)=\arg (u/z)-\pi \,\mathrm{sign}(\arg (u/z))$. Therefore, the condition $\arg (-u/z)$ $\notin [0,-\arg z]$ is equivalent to the condition $\vert \arg (u/z)+\arg z\vert <\pi$. Now, using that

$$\begin{aligned} \vert \arg (u/z)+\arg z\vert =\left\{ {\begin{matrix} \vert \arg u\vert (<\pi )&{} \quad \mathrm{if}\quad \vert \arg u-\arg z\vert <\pi , \\ \vert \arg u\pm 2\pi \vert (\ge \pi )&{} \quad \mathrm{if}\quad \vert \arg u-\arg z\vert \ge \pi , \end{matrix}}\right. \end{aligned}$$

we deduce that $\vert \arg (u/z)+\arg z\vert<\pi \Longleftrightarrow \vert \arg u-\arg z\vert <\pi$, and then, the condition $\arg (-u/z)$ $\notin [0,-\arg z]$ is equivalent to the condition $\vert \arg u-\arg z\vert <\pi$.

But moreover, when $\vert \arg (u/z)+\arg z\vert <\pi$ we have that $\sqrt{z(u/z)}=\sqrt{z}\sqrt{u/z}$, and using that $\vert \arg (s+u/z)\vert \le \vert \arg (u/z)\vert$ $\forall$ $s\ge 0$, we also have that $\sqrt{z(s+u/z)}=\sqrt{z}\sqrt{s+u/z}$ $\forall$ $s\ge 0$. Therefore, when $\vert \arg x-\arg z\vert <\pi$ and $\vert \arg y-\arg z\vert <\pi$,

$$\begin{aligned} R_{F}(x,y,z)={1\over 2\sqrt{z}}\int _0^{\infty }{ds\over \sqrt{s+x/z}\sqrt{s+y/z}\sqrt{s+1}}. \end{aligned}$$

(29)

Then, the connection formula (3), and the expansions for $R_F(x,y,z)$ that we obtain when we combine (3) with the expansions derived for F(x, y) in Sect. 3 hold, not only for $z>0$ and $x,y\in \mathbb {C}{\setminus }(-\infty , 0]$, but in the bigger domain:

$$\begin{aligned} (x,y,z)\in \Lambda :=\lbrace (x,y,z)\in (\mathbb {C}{\setminus }(-\infty ,0])^3;\, \vert \arg x-\arg z\vert<\pi ,\,\,\vert \arg y-\arg z\vert <\pi \rbrace . \end{aligned}$$

Figure 2 illustrates the shape of the $x-$domain $\Lambda$ for fixed z (the $y-$domain for fixed z is analogous). By using the symmetry of $R_F(x,y,z)$, we may interchange the rolls of x and z or y and z.

Fig. 2

The argument of the variable x is restricted to the sector $\arg x\in (\arg z-\pi ,\arg z+\pi )\bigcap (-\pi ,\pi ]$. Different shapes of the $x-$section of the region $\Lambda$ for different arguments of z (green region in all the pictures) (color figure online)

Finally, we give some numerical experiments that illustrate the accuracy and uniform character of the expansions derived in Theorems 1 and 2. In the numerical tables of this subsection we have computed the Relative Error, $E_{Rel}^n(x,y)$, and compared to the relative error bound $B_{Rel}^n(x,y)$. They are defined in the form:

$$\begin{aligned} E_{Rel}^n:=\dfrac{|F_n(x,y)-F(x,y)|}{|F(x,y)|}, \qquad \qquad B_{Rel}^n:=\dfrac{|R_n(x,y)|}{|F(x,y)|}, \end{aligned}$$

where $F_n(x,y)$ represents the sum of the first n terms of the series in the right hand side of (16) or (22). The term $R_n(x,y)$ represents the error bound given in the right hand side of (18), (23) or (24). In Tables 1 and 2 we compute $E_{Rel}^n(x,y)$ and $B_{Rel}^n(x,y)$ for several fixed values of x and along some rays $y=\vert y\vert e^{i\arg y}$ for several values of $\arg y$.

Table 1 Relative error (with $F_n(x,y)$ evaluated by using (16)) and relative error bound (18) for $x=2 e^{i\,\pi /5}$; several values of $y=\vert y\vert \,e^{i\arg y}$ and order n of the approximation

Table 2 Relative error (with $F_n(x,y)$ evaluated by using (22)) and relative error bound (23) for $x=1/3 e^{i\,\pi /5}$; several values of $y=\vert y\vert \,e^{i\arg y}$ and order n of the approximation

In Fig. 3 we plot the function F(x, y) and several orders of the approximations $F_n(x,y)$ given in Theorems 1 and 2 for fixed values of the variable x in different rays of the $y-$complex plane. The uniform and convergent character of the expansions are exhibited. On the other hand, in Fig. 4 we compare the approximation of $R_F(x,y,z)$ derived from (22) and (3) to the convergent and asymptotic approximations of $R_F(x,y,z)$ given in [24, Corollary 1, Eq. (26)] for large and small values of $y>0$, with fixed positive values of x and z. The expansion given in [24, Corollary 1, Eq. (26)] is only valid for $x<y<z$; but using the symmetry of the symmetric standard elliptic integral, we may use the approximation of $R_F(x,y,z)$ for small values of y, and the approximation of $R_F(x,z,y)$ for large values of y. The picture illustrates the uniform character of expansion given in Theorem 2 above, in contrast to the expansions given in [24, Corollary 1, Eq. (26)].

Fig. 3

Graphics of F(x, y) (black, dashed) and the approximations given by theorems 2 and 1 with $n=1$ (blue), $n=2$ (red) and $n=3$ (green) for different values of the fixed variable x and different intervals of the uniform variable y, with w(x) taken according to Lemma 2. We have taken $x=0.7$ and $y \in (-1,15)$ (top, left); $x=2.3$ and $y \in (-1,15)$ (top right); and $x=2 e^{\pi i /3}$ and $y \in (-10 e^{i\pi /4}, 10 e^{i\pi /4})$ (bottom). The graphic on the bottom left corresponds to the real part of the functions whereas the picture on the bottom right represents the imaginary part. The graphics are similar for others values of x and y. The graphics show the uniform and the convergent character of the expansions (color figure online)

Fig. 4

Relative errors in the approximation of $R_F(1,y,2)$ for $y\in [0,6]$. The blue line represents the relative error provided by the series expansion (22), using the connection formula (3). The red line represents the relative error provided by the series expansion given in [24, Corollary 1, Eq. (26)] for small values of y. The green line represents the relative error provided by the series expansion given in [24, Corollary 1, Eq. (26)] for large values of y. We have taken the same number of terms $n=5$ for the three approximations (color figure online)

All the computations of this section have been carried out by using the symbolic manipulation program Wolfram Mathematica 12.2. In particular, the “exact” value of F(x, y) or $R_F(x,y,z)$ is computed by means of numerical integration with the command “NIntegrate”.