Abstract
A topological space is Suslin (Lusin) if it is a continuous (and bijective) image of a Polish space. For a Tychonoff space X let \(C_p(X)\), \(C_k(X)\) and \(C_{{\downarrow }{\mathsf {F}}}(X)\) be the space of continuous real-valued functions on X, endowed with the topology of pointwise convergence, the compact-open topology, and the Fell hypograph topology, respectively. For a metrizable space X we prove the equivalence of the following statements: (1) X is \(\sigma \)-compact, (2) \(C_p(X)\) is Suslin, (3) \(C_k(X)\) is Suslin, (4) \(C_{{\downarrow }{\mathsf {F}}}(X)\) is Suslin, (5) \(C_p(X)\) is Lusin, (6) \(C_k(X)\) is Lusin, (7) \(C_{{\downarrow }{\mathsf {F}}}(X)\) is Lusin, (8) \(C_p(X)\) is \(F_\sigma \)-Lusin, (9) \(C_k(X)\) is \(F_\sigma \)-Lusin, (10) \(C_{{\downarrow }{\mathsf {F}}}(X)\) is \(C_{\delta \sigma }\)-Lusin. Also we construct an example of a sequential \(\aleph _0\)-space X with a unique non-isolated point such that the function spaces \(C_p(X)\), \(C_k(X)\) and \(C_{{\downarrow }{\mathsf {F}}}(X)\) are non-Suslin.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we study the descriptive properties of the spaces \(C_p(X)\), \(C_k(X)\) and \(C_{{\downarrow }{\mathsf {F}}}(X)\) of continuous real-valued functions on a Tychonoff space X.
The function space \(C_p(X)\) is the space C(X) of continuous real-valued functions on X, endowed with the topology of pointwise convergence. This topology is generated by the subbase consisting of the sets
where \(x\in X\) and r is a real number. The function spaces \(C_p(X)\) were thoroughly studied in the monographs [1] and [16,17,18].
The function space \(C_k(X)\) is the space C(X) endowed with the compact-open topology. This topology is generated by the subbase consisting of the sets
where K is a nonempty compact set in X and r is a real number. The function spaces \(C_k(X)\) are also well-studied in General Topology [7, 12, §3.4] and Functional Analysis [9].
Our third object of study is the function space \(C_{{\downarrow }{\mathsf {F}}}(X)\). It is the space C(X) endowed with the Fell hypograph topology. This topology is generated by the subbase consisting of the sets
where K is a nonempty compact subset of X, U is a nonempty open set in X, and r is a real number.
The study of the function spaces \(C_{{\downarrow }{\mathsf {F}}}(X)\) was initiated by McCoy and Ntantu [11] and continued in [19,20,21,22,23,24,25].
The function spaces \(C_p(X)\) and \(C_k(X)\) are Tychonoff for any topological space X. In contrast, \(C_{{\downarrow }{\mathsf {F}}}(X)\) is Tychonoff only for weakly locally compact spaces X.
A space X is defined to be weakly locally compact if for every compact set K in X there exists an open set U in X such that \(K\subseteq \overline{U}\) and \(\overline{U}\) is compact. The Fréchet–Urysohn fan (see [1, III.1.8]) is an example of a weakly locally compact space, which is not locally compact.
The following characterization of the (complete) regularity of the function spaces \(C_{{\downarrow }{\mathsf {F}}}(X)\) can be found in [11, Theorem 3.7].
Theorem 1.1
(McCoy, Ntantu) For a Tychonoff space X, the following statements are equivalent:
-
(1)
\(C_{{\downarrow }{\mathsf {F}}}(X)\) is a Tychonoff space.
-
(2)
\(C_{{\downarrow }{\mathsf {F}}}(X)\) is a regular space.
-
(3)
The space X is weakly locally compact.
In this paper we shall be interested in descriptive properties of the function spaces, i.e., properties that can be described in terms of Borel sets.
Let us recall that a set A in a topological space X is called
-
Borel if A belongs to the smallest \(\sigma \)-algebra of sets in X, containing all open subsets in X;
-
constructible if A belongs to the smallest algebra of sets in X, containing all open sets in X;
-
clopen if it is both open and closed;
-
an \(F_\sigma \)-set if A is a countable union of closed sets in X;
-
a \(G_\delta \)-set if A is a countable intersection of open sets in X;
-
a \(C_\sigma \)-set if A is a countable union of constructible sets in X;
-
a \(C_\delta \)-set if A is a countable intersection of constructible sets in X;
-
an \(C_{\sigma \delta }\)-set (resp. \(F_{\sigma \delta }\)-set) if A is a countable intersection of \(C_\sigma \)-sets (resp. \(F_\sigma \)-sets) in X;
-
an \(C_{\delta \sigma }\)-set (resp. \(G_{\delta \sigma }\)-set) if A is a countable union of \(C_\delta \)-sets (resp. \(G_\delta \)-sets) in X.
De Morgan’s laws imply that each constructible set in a topological space can be written as a finite union \((U_1\cap F_1)\cup \cdots \cup (U_n\cap F_n)\) of intersections \(U_i\cap F_i\) of open and closed sets.
For any set in a topological space we have the following implications.

A topological space X is called perfect if each open set in X is of type \(F_\sigma \). For example, each metrizable space is perfect. In perfect spaces the above diagram simplifies to the following form.

Let \(\varGamma \) be a class of Borel sets in topological spaces. A function \(f:X\rightarrow Y\) between topological spaces is called \(\varGamma \)-measurable if for any open set \(U\subseteq Y\) the preimage \(f^{-1}[U]\) is Borel of class \(\varGamma \) in X. In particular, a function \(f:X\rightarrow Y\) is continuous if and only if it is G-measurable for the class G of open sets in topological spaces.
A topological space X is defined to be
-
Polish if it is homeomorphic to a separable complete metric space;
-
Suslin if it is the image of a Polish space under a continuous map;
-
Lusin if it is the image of a Polish space under a continuous bijective map;
-
\(\varGamma \)-Lusin for a Borel class \(\varGamma \) if it is the image of a Polish space P under a continuous bijective map \(f:P\rightarrow X\) such that the inverse map \(f^{-1}:X\rightarrow P\) is \(\varGamma \)-measurable.
In the role of the class \(\varGamma \) we shall consider the (additive) Borel classes G, \(F_\sigma \), \(C_\sigma \), \(C_{\delta \sigma }\), \(G_{\delta \sigma }\), B of open sets, \(F_\sigma \)-sets, \(C_\sigma \)-sets, \(C_{\delta \sigma }\)-sets, \(G_{\delta \sigma }\)-sets, Borel sets in topological spaces, respectively.
For any topological space we have the implications:
For regular spaces some implications in this chain turn into equivalences (see Theorem 3.4):
By Lusin–Suslin Theorem [10, 15.1], a subspace X of a Polish space P is Lusin if and only if X is a Borel subset of P. By the famous result of Suslin [10, 14.2], each uncountable Polish space contains a Suslin subset, which is not Borel and hence is not Lusin. In the class of metrizable spaces, Lusin and Suslin spaces were defined by Bourbaki in [5].
It is well-known [7, 4.3.26] that each Polish (= G-Lusin) space X is a \(G_\delta \)-set in any Tychonoff space containing X as a subspace. In Theorem 3.1 we shall prove that each \(F_\sigma \)-Lusin space X is a \(C_{\sigma \delta }\)-set in each Hausdorff space containing X as a subspace.
Let us observe that each Suslin space has a countable network, being a continuous image of a Polish space (which has a countable base).
We recall that a family \({\mathcal {N}}\) of subsets of a topological space X is called
-
a network if for every open set \(U\subseteq X\) and point \(x\in U\), there is a set \(N \in {\mathcal {N}}\) such that \(x\in N\subseteq U\);
-
a k-network if for every open set \(U\subseteq X\) and compact subset \(K\subseteq U\), there is a finite subfamily \({\mathcal {F}}\subseteq {\mathcal {N}}\) such that \(K \subseteq \bigcup {\mathcal {F}} \ \subseteq U\).
A topological space X is called
-
cosmic if X is regular and has a countable network;
-
an \(\aleph _0\)-space if X is regular and has a countable k-network.
For any topological space we have the following implications (see [8, §4]):
Function spaces \(C_{{\downarrow }{\mathsf {F}}}(X)\) and \(C_k(X)\) possessing countable networks were characterized in [11, Theorem 3.7 and 4.5] and [13] (see also [12, §4.1]).
Theorem 1.2
(McCoy, Ntantu, Michael) For a Tychonoff space X the following conditions are equivalent:
-
(1)
the function space \(C_{{\downarrow }{\mathsf {F}}}(X)\) has a countable network;
-
(2)
the function space \(C_k(X)\) is cosmic;
-
(3)
the function space \(C_k(X)\) is an \(\aleph _0\)-space;
-
(4)
X is an \(\aleph _0\)-space.
The following characterization of cosmic spaces \(C_p(X)\) is well-known and can be found in [12, 4.1.3] or [1, I.1.3].
Theorem 1.3
A Tychonoff space X is cosmic if and only if \(C_p(X)\) is cosmic.
The following fundamental result is due to Calbrix [6] (see also Theorem 9.7 in [9, p.208]).
Theorem 1.4
(Calbrix) If for a Tychonoff space X the function space \(C_p(X)\) is Suslin, then X is \(\sigma \)-compact.
For an Ascoli space X the Suslin property of the function space \(C_k(X)\) can be characterized in terms of \({\mathbb {R}}\)-universal \(\omega ^\omega \)-based uniformities.
Let us recall that a topological space X is called
-
Fréchet–Urysohn if for each set \(A\subseteq X\) and point \(a\in {\bar{A}}\) there exists a sequence \(\{a_n\}_{n\in \omega }\subseteq A\) that converges to a;
-
sequential if a subset \(A\subseteq X\) is closed in X if and only if A contains the limits of all sequences \(\{a_n\}_{n\in \omega }\subseteq A\) that converge in X;
-
a k-space if a subset \(A\subseteq X\) is closed in X if and only if for any compact subset \(K\subseteq X\) the intersection \(A\cap K\) is closed in K;
-
a
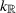 -space if a function \(f:X\rightarrow {\mathbb {R}}\) is continuous if and only if for every compact subset \(K\subseteq X\) the restriction \(f{\restriction }K\) is continuous;
-space if a function \(f:X\rightarrow {\mathbb {R}}\) is continuous if and only if for every compact subset \(K\subseteq X\) the restriction \(f{\restriction }K\) is continuous; -
Ascoli if the canonical map \(\delta :X\rightarrow C_k(C_k(X))\), \(\delta :x\mapsto \delta _x\), is continuous.
The canonical map assigns to each point x the Dirac functional \(\delta _x:C_k(X)\rightarrow {\mathbb {R}}\), \(\delta _x:f\mapsto f(x)\).
By [15], each Tychonoff  -space is Ascoli. Therefore, for any Tychonoff space we obtain the following implications:
-space is Ascoli. Therefore, for any Tychonoff space we obtain the following implications:
None of these implications can be reversed, see Examples 1.6.18, 1.6.19 in [7, 14], and [4, 6.7].
Next, we recall some information on \(\omega ^\omega \)-based uniformities. Here we consider \(\omega ^\omega \) as a partially ordered space endowed with the partial order \(\le \) defined by \(\alpha \le \beta \) iff \(\alpha (n)\le \beta (n)\) for all \(n\in \omega \).
A uniformity \({\mathcal {U}}\) on a set X is called \(\omega ^\omega \)-based if it has a base \((U_\alpha )_{\alpha \in \omega ^\omega }\) such that \(U_\beta \subseteq U_\alpha \) for any \(\alpha \le \beta \) in \(\omega ^\omega \). For example, any metrizable uniformity is \(\omega ^\omega \)-based.
A uniformity \({\mathcal {U}}\) on a topological space X is called \({\mathbb {R}}\)-universal if it generates the topology of X and every continuous function \(f:X\rightarrow {\mathbb {R}}\) is uniformly continuous in the uniformity \({\mathcal {U}}\).
A topological space X is called universally\(\omega ^\omega \)-based if its universal uniformity is \(\omega ^\omega \)-based. The universal uniformity of X is generated by the family of all continuous pseudometrics on X.
Theorem 1.5
For an (Ascoli) Tychonoff space X the function space \(C_k(X)\) is Suslin if (and only if) X is separable and has an \({\mathbb {R}}\)-universal \(\omega ^\omega \)-based uniformity.
This theorem will be proved in Sect. 2. Now we discuss the descriptive properties of function spaces on \(\varGamma \)-quotient spaces.
We say that a topological space X is a quotient of a topological space M if there exists a surjective quotient map \(f:M\rightarrow X\). The quotient property of f means that a subset \(U\subseteq X\) is open if and only if its preimage \(f^{-1}[U]\) in open in M.
A topological space X is called \(\varGamma \)-quotient for a Borel class \(\varGamma \) if X is a quotient of some space of class \(\varGamma \) in a compact metrizable space.
In particular, a G-quotient space is a quotient of a locally compact Polish space and an \(F_\sigma \)-quotient space is a quotient of a \(\sigma \)-compact metrizable space.
We recall that a topological space is Lashnev if it is the image of a metrizable space under a continuous closed map. It is known (see [8, 11.3] or [2, §8.2]) that separable Lashnev spaces are Fréchet–Urysohn \(\aleph _0\)-spaces.
The following characterization is proved in [2, 7.8.10 and 8.3.1].
Proposition 1.6
A (separable Lashnev) Tychonoff space X is universally \(\omega ^\omega \)-based if (and only if) X is \(F_\sigma \)-quotient.
We recall that a Tychonoff space is universally \(\omega ^\omega \)-based if its universal uniformity of X has an \(\omega ^\omega \)-base.
Therefore, for any Tychonoff space X we have the implications:
where the last implication can be reversed for separable Lashnev spaces.
The following theorem is the main result of this paper.
Theorem 1.7
For a Tychonoff space X consider the following statements:
-
(1)
X is G-quotient;
-
(2)
\(C_k(X)\) is Polish;
-
(3)
\(C_{{\downarrow }{\mathsf {F}}}(X)\) is \(C_\sigma \)-Lusin;
-
(4)
X is \(F_\sigma \)-quotient;
-
(5)
\(C_p(X)\), \(C_k(X)\) are \(F_\sigma \)-Lusin and \(C_{\downarrow {\mathsf {F}}}(X)\) is \(C_{\delta \sigma }\)-Lusin;
-
(6)
\(C_p(X)\) is Lusin and X is an \(\aleph _0\)-space;
-
(7)
\(C_k(X)\) is Lusin;
-
(8)
\(C_{\downarrow {\mathsf {F}}}(X)\) is Lusin;
-
(9)
\(C_p(X)\) is Suslin and X is an \(\aleph _0\)-space;
-
(10)
\(C_k(X)\) is Suslin;
-
(11)
\(C_{\downarrow {\mathsf {F}}}(X)\) is Suslin;
-
(12)
X is \(\sigma \)-compact.
Then \((3)\Leftarrow (2)\Leftrightarrow (1)\Rightarrow (4)\Rightarrow (5)\Rightarrow (6)\Leftrightarrow (7)\Leftrightarrow (8)\Rightarrow (9)\Leftrightarrow (10)\Leftrightarrow (11)\Rightarrow (12)\).
Theorem 1.7 will be proved in Sect. 6 after some preliminary work done in Sects. 3, 4 and 5. This theorem implies the following characterization.
Corollary 1.8
For a metrizable space X the following statements are equivalent:
-
(1)
X is \(\sigma \)-compact;
-
(2)
\(C_p(X)\) is \(F_\sigma \)-Lusin;
-
(3)
\(C_k(X)\) is \(F_\sigma \)-Lusin;
-
(4)
\(C_{\downarrow {\mathsf {F}}}(X)\) is \(C_{\delta \sigma }\)-Lusin;
-
(5)
\(C_p(X)\) is Lusin;
-
(6)
\(C_k(X)\) is Lusin;
-
(7)
\(C_{\downarrow {\mathsf {F}}}(X)\) is Lusin;
-
(8)
\(C_p(X)\) is Suslin;
-
(9)
\(C_k(X)\) is Suslin;
-
(10)
\(C_{\downarrow {\mathsf {F}}}(X)\) is Suslin.
Theorem 1.7(3), Corollary 1.8(3) (and Theorem 1.1) suggest the following open problem.
Problem 1.9
Is the function space \(C_{{\downarrow }{\mathsf {F}}}(X)\)\(F_\sigma \)-Lusin for any metrizable \(\sigma \)-compact (weakly locally compact) space X?
The implications of Theorems 1.7, 1.4 and 1.5 are represented in the following diagram holding for any Tychonoff space X.

The following proposition shows that the last implication in the diagram (established by Calbrix’s Theorem 1.4) cannot be reversed even for countable Lashnev (and hence \(\aleph _0\)-spaces) with a unique non-isolated point. This proposition also implies that Theorem 5.7.4 in [12] is incorrect (that theorem claims that for any sequential \(\sigma \)-compact \(\aleph _0\)-space X the function space \(C_k(X)\) is Suslin).
Proposition 1.10
Let \(X=M/A\) be the quotient space of a metrizable space M by a closed nowhere dense subset \(A\subset M\). If the function space \(C_k(X)\) is Suslin, then the space M is \(\sigma \)-compact and hence X is an \(F_\sigma \)-quotient space.
Proof
The quotient space \(X=M/A\) of the metrizable space M is a sequential Tychonoff space and hence Ascoli. If the function space \(C_k(X)\) is Suslin, then X cosmic by Theorem 1.3, and by Theorem 1.5, the topology of X is generated by some \(\omega ^\omega \)-based uniformity. By Corollary 8.2.3 [2], the set A is \(\sigma \)-compact. By Theorem 1.4, the cosmic space X is \(\sigma \)-compact and so is its open subspace \(X{\setminus }\{A\}\), which is homeomorphic to \(M{\setminus } A\). Then \(M=A\cup (M{\setminus } A)\) is \(\sigma \)-compact and hence X is \(F_\sigma \)-quotient. \(\square \)
Example 1.11
Let \(\omega ^{<\omega }=\bigcup _{n\in \omega }\omega ^n\) be the family of all functions \(x:n\rightarrow \omega \) defined on finite ordinals \(n\in \omega \). Let \(\omega ^{\le \omega }=\omega ^{<\omega }\cup \omega ^\omega \). For any function \(x\in \omega ^{\le \omega }\) defined on an ordinal \(n\le \omega \) and any ordinal \(k\le \omega \) denote by \(x{\restriction }k\) the restriction of x to the ordinal \(k\cap n=\min \{n,k\}\). The set \(\omega ^{\le \omega }\) carries a natural partial order \(\le \) defined by \(x\le y\) iff there exists an ordinal \(n\le \omega \) such that \(x=y{\restriction }n\). The space \(\omega ^{\le \omega }\) is endowed with the topology \(\tau \) generated by the countable base consisting of the sets \({\uparrow }x=\{y\in \omega ^{\le \omega }:x\le y\}\) where \(x\in \omega ^{<\omega }\). It is easy to see that \((\omega ^{\le \omega },\tau )\) is a Polish space, \(\omega ^{<\omega }\) is a dense discrete subspace in \(\omega ^{\le \omega }\) and \(\omega ^\omega \) is a closed nowhere dense subset in \(\omega ^{\le \omega }\). Consider the quotient space \(X=\omega ^{\le \omega }/{\omega ^\omega }\) and observe that X is a countable sequential \(\aleph _0\)-space with a unique non-isolated point. Since the space \(\omega ^{\le \omega }\) is not \(\sigma \)-compact, the function spaces \(C_p(X)\), \(C_k(X)\) and \(C_{{\downarrow }{\mathsf {F}}}(X)\) are not Suslin according to Proposition 1.10. In Sect. 7 we shall present an alternative self-contained proof of this fact.
Observe that the space \(X=M/A\) in Proposition 1.10 is Lashnev, i.e., the image of a metrizable space under a closed continuous map.
Problem 1.12
Assume that a Tychonoff space X is Lashnev and its function space \(C_k(X)\) is Suslin. Is X an \(F_\sigma \)-quotient space?
2 The Suslin property of the function spaces on Ascoli spaces
In this section we shall prove Theorem 1.5. To prove the “if” part of this theorem, assume that a Tychonoff space X is separable and has an \({\mathbb {R}}\)-universal \(\omega ^\omega \)-based uniformity. By Theorem 7.5.1(18) of [2], the function space \(C_k(X)\) is Suslin.
To prove the “only if” part of Theorem 1.5, assume that the space X is Ascoli and the function space \(C_k(X)\) is Suslin. By Theorem 1.2, the space X is separable. By the definition of an Ascoli space, the canonical map \(\delta :X\rightarrow C_k(C_k(X))\) is continuous. Since the space \(C_k(X)\) is Suslin, there exists a continuous surjective map \(\xi :\omega ^{\mathbb {N}}\rightarrow C_k(X)\). Here \({\mathbb {N}}=\omega \setminus \{0\}\). For any \(\alpha \in \omega ^{\mathbb {N}}\) the subspace \({\downarrow }\alpha =\{\beta \in \omega ^{\mathbb {N}}:\beta \le \alpha \}\) of \(\omega ^{\mathbb {N}}\) is compact and so is its continuous image \(K_\alpha =\xi ({\downarrow }\alpha )\subseteq C_k(X)\). Observe that \(K_\alpha \subseteq K_\beta \) for any \(\alpha \le \beta \) in \(\omega ^\omega \).
For every \(\alpha \in \omega ^\omega \) consider the entourage
of the diagonal in \(X\times X\). The continuity of the map \(\delta :X\rightarrow C_k(C_k(X))\) implies that \(U_\alpha \) is an open neighborhood of the diagonal in \(X\times X\). It is easy to see that \((U_\alpha )_{\alpha \in \omega ^\omega }\) is an \(\omega ^\omega \)-base of some uniformity \({\mathcal {U}}\) on X. To see that this uniformity in \({\mathbb {R}}\)-universal, we need to show that every function \(f\in C(X)\) is uniformly continuous with respect to the uniformity \({\mathcal {U}}\). Given any \(\varepsilon >0\), find \(\alpha \in \omega ^\omega \) such that \(2^{-\alpha (0)}<\varepsilon \) and \(f=\xi (\alpha {\restriction }{\mathbb {N}})\). Then for any pair \((x,y)\in U_\alpha \in {\mathcal {U}}\), we get
which means that f is uniformly continuous.
3 Some results on Lusin and Suslin spaces
Theorem 3.1
Each \(F_\sigma \)-Lusin subspace X of a Hausdorff topological space Y is a \(C_{\sigma \delta }\)-set in Y. More precisely, \(X=A\cap B\) for some \(G_\delta \)-set \(A\subseteq Y\) and some \(F_{\sigma \delta }\)-set \(B\subseteq Y\).
Proof
Write X as the image of a Polish space P under a continuous bijective map \(f:P\rightarrow X\) with \(F_\sigma \)-measurable inverse \(f^{-1}:X\rightarrow P\). Fix a complete metric d that generates the topology of the Polish space X.
For every \(n\in \omega \) fix a countable open cover \({\mathcal {U}}_n\) of X by sets of d-diameter \(<2^{-n}\). By the choice of the map f, for every \(U\in {\mathcal {U}}_n\) the image f[U] is an \(F_\sigma \)-set in X. Consequently, \(f[U]=\bigcup {\mathcal {F}}_{n,U}\) for some countable family \({\mathcal {F}}_{n,U}\) of closed sets in X. Let \({\mathcal {F}}_n=\bigcup _{U\in {\mathcal {U}}_n}{\mathcal {F}}_{n,U}\) and \({\mathcal {F}}=\bigcup _{n\in \omega }{\mathcal {F}}_n\). Therefore, \({\mathcal {F}}\) is a countable family of closed sets in X. It follows that each set \(F\in {\mathcal {F}}\) is equal to the intersection \(X\cap {\bar{F}}\) of X and the closure \({\bar{F}}\) of F in the space Y. Observe that for any sets \(F_1,\dots ,F_n\in {\mathcal {F}}\) we get \({\bar{F}}_1\cap \dots {\bar{F}}_n\cap X=F_1\cap \dots \cap F_n\).
Consequently,
is a \(G_\delta \)-set in Y containing X. Now consider the \(F_{\sigma \delta }\)-set \(B=\bigcap _{n\in \omega }\bigcup _{F\in {\mathcal {F}}_n}{\bar{F}}\) in Y and observe that \(A\cap B\) is a \(C_{\sigma \delta }\)-set in Y. We claim that \(X=A\cap B\). The inclusion \(X\subseteq A\cap B\) is obvious. Assuming that \(X\ne A\cap B\), find a point \(y\in A\cap B{\setminus } X\).
Then for every \(n\in \omega \) there exists a set \(F_n\in {\mathcal {F}}_n\) such that \(y\in {\bar{F}}_n\). For the set \(F_n\) find an open set \(U_n\in {\mathcal {U}}_n\) such that \(F_n\subseteq f[U_n]\) and hence \(f^{-1}[F_n]\subseteq U_n\) has d-diameter \(<2^{-n}\).
We claim that for every \(n\in \omega \) the intersection \(F_0\cap \dots \cap F_n\) is not empty. Assuming that this intersection is empty, we would conclude that \(y\in {\bar{F}}_0\cap \dots \cap {\bar{F}}_n\) is contained in \(Y\setminus A\), which contradicts the choice of y. Therefore, the family of closed sets \((F_n)_{n\in \omega }\) is centered and so is the family \((f^{-1}[F_n])_{n\in \omega }\). Since each set \(f^{-1}[F_n]\) has d-diameter \(<2^{-n}\), the completeness of the metric d ensures that the intersection \(\bigcap _{n\in \omega }f^{-1}[F_n]\) contains a unique point \(x\in X\).
By the Hausdorff property of Y, the point f(x) has an open neighborhood \(V\subseteq Y\) whose closure does not contain the point y. By the continuity of f at x, there exists \(n\in \omega \) such that \(f^{-1}[V]\) contain the ball \(B(x;2^{-n})=\{z\in X:d(x,z)<2^{-n}\}\). Then \(f^{-1}[F_n]\subseteq B(x;2^{-n})\) and hence \(F_n=f[f^{-1}[F_n]]\subseteq V\). Finally, \(y\in {\bar{F}}_n\subseteq {\bar{V}}\), which contradicts the choice of V. This contradiction completes the proof of the equality \(X=A\cap B\). \(\square \)
We do not know if Theorem 3.1 generalizes to higher Borel classes.
Problem 3.2
Let X be a \(G_{\delta \sigma }\)-Lusin subspace of a regular topological space Y. Is X a \(C_{\delta \sigma \delta }\)-set (=a countable intersection of \(C_{\delta \sigma }\)-sets) in Y?
Let us recall that a map \(f:X\rightarrow Y\) between topological spaces is Borel if for any open set \(U\subseteq Y\) the preimage \(f^{-1}[U]\) is a Borel subset of X.
The following characterization of Suslin spaces was proved in [3, 2.5].
Theorem 3.3
A cosmic space X is Suslin if and only if it is the image of a Suslin space Z under a surjective Borel map \(f:Z\rightarrow X\).
A similar characterization holds for Lusin spaces.
Theorem 3.4
For a cosmic space X the following conditions are equivalent:
-
(1)
X is Lusin;
-
(2)
X is B-Lusin;
-
(3)
X is the image of a Lusin space Z under a bijective Borel map \(f:Z\rightarrow X\).
Proof
\((1)\Rightarrow (2)\): Assuming that X is Lusin, find a Polish space P and a continuous bijective map \(f:P\rightarrow X\). The space X is cosmic, being a continuous image of the Polish space. By [8, 2.9], the cosmic space X is submetrizable and hence admits a continuous injective map \(g:X\rightarrow Y\) to a Polish space Y. By Lusin–Suslin Theorem [10, 15.1], for every open set \(U\subseteq P\) the image \(g\circ f[U]\) is a Borel subset of the Polish space Y. The continuity of the map g implies that the set \(f[U]=g^{-1}[g\circ f[U]]\) is Borel in X. This means that the space X is B-Lusin.
The implication \((2)\Rightarrow (3)\) is trivial.
\((3)\Rightarrow (1)\): Assume that the cosmic space X is the image of a Lusin space L under a bijective Borel map \(f:L\rightarrow X\). By the definition, the Lusin space L is the image of a Polish space P under a continuous bijective map \(g:P\rightarrow L\). Then X is the image of the Polish space under the Borel bijective map \(h=f\circ g:P\rightarrow X\). Being cosmic, the space X has a countable network \({\mathcal {N}}\) consisting of closed subsets of X. Since the map h is Borel, for every \(N\in {\mathcal {N}}\) the preimage \(h^{-1}[N]\) is a Borel subset of the Polish space P. By [10, 13.5], there exists a continuous bijective map \(\xi :Z\rightarrow P\) from a Polish space Z such that for every \(N\in {\mathcal {N}}\) the Borel set \(\xi ^{-1}[h^{-1}[N]]\) is open in Z. Consider the map \(\varphi =h\circ \xi :Z\rightarrow X\) and observe that for any open set \(U\subseteq X\) the preimage \(\varphi ^{-1}[U]=\bigcup \{\varphi ^{-1}[N]:N\in {\mathcal {N}},\;N\subseteq U\}\) is open in Z, witnessing that the bijective map \(\varphi :Z\rightarrow X\) is continuous and hence X is Lusin. \(\square \)
4 Borel properties of the identity maps between various function spaces
It is clear that for any Tychonoff space X the identity maps \(C_k(X)\rightarrow C_p(X)\) and \(C_k(X)\rightarrow C_{{\downarrow }{\mathsf {F}}}(X)\) are continuous.
Lemma 4.1
For any \(\aleph _0\)-space X, the identity map \(C_p(X)\rightarrow C_k(X)\) is \(F_\sigma \)-measurable.
Proof
By Theorem 1.2, the function space \(C_k(X)\) has a countable network and hence is hereditarily Lindelöf. Then it suffices to find a subbase of the topology of \(C_k(X)\) consisting of the sets which are Borel in the topology of the space \(C_p(X)\). We claim that the standard subbase of \(C_k(X)\) has this property. Given a compact set \(K\subseteq X\) and a real number r, we need to check that the open sets
are Borel in \(C_p(X)\). The compact subset K of the \(\aleph _0\)-space has a countable network and hence is separable. Consequently, we can fix a countable dense set \(\{x_m\}_{m\in \omega }\) in K.
Now observe that the sets
are Borel of type \(F_{\sigma }\) in \(C_p(X)\). \(\square \)
Lemma 4.2
For any cosmic space X, the identity map \(C_{{\downarrow }{\mathsf {F}}}(X)\rightarrow C_p(X)\) is \(C_\sigma \)-measurable.
Proof
By Theorem 1.3, the function space \(C_p(X)\) has a countable network and hence is hereditarily Lindelöf. Then it suffices to find a subbase of the topology of \(C_p(X)\) consisting of sets which are of type \(C_\sigma \) in the Fell hypograph topology. We claim that the standard subbase of \(C_p(X)\) has this property. Given a point \(x\in X\) and a real number r, we need to check that the open sets
are Borel of type \(C_\sigma \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\). The set \(\lceil x;r\rceil \) is open in \(C_{{\downarrow }{\mathsf {F}}}(X)\) and hence \(C_\sigma \) by the definition of the Fell hypograph topology. Since
the set \(\lfloor K;r\rfloor \) is Borel of type \(F_\sigma \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\). \(\square \)
Lemma 4.3
For any \(\aleph _0\)-space X, the identity map \(C_{{\downarrow }{\mathsf {F}}}(X)\rightarrow C_k(X)\) is \(C_\sigma \)-measurable.
Proof
By Theorem 1.2, the function space \(C_k(X)\) has a countable network and hence is hereditarily Lindelöf. Then it suffices to find a subbase of the topology of \(C_k(X)\) consisting of sets which are of type \(F_\sigma \) in the Fell hypograph topology. We claim that the standard subbase of \(C_k(X)\) has this property. Given a nonempty compact set \(K\subseteq X\) and a real number r, we need to check that the open sets
are Borel of class \(C_\sigma \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\). The set \(\lceil K;r\rceil \) is open in \(C_{{\downarrow }{\mathsf {F}}}(X)\) by the definition of the Fell hypograph topology.
The compact subset K of the \(\aleph _0\)-space has a countable network \(\{K_n\}_{n\in \omega }\) consisting of closed (and hence compact) sets in K.
Since
the set \(\lfloor K;r\rfloor \) is Borel of type \(F_\sigma \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\). \(\square \)
5 Function spaces on \(F_\sigma \)-quotient spaces
Lemma 5.1
For any \(F_\sigma \)-quotient Tychonoff space X, the function spaces \(C_p(X)\) and \(C_k(X)\) are \(F_\sigma \)-Lusin and \(C_{{\downarrow }{\mathsf {F}}}(X)\) is \(C_{\delta \sigma }\)-Lusin.
Proof
By the definition of an \(F_\sigma \)-quotient space, there exists a quotient surjective map \(q:M\rightarrow X\) defined on a \(\sigma \)-compact metrizable space M. First we establish two properties of the quotient map q.
Claim 5.2
For any sequence \(\{x_n\}_{n\in \omega }\subseteq X\) that accumulates at some point \(x\in X\) there exists a sequence \(\{z_k\}_{k\in \omega }\subseteq q^{-1}[\{x_n\}_{n\in \omega }]\) that converges to a point \(z\in q^{-1}(x)\).
Proof
If the set \(\varOmega =\{n\in \omega :x_n=x\}\) is infinite, then take any point \(z\in q^{-1}(x)\) and put \(z_k=z\) for all \(k\in \varOmega \). It is clear that the sequence \((z_k)_{k\in \varOmega }\) converges to z and \(\{z_k\}_{k\in \varOmega }\subseteq q^{-1}[\{x_n\}_{n\in \varOmega }]\subseteq q^{-1}[\{x_n\}_{n\in \omega }]\).
So, we assume that the set \(\varOmega \) is finite. Then the set \(A=\{x_n:n\in \omega \setminus \varOmega \}\) is not closed in X and by the quotient property of q, the preimage \(q^{-1}(A)\) is not closed in M. Since M is metrizable, there exists a sequence \(\{z_k\}_{k\in \omega }\subseteq q^{-1}[A]\), convergent to a point \(z\notin q^{-1}[A]\). The continuity of q implies that \(q(z)\in {\bar{A}}\setminus A=\{x\}\). \(\square \)
Claim 5.3
For every compact set \(K\subseteq X\) and a cover \({\mathcal {U}}\) of the set \(q^{-1}[K]\) by open subsets of M there exists a finite subfamily \({\mathcal {F}}\subseteq {\mathcal {U}}\) such that \(K\subseteq \bigcup _{U\in {\mathcal {F}}}q[U]\).
Proof
Since the \(\sigma \)-compact space M is Lindelöf, the open cover \({\mathcal {U}}\) of the closed set \(q^{-1}[K]\) contains a countable subcover \({\mathcal {V}}\). We can choose an enumeration \(\{U_n\}_{n\in \omega }\) of the countable family \({\mathcal {V}}\) such that \(q^{-1}[K]\subseteq \bigcup _{n=k}^\infty U_n\) and hence \(K\subseteq \bigcup _{n=k}^\infty q[U_n]\) for every \(k\in \omega \).
To finish the proof of the claim, it suffices to find \(n\in \omega \) such that \(K\subseteq \bigcup _{k\le n}q[U_k]\). Assuming that no such number n exists, for every \(n\in \omega \) we can choose a point \(x_n\in K\setminus \bigcup _{k\le n}q[U_k]\). By the compactness of K, the sequence \((x_n)_{n\in \omega }\) accumulates at some point \(x\in K\). Since \(K\subseteq \bigcup _{n\in \omega }q[U_n]\), there exists a number \(k\in \omega \) such that \(x\in q[U_k]\). Then \(x\notin \{x_n\}_{n>k}\).
By Claim 5.2, there exists a sequence \(\{z_n\}_{n\in \omega }\subseteq q^{-1}[\{x_n\}_{n>k}]\) that converges to a point \(z\in q^{-1}(x)\subseteq q^{-1}[K]\). Since \(\{U_n\}_{n>k}\) is a cover of \(q^{-1}[K]\), the point z belongs to some set \(U_n\) with \(n>k\). Since the sequence \((z_m)_{m\in \omega }\) converges to the point \(z\in U_n\), there exists a number \(m>n\) such that \(z_m\in U_n\setminus q^{-1}[\{x_{k+1},\dots ,x_n\}]\). Then \(q(z_m)=x_i\) for some \(i>n\) and hence \(x_i=q(z_m)\in q[U_n]\), which contradicts the choice of \(x_i\). \(\square \)
Write the \(\sigma \)-compact space M as the countable union \(M=\bigcup _{n\in \omega }M_n\) of an increasing sequence \((M_n)_{n\in \omega }\) of compact subsets of M. Fix a countable subset \(D\subseteq M\) such that for any \(n\in \omega \) the intersection \(D\cap M_n\) is dense in \(M_n\). Also fix a metric d generating the topology of M. For a point \(x\in M\) and a positive real number \(\varepsilon \) let \(B(x;\varepsilon )=\{y\in M:d(y,x)<\varepsilon \}\) be the \(\varepsilon \)-ball centered at x and \(D(x;\varepsilon ):=D\cap B(x;\varepsilon )\) be the trace of the ball \(B(x,\varepsilon )\) on D. For every \(n\in \omega \) let \(Q_n=\{(x,y)\in M_n\times M_n:q(x)=q(y)\}\).
In the Polish space \(\omega ^\omega \times {\mathbb {R}}^D\) consider the \(G_\delta \)-subset
Observe that for every \((\alpha ,f)\in P\) and every \(n\in \omega \) the restriction \(f{\restriction }D\cap M_n\) is a uniformly continuous function, which admits a uniformly continuous extension \({\bar{f}}_n:M_n\rightarrow {\mathbb {R}}\) to \(M_n\) (by the density of \(D\cap M_n\) in \(M_n\)). Taking into account that \(D\cap M_n\subseteq D\cap M_{n+1}\), we conclude that \({\bar{f}}_n={\bar{f}}_{n+1}{\restriction }M_n\), which allows us to define a function \({\bar{f}}:M\rightarrow {\mathbb {R}}\) such that \({\bar{f}}{\restriction }M_n=f_n\) for all \(n\in \omega \). We claim that the function \({\bar{f}}\) is continuous. Indeed, for any \(x\in M\) and any \(\varepsilon >0\), we can find \(n\in \omega \) such that \(x\in M_n\) and \(\frac{1}{2^n}<\frac{1}{3}\varepsilon \). We claim that \(|{\bar{f}}(x)-{\bar{f}}(y)|<\varepsilon \) for any \(y\in M\) with \({d}(x,y)<\frac{1}{2^{\alpha (n)}}\). Find a number \(m\ge n\) such that \(y\in M_m\). By the continuity of the map \({\bar{f}}{\restriction }M_m\) and the density of \(D\cap M_k\) in \(M_k\) for \(k\in \{n,m\}\), there exist points \(x'\in D\cap M_n\) and \(y'\in D\cap M_m\) such that \({d}(x',y')<\frac{1}{2^{\alpha (n)}}\), \(|{\bar{f}}(x)-{\bar{f}}(x')|<\frac{1}{3}\varepsilon \) and \(|{\bar{f}}(y)-{\bar{f}}(y')|<\frac{1}{3}\varepsilon \). Then
Therefore the function \({\bar{f}}\) is continuous.
Next, we show that \({\bar{f}}(x)={\bar{f}}(y)\) for any \(x,y\in M\) with \(q(x)=q(y)\). Assuming that \({\bar{f}}(x)\ne {\bar{f}}(y)\), we can find \(n\in \omega \) such that \(x,y\in M_n\) and \(|f(x)-f(y)|>\frac{3}{2^n}\). Then \((x,y)\in Q_n\). By the density of D in M, there exist points \(x'\in D(x;\frac{1}{2^{\alpha (n)}})\) and \(y'\in D(y;\frac{1}{2^{\alpha (n)}})\) such that \(|f(x')-f(y')|=|{\bar{f}}(x')-{\bar{f}}(y')|>\frac{3}{2^n}\). But this contradicts the inclusion \((\alpha ,f)\in P\). This contradiction shows that \({\bar{f}}={{\tilde{f}}}\circ q\) for some function \({{\tilde{f}}}:X\rightarrow {\mathbb {R}}\). Since the map q is quotient, the function \({{\tilde{f}}}:X\rightarrow {\mathbb {R}}\) is continuous.
So, we can consider the function \(\xi :P\rightarrow C(X)\) assigning to each pair \((\alpha ,f)\) the (unique) continuous function \({{\tilde{f}}}:X\rightarrow {\mathbb {R}}\) such that \(f={{\tilde{f}}}\circ q{\restriction }D\).
Claim 5.4
The function \(\xi :P\rightarrow C(X)\) is surjective.
Proof
Let \(\varphi :X\rightarrow {\mathbb {R}}\) be any continuous function. For every \(n\in \omega \), the continuity of the function \(\psi =\varphi \circ q\) at points of the compact set \(M_n\) yields a number \(\alpha (n)\in \omega \) such that \(|\psi (x)-\psi (y)|\le 2^{-n}\) for any \(x\in M_n\) and \(y\in M\) with \({d}(x,y)<2^{-\alpha (n)}\). We can assume that \(\alpha (n)\) is the smallest possible number with this property. Then there exists \(x\in M_n\) and \(y\in M\) such that \({d}(x,y)<2^{1-\alpha (n)}\) and \(|\psi (x)-\psi (y)|>2^{-n}\). By the density of the sets \(D\cap M_n\) in \(M_n\) and D in M, there are points \(x'\in M_n\cap D\) and \(y'\in D\) such that \({d}(x',y')<2^{1-\alpha (n)}\) and \(|\psi (x')-\psi (y')|>2^{-n}\). It is easy to see that the pair \((\alpha ,\psi {\restriction }D)\) belongs to the first two sets in the definition of the set P.
Let us show that \((\alpha ,\psi {\restriction }D)\) also belongs to the third set. Assuming that this is not true, we can find \(n\in \omega \), \((x,y)\in Q_n\) and points \(x'\in D(x;2^{-\alpha (n)})\), \(y'\in D(y;2^{-\alpha (n)})\) such that \(|\psi (x')-\psi (y')|>\frac{3}{2^n}\). It follows that \(x\in M_n\cap D(x';2^{-\alpha (n)})\) and \(y\in M_n\cap D(y';2^{-\alpha (n)})\). By the density of the set \(D\cap M_n\) in M, there are points \(x''\in M_n\cap D(x';2^{-\alpha (n)})\) and \(y''\in M_n\cap D(y';2^{-\alpha (n)})\) such that \(\max \{|\psi (x)-\psi (x'')|,|\psi (y)-\psi (y'')|\}<\frac{1}{2^{n+1}}\). Since \(x'\in D(x'';2^{-\alpha (n)})\) and \(y'\in D(y'';2^{-\alpha (n)})\), the choice of \(\alpha (n)\) ensures that \(\max \{|\psi (x'')-\psi (x')|,|\psi (y'')-\psi (y')|\}\le \frac{1}{2^n}\). It follows from \((x,y)\in Q_n\) that \(q(x)=q(y)\) and hence \(\psi (x)=\varphi (q(x))=\varphi (q(y))=\psi (y)\). Then
which is a contradiction finishing the proof of the inclusion \((\alpha ,\psi {\restriction }D)\in P\).
Observe that for the function \(f=\psi {\restriction }D\), we get \({\bar{f}}=\psi \) and \(\varphi ={{\tilde{f}}}=\xi (\alpha ,f)\), which means that the function \(\xi \) is surjective. \(\square \)
Claim 5.5
The function \(\xi :P\rightarrow C(X)\) is injective.
Proof
Assume that \((\alpha ,f),(\beta ,g)\in P\) are two pairs such that \({{\tilde{f}}}={{\tilde{g}}}\), where \({{\tilde{f}}}=\xi (\alpha ,f)\) and \({{\tilde{g}}}=\xi (\beta ,g)\). Then \(f={{\tilde{f}}}\circ q{\restriction }D={{\tilde{g}}}\circ q{\restriction }D=g\).
It remains to prove that \(\alpha =\beta \). Assuming that \(\alpha \ne \beta \), we can find \(n\in \omega \) such that \(\alpha (n)\ne \beta (n)\). We lose no generality assuming that \(\alpha (n)<\beta (n)\). Since \((\beta ,g)\in P\), there exist points \(x\in D\cap M_n\) and \(y\in D(x;2^{1-\beta (n)})\) such that \(|g(x)-g(y)|>2^{-n}\). The strict inequality \(\alpha (n)<\beta (n)\) implies \(2^{-\alpha (n)}\ge 2^{1-\beta (n)}\) and hence \(y\in D(x;2^{1-\beta (n)})\subseteq D(x;2^{-\alpha (n)})\). Then we get points \(x\in D\cap M_n\) and \(y\in D(x;2^{-\alpha (n)})\) such that \(|f(x)-f(y)|=|g(x)-g(y)|>2^{-n}\). But this contradicts the inclusion \((\alpha ,f)\in P\). \(\square \)
Claim 5.6
The function \(\xi :P\rightarrow C_k(X)\) is continuous.
Proof
By [8, 11.3], the \(F_\sigma \)-quotient space X is an \(\aleph _0\)-space. By Theorem 1.2, the function space \(C_k(X)\) is cosmic and hence hereditarily Lindelöf. So, it suffices to show that for any nonempty compact set \(K\subseteq X\) and any real number r the sets \(\xi ^{-1}\big [\lfloor K;r\rfloor \big ]\) and \(\xi ^{-1}\big [\lceil K;r\rceil \big ]\) are open in P.
To see that \(\xi ^{-1}\big [\lfloor K;r\rfloor \big ]\) is open, take any pair \((\alpha ,f)\in \xi ^{-1}\big [\lfloor K;r\rfloor \big ]\). Consider the function \({{\tilde{f}}}=\xi (\alpha ,f)\). Since \({{\tilde{f}}}\in \lfloor K;r\rfloor \), there exists an open neighborhood \(U\subseteq X\) of K and a number \(n\in \omega \) such that \(r+\tfrac{2}{2^n}<\inf {{\tilde{f}}}(U)\).
For every \(z\in q^{-1}[K]\) we can find a number \(k\ge n\) such that \(z\in M_k\). By the density of the set \(D\cap M_k\) in \(M_k\), there exists a point \(x\in D\cap M_k\cap q^{-1}[U]\cap B(z;2^{-\alpha (k)})\). Then \(z\in B(x;2^{-\alpha (k)})\). Therefore,
By Claim 5.3, there exists \(m\ge n\) and a finite subset \(F\subseteq D\cap q^{-1}[U]\) such that
Consider the open neighborhood
of \((\alpha ,f)\) in P.
We claim that \(\xi [W]\subseteq \lfloor K;r\rfloor \). Take any pair \((\beta ,g)\in W\) and consider the function \({{\tilde{g}}}=\xi (\beta ,g)\). Given any point \(y\in K\) we should prove that \({{\tilde{g}}}(y)>r\). Find \(k\in [n,m]\) and \(x\in F\cap M_k\) such that \(y\in q[B(x,2^{-\alpha (k)})]\). Then \(y=q(z)\) for some \(z\in B(x,2^{-\alpha (k)})\). The inclusion \((\beta ,g)\in W\) ensures that \(g(x)>r+\frac{1}{2^n}\). Let \({\bar{g}}:X\rightarrow {\mathbb {R}}\) be the (unique) continuous function extending the function g. We claim that \(|{\bar{g}}(z)-g(x)|\le \frac{1}{2^k}\). To derive a contradiction, assume that \(|{\bar{g}}(z)-g(x)|>\frac{1}{2^k}\). By the continuity of \({\bar{g}}\) and the density of D in M, there exists a point \(t\in D\) such that \(d(t,z)<2^{-\alpha (k)}-d(z,x)\) and \(|{\bar{g}}(t)-{\bar{g}}(z)|<|{\bar{g}}(z)-g(x)|-\frac{1}{2^k}\). Then \(t\in B(x;2^{-\alpha (k)})\) and \(|{\bar{g}}(t)-g(x)|>\frac{1}{2^k}\). The inclusion \((\beta ,g)\in W\) guarantees that \(\beta (k)=\alpha (k)\). Then \(x\in D\cap M_k\) and \(t\in D\cap B(x;2^{-\beta (k)})\) are two points with \(|g(t)-g(x)|>\frac{1}{2^k}\), which contradicts the inclusion \((\beta ,g)\in P\). This contradiction shows that \(|{\bar{g}}(z)-g(x)|\le \frac{1}{2^k}\le \frac{1}{2^n}\). Then
Therefore, \(W\subseteq \xi ^{-1}\big [\lfloor K;r\rfloor \big ]\) and the set \(\xi ^{-1}\big [\lfloor K;r\rfloor \big ]\) is open in P. By analogy we can prove that the set \(\xi ^{-1}\big [\lceil K;r\rceil \big ]\) is open in P. \(\square \)
Claim 5.7
The function \(\xi ^{-1}:C_p(X)\rightarrow P\) is \(F_\sigma \)-measurable.
Proof
Since the Polish space P is hereditarily Lindelöf, it suffices to show that for any \((n,m)\in \omega \), point \(x\in D\) and real number r, the images of the subbasic open sets
and
under the map \(\xi \) are \(F_\sigma \)-sets in \(C_p(X)\). We shall prove that the images of these sets are open or closed (and hence \(F_\sigma \)) in \(C_p(X)\).
Observe that the set
-
\(\xi [P_{n\le m}]=\{f\in C(X):\forall x\in D\cap X_n\;\forall y\in D(x,\frac{1}{2^{m}})\; |f\circ q(x)-f\circ q(y)|\le \tfrac{1}{2^n}\}\) is closed in \(C_p(X)\),
-
\(\xi [P_{n\ge m}]=\{f\in C(X):\exists x\in D\cap X_n\;\exists y\in D(x,\frac{2}{2^{m}})\; |f\circ q(x)-f\circ q(y)|>\frac{1}{2^n}\}\) is open in \(C_p(X)\),
-
\(\xi [P_{x<r}]=\{f\in C(X):f\circ q(x)<r\}\) and \(\xi (P_{x>r})=\{f\in C(X):f\circ q(x)>r\}\) are open in \(C_p(X)\).\(\square \)
Claim 5.8
For every \(x,y\in X\) and \(\varepsilon >0\) the set \(E=\{f\in C_{{\downarrow }{\mathsf {F}}}(X):|f(x)-f(y)|>\varepsilon \}\) is of type \(C_\sigma \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\).
Proof
Let \({\mathbb {Q}}\) be the set of rational numbers and \(Q=\{(p,q)\in {\mathbb {Q}}\times {\mathbb {Q}}:p+\varepsilon <q\}\). Observe that
is of type \(C_\sigma \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\). \(\square \)
Claim 5.9
The function \(\xi ^{-1}:C_{{\downarrow }{\mathsf {F}}}(X)\rightarrow P\) is \(C_{\delta \sigma }\)-measurable.
Proof
Similarly as in Claim 5.7, it suffices to check that for any \((n,m)\in \omega \), point \(x\in D\) and real number r, the images of the subbasic open sets \(P_{n\le m},P_{n\ge m},P_{x>r}\), \(P_{x<r}\) under the map \(\xi \) are \(C_{\delta \sigma }\)-sets in \(C_{{\downarrow }{\mathsf {F}}}(X)\). We shall prove that the images of these sets are of type \(C_\sigma \) or \(C_\delta \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\).
By Claim 5.8, the set
-
\(\xi [P_{n\le m}]=\{f\in C(X):\forall x\in D\cap X_n\;\forall y\in D(x,\frac{1}{2^{m}})\;\; |f\circ q(x)-f\circ q(y)|\le \frac{1}{2^n}\}\) is of type \(C_\delta \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\),
-
\(\xi [P_{n\ge m}]=\{f\in C_p(X):\exists x\in D\cap X_n\;\exists y\in D(x,\frac{2}{2^{m}})\;\; |f(x)-f(y)|>\frac{1}{2^n}\}\) is of type \(C_\sigma \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\),
-
\(\xi [P_{x<r}]=\{f\in C(X):f(q(x))<r\}\) is open in \(C_{{\downarrow }{\mathsf {F}}}(X)\),
-
\(\xi [P_{x>r}]=\{f\in C(X):f(q(x))>r\}=\bigcup _{n\in \omega }\{f\in C(X):f(q(x))\ge r+\frac{1}{2^n}\}= \bigcup _{n\in \omega }(C(X)\setminus \lceil q(x);r+\frac{1}{2^n}\rceil )\) is of type \(F_\sigma \) in \(C_{{\downarrow }{\mathsf {F}}}(X)\). \(\square \)
Claim 5.10
The function space \(C_p(X)\) is \(F_\sigma \)-Lusin.
Proof
By Claims 5.4, 5.5 and 5.6, the map \(\xi :P\rightarrow C_k(X)\) is bijective and continuous. Since the identity map \(C_k(X)\rightarrow C_p(X)\) is continuous, the map \(\xi :P\rightarrow C_p(X)\) is continuous as the composition of two continuous maps. By Claim 5.7, the inverse map \(\xi ^{-1}:C_p(X)\rightarrow P\) is \(F_\sigma \)-measurable, which implies that the space \(C_p(X)\) is \(F_\sigma \)-Lusin. \(\square \)
Claim 5.11
The function space \(C_k(X)\) is \(F_\sigma \)-Lusin.
Proof
By Claims 5.4, 5.5 and 5.6, the map \(\xi :P\rightarrow C_k(X)\) is bijective and continuous. By Claim 5.7 the map \(\xi ^{-1}:C_p(X)\rightarrow P\) is \(F_\sigma \)-measurable. The continuity of the identity map \(C_k(X)\rightarrow C_p(X)\) implies that the map \(\xi ^{-1}:C_k(X)\rightarrow P\) is \(F_\sigma \)-measurable (as the composition of a continuous and \(F_\sigma \)-measurable maps). Now we see that the Polish space P and the map \(\xi :P\rightarrow C_k(X)\) witness that the space \(C_k(X)\) is \(F_\sigma \)-Lusin. \(\square \)
Claim 5.12
The function space \(C_{{\downarrow }{\mathsf {F}}}(X)\) is \(C_{\delta \sigma }\)-Lusin.
Proof
By Claims 5.4, 5.5 and 5.6, the map \(\xi :P\rightarrow C_k(X)\) is bijective and continuous. Since the identity map \(C_k(X)\rightarrow C_{{\downarrow }{\mathsf {F}}}(X)\) is continuous, the map \(\xi :P\rightarrow C_{{\downarrow }{\mathsf {F}}}(X)\) is continuous (as the composition of two continuous maps). By Claim 5.9, the inverse map \(\xi ^{-1}:C_{{\downarrow }{\mathsf {F}}}(X)\rightarrow P\) is \(C_{\delta \sigma }\)-measurable, which implies that the space \(C_p(X)\) is \(C_{\delta \sigma }\)-Lusin. \(\square \)
6 Proof of Theorem 1.7
In this section, for a Tychonoff space X we shall prove the implications
of Theorem 1.7.
\((2)\Rightarrow (3)\) Assume that the function space \(C_k(X)\) is Polish. The continuity of the identity map \(C_k(X)\rightarrow C_{{\downarrow }{\mathsf {F}}}(X)\) implies that the space \(C_{{\downarrow }{\mathsf {F}}}(X)\) is Lusin. Since the identity map \(C_{{\downarrow }{\mathsf {F}}}(X)\rightarrow C_k(X)\) is \(C_\sigma \)-measurable (by Lemma 4.3), the space \(C_{{\downarrow }{\mathsf {F}}}(X)\) is \(C_\sigma \)-Lusin.
\((2)\Rightarrow (1)\) If the function space \(C_k(X)\) is Polish, then by Corollary 5.2.5 in [12], X is a cosmic hemicompact k-space. The hemicompactness of X yields an increasing sequence \((K_n)_{n\in \omega }\) of compact sets in X such that each compact subset of X is contained in some set \(K_n\). Consider the locally compact subspace \(M=\bigcup _{n\in \omega }(K_n\times \{n\})\) of the product \(X\times \omega \) where the ordinal \(\omega \) is endowed with the discrete topology. Let \(q:M\rightarrow X\) be the natural projection. We claim that the map q is quotient. Indeed, take any subset \(A\subseteq X\) such that the preimage \(q^{-1}[A]\) is closed in X. Then \(A\cap K_n\) is closed in \(K_n\) for every \(n\in \omega \). Since each compact set \(K\subseteq X\) is contained in some \(K_n\), the intersection \(A\cap K=(A\cap K_n)\cap K\) is closed in K. Since X is a k-space, the set A is closed in X. Therefore, the map q is quotient. Since M is open in its one-point compactification, the space X is G-quotient.
\((1)\Rightarrow (2)\) Assume that X is G-quotient and find a quotient surjective map \(q:M\rightarrow X\) defined on an open subspace M of a compact metrizable space. Write the locally compact space M as the countable union \(M=\bigcup _{n\in \omega }U_n\) of an increasing sequence \((U_n)_{n\in \omega }\) of open sets such that each set \(U_n\) has compact closure \(\overline{U_n}\), contained in \(U_{n+1}\). By Claim 5.3, for every compact set \(K\subseteq X\) there exists a number \(n\in \omega \) such that \(K\subseteq q[U_n]\subseteq q[\overline{U_n}]\). Now we see that the sequence of compact sets \((q[\overline{U_n}])_{n\in \omega }\) witnesses that the space X is hemicompact. By Theorem 11.3 [8], X is a cosmic k-space, and by Corollary 5.2.5 of [12], for the cosmic hemicompact k-space X, the function space \(C_k(X)\) is Polish.
The implication \((1)\Rightarrow (4)\) is trivial, \((4)\Rightarrow (5)\) is proved in Lemma 5.1 and \((5)\Rightarrow (7)\) is trivial. The implication \((7)\Rightarrow (8)\) follows from the continuity of the identity map \(C_k(X)\rightarrow C_{{\downarrow }{\mathsf {F}}}(X)\).
\((8)\Rightarrow (6)\) Assume that the space \(C_{{\downarrow }{\mathsf {F}}}(X)\) is Lusin. Then \(C_{{\downarrow }{\mathsf {F}}}(X)\) has a countable network and X is an \(\aleph _0\)-space by Theorem 1.2. By Theorem 1.3, the function space \(C_p(X)\) is cosmic. By Lemma 4.2, the identity map \(C_{{\downarrow }{\mathsf {F}}}(X)\rightarrow C_p(X)\) is Borel and by Theorem 3.4, the cosmic space \(C_p(X)\) is Lusin.
\((6)\Rightarrow (7)\) Assume that \(C_p(X)\) is Lusin and X is an \(\aleph _0\)-space. By Theorem 1.2, the function space \(C_k(X)\) is cosmic. By Lemma 4.1, the identity map \(C_p(X)\rightarrow C_k(X)\) is Borel and by Theorem 3.4, the cosmic space \(C_k(X)\) is Lusin.
The implication \((7)\Rightarrow (10)\) is trivial and \((10)\Rightarrow (11)\) follows from the continuity of the identity map \(C_k(X)\rightarrow C_{{\downarrow }{\mathsf {F}}}(X)\).
\((11)\Rightarrow (9)\) Assume that the space \(C_{{\downarrow }{\mathsf {F}}}(X)\) is Suslin. Then \(C_{{\downarrow }{\mathsf {F}}}(X)\) has a countable network and X is an \(\aleph _0\)-space by Theorem 1.2. By Theorem 1.3, the function space \(C_p(X)\) is cosmic. By Lemma 4.2, the identity map \(C_{{\downarrow }{\mathsf {F}}}(X)\rightarrow C_p(X)\) is Borel and by Theorem3.3, the space \(C_p(X)\) is Suslin.
\((9)\Rightarrow (10)\) Assume that \(C_p(X)\) is Suslin and X is an \(\aleph _0\)-space. By Theorem 1.2, the function space \(C_k(X)\) is cosmic. By Lemma 4.1, the identity map \(C_p(X)\rightarrow C_k(X)\) is Borel and by Theorem 3.3, the space \(C_k(X)\) is Suslin.
\((10)\Rightarrow (12)\) If the space \(C_k(X)\) is Suslin, then so is the space \(C_p(X)\) (being a continuous image of \(C_k(X)\). By Calbrix’s Theorem 1.4, the space X is \(\sigma \)-compact.
7 Discussing Example 1.11
In this section we prove that for the quotient space \(X=\omega ^{\le \omega }/\omega ^\omega \) from Example 1.11, the function spaces \(C_p(X)\), \(C_k(X)\) and \(C_{{\downarrow }{\mathsf {F}}}(X)\) are non-Suslin.
For a topological space T denote by \(T'\) the set of non-isolated points of T and observe that
is a closed linear subspace of \(C_p(T)\).
We recall that the discrete subspace \(\omega ^{<\omega }\) of the Polish space \(\omega ^{\le \omega }=\omega ^{<\omega }\cup \omega ^\omega \) carries the partial order \(\le \) defined by \(x\le y\) iff \(x=y{\restriction }n\) for some \(n\in \omega \). Endowed with this partial order, the set \(\omega ^{<\omega }\) is a tree (which means that for any \(x\in \omega ^{<\omega }\) the set \({\downarrow }x=\{y\in \omega ^{<\omega }:y\le x\}\) is finite and linearly ordered). A subtree T of \(\omega ^{<\omega }\) is well-founded if it contains no infinite linearly ordered subsets.
In the function space \(C_p(\omega ^{\le \omega })\) consider the closed subspace
consisting of non-increasing continuous functions \(f:\omega ^{\le \omega }\rightarrow \{0,1\}\) that vanish on the subspace \(\omega ^\omega \).
For any function \(f\in M_0(\omega ^{\le \omega })\) the preimage \(f^{-1}(1)\) is a well-founded subtree of the tree \(\omega ^{<\omega }\). So, the space \(M_0(\omega ^{\le \omega })\) can be identified with the space WF of well-founded trees on \(\omega \). By [10, 32.B], the space WF is coanalytic but not analytic and so is the space \(M_0(\omega ^{\le \omega })\). Let us recall that a subset A of a Polish space P is analytic (resp. coanalytic) if the space A (resp. \(P\setminus A\)) is Suslin.
Consider the quotient space \(X=\omega ^{\le \omega }/\omega ^\omega \) of the Polish space \(\omega ^{\le \omega }\) by its closed nowhere dense subspace \(\omega ^\omega \). It is clear that X is a countable Tychonoff space with a unique non-isolated point \(\{\omega ^\omega \}\). By [8, 11.3], X is a sequential \(\aleph _0\)-space.
Claim 7.1
The function space \(C'_p(X)=\big \{f\in C_p(X):f[X']\subseteq \{0\}\big \}\) is not Suslin.
Proof
Let \(q:\omega ^{\le \omega }\rightarrow X\) be the quotient map. It induces a continuous map \(q^*:C_p(X)\rightarrow C_p(\omega ^{\le \omega })\), \(q^*:f\mapsto f\circ q\). Observe that \(q^*[C_p'(X)]=C'_p(\omega ^{\le \omega })\), where \(C_p'(\omega ^{\le \omega })=\{f\in C_p(\omega ^{\le \omega }):f[\omega ^\omega ]\subseteq \{0\}\}\). Assuming that the space \(C_p'(X)\) is Suslin, we would conclude that its continuous image \(C'_p(\omega ^{\le \omega })\) is Suslin. On the other hand, \(C_p'(\omega ^{\le \omega })\) contains the non-analytic space \(M_0(\omega ^{\le \omega })\) as a closed subspace and hence \(C_p'(\omega ^{\le \omega })\) cannot be Suslin. \(\square \)
Claim 7.2
The function spaces \(C_p(X),C_k(X)\) and \(C_{{\downarrow }{\mathsf {F}}}(X)\) are non-Suslin.
Proof
The space \(C_p(X)\) is not Suslin since it contains the closed subspace \(C'_p(X)\) which is not Suslin by Claim 7.1. By Theorem 1.7, the space \(C_k(X)\) and \(C_{{\downarrow }{\mathsf {F}}}(X)\) are not Suslin, too. \(\square \)
References
Arkhangel’skiĭ, A.V.: Topological Function Spaces. Kluwer Academic Publ. Group, Dordrecht (1992)
Banakh, T.: Topological spaces with an \(\omega ^{\omega }\)-base. Dissert. Math. 538, 1–141 (2019)
Banakh, T.: Banalytic spaces and characterization of Polish groups. Lett. Math. Sci. (in press). http://www.prior-sci-pub.com/lims_2019art1.html
Banakh, T., Gabriyelyan, S.: On the \(C_k\)-stable closure of the class of (separable) metrizable spaces. Monatsh. Math. 180(1), 39–64 (2016)
Bourbaki, N.: General Topology. Chapters 5–10, Elements of Mathematics. Springer, Berlin (1989)
Calbrix, J.: Espaces \(K_{ }\) et espaces des applications continues. Bull. Soc. Math. Fr. 113(2), 183–203 (1985)
Engelking, R.: General Topology. Heldermann, Berlin (1989)
Gruenhage, G.: Generalized metric spaces. In: Handbook of Set-theoretic Topology, pp. 423–501. North-Holland, Amsterdam (1984)
Ka̧kol, J., Kubiś, W., López-Pellicer, M.: Descriptive topology in selected topics of functional analysis, Developments in Mathematics, vol. 24. Springer, Berlin (2011)
Kechris, A.: Classical Descriptive Set Theory. Springer, New York (1995)
McCoy, R., Ntantu, I.: Properties of C(X) with the epi-topology. Boll. Unione Mat. Ital. B (7) 6, 507–532 (1992)
McCoy, R., Ntantu, I.: Topological properties of spaces of continuous functions, Lecture Notes in Mathematics, vol. 1315. Springer, Berlin (1988)
Michael, E.: \(\aleph _0\)-spaces. J. Math. Mech. 15, 983–1002 (1966)
Michael, E.: On \(k\)-spaces, \(k_{R}\)-spaces and \(k(X)\). Pac. J. Math. 47, 487–498 (1973)
Noble, N.: Ascoli theorems and the exponential map. Trans. Am. Math. Soc. 143, 393–411 (1969)
Tkachuk, V.: A \(C_p\)-Theory Problem Book. Special Features of Function Spaces. Springer, Cham (2014)
Tkachuk, V.: A \(C_p\)-Theory Problem Book. Compactness in Function Spaces. Springer, Cham (2015)
Tkachuk, V.: A \(C_p\)-Theory Problem Book. Functional Equivalencies. Springer, Cham (2016)
Wang, L., Banakh, T.: Baire category properties of function spaces with the Fell hypograph topology. Topol. Appl. 265, 106817 (2019)
Yang, Z., Chen, L., Zheng, Y.: Topological classification of function spaces with the Fell topology III. Topol. Appl. 197, 112–132 (2016)
Yang, Z., Hu, S., Wei, G.: Topological structures of the space of continuous functions on a non-compact space with the Fell topology. Topol. Proc. 41, 17–38 (2013)
Yang, Y., Zhang, B.: The hyperspace of the hypographs of continuous maps with the Fell topology. Acta Math. Sin. Engl. Ser. 28, 57–66 (2012)
Yang, Y., Yan, P.: Topological classification of function spaces with the Fell topology I. Topol. Appl. 178, 146–159 (2014)
Yang, H., Yang, Y., Zheng, Y.: Topological classification of function spaces with the Fell topology IV. Topol. Appl. 228, 222–235 (2017)
Yang, Z., Zheng, Y., Chen, J.: Topological classification of function spaces with the Fell topology II. Topol. Appl. 187, 82–96 (2015)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Leijie Wang was supported by National Science Foundation of China (Grant No. 11971287).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Banakh, T., Wang, L. Lusin and Suslin properties of function spaces. RACSAM 114, 133 (2020). https://doi.org/10.1007/s13398-020-00862-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13398-020-00862-y
Keywords
- Fell hypograph topology
- Compact-open topology
- pointwise convergence topology
- Lusin space
- Suslin space
- \(\aleph _0\)-Space
- Cosmic space
- \(\omega ^\omega \)-Base




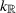 -space if a function
-space if a function