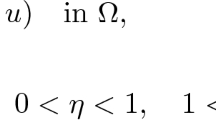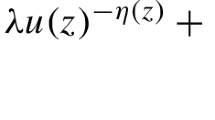Positive solutions for nonlinear parametric singular Dirichlet problems

Abstract

We consider a nonlinear parametric Dirichlet problem driven by the p-Laplace differential operator and a reaction which has the competing effects of a parametric singular term and of a Carathéodory perturbation which is ($p-1$)-linear near $+\infty$. The problem is uniformly nonresonant with respect to the principal eigenvalue of $(-\Delta _p,W^{1,p}_0(\Omega ))$. We look for positive solutions and prove a bifurcation-type theorem describing in an exact way the dependence of the set of positive solutions on the parameter $\lambda >0$.

1 Introduction

Let $\Omega \subseteq \mathbb R^N$ be a bounded domain with $C^2$-boundary $\partial \Omega$. In this paper we study the following nonlinear parametric singular Dirichlet problem:

In this problem, $\Delta _p$ denotes the p-Laplacian differential operator defined by

$$\begin{aligned} \Delta _pu=\mathrm{div}\,(|Du|^{p-2}Du)\quad \hbox {for all}\,\,u\in W^{1,p}_0(\Omega ),\quad 1<p<\infty . \end{aligned}$$

On the right-hand side of ($P_{\lambda }$) (the reaction of the problem), we have a parametric singular term $u\mapsto \lambda u^{-\gamma }$ with $\lambda >0$ being the parameter and $0<\gamma <1$. Also, there is a Carathéodory perturbation f(z, x) (that is, for all $x\in \mathbb R$ the mapping $z\mapsto f(z,x)$ is measurable and for almost all $z\in \Omega$ the mapping $x\mapsto f(z,x)$ is continuous). We assume that $f(z,\cdot )$ exhibits $(p-1)$-linear growth near $+\infty$.

We are looking for positive solutions of problem ($P_{\lambda }$). Our aim is to describe in a precise way the dependence on the parameter $\lambda >0$ of the set of positive solutions.

We prove a bifurcation-type property, which is the main result of our paper. Concerning the hypotheses H(f) on the perturbation f(z, x) and the other notation used in the statement of the theorem, we refer to Sect. 2. The main result of the present paper is stated in the following theorem.

Theorem A

If hypotheses H(f) hold, then there exists $\lambda ^*\in (0,+\infty )$ such that

• (a) for every $\lambda \in (0,\lambda ^*)$, problem ($P_{\lambda }$) has at least two positive solutions

  $$\begin{aligned} u_\lambda ,\hat{u}_\lambda \in \mathrm{int}\,C_+,\quad u_\lambda \ne \hat{u}_\lambda ,\quad u_\lambda \leqslant \hat{u}_\lambda ; \end{aligned}$$

• (b) for $\lambda =\lambda ^*$, problem ($P_{\lambda }$) has at least one positive solution

  $$\begin{aligned} u^*_\lambda \in \mathrm{int}\,C_+; \end{aligned}$$

• (c) for $\lambda >\lambda ^*$, problem ($P_{\lambda }$) has no positive solutions.

In the past, singular problems were studied in the context of semilinear equations (that is, $p=2$). We mention the works of Coclite and Palmieri [2], Ghergu and Rădulescu [5], Hirano et al. [10], Lair and Shaker [11] and Sun et al. [21]. A detailed bibliography and additional topics on the subject, can be found in the book of Ghergu and Rădulescu [6]. For nonlinear equations driven by the p-Laplacian, we mention the works of Giacomoni et al. [7], Papageorgiou et al. [16, 17], Papageorgiou and Smyrlis [18] and Perera and Zhang [19]. Of the aforementioned papers, closest to our work here is that of Papageorgiou and Smyrlis [18], where the authors also deal with a parametric singular problem and prove a bifurcation-type result. In their problem, the perturbation f(z, x) is ($p-1$)-superlinear in $x\in \mathbb R$ near $+\infty$. So, our present work complements the results of [18], by considering equations in which the reaction has the competing effects of a singular term and of a $(p-1)$-linear term.

Our approach uses variational tools together with suitable truncation and comparison techniques.

2 Preliminaries and hypotheses

Let X be a Banach space and $X^*$ its topological dual. By $\left\langle \cdot ,\cdot \right\rangle$ we denote the duality brackets of the pair $(X^*,X)$. Given $\varphi \in C^1(X,\mathbb R)$, we say that $\varphi$ satisfies the “Cerami condition” (the “C-condition” for short), if the following property holds:

“Every sequence $\{u_n\}_{n\geqslant 1}\subseteq X$ such that

$$\begin{aligned} \{\varphi (u_n)\}_{n\geqslant 1}\subseteq \mathbb R\ \hbox { is bounded and }\,(1+||u_n||)\varphi '(u_n)\rightarrow 0 \hbox { in } X^*\,\mathrm{as}\,n\rightarrow \infty , \end{aligned}$$

admits a strongly convergent subsequence.”

Using this notion, we can state the “mountain pass theorem”.

Theorem 1

(Mountain pass theorem) Assume that $\varphi \in C^1(X,\mathbb R)$ satisfies the C-condition, $u_0,u_1\in X, ||u_1-u_0||>\rho >0$,

$$\begin{aligned} \max \{\varphi (u_0),\varphi (u_1)\}<\inf \{\varphi (u):||u-u_0||=\rho \}=m_{\rho } \end{aligned}$$

and $c=\inf \nolimits _{\gamma \in \Gamma }\max \nolimits _{0\leqslant t\leqslant 1}\ \varphi (\gamma (t))$ with $\Gamma =\{\gamma \in C([0,1],X):\gamma (0)=u_0,\gamma (1)=u_1\}$. Then $c\geqslant m_{\rho }$ and c is a critical value of $\varphi$ (that is, we can find $\hat{u}\in X$ such that $\varphi '(\hat{u})=0$ and $\varphi (\hat{u})=c$).

The analysis of problem ($P_{\lambda }$) will involve the Sobolev space $W^{1,p}_0(\Omega )$ and the Banach space

$$\begin{aligned} C^1_0(\overline{\Omega })=\left\{ u\in C^1(\overline{\Omega }):u|_{\partial \Omega }=0\right\} . \end{aligned}$$

We denote by $||\cdot ||$ the norm of $W^{1,p}_0(\Omega )$. On account of the Poincaré inequality, we have

$$\begin{aligned} ||u||=||Du||_p\quad \hbox {for all}\,\,u\in W^{1,p}_0(\Omega ). \end{aligned}$$

The space $C^1_0(\overline{\Omega })$ is an ordered Banach space with positive (order) cone

$$\begin{aligned} C_+=\left\{ u\in C^1_0(\overline{\Omega }):u(z)\geqslant 0\ \hbox {for all}\ z\in \overline{\Omega }\right\} . \end{aligned}$$

This cone has a nonempty interior given by

$$\begin{aligned} \mathrm{int}\, C_+=\left\{ u\in C_+:u(z)>0\ \hbox {for all}\ z\in \Omega ,\ \left. \frac{\partial u}{\partial n}\right| _{\partial \Omega }<0\right\} . \end{aligned}$$

Here, $n(\cdot )$ denotes the outward unit normal on $\partial \Omega$.

Let $h_1,h_2\in L^{\infty }(\Omega )$. We write $h_1\prec h_2$, if for every compact $K\subseteq \Omega$, we can find $c_K>0$ such that $c_K\leqslant h_2(z)-h_1(z)$ for almost all $z\in K$. Note that, if $h_1,h_2\in C(\Omega )$ and $h_1(z)<h_2(z)$ for all $z\in \Omega$, then $h_1\prec h_2$.

The next strong comparison principle can be found in Papageorgiou and Smyrlis [18, Proposition 4] (see also Giacomoni et al. [7, Theorem 2.3]).

Proposition 2

If $\hat{\xi }\geqslant 0,h_1,h_2\in L^{\infty }(\Omega ), h_1\prec h_2,u_1\in C_+$ with $u_1(z)>0$ for all $z\in \Omega , u_2\in \mathrm{int}\, C_+$ and

$$\begin{aligned}&-\Delta _pu_1(z)+\hat{\xi }u_1(z)^{p-1}-\lambda u_1(z)^{-\gamma }=h_1(z),\\&-\Delta _pu_2(z)+\hat{\xi }u_2(z)^{p-1}-\lambda u_2(z)^{-\gamma }=h_2(z)\quad \hbox {for almost all}\,\,z\in \Omega , \end{aligned}$$

then $u_2-u_1\in \mathrm{int}\, C_+.$

We denote by $A\,{:}\,W^{1,p}_0(\Omega )\rightarrow W^{-1,p'}(\Omega )=W^{1,p}_0(\Omega )^*\left( \frac{1}{p}+\frac{1}{p'}=1\right)$ the nonlinear map defined by

$$\begin{aligned} \left\langle A(u),h\right\rangle =\int _{\Omega }|Du|^{p-2}(Du,Dh)_{\mathbb R^N}dz\quad \hbox {for all}\,\, u,h\in W^{1,p}_0(\Omega ). \end{aligned}$$

This map has the following properties (see Motreanu et al. [15, p. 40]).

Proposition 3

The map $A\,{:}\,W^{1,p}_0(\Omega )\rightarrow W^{-1,p'}(\Omega )$ is bounded (that is, A maps bounded sets to bounded sets), continuous, strictly monotone and of type $(S)_+$, that is, if $u_n{\mathop {\rightarrow }\limits ^{w}}u$ in $W^{1,p}_0(\Omega )$ and $\limsup \nolimits _{n\rightarrow \infty }\left\langle A(u_n),u_n-u\right\rangle \leqslant 0$, then $u_n\rightarrow u$ in $W^{1,p}_0(\Omega )$.

Consider the following nonlinear eigenvalue problem

$$\begin{aligned} -\Delta _pu(z)=\hat{\lambda }|u(z)|^{p-2}u(z)\quad \hbox {in}\,\,Omega,\ u|_{\partial \Omega }=0. \end{aligned}$$

(1)

We say that $\hat{\lambda }\in \mathbb R$ is an “eigenvalue” of ($-\Delta _p,W^{1,p}_0(\Omega )$) if problem (1) admits a nontrivial solution $\hat{u}\in W^{1,p}_0(\Omega )$, known as an “eigenfunction” corresponding to $\hat{\lambda }$. The nonlinear regularity theory (see Gasinski and Papageorgiou [3, pp. 737–738]) implies that $\hat{u}\in C^1_0(\overline{\Omega })$. There is a smallest eigenvalue $\hat{\lambda }_1>0$ with the following properties:

• $\hat{\lambda }_1>0$ is isolated (that is, if $\hat{\sigma }(p)$ denotes the spectrum of ($-\Delta _p,W^{1,p}_0(\Omega )$) then we can find $\epsilon >0$ such that $(\hat{\lambda }_1,\hat{\lambda }_1+\epsilon )\cap \hat{\sigma }(p)=0$);

• $\hat{\lambda }_1$ is simple (that is, if $\hat{u},\hat{v}\in C^1_0(\overline{\Omega })$ are eigenfunctions corresponding to $\hat{\lambda }_1$, then $\hat{u}=\xi \hat{v}$ for some $\xi \in \mathbb R\backslash \{0\}$);

• $$\begin{aligned} \hat{\lambda }_1=\inf \left\{ \frac{||Du||^p_p}{||u||^p_p}:u\in W^{1,p}_0(\Omega ),u\ne 0\right\} . \end{aligned}$$

  (2)

It follows from the above properties that the eigenfunctions corresponding to $\hat{\lambda }_1$ do not change sign. We denote by $\hat{u}_1$ the positive, $L^p$-normalized (that is, $||\hat{u}_1||_p=1$) eigenfunction corresponding to $\hat{\lambda }_1>0$. From the nonlinear maximum principle (see, for example, Gasinski and Papageorgiou [3, p. 738]), we have $\hat{u}_1\in \mathrm{int}\, C_+$. Any eigenfunction corresponding to an eigenvalue $\hat{\lambda }\ne \hat{\lambda }_1$, is nodal (that is, sign-changing). More details about the spectrum of $(-\Delta _p,W^{1,p}_0(\Omega ))$ can be found in [3, 15].

We can also consider a weighted version of the eigenvalue problem (1). So, let $m\in L^{\infty }(\Omega ), m(z)\geqslant 0$ for almost all $z\in \Omega ,\ m\ne 0$. We consider the following nonlinear eigenvalue problem:

$$\begin{aligned} -\Delta _pu(z)=\tilde{\lambda }m(z)|u(z)|^{p-2}u(z)\quad \hbox {in}\,\,\Omega ,\ u|_{\partial \Omega }=0. \end{aligned}$$

(3)

This problem has the same properties as (1). So, there is a smallest eigenvalue $\tilde{\lambda }_1(m)>0$ which is isolated, simple and admits the following variational characterization

$$\begin{aligned} \tilde{\lambda }_1(m)=\inf \left\{ \frac{||Du||^p_p}{\int _{\Omega }m(z)|u|^pdz}:u\in W^{1,p}_0(\Omega ),u\ne 0\right\} . \end{aligned}$$

Also the eigenfunctions corresponding to $\tilde{\lambda }_1(m)$ have a fixed sign and we denote by $\tilde{u}_1(m)$ the positive, $L^p$-normalized eigenfunction. We have $\tilde{u}_1(m)\in \mathrm{int}\, C_+$. These properties lead to the following monotonicity property of the map $m\mapsto \tilde{\lambda }_1(m)$.

Proposition 4

If $m_1,m_2\in L^{\infty }(\Omega ),0\leqslant m_1(z)\leqslant m_2(z)$ for almost all $z\in \Omega$ and both inequalities are strict on sets of positive measure, then $\tilde{\lambda }_1(m_2)<\tilde{\lambda }_1(m_1)$.

Given $x\in \mathbb R$, we set $x^{\pm }=\max \{\pm x, 0\}$. Then for $u\in W^{1,p}_0(\Omega )$, we set $u^{\pm }(\cdot )=u(\cdot )^{\pm }$. We know that

$$\begin{aligned} u^{\pm }\in W^{1,p}_0(\Omega ),\quad |u|=u^++u^-,\quad u=u^+-u^-. \end{aligned}$$

If $g\,{:}\,\Omega \times \mathbb R$ is a measurable function (for example, a Carathéodory function), then by $N_g(\cdot )$ we denote the Nemytski map corresponding to $g(\cdot ,\cdot )$ defined by

$$\begin{aligned} N_g(u)(\cdot )=g(\cdot ,u(\cdot ))\quad \hbox {for all}\,\, u\in W^{1,p}_0(\Omega ). \end{aligned}$$

Given $v,u\in W^{1,p}_0(\Omega )$ with $v\leqslant u$, we define the order interval [v, u] by

$$\begin{aligned}{}[v,u]=\left\{ y\in W^{1,p}_0(\Omega ):v(z)\leqslant y(z)\leqslant u(z)\ \hbox {for almost all}\ z\in \Omega \right\} . \end{aligned}$$

The hypotheses on the perturbation f(z, x) are the following:

$H(f)\,{:}\,f\,{:}\,\Omega \times \mathbb R\leftarrow \mathbb R$ is a Carathéodory function such that $f(z,0)=0$ for almost all $z\in \Omega$ and

• (i) for every $\rho >0$, there exists $a_{\rho }\in L^{\infty }(\Omega )$ such that

  $$\begin{aligned} |f(z,x)|\leqslant a_{\rho }(z)\ \hbox {for almost all}\ z\in \Omega ,\ \hbox {and all}\ 0\leqslant x\leqslant \rho ; \end{aligned}$$

• (ii) $\hat{\lambda }_1<\eta \leqslant \liminf \nolimits _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}}\leqslant \limsup \nolimits _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}}\leqslant \hat{\eta }$ uniformly for almost all $z\in \Omega ;$

• (iii) there exists a function $w\in C^1(\overline{\Omega })$ such that

  $$\begin{aligned} w(z)\geqslant c_0>0\ \hbox {for all}\ z\in \overline{\Omega },\ \Delta _pw\in L^{\infty }(\Omega )\ \hbox {with}\ \Delta _pw(z)\leqslant 0\ \hbox {for almost all}\ z\in \Omega , \end{aligned}$$

  and for every compact $K\subseteq \Omega$ we can find $c_K>0$ such that

  $$\begin{aligned} w(z)^{-\gamma }+f(z,w(z))\leqslant -c_K<0\quad \hbox {for almost all}\,\, z\in K; \end{aligned}$$

• (iv) there exists $\delta _0\in (0,c_0)$ such that for every compact $K\subseteq \Omega$

  $$\begin{aligned} f(z,x)\geqslant \hat{c}_K>0\quad \hbox {for almost all}\,\, z\in K,\quad \hbox {and all}\,\, x\in \left( 0,\delta _0\right] ; \end{aligned}$$

• (v) for every $\rho >0$, there exists $\hat{\xi }_{\rho }>0$ such that for almost all $z\in \Omega$ the function

  $$\begin{aligned} x\mapsto f(z,x)+\hat{\xi }_{\rho }x^{p-1} \end{aligned}$$

  is nondecreasing on $[0,\rho ]$.

Remark 1

Since we are looking for positive solutions and all the above hypotheses concern the positive semiaxis $\mathbb R_+=\left[ 0,+\infty \right)$, we may assume without any loss of generality that

$$\begin{aligned} f(z,x)=0\quad \hbox {for almost all}\, z\in \Omega ,\quad \hbox {and all}\,\,x\leqslant 0. \end{aligned}$$

(4)

Hypothesis H(f)(iii) implies that asymptotically at $+\infty$ we have uniform nonresonance with respect to the principal eigenvalue $\hat{\lambda }_1>0$ of $(-\Delta _p,W^{1,p}_0(\Omega ))$. The resonant case was recently examined for nonparametric singular Dirichlet problems by Papageorgiou et al. [16].

Example 1

The following functions satisfy hypotheses H(f). For the sake of simplicity we drop the z-dependence:

$$\begin{aligned} f(x)=\left\{ \begin{array}{l@{\quad }l} x^{\tau -1}-3x^{\vartheta -1}&{}\hbox {if}\,\,0\leqslant x\leqslant 1\\ \eta x^{p-1}-(\eta +2)x^{q-1}&{}\hbox {if}\,\,1<x \end{array}\right\} \ (\hbox {see } (4)) \end{aligned}$$

with $1<\tau<\vartheta , 1<q<p$ and $\eta >\hat{\lambda }_1$; and

$$\begin{aligned} f(x)=\left\{ \begin{array}{l@{\quad }l} 2\sin (2\pi x)&{}\hbox {if}\,\,0\leqslant x\leqslant 1\\ \eta (x^{p-1}-x^{q-1})&{}\hbox {if}\,\,1<x \end{array}\right. \end{aligned}$$

with $\eta >\hat{\lambda }_1, 1<q<p$.

3 A purely singular problem

In this section we deal with the following purely singular parametric problem:

The next proposition establishes the existence and $\lambda$-dependence of the positive solutions for problem ($Au_{\lambda }$).

Proposition 5

For every $\lambda >0$ problem ($Au_{\lambda }$) admits a unique solution $\tilde{u}_{\lambda }\in \mathrm{int}\, C_+$, the map $\lambda \mapsto \tilde{u}_{\lambda }$ is nondecreasing from $(0,\infty )$ into $C^1_0(\overline{\Omega })$ (that is, if $0<\vartheta <\lambda$, then $\tilde{u}_{\vartheta }\leqslant \tilde{u}_{\lambda }$) and $||\tilde{u}_{\lambda }||_{C^1_0(\overline{\Omega })}\rightarrow 0$ as $\lambda \rightarrow 0^+$.

Proof

The existence of a unique solution $\tilde{u}_{\lambda }\in \mathrm{int}\, C_+$ follows from Proposition 5 of Papageorgiou and Smyrlis [18].

Let $0<\vartheta <\lambda$ and let $\tilde{u}_{\vartheta },\tilde{u}_{\lambda }\in \mathrm{int}\, C_+$ be the corresponding unique solutions of problem ($Au_{\lambda }$). Evidently, $\tilde{u}^{p'}_{\vartheta }\in \mathrm{int}\, C_+\left( \frac{1}{p}+\frac{1}{p'}=1\right)$ and so by Proposition 2.1 of Marano and Papageorgiou [14], we can find $c_1>0$ such that

$$\begin{aligned} \hat{u}_1\leqslant c_1\tilde{u}^{p'}_{\vartheta },\Rightarrow & {} \hat{u}_1^{1/p'}\leqslant c_1^{1/p'}\tilde{u}_{\vartheta },\\\Rightarrow & {} \tilde{u}^{-\gamma }_{\vartheta }\leqslant c_2\hat{u}_1^{-\gamma /p'}\quad \hbox {for some}\,\,c_2>0. \end{aligned}$$

The lemma of Lazer and McKenna [12, p. 726], implies that $\hat{u}_1^{-\gamma /p'}\in L^{p'}(\Omega )$. Therefore $\tilde{u}_{\vartheta }^{-\gamma }\in L^{p'}(\Omega )$. We introduce the Carathéodory function $g_{\lambda }(z,x)$ defined by

$$\begin{aligned} g_{\lambda }(z,x)=\left\{ \begin{array}{l@{\quad }l} \lambda \tilde{u}_{\vartheta }^{-\gamma }&{}\hbox {if}\ x\leqslant \tilde{u}_{\vartheta }(z)\\ \lambda x^{-\gamma }&{}\hbox {if}\ \tilde{u}_{\vartheta }(z)<x. \end{array}\right. \end{aligned}$$

(5)

We set $G_{\lambda }(z,x)=\int ^x_0g_{\lambda }(z,s)ds$ and consider the functional $\hat{\psi }_{\lambda }:W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \hat{\psi }_{\lambda }(u)=\frac{1}{p}||Du||^p_p-\int _{\Omega }G_{\lambda }(z,u)dz\quad \hbox {for all}\,\, u\in W^{1,p}_0(\Omega ). \end{aligned}$$

Proposition 3 of Papageorgiou and Smyrlis [18] implies that $\hat{\psi }_{\lambda }\in C^1(W^{1,p}_0(\Omega ))$. From (5) and since $\tilde{u}_{\vartheta }^{-\gamma }\in L^{p'}(\Omega )$ it follows that $\hat{\psi }_{\lambda }(\cdot )$ is coercive. Also, via the Sobolev embedding theorem, we see that $\hat{\psi }_{\lambda }(\cdot )$ is sequentially weakly lower semicontinuous. So, by the Weierstrass–Tonelli theorem, we can find $\bar{u}_{\lambda }\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \hat{\psi }_{\lambda }(\bar{u}_{\lambda })= & {} \inf \left\{ \hat{\psi }_{\lambda }(u):u\in W^{1,p}_0(\Omega )\right\} ,\Rightarrow \hat{\psi }'_{\lambda }(\bar{u}_{\lambda })=0,\nonumber \\\Rightarrow & {} \left\langle A(\bar{u}_{\lambda }),h\right\rangle =\int _{\Omega }g_{\lambda }(z,\bar{u}_{\lambda })hdz \quad \hbox {for all}\,\,h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(6)

In (3) we choose $h=(\tilde{u}_{\vartheta }-\bar{u}_{\lambda })^+\in W^{1,p}_0(\Omega )$. We have

$$\begin{aligned} \left\langle A(\bar{u}_{\lambda }),(\tilde{u}_{\vartheta }-\bar{u}_{\lambda })^+\right\rangle= & {} \int _{\Omega }\lambda \tilde{u}_{\vartheta }^{-\gamma }(\tilde{u}_{\vartheta }-\bar{u}_{\lambda })^+dz\ (\hbox {see } (5))\nonumber \\\geqslant & {} \int _{\Omega }\vartheta \tilde{u}_{\vartheta }^{-\gamma }(\tilde{u}_{\vartheta }-\bar{u}_{\lambda })dz\ (\hbox {since}\ \vartheta <\lambda )\nonumber \\= & {} \left\langle A(\tilde{u}_{\vartheta }),(\tilde{u}_{\vartheta }-\bar{u}_{\lambda })^+\right\rangle ,\Rightarrow \tilde{u}_{\vartheta }\leqslant \bar{u}_{\lambda }. \end{aligned}$$

(7)

From (5)–(7), we have

$$\begin{aligned} -\Delta _p\bar{u}_{\lambda }(z)= & {} \lambda \bar{u}_{\lambda }(z)^{-\gamma } \quad \hbox {for almost all}\,\,z\in \Omega ,\left. \bar{u}_{\lambda }\right| _{\partial \Omega }=0,\\\Rightarrow & {} \bar{u}_{\lambda }=\tilde{u}_{\lambda },\quad \Rightarrow \tilde{u}_{\vartheta }\leqslant \tilde{u}_{\lambda }\ (\hbox {see } (7)). \end{aligned}$$

Therefore the map $\lambda \mapsto \tilde{u}_{\lambda }$ is nondecreasing from $(0,+\infty )$ into $C^1_0(\overline{\Omega })$.

We have

$$\begin{aligned} \left\langle A(\tilde{u}_{\lambda }),h\right\rangle =\int _{\Omega }\lambda \tilde{u}_{\lambda }^{-\gamma }hdz\ \quad \hbox {for all}\,\,h\in W^{1,p}_0(\Omega ). \end{aligned}$$

Choosing $h=\tilde{u}_{\lambda }\in W^{1,p}_0(\Omega )$, we obtain

$$\begin{aligned} ||D\tilde{u}_{\lambda }||^p_p= & {} \lambda \int _{\Omega }\tilde{u}_{\lambda }^{1-\gamma }dz\leqslant \lambda c_3||\tilde{u}_{\lambda }||_p\ \hbox {for some}\ c_3>0\nonumber \\&(\hbox {see Theorem 13.17 of Hewitt and Stromberg}~[9, p. 196]),\nonumber \\\Rightarrow & {} \{\tilde{u}_{\lambda }\}_{\lambda \in \left( 0,1\right] }\subseteq W^{1,p}_0(\Omega )\ \hbox {is bounded and }||\tilde{u}_{\lambda }||\rightarrow 0\ \hbox {as}\ \lambda \rightarrow 0^+. \end{aligned}$$

(8)

As in the first part of the proof, using Proposition 2.1 of Marano and Papageorgiou [14], we show that $\tilde{u}_{\lambda }^{-\gamma }\in L^r(\Omega )$ for $r>N$. Then Proposition 1.3 of Guedda and Véron [8] implies that

$$\begin{aligned} \tilde{u}_{\lambda }\in L^{\infty }(\Omega )\quad \hbox {and}\quad ||\tilde{u}_{\lambda }||_{\infty }\leqslant c_4\quad \hbox {for some}\quad c_4>0,\quad \hbox {and all}\quad 0<\lambda \leqslant 1. \end{aligned}$$

(9)

Let $k_{\lambda }=\lambda \tilde{u}^{-\gamma }_{\lambda }\in L^r(\Omega ),\lambda \in \left( 0,1\right]$ and consider the following linear Dirichlet problem

$$\begin{aligned} -\Delta v(z)=k_{\lambda }(z)\quad \hbox {in}\,\,\Omega , v|_{\partial \Omega }=0,\quad 0<\lambda \leqslant 1. \end{aligned}$$

(10)

Standard existence and regularity theory (see, for example, Struwe [20, p. 218]), implies that problem (10) has a unique solution $v_{\lambda }(\cdot )$ such that

$$\begin{aligned} v_{\lambda }\in W^{2,r}(\Omega )\subseteq C^{1,\alpha }_{0}(\overline{\Omega })=C^{1,\alpha }(\overline{\Omega })\cap C^1_0(\overline{\Omega }),\quad ||v_{\lambda }||_{C^{1,\alpha }_0(\overline{\Omega })}\leqslant c_5\end{aligned}$$

for some $c_5>0$, all $\lambda \in \left( 0,1\right]$, and with $\alpha =1-\frac{N}{r}\in (0,1)$ (recall that $r>N$). Let $\beta _{\lambda }(z)=Dv_{\lambda }(z)$. Then $\beta _{\lambda }\in C^{0,\alpha }(\overline{\Omega })$ for every $\lambda \in \left( 0,1\right]$. We have

$$\begin{aligned} -\mathrm{div}\,[|D\tilde{u}_{\lambda }|^{p-2}D\tilde{u}_{\lambda }-\beta _{\lambda }]=0\ \hbox {in}\ \Omega ,\quad \left. \ \tilde{u}_{\lambda }\right| _{\partial \Omega }=0\ (\hbox {since}\ \tilde{u}_{\lambda }\ \hbox {solves}\ Au_{\lambda }). \end{aligned}$$

Then Theorem 1 of Lieberman [13] (see also Corollary 1.1 of Guedda and Véron [8]) and (9), imply that we can find $s\in (0,1)$ and $c_6>0$ such that

$$\begin{aligned} \tilde{u}_{\lambda }\in C^{1,s}_0(\overline{\Omega })\cap \mathrm{int}\, C_+,\ ||\tilde{u}_{\lambda }||_{C^{1,s}_0(\overline{\Omega })}\leqslant c_6\quad \hbox {for all}\,\,\lambda \in \left( 0,1\right] . \end{aligned}$$

Finally, the compact embedding of $C^{1,s}_0(\overline{\Omega })$ into $C^1_0(\overline{\Omega })$ and (8) imply that

$$\begin{aligned} ||\tilde{u}_{\lambda }||_{C^1_0(\overline{\Omega })}\rightarrow 0\,\,\hbox {as}\,\,\lambda \rightarrow 0^+. \end{aligned}$$

This completes the proof. $\square$

4 Bifurcation-type theorem

Let

$$\begin{aligned} {\mathcal {L}}= & {} \{\lambda >0\,{:}\,\hbox {problem}\, (P_{\lambda })\,\hbox {admits a} \hbox {positive solution}\}\\ S_{\lambda }= & {} \hbox {the set of positive solutions for problem } (P_{\lambda }). \end{aligned}$$

Proposition 6

If hypotheses H(f) hold, then $\mathcal {L}\ne \emptyset$.

Proof

Using Proposition 5, we can find $\lambda _0\in \left( 0,1\right]$ such that

$$\begin{aligned} \tilde{u}_{\lambda }(z)\in \left( 0,\delta _0\right] \quad \hbox {for all}\,\, z\in \Omega ,\quad \hbox {all}\,\,\lambda \in \left( 0,\lambda _0\right] . \end{aligned}$$

(11)

Here, $\delta _0>0$ is as postulated by hypothesis H(f)(iv).

We fix $\lambda \in \left( 0,\lambda _0\right]$ and we consider the following truncation of the reaction in problem ($P_{\lambda }$):

$$\begin{aligned} \hat{k}_{\lambda }(z,x)=\left\{ \begin{array}{l@{\quad }l} \lambda \hat{u}_{\lambda }(z)^{-\gamma }+f(z,\tilde{u}_{\lambda }(z))&{}\hbox {if}\ x<\tilde{u}_{\lambda }(z)\\ \lambda x^{-\gamma }+f(z,x)&{}\hbox {if}\ \tilde{u}_{\lambda }\leqslant x\leqslant w(z)\\ \lambda w(z)^{-\gamma }+f(z,w(z))&{}\hbox {if}\ w(z)<x \end{array} \right. \end{aligned}$$

(12)

(recall that $\delta _0<c_0\leqslant w(z)$ for all $z\in \overline{\Omega }$). This is a Carathéodory function. We set $\hat{K}_{\lambda }(z,x)=\int ^x_0\hat{k}_{\lambda }(z,s)ds$ and consider the function $\hat{\varphi }_{\lambda }:W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \hat{\varphi }_{\lambda }(u)=\frac{1}{p}||Du||^p_p-\int _{\Omega }\hat{K}_{\lambda }(z,u)dz\quad \hbox {for all}\,\,u\in W^{1,p}_0(\Omega ). \end{aligned}$$

As before, we have $\hat{\varphi }_{\lambda }\in C^1(W^{1,p}_0(\Omega ))$. Also, it follows from (12) that

$$\begin{aligned} \hat{\varphi }(\cdot )\ \hbox {is coercive}. \end{aligned}$$

In addition, we have that

$$\begin{aligned} \hat{\varphi }_{\lambda }(\cdot )\ \hbox {is sequentially lower semicontinuous}. \end{aligned}$$

Therefore, we can find $\hat{u}_{\lambda }\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \hat{\varphi }_{\lambda }(\hat{u}_{\lambda })= & {} \inf [\hat{\varphi }_{\lambda }(u):u\in W^{1,p}_0(\Omega )],\nonumber \\\Rightarrow & {} \hat{\varphi }'_{\lambda }(\hat{u}_{\lambda })=0,\nonumber \\\Rightarrow & {} \left\langle A(\hat{u}_{\lambda }),h\right\rangle =\int _{\Omega }\hat{k}_{\lambda }(z,\hat{u}_{\lambda })hdz\quad \hbox {for all}\,\,h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(13)

In (13) we choose $h=(\tilde{u}_{\lambda }-\hat{u}_{\lambda })^+\in W^{1,p}_0(\Omega )$. Then

$$\begin{aligned} \left\langle A(\hat{u}_{\lambda }),(\tilde{u}_{\lambda }-\hat{u}_{\lambda })^+\right\rangle= & {} \int _{\Omega }[\lambda \tilde{u}_{\lambda }^{-\gamma }+f(z,\tilde{u}_{\lambda })](\tilde{u}_{\lambda }-\hat{u}_{\lambda })^+dz\ (\hbox {see } (12)))\\\geqslant & {} \int _{\Omega }\lambda \tilde{u}_{\lambda }^{-\gamma }(\tilde{u}_{\lambda }-\hat{u}_{\lambda })^+dz\\&(\hbox {see } (11)\,\mathrm{and}\,\hbox {hypothesis H(f)(iv)})\\= & {} \left\langle A(\tilde{u}_{\lambda }),(\tilde{u}_{\lambda }-\hat{u}_{\lambda })^+\right\rangle \ (\hbox {see Proposition~} 5),\\\Rightarrow & {} \tilde{u}_{\lambda }\leqslant \hat{u}_{\lambda }. \end{aligned}$$

Next, we choose $h=(\hat{u}_{\lambda }-w)^+\in W^{1,p}_0(\Omega )$ in (13). Then

$$\begin{aligned} \left\langle A(\hat{u}_{\lambda }),(\hat{u}_{\lambda }-w)^+\right\rangle= & {} \int _{\Omega }[\lambda w^{-\gamma }+f(z,w)](\hat{u}_{\lambda }-w)^+dz\ (\hbox {see } (12))\\\leqslant & {} \left\langle A(w),(\hat{u}_{\lambda }-w)^+\right\rangle \end{aligned}$$

(see hypothesis H(f)(iii) and use the nonlinear Green identity, see [3, p. 211])

$$\begin{aligned} \Rightarrow \tilde{u}_{\lambda }\leqslant w. \end{aligned}$$

So, we have proved that

$$\begin{aligned} \hat{u}_{\lambda }\in [\tilde{u}_{\lambda },w]. \end{aligned}$$

(14)

Using (12) and (14), Eq. (13) becomes

$$\begin{aligned} \left\langle A(\hat{u}_{\lambda }),h\right\rangle= & {} \int _{\Omega }[\lambda \hat{u}_{\lambda }^{-\gamma }+f(z,\hat{u}_{\lambda })]hdz\quad \hbox {for all}\,\, h\in W^{1,p}_0(\Omega ),\nonumber \\\Rightarrow & {} -\Delta _p\hat{u}_{\lambda }(z)=\lambda \hat{u}_{\lambda }(z)^{-\gamma }+f(z,\hat{u}_{\lambda }(z)) \nonumber \\&\hbox {for almost all}\,\,z\in \Omega ,\left. \hat{u}_{\lambda }\right| _{\partial \Omega }=0. \end{aligned}$$

(15)

From (14), (15) and Theorem 1 of Lieberman [13], we infer that

$$\begin{aligned}&\hat{u}_{\lambda }\in [\tilde{u}_{\lambda },w]\cap \mathrm{int}\, C_+,\quad \Rightarrow \lambda \in \mathcal {L},\quad \hat{u}_{\lambda }\in S_{\lambda }. \end{aligned}$$

This completes the proof. $\square$

A byproduct of the above proof is the following corollary.

Corollary 7

If hypotheses H(f) hold, then $S_{\lambda }\subseteq \mathrm{int}\, C_+$ for all $\lambda >0$.

The next proposition shows that $\mathcal {L}$ is an interval.

Proposition 8

If hypotheses H(f) hold, $\lambda \in \mathcal {L}$ and $\vartheta \in (0,\lambda )$, then $\vartheta \in \mathcal {L}.$

Proof

Since $\lambda \in \mathcal {L}$, we can find $u_{\lambda }\in S_{\lambda }\subseteq \mathrm{int}\, C_+$. Proposition 5 implies that we can find $\tau \in [0,\lambda _0]$ (see (11)) such that

$$\begin{aligned} \tau <\vartheta \ \hbox {and}\ \tilde{u}_{\tau }\leqslant u_{\lambda }. \end{aligned}$$

We introduce the Carathéodory function e(z, x) defined by

$$\begin{aligned} e_{\vartheta }(z,x)=\left\{ \begin{array}{l@{\quad }l} \vartheta \tilde{u}_{\tau }(z)^{-\gamma }+f(z,\tilde{u}_{\tau }(z))&{}\hbox {if}\,\,x<\tilde{u}_{\tau }(z)\\ \vartheta x^{-\gamma }+f(z,x)&{}\hbox {if}\,\,\,\tilde{u}_{\tau }(z)\leqslant x\leqslant u_{\lambda }(z)\\ \vartheta u_{\lambda }(z)^{-\gamma }+f(z,u_{\lambda }(z))&{}\hbox {if}\,\, u_{\lambda }(z)<x. \end{array}\right. \end{aligned}$$

(16)

We set $E_{\vartheta }(z,x)=\int ^x_0 e_{\vartheta }(z,s)ds$ and consider the functional $\hat{\psi }_{\vartheta }:W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \hat{\psi }_{\vartheta }(u)=\frac{1}{p}||Du||^p_p-\int _{\Omega }E_{\vartheta }(z,u)dz\quad \hbox {for all}\,\,u\in W^{1,p}_0(\Omega ). \end{aligned}$$

We know that $\hat{\psi }_{\vartheta }\in C^1(W^{1,p}_0(\Omega ))$. Moreover, $\hat{\psi }_{\vartheta }$ is coercive (see (16)) and sequentially weakly lower semicontinuous. So, we can find $u_{\vartheta }\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned}&\hat{\psi }_{\vartheta }(u_{\vartheta })=\inf \left\{ \hat{\psi }_{\vartheta }(u):u\in W^{1,p}_0(\Omega )\right\} ,\Rightarrow \hat{\psi }'_{\vartheta }(u_{\vartheta })=0, \nonumber \\\Rightarrow & {} \left\langle A(u_{\vartheta }),h\right\rangle =\int _{\Omega }e_{\vartheta }(z,u_{\vartheta })hdz\quad \hbox {for all}\,\,h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(17)

In (17) we first choose $h=(\tilde{u}_{\tau }-u_{\vartheta })^+\in W^{1,p}_0(\Omega )$. Then

$$\begin{aligned} \left\langle A(u_{\vartheta }),(\tilde{u}_{\tau }-u_{\vartheta })^+\right\rangle= & {} \int _{\Omega }[\vartheta \tilde{u}_{\tau }^{-\gamma }+f(z,\tilde{u}_{\tau })](\tilde{u}_{\tau }-u_{\vartheta })^+dz\ (\hbox {see } (16))\\\geqslant & {} \int _{\Omega }\vartheta \tilde{u}_{\tau }^{-\gamma }(\tilde{u}_{\tau }-u_{\vartheta })^+dz\\&(\hbox {since}\ \tau \leqslant \lambda _0,\ \hbox {see } (11) \hbox { and hypothesis}\ H(f)(iv))\\\geqslant & {} \int _{\Omega }\tau \tilde{u}_{\tau }^{-\gamma }(\tilde{u}_{\tau }-u_{\vartheta })^+dz\ (\hbox {recall that}\ \tau <\vartheta )\\= & {} \left\langle A(u_{\tau }),(\tilde{u}_{\tau }-u_{\vartheta })^+\right\rangle \ (\hbox {see Proposition~} (5)),\\\Rightarrow & {} \tilde{u}_{\tau }\leqslant u_{\vartheta }. \end{aligned}$$

Next, in (17) we choose $h=(u_{\vartheta }-u_{\lambda })^+\in W^{1,p}_0(\Omega )$. Then

$$\begin{aligned} \left\langle A(u_{\vartheta }),(u_{\vartheta }-u_{\lambda })^+\right\rangle= & {} \int _{\Omega }[\vartheta u_{\lambda }^{-\gamma }+f(z,u_{\lambda })](u_{\vartheta }-u_{\lambda })^+dz\ (\hbox {see } (16)\\\leqslant & {} \int _{\Omega }[\lambda u_{\lambda }^{-\gamma }+f(z,u_{\lambda })](u_{\vartheta }-u_{\lambda })^+dz\ (\hbox {since}\ \vartheta <\lambda )\\= & {} \left\langle A(u_{\lambda }),(u_{\vartheta }-u_{\lambda })^+\right\rangle \ (\hbox {since}\ u_{\lambda }\in S_{\lambda }),\\\Rightarrow & {} u_{\vartheta }\leqslant u_{\lambda }. \end{aligned}$$

So, we have proved that

$$\begin{aligned} u_{\vartheta }\in [\tilde{u}_{\tau },u_{\lambda }]. \end{aligned}$$

(18)

It follows from (16), (17) and (18) that

$$\begin{aligned}\vartheta \in \mathcal {L}\ \hbox {and}\ u_{\vartheta }\in S_{\vartheta }\subseteq \mathrm{int}\, C_+.\end{aligned}$$

The proof is now complete. $\square$

An interesting byproduct of the above proof is the following result.

Corollary 9

If hypotheses H(f) hold, $\lambda \in \mathcal {L},u_{\lambda }\in S_{\lambda }\subseteq \mathrm{int}\, C_+$, and $\vartheta <\lambda$, then $\vartheta \in \mathcal {L}$ and we can find $u_{\vartheta }\in S_{\vartheta }\subseteq \mathrm{int}\, C_+$ such that $u_{\vartheta }\leqslant u_{\lambda }$.

In fact, we can improve the above result as follows.

Proposition 10

If hypotheses H(f) hold, $\lambda \in \mathcal {L},u_{\lambda }\in S_{\lambda }\subseteq \mathrm{int}\, C_+$, and $\vartheta <\lambda$, then $\vartheta \in \mathcal {L}$ and we can find $u_{\vartheta }\in S_{\vartheta }\subseteq \mathrm{int}\, C_+$ such that $u_{\lambda }-u_{\vartheta }\in \mathrm{int}\, C_+$.

Proof

From Corollary 9 we know that $\vartheta \in \mathcal {L}$ and we can find $u_{\vartheta }\in S_{\vartheta }\subseteq \mathrm{int}\, C_+$ such that

$$\begin{aligned} u_{\vartheta }\leqslant u_{\lambda }. \end{aligned}$$

(19)

Let $\rho =||u_{\lambda }||_{\infty }$ and let $\hat{\xi }_{\rho }>0$ be as postulated by hypothesis H(f)(v). Then

$$\begin{aligned}&-\Delta _pu_{\vartheta }+\hat{\xi }_pu_{\vartheta }^{p-1}-\lambda u_{\vartheta }^{-\gamma }\\&\quad =-(\lambda -\vartheta )u_{\vartheta }^{-\gamma }+f(z,u_{\vartheta })+\hat{\xi }_{\rho }u_{\vartheta }^{p-1}\\&\quad \leqslant f(z,u_{\lambda })+\hat{\xi }_{\rho }u_{\lambda }^{p-1}\ (\hbox {recall that}\ \vartheta <\lambda \ \hbox {and see } (19) \hbox { and hypothesis}\ H(f)(v))\\&\quad =-\Delta _pu_{\lambda }+\hat{\xi }_{\rho }u_{\lambda }^{p-1}-\lambda u_{\lambda }^{-\gamma }\ (\hbox {since}\ u_{\lambda }\in S_{\lambda }). \end{aligned}$$

We set

$$\begin{aligned}&h_1(z)=f(z,u_{\vartheta }(z))+\hat{\xi }_{\rho }u_{\vartheta }(z)^{p-1}-(\lambda -\vartheta )u_{\vartheta }(z)^{-\gamma }\\&h_2(z)=f(z,u_{\lambda }(z))+\hat{\xi }_{\rho }u_{\lambda }(z)^{p-1}. \end{aligned}$$

We have

$$\begin{aligned} h_2(z)-h_1(z)\geqslant (\lambda -\vartheta )u_{\vartheta }(z)^{-\gamma }\geqslant (\lambda -\vartheta )\rho ^{-\gamma }\ \hbox {for almost all}\ z\in \Omega \end{aligned}$$

(see (19) and hypotheses H(f)(v)).

We can apply Proposition 2 and conclude that

$$\begin{aligned}u_{\lambda }-u_{\vartheta }\in \mathrm{int}\, C_+.\end{aligned}$$

The proof is now complete. $\square$

Denote $\lambda ^*=\sup \mathcal {L}.$

Proposition 11

If hypotheses h(f) hold, then $\lambda ^*<+\infty$.

Proof

Let $\epsilon >0$ be such that $\hat{\lambda }_1+\epsilon <\eta$ (see hypothesis H(f)(ii)). We can find $M>0$ such that

$$\begin{aligned} f(z,x)\geqslant [\hat{\lambda }_1+\epsilon ]x^{p-1}\ \hbox {for almost all}\ z\in \Omega ,\ \hbox {and all}\ x\geqslant M. \end{aligned}$$

(20)

Also, hypothesis H(f)(i) implies that we can find large enough $\tilde{\lambda }>0$ such that

$$\begin{aligned} \tilde{\lambda }M^{-\gamma }+f(z,x)\geqslant [\hat{\lambda }_1+\epsilon ]M^{p-1}\ \hbox {for almost all}\ z\in \Omega ,\ \hbox {and all}\ 0\leqslant x\leqslant M. \end{aligned}$$

(21)

It follows from (20) and (21) that

$$\begin{aligned} \tilde{\lambda }x^{-\gamma }+f(z,x)\geqslant [\hat{\lambda }_1+\epsilon ]x^{p-1}\ \hbox {for almost all}\ z\in \Omega ,\ \hbox {and all}\ x\geqslant 0. \end{aligned}$$

(22)

Let $\lambda >\tilde{\lambda }$ and suppose that $\lambda \in \mathcal {L}$. Then we can find $u_{\lambda }\in S_{\lambda }\subseteq \mathrm{int}\, C_+$. We have

$$\begin{aligned} -\Delta _pu_{\lambda }= & {} \lambda u_{\lambda }^{-\gamma }+f(z,u_{\lambda })>\tilde{\lambda }u_{\lambda }^{-\gamma }+f(z,u_{\lambda })\nonumber \\\geqslant & {} [\hat{\lambda }_1+\epsilon ]u_{\lambda }^{p-1}\ \hbox {for a.a.}\ z\in \Omega \ (\hbox {see } (22)). \end{aligned}$$

(23)

Since $u_{\lambda }\in \mathrm{int}\, C_+$, we can find $t\in (0,1)$ so small that

$$\begin{aligned} \hat{y}_1=t\hat{u}_1\leqslant u_{\lambda } \end{aligned}$$

(24)

(see Proposition 2.1 of Marano and Papageorgiou [14]). We have

$$\begin{aligned} -\Delta _p\hat{y}_1=\hat{\lambda }_1\hat{y}_1^{p-1}<[\hat{\lambda }_1+\epsilon ]\hat{y}_1^{p-1}\ \quad \hbox {for almost all}\,\, z\in \Omega . \end{aligned}$$

(25)

Using (24), we can define the Carathéodory function $\beta (z,x)$ as follows

$$\begin{aligned} \beta (z,x)=\left\{ \begin{array}{l@{\quad }l@{\quad }l} &{} [\hat{\lambda }_1 + \epsilon ]\hat{y}_1(z)^{p-1}&{} \hbox {if}\ x<\hat{y}_1(z)\\ &{} [\hat{\lambda }_1 + \epsilon ]x^{p-1} &{} \hbox {if}\ \hat{y}_1(z)\leqslant x\leqslant u_{\lambda }(z)\\ &{} [\hat{\lambda }_1 + \epsilon ]u_{\lambda }(z)^{p-1}&{} \hbox {if}\ u_{\lambda }(z)<x. \end{array}\right. \end{aligned}$$

(26)

We set $B(z,x)=\int ^x_0\beta (z,s)ds$ and consider the $C^1$-functional $\sigma :W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned}\sigma (u)=\frac{1}{p}||Du||^p_p-\int _{\Omega }B(z,u)dz\ \hbox {for all}\ u\in W^{1,p}_0(\Omega ).\end{aligned}$$

From (26) it is clear that $\sigma (\cdot )$ is coercive. Also, it is sequentially weakly lower semicontinuous. So, we can find $\bar{u}\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned}&\sigma (\bar{u})=\inf \{\sigma (u):u\in W^{1,p}_0(\Omega )\},\nonumber \\&\quad \Rightarrow \sigma '(\bar{u})=0,\nonumber \\\Rightarrow & {} \left\langle A(\bar{u}),h\right\rangle =\int _{\Omega }\beta (z,\bar{u})hdz\ \hbox {for all}\ h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(27)

In (27) we first choose $h=(\hat{y}_1-\bar{u})^+\in W^{1,p}_0(\Omega )$. Then

$$\begin{aligned} \left\langle A(\bar{u}),(\hat{y}_1-\bar{u})^+\right\rangle= & {} \int _{\Omega }[\hat{\lambda }_1+\epsilon ]\hat{y}_1^{p-1}(\hat{y}_1-\bar{u})^+dz\ (\hbox {see } (26))\\\geqslant & {} \left\langle A(\hat{y}_1),(\hat{y}_1-\hat{u})^+\right\rangle \ (\hbox {see } (25)),\\\Rightarrow & {} \hat{y}_1 \leqslant \bar{u}. \end{aligned}$$

Also, in (27) we choose $h=(\bar{u}-u_{\lambda })^+\in W^{1,p}_0(\Omega )$. Then

$$\begin{aligned} \left\langle A(\bar{u}),(\bar{u}-u_{\lambda })^+\right\rangle= & {} \int _{\Omega }[\hat{\lambda }_1+\epsilon ]u_{\lambda }^{p-1}(\bar{u}-u_{\lambda })^+dz\ (\hbox {see } (26))\\\leqslant & {} \left\langle A(u_{\lambda }),(\bar{u}-u_{\lambda })^+\right\rangle \ (\hbox {see }),\\\Rightarrow & {} \bar{u}\leqslant u_{\lambda }. \end{aligned}$$

So, we have proved that

$$\begin{aligned} \bar{u}\in [\hat{y}_1,u_{\lambda }]. \end{aligned}$$

(28)

It follows from (26)–(28) that

$$\begin{aligned}&-\Delta _p\bar{u}(z)=[\hat{\lambda }_1+\epsilon ]\bar{u}(z)^{p-1}\ \hbox {for almost all}\ z\in \Omega ,\ \bar{u}|_{\partial \Omega }=0,\\&\quad \Rightarrow \bar{u}\in C^1_0(\overline{\Omega })\ \hbox {must be nodal, a contradiction }(\hbox {see } (28)). \end{aligned}$$

Therefore we have $\lambda ^*\leqslant \tilde{\lambda }<+\infty$. $\square$

Next, we show that the critical parameter $\lambda ^*>0$ is admissible.

Proposition 12

If hypotheses H(f) hold, then $\lambda ^*\in \mathcal {L}$.

Proof

Let $\{\lambda _n\}_{n\geqslant 1}\subseteq (0,\lambda ^*)$ and assume that $\lambda _n\rightarrow (\lambda ^*)^{-}$ as $n\rightarrow \infty$. We can find $u_n=u_{\lambda _n}\in S_{\lambda _n}\subseteq \mathrm{int}\,C_+$ for all $n\in \mathbb N$. Then

$$\begin{aligned} \langle A(u_n),h\rangle = \int _\Omega [\lambda _n u_n^{-\gamma }+f(z,u_n)]hdz\ \hbox {for all}\ h\in W^{1,p}_0(\lambda ),\quad \hbox {all}\,\, n\in \mathbb N. \end{aligned}$$

(29)

Suppose that $||u_n||\rightarrow \infty$. We set $y_n=\frac{u_n}{||u_n||}\ n\in \mathbb N$. Then $||y_n||=1, y_n\geqslant 0$ for all $n\in \mathbb N$. So, we may assume that

$$\begin{aligned} y_n\xrightarrow {w}y\ \hbox {in}\ W^{1,p}_0(\Omega )\quad \hbox {and}\,\, y_n\rightarrow y\ \hbox {in}\ L^p(\Omega )\,\, \hbox {as}\,\, n\rightarrow \infty . \end{aligned}$$

(30)

From (29) we have

$$\begin{aligned} \langle A(y_n),h\rangle = \int _\Omega \left[ \frac{\lambda _n}{||u_n||^{p+\gamma -1}}y^{-\gamma }_n + \frac{N_f(u_n)}{||u_n||^{p-1}}\right] hdz\quad \hbox {for all}\,\,h\in W^{1,p}_0(\Omega ),\ n\in \mathbb N. \end{aligned}$$

(31)

Hypotheses H(f)(i), (ii) imply that

$$\begin{aligned} |f(z,x)|\leqslant c_7[1+x^{p-1}]\ \hbox {for almost all}\ z\in \Omega ,\ \hbox {all}\ x\geqslant 0,\ \hbox {and some}\ c_7>0. \end{aligned}$$

This growth condition implies that

$$\begin{aligned} \left\{ \frac{N_f(u_n)}{||u_n||^{p-1}}\right\} _{n\geqslant 1}\subseteq L^{p'}(\Omega )\ \hbox {is bounded}. \end{aligned}$$

(32)

Then (32) and hypothesis H(f)(ii) imply that at least for a subsequence, we have

$$\begin{aligned}&\frac{N_f(u_n)}{||u_n||^{p-1}}\xrightarrow {w}\eta _0(z)y^{p-1}\ \hbox {in}\ L^{p'}(\Omega )\ \hbox {as}\ n\rightarrow \infty ,\nonumber \\&\quad \hbox {with}\ \eta \leqslant \eta _0(z)\leqslant \hat{\eta }\ \hbox {for almost all}\ z\in \Omega \nonumber \\&\quad \hbox {(see}\,[1, proof of Proposition 16]). \end{aligned}$$

(33)

In (31) we choose $h=y_n-y\in W^{1,p}_0(\Omega )$, pass to the limit as $n\rightarrow \infty$, and use (30) and (32). Then

$$\begin{aligned}&\lim _{n\rightarrow \infty }\langle A(y_n),y_n-y\rangle =0, \nonumber \\ \Rightarrow&y_n\rightarrow y\ \hbox {in}\ W^{1,p}_0(\Omega )\ (\hbox {see Proposition~} 3), \hbox { hence}\ ||y||=1,\ y\geqslant 0. \end{aligned}$$

(34)

Therefore, if in (31) we pass to the limit as $n\rightarrow \infty$ and use (34) and (33), then

$$\begin{aligned}&\langle A(y),h\rangle = \int _\Omega \eta _0(z)y^{p-1}hdz\ \hbox {for all}\ h\in W^{1,p}_0(\Omega ), \nonumber \\ \Rightarrow&-\Delta _py(z)=\eta _0(z)y(z)^{p-1}\ \hbox {for almost all}\ z\in \Omega , \ y|_{\partial \Omega }=0. \end{aligned}$$

(35)

Since $\eta \leqslant \eta _0(z)\leqslant \hat{\eta }$ for almost all $z\in \Omega$ (see (33)), using Proposition 4, we have

$$\begin{aligned} \tilde{\lambda }_1(\eta _0)\leqslant \tilde{\lambda }_1(\eta )<\tilde{\lambda }_1(\hat{\lambda _1})=1. \end{aligned}$$

So, from (35) and since $||y||=1$ (see (34)), it follows that y must be nodal, a contradiction (see (34)). Therefore

$$\begin{aligned} \{u_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )\ \hbox {is bounded}. \end{aligned}$$

Hence, we may assume that

$$\begin{aligned} u_n\xrightarrow {w}u^*\ \hbox {in}\ W^{1,p}_0(\Omega )\ \hbox {and}\ u_n\rightarrow u^*\ \hbox {in}\ L^p(\Omega )\ \hbox {as}\ n\rightarrow \infty . \end{aligned}$$

(36)

On account of Corollary 9, we may assume that $\{u_n\}_{n\geqslant 1}$ is nondecreasing. Therefore $u^*\ne 0$. Also, we have

$$\begin{aligned} 0\leqslant (u^*)^{-\gamma }\leqslant u_n^{-\gamma }\leqslant u_1^{-\gamma }\in L^{p'}(\Omega )\quad \hbox {for all}\,\,n\in \mathbb N. \end{aligned}$$

(37)

From (36) and by passing to a subsequence if necessary, we can say that

$$\begin{aligned} u_n(z)^{-\gamma }\rightarrow u^*(z)^{-\gamma }\quad \hbox {for almost all}\,\, z\in \Omega . \end{aligned}$$

(38)

From (37), (38) and Problem 1.19 of Gasinski and Papageorgiou [4], we have that

$$\begin{aligned} u_n^{-\gamma }\xrightarrow {w}(u^*)^{-\gamma }\ \hbox {in}\ L^{p'}(\Omega )\ \hbox {as}\ n\rightarrow \infty . \end{aligned}$$

(39)

If in (29) we choose $h=u_n-u^*\in W^{1,p}_0(\Omega )$, pass to the limit as $n\rightarrow \infty$ and use (39) and the fact that $\{N_f(u_n)\}_{n\geqslant 1}\subseteq L^{p'}(\Omega )$ is bounded, then

$$\begin{aligned}&\lim _{n\rightarrow \infty }\langle A(u_n),u_n-u^*\rangle =0, \nonumber \\&\quad \Rightarrow u_n\rightarrow u^*\ \hbox {in}\ W^{1,p}_0(\Omega )\ (\hbox {see Proposition~} 3). \end{aligned}$$

(40)

Finally, in (29) we pass to the limit as $n\rightarrow \infty$ and use (39) and (40). We obtain

$$\begin{aligned}&\langle A(u^*),h\rangle = \int _\Omega [\lambda ^*(u^*)^{-\gamma } + f(z,u^*)]hdz\ \hbox {for all}\ h\in W^{1,p}_0(\Omega ), \\&\quad \Rightarrow u^*\in S_{\lambda ^*}\subseteq \mathrm{int}\,C_+\ \hbox {and}\ \lambda ^*\in \mathcal {L}. \end{aligned}$$

This completes the proof. $\square$

We have proved that

$$\begin{aligned} \mathcal {L}=(0,\lambda ^*]. \end{aligned}$$

Proposition 13

If hypotheses H(f) hold and $\lambda \in (0,\lambda ^*)$, then problem $(P_\lambda )$ admits at least two positive solutions

$$\begin{aligned} u_\lambda ,\hat{u}_\lambda \in \mathrm{int}\,C_+,\quad \hat{u}_{\lambda }-u_\lambda \in C_+\backslash \{0\}. \end{aligned}$$

Proof

Let $u^*\in S_{\lambda ^*}\subseteq \mathrm{int}\,C_+$ (see Proposition 12). Invoking Proposition 10, we can find $u_\lambda \in S_\lambda \subseteq \mathrm{int}\,C_+$ such that

$$\begin{aligned} u^*-u_\lambda \in \mathrm{int}\,C_+. \end{aligned}$$

(41)

We consider the Carathéodory function $\tau _\lambda (z,x)$ defined by

$$\begin{aligned} \tau _\lambda (z,x)=\left\{ \begin{array}{l@{\quad }l} \lambda u_\lambda (z)^{-\gamma } + f(z,u_\lambda (z)) &{} \hbox {if}\,\, x\leqslant u_\lambda (z) \\ \lambda x^{-\gamma } + f(z,x) &{} \hbox {if}\,\,u_\lambda (z)<x. \end{array} \right. \end{aligned}$$

(42)

Recall that $u_\lambda ^{-\gamma }\in L^{p'}(\Omega )$ (see the proof of Proposition 5). We set $T_\lambda (z,x)=\int ^x_0\tau _\lambda (z,s)ds$ and consider the functional $\tilde{\varphi }_\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \tilde{\varphi }_\lambda (u)=\frac{1}{p}||Du||^p_p - \int _\Omega T_\lambda (z,u)dz\ \hbox {for all}\ u\in W^{1,p}_0(\Omega ). \end{aligned}$$

We know that $\tilde{\varphi }_\lambda \in C^1(W^{1,p}_0(\Omega ))$. Let $K_{\tilde{\varphi }_\lambda }=\{u\in W^{1,p}_0(\Omega ):\tilde{\varphi }_\lambda '(u)=0\}$ (the critical set of $\tilde{\varphi }_\lambda$). Also, for $u\in W^{1,p}_0(\Omega )$, we set

$$\begin{aligned}{}[u)=\{v\in W^{1,p}(\Omega ):u(z)\leqslant v(z)\quad \hbox {for almost all}\,\, z\in \Omega \}.\end{aligned}$$

Claim 1

$K_{\tilde{\varphi _\lambda }}\subseteq [u_\lambda )\cap \mathrm{int}\,C_+$.

Let $u\in K_{\tilde{\varphi }_\lambda }$. We have

$$\begin{aligned} \langle A(u),h\rangle = \int _\Omega \tau _\lambda (z,u)hdz\quad \hbox {for all}\,\, h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(43)

We choose $h=(u_\lambda -u)^+\in W^{1,p}_0(\Omega )$. Then

$$\begin{aligned} \langle A(u),(u_\lambda -u)^+\rangle= & {} \int _\lambda [\lambda u_\lambda ^{-\gamma } + f(z,u_\lambda )](u_\lambda -u)^+dz\ (\hbox {see } (42)) \nonumber \\= & {} \langle A(u_\lambda ), (u_\lambda -u)^+\rangle \ (\hbox {since }u_\lambda \in S_\lambda ), \nonumber \\\Rightarrow & {} u_\lambda \leqslant u. \end{aligned}$$

(44)

From (42)–(44), we obtain

$$\begin{aligned} \langle A(u),h\rangle= & {} \int _\Omega [\lambda u^{-\gamma } + f(z,u)]hdz\ \hbox {for all}\ h\in W^{1,p}_0(\Omega ), \\\Rightarrow & {} u\in S_\lambda \subseteq \mathrm{int}\,C_+\ \hbox {and}\ u_\lambda \leqslant u, \\\Rightarrow & {} u\in [u_\lambda )\cap \mathrm{int}\,C_+. \end{aligned}$$

This proves Claim 1.

Note that $u_\lambda \in K_{\tilde{\varphi }_\lambda }$. We may assume that

$$\begin{aligned} K_{\tilde{\varphi }_\lambda }\cap [u_\lambda ,u^*]=\{u_\lambda \}, \end{aligned}$$

(45)

or otherwise we already have a second positive smooth solution for problem $P_{\lambda }$ (see (42)) and so we are done.

We introduce the following Carathéodory function

$$\begin{aligned} \hat{\tau }_\lambda (z,x)=\left\{ \begin{array}{l@{\quad }l} \tau _\lambda (z,x) &{} \hbox {if}\,\ x\leqslant u^*(z) \\ \tau _\lambda (z,u^*(z)) &{} \hbox {if}\,\ u^*(z)<x. \end{array} \right. \end{aligned}$$

(46)

We set $\hat{T_\lambda }(z,x)=\int ^x_0\hat{\tau }_\lambda (z,s)ds$ and consider the $C^1$-functional $\hat{\varphi }_\lambda :W^{1,p}(\Omega )\rightarrow \mathbb R$ defined by

$$\begin{aligned} \hat{\varphi }_\lambda (u)=\frac{1}{p}||Du||^p_p - \int _\Omega \hat{T_\lambda }(z,u)dz\ \hbox {for all}\ u\in W^{1,p}_0(\Omega ). \end{aligned}$$

This functional is coercive (see (46)) and sequentially weakly lower semicontinuous. Hence we can find $\tilde{u}_\lambda \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \hat{\varphi }_\lambda (\tilde{u}_\lambda )= & {} \inf \{\hat{\varphi }_\lambda (u):u\in W^{1,p}_0(\Omega )\}, \nonumber \\\Rightarrow & {} \hat{\varphi }'_{\lambda }(\tilde{u}_\lambda )=0, \nonumber \\\Rightarrow & {} \langle A(\tilde{u}_\lambda ),h\rangle = \int _\Omega \hat{\tau }_\lambda (z,\tilde{u}_\lambda )hdz\ \hbox {for all}\ h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(47)

In (47) we choose $h=(u_\lambda -\tilde{u}_\lambda )^+\in W^{1,p}_0(\Omega )$ and $h=(\tilde{u}_\lambda -u^*)^+\in W^{1,p}_0(\Omega )$ and obtain that

$$\begin{aligned} \tilde{u}_\lambda \in [u_\lambda ,u^*]. \end{aligned}$$

(48)

From (46)–(48) we infer that

$$\begin{aligned} \tilde{u}_\lambda \in K_{\tilde{\varphi }_\lambda }\cap [u_\lambda ,u^*], \quad \Rightarrow \tilde{u}_\lambda = u_\lambda \ \hbox {(see } (45)). \end{aligned}$$

From (42) and (46) it is clear that

$$\begin{aligned} \tilde{\varphi }_\lambda |_{[0,u^*]}=\hat{\varphi }_\lambda |_{[0,u^*]}. \end{aligned}$$

Also, $u_\lambda$ is a minimizer of $\hat{\varphi }_\lambda$. Since $u^*-u_\lambda \in \mathrm{int}\,C_+$ (see (41)), it follows that

$$\begin{aligned}&u_\lambda \ \hbox {is a local}\ C^1_0(\overline{\Omega })-\hbox {minimizer of}\ \tilde{\varphi }_\lambda , \nonumber \\&\quad \Rightarrow u_\lambda \ \hbox {is a local}\ W^{1,p}_0(\Omega )-\hbox {minimizer of}\ \tilde{\varphi }_\lambda . \nonumber \\&\quad (\hbox {see Motreanu et al.}\,[15, \hbox {Theorem 12.18, p. 409}]). \end{aligned}$$

(49)

We assume that $K_{\tilde{\varphi }_\lambda }$ is finite or otherwise on account of Claim 1, we already have an infinity of positive smooth solutions for problem $P_{\lambda }$ bigger than $u_\lambda$ and so we are done. Because of (49), we can find $\rho \in (0,1)$ small such that

$$\begin{aligned}&\tilde{\varphi }_\lambda (u_\lambda )<\inf \{\tilde{\varphi }_\lambda (u):||u-u_\lambda ||=\rho \}=\tilde{m}_\lambda \nonumber \\&\quad (\hbox {see Aizicovici et al.}~[1, \hbox {proof of Proposition 29}]). \end{aligned}$$

(50)

Hypothesis H(f)(ii) implies that

$$\begin{aligned} \tilde{\varphi }_\lambda (t\hat{u}_1)\rightarrow -\infty \ \hbox {as}\ t\rightarrow +\infty . \end{aligned}$$

(51)

Claim 2

$\tilde{\varphi }_\lambda$ satisfies the C-condition.

Let $\{u_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )$ such that $\{\tilde{\varphi }_\lambda (u_n)\}_{n\geqslant 1}\subseteq \mathbb R$ is bounded and

$$\begin{aligned} (1+||u_n||)\tilde{\varphi }_\lambda '(u_n)\rightarrow 0\ \hbox {in}\ W^{-1,p'}(\Omega )=W^{1,p}_0(\Omega )^*\ \hbox {as}\ n\rightarrow \infty . \end{aligned}$$

We have

$$\begin{aligned} |\langle A(u_n),h\rangle - \int _\Omega \tau _\lambda (z,u_n)hdz| \leqslant \frac{\varepsilon _n||h||}{1+||u_n||}\ \hbox {for all}\ h\in W^{1,p}_0(\Omega ),\ \hbox {with}\ \varepsilon _n\rightarrow 0^+. \end{aligned}$$

(52)

We choose $h=-u^-_n\in W^{1,p}_0(\Omega )$ in (52) and also use (42). Then

$$\begin{aligned}&||Du^-_n||^p_p \leqslant c_8||u^-_n||\ \hbox {for some}\ c_8>0, \hbox {and all}\ n\in \mathbb N, \nonumber \\&\quad \Rightarrow \{u^-_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )\ \hbox {is bounded}. \end{aligned}$$

(53)

Suppose that $||u^+_n||\rightarrow \infty$ and let $y_n=\frac{u^+_n}{||u^+_n||}\ n\in \mathbb N$. Then $||y_n||=1,y_n\geqslant 0$ for all $n\in \mathbb N$. So, we may assume that

$$\begin{aligned} y_n\xrightarrow {w}y\ \hbox {in}\ W^{1,p}_0(\Omega )\quad \hbox {and}\,\, y_n\rightarrow y\ \hbox {in}\ L^p(\Omega ),\ y\geqslant 0. \end{aligned}$$

(54)

From (52) and (53), we have

$$\begin{aligned} |\langle A(y_n),h\rangle - \int _\Omega \frac{N_{\tau _\lambda }(u_n^+)}{||u_n^+||^{p-1}}hdz| \leqslant \varepsilon _n'||h||\ \hbox {for all}\ h\in W^{1,p}_0(\Omega ),\quad \hbox {with}\,\, \varepsilon _n'\rightarrow 0. \end{aligned}$$

(55)

From (42) and hypothesis H(f)(ii), we have

$$\begin{aligned}&\frac{N_{\tau _\lambda }(u_n^+)}{||u_n^+||^{p-1}}\xrightarrow {w} \eta _0(z)y^{p-1}\,\,\hbox {in}\,\,L^{p'}(\Omega )\ \hbox {as}\ n\rightarrow \infty \ \nonumber \\&\quad \hbox {with}\ \eta \leqslant \eta _0(z)\leqslant \hat{\eta }\,\,\hbox {for almost all}\,\,z\in \Omega .\ (\hbox {see } (33)). \end{aligned}$$

(56)

In (55) we choose $h=y_n-y\in W^{1,p}_0(\Omega )$ and pass to the limit as $n\rightarrow \infty$. Then

$$\begin{aligned}&\lim _{n\rightarrow \infty }\langle A(y_n),y_n-y\rangle =0, \nonumber \\&\quad \Rightarrow y_n\rightarrow y\ \hbox {in}\ W^{1,p}_0(\Omega )\ (\hbox {see Proposition~} 3), \hbox {hence}\ ||y||=1, y\geqslant 0. \end{aligned}$$

(57)

Then passing to the limit as $n\rightarrow \infty$ in (55) and using (56) and (57), we obtain

$$\begin{aligned}&\langle A(y),h\rangle = \int _\Omega \eta _0(z)y^{p-1}hdz\ \hbox {for all}\ h\in W^{1,p}_0(\Omega ), \nonumber \\&\quad \Rightarrow -\Delta _py(z)=\eta _0(z)y(z)^{p-1}\ \hbox {for almost all}\ z\in \Omega , y|_{\partial \Omega }=0. \end{aligned}$$

(58)

As before, using Proposition 4, we have

$$\begin{aligned}&\tilde{\lambda }_1(\eta _0)\leqslant \tilde{\lambda }_1(\eta )<\tilde{\lambda }_1(\hat{\lambda }_1)=1, \\\Rightarrow & {} y\ \hbox {must be nodal }(\hbox {see } (58), (57)), \hbox {a contradiction}\,(\hbox {see}~ (57)). \end{aligned}$$

This proves that $\{u^+_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )$ is bounded. Hence

$$\begin{aligned} \{u_n\}_{n\geqslant 1}\subseteq W^{1,p}_0(\Omega )\ \hbox {is bounded }\,(\mathrm{see}\,). \end{aligned}$$

So, we may assume that

$$\begin{aligned} u_n\xrightarrow {w}u\ \hbox {in}\ W^{1,p}_0(\Omega )\ \hbox {and}\ u_n\rightarrow u\ \hbox {in}\ L^p(\Omega )\ \hbox {as}\ n\rightarrow \infty . \end{aligned}$$

(59)

In (52) we choose $h=u_n-u\in W^{1,p}_0(\Omega )$, pass to the limit as $n\rightarrow \infty$ and use (59). Then

$$\begin{aligned}&\lim _{n\rightarrow \infty }\langle A(u_n),u_n-u\rangle = 0, \\&\quad \Rightarrow u_n\rightarrow u\ \hbox {in}\ W^{1,p}_0(\Omega )\ \hbox {(see Proposition 3)}. \end{aligned}$$

This proves Claim 2.

On account of (50), (51) and Claim 2 we can apply Theorem 1 (the mountain pass theorem) and find $\hat{u}_\lambda \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned}&\hat{u}_\lambda \in K_{\tilde{\varphi }_\lambda }\subseteq [u_\lambda )\cap \mathrm{int}\,C_+\ (\hbox {see Claim~}) (see Claim 1), \\&\quad \tilde{m_\lambda }\leqslant \tilde{\varphi }_\lambda (\hat{u}_\lambda )\ (\hbox {see } (50)),\quad \hbox {hence}\ \hat{u}_\lambda \ne u_\lambda . \end{aligned}$$

Therefore $\hat{u}_\lambda \in \mathrm{int}\,C_+$ is the second positive solution of $P_{\lambda }$ and

$$\begin{aligned} \hat{u}_\lambda - u_\lambda \in C_+\backslash \{0\}. \end{aligned}$$

The proof is now complete. $\square$

Therefore we have also proved Theorem A, which is the main result of this paper.

Remark 2

An interesting open problem is whether there is such a bifurcation-type theorem for resonant problems, that is,

$$\begin{aligned} \hat{\lambda }_1\leqslant \liminf _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}} \leqslant \limsup _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}}\leqslant \hat{\eta }\ \hbox {uniformly for almost all}\ z\in \Omega \end{aligned}$$

or even for the nonuniformly nonresonant problems, that is,

$$\begin{aligned} \eta (z)\leqslant \liminf \limits _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}}\leqslant \limsup \limits _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}}\leqslant \hat{\eta }\ \hbox {uniformly for almost all}\ z\in \Omega \end{aligned}$$

with $\eta \in L^\infty (\Omega )$ such that

$$\begin{aligned} \hat{\lambda }_1\leqslant \eta (z)\ \hbox {for almost all}\ z\in \Omega ,\ \eta \not \equiv \hat{\lambda }_1. \end{aligned}$$

In both cases it seems to be difficult to show that $\lambda ^*<\infty$. Additional conditions on $f(z,\cdot )$ might be needed.