Abstract
We study the stationary Stokes system with variable coefficients in the whole space, a half space, and on bounded Lipschitz domains. In the whole and half spaces, we obtain a priori \(\dot{W}^1_q\)-estimates for any \(q\in [2,\infty )\) when the coefficients are merely measurable functions in one fixed direction. For the system on bounded Lipschitz domains with a small Lipschitz constant, we obtain a \(W^1_q\)-estimate and prove the solvability for any \(q\in (1,\infty )\) when the coefficients are merely measurable functions in one direction and have locally small mean oscillations in the orthogonal directions in each small ball, where the direction is allowed to depend on the ball.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we study \(W^1_q\)-estimates and the solvability of the stationary Stokes system with variable coefficients in the whole space, a half space, and on bounded Lipschitz domains. The regularity theory for the linear Stokes system has important applications in mathematical fluid dynamics, for instance, the Navier–Stokes equations. This theory has been extensively studied over the last fifty years by many authors. For the classical Stokes system with the Laplace operator in smooth domains, i.e.,
with the non-homogeneous Dirichlet boundary condition \(u=\varphi \) on \(\partial \Omega \), we refer the reader to Ladyženskaya [27], Sobolevskiĭ [33], Cattabriga [8], Vorovič and Judovič [34], and Amrouche and Girault [3]. In particular, for any \(q\in (1,\infty )\), the following \(W^1_q\)-estimate was obtained by Cattabriga [8] for the system in a bounded \(C^{2}\) domain \(\Omega \subset \mathbb {R}^3\):
The proof is based on the explicit representation of solutions using fundamental solutions. By using a result by Agmon et al. [2] for elliptic systems together with an interpolation argument, Cattabriga’s result was later extended by Amrouche and Girault [3] to a bounded \(C^{1,1}\) domain \(\Omega \subset \mathbb {R}^d\), for any \(d\ge 2\). The system (1.1) on a bounded Lipschitz domain was first studied by Galdi et al. [18]. They proved \(W^1_q\)-estimates and solvability under the assumption that the Lipschitz constant of the domain is sufficiently small. The problem was studied by Fabes et al. [16] in the case of arbitrary Lipschitz domains with the range of q restricted, using the layer potential method and Rellich identities. For this line of research, see also [6, 19, 30,31,32] and references therein, some of which obtain estimates in Besov spaces.
We are interested in the Stokes system with variable coefficients:
where \(\Omega \subseteq \mathbb {R}^d\) and \(\mathcal {L}\) is a strongly elliptic operator, given by
for \(\alpha ,\beta =1,\ldots ,d\). Here and throughout the paper, we use the Einstein summation convention on repeated indices. Such type of systems were considered by Giaquinta and Modica [20], where they obtained various regularity results for both linear and nonlinear Stokes systems when the coefficients are sufficiently regular. Besides its mathematical interests, the system (1.2) is also partly motivated by the study of inhomogeneous fluids with density dependent viscosity (see, for instance, [1, 28, 29]), as well as equations describing flows of shear thinning and shear thickening fluids with viscosity depending on pressure (see, for instance, [7, 17]). See also Dindoš and Mitrea [11] for its relation to the Navier–Stokes system in general Riemannian manifolds.
In this paper, we allow coefficients \(A^{\alpha \beta }\) to be merely measurable in one direction. In particular, they may have jump discontinuities, so that the system can be used to model, for example, the motion of two fluids with interfacial boundaries. The system (1.2) is considered in the whole space, a half space, and on bounded Lipschitz domains. In the whole and half spaces, we obtain a priori \(\dot{W}^1_q\)-estimates for any \(q\in [2,\infty )\) in the case that the coefficients are merely measurable functions in one fixed direction (see Theorem 2.1). For the system on bounded Lipschitz domains with a small Lipschitz constant, we prove a \(W^1_q\)-estimate and solvability for (1.2) with any \(q\in (1,\infty )\), when the coefficients are merely measurable functions in one direction and have locally small mean oscillations in the orthogonal directions in each small ball, with the direction depending on the ball (see Theorem 2.6). These results extend the aforementioned results from [18] for the classical Stokes system (1.1), and the recent study [9] for (1.2) with coefficients having small mean oscillations in all directions. We note that the class of coefficients considered in this paper was first introduced by Kim and Krylov [23] and Krylov [25], where they established the \(W^2_p\)-estimate for non-divergence form second-order elliptic equations in the whole space. Subsequently, such coefficients were also treated in [13, 14] for second- and higher-order elliptic and parabolic systems in regular and irregular domains.
Let us now provide an outline of the proofs of Theorems 2.1 and 2.6. Our argument is completely different from the methods in [3, 8, 18], and is based on pointwise sharp and maximal function estimates in the spirit of [23,24,25] for second-order elliptic equations. Such estimates rely on the \(C^{1,\alpha }\) regularity of solutions to the homogeneous system. Here, the main difficulty is that because the coefficients are measurable in one direction, say \(x_1\), it is impossible to obtain a Hölder estimate of the full gradient Du. To this end, instead of considering Du itself, we exploit an idea given in [14] to estimate certain linear combinations of Du and p:
Here and throughout the paper, \(D_{x'}u\) denotes the partial derivative of u in the \(x_i\) direction, \(i=2,\ldots ,d\), where \(x = (x_1, x') = (x_1, x_2, \ldots ,x_d) \in \mathbb {R}^d\). For the Stokes system, the presence of the pressure term p gives an added difficulty, because in the usual \(L_2\)-estimate, instead of p one can only bound \(p-(p)\) by Du, instead of p. See, for instance, Lemma 3.5. Nevertheless, in Lemma 4.2 we show that for the homogeneous Stokes system and any integer \(k\ge 1\), the \(L_2\)-norm of \(D_{x'}^k p\) in a smaller ball can be controlled by that of Du in a larger ball. Finally, in order to deal with the system (1.2) in a Lipschitz domain, we apply a version of the Fefferman–Stein sharp function theorem for spaces of homogeneous type, which was recently proved in [12] (cf. Lemma 7.3). Furthermore, we employ a delicate cut-off argument, together with Hardy’s inequality, which was first used in [13] and also in the recent paper [9].
In a subsequent paper, we will study weighted \(W^1_q\)-estimates and the solvability of the Stokes system (1.2) in more general Reifenberg flat domains, with the same class of coefficients. We note that an a priori \(W^1_q\)-estimate in Reifenberg flat domains was obtained in [9], under the condition that the coefficients have sufficiently small mean oscillations in all directions.
The remainder of this paper is organized as follows. We state the main theorems in the following section. Section 3 contains some auxiliary results, including \(L_2\)-estimates and Caccioppoli type inequalities. In Sect. 4, we prove interior and boundary \(L_\infty \) and Hölder estimates for derivatives of solutions, while in Sect. 5 we establish the interior and boundary mean oscillation estimates for the system in the whole space and in a half space. Section 6 is devoted to the proof of Theorem 2.1. Finally, we consider the system (1.2) in a Lipschitz domain with a small Lipschitz constant in Sect. 7.
We conclude this section by introducing some notation. We fix a half space to be \(\mathbb {R}^d_+\), defined by
Let \(B_r(x_0)\) be the Euclidean ball of radius r in \(\mathbb {R}^d\) centered at \(x_0\in \mathbb {R}^d\), and let \(B^+_r(x_0)\) be the half ball
A ball in \(\mathbb {R}^{d-1}\) is denoted by
We use the abbreviations \(B_r := B_r(0), B_r^+ := B_r^+(0)\) where \(0\in \mathbb {R}^d\), and \(B_r' := B_r'(0)\) where \(0 \in \mathbb {R}^{d-1}\).
For a locally integrable function f, we define its average on \(\Omega \) by

We shall use the following function spaces:
Finally, let \(\mathring{W}_q^1(\Omega )\) be the completion of \(C^\infty _0(\Omega )\) in \(W_q^1(\Omega )\), and \(\mathring{W}_q^1(\Omega )^d=\big (\mathring{W}_q^1(\Omega )\big )^d\).
2 Main results
In this section, we state our main results and the assumptions required for them. Throughout this paper, the coefficients \(A^{\alpha \beta }\) are bounded and satisfy the strong ellipticity condition, i.e., there exists a constant \(\delta \in (0,1)\) such that
for any \(\xi _\alpha \in \mathbb {R}^d\), \(\alpha = 1, \ldots , d\). Owing to the trace-extension theorem on Lipschitz domains, in the sequel we only consider the homogeneous boundary condition \(u=0\) on \(\partial \Omega \), without loss of generality.
We say that \((u,p)\in W_q^1(\Omega )^d\times L_q(\Omega )\) is a solution to (1.2) if for any \(\psi = (\psi _1, \ldots , \psi _d) \in C_0^\infty (\Omega )^{d}\), we have that
where
Our first results concern a priori \(L_q\)-estimates of the Stokes system defined in \(\mathbb {R}^d\) or \(\mathbb {R}^d_+\), when the coefficients \(A^{\alpha \beta }\) are merely measurable functions of only \(x_1\). In this case, throughout the paper, we set
where \(A^{\alpha \beta }(x_1) = [A^{\alpha \beta }_{ij}(x_1)]_{i,j=1}^d\). Note that we do not impose any regularity assumptions on \(A^{\alpha \beta }(x_1)\).
Theorem 2.1
Let \(q \in [2,\infty )\), and let \(\Omega \) be either \(\mathbb {R}^d\) or \(\mathbb {R}^d_+\) and \(A^{\alpha \beta } = A^{\alpha \beta }(x_1)\), i.e., \(\mathcal {L}= \mathcal {L}_0\). If \((u,p) \in W_q^1(\Omega )^d \times L_q(\Omega )\) satisfies
where \(f_\alpha , g \in L_q(\Omega )\), then we have that
where \(N=N(d,\delta ,q)\).
Remark 2.2
In Theorem 2.1 we only consider the case that \(q \in [2,\infty )\) to simplify the exposition and to present our approach in the most transparent way. Indeed, if \(q = 2\), the theorem holds even with measurable \(A^{\alpha \beta }(x)\). See Theorem 3.4. Thus, in the proof of Theorem 2.1 we focus on the case \(q \in (2,\infty )\), the proof of which well illustrates, in the simplest setting, our arguments based on mean oscillation estimates together with the sharp function and the maximal function theorems. One can prove the other case, with \(q \in (1,2)\), by using Theorem 2.6 below. This will be discussed in a more general setting with weights in a forthcoming paper [15].
Next, when the Stokes system is defined in a bounded Lipschitz \(\Omega \) with a small Lipschitz constant, we show that the system is uniquely solvable in \(L_q(\Omega )\) spaces. In this case, we allow coefficients not only to be measurable locally in one direction (near the boundary the direction is almost perpendicular to the boundary of the domain), but also to have small mean oscillations in the other directions. To present this result, we require the following assumptions.
Assumption 2.3
For any \(x_0 \in \partial \Omega \) and \(0 < r \le R_0\), there is a coordinate system depending on \(x_0\) and r such that in the new coordinate system we have
where \(\phi : \mathbb {R}^{d-1} \rightarrow \mathbb {R}\) is a Lipschitz function with
Assumption 2.4
(\(\gamma , \rho \)). Let \(\gamma , \rho \in (0,1/16)\). There exists \(R_1 \in (0, R_0]\) satisfying the following.
-
(1)
For \(x_0 \in \Omega \) and \(0 < r \le \min \{R_1, {\text {dist}}(x_0, \partial \Omega )\}\), there is a coordinate system depending on \(x_0\) and r such that in this new coordinate system we have that
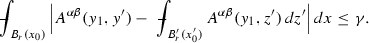 (2.3)
(2.3) -
(2)
For any \(x_0 \in \partial \Omega \) and \(0 < r \le R_1\), there is a coordinate system depending on \(x_0\) and r such that in the new coordinate system we have that (2.3) holds, and
$$\begin{aligned} \Omega \cap B_r(x_0) = \{x \in B_r(x_0)\, :\, x_1 >\phi (x')\}, \end{aligned}$$where \(\phi : \mathbb {R}^{d-1} \rightarrow \mathbb {R}\) is a Lipschitz function with
$$\begin{aligned} \sup _{\begin{array}{c} x', \, y' \in B_r'(x_0')\\ x' \ne y' \end{array}}\frac{|\phi (y')-\phi (x')|}{|y'-x'|}\le \rho . \end{aligned}$$
Remark 2.5
Clearly, Assumption 2.4 (2) is stronger than Assumption 2.3. However, we state these two assumptions separately for the following reason. As seen in Theorem 2.6, we specify the class of bounded Lipschitz domains for which the results of the theorem hold in terms of the flatness parameter \(\rho \). Thus, having two separate assumptions means that in Theorem 2.6 we specify a subclass of the class of domains satisfying Assumption 2.3. The necessity of such a hierarchy of classes of domains is that when determining the size of \(\rho \) in Theorem 2.6, we need some information about domains and their boundaries. In particular, the maximal function and sharp function theorems on bounded domains we use in this paper require such information. Thus, without Assumption 2.3, the size of \(\rho \) is to be determined by a set of parameters including \(R_1\). In this case, i.e., when \(\rho \) is given by \(R_1\), even a smooth domain \(\Omega \) may not satisfy Assumption 2.4 (2) if \(R_1\) is too large for the boundary to have \(\rho \) flatness on \(\Omega \cap B_{R_1}(x_0)\). With two assumptions as above, every smooth domain satisfies Assumption 2.4 (2) for any \(\rho \) by choosing a sufficiently small \(R_1\).
Theorem 2.6
Let \(q ,q_1\in (1,\infty )\) satisfying \(q_1 \ge q d/(q+d)\), \(K > 0\), and let \(\Omega \) be bounded (\({\text {diam}}\Omega \le K\)). Then, there exist constants \((\gamma , \rho ) = (\gamma , \rho )(d,\delta ,R_0, K, q) \in (0,1/16)\) such that, under Assumptions 2.3 and 2.4 \((\gamma , \rho )\), for \((u,p) \in W_q^1(\Omega )^d \times L_q(\Omega )\) satisfying \((p)_\Omega = 0\) and
where \(f \in L_{q_1}(\Omega )\), \(f_\alpha , g \in L_q(\Omega )\), we have that
where \(N>0\) is a constant depending only on d, \(\delta \), \(R_0\), \(R_1\), K, q, and \(q_1\). Moreover, for \(f \in L_{q_1}(\Omega )\), \(f_\alpha , g \in L_q(\Omega )\) with \((g)_\Omega = 0\), there exists a unique \((u,p) \in W_q^1(\Omega )^d \times L_q(\Omega )\) satisfying \((p)_\Omega = 0\) and (2.4).
3 Auxiliary results
In this section, we assume that the coefficients \(A^{\alpha \beta }\) are measurable functions of \(x \in \mathbb {R}^d\). That is, no regularity assumptions are imposed on \(A^{\alpha \beta }\).
We impose the following assumption on a bounded domain \(\Omega \subset \mathbb {R}^d\) in Lemma 3.3 below.
Assumption 3.1
For any \(g \in L_2(\Omega )\) such that \(\int _{\Omega } g \, dx = 0\), there exist \(B g \in \mathring{W}_2^1(\Omega )^d\) and a constant \(K_1>0\) depending only on d and \(\Omega \) such that
Remark 3.2
If \(\Omega = B_R\) or \(\Omega = B_R^+\), it follows from a scaling argument that the constant \(K_1\) depends only on the dimension d. If \(\Omega \) is a bounded Lipschitz domain satisfying Assumption 2.3, then Assumption 3.1 is satisfied with \(K_1\) depending only on d, \(R_0\), and \({\text {diam}} \Omega \). If 1 / 16 in Assumption 2.3 is replaced by \(\rho \) and \(\rho \in [0,\rho _0]\), the constant \(K_1\) can be chosen so that it depends only on d, \(R_0\), \({\text {diam}}\Omega \), and \(\rho _0\). See, for instance, [5].
Lemma 3.3
Let \(\Omega \subset \mathbb {R}^d\) be a bounded domain which satisfies Assumption 3.1, and \(f, f_\alpha , g \in L_2(\Omega )\) with \((g)_\Omega = 0\). Then, there exists a unique \((u,p) \in W_2^{1}(\Omega )^d \times L_2(\Omega )\) with \((p)_\Omega = 0\) satisfying
Moreover, we have that
where \(N = N(d,\delta , K_1)\). If \(\Omega = B_R(x_0)\), \(x_0 \in \mathbb {R}^d\), or \(\Omega = B^+_R(x_0)\), \(x_0 \in \partial \mathbb {R}^d_+\), then we have that
where \(N=N(d,\delta )\).
Proof
See, for instance, [9, Lemma 3.1]. \(\square \)
As far as a priori estimates are concerned, one can have \(\Omega =\mathbb {R}^d\) or \(\Omega = \mathbb {R}^d_+\) in Lemma 3.3 if \(f \equiv 0\). In this case we do not necessarily need that the integral of p over \(\Omega \) is zero. For completeness and later reference, we state and prove this result in the theorem below.
Recall that we say that \((u,p) \in W_2^1(\Omega )^d \times L_2(\Omega )\) satisfies, for instance, \(\mathcal {L}u + \nabla p = 0\) in \(\Omega \), if
for all \(\psi \in C_0^\infty (\Omega )^d\). One can easily see that \(C_0^\infty (\Omega )^d\) can be replaced by \(\mathring{W}_2^1(\Omega )^d\).
Theorem 3.4
Let \(\Omega \) be either \(\mathbb {R}^d\) or \(\mathbb {R}^d_+\). If \((u,p) \in W_2^1(\Omega )^d \times L_2(\Omega )\) satisfies
where \(f_\alpha , g \in L_2(\Omega )\), then we have that
where \(N=N(d,\delta )\).
Proof
Since \(u \in \mathring{W}_2^1(\Omega )^d\), we use u as a test function to obtain that
From this, the ellipticity condition, and Young’s inequality, we have that
for any \(\varepsilon _0 > 0\), where \(N=N(d,\delta )\).
Now, for any \(\varepsilon >0\), we can find \(R> 0\) and \(p_\varepsilon \in L_2(\Omega )\) such that \({\text {supp}} p_\varepsilon \subset B_R\), \(\int _{\Omega } p_{\varepsilon } \, dx = 0\), and \(\Vert p - p_\varepsilon \Vert _{L_2(\Omega )} < \varepsilon \). To do this, because \(p \in L_2(\Omega )\), we first find a function \(p_1\) with a compact support in \(B_{R_1}\) such that
If \(\int _{\Omega } p_1 \, dx = 0\), we set \(R = R_1\) and \(p_\varepsilon = p_1\). Otherwise, set
and \(R_2\) is a positive number satisfying
Then, we see that
Thus, it suffices to take \(R = \max \{ R_1, R_2\}\) and \(p_\varepsilon = p_1 - g\).
Thanks to the fact that \((p_{\varepsilon })_{B_R} = 0\) or \((p_{\varepsilon })_{B_R^+} = 0\), there exists a solution \(\psi \in \mathring{W}_2^1(B_R)^d\) or \(\psi \in \mathring{W}_2^1(B_R^+)^d\) satisfying the divergence equation
in \(B_R\) or \(B_R^+\). Extend \(\psi \) to be zero on \(\mathbb {R}^d {\setminus } B_R\) or \(\mathbb {R}^d_+ {\setminus } B_R^+\). Then we have \(\psi \in \mathring{W}_2^1(\Omega )^d\) and
By applying \(\psi \) as a test function to the system, we have that
From this, Young’s inequality, and (3.2), it follows that
for any \(\varepsilon _1 > 0\), where \(N=N(d,\delta )\). Since \(\varepsilon > 0\) is arbitrary, from the above inequality we obtain that
which combined with (3.1) proves the desired inequality. \(\square \)
In the lemmas below, we do not necessarily have that \((p)_{B_R} = 0\) or \((p)_{B_R^+} = 0\) unless specified. We note that by now these lemmas are fairly standard results, and we present them here for the sake of completeness. See, for instance, [22] and [9], and also [20] under slightly different conditions on the coefficients.
Lemma 3.5
Let \(R>0\). If \((u,p) \in W_2^1(B_R)^d \times L_2(B_R)\) satisfies
then
where \(N=N(d,\delta )\). The same estimate holds if \(B_R\) is replaced by \(B_R^+\).
Proof
We only prove the case with \(B_R^+\), because the other case is similar. By Remark 3.2, one can find \(\psi \in \mathring{W}_2^1(B_R^+)^d\) satisfying
and
where \(N = N(d)\). Then, apply \(\psi \) to (3.3) as a test function, and use Young’s inequality and (3.5), to get (3.4) with \(B_R^+\) in place of \(B_R\). \(\square \)
Lemma 3.6
Let \(0< r < R\).
-
(1)
If \((u,p) \in W_2^1(B_R)^d \times L_2(B_R)\) satisfies
$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {L}u + \nabla p = 0 &{}\quad \text {in}\,\,B_R,\\ {\text {div}} u = 0 &{}\quad \text {in}\,\,B_R, \end{array} \right. \end{aligned}$$(3.6)then for any \(\varepsilon > 0\), we have that
$$\begin{aligned} \int _{B_r} |Du|^2 \, dx \le N (R-r)^{-2} \int _{B_R}|u|^2 \, dx + \varepsilon \int _{B_R} |Du|^2 \, dx, \end{aligned}$$(3.7)where \(N = N(d,\delta ,\varepsilon )\).
-
(2)
If \((u,p) \in W_2^1(B_R^+)^d \times L_2(B_R^+)\) satisfies
$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {L}u + \nabla p = 0 &{}\quad \text {in}\,\,B_R^+,\\ {\text {div}} u = 0 &{}\quad \text {in}\,\,B_R^+,\\ u=0 &{}\quad \text {on}\,\, B_R \cap \partial \mathbb {R}^d_+, \end{array} \right. \end{aligned}$$(3.8)then for any \(\varepsilon >0\), we have that (3.7) holds with \(B_r^+\) and \(B_R^+\) replacing \(B_r\) and \(B_R\), respectively, where \(N = N(d,\delta , \varepsilon )\).
Proof
We only prove the second assertion of the lemma, because the first is the same with obvious modifications.
Set \(\eta \) to be an infinitely differentiable function on \(\mathbb {R}^d\), such that
Then, we apply \(\eta ^2 u\) to (3.8) as a test function (because \((\eta ^2 u)|_{\partial B_R^+} = 0\)), to obtain that
From this and the fact that \(\int _{B_R^+} {\text {div}} (\eta ^2 u) \, dx = 0\), we have that
Together with (3.9), the ellipticity condition, Young’s inequality, and the fact that \({\text {div}}u = 0\), this shows that
for any \(\varepsilon > 0\). The desired estimate follows by combining this with Lemma 3.5, and the fact that \(\eta = 1\) on \(B_r\). \(\square \)
Lemma 3.7
Let \(0< r < R\).
-
(1)
If \((u,p) \in W_2^1(B_R)^d \times L_2(B_R)\) satisfies (3.6), then we have that
$$\begin{aligned} \int _{B_r} |Du|^2 \, dx \le N (R-r)^{-2} \int _{B_R} |u|^2 \, dx, \end{aligned}$$(3.10)where \(N=N(d,\delta )\).
-
(2)
If \((u,p) \in W_2^1(B_R^+)^d \times L_2(B_R^+)\) satisfies (3.8), then we have that (3.10) holds, with \(B_r^+\) and \(B_R^+\) replacing \(B_r\) and \(B_R\), respectively.
Proof
To prove the lemma one may use the so called \(\varepsilon \)-lemma given in [20, Lemma 0.5]. However, in this case, it is easier to employ the following well-known argument (see, for instance, the proof of [23, Lemma 4.2]). Set
Then, by Lemma 3.6 we have that
for any \(\varepsilon > 0\), where \(N=N(d,\delta ,\varepsilon )\). By multiplying both sides of the above inequality by \(\varepsilon ^k\) and summing the terms with respect to \(k = 0, 1, \ldots \), we obtain that
where each summation is finite upon choosing, for instance, \(\varepsilon = 1/8\). Since the first summation on the right-hand side of the above inequality is bounded by \(\int _{B_R}|u|^2 \, dx\), we can arrive at (3.10) by subtracting \(\sum _{k=1}^\infty \varepsilon ^k \int _{B_{R_k}} |Du|^2 \, dx\) from both sides of the above inequality. The other case for half balls is proved in the same way. \(\square \)
4 \(L_\infty \) and Hölder estimates
In this section, we prove \(L_\infty \) and Hölder estimates of certain linear combinations of Du and p, which are crucial for proving our main results. Recall the operator \(\mathcal {L}_0\) given in (2.1), where the coefficients are functions of \(x_1\) only. In this case, if a sufficiently smooth (u, p) satisfies \(\mathcal {L}_0 u + \nabla p = 0\) in \(\Omega \subset \mathbb {R}^d\), we see that
in \(\Omega \). Set \(U = \left( U_1, U_2, \ldots , U_d\right) ^{{\text {tr}}}\), where
That is,
Here and throughout we write \(D D_{x'}^k u\), \(k=0,1, \ldots \), to denote \(D^\vartheta u\), where \(\vartheta \) is a multi-index such that \(\vartheta = (\vartheta _1, \ldots , \vartheta _d)\) with \(\vartheta _1 = 0, 1\) and \(|\vartheta | = k+1\).
Lemma 4.1
Let \(0< r < R\), and let \(\ell \) be a constant.
-
(1)
If \((u,p) \in W_2^1(B_R)^d \times L_2(B_R)\) satisfies
$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {L}_0 u + \nabla p = 0 &{}\quad \text {in}\,\,B_R, \\ {\text {div}} u = \ell &{}\quad \text {in}\,\,B_R, \end{array} \right. \end{aligned}$$(4.3)then \(DD_{x'} u \in L_2(B_r)\), and
$$\begin{aligned} \int _{B_r} |DD_{x'}u|^2 \, dx \le N(R-r)^{-2} \int _{B_R} |Du|^2 \, dx, \end{aligned}$$(4.4)where \(N=N(d,\delta )\).
-
(2)
If \((u,p) \in W_2^1(B_R^+)^d \times L_2(B_R^+)\) satisfies
$$\begin{aligned} \left\{ \begin{array}{ll} \mathcal {L}_0 u + \nabla p = 0 &{} \quad \text {in}\,\,B_R^+,\\ {\text {div}} u = \ell &{}\quad \text {in}\,\,B_R^+, \\ u = 0 &{}\quad \text {on}\,\, B_R \cap \partial \mathbb {R}^d_+, \end{array} \right. \end{aligned}$$(4.5)then \(DD_{x'}u \in L_2(B_r^+)\), \(D_{x'} u = 0\) on \(B_r \cap \partial \mathbb {R}^d_+\), and (4.4) is satisfied with \(B_r^+\) and \(B_R^+\) replacing \(B_r\) and \(B_R\), respectively.
Proof
We only deal with the second assertion here. Set \(\delta _{j,h} f\) to be the difference quotient of f with respect to \(x_j\), i.e.,
and let \(R_1 = (R+r)/2\). Then, since the coefficients are functions of \(x_1\) only, we have for \(0< h < (R-r)/2\) that
where \(j=2,\ldots ,d\). By applying Lemma 3.7 to (4.6), we have that
which we can combine with the standard finite difference argument to imply the desired conclusion. \(\square \)
To estimate U, we also need to bound \(D_{x'} p \in L_2(B_r)\), as in the following key lemma.
Lemma 4.2
Let \(0< r < R\), and let \(\ell \) be a constant.
-
(1)
If \((u,p) \in W_2^1(B_R)^d \times L_2(B_R)\) satisfies (4.3) in \(B_R\), then \(D_{x'}p \in L_2(B_r)\) and
$$\begin{aligned} \int _{B_r}|D_{x'}p|^2\,dx\le N(R-r)^{-2} \int _{B_R}|Du|^2\,dx, \end{aligned}$$(4.7)where \(N = N(d,\delta )>0\).
-
(2)
If \((u,p) \in W_2^1(B_R^+)^d \times L_2(B_R^+)\) satisfies (4.5) in \(B_R^+\), then \(D_{x'}p \in L_2(B_r^+)\), and (4.7) is satisfied with \(B_r^+\) and \(B_R^+\) replacing \(B_r\) and \(B_R\), respectively.
Proof
We only prove the second assertion here. Define \(\delta _{j,h} f\) as in the proof of Lemma 4.1, and set \(R_1 = (2R+r)/3\). Then, for \(0< h < (R-r)/3\), we have that
in \(B_{R_1}^+\), where \(j=2,\ldots ,d\). Set \(R_2 = (R+2r)/3\), and let \(\eta \) be an infinitely differentiable function on \(\mathbb {R}^d\) such that
Find a function \(\psi \in \mathring{W}_2^1(B_{R_1}^+)^d\) such that
in \(B_{R_1}^+\), where \(c := (p)_{B_R^+}\). Note that
Then, by Remark 3.2 we have that
Since
it follows that
Then, applying \(\psi \) to (4.8) as a test function, we have that
Thus, we have that
By Young’s inequality and (4.9), we have for any \(\varepsilon \in (0,1)\) that
Here, we note that
where the last term is estimated by
In addition, note that
and by Lemma 4.1 and the properties of \(\delta _{j,h}\), it holds that
where \(R_1< R' < R\). By using the above inequalities combined with (4.10), (4.9), and Lemma 3.5, and choosing a sufficiently small \(\varepsilon >0\), we obtain that
Together with the properties of the finite difference operator, this proves the desired inequality. \(\square \)
As usual, by \([u]_{C^\tau (\Omega )}\), \(\tau \in (0,1)\), we denote the Hölder semi-norm of u defined by
The following interior and boundary \(L_\infty \) and Hölder estimates constitute the main results of this section.
Lemma 4.3
Let \(\ell \) be a constant, and let \((u,p) \in W_2^1(B_2)^d \times L_2(B_2)\) satisfy (4.3) with \(R=2\). Then, we have that
and
where \(N=N(d,\delta )\).
Proof
See the proof of Lemma 4.4 below, with obvious modifications. \(\square \)
Lemma 4.4
Let \(\ell \) be a constant, and let \((u,p) \in W_2^1(B_2^+)^d \times L_2(B_2^+)\) satisfy (4.5) with \(R=2\). Then, we have that
and
where \(N=N(d,\delta )\).
Proof
From Lemmas 4.1 and 4.2, we have that \((D_{x'} u, D_{x'}p) \in W_2^1(B_{r_1}^+)^d \times L_2(B_{r_1}^+)\) and
where \(1< r_1 < 2\). Moreover, \((D_{x'} u, D_{x'} p)\) satisfies
Then, we apply Lemmas 4.1 and 4.2 again as above, with \(r_2\) in place of \(r_1\) and with \(r_1\) in place of 1, where \(1< r_2< r_1 < 2\). By repeating this process, we see that \((D_{x'}^k u, D_{x'}^k p)\) belongs to \(W_2^1(B_r^+)^d \times L_2(B_r^+)\) with \(D_{x'}^k u = 0\) on \(B_r \cap \partial \mathbb {R}^d_+\), and satisfies
for any \(r \in [1,2)\) and \(k=1,2,\ldots \). In particular, this estimate means that \(D_{x'}u\) has one derivative in \(x_1\) and sufficiently many derivatives in \(x_i\), \(i=2,\ldots ,d\), the \(L_2(B_1^+)\) norms of which are bounded by \(\Vert Du\Vert _{L_2(B_2^+)}\). Then, by the anisotropic Sobolev embedding theorem with \(k> (d-1)/2\) (see, for instance, the proof [14, Lemma 3.5]), we get that
Now, we prove the Hölder semi-norm estimate of U and the sup-norm estimate of \(U_i\), \(i = 2, \ldots , d\). Set
By the definitions of U and \(\tilde{U}\), we have that
where \(k=1,2,\ldots \). In combination with (4.11), this shows that
Similarly, since the \(D_{\alpha \beta }u\) terms on the right-hand side of (4.1) are of the form \(D D_{x'} u\), we have that
where \(k=0,1,2,\ldots \). To estimate \(\Vert \tilde{U}\Vert _{L_2(B_1^+)}\), we apply Lemma 3.5 with \(R=1\) to obtain that
where \(N=N(d,\delta )\). Together with the definition of \(\tilde{U}\), this shows that
Together with (4.12) and (4.13), and using the anisotropic Sobolev embedding as above with \(k>(d-1)/2\), this gives that
Since \(\left[ U\right] _{C^{1/2}(B_1^+)} = \big [\tilde{U}\big ]_{C^{1/2}(B_1^+)}\) and \(\tilde{U}_i = U_i\), \(i = 2, \ldots , d\), we have obtained the desired inequalities. Thus, the lemma is proved. \(\square \)
5 Mean oscillation estimates
In this section, we prove our mean oscillation estimates using the Hölder estimates developed in Sect. 4 and the \(L_2\)-estimates of the Stokes system given in Lemma 3.3. Throughout this section, we consider the operator \(\mathcal {L}_0\), i.e., the coefficients \(A^{\alpha \beta }\) are measurable functions of \(x_1\) only.
Lemma 5.1
Let \(r \in (0,\infty )\), \(\kappa \ge 2\), \(x_0 \in \mathbb {R}^d\), and \(f_\alpha , g \in L_2(B_{\kappa r}(x_0))\). If \((u,p) \in W_2^1(B_{\kappa r}(x_0))^d \times L_2(B_{\kappa r}(x_0))\) satisfies
then
where \(N=N(d,\delta )\).
Proof
This lemma follows as a consequence of Lemmas 3.3 and 4.3. See Case 2 in the proof of Lemma 5.2 below. \(\square \)
Lemma 5.2
Let \(r \in (0,\infty )\), \(\kappa \ge 16\), \(x_0 \in \overline{\mathbb {R}^d_+}\), and \( f_\alpha , g \in L_2(B^+_{\kappa r}(x_0))\). If \((u,p) \in W_2^1(B_{\kappa r}^+(x_0))^d \times L_2(B_{\kappa r}^+(x_0))\) satisfies
then
where \(N=N(d,\delta )\).
Proof
Denote the first coordinate of \(x_0\) by \({x_0}_1\). We consider the following two cases.
Case 1 \({x_0}_1 \ge \kappa r/8\). In this case, we have that
and \(\kappa /8\ge 2\). Then, the estimate (5.1) follows from Lemma 5.1.
Case 2 \({x_0}_1 < \kappa r/8\). Set \(y_0 = (0,x_0')\). Then, we have that
Considering dilation, it suffices to prove (5.1) when \(r = 4/\kappa \le 1/4\) and \({x_0}_1 < 1/2\). Furthermore, we assume that \(y_0 = 0\). By Lemma 3.3, there exists \((w,p_1) \in \mathring{W}_2^1(B_2^+)^d \times L_2(B_2^+)\) such that \((p_1)_{B_2^+} = 0\),
and
where \(N=N(d,\delta )\). In particular, we have that \(w = 0\) on \(B_2 \cap \partial \mathbb {R}^d_+\). The estimate (5.3) clearly implies that
where \(N=N(d,\delta )\).
Now, we set \((v,p_2) = (u,p) - (w,p_1)\), which satisfies
Then, by Lemma 4.4,
where \(N=N(d,\delta )\). Similarly, we have that
where V is defined in exactly the same way as U in (4.2) with v in place of u. Then, it follows from the triangle inequality that
where \(N=N(d,\delta )\). Together with the estimates (5.3) and (5.4), and the fact that \(u = v+w\), this shows that
It only remains to observe that the right-hand side is bounded by that of (5.1), because of (5.2).
We can similarly obtain the desired estimate for U. Thus, the lemma is proved. \(\square \)
6 Proof of Theorem 2.1
In this section, we complete the proof of Theorem 2.1. We use the following filtration of partitions of \(\mathbb {R}^d\):
where \(n \in \mathbb {Z}\) and
For a filtration of partitions of \(\mathbb {R}^d_+\), we replace \(i_1 \in \mathbb {Z}\) by \(i_1 \in \{0,1,2,\ldots ,\}\). Using these filtrations, we define the sharp function of \(f \in L_{1, {\text {loc}}}(\Omega )\), where \(\Omega = \mathbb {R}^d\) or \(\Omega = \mathbb {R}^d_+\), by

where the supremum is taken with respect to all \(C_n \in \mathbb {C}_n\) containing x, where \(n \in \mathbb {Z}\). The maximal function of f in \(\mathbb {R}^d\) or \(\mathbb {R}^+\) is defined by

where \(\Omega = \mathbb {R}^d\) or \(\Omega = \mathbb {R}^d_+\), and the supremum is taken with respect to all \(B_r(x_0)\) containing x with \(r > 0\), where \(x_0\in \bar{\Omega }\).
Proof of Theorem 2.1
Because Theorem 3.4 covers the case with \(q=2\), we assume that \(q \in (2,\infty )\). We prove the case when \(\Omega = \mathbb {R}^d_+\). The other case is simpler.
For \(x \in \mathbb {R}^d_+\) and \(C_n \in \mathbb {C}_n\) such that \(x \in C_n\), find \(x_0 \in \mathbb {R}^d_+\) and the smallest \(r \in (0,\infty )\) (indeed, \(r = 2^{-n-1}\sqrt{d}\)) satisfying \(C_n \subset B_r(x_0)\) and

Since \((u,p) \in W_2^1(B_{\kappa r}^+(x_0))^d \times L_2(B_{\kappa r}^+(x_0))\), it follows from Lemma 5.2 that we have the mean oscillation estimate (5.1) for \(\kappa \ge 16\). Moreover, each term in the right-hand side of (5.1) is bounded by its maximal function at x. From this and (6.2), we have that
for \(x \in C_n\) and \(\kappa \ge 16\), where \(N=N(d,\delta )\). By taking the supremum of the left-hand side of the above inequality with respect to all \(C_n \ni x\), \(n \in \mathbb {Z}\), we obtain that
for \(x \in \mathbb {R}^d_+\) and \(\kappa \ge 16\). Then, we employ the Fefferman–Stein theorem on sharp functions (see, for instance, [26, Theorem 3.2.10]) and the maximal function theorem (see, for instance, [26, Theorem 3.3.2] or Lemma 7.2 in this paper, which also holds when \(\Omega = \mathbb {R}^d_+\) with \(N=N(d,q)\)) on the above pointwise estimate, to obtain that
where \(L_q = L_q(\mathbb {R}^d_+)\) and \(N = N(d,\delta ,p)\). Note that on the left-hand side of the above inequality we do not yet have \(L_q\)-norms of \(D_1u_i\), \(i=1,2,\ldots ,d\), and p. To obtain \(L_q\)-estimates of such terms, we first note the relation
Using this and (6.3), we have that
Then, we use the relation
which follows from the definition of \(U_i\), \(i=2,\ldots ,d\). By the ellipticity condition on \(A^{\alpha \beta }\), it follows that the \((d-1)\times (d-1)\) matrix \([A_{ij}^{11}]_{i,j=2}^d\) is invertible. Thus, from (6.5) and (6.4) we have that
Upon taking a sufficiently large \(\kappa \ge 16\), which depends only on d, \(\delta \), and q, such that \(N \kappa ^{-1/2} \le 1/2\), we arrive at
Finally, from this estimate and the definition of \(U_1\), we see that the \(L_q\)-norm of p is bounded by the right-hand side of (2.2). By this and (6.6), we can conclude that the estimate (2.2) holds, and the theorem is proved. \(\square \)
7 Proof of Theorem 2.6
This section is devoted to the proof of Theorem 2.6. For any \(x_0\in \mathbb {R}^d\) and \(r>0\), denote
We first derive the following mean oscillation estimate.
Lemma 7.1
Let \(\mu , \nu \in (1,\infty )\) be such that \(1/\mu + 1/\nu = 1\) and \(\kappa \ge 32\). Then, under Assumption 2.4\((\gamma ,\rho )\) such that \(\rho \kappa \le 1/4\), for any \(r \in (0, R_1/\kappa ]\), \(x_0 \in \overline{\Omega }\), and
satisfying
where \(f_\alpha \in L_{2}(\Omega _{\kappa r}(x_0))\), there exists a \(d^2\)-dimensional vector-valued function \(\mathcal {U}\) on \(\Omega _{\kappa r}(x_0)\) such that on \(\Omega _{\kappa r}(x_0)\),
and
where \(N=N(d,\delta , \mu )\).
Proof
We mainly follow the proof of Proposition 7.10 in [13], where \(\mathbb {R}^d_+\) instead of \(\Omega \) is considered. Let \(\tilde{x}\in \partial \Omega \) be such that \(|x_0 -\tilde{x}|=\text {dist}(x_0,\partial \Omega )\). As in the proof of Lemma 5.2, we consider two cases.
Case 1 \(|x_0 -\tilde{x}|\ge \kappa r/16\). In this case, we have that
Since \(\kappa /16\ge 2\), (7.3) follows from Lemma 5.1, by using a rotation of coordinates and setting
where for \(i = 2, \ldots ,d\), \(U_i\) are given as in (7.16) below. See the proof for Case 2. As in the proof of Theorem 2.1, by using the definition of U, we see that (7.2) is satisfied.
Case 2 \(|x_0 -\tilde{x}|< \kappa r/16\). Without loss of generality, one may assume that \(\tilde{x}\) is the origin. Note that
Denote \(R=\kappa r/2 \, (\le R_1/2)\). Due to Assumption 2.4, we can take an orthogonal transformation to obtain that
and

where

Take a smooth function \(\chi \) on \(\mathbb {R}\) such that
Denote \(\mathcal {L}_0\) to be the elliptic operator with the coefficients \(\bar{A}^{\alpha \beta }\) from (7.5). Let \(\hat{u}=\chi u\), which vanishes on \(B_R\cap \{x_1\le \rho R\}\). From (7.1), it is easily seen that \((\hat{u},p)\) satisfies
where
For \(\tau \in [0,\infty )\), set
where \(0 \in \mathbb {R}^{d-1}\). Since \(\rho \in (0,1/16)\), we have that
By Lemma 3.3, there is a unique solution
satisfying \((p_1)_{\widetilde{B}^+_{3R/4}(\rho R,0)}=0\) and
Moreover, it holds that
where \(\Vert \cdot \Vert _{L_2}=\Vert \cdot \Vert _{L_2(\widetilde{B}^+_{3R/4}(\rho R,0))}\) and \(N = N(d,\delta )\). Using the fact that \(|A^{\alpha \beta }| \le \delta ^{-1}\), together with (7.4) and Hölder’s inequality, it follows that
Since \(\chi -1\) is supported on \(\{x_1\le 2\rho R\}\), Hölder’s inequality implies that
Using Hölder’s inequality again, together with the fact that \(\chi '\) is supported on \(\{\rho R \le x_1 \le 2\rho R\}\), we have that
where the last inequality follows from Hardy’s inequality, using the boundary condition \(u = 0\) on \(\partial \Omega \) and the observation that
for \((x_1,x') \in \Omega _R\), where \(\Omega _R\) is given by \(\{ x \in B_R: x_1 > \phi (x')\}\). The inequalities (7.9), (7.10), and (7.11), together with (7.8), imply that
We extend \(\hat{w}\) to be zero in \(\Omega _{3R/4}(\rho R,0)\cap \{x_1<\rho R\}\), so that \(\hat{w}\in W^{1}_2(\Omega _{3R/4}(\rho R,0))\), and we let
By the same reasoning as in (7.10) and (7.11), we have that
From this and (7.12), we deduce that
Note that, because \(\kappa \rho \le 1/4\), it holds that
Thus, from (7.13) we also obtain that
Next, we define \(v= u- w\) \((=\chi u-\hat{w})\) in \(\Omega _{3R/4}(\rho R,0)\) and \(p_2=p-p_1\) in \(\widetilde{B}^+_{3R/4}(\rho R,0)\). From (7.6) and (7.7), it is easily seen that \((v,p_2)\) satisfies
Denote
We have that \(\mathcal {D}_2\subset \mathcal {D}_3\) and \(|\mathcal {D}_1|\le N\kappa \rho |\Omega _{r}(x_0)|\), where the latter follows from the fact that \(\mathcal {D}_1 = \Omega _r(x_0) \cap \{ - \rho R \le x_1 \le \rho R\}\). We set
where the coefficients \(\bar{A}^{1\beta }(x_1)\) are taken from (7.5). Note that \(v=V_i=0\) in \(\mathcal {D}_1\). Then, by applying Lemma 4.4 with a dilation, we get that
Now, we set \(\mathcal {U}=(D_{x'}u,{\text {div}} u, U_2,\ldots ,U_d)\), where
Note that \(\mathcal {U}\) satisfies (7.2). From the triangle inequality, (7.15), and the fact that \(|\Omega _{2R}(x_0)| \le N \kappa ^d |\Omega _r(x_0)|\) by the condition that \(\kappa \rho \le 1/4\), we have that
where we bound the second and last terms on the right-hand side of the last inequality by using (7.13) and (7.14). This completes the proof of Lemma 7.1. \(\square \)
Before we present the proof of Theorem 2.6, we note that a Lipschitz domain \(\Omega \) in \(\mathbb {R}^d\) satisfying Assumption 2.3 with \({\text {diam}}\Omega \le K\) is a space of homogeneous type, which is endowed with the Euclidean distance and a doubling measure \(\mu \) that is naturally inherited from the Lebesgue measure. Owing to a result by Christ [10, Theorem 11] (also see [21]), there exists a filtration of partitions of \(\Omega \) in the following sense. For each \(n\in \mathbb {Z}\), there exists a collection of disjoint open subsets \(\mathbb {C}_n:=\{Q_\alpha ^n\,:\,\alpha \in I_n\}\) for some index set \(I_n\), satisfying the following properties:
-
(1)
For any \(n\in \mathbb {Z}\), \(\mu (\Omega {\setminus } \bigcup _{\alpha }Q_\alpha ^n)=0\);
-
(2)
For each n and \(\alpha \in I_n\), there exists a unique \(\beta \in I_{n-1}\) such that \(Q_\alpha ^n\subset Q_\beta ^{n-1}\);
-
(3)
For each n and \(\alpha \in I_n\), \(\text {diam}(Q_\alpha ^n)\le N_0\delta _0^n\);
-
(4)
Each \(Q_\alpha ^n\) contains some ball \(\Omega _{\varepsilon _0\delta _0^n}(z_\alpha ^n)\);
for some constants \(\delta _0\in (0,1)\), \(\varepsilon _0>0\), and \(N_0\) depending only on d, \(R_0\), and K.
For any \(f\in L_{1,\text {loc}}(\Omega )\), recall the definition of a maximal function in (6.1) with a bounded Lipschitz domain \(\Omega \) in place of \(\mathbb {R}^d\) or \(\mathbb {R}^d_+\):

Lemma 7.2
Let \(q \in (1,\infty )\) and \(\Omega \) satisfy Assumption 2.3 with \({\text {diam}}\Omega \le K\). Then, for any \(f\in L_q(\Omega )\), we have that
where \(N>0\) is a constant depending only on d, q, \(R_0\), and K.
Proof
Since \(\Omega \) is a space of homogeneous type, the lemma follows from the Hardy–Littlewood maximal function theorem for spaces of homogeneous type. See, for instance, [4]. Also see [12, Theorem 2.2]. \(\square \)
Lemma 7.3
Let \(q \in (1,\infty )\) and \(\Omega \) satisfy Assumption 2.3 with \({\text {diam}}\Omega \le K\). Suppose that
and that for each \(n \in \mathbb {Z}\) and \(Q \in \mathbb {C}_n\), there exists a measurable function \(F^Q\) on Q such that

for some constant \(N_0>0\). Then, we have that
where \(N>0\) is a constant depending only on d, q, \(R_0\), and K.
Proof
This lemma is a special case of Theorem 2.4 of [12], in which \(A_q\) weights are considered. When there is no weight as in the lemma, it is easily seen that \(\beta \) in that theorem is equal to 1. \(\square \)
We are now ready to present the proof of Theorem 2.6.
Proof of Theorem 2.6
We only derive the a priori estimate (2.5). The solvability then follows from (2.5), the Poincaré inequality, and the method of continuity. Furthermore, we assume that \(f \equiv 0\). Otherwise, for \(B_R \supseteq \Omega \), we find \(w \in W_{q_1}^2(B_R)\) such that \(\Delta w = f 1_{\Omega }\) in \(B_R\) and \(w|_{\partial B_R} = 0\). Then, we consider
where from the Sobolev embedding theorem and the well-known \(L_{q_1}\)-estimate for the Laplace equation we have that
We consider the two cases with \(q >2\) and \(q\in (1,2)\). The case with \(q=2\) follows from Lemma 3.3.
Case 1 \(q>2\). We take \(\mu \in (1,\infty )\), depending only on q, such that \(2\mu <q\), and we let \(\kappa \ge 32\) be a constant to be specified. By the properties (3) and (4) described above, for each Q in the partitions there exist \(r \in (0,\infty )\) and \(x_0 \in \bar{\Omega }\) such that
where N depends only on d, \(R_0\), and K. See Remark 7.3 in [12]. In order to apply Lemma 7.3, we take \(F=|Du|\), \(H=N|Du|\), where \(N = N(d,\delta ,q) \ge 1\) from (7.2), and
For \(F^Q\), we consider two cases. When \(\kappa r\le R_1\), we choose \(F^Q=\mathcal {U}\), where \(\mathcal {U}\) is from Lemma 7.1. Thanks to (7.2), (7.3), and (7.19), we have that (7.17) holds with \(N_0\) depending only on d, \(\delta \), \(R_0\), K, and q. Otherwise, i.e., if \(r>R_1/\kappa \) we take \(F^Q=|Du|\). Then, by (7.19) we have

where \(N = N(d, R_0, K)\). Since \(|\Omega _{R_1/\kappa }(x_0)|^{-1}\le NR_1^{-d}\kappa ^{d}\), we still get that (7.17) holds with \(N_0\) depending only on d, \(R_0\), and K. Therefore, the conditions in Lemma 7.3 are satisfied. From (7.18), we obtain that
where \(N = N(d,\delta ,R_0,K,q)\). By Lemma 7.2, the right-hand side above is bounded by
Upon taking sufficiently large \(\kappa \), then sufficiently small \(\gamma \) and \(\rho \), depending on d, \(\delta \), \(R_0\), K, and q (but independent of \(R_1\)), so that
we get that
Since \(\Omega \) is bounded, we have that \(f_\alpha ,g\in L_2(\Omega )\). Thus, by Lemma 3.3 (also see Remark 3.2) and Hölder’s inequality,
where \(N=N(d,\delta ,R_0, K, \rho ,q)\). Combining this with (7.20) yields that
where \(N = N(d,\delta ,R_0,R_1,K,q)\). Next, we estimate p. For any \(\eta \in L_{q'}(\Omega )\) with \(q'=q/(q-1)\), it follows from the solvability of the divergence equation in Lipschitz domains (cf. [5]) that there exists \(\psi \in \mathring{W}_{q'}^1(\Omega )^d\) such that
where \(N>0\) is a constant depending only on d, \(R_0\), K, and \(q'\). We test the first equation of (2.4) by \(\psi \), and using the fact that \((p)_\Omega = 0\) we obtain
which combined with (7.21) and (7.22) yields
Since \(\eta \in L_{q'}(\Omega )\) is arbitrary, we can infer that
which together with (7.21) implies that (2.5) holds.
Case 2 \(q\in (1,2)\). We employ a duality argument. Let \(q'=q/(q-1)\in (2,\infty )\) and \((\gamma , \rho ) = (\gamma , \rho )(d,\delta ,R_0,K,q')\) from Case 1. Then, for any \(\eta =(\eta _{\alpha })\), where \(\eta _\alpha \in L_{q'}(\Omega )^d\) for \(\alpha =1,\ldots ,d\), there exists a unique solution \((v,\pi ) \in W_{q'}^{1}(\Omega )^d \times L_{q'}(\Omega )\) with \((\pi )_\Omega = 0\) satisfying
where \(A^{\alpha \beta }_{{\text {tr}}}\) is the transpose of the matrix \(A^{\alpha \beta }\) for each \(\alpha ,\beta =1,\ldots ,d\). Moreover, we have that
where \(N = N(d,\delta ,R_0,R_1,K,q')\). Then, we test the equation of \((v,\pi )\) by u, to obtain
From this and (7.23), we get that
Since \(\eta \in \big (L_{q'}(\Omega )\big )^{d^2}\) is arbitrary, we obtain that (7.21) holds. The estimate of p is the same as in Case 1. Thus, the theorem is proved. \(\square \)
References
Abidi, H., Gui, G., Zhang, P.: On the decay and stability of global solutions to the 3D inhomogeneous Navier–Stokes equations. Commun. Pure Appl. Math. 64(6), 832–881 (2011)
Agmon, S., Douglis, A., Nirenberg, L.: Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions. II. Commun. Pure Appl. Math. 17, 35–92 (1964)
Amrouche, C., Girault, V.: On the existence and regularity of the solution of Stokes problem in arbitrary dimension. Proc. Jpn. Acad. Ser. A Math. Sci. 67(5), 171–175 (1991)
Aimar, Hugo, Macías, Roberto A.: Weighted norm inequalities for the Hardy-Littlewood maximal operator on spaces of homogeneous type. Proc. Am. Math. Soc. 91(2), 213–216 (1984)
Auscher, Pascal: Russ, Emmanuel, Tchamitchian, Philippe: Hardy Sobolev spaces on strongly Lipschitz domains of \(\mathbb{R}^n\). J. Funct. Anal. 218(1), 54–109 (2005)
Brown, R.M., Shen, Z.: Estimates for the Stokes operator in Lipschitz domains. Indiana Univ. Math. J. 44(4), 1183–1206 (1995)
Bulíček, M., Málek, J., Rajagopal, K.R.: Navier’s slip and evolutionary Navier–Stokes-like systems with pressure and shear-rate dependent viscosity. Indiana Univ. Math. J. 56(1), 51–85 (2007)
Cattabriga, L.: Su un problema al contorno relativo al sistema di equazioni di Stokes. Rend. Sem. Mat. Univ. Padova 31, 308–340 (1961)
Choi, Jongkeun: Lee, Ki-Ahm: The green function for the Stokes system with measurable coefficients. Commun. Pure Appl. Anal. 16(6), 1989–2022 (2017)
Christ, Michael: A \(T(b)\) theorem with remarks on analytic capacity and the Cauchy integral. Colloq. Math. 60/61(2), 601–628 (1990)
Dindoš, M., Mitrea, M.: The stationary Navier–Stokes system in nonsmooth manifolds: the Poisson problem in Lipschitz and \(C^1\) domains. Arch. Ration. Mech. Anal. 174(1), 1–47 (2004)
Dong, H., Kim, D.: On \(L_p\)-estimates for elliptic and parabolic equations with \(A_p\) weights. Trans. Am. Math. Soc. arXiv:1603.07844 (2016). (to appear)
Dong, H., Kim, D.: Higher order elliptic and parabolic systems with variably partially BMO coefficients in regular and irregular domains. J. Funct. Anal. 261(11), 3279–3327 (2011)
Dong, H., Kim, D.: Parabolic and elliptic systems in divergence form with variably partially BMO coefficients. SIAM J. Math. Anal. 43(3), 1075–1098 (2011)
Dong, H., Kim, D.: Weighted L\(_q\)-estimates for stationary Stokes system with partially BMO coefficients. J. Differ. Equ. 264(7), 4603–4649 (2018)
Fabes, E.B., Kenig, C.E., Verchota, G.C.: The Dirichlet problem for the Stokes system on Lipschitz domains. Duke Math. J. 57(3), 769–793 (1988)
Franta, M., Málek, J., Rajagopal, K.R.: On steady flows of fluids with pressure- and shear-dependent viscosities. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 461(2055), 651–670 (2005)
Galdi, G.P., Simader, C.G., Sohr, H.: On the Stokes problem in Lipschitz domains. Ann. Math. Pure Appl. 4(167), 147–163 (1994)
Geng, J., Kilty, J.: The \(L^p\) regularity problem for the Stokes system on Lipschitz domains. J. Differ. Equ. 259(4), 1275–1296 (2015)
Giaquinta, M., Modica, G.: Nonlinear systems of the type of the stationary Navier–Stokes system. J. Reine Angew. Math. 330, 173–214 (1982)
Hytönen, T., Kairema, A.: Systems of dyadic cubes in a doubling metric space. Colloq. Math. 126(1), 1–33 (2012)
Kang, Kyungkeun: On regularity of stationary Stokes and Navier–Stokes equations near boundary. J. Math. Fluid Mech. 6(1), 78–101 (2004)
Kim, Doyoon: Krylov, N.V.: Elliptic differential equations with coefficients measurable with respect to one variable and VMO with respect to the others. SIAM J. Math. Anal. 39(2), 489–506 (2007)
Krylov, N.V.: Parabolic and elliptic equations with VMO coefficients. Commun. Partial Differ. Equ. 32(1–3), 453–475 (2007)
Krylov, N.V.: Second-order elliptic equations with variably partially VMO coefficients. J. Funct. Anal. 257(6), 1695–1712 (2009)
Krylov, N.V.: Lectures on Elliptic and Parabolic Equations in Sobolev Spaces, Volume 96 of Graduate Studies in Mathematics. American Mathematical Society, Providence (2008)
Ladyženskaya, O.A.: Investigation of the Navier–Stokes equation for stationary motion of an incompressible fluid. Uspehi Mat. Nauk 14(3), 75–97 (1959)
Lions, P.-L.: Mathematical Topics in Fluid Mechanics. Vol. 1. Incompressible Models. Oxford Lecture Series in Mathematics and Its Applications, 3, vol. 1, p. xiv+237. Oxford Science Publications, New York (1996)
Ladyženskaya, O.A., Solonnikov, V.A.: The unique solvability of an initial-boundary value problem for viscous incompressible inhomogeneous fluids. Boundary value problems of mathematical physics, and related questions of the theory of functions, 8. Zap. Naučn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 52, 52–109, 218–219 (1975)
Mitrea, M., Taylor, M.: Navier–Stokes equations on Lipschitz domains in Riemannian manifolds. Math. Ann. 321(4), 955–987 (2001)
Mitrea, M., Wright, M.: Boundary value problems for the Stokes system in arbitrary Lipschitz domains. Astérisque No. 344, viii+241 pp (2012)
Shen, Z.: A note on the Dirichlet problem for the Stokes system in Lipschitz domains. Proc. Am. Math. Soc. 123(3), 801–811 (1995)
Sobolevskiĭ, P.E.: On the smoothness of generalized solutions of the Navier–Stokes equations. Dokl. Akad. Nauk SSSR 131, 758–760 (1960). (Russian; translated as Soviet Math. Dokl., 1:341–343)
Vorovič, I.I., Judovič, V.I.: Steady flow of a viscous incompressible fluid. Mat. Sb. (N.S.) 53(95), 393–428 (1961). (Russian)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Neil Trudinger.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
H. Dong was partially supported by the NSF under agreements DMS-1056737 and DMS-1600593.
D. Kim was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2016R1D1A1B03934369).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dong, H., Kim, D. \(L_q\)-estimates for stationary Stokes system with coefficients measurable in one direction. Bull. Math. Sci. (2018). https://doi.org/10.1007/s13373-018-0120-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13373-018-0120-6