1 Introduction

Peristalsis, a series of muscular contractions that resemble waves, helps food move through the digestive system. It happens in the stomach after beginning in the oesophagus, where strong waves of smooth muscle transport eaten food pellets. As part of the digestive process, food is subjected to churning movements in the stomach and then transferred to the small intestine. This movement results in the formation of chyme, a liquid mixture. The presence of chyme in the small intestine reactivates peristalsis, the rhythmic contraction and relaxation of intestinal muscles. Extending a portion of the intestine makes it possible to observe its undulating movements more clearly. These movements aid in the passage of nutrients through the walls of the small intestine, allowing them to access the circulatory system. Peristalsis in the large intestine facilitates water absorption from partially digested food into circulation and optimises the overall process. The remaining waste items are subsequently expelled using the rectum and anus. Peristaltic motion is thought to be the primary mechanism for spermatozoa movement in the cervical canal, bile transport in the bile duct, and urine transport in the ureter. Due to their wide range of uses, fluids with non-Newtonian properties are preferable to those with Newtonian properties. Engineering, science, and business are a few examples. Several models in the scientific and general literature can be used to understand these fluids’ range of flow behaviour. This idea is used in various engineering devices, including dialysis machines, roller pumps, and heart–lung machines. Given the importance of peristalsis, numerous researchers [1,2,3,4,5] have studied it in mechanical and physiological situations with different geometries.

When the strain rate and the distracting speed component are equal at the limit, a phenomenon known as the wall slide occurs. This phenomenon takes on more importance in situations of fractional slip when working with circular systems made up of foams, emulsions, suspensions, and polymer arrangements. The wall-sliding effect during peristaltic flow can be used for various purposes, including cleaning prosthetic heart valves, inner depressions, and other biological applications. Shehzad et al. [6] investigated the peristaltic mechanism in a curved channel with a radial magnetic field and Carreau-Yasuda (CY) fluid while the slip condition was considered at the channel. The peristalsis of a Bingham fluid was studied by Lakshminarayana et al. [7] in an inclined tapered porous conduit with elastic walls. Joule heating and slip were both examined in their studies. The peristalsis of a tangent hyperbolic liquid in a curved conduit was investigated by Farooq et al. [8]. Conditions relating to temperature, concentration, and velocity slip were studied. Low Reynolds number and long wavelength approximation were employed to analyse the effect of slip parameters on temperature, velocity, and concentration. Imran et al. [9] investigated peristalsis in a flexible conduit by considering the impact of hall current and ion slip. The mathematical model developed was predicated on the assumptions of a low Reynolds number and a long wavelength. In addition, magnetohydrodynamics (MHD) Casson fluid slip flow in an inclined channel with changing fluid characteristics was investigated by Prasad et al. [10].

Understanding fluid dynamics, especially as it pertains to describing natural fluids, necessitates the study of heat transport characteristics. To keep homeostasis, the human body uses four ways to transfer heat: conduction, radiation, convection, and evaporation. In these operations, heat is dissipated from a warmer environment to a cooler one. Therefore, internal and external factors like temperature affect the heat transfer rate between the components. The effect of flexible wall elasticity on the peristaltic motion of an incompressible viscous fluid was investigated in a study by Radhakrishnamacharya and Srinivasulu [11]. Incorporating heat transfer phenomena in a two-dimensional uniform duct broadened the scope of this investigation. A two-dimensional asymmetric channel was used to study the consequences of heat transmission. The movement of a viscous, incompressible fluid, set in motion by the propagation of sinusoidal waves, is responsible for the apparent asymmetry. Changing the amplitudes and phases of the peristaltic wave patterns on the walls produced asymmetry in the channel. Srinivas and Kothandapani [12]  adopted a wave frame reference that propagated at the same rate as the wave in their study. The momentum and energy equations were linearised using the long wavelength approximation and a small Reynolds number. Thermodynamic irreversibilities due to heat transfer were studied by Khan et al. [13] in the context of magneto-Carreau nano-liquid peristalsis. Extensive wavelengths and low Reynolds numbers were the primary focus of the studies. Both varying viscosity and thermal conductivity were accounted for in the research. Heat and mass transfer characteristics in MHD peristaltic flow within a narrow, permeable channel were studied by Vaidya et al. [14] by considering the impact of varying thermal conductivities in their analysis. Porous boundaries, wall characteristics, long wavelengths, and low Reynolds values were meticulously examined. Rajashekhar et al. [15] studied the intricate dynamics of peristaltic motion in a Ree-Eyring liquid using a model that considers a uniformly compliant conduit. The effects of different thermal conductivities and viscosities were investigated.

The study of magnetohydrodynamics (MHD) in fluid flows offers valuable insights into the complex interaction between electromagnetic fields and fluid movement. Integrating these ideas has shown value in many areas, laying the groundwork for many practical applications. Magnetic fields can direct tailored drug delivery systems in biomedical applications. This approach ensures exact medication administration, decreasing side effects and maximising therapy. MHD also improves industrial fluid transportation efficiency. Magnetic fields can manipulate fluid flows in numerous sectors to optimise manufacturing processes, reduce energy consumption, and improve operational efficiency. Due to its relevance to the flow of conductive physiological fluids like blood, the study of MHD flow in a channel with elastic, rhythmically contracting walls is essential. In addition, theoretical studies on peristaltic MHD compressor operation are required. As a bonus, patients with arterial problems like arterial stenosis or arteriosclerosis can benefit from the magnetic field's influence by using it as a blood pump during cardiac treatments. Hayat et al. [16] created a mathematical model for the peristaltic motion of a Johnson–Segalman fluid with MHD in a planar flow structure using nonlinear partial differential equations. The Lie-group method was used to find a complete solution for the basic nonlinear partial differential equation. Assuming long-wavelength and low-Reynolds number conditions, Srinivas et al. [17] explored the peristaltic transport of the magnetohydrodynamic heat transfer in a channel with slip conditions and elastic wall properties. The impacts of temperature-dependent variable features on the peristaltic mechanism of a third-order fluid are studied by Lathif et al. [18] in a symmetric channel. Viscous dissipation and MHD fluids were considered as well. Tanveer and Malik [19] sought to provide a comprehensive analysis linking the novel concept of a porous medium with modified Darcy's law. Nanofluid mobility is studied using the Ree-Eyring fluid model. The study also included the factors such as changing viscosity, MHD, viscous diffusion, and thermo-diffusion (Soret) effects affecting flow kinetics. Khan and Rasfat [20] studied the effects of MHD on compressible Jeffrey fluid and the impact of thermal radiation on heat transmission.

In recent studies, researchers focused on the impact of varying fluid properties, including viscosity and thermal conductivity. Fluid dynamics analysis and comprehension get more complicated when changeable fluid parameters are considered. The presence of changing qualities like viscosity, density, and thermal conductivity makes fluid flow phenomena dynamic. The observed variation is due to changes in temperature, pressure, and fluid system composition. Variable fluid characteristics are essential in conditions with a wide range of temperatures, high pressures, and complex flow geometries. Jet engine combustion processes vary in temperature and pressure in aerospace engineering. These differences change fluid characteristics, which affect the engine performance. In biological systems, temperature and cellular composition affect viscosity, density, and blood flow. Complex mathematical models and computer methods are needed to analyse fluid systems with changeable properties. Analytical and numerical simulations are essential for capturing the intricate interaction between fluid dynamics and property fluctuations. Accurate predictions are crucial in engineering, industrial, and scientific research. Understanding the effects of changeable fluid characteristics helps to optimise systems, enhance energy efficiency, and provide robust solutions for practical applications. The complex yet essential aspect of fluid dynamics drives engineering and science. Rajashekhar et al. [21] studied the peristaltic transport of Casson liquid in an inclined porous tube heated by convection. The effects of varying viscosity and thermal conductivity on flow were investigated by considering that viscosity varies in the radial plane and thermal conductivity is temperature dependent. The effects of a compliant wall and diverse liquid characteristics on the peristaltic flow of a Rabinowitsch liquid in an inclined channel were explored by Vaidya et al. [22]. The study also found a link between the channel's width and the liquid's thickness. Manjunatha et al. [23] studied the peristaltic behaviour of a Bingham liquid in a porous tube with changing liquid properties that was convectively heated. Recently Balachandra et al. [24] examined the effects of slip on a Ree-Eyring liquid peristaltic flow in an inclined channel, highlighting the role of variable viscosity and velocity slip parameters in generating velocity profiles. Rajashekhar et al. [25] investigated the role of heat transmission and electroosmosis on MHD peristaltic pumping in a microchannel with multiple slip effects and diverse fluid properties.

When conducting a comparative study between the Eyring–Powell model and other non-Newtonian fluid models, several advantages of the former become apparent. The derivation of this concept is based on liquid kinetic theory rather than empirical relationships. Another benefit is its ability to accurately demonstrate Newtonian behaviour across a wide range of shear rates, including low and high values. In their study, Hayat et al. [26] examined the influence of convective conditions and chemical activities on the peristaltic flow of Eyring–Powell fluid. Hina [27] extensively studied slip and MHD on Eyring–Powell fluid peristaltic transport. A study examined the conduit's dynamic character in a channel with a compliant wall structure. By incorporating heat and mass transfer processes, the study improved its understanding of the system's behaviour under different circumstances. Tanveer et al. [28] investigated the peristaltic mechanics of Eyring–Powell nanofluid compliance with the curved tube walls, enhancing the system's diverse properties. A comprehensive approach was used to analyse this data, applying mass, momentum, energy, and concentration conservation principles. This multifunctional method analysed the intricate interaction of elements affecting fluid dynamics in a dynamic environment. Yasin et al. [29] significantly contributed to the field with their collective perspective inquiry. The study examined the impact of slip and Hall current on peristaltic transport, specifically in MHD Eyring–Powell fluid. The effect of variable fluid properties on Eyring Powell Fluid Peristaltic Transport was investigated by Balachandra et al. [30], with a specific focus on the inclined uniform channel.

The current study, in detail, examines the mechanism of peristalsis, a crucial biological and industrial activity. Understanding this phenomenon is crucial since it affects many physiological and technical systems. The theoretical study focuses on fluid dynamics, heat transport, and mass transmission to explain the peristaltic flow. The analysis relies on the fundamental concepts to understand the complicated behaviour of peristalsis. Additionally, peristaltic flow parameters such as fluid properties, conduit configuration, external forces, and wall compliance are investigated. This study aims to comprehensively understand the intricate relationship among these various components and their combined impact on peristaltic motion through analysis. The research builds a solid foundation by incorporating earlier knowledge and investigations. The current investigation studies the effect of magnetic field in peristaltic flow. Eyring Powell fluid rheology, which characterises shear-thinning non-Newtonian fluids, is also essential; hence, it is considered in the current study. Understanding their peristalsis behaviour is crucial since biological and industrial applications use such fluids. The study also considers fluid parameters like varying viscosity, density, and thermal conductivity. These features must be examined under diverse situations to understand the peristaltic flow. This study is significant for young researchers, engineers, and practitioners exploring and applying peristaltic transport in many applications. It uncovers peristaltic flow mechanics and determinants, enabling biological and industrial advances. The present mathematical model improves transport systems in numerous domains by improving our understanding of peristalsis, benefiting science and practice.

2 Mathematical Formulations

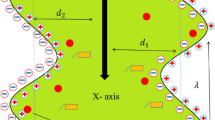
Consider the peristaltic flow of a viscous, incompressible Eyring–Powell fluid moving through an axis-symmetric, uniform channel. The movement of the fluid along the walls of the channel is caused by sinusoidal wave trains with wavelengths \(\lambda\) and wave speed \(c\).

The expression given below defines the channel's geometry.

$$H^{\prime} = a^{\prime} + b^{\prime} \sin \left[ {\frac{2\pi }{\lambda }\left( {x^{\prime} - ct^{\prime}} \right)} \right]$$
(1)

where \(H^{\prime}\) is the uniform wave in which \(a^{\prime}\), \(b^{\prime}\) and \(t^{\prime}\) represent the radius, wave amplitude, and time, respectively (Fig. 1).

Fig. 1
figure 1

Geometry of the inclined uniform channel

Full size image

The incompressibility conditions for the equation of continuity, equation of momentum and equation for energy are written as

Continuity Equation:

$$\frac{{ \partial u^{\prime}}}{{\partial x^{\prime}}} + \frac{{\partial w^{\prime}}}{{\partial y^{\prime}}} = 0$$
(2)

Momentum Equation:

$$\rho \left[ {\frac{{\partial u^{\prime}}}{\partial t^{\prime}} + u^{\prime} \frac{{\partial u^{\prime}}}{\partial x^{\prime}} + w^{\prime}\frac{\partial u^{\prime}}{{\partial y^{\prime}}}} \right] = - \frac{{\partial p^{\prime}}}{{\partial x^{\prime}}} + \frac{{\partial \tau^{\prime}_{{x^{\prime}x^{\prime}}} }}{{\partial x^{\prime}}} + \frac{{\partial \tau^{\prime}_{{x^{\prime}y^{\prime}}} }}{{\partial y^{\prime}}} + \rho g\sin \phi - \sigma_{0} B_{0}^{2} u$$
(3)
$$\rho \left[ {\frac{{\partial w^{\prime}}}{{\partial t^{\prime}}} + u^{\prime}\frac{{\partial w^{\prime}}}{{\partial x^{\prime}}} + w^{\prime}\frac{{\partial w^{\prime}}}{{\partial y^{\prime}}}} \right] = - \frac{{\partial p^{\prime}}}{{\partial y^{\prime}}} + \frac{{\partial \tau^{\prime}_{{x^{\prime}y^{\prime}}} }}{{\partial x^{\prime}}} + \frac{{\partial \tau^{\prime}_{{y^{\prime}y^{\prime}}} }}{{\partial y^{\prime}}}$$
(4)

Energy Equation:

$$\rho C_{P} \left[ {\frac{{\partial T^{\prime}}}{{\partial t^{\prime}}} + u^{\prime}\frac{{\partial T^{\prime}}}{{\partial x^{\prime}}} + w^{\prime}\frac{{\partial T^{\prime}}}{{\partial y^{\prime}}}} \right] = \frac{\partial }{{\partial x^{\prime}}}\left( {k\left( {T^{\prime}} \right)\frac{{\partial T^{\prime}}}{{\partial x^{\prime}}}} \right) + \frac{\partial }{{\partial y^{\prime}}}\left( {k\left( {T^{\prime}} \right)\frac{{\partial T^{\prime}}}{{\partial y^{\prime}}}} \right) + \tau^{\prime}_{{x^{\prime}x^{\prime}}} \frac{{\partial u^{\prime}}}{{\partial x^{\prime}}} + \tau^{\prime}_{{y^{\prime}y^{\prime}}} \frac{{\partial w^{\prime}}}{{\partial y^{\prime}}} + \tau^{\prime}_{{x^{\prime}y^{\prime}}} \left( {\frac{{\partial u^{\prime}}}{{\partial y^{\prime}}} + \frac{{\partial w^{\prime}}}{{\partial x^{\prime}}}} \right)$$
(5)

Concentration Equation:

$$\left[ {\frac{{\partial C^{\prime}}}{{\partial t^{\prime}}} + u^{\prime}\frac{{\partial C^{\prime}}}{{\partial x^{\prime}}} + w^{\prime}\frac{{\partial C^{\prime}}}{{\partial y^{\prime}}}} \right] = D\left[ {\frac{{\partial^{2} C^{\prime}}}{{\partial x^{{\prime}{2}} }} + \frac{{\partial^{2} C^{\prime}}}{{\partial y^{{\prime}{2}} }}} \right] + \frac{{DK_{{\text{T}}} }}{{T_{{\text{m}}} }} \left[ {\frac{{\partial^{2} T^{\prime}}}{{\partial x^{{\prime}{2}} }} + \frac{{\partial^{2} T^{\prime}}}{{\partial y^{{\prime}{2}} }}} \right].$$
(6)

where velocity components in the radial and axial directions are denoted as \(u^{\prime}\), and \(w^{\prime}\) respectively. The fluid density is denoted by \(\rho\), the pressure is denoted by \(p^{\prime}\) and the extra stress components are represented by \(\tau^{\prime}_{{x^{\prime}x^{\prime}}} ,\) \(\tau^{\prime}_{{x^{\prime}y^{\prime}}} ,\) and \(\tau^{\prime}_{{y^{\prime}y^{\prime}}}\). Additionally, \(T^{\prime}\) and \(C_{P}\) represent the temperature, and specific heat at constant volume, respectively. \(k\left( {T^{\prime}} \right)\) denotes the variable thermal conductivity, \(D\)—the coefficient of mass diffusivity, \(T_{{\text{m}}}\)—the mean temperature, \(K_{{\text{T}}}\)-the thermal diffusion ratio.

The elastic wall motion equation is given by

$$L\left( P \right) = P - P_{0} ,$$
(7)

where \(P_{0} \left( { = 0} \right)\) denotes the pressure exerted on the exterior wall due to muscle tension.

Here, the linear operator \(L\) influences membrane stretching accompanied by the centre of viscous damping and is denoted as

$$L = - \tau \frac{{\partial^{2} }}{{\partial x^{2} }} + m_{1} \frac{{\partial^{2} }}{{\partial t^{2} }} + n_{1} \frac{\partial }{\partial t} + n_{2} \frac{{\partial^{4} }}{{\partial x^{4} }} + H,$$
(8)

where \(n_{1}\) is the viscous damping coefficient, \(n_{2}\) is the rigidity of the plate, \(m_{1}\) denotes the mass per unit area, \(H\) denotes the spring stiffness and \(\tau\) denotes the elastic tension.

$$\frac{\partial p}{{\partial x}} = E_{1} \frac{{\partial^{3} h}}{{\partial x^{3} }} + E_{2} \frac{{\partial^{3} h}}{{\partial t^{2} \partial x}} + E_{3} \frac{{\partial^{3} h}}{{\partial t\partial x^{2} }} + E_{4} \frac{{\partial^{5} h}}{{\partial x^{5} }} + E_{5} \frac{\partial h}{{\partial x}} ,$$
(9)

The non-dimensional quantities considered are given below

$$ \begin{aligned} & x = \frac{{x^{\prime}}}{\lambda } , y = \frac{{y^{\prime}}}{{a^{\prime}}} , u = \frac{{u^{\prime}}}{c}, w = \frac{{\lambda w^{\prime}}}{{ca^{\prime}}} ,\\ &\tau_{xx } = \frac{{a^{\prime}\tau^{\prime}_{{x^{\prime}x^{\prime}}} }}{c \mu } , \tau_{xy } = \frac{{ a^{\prime}\tau{\prime}_{{x^{\prime}y^{\prime}}} }}{c \mu } , \tau_{yy} = \frac{{a^{\prime}\tau_{{y^{\prime}y^{\prime} }}{\prime} }}{c \mu } , \\ & {\text{Re}} = \frac{{a^{\prime} c \rho }}{\mu } , \vartheta = \frac{{\mu_{0} }}{\rho } , p = \frac{{a^{{\prime}{2}} p^{\prime}}}{c \lambda \mu } ,\\ & \theta = \frac{{T^{\prime} - T^{\prime}_{0} }}{{T_{1} - T_{0} }} , \Pr = \frac{{\mu C_{P} }}{{k_{1} }} {\text{Ec}} = \frac{{c^{2} }}{{\delta T_{0} }}, {\text{Br}} = {\text{Ec}} \Pr , \\ & \sigma = \frac{{C^{\prime} - C^{\prime}_{0} }}{{C^{\prime}_{0} }}, \psi = \frac{{\psi^{\prime}}}{{a^{\prime}c}} , \mu_{0}{\prime} = \frac{{\mu_{0} }}{\mu }, \\ & Sr = \frac{{\rho DK_{T} \left( {T^{\prime} - T^{\prime}_{0} } \right)}}{{T_{m} C^{\prime}_{0} }}, {\text{Sc}} = \frac{\mu }{\rho D} ,\\ & F = \frac{\mu c}{{\rho ga^{\prime}}} , M = \sqrt {\frac{\sigma }{\mu }} B_{0} , \\ & \delta = \frac{{a^{\prime}}}{\lambda }, \epsilon = \frac{{b^{\prime}}}{{a^{\prime}}} , t = \frac{{c t^{\prime}}}{\lambda } , E_{1} = \frac{{ - \sigma a^{{\prime}{3}} }}{{\lambda^{3} \mu c}},\\ & E_{2} = \frac{{m a^{{\prime}{3}} c}}{{\lambda^{3} \mu }}, E_{3} = \frac{{ a^{{\prime}{3}} c}}{{\lambda^{3} \mu }}, E_{4} = \frac{{m_{3} a^{{^{{\prime}{3}} }} }}{{\lambda^{5} \mu_{0} c}},E_{5} = \frac{{Ha^{{\prime}{3}} }}{{\lambda \mu_{0} c}} , \\ & h = \frac{{H^{\prime}}}{{a^{\prime}}} = 1 + \epsilon \sin \left( {2\pi \left( {x - t} \right)} \right) \\ \end{aligned} $$
(10)

On utilizing the non-dimensional transformations from Eq. (10), the governing equations can be expressed as,

Continuity Equation:

$$\delta \frac{ \partial u}{{\partial x}} + \frac{\partial w}{{\partial y}} = 0$$
(11)

Momentum Equation:

$${\text{Re}} \left[ {\delta u \frac{ \partial u}{{\partial x}} + w\frac{\partial u}{{\partial y}}} \right] = - \frac{\partial p}{{\partial x}} + \delta \frac{{\partial \tau_{xx} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y} + \frac{\sin \phi }{F} - M^{2} \left( {u + 1} \right)$$
(12)
$${\text{Re}} \delta \left[ {\delta u\frac{ \partial w}{{\partial x}} + w\frac{ \partial w}{{\partial y}}} \right] = - \frac{\partial p}{{\partial y}} + \delta^{2} \frac{{\partial \tau_{xy} }}{\partial x} + \delta \frac{{\partial \tau_{yy} }}{\partial y}$$
(13)

Energy Equation:

$$ \begin{aligned} &{\text{Re}} \delta \left[ {\delta u\frac{\partial \theta }{{\partial x}} + w\frac{\partial \theta }{{\partial y}}} \right] \\ & \quad = Ec\left[ {\left( {\delta \tau_{xx} \frac{\partial u}{{\partial x}} + \tau_{yy} \frac{\partial w}{{\partial y}} } \right) + \tau_{xy} \left( {\delta \frac{\partial w}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right)} \right] \\ & \qquad + \frac{1}{\Pr } \left[ {\delta^{2} \frac{\partial }{\partial x}\left( {k\left( \theta \right)\frac{\partial \theta }{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {k\left( \theta \right)\frac{\partial \theta }{{\partial y}}} \right)} \right] \\ \end{aligned} $$
(14)

Concentration Equation:

$${\text{Re}} \left[ {\delta u\frac{\partial \sigma }{{\partial x}} + w\frac{\partial \sigma }{{\partial y}}} \right] = \frac{1}{{{\text{Sc}}}}\left[ {\delta^{2} \frac{{\partial^{2} \sigma }}{{\partial x^{2} }} + \frac{{\partial^{2} \sigma }}{{\partial y^{2} }}} \right] + {\text{Sr}} \left[ {\delta^{2} \frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right]$$
(15)

By implementing long wavelength and small Reynolds number assumptions, Eqs. (11)–(15) takes the form,

Velocity Equation:

$$\frac{{\partial \tau_{xy} }}{\partial y} = \left( {\frac{\partial p}{{\partial x}}} \right) - \frac{\sin \phi }{F} + M^{2} \left( {\frac{\partial \psi }{{\partial y}} + 1} \right)$$
(16)
$$\frac{\partial p}{{\partial y}} = 0$$
(17)

Temperature Equation:

$$\frac{\partial }{\partial y}\left\{ {k\left( \theta \right)\frac{\partial \theta }{{\partial y}}} \right\} + {\text{Br}} \tau_{xy} \frac{{\partial^{2} \psi }}{{\partial y^{2} }} = 0$$
(18)

Concentration Equation:

$$\frac{{\partial^{2} \sigma }}{{\partial y^{2} }} + {\text{Sc}}\,{\text{Sr}}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} = 0$$
(19)

The constitutive equation for the Eyring Powell fluid, represented as \(\tau_{xy }\), is given by the following expression:

$$\tau_{xy} = \left\{ {\mu \left( y \right) + B} \right\} \frac{{\partial^{2} \psi }}{{\partial y^{2} }} - \frac{A}{3}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{3}$$
(20)

The dimensionless slip boundary conditions are given by

$$\frac{{\partial^{2} \psi }}{{ \partial y^{2} }} = 0, \frac{\partial \theta }{{\partial y}} = 0 , \frac{\partial \sigma }{{\partial y}} = 0\quad {\text{at}}\quad y = 0$$
(21)
$$\frac{\partial \psi }{{ \partial y}} + \eta_{1} \tau_{xy} = - 1, \theta + \eta_{2} \frac{\partial \theta }{{\partial y}} = 1, \sigma + \eta_{3} \frac{\partial \sigma }{{\partial y}} = 1 \quad {\text{at}}\quad y = h$$
(22)

The following expressions describe the variations in viscosity, represented by \(\mu \left( y \right)\), and thermal conductivity, represented by \(k\left( \theta \right)\), across the breadth of the channel:

$$\mu \left( y \right) = 1 - \alpha_{1} y\quad \alpha_{1} < < 1$$
(23a)
$$k\left( \theta \right) = 1 + \alpha_{2} \theta \quad \alpha_{2} < < 1$$
(23b)

where \(\alpha_{1}\) and \(\alpha_{2}\) represent the coefficients that governs the variable viscosity and thermal conductivity.

3 Solution Methodology

Consider Eq. (16). By taking \(P = \frac{\partial p}{{\partial x}}\) and \(f = \frac{\sin \phi }{F}\), and integrate. Compare the obtained solution with Eq. (20).

Then,

$$\left( {P - f + M^{2} } \right) y + M^{2} \psi = \left( {1 - \alpha_{1} y + B} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} - \frac{A}{3}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{3}$$
(24)
$$\frac{\partial }{\partial y}\left\{ {k\left( \theta \right)\frac{\partial \theta }{{\partial y}}} \right\} + {\text{Br }}\left\{ {\left( {1 - \alpha_{1} y + B} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} - \frac{A}{3}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{3} } \right\}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) = 0$$
(25)

Due to the inherent nonlinearity of Eqs. (24) and (25), it is impossible to derive an exact analytical solution. As a result, a different methodology is adopted that employs the perturbation method's capabilities to elucidate the solutions. This approach is frequently observed when complex nonlinear equations are prevalent. It enables us to estimate the solutions methodically and gain a deep understanding of the fundamental dynamics. The perturbation method initiates a systematic expansion procedure in which the solutions are represented as a series of terms. This method simplifies complex nonlinear equations into a more manageable format that accurately depicts the behaviour under study.

3.1 Perturbation Technique

The series perturbation method is used to solve the stream function and temperature expression using the following equations.

$$\psi = {\Sigma }A^{n} \psi_{n}$$
(26a)
$$\theta = {\Sigma }A^{n} \theta_{n}$$
(26b)

3.1.1 Stream Function

On ignoring \(O\left( {A^{2} } \right)\) terms in Eq. (26a), expression for streamline is obtained as

$$\psi = \psi_{0} + A \psi_{1}$$
(27)
3.1.1.1 Zeroth-Order Streamline System
$$ \begin{aligned} & \left( {P - f + M^{2} } \right) y + M^{2} \psi_{0} = \left( {1 - \alpha_{1} y + B} \right) \frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }} \\ & \frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }} = 0 \quad {\text{at}}\quad y = 0 \;{\text{and}}\;\frac{{\partial \psi_{0} }}{\partial y} + \eta_{1} \left( {1 - \alpha_{1} y + B} \right)\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }} \\ & \quad = - 1\quad {\text{at}}\quad y = h \end{aligned}$$
(28)

Due to the inherent nonlinearity of the equations above, the solutions are derived using the double perturbation technique.

$$\psi_{i} = \Sigma \alpha_{1}^{j} \psi_{ij} , \;{\text{where}}\quad i = \left\{ {0, 1} \right\} , 0 \le j \le n$$
(29)

To obtain the solution for zeroth-order stream function, higher-order terms, say \(O\left( {\alpha_{1}^{2} } \right)\) are ignored for \(i = 0\), then the equation obtained are as follows:

$$\psi_{0} = \psi_{00} + \alpha_{1} \psi_{01}$$
(30)

Zeroth-Order System

$$\begin{aligned} & \frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }} - \frac{{M^{2} }}{{\left( {1 + B} \right)}}\psi_{00} = \frac{{\left( {P - f + M^{2} } \right) }}{{\left( {1 + B} \right)}}y \\ & \frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }} = 0\quad {\text{at}}\quad y = 0 \;\quad{\text{and}}\; \\ & \frac{{\partial \psi_{00} }}{\partial y} + \eta_{1} \left( {1 + B} \right)\frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }} = - 1\quad {\text{at}}\quad y = h \end{aligned}$$
(31)

First-Order System

$$\begin{aligned} & \frac{{\partial^{2} \psi_{01} }}{{\partial y^{2} }} - \frac{{M^{2} }}{{\left( {1 + B} \right)}}\psi_{01} = y \frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }} \\ & \frac{{\partial^{2} \psi_{01} }}{{\partial y^{2} }} = 0\quad {\text{at}}\quad y = 0\;{\text{ and}}\;\\ & \frac{{\partial \psi_{01} }}{\partial y} + \eta_{1} \left( {1 + B} \right)\frac{{\partial^{2} \psi_{01} }}{{\partial y^{2} }} + \eta_{1} y \frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }} = 0 \quad {\text{at}} \quad y = h \end{aligned}$$
(32)
3.1.1.2 First-Order Streamline System
$$\begin{aligned} & \left\{ {1 - \alpha_{1} y + B} \right\} \frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }}- M^{2} \psi_{1} - \frac{1}{3}\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)^{3} = 0 \\ & \frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }} = 0\quad {\text{at}}\quad y = 0 \;\qquad{\text{and}}\; \\ & \frac{{\partial \psi_{1} }}{\partial y} + \eta_{1} \left\{ {\left( {1 - \alpha_{1} y + B} \right) \frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }} - \frac{1}{3}\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)^{3} } \right\} = 0\quad {\text{at}}\quad y = h \end{aligned}$$
(33)

To obtain the solution for first-order stream function, higher-order terms are ignored, i.e., \(O\left( {\alpha_{1}^{2} } \right)\), for \(i = 1\), then the equation obtained are as follows:

$$\psi_{1} = \psi_{10} + \alpha_{1} \psi_{11}$$
(34)

Zeroth-Order System

$$\begin{aligned} & \frac{{\partial^{2} \psi_{10} }}{{\partial y^{2} }} - \frac{{M^{2} }}{{\left( {1 + B} \right)}}\psi_{10} = \frac{1}{{3\left( {1 + B} \right)}}\left( {\frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }}} \right)^{3} \\ & \frac{{\partial^{2} \psi_{10} }}{{\partial y^{2} }} = 0\quad {\text{at}}\quad y = 0 \;\quad{\text{and }}\; \\ & \frac{{\partial \psi_{10} }}{\partial y} + \eta_{1} \left\{ {\left( {1 + B} \right) \frac{{\partial^{2} \psi_{10} }}{{\partial y^{2} }} - \frac{1}{3}\left( {\frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }}} \right)^{3} } \right\} = 0\quad {\text{at}}\quad y = h \end{aligned}$$
(35)

First-Order System

$$ \begin{aligned} & \frac{{\partial^{2} \psi_{11} }}{{\partial y^{2} }} - \frac{{M^{2} }}{{\left( {1 + B} \right)}}\psi_{11} \\ & \quad = \frac{1}{{\left( {1 + B} \right)}}\left[ {y \frac{{\partial^{2} \psi_{10} }}{{\partial y^{2} }} + \left( {\frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }}} \right)^{2} \left( { \frac{{\partial^{2} \psi_{10} }}{{\partial y^{2} }}} \right)} \right] \\ & \frac{{\partial^{2} \psi_{11} }}{{\partial y^{2} }} = 0\quad {\text{at}}\quad y = 0\;{\text{and}}\; \frac{{\partial \psi_{11} }}{\partial y} \\ & \qquad + \eta_{1} \left\{ {\left( {1 + B} \right) \frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }} - y \frac{{\partial^{2} \psi_{10} }}{{\partial y^{2} }} - \left( {\frac{{\partial^{2} \psi_{00} }}{{\partial y^{2} }}} \right)^{2} \left( { \frac{{\partial^{2} \psi_{10} }}{{\partial y^{2} }}} \right)} \right\} \\ & \quad = 0\quad {\text{at}}\quad y = h \\ \end{aligned} $$
(36)

Solving and combining Eqs. (31), (32), (35), and (36), the expression for stream function is obtained as,

$$\psi = \psi_{00} + \alpha_{1} \psi_{01} + A \psi_{10} + A \alpha_{1} \psi_{11}$$
(37)

Utilising the equation \(u = \frac{\partial \psi }{{\partial y}}\), the analytical solution for velocity could be determined.

3.1.2 Temperature Expression

On ignoring \(O\left( {A^{2} } \right)\) terms in Eq. (26b), the expression for temperature is considered as

$$\theta = \theta_{0} + A \theta_{1}$$
(38)

Using Eq. (38) in Eq. (25) and grouping the terms, the following equations are obtained as.

3.1.2.1 Zeroth-Order Temperature System
$$\begin{aligned} & \frac{{\partial \theta_{0} }}{\partial y} + \alpha_{2} \theta_{0} \frac{{\partial \theta_{0} }}{\partial y} + \smallint {\text{Br }} \left\{ {\left( {1 - \alpha_{1} y + B} \right)\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)^{2} } \right\} \partial y = 0 \\ & \frac{{\partial \theta_{0} }}{\partial y} = 0\quad {\text{at}}\quad y = 0\;\quad{\text{and}}\;\quad\theta_{0} + \eta_{2} \frac{{\partial \theta_{0} }}{\partial y} = 1\quad {\text{at}}\quad y = h \\ \end{aligned}$$
(39)

The above-mentioned equations are inherently nonlinear, hence to obtain the solutions, the double perturbation approach is used.

$$\theta_{i} = \Sigma \alpha_{2}^{j} \theta_{ij} ,\;{\text{ where}}\quad i = \left\{ {0, 1} \right\} , 0 \le j \le n$$
(40)

To acquire more concise and direct temperature solutions, we disregard higher-order terms \(O\left( {\alpha_{2}^{2} } \right)\) in the above equation. Consequently, the subsequent equations for temperature are formulated for \(i = 0\) as,

$$\theta_{0} = \theta_{00} + \alpha_{2} \theta_{01}$$
(41)

Zeroth-Order System

$$\begin{aligned} & \frac{{\partial \theta_{00} }}{\partial y} + \smallint {\text{Br}} \left\{ {\left( {1 - \alpha_{1} y + B} \right)\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)^{2} } \right\} \partial y = 0 \\ & \frac{{\partial \theta_{00} }}{\partial y} = 0 \quad {\text{at}}\quad y = 0 \;\quad{\text{and}}\;\quad \theta_{00} + \eta_{2} \frac{{\partial \theta_{00} }}{\partial y} = 1\quad {\text{at}}\quad y = h \\ \end{aligned}$$
(42)

First-Order System

$$\begin{aligned} & \frac{{\partial \theta_{01} }}{\partial y} + \theta_{00} \frac{{\partial \theta_{00} }}{\partial y} = 0 \\ & \frac{{\partial \theta_{01} }}{\partial y} = 0\quad {\text{at}}\quad y = 0\;\quad{\text{and}}\;\quad \theta_{01} + \eta_{2} \frac{{\partial \theta_{01} }}{\partial y} = 0 \quad {\text{at}}\quad y = h \\ \end{aligned}$$
(43)
3.1.2.2 First-Order Temperature System
$$\begin{aligned} & \frac{{\partial \theta_{1} }}{\partial y} + \alpha_{2} \theta_{0} \frac{{\partial \theta_{1} }}{\partial y} + \alpha_{2} \theta_{1} \frac{{\partial \theta_{0} }}{\partial y} \\ & \qquad + \smallint {\text{Br}} \left\{ {2\left( {1 - \alpha_{1} y + B} \right)\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)\left( {\frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }}} \right) - \frac{1}{3}\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)^{4} } \right\} \partial y = 0 \\ & \frac{{\partial \theta_{1} }}{\partial y} = 0\quad {\text{at}}\quad y = 0\;\quad{\text{and}}\;\quad \theta_{1} + \eta_{2} \frac{{\partial \theta_{1} }}{\partial y} = 0 \quad {\text{at}}\quad y = h \\ \end{aligned}$$
(44)

Higher-order elements beyond \(O\left( {\alpha_{2}^{2} } \right)\) in Eq. (40) are ignored to simplify temperature solutions for \(i = 1\). The preceding approach yields the following equations that describe temperature.

$$\theta_{1} = \theta_{10} + \alpha_{2} \theta_{11}$$
(45)

Zeroth-Order System

$$\begin{aligned} & \frac{{\partial \theta_{10} }}{\partial y} + \smallint {\text{Br }}\left\{ {2\left( {1 - \alpha_{1} y + B} \right)\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)\left( {\frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }}} \right) - \frac{1}{3}\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)^{4} } \right\}\partial y = 0 \\ & \frac{{\partial \theta_{10} }}{\partial y} = 0\quad {\text{at}}\quad y = 0\;\quad{\text{and}}\; \quad\theta_{10} + \eta_{2} \frac{{\partial \theta_{10} }}{\partial y} = 0 \quad {\text{at}}\quad y = h \\ \end{aligned}$$
(46)

First-Order System

$$\begin{aligned} & \frac{{\partial \theta_{11} }}{\partial y} + \theta_{00} \frac{{\partial \theta_{10} }}{\partial y} + \theta_{10} \frac{{\partial \theta_{00} }}{\partial y} = 0 \\ & \frac{{\partial \theta_{11} }}{\partial y} = 0\quad {\text{at}}\quad y = 0\;\quad{\text{and}}\; \quad\theta_{11} + \eta_{2} \frac{{\partial \theta_{11} }}{\partial y} = 0\quad {\text{at}}\quad y = h \\ \end{aligned}$$
(47)

By solving Eqs. (42), (43), (46) and (47) analytically, and substituting in Eq. (38), the expression for temperature function is obtained as

$${\text{i}}.{\text{e}}.,\quad \theta = \theta_{00} + \alpha_{2} \theta_{01} + A \theta_{10} + A \alpha_{2} \theta_{11}$$
(48)

By solving Eq. (19) the analytical solution for the concentration is obtained. Using MATLAB R2023a programming language, the velocity expression, temperature equation, concentration, and stream function solutions are graphically represented.

3.2 Expression for Different Waveforms

The following are the nondimensional expressions for sinusoidal, square, triangular, and trapezoidal wave forms:

  1. a.

    Sinusoidal wave:

    $$h\left( {x,t} \right) = 1 + \epsilon {\text{ sin}} \left[ {\frac{2\pi }{\lambda }\left( {x - ct} \right)} \right]$$
  2. b.

    Square wave:

    $$h\left( {x,t} \right) = 1 + \epsilon \left[ {\frac{4}{\pi }\mathop \sum \limits_{\xi = 1}^{\infty } \frac{{\left( { - 1} \right)^{\xi + 1} }}{{\left( {2\xi - 1} \right)}}{\text{ cos}} \left[ {\left( {2\xi - 1} \right)2\pi \left( {x - ct} \right)} \right]} \right]$$
  3. c.

    Triangular wave:

    $$h\left( {x,t} \right) = 1 + \epsilon \left[ {\frac{8}{{\pi^{3} }}\mathop \sum \limits_{\xi = 1}^{\infty } \frac{{\left( { - 1} \right)^{\xi + 1} }}{{\left( {2\xi - 1} \right)^{2} }}{\text{ sin}} \left[ {\left( {2\xi - 1} \right)2\pi \left( {x - ct} \right)} \right]} \right]$$
  4. d.

    Trapezoidal wave

    $$h\left( {x,t} \right) = 1 + \epsilon \left[ {\frac{32}{{\pi^{2} }}\mathop \sum \limits_{\xi = 1}^{\infty } \frac{{{\text{ sin}} \left( {\frac{\pi }{8}} \right)\left( {2\xi - 1} \right)}}{{\left( {2\xi - 1} \right)^{2} }}{\text{ sin}} \left[ {\left( {2\xi - 1} \right)2\pi \left( {x - ct} \right)} \right]} \right]$$

4 Results and Discussion

The previous section analysed the fluid flow, heat, and mass transfer of a Eyring Powell fluid flowing down a uniform channel under different conditions using the Perturbation Technique. The effects of changing fluid properties are evaluated in this section. MATLAB R2023a illustrates flow quantities and physiological activity metrics. Additionally, Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 indicates the influence of physiological parameters on velocity, temperature, concentration, different waveforms, and contour graphs for streamlines.

Fig. 2
figure 2

Variation of velocity profiles when E1 = 0.4, E2 = 0.1, E3 = 0.01, E4 = 0.001, E5 = 0.1, A = 0.01, B = 2, x = 0.2, F = 2, \(\phi = \frac{\pi }{4}\), α1 = 0.02, t = 0.1, \(\epsilon = 0.3\), \(\eta_{1} = 0.2\), M = 2

Full size image
Fig. 3
figure 3

Variation of temperature profiles when E1 = 0.4, E2 = 0.1, E3 = 0.01, E4 = 0.001, E5 = 0.1, A = 0.01, B = 2, x = 0.2, F = 2, \(\phi = \frac{\pi }{4}\), α1 = 0.02, t = 0.1, \(\epsilon = 0.3\), \(\eta_{1} = 0.2\), M = 2, α2 = 0.02, \(\eta_{2} = 0.2\), Br = 2

Full size image
Fig. 4
figure 4

Variation of concentration profiles when E1 = 0.4, E2 = 0.1, E3 = 0.01, E4 = 0.001, E5 = 0.1, A = 0.01, B = 2, x = 0.2, F = 2, \(\phi = \frac{\pi }{4}\), α1 = 0.02, t = 0.1, \(\epsilon = 0.3\), \(\eta_{1} = 0.2\), M = 2, α2 = 0.02, \(\eta_{2} = 0.2\), Br = 2, Sc = 1, Sr = 1, \(\eta_{3} = 0.2\)

Full size image
Fig. 5
figure 5

Variation of velocity profiles for different values of A for different wave forms a sinusoidal, b square, c triangular, d trapezoidal when E1 = 0.4, E2 = 0.1, E3 = 0.01, E4 = 0.001, E5 = 0.1, A = 0.01, B = 2, x = 0.2, F = 2, \(\phi = \frac{\pi }{4}\), α1 = 0.02, t = 0.1, \(\epsilon = 0.3\), \(\eta_{1} = 0.2\), M = 2

Full size image
Fig. 6
figure 6

Variation of velocity profiles for different values of B for different wave forms a sinusoidal, b square, c triangular, d trapezoidal when E1 = 0.4, E2 = 0.1, E3 = 0.01, E4 = 0.001, E5 = 0.1, A = 0.01, B = 2, x = 0.2, F = 2, \(\phi = \frac{\pi }{4}\), α1 = 0.02, t = 0.1, \(\epsilon = 0.3\), \(\eta_{1} = 0.2\), M = 2

Full size image
Fig. 7
figure 7

Variation of velocity profiles for different values of M for different wave forms a sinusoidal, b square, c triangular, d trapezoidal when E1 = 0.4, E2 = 0.1, E3 = 0.01, E4 = 0.001, E5 = 0.1, A = 0.01, B = 2, x = 0.2, F = 2, \(\phi = \frac{\pi }{4}\), α1 = 0.02, t = 0.1, \(\epsilon = 0.3\), \(\eta_{1} = 0.2\), M = 2

Full size image
Fig. 8
figure 8

Variation of streamlines for a A = 0.01, b A = 0.05

Full size image
Fig. 9
figure 9

Variation of streamlines for a B = 1.5, b B = 2.5

Full size image
Fig. 10
figure 10

Variation of streamlines for a α1 = 0.01, b α1 = 0.04

Full size image
Fig. 11
figure 11

Variation of streamlines for a \(\eta_{1} = 0.00\), b \(\eta_{1} = 0.02\)

Full size image
Fig. 12
figure 12

Variation of streamlines for a M = 2, b M = 2.5

Full size image

4.1 Velocity Profiles

Examining velocity profiles shows fascinating differences brought on by carefully adjusting fitting parameters, as seen in Fig. 2a–g. A comprehensive examination of these graphs reveals distinct patterns dictating the effect of various parameters on axial velocity. Figure 2a demonstrates a substantial association between Eyring–Powell Fluid parameter \(A\) and axial velocity. Axial velocity rises with fluid parameter \(A\). In contrast, Fig. 2b shows that increasing parameter \(B\) decreases velocity. Figure 2c, d offers informative visuals on the effects of varying viscosity and slip parameters, respectively. The graphical representations convey the importance of these characteristics in determining velocity profiles. Thus, they demonstrate the enhanced velocity profiles caused by these factors. Further examining the magnetic effect yields an intriguing relationship between magnetic and fluid velocity, as illustrated in Fig. 2e. The graphical representation shown below supports the observation that an increase in magnetic effect results in a noticeable drop in fluid velocity. Figure 2f illustrates the correlation between inclination angles and their impact on fluid velocity. Increasing the inclination angle increases fluid velocity. Figure 2g emphasizes the impact of wall attributes, is the focal point of the analysis. Attributes like mass characterization, wall tension, and damping characteristics are essential for coordinating components, like a symphony. Recalibration of factors like wall stiffness and elasticity considerably impacts velocity for its subtle nature. Velocity increases with increases in mass characterization and wall tension parameters and decreases with increases in wall damping parameters. Notably, a slight change in the wall stiffness parameter results in a substantial decrease in velocity. A similar trend is seen when adjusting the wall elasticity parameter, with more elasticity resulting in a flatter velocity distribution.

4.2 Temperature Profiles

Figure 3a–j shows the temperature variations for various parameters. The temperature profiles are seen to grow as the Eyring Powell fluid parameter \(A\) is increased in Fig. 3a, but the material parameter \(B\) exhibits the reverse tendency in Fig. 3b. The effect of varying viscosity over temperature is depicted in Fig. 3c. It demonstrates that increasing variable viscosity lowers temperature profiles while increasing the value of \({\alpha }_{2}\) exhibits a dual behaviour for temperature profiles, as seen in Fig. 3d. The temperature profiles change for velocity slip and thermal slip parameters is shown in Fig. 3e, f respectively. As the velocity slip increases, there is a corresponding reduction in the temperature profiles. Similarly, an increase in \({\eta }_{2}\) leads to a decrease in the temperature profile. Figure 3g illustrates the temperature variation corresponding to various magnetic parameters. It can be observed that a rise in the magnetic parameter leads to a decrease in the temperature profiles. Furthermore, Fig. 3h demonstrates a significant rise in temperature with the rise of the Brinkmann number. Figure 3i shows a direct relationship between the inclination angle and the fluid temperature increases. In the analysis of the temperature variation depicted in Fig. 3j, it can be observed that a rise in the wall tension and mass characterization parameters leads to a corresponding rise in temperature. Conversely, the damping parameter exhibits an inversing relationship with temperature. Moreover, an augmentation in the wall damping and stiffness parameters results in a decrease in temperature profiles. The increase in the wall elasticity parameter has a minimal impact on the temperature profile, causing only a slight decline.

4.3 Concentration Profile

Figure 4a–l illustrates the impact of essential parameters on the concentration profiles. In Fig. 4a, it has been observed that an increase in the Eyring Powell fluid parameter \(A\) results a decrease in the concentration profile. Conversely, Fig. 4b illustrates a contrasting trend for the material parameter \(B\), where an increase in \(B\) leads to an increase in the concentration profiles. Figure 4c demonstrate that the enhancement of concentration profiles is observed with an increase in variable viscosity, whereas an increase in variable thermal conductivity yields the opposite behaviour (see Fig. 4d). The higher concentration caused by increasing velocity slip and thermal slip parameters is seen in Fig. 4e, f. For the concentration slip parameter, the opposite behaviour has been seen. When the concentration slip parameter is raised, the concentration decreases (see Fig. 4g). The fluctuation of concentration for changing magnetic parameters is depicted in Fig. 4h. The concentration profiles are increased as the magnetic parameter is increased Fig. 4i, j depict the variance in concentration profile for different Scmidth and Soret number values, respectively. Both factors exhibit similar behaviour; that is, raising these values lowers the concentration profiles. A notable concentration fluctuation for the Brinkmann number can be observed in Fig. 4k. The concentration decreases as the Brinkmann number increases. Figure 4l shows the fluctuation of concentration on wall characteristics. For an increase in wall tension and mass characterisation parameter, a drop in concentration profile is seen. When compared to temperature and velocity profiles, this tendency is opposite in nature. The concentration profiles show a significant improvement as the wall damping value rises. Both \({E}_{4}\) and \({E}_{5}\) exhibits comparable behaviour. Both the wall rigidity and elasticity parameter enhances the concentration profiles.

4.4 Wave Forms

The significance of waveforms is derived from the fact that they affect the operation and behaviour of a system. Waveforms are paramount when determining effectiveness and performance in various fluid mechanics applications. The four standard waveforms: sinusoidal, square, triangle, and trapezoidal, are drawn offering something unique and valuable. Waveforms are essential components in a wide variety of applications involving fluid mechanics. These applications include hydraulic testing, flow visualisation techniques, flow control experiments, and cardiovascular research. These aid researchers and engineers in their quest to better understand and build liquid systems by allowing them to simulate real-world settings, investigate flow instabilities, and optimise flow control tactics.

To obtain insight into the impact that different waveforms (sinusoidal, square, triangle, and trapezoidal) have on fluid flow features and the distribution of velocity within channels, an analysis was carried out on the velocity profiles for each of the distinct waveforms. Figure 5a–d and 6a–d show that the fluid parameter \(A\) and \(B\) has been analysed, respectively. This study aims to understand the fluid flow behaviour when Eyring Powell Fluid is considered through different waveforms. This insight can improve the efficiency of velocity control and manipulation systems. It is important to note that when the fluid parameter \(A\) goes up, the flow rate also goes up, as seen in Fig. 5, showing the velocity profiles. Also, all the graphs displaying the velocity profiles show that the fluid rate decreases when the fluid parameter \(B\) increases (see Fig. 6). This study aims to understand fluid flow behaviour better when subjected to various magnetic parameters and waveforms (see Fig. 7a–d. This knowledge can improve the performance of systems that rely on magnetic effects for controlling and changing velocity. One possible use of this knowledge is in the aerospace industry. It is important to note that an increase in the magnetic parameter leads to a drop in the fluid rate. This can be seen in every picture that depicts the velocity profiles, and it is something that should be taken into consideration.

4.5 Trapping Phenomenon

Trapping is essential to analyse peristaltic motion in biological fluids, as it provides insight into the formation of boluses through enclosed streamlines. Figures 8, 9, 10, 11 and 12 examine the physiological indicators along these streamlines. Figure 5 illustrates the variation in streamlines for different values of the fluid parameter \(A\). The correlation between the number of bolus formations and the importance of \(A\) is positive. In contrast, Fig. 6 exhibits a contrasting behaviour for fluid parameter \(B\). As the value of \(B\) increases, fewer boluses are administered. The influence of viscosity and velocity slip parameters on the confined bolus is depicted in Figs. 10 and 11. The presented graphs illustrate that the number of bolus formations increases as the viscosity and velocity slip parameters are altered. The relationship between the magnetic parameter and the number of confined boluses is depicted in Fig. 12. As the magnetic parameter is increased, there is a corresponding decrease in the number of trapped boluses.

5 Validation

The current model validates theoretical results with the existing model from Hina [27] as shown in Fig. 13. The newly introduced parameters such as, variable viscosity, variable thermal conductivity as well as angle of inclination has been set to zero to validate the results graphically. It can be noted that the model is in good agreement with the existing model. Figure 13a represents the velocity profiles; Fig. 13b represents Temperature profile and Fig. 13c represents concentration profiles. In the present model a variation is observed due to the boundary conditions considered different from that of Hina [27]. Also, the present model reduces to Hina [27] model when same boundary conditions are considered.

Fig. 13
figure 13

Validation of current model with Hina [27] for a velocity profile, b temperature profile and c concentration profile when \(E_{1} = 0.4,E_{2} = 0.1, E_{3} = 0.01\), \(A = 0.01, B = 2, x = 0.2, t = 0.1,\) \(\epsilon = 0.3, \eta_{1} = 0.01, M = 2, \eta_{2} = 0.02\), \({\text{Br}} = 2, {\text{Sc}} = 1, {\text{S}}r = 1, \eta_{3} = 0.02\)

Full size image

6 Conclusion

The present mathematical model investigates the peristaltic transport, specifically concentrating on the behaviour of Eyring–Powell fluid in the presence of a magnetic field, yields the significant and applicable findings theoretically. Slip boundary conditions were included in a uniform channel model to examine these phenomena. Velocity profiles for sinusoidal, square, triangular, and trapezoidal waveforms were analysed to determine their effects on fluid flow. The investigation centred on determining the applicability of this research in various fields, including biomedical engineering, medicine, and technology. The following conclusions can be drawn from the study:

  • Flow rate is positively correlated with fluid parameter \(A\), whereas flow rate decreases with an increase in fluid parameter \(B\).

  • The velocity is substantially influenced by the characteristics of the wall, such as its stiffness and elasticity.

  • Comprehending fluid flow behaviour in diverse magnetic parameters and waveforms can improve systems that depend on magnetic effects to regulate velocity.

  • Improvement in concentration profiles is noticed when considering viscosity and thermal conductivity, which thoroughly comprehends fluid behaviour related to various factors.

  • A direct correlation exists between temperature increase and damping, while rigidity and elasticity demonstrate the opposite relationship. This condition affects several biological and physiological systems and is essential for understanding system thermodynamics.

  • Number of Bolus formations increase in response to changes in velocity slip and viscosity parameters.