1 Introduction

Portland Cement Concrete (PCC) is the composite material produced by mixing coarse aggregates (i.e., gravel), fine aggregates (i.e., sand), Portland Cement (PC), water, and optionally admixtures (e.g., chemical additives, fly ash, and steel slag) [1,2,3]. PCC is the world's most widely used construction material, mainly employed for constructing buildings and pavements [4,5,6]. Notoriously, the high consumption of time and financial resources for its proper experimental characterization implies that designers must resort to indirect methods [7,8,9]. However, the traditional mathematical models used for these purposes have been confirmed to be inaccurate and unreliable [10,11,12]. The preceding has led the estimation of PCC's engineering properties to focus on developing advanced computational models [13,14,15]. Within this field of research, Artificial Intelligence (AI)-based models stand out for their high precision and ability to adapt to new types of mixture designs not considered during the model creation stage [8, 14, 16].

Table 1 summarizes a literature review on estimating PCC's engineering properties using AI techniques. This table shows that most previous investigations focused on predicting Compressive Strength (ComS) and Tensile Strength (TenS). The preceding is expected since the ComS and TenS are the most relevant properties (regarding the characterization of the PCC's mechanical behaviour) to design structural elements and rigid pavements, respectively [17,18,19]. On the other hand, Table 1 also reveals a critical gap in the state-of-the-art, i.e., in none of the consulted research, Poisson's Ratio (v) and Elastic Modulus (E) are considered output variables. In this regard, the aforementioned computational models did not take into account the strong relationship that exists between the resistance-related properties with the v and E. In other words, previous case studies do not guarantee that for each evaluated dataset (i.e., a set of experimental data), the physical associations between v, E, ComS, and TenS would be simultaneously maintained.

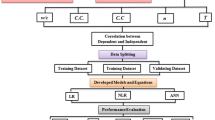
Table 1 Literature review on estimating PCC's engineering properties using AI techniques
Full size table

The present research aims to overcome the previously explained literature gap. Consequently, a computational model is proposed using the Long-Term Pavement Performance (LTPP) database as the data source [23]. Specifically, a Machine Learning (ML) technique called Artificial Neural Network (ANN) is employed for this purpose. From the LTPP database, experimental information from multiple PCC samples was extracted. The experimental information includes design variables and laboratory testing results (i.e., v, E, ComS, and TenS). In turn, the PCC's design variables comprise the following parameters: volumetric air content (VairC), volumetric aggregate content (VaggC), volumetric PC content (VpcC), volumetric water content (VwC), gravimetric water-to-cement ratio (GwcR), and specific gravity (Gs). Notoriously, it is expected that the proposed ANN model can be used (by agencies, designers and the scientific community) to forecast the PCC's engineering properties (v, E, ComS, and TenS) when experimental measurements are not feasible.

Below is described the structure of the present manuscript. Initially, Sect. 2 describes the origin of the data used to develop the ML-based model. Next, Sect. 3 introduces the computational methods employed, and the basic concepts of ANNs are also explained. Then, Sect. 4 exhibits a deep discussion about the exactness and accuracy of the proposed computational model. It is important to highlight that the discussion section includes several SHapley Additive exPlanations (SHAP) assessments and running time analyses. Finally, Sect. 5 summarises the research and offers the main findings and conclusions achieved throughout the investigation.

2 Data Source

All the data employed in this investigation was extracted from the LTPP database. The LTPP's information management system has operated since 1988 and is managed by the Federal Highway Administration (i.e., part of the US Department of Transportation) [24,25,26,27]. The LTPP database comprises exhaustive information about design parameters, laboratory characterization of materials, climate variables, in-situ performance, and life-cycle behaviour on over 2500 pavement test sections in the USA and Canada [28,29,30,31].

With the aim of filtering the relevant information (for this study) from the LTPP database, it was decided to solely consider the experimental dataset that simultaneously contains information about VairC, VaggC, VpcC, VwC, GwcR, Gs, v, E, ComS, and TenS. Furthermore, the datasets were manually scanned to discard those with missing information. Consequently, a total number of 75 datasets were finally obtained from experimental/laboratory works that were developed in the US states of Alabama, Arizona, Arkansas, California, Colorado, Delaware, Illinois, Indiana, Iowa, Kansas, Michigan, Missouri, North Carolina, North Dakota, Ohio, Oklahoma, Texas, Washington, and Wisconsin. In this regard, it is essential to highlight that all datasets used in this research are available for free download on the LTPP's website. Table 2 presents the adopted datasets' statistical description (i.e., each variable's minimum, maximum, mean, median, standard deviation, kurtosis, and skewness values). Also, Fig. 1 shows a scatterplot matrix to depict the considered parameters' variability and correlation. From Fig. 1, it is clear that there is no marked trend between the input data (i.e., the design variables comprised by the VairC, VaggC, VpcC, VwC, GwcR, and Gs) and the output data (i.e., the laboratory testing results comprised by v, E, ComS, and TenS).

Table 2 Basic statistical description of the adopted variables
Full size table
Fig. 1
figure 1

Correlation and variability of the considered variables. Units: VairC (%); VaggC (%); VpcC (%); VwC (%); GwcR (-); Gs (-); v (-); E (GPa); ComS (MPa); TenS (MPa)

Full size image

2.1 Definition of New Input Variables

According to Fig. 1, there is no strong correlation between the input and output variables (at least in their current form). Therefore, in order to generate more relationships between the considered properties, it was decided to create four new input variables, namely volumetric water-to-cement ratio (VwcR), volumetric paste content (VpasteC), aggregate-to-paste ratio (AggPasR), and paste to air ratio (PasAirR). Equations (1), (2), (3), and (4) show the mathematical formulations for calculating VwcR, VpasteC, AggPasR, and PasAirR, respectively. In Eq. (1), Gs_pc refers to the specific gravity of the PC, which was assumed as a typical value of 3.1 [32,33,34].

$$VwcR = GwcR*Gs\_pc$$
(1)
$$VpasteC = VpcC + VwC$$
(2)
$$AggPasR = \frac{VaggC}{{VpasteC}}$$
(3)
$$PasAirR = \frac{VpasteC}{{VairC}}$$
(4)

2.2 Feature Scaling

According to Table 2, the input and output variables present different units and magnitudes, making the learning process of ANNs demanding. In order to simplify the artificial learning procedure, it was decided to apply a feature scaling technique called standardization; Eq. (5) shows its mathematical definition [35]. The standardization process transforms data arrays, obtaining a new one with three principal characteristics [36, 37]: (i) mean equal to 0, (ii) standard deviation equal to 1, (iii) and most data points are between the range [− 1, 1]. Table 3 exhibits the basic statistical description of the transformed variables; in this table, it is clear that the standardized variables present the expected (and previously explained) features.

$$Standardized\;value = \frac{Original\;value - Mean}{{Standard\;deviation}}$$
(5)
Table 3 Statistical description of the variables after the standardization process
Full size table

2.3 Data Augmentation

The main limitation of this study is that the employed database is only composed of 75 datasets. That amount of data is minimal; hence, an ML-based computational model created solely by that data could suffer from overfitting phenomena [38,39,40]. In order to avoid overfitting, it was decided to apply two techniques: (i) data augmentation during the data preprocessing stage and (ii) early stopping during the learning process stage. The early stopping technique is explained later in the manuscript. On the other hand, the data augmentation technique is just described below.

Data augmentation is one of the most powerful techniques to avoid overfitting [41,42,43]. Moreover, this technique stands out due to its simplicity [44, 45]. The data augmentation consists of conducting the model's learning process by considering several slightly altered copies of the original datasets together with the authentic ones [46,47,48]. Thus, for this research, it was decided to create 9 modified copies of each of the original datasets. Each modified copy was formed by affecting the authentic values with a pseudo-random distortion of between ± 3%. This low alteration ratio was selected to ensure that the physical consistency of the concrete mix designs was maintained. In this regard, 675 artificial datasets were obtained, which, added to the 75 original datasets, yields a total of 750. For the subsequent learning process (that is, the design of the ANN architecture and its performance assessments), the embraced database was separated as follows: 70% (i.e., 525 datasets) for the training process, 20% (i.e., 150 datasets) for the testing process, and 10% (i.e., the remaining 75 datasets) for the validation. It is crucial to highlight that this classification is accomplished using a random shuffle.

3 Methods

A broad set of ML-based computational techniques can be used for regression/forecasting problems, e.g., ANNs, bagging regressors, decision trees, lasso regression, random forests, and support vector machines [49,50,51,52]. In this research, it was decided to apply ANNs to estimate the PCC's engineering properties (v, E, ComS, and TenS). The ANNs are one of the most popular deep-learning techniques because they allow for establishing correlations between variables that did not present a strong relationship [22, 45, 53]. The internal working of the ANNs is based on replicating the logic of the human brain's neural connections [11, 54, 55]. Specifically, in this study, it was decided to apply a type of ANN called Deep Neural Networks (DNNs). The DNNs are defined as ANNs with at least two hidden layers and densely linked neurons (i.e., it is necessary to establish all the possible connections between neurons) [9, 39, 54]. Figure 2 shows the base architecture of DNNs.

Fig. 2
figure 2

Base architecture of DNNs. Adapted from: [54, 56]. Legend: ki, kh, ko, k1, and k2 are integer numbers equal to or greater than two

Full size image

Based on the DNN canonical architecture shown in Fig. 2, the following aspects could be highlighted for this case study: (i) the input layer comprises 10 neurons (i.e., each neuron for each input variable presented in Table 3); (ii) the output layer comprises 4 neurons (i.e., each neuron for each output variable presented in Table 3); and (iii) the number of hidden layers and their number of neurons should be determined. In order to obtain a suitable configuration of the number of hidden layers and neurons, an extensive inspection of the possible combinations was carried out. In this way, the most appropriate DNN architecture was found, as indicated in Fig. 3. According to Fig. 3, there are four hidden layers. Respectively, the first, second, third and fourth hidden layers are composed of 800, 640, 160, and 40 neurons. Therefore, the proposed DNN is formed by 6 layers, 1654 neurons, and 630,604 trainable parameters. The procedure to calculate the total number of trainable parameters is exhibited in Table 4.

Fig. 3
figure 3

Proposed DNN

Full size image
Table 4 Calculation of the total number of trainable parameters for the proposed DNN
Full size table

In Fig. 3, two characteristics stand out: (i) all the hidden layers are affected by the hyperbolic tangent (tanh) activation function, and (ii) the proposed DNN is executed under a first-order gradient-based optimization method called Adamax. On the one hand, tanh is one of the most helpful activation functions because it causes all data coming out of a layer to be between the closed interval from -1 to 1 [57,58,59]. The preceding is particularly desirable in this case study because, according to Table 3, most of the data points (for both input and output variables) are comprehended within that range. In this regard, it was deliberately designed that the output layer would not have an activation function so that the few data outside the interval [− 1, 1] could be adequately predicted. On the other hand, Adamax is a variant of the traditional Adam optimization method [41, 60]. The internal functioning of Adamax is based on the infinity norm concept, which allows a high capacity to modify the learning rate according to the features of the input data [60, 61]. Algorithm 1 explains in detail the optimization procedure applied by Adamax [62, 63]. Also, Table 5 shows the hyperparameter values adopted for this case study.

Table 5 Selected hyperparameter values for the Adamax optimizer
Full size table
Algorithm 1
figure a

Pseudocode of the internal working of the Adamax optimizer. Adapted from: [62, 63].

Full size image

t - iteration index; m - first moment vector; u - exponentially weighted infinity norm; w - convergence parameter (weight variable); T - number of iterations to reach the convergence; gt - gradient; β1 - exponential decay rate for the first moment estimates; β2 - exponential decay rate for the exponentially weighted infinity norm; lr - learning rate; ε - small constant for numerical stability

In order to make this research reproducible, duplicatable, and replicable, Algorithm 2 shows the simplified pseudocode of the proposed DNN. Further, the authors publicly share the computational model to the following GitHub repository (programmed in Python language): https://github.com/rpoloe/PCC. It is essential to highlight that the authors bring an open license to guarantee the unrestricted use, modification, and distribution of the codes hosted in this repository. From Algorithm 2, four aspects should be discussed: (i) the selected loss function, (ii) the error metrics employed, and (iii) the required number of epochs.

The Mean Square Error (MSE) was chosen as the loss function. Equation (6) explains it [54, 56]. The MSE is one of the most common loss functions because it maximizes the differences between predicted and expected values [55, 64, 65]. Furthermore, four additional error metrics were considered, namely Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Mean Squared Logarithmic Error (MSLE), and the Logarithm of the Hyperbolic Cosine of the Error (LHCE). Respectively, Eqs. (7), (8), (9), and (10) define the MAE, MAPE, MSLE, and LHCE [54, 56]. On the other hand, the early stopping technique demarcated the required number of epochs (i.e., cycles of training and testing). This technique consists of determining the maximum number of epochs that the optimization process can reach before stopping learning, which is evidenced when, in the error functions (in this case, MSE, MAE, MAPE, MSLE, and LHCE), the assumed error changes from a decreasing trend to an ascending one [40, 54, 66]. In other words, the early stopping technique consists of locating the moment of maximum precision [54, 67, 68]. For the proposed DNN, the instant when learning stagnated varied between 600 and 1400 epochs (depending on the error metrics). Thus, with the aim of adopting a conservative number of epochs, this was set at 500.

$${\text{MSE}} = \frac{1}{{\text{n}}}\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {{\text{OD}}^{{\text{i}}} - {\text{ED}}^{{\text{i}}} } \right)^{2}$$
(6)
$${\text{MAE}} = \frac{1}{{\text{n}}}\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} \left| {{\text{OD}}^{{\text{i}}} - {\text{ED}}^{{\text{i}}} } \right|$$
(7)
$${\text{MAPE}} = \frac{1}{{\text{n}}}\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} \left| {\frac{{{\text{OD}}^{{\text{i}}} - {\text{ED}}^{{\text{i}}} }}{{{\text{OD}}^{{\text{i}}} }}} \right|$$
(8)
$${\text{MSLE}} = \frac{1}{{\text{n}}}\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {{\text{ln}}\left( {1 + {\text{OD}}^{{\text{i}}} } \right) - {\text{ln}}\left( {1 + {\text{ED}}^{{\text{i}}} } \right)} \right)^{2}$$
(9)
$${\text{LHCE}} = \frac{1}{{\text{n}}}\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {\frac{{{\text{e}}^{{{\text{OD}}^{{\text{i}}} - {\text{ED}}^{{\text{i}}} }} + {\text{e}}^{{{\text{ED}}^{{\text{i}}} - {\text{OD}}^{{\text{i}}} }} }}{2}} \right){ }$$
(10)

where n—number of data points. i—data index. OD—observed/experimental data. ED—estimated data.

Algorithm 2
figure b

Simplified pseudocode to create the proposed DNN

Full size image

4 Discussion

4.1 Model’s Exactness

Figure 4 compares the measured and predicted values of the PCC's engineering properties through 1:1 line plots. This figure clearly shows that the proposed DNN model can assemble forecasting with almost perfect accuracy. Regardless of the origin of the datasets (i.e., training, testing, or validation), the computational model is able to reproduce the laboratory-tested behaviour. It is paramount to emphasise that the training and testing datasets are employed along the supervised learning process, but the model has no prior knowledge of the validation datasets [69, 70]. Therefore, the validation datasets corroborate whether the DNN architecture can forecast never-before-observed scenarios [71, 72]. Thus, based on Fig. 4, it is possible to recognise the almost perfect estimation capacity of the proposed computational model. Besides, several goodness-of-fit parameters are examined in Fig. 5 and Table 6. These parameters are the previously introduced error metrics and the coefficient of determination (R2). Table 6 shows the goodness-of-fit parameters at the first and last epochs, as well as the “initial/final” error ratio. From this table, the following findings can be drawn. First, at the final epoch, the prediction errors of the DNN model are close to zero (0). Second, the error metrics that best capture the improving behaviour of the DNN architecture through the epochs are MSE and MSLE. Third, at the initial epoch, the accuracy of the estimations according to the R2 parameters was between 2.7–11.7%, 0.5–2.3%, 19.4–24.6%, and 0.4–6.0% for v, E, ComS, and TenS, respectively. Fourth, at the final epoch, the accuracy of the estimations according to the R2 parameters was higher than 99.8% for all the forecasted properties. Also, Fig. 5 provides a detailed explanation of the error evolution along the epochs, which reveals that overfitting and underfitting are not occurring.

Fig. 4
figure 4

Comparison of measured and predicted values (1:1 lines)

Full size image
Fig. 5
figure 5

Statistical evaluation of the proposed DNN

Full size image
Table 6 Summary of goodness-of-fit parameters determined for the proposed DNN
Full size table

4.2 SHAP Assessments

Figure 6 exhibits four SHAP assessments on the proposed DNN: a summary plot, a waterfall plot, a decision plot for the training datasets, and a decision plot for the testing datasets. The summary plot represents a SHAP global interpretation of the DNN model, whilst the other charts correspond to SHAP local interpretations [54, 73]. According to these plots, it is possible to draw the following findings. In the summary plot, each input variable has an associated SHAP value. Higher SHAP values indicate more influence on the global predictive response of the DNN model [74, 75]. Therefore, the Gs, VairC, AggPasR, PasAirR, and GwcR are the input variables with more weight in the computational model. Thus, it is clear that creating new variables was a valuable strategy for this case study. In the waterfall plot, the input variables marked with red color (i.e., solely Gs and VairC) display a positive contribution to the output variables, whilst the blue color (i.e., all the input variables except Gs and VairC) denotes a negative one. This behaviour is helpful for the user to understand how the DNN model internally works [76, 77]. Meanwhile, the decision plots do not provide meaningful information individually since they reveal the learning trend followed by the DNN model [75, 77]. However, when comparing the decision plots for the training and testing datasets, it is notable that they follow a very similar trajectory. Hence, it is evidenced that the two phases of the learning process are congruent, which is desired [78, 79].

Fig. 6
figure 6

SHAP assessments for the proposed DNN model

Full size image

4.3 Running Time

The running time of ML-based computational models is an important parameter to assess the feasibility of their implementation in the daily-basis engineering practice [52, 56]. For this purpose, the proposed DNN model was evaluated using Python's native "TIME" module. Thus, the proposed DNN was executed on 100 independent occasions; Fig. 7 shows these results. According to this graph, the minimum, maximum, and average rutting times were 54.70, 87.47, and 66.01 s, respectively. Also, the standard deviation of the measurements was 10.15 s. Therefore, the proposed DNN requires approximately one minute for its execution, i.e., an acceptable magnitude within the context of civil engineering [52, 54]. It is essential to highlight that the running time depends primarily on the software and hardware used [80,81,82]. Hence, in order to be transparent, the ones used in this research are detailed below. On the one hand, Google Colab (a hosted Jupyter Notebook service) was utilized as the development environment. On the other hand, the NVIDIA® V100 Tensor Core GPU was adopted as the acceleration hardware.

Fig. 7
figure 7

Analysis of running time for the proposed DNN

Full size image

4.4 Model’s Limitations

The central limitation of the proposed DNN model is associated with the adopted database. The DNN architecture was trained, tested, and validated with 750 datasets. Nonetheless, only 75 datasets were obtained experimentally (from the LTPP database), and the other 675 datasets were artificially created through the data augmentation technique. Although this technique has been widely used in the literature to improve limited databases in ML-related regression problems [42,43,44,45, 83,84,85], the new modified database may not be broad enough to cover all physically/phenomenologically conceivable scenarios [44, 86, 87]. Therefore, the proposed DNN model may not yield highly accurate predictions of engineering properties (v, E, ComS, and TenS) for PCC mix designs that incorporate unconventional proportions of raw materials.

Another limitation of the computational model is that it is designed to forecast ordinary PCC's engineering properties (v, E, ComS, and TenS). In other words, the proposed DNN model is not able to predict the performance-related properties of mix designs that contain additives or supplementary cementitious materials (e.g., blast furnace slag, coal bottom ash, coal fly ash, metakaolin, palm oil ash, rice husk ash, silica fume, and steel slag [4, 88,89,90]). The preceding is particularly important considering that modified PCCs are increasingly used to construct buildings and rigid pavement.

5 Conclusions

In this investigation, an ML-based computational model was developed to estimate the engineering properties of the PCC, namely v, E, ComS, and TenS. Specifically, the ANN technique was employed as the primary computational method. In this regard, the LTPP database was utilized as the data source for the experimental/laboratory information. Eventually, a DNN architecture was proposed and evaluated with 1:1 lines, goodness-of-fit parameters, SHAP assessments, and running time analyses. Thus, the main conclusions that can be drawn from this study are presented below:

  • The data preprocessing techniques (i.e., the definition of new input variables, feature scaling, and data augmentation) were necessary to obtain a proper ML-based computational model.

  • The most suitable DNN architecture comprised one 10-neuron input layer (each neuron for each input variable), four hidden layers, and one 4-neuron output layer (each neuron for each output variable). The hidden layers subsequently had the following number of neurons: 800, 640, 160 and 40. Also, the tanh activation function was added for all the hidden layers.

  • Notoriously, the proposed DNN shows an accuracy higher than 99.8%, which makes it a valuable tool for estimating the engineering properties of PCC when there is no possibility of experimental measurements.

  • The SHAP assessments demonstrated that the input variables more critical for the proposed DNN model were the Gs, VairC, AggPasR, PasAirR, and GwcR.

  • The average running time of the proposed DNN model is approximately one minute, which implies a relatively low time quantity. In this regard, the model's speed is expected to be an attractive feature for potential users.

  • Although the proposed DNN model is limited by the few original datasets, its most significant advantage is that it can be easily used for transfer learning. Accordingly, other researchers and designers can adjust/fine-tune the model for their contexts. Hence, the authors publicly share the computational model assembled in this study through an open-access GitHub repository.