Online monitoring of dynamic networks using flexible multivariate control charts

Abstract

Change-point detection in dynamic networks is a challenging task which is particularly due to the complex nature of temporal graphs. Existing approaches are based on the extraction of a network’s information by the reduction to a model or to a single metric. Whereas the former one requires restrictive assumptions and has limited applicability for real-world social networks, the latter one may suffer from a huge information loss. We demonstrate that an extension to a well-balanced multivariate approach that uses multiple metrics jointly to cover the relevant network information can overcome both issues, since it is applicable to arbitrary network shapes and promises to strongly mitigate the information loss. In this context, we give guidelines on the crucial questions of how to properly choose a suitable multivariate metric set together with the choice of a meaningful parametric or nonparametric control chart and show that an improper application may easily lead to unsatisfying results. Furthermore, we identify a solution that achieves reasonable performances in flexible circumstances in order to give a reliably applicable approach for various types of social networks and application fields. Our findings are supported by the use of extensive simulation studies, and its applicability is demonstrated on two real-world data sets from economics and social sciences.

1 Introduction

Dynamic networks play an important role in many different application fields nowadays, ranging from biological (Bassett and Sporns 2017; Prill et al. 2005) and social sciences (Sarkar and Moore 2005; Carrington et al. 2005) to logistic and transportation processes (Lee and Dong 2009). Suppose we observe a dynamic network ${\mathcal {D}} = \{D_t, t = 1, \ldots , T\}$ which is a sequence of snapshots of the network of interest at various time points t. Each of these single networks $D_t$ consists of a set of nodes $V_t$ that may be connected through a set of links $E_t$. Note that we do not only allow the number and positions of edges to differ between different time points, but also the number of nodes may change. It is often of interest to decide whether there are differences in the (dynamic) stochastic network generating process between different time points, e.g., due to a changed consumer behavior in marketing networks, an increased communication in social networks, or a failure of a working machine in a manufacturing process. Other scenarios involve financial market analysis (Durante and Dunson 2014), network traffic monitoring (Sun et al. 2006), or connectomic applications (Durante et al. 2017). Relevant statistical analysis procedures for such tasks are two-sample tests and change-point detection. Although our results can be employed for classical testing procedures as well, we focus on the latter one in our work.

The main purpose of change-point detection (Basseville and Nikiforov 1993; Montgomery 2012) is to identify time points at which the structure of a dynamic network changes in a meaningful way. Traditionally, there are two perspectives toward this issue. One approach is to observe the whole sample ${\mathcal {D}} =\{D_1,\ldots ,D_T\}$ of interest first and to decide afterward if one or more changes have happened (offline change-point detection). Another approach is to monitor the process sequentially in real-time in order to make an immediate decision at each newly observed time point (online monitoring). Our results hold for both scenarios, but for clarity of exposition we mainly focus on the usually more difficult and, in practice, often more relevant task of online monitoring in the following.

In classical data setups of statistical process control, a time series of scalar values is monitored which means that the detection is mostly limited to a shift of the mean or variance of the observed measurement. Statistical network data, however, covers a lot more information compared to classical data setups (relationships, intensities etc.). Dynamic networks even add another dimension by the consideration of the time component. This has, on the one hand, the advantage of offering a more informative representation of an underlying system enabling, e.g., a better interpretation of observed changes. On the other hand, the derivation of statistical inference approaches gets more challenging. For the task of online monitoring, there are two main issues in this context. First, it is not clear how a change might look like and, second, a direct transfer of traditional monitoring approaches to dynamic network data is hardly feasible as the process is described by a time series of networks and not by a time series of scalar values anymore. It is therefore crucial to a) be aware of possible changes in network data and b) construct monitoring strategies that are suitable for network data.

1.1 Related work

Regarding a), it is not intuitively clear how a change may look like, since there is not only one but many, partly dependent, components which may trigger a change in network structure. A straightforward definition is presented in Ranshous et al. (2015) by assigning a change to time point t, if $|f(D_t) - f(D_{t-1})|> c_0$ and $|f(D_t) - f(D_{t+1})|\le c_0$ for some scoring function $f: D_t \mapsto {\mathbb {R}}$ and a threshold $c_0$. However, this approach is largely limited to the suitability of the applied scoring function as it addresses only those changes, for which f(.) is able to capture the relevant information. In a more comprehensive context, the need of categorizing network changes with respect to their structural levels including nodes, communities or subgraphs is mentioned in Hewapathirana (2019). Such a general categorization to handle this issue is presented in Flossdorf and Jentsch (2021). It covers global as well as local changes of single components (e.g., nodes and links) and addresses their combinations such that more complex structural changes (e.g., in blockmodels) are also considered.

Regarding b), monitoring strategies for dynamic network data are typically based on a reduction of the complexity of the underlying time series of networks. There exist various methods to do so which can be subdivided in model-based, embedding-based and metric-based approaches. For the model-based methods, a dynamic network model is fitted and the specific parameters or residuals are then monitored with a traditional control chart. Examples are state space models (Zou and Li 2017), degree-corrected stochastic blockmodels (Wilson et al. 2019), temporal exponential random graph models (Malinovskaya and Otto 2021), or Poisson regression models (Farahani et al. 2017; Motalebi et al. 2021). However, the model-based approach commonly requires potentially restrictive assumptions like a fixed node set (same nodes for each time point, no node dynamics) or knowledge of the underlying network structure. These assumptions are often too strong, since they can only be used for a small field of applications. Furthermore, they allow to detect only a limited number of changes while ignoring those which does not affect the fitted model.

A related approach is the usage of embedding techniques. In a nutshell, the main goal of network embedding is to learn a mapping function in order to map each single node to a lower-dimensional vector. This results in a latent lower-dimensional feature representation of a graph that reduces noise and redudant information, but still aims to maintain important structural information (Cui et al. 2018). There exist various of these network representation methods such as node2vec (Grover and Leskovec 2016) and DeepWalk (Perozzi et al. 2014) that are developed based on random walks. Other approaches use matrix factorization (Belkin and Niyogi 2001; Ou et al. 2016). Whereas these are specifically designed for static networks, there also exist versions for dynamic networks like temporalnode2vec (Haddad et al. 2020) and DynamicTriad (Zhou et al. 2018). A thorough analysis of the stability of such embedding approaches can be found in Gürsoy et al. (2021), where also the importance for ensuring alignment is stressed as misaligned embeddings might negatively impact the performance for dynamic network inference tasks such as change detection. For the usage of change detection, embedding methods are particularly used to detect vertex-based changes in a time series of graphs like, e.g., detecting vandal users in online social networks using a vector autoregression approach (Li et al. 2019). Moreover, Hewapathirana et al. (2020) propose a spectral embedding method that particularly addresses sparsity and degree heterogeneity. Lin et al. (2022) construct an embedding change detection approach with a focus on node coordinates in a latent space that are used to model edge dependencies. Further approaches involve Sun and Liu (2018), Grattarola et al. (2019), Duan et al. (2020), and Xie et al. (2023).

Lastly, metric-based approaches summarize the network information by assigning a single metric or a combination of different metrics to each $D_t$. Hence, they are more flexible as they can be applied to arbitrary types of networks. Exceptions are similarity measures like DeltaCon (Koutra et al. 2016) or Graph Edit Distance (Bunke et al. 2007) which sequentially compare each $D_t$ to a reference network. For those approaches, a fixed node set is obviously required. This is not the case for any other network metric that is calculated with the sole information of $D_t$. Recent works used centrality metrics (McCulloh and Carley 2011), matrix characteristics (Barnett and Onnela 2016; Hazrati-Marangaloo and Noorossana 2021), scan statistics (Neil et al. 2013), or further network metrics like the clustering coefficient (Kendrick et al. 2018). The application under the consideration of time dependency is discussed in Ofori-Boateng et al. (2021). Obviously though, univariate metric-based methods tend to lead to flexibility issues. A single metric is only able to capture some, but not all information that might be relevant for change detection. Therefore, in Flossdorf and Jentsch (2021), such metrics are analyzed in dependent and independent setups and evaluated with respect to their individual suitability in various situations. A multivariate usage of three network centrality metrics and the network density in a multivariate EWMA chart is studied in Salmasnia et al. (2020). However, a fixed node set as well as a Gaussian distribution for each involved metric is assumed which noticeably reduces the flexibility advantage that metric-based approaches have compared to the other mentioned categories of network change detection.

1.2 Contribution

We expand on the univariate results of the metric-based approaches and study a monitoring method that uses a multivariate set of metrics. We illustrate that such a multivariate approach overcomes the mentioned issues of model-based and other metric-based methods, since it is ad hoc applicable without restrictive assumptions and provides flexibility gains as the relevant information is now simultaneously captured by multiple metrics of various types. We base our analysis on theoretical considerations, simulation-based evidences and practical applications. The need of such a multivariate analysis is mentioned in the univariate literature (McCulloh and Carley 2011; Flossdorf and Jentsch 2021). Contrary to the multivariate investigations in Salmasnia et al. (2020), we do not limit our analysis on a certain set of metrics or control chart and also allow for arbitrary network structures including a dynamic node set and a nonparametric setup. Our primary objective is to present a solution on how exactly a general multivariate procedure shall be implemented and performed. In this context, we identify three challenges that are crucial for a succesful application: a) a sound choice of a set of network metrics, b) their combination with a suitable choice of control charting procedures, and c) the final interpretation of the results. We introduce strategical guidelines to solve these challenges and demonstrate that ignoring them could easily lead to erroneous conclusions and unsatisfying results. We identify a balanced solution that achieves reliable performances in various situations as well as propose solutions that are specialized for more specific scenarios. To support the flexibility of this study, we study both distribution-free and parametric monitoring schemes.

The paper is organized as follows: Sect. 2 offers a short recap of the necessary theory regarding change detection in network data and multivariate control charts. In Sect. 3, we formulate the multivariate network change detection procedure in details and study the suitability of different metric sets, various control charts, and the interaction of both. The results are supported by an extensive simulation study in Sect. 4 which confirms the reliability in various change situations and shows superior performance compared to univariate approaches. In Sect. 5, the procedure is applied to two real-world social network data sets. Section 6 contains some concluding remarks.

2 Existing foundations

In this section, we recap the existing concepts of change detection in network data as well as of traditional statistical process control that are necessary for the introduction of the methodology in Sect. 3.

2.1 Changes in network data

The first challenge is to understand which types of changes may happen in network data. Because a dynamic network consists of various structural elements, a simple shift of location or scale parameters like in traditional scenarios does not exist. As explained above, we focus on a flexible setup and prefer general types of changes (Hewapathirana 2019) rather than specialized changes and therefore follow the change definition of Flossdorf and Jentsch (2021). In this context, the idea is to consider the influence of each structural network element to obtain a thorough categorization of possible changes. These elements are a) links, b) nodes, and c) extra information that may be put on either nodes or links (i.e., covariates, attributes). Each element is assumed to be able to trigger a change either in a global or local manner. A short summary of all scenarios is listed below. Note that we do not consider changes caused by covariates here, since their type of occurrence is hugely dependent on the underlying application field.

• Global Link Change (GLC): The change is triggered by a significantly increased or decreased link amount. This is assumed to happen globally, i.e., the changed link probability affects each node equally.

• Local Link Change (LLC): Similar to GLCs, but the changed link behavior only affects a few nodes which either get more or less influence, i.e., the network structure changes to a more centralized or flat hierarchy.

• Global Node Change (GNC): The node amount increases or decreases significantly, because new nodes enter the network or existing ones leave it.

• Local Node Change (LNC): Only a few influential nodes enter or leave the network which results in a significant impact on the network structure.

Fig. 1

Real-world example for a mixed-type change (MTC): Enron E-mail communication

Table 1 Examples and application scenarios

While all of these changes may occur individually, it is likely that some of them happen simultaneously, e.g., a global increase of links may be the consequence of the entry of new nodes in the network. This is referred to as mixed-type changes (MTC), which also enables capturing more complex change scenarios like those in blockmodels or subgraphs. A real-world social network example for MTCs is depicted in Fig. 1. It shows the e-mail communication between employees of the former US company Enron. It is quite obvious that the overall structure of the network has not changed drastically between the both observed time points. Hence, we have no hint to local changes. However, we can observe a clearly reduced node and link amount in Fig. 1 compared to Fig. 1. The network hence got more sparse both in terms of nodes and links which hints to a mixed-type change of GLC and GNC. Further typical examples and relevant application scenarios for the different types of change are given in Table 1.

2.2 Metric-based network monitoring

We already briefly discussed possible complexity reduction procedures in order to monitor a temporal series of graphs which involves model-based and metric-based approaches. The former one is quite restrictive and not applicable ad hoc, e.g., parametric assumptions have to be met. This also affects that only a few model-specific change types can be detected, e.g., LNCs and GNCs are ignored due to the common assumption of a fixed node set. Those restrictions are especially unfavorable, if the structure and behavior of the network of interest is not explicitly known beforehand. Dynamic networks are commonly quite prone to this issue due to their high dimensionality and potentially high dynamics.

The complexity reduction step of the metric-based procedure is even more radical, but those approaches provide a more flexible monitoring tool without restrictions for a broad application field. Consider that each network $D_t$ of the dynamic network ${\mathcal {D}}$ is reduced to a scalar $f(D_t) = s_t$. Thus, the vector ${\textbf{s}} = (s_1, \ldots , s_T)$ contains the captured information of the applied metric to ${\mathcal {D}}$. Below, we give a summary of typical metrics that are common choices when dealing with network monitoring. For instance, the Frobenius norm is studied in Barnett and Onnela (2016), the Spectral norm in Chen et al. (2021) and as it is equal to the largest eigenvalue for undirected networks also in parts in Hazrati-Marangaloo and Noorossana (2021), the centrality metrics in McCulloh and Carley (2011), Salmasnia et al. (2020), and Ofori-Boateng et al. (2021). Note that the matrix norms are calculated based on the temporal series of adjacency matrices $A_t \in {\mathbb {R}}^{n_t \times n_t}$ of the networks $D_t$, where $n_t$ is the number of nodes at time point t. For the sake of simplicity, we mainly focus on undirected and unweighted networks which means that a matrix entry $a_{t,ij} = 1$, if a link between nodes i and j exists, and $a_{t,ij} = 0$ otherwise.

• Frobenius norm (F): $\sqrt{\sum \limits _{i = 1}^{n_t} \sum \limits _{j = 1}^{n_t} a_{t,ij}^2}$.

• Spectral norm (S): $\max \limits _{\left\Vert x \right\Vert _2 = 1} \left\Vert A_t x \right\Vert _2$.

• Closeness centrality (C): $c_i^C = (\frac{1}{n-1}\sum \limits _{j \in V} \text {d}(i,j))^{-1}$.

• Degree centrality (D): $c_i^D = \sum \limits _{j = 1}^{n_t} a_{t,ij}$.

• Betweenness centrality (B): $c_i^B = \sum \limits _{i \ne j \ne l}\frac{\sigma _{jl}(i)}{\sigma _{jl}}$.

• Eigenvector centrality (E): $c_i^E = \frac{1}{\lambda }{\sum \limits _{j=1}^{n_t}} a_{t,ij} c_j^E$.

In this context, d(i, j) denotes the shortest path between two nodes i and j, $\sigma _{jl}(i)$ the number of shortest path between two nodes j and l (that pass through node i), and $\lambda$ the largest eigenvalue of $A_t$.

Whereas the matrix norms are global metrics for the whole network $D_t$, the centrality scores are locally defined for each node. To transform them into a global network metric, we consider two approaches. On the one hand, this involves the average score over all nodes, i.e.,

$$\begin{aligned} c_{\text {avg}} = \frac{1}{n} \sum _{i \in V} c_i. \end{aligned}$$

On the other hand, we can use a scale metric by taking the deviation to the largest observed score

$$\begin{aligned} c_{\text {dev}} = \sum _{i \in V} (\max _{j \in V} (c_j) - c_i). \end{aligned}$$

We specify the used version in the following by noting an m or d index (e.g., C$_m$ for mean Closeness and C$_d$ for Closeness deviation). Note that for the eigenvector centrality, both versions are affine linear transformations to each other and therefore achieve equal monitoring performances. It is possible to use any other network metric as well, e.g., the Average Path Length or the Clustering Coefficient like in Kendrick et al. (2018), but many are strongly related to the presented ones and do not contribute added value (Flossdorf and Jentsch 2021).

2.3 General online monitoring procedure

The main goal of online monitoring is to detect anomalies in a process as soon as possible after their occurrence. Typically, the process of interest is subdivided into two phases. In Phase I, it is assumed that the process is somewhat stable and reliably represents the typical state of the underlying system without meaningful deviations. The system is then called to be in-control. In Phase II, the actual monitoring takes place by deciding if an incoming signal sufficiently matches the in-control state. An alarm is triggered if this is not the case and the signal is classified as out-of-control (Basseville and Nikiforov 1993).

Consider $\{Y_t, t=1, \ldots , T\}$ to be a sequence of a random variable of interest with conditional density $P_{\theta }(Y_t \mid Y_{t-1},..., Y_{1})$ and $\tau$ to be the unknown change time. If $\tau > t$, then the conditional density parameter $\theta$ is constant with $\theta = \theta _1$. For $\tau \le t$, it applies $\theta = \theta _2$. The goal is to detect the anomaly as soon as possible with a fixed rate of false alarms before $\tau$. An estimation of $\theta _1$ and $\theta _2$ is often not necessary, but might be useful for interpretation purposes regarding possible reasons for a change.

In terms of the practical usage, control charts are applied. First, a metric $x_t$ is chosen which a) can be calculated for each time point t, b) covers and represents most relevant aspects of the behavior of the system (i.e., $Y_t$), and c) is able to identify all considered changes by a sensitive reaction to them. This metric serves as the main input for the control statistic $z_t$ which is calculated for the process at each time point t. Depending on the setup, $z_t$ can be the metric itself (e.g., in memory-free Shewhart charts) or some sort of transformation $z_t = g(x_t)$ (e.g., in memory-based EWMA or CUSUM charts). In Phase I, $z_t$ is expected to represent the in-control state of the system and, hence, to be a stable process without meaningful deviations. This information is used to define the upper and lower control limits $h_u$ and $h_l$. Those limits are chosen under the consideration of the desired rate of false alarms and can be derived by parametric or distribution-free procedures. In Phase II, if we observe $h_l \le z_t \le h_u$, the process is deemed in-control. Otherwise an alarm is triggered at time point t to signal a detected change.

2.4 Control charts for traditional multivariate data

In practice, it is customary to improve the monitoring procedure by taking more process metrics into account. Their independent usage in a univariate manner is possible but not recommended, since it is inefficient and may result in erroneous conclusions Montgomery (2012). Hence, the construction of multivariate control charts, which consider the metrics jointly, is of interest.

In this context, the most basic multivariate chart is the Hotelling $T^2$ chart. Suppose we observe a vector $\mathbf {x_t} = (x_{t1},..., x_{tp})$ of p different process metrics at each time point t, then the corresponding control statistic is calculated by

$$\begin{aligned} z_t = (\mathbf {x_t} - \mathbf {{\bar{x}}})' {\textbf{S}}^{-1} (\mathbf {x_t} - \mathbf {{\bar{x}}}), \end{aligned}$$

where $\mathbf {{\bar{x}}}$ and ${\textbf{S}}$ are the sample mean vector and covariance matrix of the underlying observations. Since $z_t$ mainly takes the squared deviation to the sample mean into account, it is non-negative and we expect values near zero if the process is in-control. Therefore, only an upper control limit has to be derived. This can be done under parametric assumptions with an approximation via the F-distribution which yields

$$\begin{aligned} h_u = \frac{p(n+1)(n-1)}{n^2 - np} F_{\alpha , p, n-p}, \end{aligned}$$

where n is the number of observations in Phase I and $\alpha$ the desired false alarm rate.

In many practical applications, the met distributional assumption might not be justified which can have a strong negative impact on the monitoring performance. To avoid such issues, the usage of nonparametric techniques seems promising. In this context, a bootstrap approach was proposed in Phaladiganon et al. (2011), which is able to efficiently handle the monitoring process, even if the observed data is non-Gaussian or unknown. It works as follows. First, the statistic $z_t$ is calculated for all T observations of Phase I as before, which yields the vector ${\textbf{z}} = (z_1,..., z_T)$. Subsequently, B Bootstrap samples with sample size T are drawn from ${\textbf{z}}$ and for each of those samples the $(1-\alpha )$-quantile is calculated. The upper control limit $h_u$ is then determined by taking the average over those values.

The Hotelling $T^2$ charts are multivariate extensions of a univariate Shewhart-type control chart, because they only use information of the current observation which makes them rather insensitive to small shifts. Memory-based control charts like exponential weighted moving average charts (EWMA) overcome this issue, the control statistic of a multivariate version (MEWMA) (Lowry et al. 1992) is defined as

$$\begin{aligned} z_t = {\textbf{m}}_t' \mathbf {S_t}^{-1} {\textbf{m}}_t, \end{aligned}$$

where $\mathbf {m_t}$ is recursively defined as

$$\begin{aligned} {\textbf{m}}_t = \lambda ({\textbf{x}}_t - \mathbf {{\bar{x}}}) + (1 - \lambda ) {\textbf{m}}_{t-1}. \end{aligned}$$

The estimation of the covariance matrix is given by

$$\begin{aligned} {\textbf{S}}_t = \frac{\lambda }{2 - \lambda }[1 - (1 - \lambda )^{2t}]{\textbf{S}}, \end{aligned}$$

where ${\textbf{S}}$ is the estimated covariance matrix given all observations from Phase I. While the formula of the control statistic is quite similar to the Hotelling $T^2$ chart, the main difference lies in the intermediate step of calculating ${\textbf{m}}_t$, where the smoothing parameter $\lambda \in [0,1]$ serves as a factor for providing weights to past observations and the current one. For $\lambda = 1$, the MEWMA setup corresponds to the Hotelling $T^2$ chart. Optimal control limits depending on $\lambda$, the number of variables p and the desired false alarm rate can be found in several works (Prabhu and Runger 1997; Knoth 2017). In general, MEWMA charts with small values of $\lambda$ are rather robust to the normal assumption yielding satisfying results for different distributions of the underlying data (Montgomery 2012).

3 Multivariate metric-based monitoring solutions

After the recap of the theoretical background of the existing foundations in Sect. 2, we now move on to the practical implementation of a monitoring setup for network data by combining and adapting multivariate control chart schemes with an intelligent choice of a set of network metrics. Making use of network metrics for the monitoring of networks, first, the practitioner has to choose the (multivariate) set of metrics in conjunction with a suitable control chart procedure. While there is a whole variety of (and even more combinations of) networks metrics that could be used, it is generally unclear which combination of such network metrics should be used in which dynamic network scenario to detect deviations from the control state as reliable as possible. As the further steps are rather straightforward, that is, the calculation of the corresponding control statistic and control limits (Phase I), the monitoring of new observations (Phase II) and how to stop at a detected change, the interpretation of the change is also not straightforward. In this context, note that this work aims to present a general procedure and particularly focuses on developing an ad hoc solution that is applicable to arbitrary network shapes and application fields and enables a reliable change analysis in various situations. Therefore, we present general guidelines for different categories of application scenarios and identify the most flexible solution that performs reliably even in unknown circumstances.

Table 2 Performances of the metrics in various situations

3.1 Selection of a suitable set of metrics

We use the metrics that were presented in Sect. 2.2 as these are the common choices for extracting the information of a network (McCulloh and Carley 2011; Hazrati-Marangaloo and Noorossana 2021; Chen et al. 2021; Barnett and Onnela 2016; Salmasnia et al. 2020; Ofori-Boateng et al. 2021). Because the information of a network gets reduced to a single scalar value, the resulting information loss is typically quite large. It is therefore crucial to be aware of the information a metric is able to capture in order to understand which type of change it is able to detect which was discussed in Flossdorf and Jentsch (2021). See Table 2 for a short summary of the individual suitability of the considered metrics in the presented change scenarios.

Due to the described information loss, it is not too surprising that no single metric is able to perform well in all scenarios. However, for each type of change, there exist multiple metrics that work reasonably well. Hence, it is a natural approach to use multiple metrics jointly in order to capture various pieces of information to mitigate the loss. Formally, for each $D_t$, a vector ${\textbf{s}}_t = (s_{t1},..., s_{tp})$ of p different scores is calculated at each time point t. In this work, we mainly focus on sets with $p = 3$.

In this context, the main challenge is the choice of a suitable set of metrics. The main statement of Table 2 is that most metrics either perform reasonably well in change situations that affect either the network globally (i.e., GLC, GNC) or in local change scenarios (i.e., LLC, LNC). Based on this, we may classify most metrics into two different performance groups A = {S, C$_m$, D$_m$, B$_m$}, which perform well in global change scenarios, and group B = {C$_d$, D$_d$, D$_b$} that perform superior in local setups. Remaining are the Frobenius norm, which can handle link changes but ignores node changes, and average Eigenvector Centrality that is theoretically affected by all change types but sometimes to a lesser extent.

The final choice of a suitable set of metrics is dependent on the goal and the expectations of the application. Based on the described univariate behavior of the presented metrics, we propose to consider the following multivariate monitoring strategies.

• I - Balanced Setups: This category represents the most flexible monitoring strategy. The goal is to achieve a reliable performance for as many as possible change types. Particularly, changes of moderate to high intensity should be detected. Corresponding sets include one metric from each of the performance groups A and B. The third metric is the average eigenvector centrality. This balanced setup is a promising candidate for ad hoc applications in which users do not know what to expect and how a change might look like (e.g., networks with high dynamics like social networks). Example setup: SB$_d$E.

• IIa - Balanced Setups with a focus on global changes: In this category, it is still of interest to be sensitive to as many change types as possible, but with a clear focus on the detection of global changes. This category involves all 2 vs. 1 combinations (i.e., two metrics out of group A and one out of group B). Example setup: SD$_m$C$_d$.

• IIb - Balanced Setups with a focus on local changes: The same as IIa, just with a major focus on local changes (i.e., one metric out of group A and two out of group B). Example setup: B$_d$D$_d$S.

• IIIa - Unbalanced setups for global changes: It is only of interest to detect global changes in the network - even those which are characterized by a small change intensity. The detection of other change types is not relevant. The corresponding metric sets are constructed with three metrics out of group A. Example setup: C$_m$D$_m$S.

• IIIb - Unbalanced setups for local changes: The same as IIIa, just for local changes. The metric sets are constructed with three metrics out of group B. Example setup:C$_d$D$_d$B$_d$.

• IV - Setups with a particular focus on link changes: This category represents all metric sets in which the Frobenius norm is part of, since this metric is specialized to detect link changes. Changes purely triggered by nodes can also be emphasized by combining the Frobenius norm with other metrics that are sensitive to it. Example setup: FSB$_d$.

In a nutshell, the idea behind Category I is to use one metric out of both classes A and B, in order to capture various types of information. The usage of the average eigenvector then provides some neutral perspective. This balanced setup seems to be a promising candidate for an ad hoc application in which users do not know what to expect and how a change might look like (e.g., networks with high dynamics like social networks). The other Categories offer some more unbalanced setups by 2 vs. 1 and 3 vs. 0 combinations. These are constructed for more specialized cases where the user might be interested in detecting some particular changes which frequently occur in the corresponding application (see examples in Table 1). Finally, Category VI emphasizes link changes more by taking the Fobenius norm into account.

As mentioned, we used $p = 3$ as the number of considered metrics for the development of the categorization scheme above. The usage of other values is of course possible. However, we would like to note that a higher value of p is in theory helpful for capturing more information, but is also prone to more uncertainty picked up by the monitoring procedure, which might result in power losses. Moreover, some of the metrics might be highly correlated due to a similar definition which would make the monitoring procedure less efficient for higher p and might even lead to erroneous conclusions. Moreover, values of $p > 3$ do likely not contribute added value as there are the two explained performance groups. Considering this, $p = 3$ seems to be a good trade-off between information capturing and maintaining flexibility. This is also validated by our simulation study in Sect. 4.

A particular metric set with a value of $p = 4$ is considered in Salmasnia et al. (2020). For the remainder of this paper, we denote this set by SAL. The included metrics are deviation metrics for the Betweenness, Degree, and Closeness centralities with a similar definition to B$_d$, D$_d$, and C$_d$. Additionally, the network density is used as a fourth metric. Overall, this metric set can be classified in our Category IIIb as it uses three metrics that are specifically sensitive to detect local changes. As we will see in the simulation study, the additional consideration of the density does not change much compared to the B$_d$D$_d$C$_d$ set as these metrics are highly correlated and quite dominant in their multivariate combination.

3.2 Selection of a suitable multivariate control chart

The choice of a suitable control chart setup is as important as the choice of a metric set. The monitoring performance of the parametric Hotelling $T^2$ chart is dependent on the quality of the fit of the applied F-distribution. To the best of our knowledge, no complete asymptotic inference has yet been derived for the considered network metrics due to their complex nature. Consequently, putting parametric assumptions on their joint distribution seems rather implausible. The parametric Hotelling $T^2$ chart is known to react rather sensitively to violations of its distributional assumption (Stoumbos and Sullivan 2002) and might suffer from reliability issues in this context. We expect that this is especially the case for rather unbalanced multivariate sets of metrics, since their marginal distributions tend to be more similar to each other and are sensitive to the same impact factors, which may result in a more skewed joint distribution. This behavior can particularly be observed for sets of Categories IIIa and IIIb and also for the presented one of Salmasnia et al. (2020). For more balanced setups, this effect is likely to be weakened, because different sensitivities are involved. Furthermore, we expect a worse performance of the Hotelling $T^2$ chart for lower false alarm rates $\alpha$, because the corresponding control limit $h_u$ depends on the $(1-\alpha )$-quantile of the applied distributional assumption. Higher quantiles are likely to be bad approximations for the corresponding quantiles of the empirical distribution, which is---for very low $\alpha$---sensitive to the observed extreme values that might especially play a role for rather unstable and high-dynamic processes like networks. Overall, this effect tends to be less pronounced for larger values of $\alpha$ as the quantile of interest is shifted more toward the center of the distribution. The explained impacts affect the MEWMA chart as well, but to a lesser extent. Due to the smoothing of the control statistic that involves the consideration of past observations, the chart is noticeably more robust against non-Gaussian behavior. This is particularly the case for lower values of the smoothing parameter $\lambda$ which weakens the individual influence of the current observation. However, note that inertia issues might be a consequence of this (Lowry et al. 1992).

Finally, the nonparametric Hotelling $T^2$ chart might be the safest choice for a reliably constructed control chart when using the considered metric sets. As the bootstrap procedure is directly dependent on the empirical distributions, we expect the chart to be more robust against various types of metric sets, i.e., to perform on a similar level for all sets. Obviously, its quality increases for larger sample sizes (i.e., longer in-control phase), and the bootstrap procedure ensures that it works reasonably in most cases of lower sample sizes as well. However, in the latter cases, its performance might not be superior to the parametric candidates anymore as we will see in Sect. 4.

3.3 Interpretation of the results and further analyses

To conclude, we recommend using a balanced metric set like SB$_d$E together with the nonparametric Hotellings $T^2$ chart for the most reliable solution in flexible scenarios. Regarding the interpretation of the monitoring results, note that we monitor a temporal series of networks ${\mathcal {D}} = \{D_t, t = 1, \ldots , T\}$ instead of a simple process variable $Y_t$. Hence, the change parameter $\theta$ gets more complex (see Sect. 2.3) making its interpretation in a change situation all the more important. This especially concerns the purpose of maintaining transparency and reliability of the monitoring tool. In practice, we propose to stop after a detected change and to analyze the corresponding network $D_t$ carefully. This can be handily done by descriptively analyzing the univariate values of the used metrics and applying their interpretations given in Table 2 in order to identify the underlying change type. Precise intepretation examples are given in Sect. 5.

While focussing on temporally independent setups and the related challenges in this paper, the presented procedure can be handily extended to allow also for time dependency. For instance, this can be done by fitting an ARIMA model to the multivariate series of metrics in order to monitor its residuals similar to Ofori-Boateng et al. (2021); Flossdorf and Jentsch (2021); Pincombe (2005).

4 Simulation study

To underline our findings, we execute an extensive simulation study in the following. We generate numerous example situations of each described change type and analyze the performances of the proposed multivariate metric strategies in combination with the described control chart procedures. Additionally, we compare their results with the corresponding univariate metric performances as studied in McCulloh and Carley (2011), Ofori-Boateng et al. (2021), or Barnett and Onnela (2016) and with the multivariate approach SAL of Salmasnia et al. (2020). Recall that a comparison with typical model-based and embedding-based approaches is not feasible here in a meaningful way, as our study is designed to detect flexible changes without imposing any high-level assumptions on the network structure (e.g., fixed node set, model assumptions). In a second part, we extend the study by analyzing more practical relevant mixed-type changes in different situations of stochastic blockmodels. The code for the simulation study can be found in a GitHub repository¹ created by the authors.

Table 3 Data generation processes using Erdös-Renyi (ER) graphs

Table 4 Parameter setup for each situation according to Table 3 with $n = 50$

4.1 Setup

We generate sampling data for each of the four described change types of Sect. 2.1 (GLC, LLC, GNC, and LNC). For each of those, we execute three sub-situations with varying change intensities (small, moderate, and heavy). This results in 12 scenarios in total, which are repeated 1000 times to obtain a reliable performance analysis. The data generating processes as well as their different parameter setups to control the intensity are given in Tables 3 and 4.

For each situation, we simulate dynamic networks of length $T = 1400$ and use the first 1000 observations as Phase I in order to reliably calibrate the control chart. The change time is set to happen at time point $\tau = 1050$. The control limits of the control charts are set with a false alarm rate of $\alpha = 1\%$. While the rather large number of observations in Phase I is interesting to obtain meaningful findings about the theoretical performances and the suitability of the metric sets, we are aware that, from a practical point of view, those numbers are usually hard to provide in real-world applications. To this purpose, we examine the performances in practically more relevant simulation settings in Sect. 4.4 and analyze real-world networks in Sect. 5.

For all scenarios, we evaluate the performances of all triple combinations of the presented metrics and particularly focus on the results of the multivariate metric set categories that were derived in Sect. 3.1. We evaluate their performance in combination with all three presented control chart procedures and compare the results with the univariate approaches. As performance measures, we use $\text {ARL}_0$ and $\text {ARL}_1$. The $\text {ARL}_0$ is defined as the in-control average run length which can reach an optimal value of $\frac{1}{\alpha } = 100$ in our setup. On the other hand, $\text {ARL}_1$ calculates the post-change average run length which measures the delay to detection, i.e., the number of time points an alarm is sent after the actual change has occurred.

To maintain comparability across the univariate and multivariate setups, we compare memory-free settings and memory-based procedures separately. Hence, the parametric and nonparametric Hotellings $T^2$ charts are compared with the Shewhart chart and the MEWMA chart with the EWMA procedure. For the latter ones, we try different smoothing parameters $\lambda \in \{0.1, 0.2,..., 0.7\}$ and report the ones with the best results.

4.2 Phase I performances

We begin with the evaluation of the in-control state. Figure 2 illustrates the empirical false alarm rates for all considered multivariate control charts in each of the 72 examined scenarios for all three applied control chart types.

Fig. 2

Average empirical false alarm rates for all simulated situations. The desired value for $\alpha$ is 0.01

The results largely meet our expectations as the parametric Hotelling $T^2$ procedure tends to yield relatively low control limits. This particularly seems to be the case for more unbalanced setups (e.g., C$_m$D$_m$S, B$_d$C$_d$D$_d$, SAL) which tend to generate more skewed joint distributions as explained in Sect. 3.2. Overall, however, the desired fit is not reached for more balanced sets as well, since their false alarm rates lie above the desired $\alpha$ and above the ones of the other two procedures.

Fig. 3

Example situation for a comparison of the simulated empirical distribution with the corresponding F-approximation of the parametric Hotelling $T^2$ chart

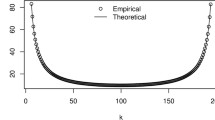
See Fig. 3 for an example of the quality of the fit where the deviation of the empirical distribution to the assumed F assumption is clearly visible, particularly at the tails of the distribution. Regarding the other control charts, the results support the statement that MEWMA is more robust against possible parametric violations. However, the nonparametric bootstrap approach clearly yields the most reliable in-control results for the rather long in-control phase and the small value of $\alpha$.

4.3 Phase II performances

We saw that the charts produce quite different $\text {ARL}_0$ values, although they were designed to hold a common fixed false alarm rate. Obviously, charts with a lower $\text {ARL}_0$ will produce lower values of $\text {ARL}_1$ on the same data set, since the control limit $h_u$ is lower. Hence, the $\text {ARL}_1$ results should only be compared between the same applied control chart type. As the bootstrap chart achieved the most reliable Phase I performances, we therefore report the Phase II results only for the bootstrap chart and concentrate on the performance differences of the applied metric sets. See Table 5 for an overview of the results for the univariate procedure and the representatives of the multivariate monitoring strategies. The results for all 84 triple combinations are given in Tables 8, 9, 10, 11, 12, 13 and 14 in the Appendix.

Table 5 $\text {ARL}_1$ for the studied change types. Best $\text {ARL}_1$ for each scenario across all setups (univariate and multivariate) is printed in bold

Overall, the results meet our expectations. The univariate metrics might perform reasonably in special scenarios, but show clear weaknesses in others. The multivariate procedures, on the other hand, perform clearly more reliable over all situations and are more robust to the underlying change type which underlines the improved flexibility compared to the univariate approach. On a further note, the results are handily interpretable and are aligned with the statements of our derived categorization of Sect. 3.1. We can, e.g., take a closer look at the performance of a representative of Category I, i.e., the balanced set SB$_d$E (consisting of S, B$_d$, and E). Regarding the involved univariate performances, S is able to handle global changes, but has problems with LLCs and especially LNCs. For B$_d$, the behavior is vice versa. Their joint monitoring, however, leads to promising results for all scenarios, since their effects are combined. The additional consideration of E, which is in theory sensitive to all types, but to a lesser extent, serves slightly supportive to all impacts and as an overall smoothing factor. The behavior for more unbalanced multivariate setups of Categories IIa, IIb, IIIa, IIIb is similar as they provide more flexibility overall compared to the involved univariate candidates. Particularly, the $\text {ARL}_1$ for the “non-specialized" cases (i.e., the cases, for which all involved metrics are not really suitable) improved as the small sensitivities of the single metrics have a larger impact if they are considered jointly, see, e.g., the B$_d$C$_d$D$_d$ performance for GNCs or the C$_m$D$_m$S performance for LLCs. Despite the improved performance compared to the univariate metrics, the values are obviously higher than those of more balanced setups in these situations. Moreover, it is somewhat surprising that they also do not clearly outperform the more balanced sets in “specialized" cases, for which they are mainly constructed.

Lastly, the results for the performance of SAL underline our previous interpretations as this metric set achieves reasonable results for local changes, but struggles more in global change cases compared to other multivariate sets. This behavior underlines our classification into Category IIIb of Sect. 3.1. Furthermore, the additional consideration of the network density as a fourth metric compared to the set B$_d$C$_d$D$_d$ seems to not contribute relevant added value as the performances are quite similar.

4.4 Extension to mixed-type changes

While this examination under rather rigid settings gave us crucial insights on the theoretical performance limits of the considered monitoring applications, we now examine if the studied behaviors still hold in practically more relevant application examples. For this purpose, we consider mixed-type changes (MTC) in the popular scenario of community changes in stochastic blockmodels (SBM) (Holland et al. 1983). The explicit setups can be found in Table 6, where K represents the number of communities, $p_i$ the intra-group link probability of group $i \in \{1,..., K\}$, $p_{ij}$ the inter-group link probability between groups i and j, and $n_i$ the number of nodes in group i. Furthermore, we reduce the length of the in-control phase to 100 in order to examine the performance of the charts in more data-restrictive circumstances. Due to the shorter in-control length, we set the false alarm rate to $\alpha = 5\%$.

Table 6 SBM parameter setups for the community changes

Fig. 4

Average empirical false alarm rates for all simulated situations

Table 7 $\text {ARL}_1$ for the community changes. Best $\text {ARL}_1$ for each scenario across all setups is printed in bold

The in-control results shown in Fig. 4 are different to those before. Whereas the nonparametric version clearly outperformed the parametric control charts in Sect. 4.2, the performances are more equal now. The nonparametric approach suffers from the shorter in-control length, because the estimation of the theoretical distribution becomes more unreliable by applying a smaller data sample to the bootstrap procedure. However, the chart still performs reasonably as it only lies approx. $0.5\%$ above the desired $\alpha$. Another advantage is the robustness against different metric sets. Overall, the parametric control charts perform better than before and reach similar performances for more balanced metric sets to the nonparametric candidate. An explanation is the higher value of $\alpha$, for which the charts are designed, as explained in Sect. 3.2. However, the sensitivity to the applied metric set still holds as the performance gets quite unstable for unbalanced sets.

The $\text {ARL}_1$ results in Table 7 can be interpreted similarly as before. Situation 1 describes a change with an increased popularity of the whole network with an increased inter- and intra-communication (link amount) and the arrival of new members which can be seen as a MTC of GNC and GLC. Apart from some univariate deviation centralities, all considered metric sets perform well. The second scenario addresses changes, where the importance between two groups is shifted, which results in an increased communication of one group and a decreased communication in the other. While most univariate metrics are not able to handle this change type as their $\text {ARL}_1$ does match their set $\text {ARL}_0$, the multivariate sets perform reasonably, particularly the more balanced ones. The last two situations address changes in the number of communities, e.g., a split of one group into two different ones. For the third situation, the link probability in both new groups stays the same as before which results in an overall decreased link amount due to the decreased link probability of those nodes, which were in one group before and are in different ones afterward. Hence, it is a relatively easy GLC situation and all applied metrics achieve a satisfactory performance. We designed the last scenario such that the overall link probability stays the same after the split. This makes the detection more challenging which results in higher $\text {ARL}_1$ values. However, the multivariate sets again underline their superior flexibility as they achieve better performances in this situation than their univariate counterparts.

5 Empirical data examples

To further underline the applicability and the handling of the approach, we analyze two real-world dynamic networks from economics and social sciences.

5.1 International trade data

This publicly available data set from the World Trade Organization (WTO) contains all reported international import–export relationships that are responsible for 90% of the overall worldwide trade volume. The data is collected quarterly and contains the time span of Q1 2010 - Q1 2022 which results in a dynamic network of $T = 49$ time points. For the selection of the in-control phase, we use the first 22 time points, i.e., the time span Q1 2010–Q2 2015. We are not aware of major trading conflicts in this time period and therefore expect stable behavior. As this in-control phase is rather short, we use the bootstrap Hotellings $T^2$ chart, because it promises to yield the most reliable results in these circumstances compared to the other charts as we saw in the simulation study. We do not expect a particular change type, since changes triggered by nodes and links both in a global and in a local fashion are conceivable. Therefore, we use the balanced metric set SB$_d$E in order to increase the probability for the detection of arbitrary change types. The result is shown in the upper part of Fig. 5.

Fig. 5

Control charts using a balanced metric set (upper chart) and an unbalanced metric set (lower chart). In-control phase ends in Q2 2015. Red dots signalize alarms

The procedure detects a change in Q2 2020 that is probably triggered by the corona pandemic. Many countries were forced to reduce their trading activities and mainly restrict them to neighboring states and the most important partner nations. This behavior pushed the trade network to a more centralized layout with leading trade nations as the hubs. Consequently, we can classify the observed change as a local change. Interestingly, we cannot detect global changes for this data as more unbalanced metric sets, that are focussed on global change types, do not trigger an alarm. This is visualized in the lower control chart of Fig. 5, for which we used the metric set C$_m$D$_m$S. Hence, the pandemic apparently did not have a huge influence on the amount of relationships that are responsible for 90% of the overall worldwide trade volume, but it did change the network on a structural level as explained. This example again underlines the importance of a careful execution of the procedure and the flexibility advantage of a balanced metric set.

5.2 Enron email data

This data contains the email communication network between employees of the former US company Enron that has been made public by the US Department of Justice and was rigorously analyzed in many publications (Priebe et al. 2005; Park et al. 2009; Chapanond et al. 2005). It comprises a time span from January 2000 until April 2002 on a monthly level. This results in T = 28 time points, from which we use the first 17 for the in-control phase and we aim to detect the effects of the accounting fraud scandal in the late 2001 s and early 2002 s. We again use the unbalanced metric set SB$_d$E in a bootstrap Hotellings $T^2$ chart in order to be flexible regarding the existence of different types of change. The output of the resulting control chart is depicted in Fig. 6.

Fig. 6

Control Chart with SB$_d$E for the Enron data. In-control phase ends in May 2001. Red dots signalize alarms

The procedure triggers alarms that are in accordance with other social network analyses of this data set (Kendrick et al. 2018). In June 2001, the CEO Jeffrey Skilling tried to fire the chairman and former CEO Kenneth Lay, in September/October 2001 Enron reported a huge loss and it was announced that a SEC (Security and Exchange Commission) inquiry has become a formal investigation, and in February/March 2002 more and more details of the fraud were made public.

6 Conclusion

The detection of temporal differences in a time series of graphs is a rather challenging task due to the complex nature of dynamic networks. We proposed an extension of a metric-based approach to a multivariate setup and its combination with suitable control charting procedures involving parametric as well as nonparametric setups. We explicitly explained the challenges of such a multivariate design and presented recommendations including a sound choice of a suitable set of metrics, its combination with a suitable control chart, and the final interpretation of the results. We particularly recommend to use a balanced metric set like SB$_d$E together with a nonparametric control chart like the bootstrap Hotelling $T^2$ chart in order to achieve reliable results in flexible change situations. We further validated our statements with the help of a simulation study and some real-world examples in which a thoroughly designed multivariate approach outperforms the univariate procedure by offering a more flexible solution to the problem of change detection in social network analysis. As a main part of this paper was studying and evaluating different multivariate network metric sets and their capability of capturing relevant network information, the results can be beneficial for further statistical analysis procedures. In our view, this especially yields for statistical testing procedures (e.g., goodness-of-fit, two-sample tests) for network data where test statistics (i.e., metrics) need to be derived that characterize the network structure as comprehensively as possible. Furthermore, our results can be beneficial also for researchers that aim to derive network monitoring procedures for a certain application scenario, e.g., with pre-known network structures (like in model-based approaches). In this context, our results can be used as a benchmark method as it is particularly designed for detecting changes of more general form.

Appendix

On the next pages: Tables for the performance of all potential metric sets for Sect. 4.3.

Table 8 $\text {ARL}_1$ multivariate performances

Table 9 $\text {ARL}_1$ multivariate performances

Table 10 $\text {ARL}_1$ multivariate performances

Table 11 $\text {ARL}_1$ multivariate performances

Table 12 $\text {ARL}_1$ multivariate performances

Table 13 $\text {ARL}_1$ multivariate performances

Table 14 $\text {ARL}_1$ multivariate performances