Kinetic and thermal simulation of water droplets in icing wind tunnels

Abstract

Within the certification process of aircraft, tests under specific icing conditions are required. For such safety relevant tests—which are performed under defined and repeatable test conditions—specially equipped Icing Wind Tunnels (IWT) are required. In such IWTs, supercooled water droplets are created with the aid of a spray system injecting pre-tempered water droplets of specific diameters into the free stream air flow. Especially tests with a droplet size up to 2mm (Supercooled Large Droplets - SLDs) are of great importance. SLDs are difficult to generate under laboratory conditions in IWT since usually the available droplet flight time from the injection location to the impact position on the test object is insufficient to reliably cool down a droplet at least to freezing temperature. To investigate the limitations associated with the application of SLD, the current work provides a method to allow detailed insight into the behavior of droplets on the path from the injection spray nozzle to the test section. In this work a state space model of a single droplet is derived that combines the kinetic aspects, thermal properties as well as the governing differential equations for motion, convective heat transfer at the droplet surface and heat conduction inside the droplet. Beside the states for the droplet’s position and velocity in space, the state space vector comprises various fluid and thermodynamic parameters. The droplet-internal temperature distribution is modelled by a discrete one-dimensional spherical shell model that also incorporates the aggregate phase (freezing mass fraction) at each shell node. This approach allows, therefore, the simulation of potential droplet phase change processes (freezing/melting) as well. With the model at hand, the influence of various boundary conditions (initial droplet temperature, flow field, ambient air temperature, etc.) can be determined and evaluated. As a result, concrete measures to achieve a desired operating condition (e.g. droplet temperature at the test object) for various model assumptions can be derived. In addition, the simulation model facilitates the prediction of the droplet diameter threshold for ensuring a supercooled state upon the impact on the test object. The governing theoretical influences are described, and various simulation results for representative test conditions that occur at the Rail-Tec-Arsenal (RTA) in Vienna are presented.

1 Introduction

The problem arising due to icing of aircraft components is inevitable, and various fields of research and experiments are dealing with an exact description of the complex processes involved. There exist several approaches that try to tackle the process of ice accretion in a numerical way [1].

For the application of SLD testing within Icing Wind tunnels, two major concerns arise: Firstly, the overall heat transfer to reach a supercooled state of the droplets must be achieved, and secondly, gravitational influences and momentum of the droplets may restrict the usable test section area [2]. To allow for the investigation of the temperature of a water droplet within an IWT such as the RTA icing wind tunnel and for the general investigation in the layout of IWT, the described simulation model was set up. With the aid of this model, the actual temperature of a water drop can be predicted. It can be checked, whether it is theoretically possible that a water droplet reaches a “supercooled” state at the point where it impacts on a test specimen. To achieve a simulated time history of the droplet position in space, the temperature distribution within the droplet shell model and the freezing mass fraction, the governing differential equations are numerically solved. The flow field itself may be of arbitrary origin such as CFD calculations, analytical calculations or measurements. For the presentation of exemplary results within this work, the flow field is determined by means of CFD calculations. As the underlying phenomena of the cool down history as the main contribution of this work can be transferred to arbitrary layout of future IWT to be designed, any quantitative assessments of the flow field properties itself are not within the scope of this work.

A common model is documented within the work of Willbanks and Schulz [3], describing an one-dimensional, multiphase flow code (the “AEDC-1DMP” code) also incorporating a partial freezing model that is used in various studies by Al-Khalil et al. [2] and Orchard et al. [4]. The AEDC-1DMP also includes model assumptions reducing its applicability to the simulation of temperature and trajectories of SLD. The work of Orchard et al. includes an overview of simulation methods documented in literature. Various approaches incorporate evaporation and partial freezing models while having the scope of e.g. predicting the LWC content at a given test section [5] or investigating on droplets trajectories and the effects of the flow field on the cloud density variation within axisymmetric wind tunnels [6] or for predicting ice and water deposition in aeronautical mixing manifolds [7]. While basically following the same approach for the kinetic simulation of droplets exposed to a flow field, the current work is not limited to an analytic expression for the flow field. Extending the applicability to arbitrary flow fields from various sources greatly enhances the field of application to arbitrary wind tunnel layouts. Most importantly, the aforementioned models assume a lumped thermal drop model and to the best knowledge of the authors, no comparable study of inner heat transfer of large droplets within an IWT as described in the current work is available.

The approach chosen here differs from the previously methods and the current work extends the scope of the simulation and the model assumptions to better fulfill the specific requirements of SLD simulation for IWT design tasks:

• The trajectory, relative velocity and subsequently heat transfer calculations are based on a separately performed CFD calculation and are capable of handling 3-dimensional flows. Separately calculating the flow field allows more elaborated calculations including complex wind tunnel geometry, varying cross sections, fixtures etc. as well as sophisticated turbulence models.

• Gravity is of importance for the trajectory and impingement angle of SLD and is thus incorporated in the model at hand. Studies of trajectories of droplets within a 3-dimensional flow field emphasize the importance of considering gravity, especially for SLD [4, 6].

• Internal heat transfer has to be considered for larger droplets having a Biot number Bi greater than 0.1.

• The injection position, velocity and angle can be varied arbitrarily to simulate a nozzle spray cone.

• The simulation capabilities are extended to arbitrary flow fields.

Another motivation for a deeper investigation of the proposed shell model is to estimate boundaries for droplet temperatures within an IWT: The lumped model approach assumes a perfect heat transfer within the drop, resulting in a higher interface temperature and subsequently higher heat loss of the drop. Thus the cooldown potential of a drop traveling through the wind tunnel tends to be overestimated. While apparently underestimating the cooldown potential with the proposed shell model, incorporating heat conduction but no convection, an upper bound of the droplet temperature is obtained.

2 Methods

Within this section the determining parameters of the model for a single droplet are described. The model consolidates the kinetics and thermal behavior to a single state space model.

2.1 State space model of the droplet

For the simulation of the time history of a droplet, various properties are consolidated to a state space model [8]. The state vector consists of the following parameters:

$$\begin{aligned} \begin{aligned} \mathbf {X}=&(x,y,z,u,v,w,d_{drop},m_{drop},\ldots \\&\ldots Re,Nu,Bi,We,Oh,Pr,h_c,\ldots \\&\ldots e_{j=1...N_{iw}},T_{j=1...N_{iw}},f_{j=1...N_{iw}})^{T} \end{aligned} \end{aligned}$$

With x,y and z the coordinates of the actual position are denoted and u,v and w denote the corresponding velocity components. The state space contains 3-dimensional position and velocity components to maintain data integrity for a future use of a 3-dimensional vector field that is not implemented yet. The droplet diameter and the mass are saved in the parameters $d_{drop}$ and $m_{drop}$. They may change with evaporation and water density change during simulation. The relevant fluid and thermodynamical parameters are the Reynolds number (Re), the Nusselt number (Nu), the Biot number (Bi), the Weber number (We), the Ohnesorge number (Oh) and the Prandtl number (Pr) as well as the local convective heat transfer coefficient ($h_c)$. These states are required in the computation of the the governing differential equations during computation and are stored in the time series of the results. Since they mostly depend on local relative velocities, a recalculation using the flow field would be required otherwise.

2.1.1 Position

The change of position results from a pure integration of the actual velocities. This yields:

$$\begin{aligned} \begin{pmatrix} {\dot{x}}\\ {\dot{y}}\\ {\dot{z}}\end{pmatrix} = \begin{pmatrix} u\\ v\\ w \end{pmatrix} = \mathbf {V} \end{aligned}$$

(1)

No rotational motion of the droplet is considered and thus no angular position is required.

2.1.2 Velocity

The velocity components of the droplet are given by:

$$\begin{aligned} \mathbf {V} = \begin{pmatrix} u\\ v\\ w\\ \end{pmatrix} \end{aligned}$$

(2)

The drag force is given by

$$\begin{aligned} \mathbf {D} = \overbrace{\frac{C_d(Re) \cdot \rho _{air} \cdot \left| \mathbf {V}_{rel}\right| ^2}{2}}^{magnitude} \cdot \overbrace{\frac{-\mathbf {V}_{rel}}{\left| \mathbf {V}_{rel} \right| }}^{direction} \end{aligned}$$

(3)

where $\frac{C_d(Re) \cdot \rho _{air} \cdot \left| \mathbf {V}_{rel}\right| ^2}{2}$ represents the magnitude of the drag force and $-\tfrac{\mathbf {V}_{rel}}{\left| \mathbf {V}_{rel} \right| }$ determines the direction of the drag force opposing the actual relative velocity vector $\mathbf {V}_{rel}$. The slip velocity vector $\mathbf {V}_{rel}$ is calculated as the difference of the actual velocity and the local velocity of the airflow field that is known.

$$\begin{aligned} \mathbf {V}_{rel} = \mathbf {V}-\mathbf {V}_{flowfield} \end{aligned}$$

(4)

In addition, a constant gravitational force is added in vertical direction.

The change of velocity $\dot{\mathbf {V}}$ (i.e. the acceleration) is given by the attacking force divided by the mass which yields:

$$\begin{aligned} \dot{\mathbf {V}} = -\frac{1}{m_{drop}} \cdot \frac{C_d(Re) \cdot \rho _{air} \cdot \left| \mathbf {V}_{rel} \right| \cdot \mathbf {V}_{rel}}{2} \end{aligned}$$

(5)

For coefficient of drag ($C_d$) calculations of smooth spheres, various formulas can be found in literature [1, 9,10,11]. While for low Reynolds number flow ($Re < 1$), the correlation $C_d \sim \tfrac{24}{Re}$ (Stokes Law) is common among the sources, the values vary for higher Reynolds numbers. Given the stated uncertainty of single-expression curve-fit errors of up to 5% [9], up to 10% [10] or discontinuities [1], a mixture of the provided formulas seems a reasonable approach.

Munson et al. offer a graph that merges various sources over the relevant range of Reynolds numbers [12]. Finally, $C_d$ is calculated as a function of the local Reynolds number by interpolating a lookup table based on the curve depicted in Fig. 1.

Fig. 1

The drag coefficient as a function on the Reynolds number (modified from [12])

To compensate for the small diameter of the droplet relative to the mean distance between air molecules, the Cunningham correction factor $f_{cun}$ is taken into consideration [13]. The Cunningham correction factor is given by:

$$\begin{aligned} f_{cun} = 1 + 2 \cdot \frac{68 \cdot 10^{-9}}{d_{drop}} \cdot 1.257 + 0.4\cdot e^{\left( 0.55 \cdot \frac{d_{drop}}{68 \cdot 10^{-9}} \right) } \end{aligned}$$

(6)

For small droplets of 1${\upmu }$m the influence is roughly 15%, for droplet size over 20${\upmu }$m the effect vanishes.

Therefore the drag coefficient considering the slip phenomenon is altered to:

$$\begin{aligned} C_{d,slip} = \frac{C_d}{f_{cun}} \end{aligned}$$

(7)

For sake of completeness, the buoyancy force $\mathbf {F_{b}}$ is given:

$$\begin{aligned} \mathbf {F_{b}} = \begin{pmatrix} 0\\ 0\\ \frac{\pi d^3_{drop} \rho _{air}}{6}\cdot {9.81}{\text {m}}{\big /}{\text {s}}^{2}\\ \end{pmatrix} \end{aligned}$$

(8)

The buoyancy force of a water droplet within air is negligible.

2.1.3 Temperature

The temperature of the droplet changes due to convective heat transfer to the surrounding air flow, and the Reynolds number (based on the relative velocity of the droplet to the surrounding air) is used to calculate the Nusselt number. The Reynolds number is given by:

$$\begin{aligned} Re=\frac{\left| \mathbf {V}_{rel} \right| \cdot d_{drop}}{\nu _{air}} \end{aligned}$$

(9)

The Nusselt number is calculated according to the formula of Brauer/Sucker for a sphere [14, 15] valid for a range of $0 \le Re \le 3\cdot 10^5$:

$$\begin{aligned} Nu = 2 + \frac{0.66}{\left( 1+\left( 0.84 \cdot Pr^{\frac{1}{6}}\right) ^3\right) ^{\frac{1}{3}}} \cdot \frac{\left( Re\cdot Pr\right) ^{1.7}}{1+\left( Re\cdot Pr\right) ^{1.2}} \end{aligned}$$

(10)

With the calculated Nusselt number, the heat transfer coefficient $h_c$ is calculated by

$$\begin{aligned} h_c = \frac{ Nu \cdot \lambda _{air}}{d_{drop}} \end{aligned}$$

(11)

The Prandtl number is calculated using

$$\begin{aligned} Pr=\frac{\eta _{air} \cdot c_{\mathrm p,air}}{\lambda _{air}} \end{aligned}$$

(12)

and is considered as constant for the whole simulation, since the temperature of the surrounding flow field is considered as constant, and the droplet temperatures vary only within a limited range.

The thermal conductivity $\lambda _{air}$ is calculated using the following relation [16, p.524] and is kept constant ($T_{air}=\mathrm {const}$) over the whole simulation.

$$\begin{aligned} \lambda _{air} = 7.655\cdot 10^{-5} \cdot T_{air} + 0.024139 \end{aligned}$$

(13)

The actual temperature change for the water droplet in the lumped model is then given by:

$$\begin{aligned} \frac{dT}{dt} = \frac{h_c \cdot \left( T_{air}-T_{drop}\right) d_{drop}^2 \cdot \pi }{m_{drop} \cdot c_{p,water}} \end{aligned}$$

(14)

where the heat capacity of water is given as a function of temperature according to Fig.  2.

Fig. 2

The heat capacity of water as a function of the temperature [17]. The figure presents values from the IAPWS-95 formulation and experimental results. The values according IAPWS-95 (continuous line) are used for interpolation

A change in temperature results in a change of the density, which in turn yields a change of the diameter. While the diameter change due to the change of density may be negligible, the mass of the drop over the simulation is included in the state space to enable consideration of evaporation in the extended model.

The density of water is implemented as an interpolation function of the graph depicted in Fig. 3.

Fig. 3

The density of water as a function of the temperature for various values of the ambient pressure P [17]. The figure presents experimental results (rectangles and circles) and values from the IAPWS-95 formulation (continuous lines) . The line at $P={0.1}\,{\text {MPa}}$ is used as a basis for interpolation

Additional numbers are included into the state vector to enable further examination of the results even if they are not explicitly required for solving the differential equations: The Biot number Bi to emphasize applicability of the shell model versus the lumped model approach, the Weber number We to observe limitations for droplet break up [18] in further research focusing on the layout of a wind tunnel specifically designed for SLD [19].

The Biot number is defined in the current context by [20]:

$$\begin{aligned} Bi = \frac{d_{drop} \ h_c}{6\,\lambda _{drop}} \end{aligned}$$

(15)

The Weber number is defined by

$$\begin{aligned} We = \frac{\rho _{air,humid} \left| \mathbf {V}_{rel}\right| ^2 d_{drop}}{\sigma _{water}} \end{aligned}$$

(16)

and the Ohnesorge number—the ratio of viscous forces to surface tension and inertia forces—is given by

$$\begin{aligned} Oh = \frac{\mu _{water} ({\bar{T}}_{drop})}{\sqrt{\rho _{water}({\bar{T}}_{drop}) \sigma _{water} d_{drop}}}, \end{aligned}$$

(17)

where $\mu _{water}$ is the dynamic viscosity of water at the mixed mean temperature ${\bar{T}}_{drop}$. The Weber number and the Ohnesorge number are implemented for future use and additional analysis of the droplet.

2.2 Initial values

The initial values for the numerical simulation are set according to Table 1.

Table 1 States of a droplet and the initial conditions

2.3 Flow field

The governing flow field and the surrounding temperature is taken from a precomputed CFD solution given at discrete data points in conjunction with a spatial interpolation.

Based on a 3D CAD-model, a mesh was created with the commercial software package ANSYS ICEM CFD.

For simple geometries a blockstructured hexahedral mesh and for more complex geometries an unstructured tetrahedral mesh with prism layers in wall vicinity was used. For both approaches the thickness of the first element adjacent to the wall was adjusted to yield (depending on the flow velocities of the operating condition) a $Y+$ value between 0.1 and 10. With the help of mesh smoothing steps aspect ratios <100, face angles >20${^{\circ }}$ and determinants >0.3 were aimed to ensure high quality meshes.

Then, the convective flow field was determined by a 2D or 3D steady state CFD simulation, performed with the commercial software package ANSYS CFX.

For modelling the turbulent flow structure, the Reynolds-averaged Navier-Stokes (RANS) approach using the Shear Stress Transport (SST) eddy-viscosity turbulence model from Menter [22] was used. The model works by solving a turbulence/frequency-based model ($\hbox { }\ k-\omega$) at the wall and $\hbox { }\ k-\epsilon$ in the bulk flow. Menter developed advanced near-wall treatments and blending functions, that ensure a smooth transition between the two models within the ANSYS CFX software. The SST model performance has been studied in a large number of cases. In a NASA Technical Memorandum [23], SST was rated the most accurate model for aerodynamic applications.

In the case of design studies, an inlet mass flux was set as inlet boundary condition (BC). All walls are treated as hydraulically smooth with zero slip conditions. For all outlets zero relative static pressure BCs were used.

Initial conditions were adopted for various operating cases to ensure a robust and fast convergence.

All CFD simulations were performed with a continuous fluid air (treated as ideal gas) including buoyancy forces with the total energy heat model (including viscous work) to take into account compressibility effects.

The advection scheme and turbulence numerics are set to a high resolution discretization scheme. All simulations were performed with double precision and the target of a maximum Root Mean square (RMS) for the residuals for mass, momentum, energy and turbulence of ${10}^{-4}$. In addition, various monitor points inside the fluid domain reported a stable behaviour of the velocity components to approve the results as a steady state converged solution.

Calculated flow fields are available for measurement section velocities having the following values (in m/s):

$$\begin{aligned} v_{Air} \in \left\{ 30,40,45,50,60,80 \right\} \end{aligned}$$

(18)

and for measurement section static temperatures

$$\begin{aligned} T_{Air,stat} \in \left\{ -18,-13,-2 \right\} \end{aligned}$$

(19)

An example flow field that is used for calculations within this work is depicted in Fig. 4. For more detailed information on the flow field’s properties, interested readers are referred to to the work of Breitfuss [24].

Fig. 4

An example flow field for a test section velocity of 60m/s with 20 k randomly chosen velocity vectors. The clustering of vectors close to the wall and adjacent to the nozzle grid gives a clue of the increased density of the computed mesh in these areas

The initial value of the z-coordinate of the droplet corresponds to the elevation of the nozzles on the spray bar grid and ranges from -1.43m to 2.41m with a vertical bar distance of 0.11m.

2.4 Droplet size

The occurring droplet size spectra for the relevant certification specification scenarios given in CS-25 [25] were measured at the RTA Icing Wind Tunnel using a Malvern Instruments Spraytec system. The droplet spectra for the following scenarios were available for the current simulations [26]:

• 1. Median volume diameter (MVD) =20${\upmu }$m

• 2. MVD=40${\upmu }$m

• 3. Freezing Drizzle (FZDZ) with MVD > 40${\upmu }$m

• 4. Freezing Rain (FZRA) with MVD > 40${\upmu }$m

The measured droplet spectra are depicted in Fig. 5.

Fig. 5

Measured particle size and its volume percentage (blue bars). The red line depicts the cumulative distribution function

Since the droplet simulation is based on a single-droplet formulation, the actual mass fraction distribution of a specific droplet size is of no influence for now. Nevertheless, it may be used for assessing the relevance of the results obtained for a certain droplet size.

2.5 Lumped thermal droplet model

The lumped thermal droplet model assumes an uniform temperature distribution within the droplet as a result of instantaneous heat conduction. Such an assumption is only valid for droplets with a Biot number satisfying $Bi < 0.1$. At greater Bi numbers, the lumped thermal model is not valid anymore [20].

It can be shown (cf. (15)) that for a relevant initial slip velocity of up to 40 m/s a Biot number greater than 0.1 occurs for droplets greater than $d_{0} \approx {500}\,{{\upmu }{\hbox {m}}}$. For SLD, therefore, an extended thermal model has to be introduced. The icing conditions according the certification specifications CS-25, Appendix O, (SLD-Icing) have to include droplet diameters of up to 2229 ${\upmu }$m [21].

2.6 Extended thermal model of the droplet

As stated, the internal heat conduction of the droplet has to be taken into account for larger droplets within the relevant droplet size spectrum.

While the kinetic equations and the heat transfer on the droplet surface remain unchanged also for the extended thermal model of the droplet, the internal temperature distribution of the droplet is modeled as a spherical shell model. The derivation of the shell model is explained in the following sections.

2.6.1 Conservation of energy

The energy balance equation for a control volume V of one single ice water shell is given by the expression

$$\begin{aligned} \int \limits _{V}\! \rho _{iw}\ e\ dV = -\int \limits _{V}\!\nabla \cdot q_{cond} dV . \end{aligned}$$

(20)

Here e is the specific enthalpy within V, $q_{cond}$ is the conductive heat flux and $\rho _{iw}$ is the ice water shell density defined by:

$$\begin{aligned} \rho _{iw} = \left( \frac{f_i}{\rho _i} + \frac{1-f_i}{\rho _w}\right) ^{-1} \end{aligned}$$

(21)

with the ice mass fraction $0 \le f_i \le 1$ and the corresponding densities of water $\rho _w$ and ice $\rho _i$. The specific enthalpy e within V is given by:

$$\begin{aligned} \begin{aligned} e =&f_i \left[ \left( T - T_{melt}\right) c_{p,i}-L_{melt} \right] \\&\qquad + \left( 1-f_i) \right) \left( T-T_{melt} \right) \cdot c_{p,w} \end{aligned} \end{aligned}$$

(22)

with the temperature T, the temperature of phase change $T_{melt}$ and the corresponding specific latent heat $L_{melt}$ of fusion. The specific heat capacity of ice is given by $c_{p,i}$ and of water by $c_{p,w}$.

Modifying (22) by application of the mean value theorem for integrals on the left side and transforming the divergence integral on the right side of (20) to a surface integral [modified from 27] yields:

$$\begin{aligned} V \rho _{iw}\ \frac{d}{dt}e = -\int \limits _{S}\!q_{cond}\ n\cdot dS \end{aligned}$$

(23)

Having the thermal conductivity of the ice water shell $k_{iw}$ and the temperature gradient $\nabla T$ between adjacent volumes (i.e. neighbour shells) and considering $q_{cond}=-k_{iw}\nabla T$, one subsequently obtains:

$$\begin{aligned} V \rho _{iw}\ \frac{d}{dt}e&= \int \limits _{S}\!k_{iw}\nabla T\ n\cdot dS \end{aligned}$$

(24)

or

$$\begin{aligned} V \rho _{iw}\ \frac{d}{dt}e&= \int \limits _{S}\!k_{iw}\frac{\partial T}{\partial n}\cdot dS \end{aligned}$$

(25)

In analogy to 21, the thermal conductivity $k_{iw}$ of the ice water shell is given by:

$$\begin{aligned} k_{iw} = \left( \frac{f_{i,vol}}{k_i} + \frac{1-f_{i,vol}}{k_w} \right) ^{-1} \end{aligned}$$

(26)

The grid size is assumed to be uniform over $\tfrac{d}{2}$ with a radial cell size of $\Delta r=\tfrac{d}{2 \cdot N_{iw}}$ , where d is the droplet’s diameter and $N_{iw}$ is the node of the most outward spherical shell as depicted in Fig. 6. The reference state of the water species having $e=0$ is considered to be liquid water at $T_{melt}$.

Fig. 6

Grid for single droplet discretization (one-dimensional)

The following derivation of the formulas vary for three cases:

• A regular inner shell with two adjacent cells.

• The innermost shell with the node containing the droplet center

• The outermost shell with one regular adjacent cell to the inside and the air/droplet interface at the outside.

Consolidating the formulas given above, the discretized transient energy balance equation for an inner spherical shell can be derived:

$$\begin{aligned}&\rho _{iw}\left( e_{j}^{k+1}-e_{j}^{k} \right) \nonumber \\&\quad =\frac{\Delta t}{r_j^2 \Delta r} \left[ \left( r^2k_{iw}\frac{\partial T}{\partial r}\right) _{j+\frac{1}{2}} -\left( r^2k_{iw}\frac{\partial T}{\partial r}\right) _{j-\frac{1}{2}} \right] \end{aligned}$$

(27)

The full explicit transient discretization of (27) for an inner spherical shell at the timestep k is given by:

$$\begin{aligned}\frac{e_j^{k+1}-e_j^k}{\Delta t}&= \beta \left[ \left( r^2 k_{iw} \right) ^k_{j+1/2} \left( T^k_{j+1} - T^k_j\right) \right. \nonumber \\&\quad \left. - \left( r^2 k_{iw} \right) ^k_{j-1/2} \left( T^k_{j} - T^k_{j-1}\right) \right] \end{aligned}$$

(28)

The parameter $\beta$ is defined by:

$$\begin{aligned} \beta = \left[ \rho ^k_{iw,j} \ r^2_j \ \left( \Delta r \right) ^2 \right] ^{-1} \end{aligned}$$

(29)

In (28) $k^k_{iw,j+1/2}$ and $k^k_{iw,j-1/2}$ are evaluated by

$$\begin{aligned} k^k_{iw,j+1/2}&= 2\left( \frac{1}{k^k_{iw,j+1}}+\frac{1}{k^k_{iw,j }}\right) \end{aligned}$$

(30a)

$$\begin{aligned} k^k_{iw,j-1/2}&= 2\left( \frac{1}{k^k_{iw,j }}+\frac{1}{k^k_{iw,j-1}}\right) \end{aligned}$$

(30b)

The energy balance for the innermost spherical shell is given by:

$$\begin{aligned}\frac{e^{k+1}_1-e^{k}_1}{\Delta t}&= \beta \left[ \left( r^2 \right) ^k_{1/2} \Delta r\ q^k_{1/2} \right. \nonumber \\&\quad \left. + \left( r^2 k_{iw}\right) ^k_{3/2} \left( T^k_2 - T^k_1\right) \right] \end{aligned}$$

(31)

Since the innermost spherical shell exhibits a symmetry around the droplet center, the heat flux at the center is set to $q^k_{1/2} = 0$ (Adiabatic boundary condition). Thus, (31) can be reduced to:

$$\begin{aligned} \frac{e^{k+1}_1-e^{k}_1}{\Delta t}= \beta \left[ \left( r^2 k_{iw}\right) ^k_{3/2} \left( T^k_2 - T^k_1\right) \right] \end{aligned}$$

(32)

The energy balance for the outermost spherical shell (denoted by the shell node index $N_{iw}$) is then given by:

$$\begin{aligned}\frac{e^{k+1}_{N_{iw}}-e^{k}_{N_{iw}}}{\Delta t}&= \beta \left[ \left( r^2 \right) ^k_{N_{iw}+1/2}\Delta r \ q^k_{N_{iw}+1/2} \right. \nonumber \\&\quad \left. -\left( r^2 k_{iw} \right) ^k_{N_{iw}-1/2} \left( T^k_{N_{iw}} - T^k_{N_{iw}-1}\right) \right] \end{aligned}$$

(33)

Again, $k^k_{iw,j-1/2}$ can be evaluated according to (30b), and $\beta$ is given by (29).

The parameter $q^k_{N_{iw}+1/2}$ is the convective/evaporative wall heat flux at the air/droplet interface which can be broken up into two parts:

$$\begin{aligned} q^k_{N_{iw}+1/2} = q_{conv} + q_{lat} \end{aligned}$$

(34)

The convective heat flux at the air/droplet interface is denoted by $q_{conv}$ and the evaporative heat flux by $q_{lat}$.

The wall heat flux directly influences the air droplet interface temperature and thus a Dirichlet boundary condition is introduced:

$$\begin{aligned} T^k_{N_{iw}+1/2} = -\frac{q^k_{N_{iw}+1/2}\ \frac{\Delta r}{2}}{\left( k_{iw}\right) ^k_{N{iw}}} + T^k_{N_{iw}} \end{aligned}$$

(35)

The convective wall heat flux $q_{conv}$ requires the heat transfer coefficient $h_c$ given in (11) and the temperature gradient at the surface as the difference between the ambient air temperature $T_a$ and the surface Temperature $T_{N_{iw}+1/2}$ and is calculated by:

$$\begin{aligned} q_{conv} = h_c \left( T_a - T_{N_{iw}+1/2} \right) \end{aligned}$$

(36)

The evaporative heat flux $q_{lat}$ is given by:

$$\begin{aligned} q_{lat} = \varphi \ h_m\ \rho _{a,humid}\ L_{e,s}\left( \omega _a -\omega \right) \end{aligned}$$

(37)

with $\rho _{a,humid}$ as the density of humid air and $L_{e,s}$ as the latent specific heat of evaporation and sublimation. By use of a limiting factor $\varphi$ that depends on the relative humidity of the surrounding air and by implementation of $\omega _a$ as well as $\omega$ saturation of evaporation is also considered. A thorough description of the evaporation process is available in [20] and a description of the implementation is available in [28]. A detailed recap here would exceed the scope of the current work.

2.6.2 Conservation of mass

The change of the droplet’s mass with time is given by the expression

$$\begin{aligned} \frac{\mathrm {d}m_{drop}}{\mathrm {d}t}= \varphi \cdot \pi \cdot d_{drop}^2 \cdot h_m \cdot \rho _{a,humid} \cdot L_{e,s}\cdot (\omega _a - \omega ) \end{aligned}$$

(38)

with the right hand side similar to the wall heat flux as stated in (37).

The corresponding mass change of the surrounding air of the droplet is consequently given by:

$$\begin{aligned} \frac{\mathrm {d}m_a}{\mathrm {d} t}= - \frac{\mathrm {d}m_{drop}}{\mathrm {d}t} \end{aligned}$$

(39)

2.6.3 Stability criterion

The implemented extended thermal model is based on an explicit finite-difference representation and thus vulnerable to numeric stability issues while solving the implemented differential equations. Therefore a specific stability criterion has to be fulfilled as stated in [27].

$$\begin{aligned} \frac{\alpha _{drop} \Delta t}{\left( \Delta x\right) ^2} \le \frac{1}{2} \end{aligned}$$

(40)

with $\Delta x$ as the grid spacing (or relevant length i.e. $\Delta x \sim \tfrac{d_{droplet}}{2 N_{shells}}$) and the thermal diffusivity $\alpha _p$ of the particle given by:

$$\begin{aligned} \alpha _{drop} = \frac{\lambda _{drop}}{\rho _{drop}\ c_{p,drop}} \end{aligned}$$

(41)

Considering a realistic scenario with an extreme value of a droplet diameter of $d = {1}{{\upmu }{\hbox {m}}}$ this results in

$$\begin{aligned} \Delta t \approx \frac{1}{2}\left( {1e-6}{\text {m}} \right) ^2 \frac{{920}\frac{\mathrm{kg}}{\mathrm{m}^{3}}\cdot {2000}\frac{\mathrm{J K}}{\mathrm{kg}} }{{2}\frac{\mathrm{W K}}{\mathrm{m}}} \approx {4.6.10^{-7}}{\hbox {s}} \end{aligned}$$

(42)

The maximum calculated time step has to be considered in the implementation of the solver or the parametrization of adaptive time step routines.

2.7 Numerical solver

For numerically solving the given differential equations, the MATLAB-implemented solver “ode23t” is used since it can be set to handle “state variables” that shall not be integrated during the solution procedure but are rather just updated. As a basis for the set of differential equations various numbers of interest such as Weber number, Biot number, Nusselt number etc. are calculated, and no additional computational effort is required after calling the numerical solver routine.

For the time step adaption, the absolute tolerance has been set to values of $d_{drop}/100$ for all components of the droplets position, ${10}^{-8}$ for all components of the droplets velocity, ${10}^{-4}$ for the temperature and ${10}^{-6}$ for the mass. An overall relative tolerance of ${10}^{-4}$ has been set for the solver. The accuracy is checked during numerical integration by comparing the achieved results with the results of a more accurate solver of higher order at specified time intervals. Whichever of the set tolerances is to be violated triggers a time step refinement of the solver. Conversely, if all criteria are met, then a relaxation of the time step size is performed [29].

3 Results

The simulations where conducted for the relevant scenarios as stated before (Sect. 2.4). For a further detailed discussion the results for a CS-25, Appendix C simulation and a CS-25, Appendix O (SLD) simulation are given below. The used parameters for the simulation are given in Table  2.

Table 2 Overview of the used simulation parameters

3.1 CS-25 Appendix C simulation results

For the scenario “$MVD={20}\,{{\upmu }{\hbox {m}}}$” droplets with a size ranging from 7.5 ${\upmu }$m to 135${\upmu }$m are used. This range includes 99% of the measured droplets (see Fig. 5a. The majority of the droplets reaches a temperature below 0${^{\circ }}$C within a flight distance of around 4m after the injection point (Fig. 7a). Generally, the velocity of the droplets follows the free stream velocity, as shown in Fig. 7b. The effect of evaporation and density change on the droplet diameter amounts to a rather negligible reduction of 2.5% compared to the initial diameter as depicted in Fig. 7c. The equidistant distribution of the droplets over the injection array is mainly preserved, that is, no major deviation from cloud uniformity is predicted by the present simulations (Fig. 7d).

Fig. 7

Results for a CS-25-C simulation with a droplet spectrum according Fig. 5a ($MVD={20}{{\upmu }{\hbox {m}}}$)

3.2 CS-25 Appendix O simulation results

Figure 8 shows the thermal SLD simulation results of the case “Freezing Rain FZRA>${40}{{\upmu }{\hbox {m}}}$” and constitutes an experimental CS-25, Appendix O icing test at RTA’s IWT.The CS25, Appendix O simulations were performed for droplet sizes within the range of 458${\upmu }$m to 1143${\upmu }$m since, for smaller droplets of the double-peak spectrum, a sufficient cooldown behaviour has been shown in Sect. 3.1.

The increased thermal inertia of the droplets from the SLD spectrum (see Fig. 5d) causes a shallow cool down behavior and therefore requires pre-cooled water at considerable low temperatures. By pre-cooling the water to 2${^{\circ }}$C and at a static air temperature of -13${^{\circ }}$C within the wind tunnel, the mean droplet temperature of all droplets of the considered diameter spectrum cool down at least to freezing temperature before reaching the red marked test section (see Fig. 8a). However, the larger droplets do not acclimate to the ambient air temperature to such an extent as observed for a CS-25, Appendix C scenario which can clearly be seen by observing the position where the droplet center reaches 0${^{\circ }}$C in Fig. 8a. The velocity of the droplets does not completely reach the flow field’s velocity (Fig. 8b).

The effect of evaporation and density change on the droplet diameter amounts to negligible reduction of less than 0.02% compared to the initial diameter as depicted in Fig. 8c.

Fig. 8

Results for a CS-25-O simulation with a droplet spectrum according to Fig. 5d ($FZRA > {40}{{\upmu }{\hbox {m}}}$)

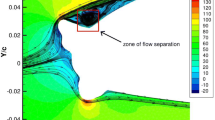
Two effects are observable at the droplets’ trajectories for CS25, Appendix O simulations. Firstly, the larger droplets do not completely follow the flow field at the contraction vane due to higher inertia and thus impinge on the icing nozzle (red line) at the position of the airflow contraction (Fig. 8d at $x \approx {4.5}{\text {m}}, y \approx {2}{\text {m}}$). Secondly, the droplets trajectories tend to divert downwards close to the test section. Although this decline may be partly explainable by the slightly downward oriented velocity vectors at the test section, gravitational effects influence the trajectories of larger droplets too. An detailed view of the flow field in the vicinity of the test section is given in Fig.9. The deviation of the flow from horizontal is compensated by adding an offset to the tilt of a test specimen to achieve the desired angle of attack, i.e. conducting a zero angle of attack test not automatically implies a horizontal alignment of the profile itself.

Fig. 9

A detailed view of the droplets’ trajectories for a CS-25, Appendix O case, overlayed with velocity vectors of the air flow in the vicinity of the test section. A downward deflected flow, partially contributing to the decline of trajectories can be observed. The position and density of trajectory lines also indicate a constrained usable area of the test section

Such phenomena are also reported within the work of Breitfuss et al., where the effectively usable area with an acceptable cloud uniformity is stated to be approximately 0.35 m in height and 2 m in width [24]. Precise knowledge of this region is required for placement of test specimen but the area is sufficiently large for wing profile icing tests. However, the droplet trajectories (Fig. 8d) confirm RTA’s capability [26, p. 8] to transport the larger droplets from the injection to certain regions of the test section.

The droplets’ mean temperatures at the test section entry are consistent over the origin of the droplets from various spraybars as depicted in Fig. 10a. Regarding the velocity of larger droplets, a dependence on the origin of the droplet can be observed, whereas the smaller droplets practically follow the free stream flow field (see Fig. 10b). While these results are given only for a CS25-O simulation, the results for relative velocity are also valid for other scenarios.

Fig. 10

Values of droplets from selected spray bars at the test section entry ($x={11.45}{\text {m}}$) for a CS-25-O simulation. The drops originate from various spray bar positions ($z_0 =$-1.0,  m-0.3 m, 0.5 m, 1.3 m, 2.0  m) and dots are color coded by droplet diameter

3.3 Comparison of the lumped thermal model and the extended thermal model

As expected, the differences between the two models considered is relevant for larger droplets of the relevant spectra. In Fig. 11a the Biot numbers along the distance travelled for various sized droplets originating from the nozzle at $z= {0.106}\,{\text {m}}$ are depicted. Droplet diameters of up to 500 ${\upmu }$m show Biot numbers below the horizontally red marked threshold of 0.1 (see Sect. 2.6) and confirm, therefore, the validity of the lumped approach. As expected, both models indicate matching simulation results in this droplet diameter domain. For diameters larger than 500 ${\upmu }$m, however, the critical Biot number of 0.1 is exceeded and the droplet-internal heat conduction included in the extended approach results in an increased cool down distance compared to the lumped approach. The difference in droplet temperature at the test section is approximately 0.2 ${^{\circ }}$C, the position where the value for the center shell reaches 0 ${^{\circ }}$C is shifted by $\approx {1}{\text {m}}$ for 500 ${\upmu }$m, by $\approx {5}\,{\text {m}}$ for 1000 ${\upmu }$m and even more for larger droplets (see Fig.  12).

Fig. 11

Relevant quantities for a CS25, Appendix O simulation

Fig. 12

Comparison of simulation results for the two different droplet models. Shown is the progression of temperature of the lumped model droplet (solid lines) and the mass averaged mean temperature of extended model droplets (dashed lines). The asterisks mark the position where the droplet center shell reaches 0${^{\circ }}$C

For the more critical case “CS25, Appendix O” with simulated droplets sizes up to 1143${\upmu }$m (see Fig. 11a) the observed Weber numbers are below 7. Critical locations for droplet deformation and break-up are after the injection and in the contraction cone due to the high relative velocities of droplets and air flow (see Fig. 11a, at position $x \approx {7}{\text {m}}$). A synopsis of various studies consolidates no breakup for a Weber number below 13 [30]. Even though these studies eventually address different ranges of density ratio $\epsilon = \tfrac{\rho _{gas}}{\rho _{liquid}}$, it is reported that the fundamental behaviour and underlying mechanisms of droplet break-up are valid for a wider range of $\epsilon$ [31] and results are applicable for the problem at hand. Based on the work of King et. al. [18], the Weber number should not exceed 15 to prevent droplet breakup.

A perfect sphere droplet shape is assumed within the model of the kinetic simulation and its applicability may be assessed as follows. An oscillatory deformation may be occurring temporarily in a phase of the droplet’s trajectory approaching the maximum Weber numbers. For a Weber Number of 2.1 a deformation (i.e. the maximum ratio of the droplets cross stream diameter to its initial diameter) of 1.2 (20%) is reported [32]. For a deformation of 20%, the drag coefficient increases from 0.44 to approximately 0.6 for ${1000}< Re < {2500}$, meaning an increase by approximately 35% [33]. The Reynolds number as a function of the distance traveled from injection for a CS25, Appendix O simulation is depicted in Fig. 11b. The simulations within this work consider the transport of a droplet from the injection nozzle to the specimen under investigation. It is known, that in the vicinity of an airfoil major droplet deformation and even breakup may occur due to high accelerations [34]. These processes take place near experimental targets and need not be considered in simulations used for the overall design and layout of an IWT.

The observed temperature differences between the lumped and the extended shell model prompts the conclusion that the influence of a droplet’s inner heat transfer on the resulting temperature is not the main contributing factor to droplet cooldown.

From a thermodynamic view, the potentially occurring oscillatory deformation [30] and the associated internal flow leads to an increased internal droplet heat exchange (forced convection) which results in approaching the lumped model assumption. An increased droplet surface may lead to enhanced heat transfer, too. The conclusion that can be drawn from this is that the extended model is likely to underpredict the cooling rate of droplets.

It is reported that the droplet’s actual temperature has little impact on the resulting shape of the accumulated ice [2] which is in close agreement with preliminary results of ongoing research of the authors. Simulations with the ICEAC2Dv2 Icing Code [35] have not proven major shape variations for droplet temperature differences within the observed variability as in Fig. 12.

This can be attributed to the fact that convective cooling of the airfoil and the just accumulated ice layer is a major contributor to the overall icing process. These assumptions of course are limited to an extent, up to when droplets are (partially) frozen. For the analysis of ice accretion on a surface under investigation, the freezing fraction has significant impact on the resulting ice shape due to completely different processes involved at impingement [36]. However, partial or complete freezing of water droplets is a frequently observed phenomenon in icing wind tunnel experiments. This the primary reason why phase transitions were considered in the current model and the ice mass fraction of the droplet approaching a surface are calculated for future utilization. In certain types of tests it is even desired to produce frozen particles rather than supercooled droplets (e.g. CS-25, Appendix P, “Mixed phase and ice crystal icing”).

4 Conclusion

Experimental icing tests are essential for the certification of aircraft based on the icing-related Appendices C and O of the CS-25 published by the European Aviation Safety Agency (EASA) [25]. The regulations shall prompt aircraft manufacturers to implement reliable and effective protective measures against hazardous icing conditions.

For demonstrating compliance to both CS-25 Appendices, manufacturers perform expensive flight experiments as well as experimental icing tests at appropriate facilities. Especially icing caused by Supercooled Large Droplets (SLD) with diameters of up to 2mm (CS-25-O) requires a profound knowledge of the kinetics and the thermal aspects a droplet experiences between its injection into an Icing Wind Tunnel (IWT) and the impact on the affected structure (e.g. a wing). SLDs are critical for experimental icing tests at IWTs since the cool down process to freezing temperature takes place relatively slowly. This paper presents a simplified (lumped) and an extended thermal model aiming at the prediction of a droplet’s temperature upon reaching the test section within an IWT. The lumped approach assumes infinite droplet-internal heat conduction processes and is thus limited to the simulation of droplets smaller than approximately 500 ${\upmu }$m.

The extended thermal approach, however, accounts for the heat conduction inside the droplet and allows the thermal simulation of SLDs of the CS-25-O spectrum as well. In addition, mass transfer aspects between air and droplet as well as potential phase change processes (freezing/melting) are implemented. The extended thermal model inevitably requires additional computational effort. It has been found that execution time is increased by roughly a factor of 20. Even though a single trajectory is simulated within several seconds, the required simulation time can play a significant role when using the model for a multi-dimensional optimization problem, e.g., the overall design of an IWT layout in the planning phase. The comparison of both thermal droplet models indicated matching results for small diameters but also justifies the higher computational effort using the extended approach for larger droplets.

The results have shown differences for the droplet’s temperature using both of the models at hand. These differences in calculated temperature subsequently only have little impact on the simulated ice shapes. Even if resulting ice shapes are similar from a geometric point of view, hence having no major impact on aerodynamic properties of the device, the mass averaged enthalpy of a droplet cloud influences the course of subsequent phenomena. For instance, the energy level directly influences the required heat flux and the effectiveness of deicing systems and their overall layout.

5 Outlook

For the future, additional validation efforts are contemplated. The Department of Aerospace Engineering at the Pennsylvania State University is currently investigating the freezing and melting behavior of single droplets by means of luminescent imaging [37] which might result in meaningful validation data for the phase change routine of the extended thermal droplet model [38]. It has to be further investigated, whether the results obtained may carry over to the application of the current model regarding the different range of Reynolds number for the cases considered.

It was shown that the model at hand provides a unified investigation approach of the influence of the flow field on the flow path as well as the thermodynamic properties of the droplets. In conjunction with investigations on the real flow field [24], further improvements on the overall capabilities may be achieved while possibly requiring only minor modifications (e.g. vanes, elongation of floor coverage at the orifice).

Moreover, the already investigated validation approaches included tests with even lower temperature within the IWT. If the critical temperature [11] of a droplet is reached, no ice accretion should be observed at a test specimen at a given distance since the then solid drops bounce off the surface. However, such tests are a precarious method and have not given fully satisfactory results so far and thus may need to be refined in a future research.

The model developed in the current research is used for the overall design and layout of a planned IWT specialized on SLD capabilities where the model has shown its potential to efficiently simulate diverse flow field properties within a multidimensional optimization [19]. The relatively low computational effort (when compared to a full 3D finite element method of a droplet) while maintaining an enhanced thermal model of a single drop also opens up possibilities to perform trajectory and thermal simulation for a whole regime of droplets. Once the time consuming calculation of a transient flow field solution is performed, even such a flow field may serve as a future basis for droplet trajectory simulation. Such investigations require only minor adaptions to the underlying data structure. By incorporating an assessment of the droplets impingement points and binning, assumptions on cloud uniformity of planned IWT facilities or measures for further improvement of existing facilities may be derived in future work.