1 Introduction

Hidden population models allow population sizes and dynamics to be estimated from partial observations and form a cornerstone of ecological methodology. Open-population models allow population sizes to vary with time and are theoretically the most interesting class of hidden population model. However, some open-population models exhibit substantial computational issues when the population sizes are large (\(N > rsim 250\)). These classes of models include N-mixture models (Royle 2004; Dail and Madsen 2011), hidden Markov models (HMMs; Zucchini et al. 2016), and integer autoregressive (INAR; Jin-Guan and Yuan 1991) models. N-mixture models are used frequently in ecological studies where under reporting is expected (e.g. Hostetter et al. 2015; Belant et al. 2016; Ward et al. 2017; Ketz et al. 2018; Parker et al. 2020). Hidden Markov models are used extensively in studying hidden stochastic processes and have been applied to study problems similar to the open-population N-mixture model (Cowen et al. 2017). Integer autoregressive models are also used to study hidden open populations (Fernández-Fontelo et al. 2016).

These hidden INAR, HMM, and N-mixture models share some similarities in their mathematical structure. In particular, owing to the transitions between unknown population states, these models require large convolutions for likelihood function calculations. These convolutions are computed many times in open-population N-mixture models due to the explicit summation over possible values of N (the total hidden population size) and the iterative nature of model fitting. In hidden INAR models, the convolutions are repeated due to the explicit sums over the possible hidden states. The HMMs formulated in Cowen et al. (2017) contain implicit summations through the multiplication of state matrices, with convolutions arising in the calculation of transition probability matrices. In all three of these hidden population model formulations, suitable upper bounds must be chosen on the size of the population. The upper bound must be chosen large enough that the fitted models are not affected by the choice of the upper bound. In practice, this means that larger study populations require large upper bounds on the summations, leading to an even larger number of computations of convolutions, and even larger computation times. These computation times can be problematic, especially when simulation studies or parametric bootstrap techniques require repeated model fitting, such as in Parker et al. (2020). Our work introduces some standard numerical methods to this class of models, leading to increased computational efficiency and increased computational precision. We use the N-mixture model (exemplified by the popular unmarked R package) as a proof of concept. Applying these methods to the hidden INAR models follows a similar procedure, due to the convolution over hidden states in the hidden INAR model likelihood function, while applying these methods to HMMs has been accomplished in previous work Cowen et al. (2017) and Mann (2006).

Large numbers of hidden states (arising from large values of N in N-mixture models, for example) lead to intractable likelihoods (see Sect. 2.2 for details). This is due to the presence of summations over states, precluding simple log transforms for numerical stability. This leads to numerical and computational issues, as integer underflow prevents the use of these classes of models on populations with larger numbers of hidden states. Integer underflow occurs when a floating point number is truncated to zero by limited machine precision (Blanchard et al. 1985). When the true parameter values of a model lay in a region of the likelihood function where underflow occurs for a particular data set, this can cause inaccurate parameter estimates. Likewise, when the observed data lay in a region of the likelihood function where underflow occurs for the true parameter values, the underflow can entirely preclude model fitting. In addition, the choice of initial values used during likelihood optimisation must be chosen to avoid regions of underflow given the observed data; otherwise, underflow at the initial values will preclude model fitting.

One solution to the integer underflow issue is to use arbitrary precision arithmetic. This is investigated and discussed in Parker (2020). This solution is far from ideal, as it exacerbates the computational complexity issue dramatically (arbitrary precision arithmetic can be hundreds or even thousands of times slower than arithmetic on double-precision floating point numbers; Bailey and Borwein (2013)). A common solution to the integer underflow issue in HMMs is to use scaling (Zucchini et al. 2016, p. 48). However, Mann (2006) discussed using the ‘log-sum-exp’ trick as an alternative.

Another solution is to use Bayesian Markov chain Monte Carlo (MCMC) methods in model fitting (see for example Ketz et al. 2018, and the textbook Kéry and Royle 2015). This approach removes the need to sum over hidden states by exploring the parameter space stochastically and can reduce the computation times involved in model fitting (and numerical stability can be achieved with simple log transforms). However, this approach requires the use of prior distributions (which in some cases may be undesirable or even indefensible and can yield more model parameters to estimate) and this approach is non-deterministic due to the stochastic nature of MCMC.

We provide several important contributions with this work. We draw attention to the mathematical similarities between three hidden population modelling frameworks and show how commonly encountered computational precision and efficiency problems can be solved in identical ways for all three frameworks. In light of the popularity of these classes of models, and the computational issues they entail, we expect our proposed solutions to be of particular interest to the ecological modelling community. We provide in our supplemental materials all of the R code necessary for simple and immediate use of these improvements to the N-mixtures framework. Similar code can be implemented for hidden INAR models without difficulty.

We note that our methods for improving computational efficiency are not applicable to general HMMs, but can be applied to any HMM which includes a convolution structure (which is the case with the HMM formulated in Cowen et al. (2017), but is not the case in general). Our methods for improving computational precision are applicable to any HMM, as shown by Mann (2006). In both cases, our main contribution is to illustrate how these methods can be extended to and used to improve the other two hidden model architectures: hidden INAR and N-mixtures.

In Sect. 2.1 we propose a solution to the computation time issue inherent to hidden open-population models through fast Fourier transforms (FFT), as is common in the signal processing literature. This method has been used successfully in HMMs (Cowen et al. 2017), but has not yet been incorporated into any software that solves N-mixture models. Application of FFT is similar for each of the three hidden population models we mention. We focus our examples on N-mixture models and improve on the state-of-the-art software package unmarked (Fiske and Chandler 2011), which we have chosen due to both the popularity of the package as well as due to its non-Bayesian implementation of N-mixture model fitting. In Sect. 4.1 we illustrate the gain in computation speeds made possible by using this technique through an application of N-mixture models to Ancient Murrelet (Synthliboramphus antiquus) chick count data (Parker et al. 2020). In Sect. 2.2 we propose solving the numerical instability of the N-mixture and hidden INAR models for large numbers of states using the numerically stable method of calculating the sum of data (using log transformations, and the log-sum-exp trick; Blanchard et al. 2020), which has already been used successfully in HMMs (Mann 2006). In Sect. 4.2 we demonstrate improvements in numerical stability through a case study with elk data (Ketz et al. 2018).

2 Methods

2.1 Improving Computational Speed Using FFT

We provide a short overview of fast Fourier transforms (FFTs). Details for the theory of FFT can be found in the references Gray and Goodman (1995) and Heckbert (1998). The FFT is a fast method of calculating a Fourier transform (FT). The Fourier transform uses integration to transform a continuous function f(x) into its frequency counterpart \({\widehat{f}}(\nu )\) (see Eq. 1). The inverse of the Fourier transform, the IFT, undoes this transformation by moving from frequency domain back to the time domain (see Eq. 2).

$$\begin{aligned} {\widehat{f}}(\nu ) = \text {FT}\left[ f(x)\right]&= \displaystyle \int _{-\infty }^{\infty } f(x) e^{-2\pi i x \nu } \mathrm {d}x, \end{aligned}$$
(1)
$$\begin{aligned} f(x) = \text {IFT}[{\widehat{f}}(\nu )]&= \displaystyle \int _{-\infty }^{\infty } {\widehat{f}}(\nu ) e^{2\pi i x \nu } \mathrm {d}\nu . \end{aligned}$$
(2)

Here i is the complex unit \(i=\sqrt{-1}\). We use discrete versions of these functions: the discrete Fourier transform (DFT) and its inverse (IDFT). The DFT operates on a length Q sequence of numbers \(\underline{\mathrm{x}}= \{x_1, x_2, \ldots , x_Q\}\) to produce the frequency domain sequence \(\widehat{\underline{\textit{x}}}= \{{\widehat{x}}_1\), \({\widehat{x}}_2,\ldots , {\widehat{x}}_Q\}\). The DFT for each component k is given in Eq. (3), while the IDFT is given in Eq. (4).

$$\begin{aligned} {\widehat{x}}_k = \text {DFT}(\underline{\textit{x}})&= \sum _{j=1}^{Q} x_j e^{\frac{-2\pi i j k}{Q+1}} \end{aligned}$$
(3)
$$\begin{aligned} x_k = \text {IDFT}(\widehat{\underline{\textit{x}}})&= \displaystyle \frac{1}{Q+1}\displaystyle \sum _{j=1}^{Q} {\widehat{x}}_j e^{\frac{2\pi i j k}{Q+1}} \end{aligned}$$
(4)

The DFT can be used to compute convolutions of discrete functions. Given two sequences of numbers \(\underline{\textit{x}}\) and \(\underline{\textit{y}}\), the convolution is as follows: \((\underline{\textit{x}} * \underline{\textit{y}})_n = \sum _{k=1}^{Q} x_k y_{n-k+1}\). Using the DFT, this can be calculated using: \((\underline{\textit{x}} * \underline{\textit{y}}) = \text {IDFT}(\text {DFT}(\underline{\textit{x}}) \cdot \text {DFT}(\underline{\textit{y}}))\). The advantage to calculating the convolution using the DFT is that for large Q, calculating the DFT and IDFT is much faster than directly calculating the many summations. Both DFT and IDFT have algorithmic complexity \({\mathcal {O}}(Q\log Q)\). Manual calculation of the convolution has algorithmic complexity \({\mathcal {O}}(Q^2)\), while calculating the convolution using the DFT has complexity \({\mathcal {O}}(Q\log Q)\) (Heckbert 1998).

Applying these ideas to calculating the model likelihoods is as simple as identifying the convolution components of the likelihood functions and replacing them with the DFT version of convolution. To illustrate, we will replace the transition matrix computations of open-population N-mixture models with FFT in Sect. 2.1.1. In the following, we will use FFT to mean the fast method of computing the DFT and the IDFT.

2.1.1 N-mixtures Transition Probability Matrix

The likelihood function for the open-population N-mixtures model from Dail and Madsen (2011) is given in Eq. (5). In this model there are four parameters: probability of detection p, initial site abundance \(\lambda \), mean population growth rate \(\gamma \), and survival probability \(\omega \). There are also two study specific constants: the number of sampling sites R, and the number of sampling occasions T. The total population at site i and time t are given by the latent variables \(N_{it}\), and the observed population counts are denoted \(n_{it}\).

The function \(P_{a,b}\) shown in Eq. (6) calculates the transition probability for moving from a population of size a to a population of size b. To calculate the likelihood equation requires calculating \(P_{a,b}\) at most \(RT(K+1)(T-1)\) times (when each \(n_{it}=0\)), where K is the upper bound on the summations and thus also the upper bound on the population size. The complexity of computing \(P_{a,b}\) is thus the main bottleneck for computing the likelihood function. \(P_{a,b}\) is a convolution of two discrete distributions and can thus be calculated efficiently using the FFT convolution.

$$\begin{aligned} L(p, \lambda , \gamma , \omega | \{ n_{it} \})&=\prod _{i=1}^{R} \left[ \sum _{N_{i1}=n_{i1}}^{K} \!\cdots \! \sum _{N_{iT}=n_{iT}}^{K} \left\{ \! \left( \!\prod _{t=1}^{T}\! \text {Bin}(n_{it}; N_{it},p) \right) \text {Pois}(N_{i1}; \lambda ) \prod _{t=2}^{T} P_{N_{it-1},N_{it}}\!\right\} \!\right] , \end{aligned}$$
(5)
$$\begin{aligned} P_{a,b}&=\sum _{c=0}^{\text {min}\{a,b\}} \text {Bin}(c;a,\omega )\text {Pois}(b-c;\gamma ). \end{aligned}$$
(6)

Here \(\text {Bin}\) and \(\text {Pois}\) denote the binomial and Poisson distribution functions, respectively. We define the transition probability matrix \(M_{K}\) to be the matrix of \(P_{a,b}\) values, where a and b vary from 0 to K.

Equation (7) illustrates the relationships between \(P_{a,b}\), \(M_K\), convolution, and FFT; let \(x_{a,c} = \text {Bin}(c;a,\omega )\) so that \(\underline{\mathrm{x}}_a = \{x_{a,0}, x_{a,1},\ldots , x_{a,\min \{a,b\}}, 0, 0, \ldots , 0\}\) (right padded with zeroes until \(\underline{\mathrm{x}}_a\) has \(K+1\) elements), and let \(y_{b,c} = \text {Pois}(b-c;\gamma )\) so that \(\underline{\mathrm{y}} = \{y_{0,c}, y_{1,c}, \ldots , y_{K,c}\}\), then \((\underline{\mathrm{x}}_a * \underline{\mathrm{y}})_b = \sum _{c=0}^{\min \{a,b\}} x_{a,c} \cdot y_{b,c} = P_{a,b}\), and \((\underline{\mathrm{x}}_a * \underline{\mathrm{y}}) = \{(\underline{\mathrm{x}}_a * \underline{\mathrm{y}})_0, (\underline{\mathrm{x}}_a * \underline{\mathrm{y}})_1, \ldots , (\underline{\mathrm{x}}_a * \underline{\mathrm{y}})_K\}\).

$$\begin{aligned} M_K = \underbrace{\begin{pmatrix} P_{0,0} &{} P_{0,1} &{} \cdots &{} P_{0,K} \\ P_{1,0} &{} P_{1,1} &{} \cdots &{} P_{1,K} \\ P_{2,0} &{} P_{2,1} &{} \cdots &{} P_{2,K} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ P_{K,0} &{} P_{K,1} &{} \cdots &{} P_{K,K} \end{pmatrix}}_{{\mathcal {O}}\big ( (K+1)^3 \big )} = \begin{pmatrix} (\underline{\mathrm{x}}_0 * \underline{\mathrm{y}}) \\ (\underline{\mathrm{x}}_1 * \underline{\mathrm{y}}) \\ (\underline{\mathrm{x}}_2 * \underline{\mathrm{y}}) \\ \vdots \\ (\underline{\mathrm{x}}_K * \underline{\mathrm{y}}) \end{pmatrix} = \underbrace{\begin{pmatrix} \text {IFFT}\big ( \text {FFT}(\underline{\mathrm{x}}_0) \cdot \text {FFT}(\underline{\mathrm{y}}) \big ) \\ \text {IFFT}\big ( \text {FFT}(\underline{\mathrm{x}}_1) \cdot \text {FFT}(\underline{\mathrm{y}}) \big ) \\ \text {IFFT}\big ( \text {FFT}(\underline{\mathrm{x}}_2) \cdot \text {FFT}(\underline{\mathrm{y}}) \big ) \\ \vdots \\ \text {IFFT}\big ( \text {FFT}(\underline{\mathrm{x}}_K) \cdot \text {FFT}(\underline{\mathrm{y}}) \big ) \end{pmatrix}}_{{\mathcal {O}}\big ( (K+1)^2\log (K+1) \big )} \end{aligned}$$
(7)

Computation of \(M_{K}\) is a large portion of the computational cost of calculating the likelihood function in open-population N-mixture models. In Fig. 1 we show a plot of the median computation times for calculating \(M_{K}\) for increasing values of K using both the manual convolution and the FFT convolution techniques. The values plotted are the median computing times over 100 runs for each value of K. Each run involved generating a random value for \(\omega \) drawn from a Beta (\(a=10\), \(b=10\)) distribution and a random value for \(\gamma \) drawn from a \(\chi ^2_K\) distribution. \(M_{K}\) was then calculated using the same \(\omega \) and \(\gamma \) for both the manual convolution method and the FFT convolution method, and computation times were calculated using the R package microbenchmark (Mersmann 2021). The error bars shown in Fig. 1 indicate minimum and maximum observed computing times. We also note that for both methods, the upper and lower quantiles are indistinguishable from the median computing times on the log plot.

Fig. 1
figure 1

Plot of log median value of computation time measured in milliseconds (out of 100 runs with randomised \(\gamma \) and \(\omega \)) versus K for computation of the transition probability matrix \(M_{K}\) using manual (grey) and the fast Fourier transform (black) convolution methods. Error bars indicate minimum and maximum computing time over the 100 runs per K. We considered \(K=\) 1, 10, 50, 100, 250, 500, and 1000

Full size image

Often, time-varying covariates for the population dynamics parameters \(\gamma \) and \(\omega \) are incorporated into N-mixture models. When this is done, the matrix \(M_{K}\) is calculated once for each time point \(t \in \{2,\ldots ,T\}\). Thus the computing time savings when using FFT are increased by a factor of up to \(T-1\) when time covariates are considered.

In Sect. 3.1 we use a simulation study to illustrate the improved computational efficiency of using the FFT method for calculating \(M_{K}\) when fitting N-mixture models. In Sect. 4.1 we apply the FFT method to improve computing efficiency for an Ancient Murrelet chick counts application.

2.2 Improving Numerical Stability

Underflow arises when machine precision is not large enough to differentiate a floating point number from zero (Blanchard et al. 1985). This situation occurs when calculating the probability of relatively rare events. As an example, consider a binomial random variable X with size parameter N and fixed probability of success \(\omega \). There are \(N+1\) possible states for the random variable X, the integers \(\{0, 1, \ldots , N\}\). Increasing N decreases the probability of observing any particular state. For large enough N, integer underflow will occur when calculating the probability \(p_X\) of even the most probable state of X.

This problem is usually solved by calculating the state probabilities \(p_X\) in log space: \(\log (p_X)\) rather than \(p_X\). When taking the log transform of the probability, the log of the probability will have relatively small absolute magnitude (i.e. within the realm of floating point precision). This solution is not immediately possible in certain likelihood equations, such as the ones associated with N-mixtures, HMMs, and hidden INAR models. The presence of summations in the likelihood functions requires transformation away from log space in order to compute the sums. To perform these summations in a numerically stable way we use the log-sum-exp trick (LSE; Blanchard et al. (2020)), which is standard in the machine learning community, and has been used for HMMs (Mann 2006), but is not used by the unmarked software. We overview the details of LSE in this section.

LSE is a method which allows two (or more) log space floating point numbers to be added outside of log space in a numerically stable way, producing a log space result. LSE works by translating the floating point numbers into a region wherein computational precision is maximised according to the IEEE 754 specification for floating points (Blanchard et al. 1985). Consider two very small floating point numbers x and y, which are being stored as \(\ell x = \log (x)\) and \(\ell y = \log (y)\). The LSE allows the sum to be calculated using Eq. (8), where \(v = \max (\ell x, \ell y)\). Without loss of generality, suppose that \(\ell x > \ell y\). Then equation 8 simplifies to: \(\text {LSE}(\ell x,\ell y) = \ell x + \log [1 + \exp (\ell y - \ell x)]\). This leaves us with a term \(\log (1+z)\) where \(z=\exp (\ell y - \ell x)\) is bounded between 0 and 1 (an interval with highest computational precision according to IEEE 754). This can be computed accurately even for very small z so long as appropriate algorithms for computing the logarithm are used (Blanchard et al. 2020). An appropriate algorithm available in R (R Core Team 2020) is provided by the function log1p.

$$\begin{aligned} \text {LSE}(\ell x,\ell y) = v + \log (\exp (\ell x - v) + \exp (\ell y - v)), \quad v = \max (\ell x, \ell y). \end{aligned}$$
(8)

The function implementing LSE can be implemented with very few lines of code; for an example implemented using R see Algorithm 1. These ideas can be used to compute convolutions in log space, so that computing the transition probability matrix \(M_{K}\) can be done with high computational precision even at large K. See Algorithm 2 for an example of implementing a log space convolution function using R.

figure a
figure b

The ability to compute arbitrary sums in log space using LSE, as well as the particular application of using LSE to compute convolutions in log space, allows for the accurate computation of log-likelihood functions involving summations and/or convolutions. This is directly applicable to the model likelihood functions for N-mixtures, HMMs, and hidden INAR models, giving them the ability to handle large numbers of discrete states in a numerically stable way.

As an illustrative example, in Sect. 3.2 we use a simulation study to compare the numerical stability of calculating the transition probability matrix of an open-population N-mixture model with and without the proposed LSE implementation. In Sect. 4.2 we apply the LSE method to solve the integer underflow issue for an Elk counts application.

3 Simulations

All simulations were computed on a single 4.0 GHz AMD Ryzen 9 3900X processor.

3.1 Computational Speed Comparison Against Unmarked

The popular R package unmarked (Fiske and Chandler 2011) contains the function pcountOpen for fitting N-mixture models of the form developed in Dail and Madsen (2011). pcountOpen is optimised using C++, making it a fast implementation of the open-population N-mixtures likelihood. However, at the time of writing this manuscript, pcountOpen uses manual convolution in calculating the transition probabilities (and does not use the FFT convolution, incurring an additional factor of \({\mathcal {O}}(K/\log (K))\) in the asymptotic complexity).

We compare the computation times for pcountOpen against the computation times for our implementation of the likelihood, which uses the FFT to compute convolutions. For this comparison, we chose \(\omega =0.8\), \(\gamma =2\), \(\lambda =30\), and \(p=0.25\) to generate a single random data set \(\{n_{it}\}\) for each combination of T and R considered. We refer to Fig. 1 to illustrate that differences in \(\omega \) and \(\gamma \) will have minimal impact on computing time for both methods. We note that in all cases considered, the unmarked parameter estimates matched the FFT parameter estimates.

The results of this simulation are summarised in Fig. 2. Due primarily to the high level of optimisation of the unmarked function, as well as the diminishing relative advantage of the FFT for small K, unmarked outperforms the FFT implementation in terms of computational speed when K is small. However, the computational speed of the FFT implementation substantially outperforms the unmarked implementation for \(K > 250\) (in a domain where unmarked requires months of computing time, our FFT implementation requires days).

Fig. 2
figure 2

Plot of the log computation time versus K using the unmarked model fitting implementation pcountOpen and the FFT-based implementation. R is the number of sampling locations, and T is the number of sampling occasions. When population size upper bound \(K=1000\), the top three lines correspond to unmarked, while the bottom three lines correspond to FFT

Full size image

The FFT method of computation as illustrated in Fig. 2 shows a non-monotonic growth pattern in terms of increasing K. This is an artefact of the FFT algorithm, and different implementations of the FFT will show different such artefacts. The FFT algorithm which we have used is implemented in base R (R Core Team 2020) and uses the mixed-radix algorithm of Singleton (1969). This implementation is known to be fastest for sequence lengths which are highly composite. As well, odd factors of the sequence length compute with four times fewer complex multiplications than the even factors, so that choice of K influences computing time through its prime factors as well as its magnitude.

3.2 Numerical Stability Comparison

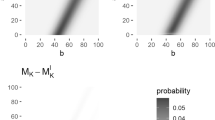
We consider the effect of numerical instability on calculation of the transition probability matrices \(M_{K}\). Figure 3 shows four matrix contour plots, with transition probabilities in log space. Each matrix was calculated with \(\omega =0.5\) and \(\gamma =1\) (according to the N-mixture model in Eqs. (5) and (6)). We note that similar results can be obtained for any given combination of \(\omega \) and \(\gamma \). In a model with site or time varying \(\gamma \) or \(\omega \), calculating the likelihood would require a separate matrix \(M_{K}\) to be calculated for each site or time. For this example we are considering a single-transition probability matrix with constant parameters. The first column of Fig. 3 illustrates the values of the transition probability matrix after calculation without using the LSE method. The second column illustrates the same, calculated using the LSE method. The first row is the matrices calculated when \(K=500\), while the second row is the matrices calculated when \(K=4,000\). The empty portions of Figs. 3a, c indicate regions where underflow has occurred. In the case of Fig. 3a, 24.03% of the matrix entries have experienced underflow. For Fig. 3c, 62.72% of the entries experienced underflow. This illustrates that underflow becomes a more prominent issue as K increases. We note that in the extreme case, when K is very large, 100% of the entries would experience underflow, as the entries of \(M_K\) tend to zero. For both choices of K, when calculating the matrix using the LSE method, zero underflows occurred. We also note that the current likelihood implementation used by the pcountOpen function of the unmarked package does not use the numerically stable LSE; thus, caution must be exercised when fitting models for large K (although small entries of \(M_K\) correspond to unlikely states, all possible product chains of entries with length \(T-1\) and with \(N_{it} \le K\) are weighted and summed together upon likelihood evaluation).

Fig. 3
figure 3

Transition probability matrices \(M_{K}\) in log space, calculated for \(K=500\), and for \(K=4000\). Each matrix was calculated with the parameter values: \(\omega =0.5\) and \(\gamma =1\). Vertical axes represent row number and horizontal axes represent column number in the \(M_{K}\) matrix. Greyscale indicates log of probability values. Subfigures a and c are calculated without using the numerically stable LSE, while b and d are calculated using the numerically stable LSE

Full size image

4 Case Studies

All case studies were computed on a single 4.0 GHz AMD Ryzen 9 3900X processor.

4.1 FFT Application

We considered a concrete example of increasing computational efficiency of N-mixture models with the FFT approach, using the Ancient Murrelet chick counts from Parker et al. (2020). The Ancient Murrelet chick count data were collected on East Limestone Island, Haida Gwaii by the Laskeek Bay Conservation Society, between 1995 and 2006. The Ancient Murrelet is a burrow nesting seabird which is a species of special concern due to dramatic population declines (see for example Bertram (1995)). Estimating the total number of chicks from the chick count data provides a measure of population health over time for the Ancient Murrelet colony. An increasing trend in chicks can indicate population growth, while a decreasing trend can indicate population decline. For the chick count data, there are six sampling sites (\(R=6\)), which are constant for each year. The sampling sites use capture funnels set each year, which allow easy counting as the chicks run from their burrows out to sea during the hatching season. There are seventeen sampling occasions (\(T=17\)), with sampling occasions lasting from early May to late June. We chose an upper bound of \(K=500\) for this study. In fitting these data, we show that the FFT implementation produces the same estimates and the same standard error estimates as the unmarked implementation, while computing more than ten times faster (Table 1). Our results show that the estimated population dynamics parameters \(\gamma \) and \(\omega \) are consistent with population decline, with the estimated number of chicks declining from 1740 with 95% confidence interval (1530, 2010) in 1995 to 950 (840, 1100) in 2006.

Table 1 Results from fitting open-population N-mixture models to the Ancient Murrelet chick count data using the unmarked implementation and the FFT implementation
Full size table

4.2 LSE Application

We considered a concrete example of increasing the computational precision of N-mixture models with the LSE approach, using the elk (Cervus elaphus nelsoni) counts from Ketz et al. (2018), which are counts of a wintering elk population located in the Estes Valley, Colorado. In this example there are \(R=2\) sampling sites, corresponding to Rocky Mountain National Park and Estes Park. There are \(T=24\) sampling occasions, with several sampling occasions per winter for each of the years 2011 to 2016. More details can be found in Ketz et al. (2018). In this case study we do not consider the movement model components from Ketz et al. (2018), and so our results here are meant only as an example illustrating the LSE approach for the large counts regime. We show that our LSE implementation of the N-mixture model succeeds in producing estimates, while the unmarked implementation fails due to numerical instability (Table 2): failing to converge because integer underflow prevents the algorithm from considering the off diagonal corners of the transition probability matrix. This can be seen in Fig. 4, which compares the transition probability matrix for the elk data calculated with and without the numerically stable LSE at the converged parameter values. For the LSE implementation, none of the elements of the matrix underflowed, whereas for the unmarked implementation 65.83% underflowed.

Fig. 4
figure 4

Transition probability matrices \(M_{K}\) in log space for the elk model, calculated for \(K=6000\) at the converged model parameter values: \({{\widehat{\omega }}}=0.7743\) and \({{\widehat{\gamma }}}=202.94\). Vertical axes represent row number and horizontal axes represent column number in the \(M_{K}\) matrix. Greyscale indicates log of probability values. The cross indicates a particular transition (\(a=2262\) to \(b=979\)) which falls into the integer underflow region. Subfigure a is calculated without using the numerically stable LSE, while b is calculated using the numerically stable LSE

Full size image
Table 2 Results from fitting open-population N-mixture models to the elk data using the log-sum-exponential (LSE) implementation
Full size table

5 Discussion

We investigated the use of fast Fourier transforms and the ‘log-sum-exp’ trick to improve computational and numerical instability issues inherent in N-mixture models when the population size is large. We compared these methods with the standard implementation found in the R package unmarked using both Ancient Murrelet and elk data.

By recognising the convolution calculations inherent to calculating the model likelihood functions, it is straightforward to replace the method of calculation from a manual convolution method to a substantially faster FFT convolution. The improvement in computational complexity for the convolution calculation is largely realised in the computation of the N-mixture model likelihood, since calculating the convolution is the most demanding aspect of the likelihood computation. This improvement is readily available to any other likelihood models which make use of convolutions, such as the hidden INAR (Fernández-Fontelo et al. 2016) and particular HMM models (Cowen et al. 2017, for example).

We have added our FFT implementation of the pcountOpen function to the R package quickNmix (Parker et al. 2022), via the function pCountOpenFFT. Our package is available on CRAN and enables researchers to quickly and easily switch between the unmarked implementation and our FFT version.

There are many cases for which the faster FFT method makes computation time more feasible. Some possibilities include large colonies of seabirds, sea lions, ungulates (elk/caribou), or insects where population surveys involve counts. One such example would be examining larger colonies of Ancient Murrelet seabirds than in Sect. 4.1. The colony on Haida Gwaii is very small compared to the neighbouring colony on Reef Island, which is estimated to contain roughly five times as many burrows (COSEWIC 2004). Especially when bootstrap methods are implemented to produce standard error estimates, such as in Parker et al. (2020), the gains in computational efficiency from using the FFT methods can be instrumental to making a large population study computationally feasible.

Implementing numerically stable log-space summations allows for the study of models with large numbers of hidden states by facilitating the calculation of the log-likelihood at high computational precision even when the likelihood function contains summations. This avoids the problem of integer underflow present in calculating the regular likelihood functions when large numbers of states are considered (such as in the large K regime of N-mixtures).

The transition probability matrix contour plots shown for the elk example in Fig. 4 illustrate why LSE can be used to fit the model to the elk data, but the unmarked implementation cannot be used. The estimated parameter values (as shown in Table 2) give rise to an estimated latent abundance for site 2 at sampling occasion 6 of \({\widehat{N}}_{2,6} = 2262\), which transitions to \({\widehat{N}}_{2,7} = 979\) at sampling occasion 7. This transition falls into the underflow region of Fig. 4a, illustrated by the blue cross. The integer underflow can be avoided by use of the numerically stable LSE in this and similar situations.

We have addressed two computational issues common to N-mixture models, hidden INAR models, and some HMMs. We have shown that the solutions to these issues compare favourably against the current implementation in the unmarked R package, and both solutions are easily implemented. For the open-population N-mixture models, we recommend using the FFT convolution method for K larger than 200, noting that the FFT method can be further improved by optimisation in C++. We also recommend the FFT method for other models which contain many convolution calculations. However, we caution that without a numerically stable FFT algorithm, integer underflow will still be an issue for large population size upper bounds such as in the N-mixture models. Therefore we recommend using the LSE method in situations where numerical instability leads to intractable model likelihoods, where higher computational precision is needed (such as when an optimisation algorithm fails to differentiate functional values at neighbouring parameter values), and when the log-likelihood will be used in calculating quantities such as AIC or BIC.