Bayesian Methods for Estimating Animal Abundance at Large Spatial Scales Using Data from Multiple Sources

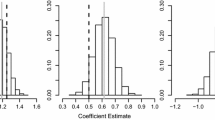
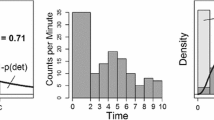
Abstract

Estimating animal distributions and abundances over large regions is of primary interest in ecology and conservation. Specifically, integrating data from reliable but expensive surveys conducted at smaller scales with cost-effective but less reliable data generated from surveys at wider scales remains a central challenge in statistical ecology. In this study, we use a Bayesian smoothing technique based on a conditionally autoregressive (CAR) prior distribution and Bayesian regression to address this problem. We illustrate the utility of our proposed methodology by integrating (i) abundance estimates of tigers in wildlife reserves from intensive photographic capture–recapture methods, and (ii) estimates of tiger habitat occupancy from indirect sign surveys, conducted over a wider region. We also investigate whether the random effects which represent the spatial association due to the CAR structure have any confounding effect on the fixed effects of the regression coefficients.

Appendices

Appendix 1: Empirical Bayes Results

An empirical Bayes version of the hierarchical Bayes estimate stated in Proposition 2.1 is given below.

Proposition 5.1

An empirical Bayes estimate of $\mathbf {\nu }^S$ and an empirical Bayes estimate of its covariance matrix are given by

$$\begin{aligned} \hat{\mathbf {\nu }}_{EB}^S= & {} \hat{\delta }^2 Q_{21}(\hat{\rho })\bigl (\hat{\sigma }^2 I_{k_1} + \hat{\delta }^2 Q_1(\hat{\rho })\bigr )^{-1}\hat{\mathbf {\nu }}(ct)\nonumber \\&+\, (\mathbf {X}^S - \hat{\delta }^2 Q_{21}(\hat{\rho })\bigl (\hat{\sigma }^2 I_{k_1} + \hat{\delta }^2 Q_1(\hat{\rho })\bigr )^{-1} \mathbf {X}^T)\hat{\mathbf {\beta }}, \end{aligned}$$

(5.1)

$$\begin{aligned} \hat{Cov}_{EB}(\mathbf {\nu }^S)= & {} \hat{\delta }^2 Q_2(\hat{\rho }) - \hat{\delta }^4 Q_{21}(\hat{\rho }) \bigl (\hat{\sigma }^2 I_{k_1} + \hat{\delta }^2 Q_1(\hat{\rho })\bigr )^{-1} Q_{12}(\hat{\rho }). \end{aligned}$$

(5.2)

Proof

Note that (2.5) yields an empirical Bayes likelihood function for $(\sigma ^2, \mathbf {\beta }, \delta ^2, \rho )$. Therefore, these parameters can be estimated by maximizing this likelihood function and obtaining the required MLE, $(\hat{\sigma }^2, \hat{\mathbf {\beta }}, \hat{\delta }^2, \hat{\rho })$. From (2.7), it follows that

$$\begin{aligned} E(\mathbf {\nu }^S | \hat{\mathbf {\nu }}(ct), \sigma ^2, \mathbf {\beta }, \delta ^2,\rho )= & {} \mathbf {X}^S\mathbf {\beta } + \delta ^2 Q_{21}(\rho )\bigl (\sigma ^2 I_{k_1} + \delta ^2 Q_1(\rho ) \bigr )^{-1}(\hat{\mathbf {\nu }}(ct) - \mathbf {X}^T\mathbf {\beta }) \nonumber \\= & {} \delta ^2 Q_{21}(\rho )\bigl (\sigma ^2 I_{k_1} + \delta ^2 Q_1(\rho )\bigr )^{-1}\hat{\mathbf {\nu }}(ct)\nonumber \\&+\, (\mathbf {X}^S - \delta ^2 Q_{21}(\rho )\bigl (\sigma ^2 I_{k_1} + \delta ^2 Q_1(\rho ) \bigr )^{-1} \mathbf {X}^T)\mathbf {\beta }. \end{aligned}$$

(5.3)

Substituting $(\sigma ^2, \mathbf {\beta }, \delta ^2,\rho )$ by $(\hat{\sigma }^2, \hat{\mathbf {\beta }}, \hat{\delta }^2, \hat{\rho })$ yields the desired empirical Bayes estimate. Similarly, since $Cov(\mathbf {\nu }^S | \hat{\mathbf {\nu }}(ct), \sigma ^2, \mathbf {\beta }, \delta ^2,\rho ) = \delta ^2 Q_2(\rho ) - \delta ^4 Q_{21}(\rho )\bigl (\sigma ^2 I_{k_1} + \delta ^2 Q_1(\rho )\bigr )^{-1} Q_{12}(\rho )$, substitution as before gives the empirical Bayes estimate of the covariance matrix. $\square$

Proposition 5.2

An empirical Bayes approximation for the estimates of abundance and its variance are, respectively, $\hat{A}_{EB} = \sum _{i=1}^{k_1+k_2} e^{\hat{\mu }_i + \hat{P}_{ii}/2}$ and $\hat{Var}_{EB}(A) = \sum _{i=1}^{k_1+k_2} e^{2\hat{\mu }_i +\hat{P}_{ii}} \bigl (e^{\hat{P}_{ii}}-1\bigr ) + \sum _{i\ne j} e^{\hat{\mu }_i + \hat{\mu }_j + (\hat{P}_{ii}+\hat{P}_{jj})/2} \bigl (e^{\hat{P}_{ij}}-1\bigr )$,

where $\hat{\mu }_i = \mu _i(\hat{\sigma }^2, \hat{\mathbf {\beta }}, \hat{\delta }^2, \hat{\rho }),\, \hat{P}_{ij} = P_{ij}(\hat{\sigma }^2, \hat{\mathbf {\beta }}, \hat{\delta }^2, \hat{\rho }).$

This follows from (2.2), arguing as above.

Appendix 2: Supplementary Material: Results for the Constrained Model

1.1 Posterior Quantities Under the Constrained Model

Following Reich et al. (2006), we set $\theta _1=0$ in (3.4) to alleviate collinearity. Then the model becomes

$$\begin{aligned} \hat{\nu }(ct) = \nu ^T + \epsilon , \, \nu ^T=\mathbf {X}^T \mathbf {\beta } + L^{\prime } \theta _2, \end{aligned}$$

(5.4)

where $\epsilon \sim N_{k_1}(\mathbf {0}, \tau _e I_{k_1})$, $\theta _2 |\tau _s \sim N_{k_1-r}(\mathbf {0}, \tau _s \widetilde{V}_{22})$, $\widetilde{V}_{22}= L V L^\prime$ and $\mathbf {X}^T$ is the matrix of covariates for the camera trap sites. $\mathbf {\beta }$ is given a flat prior and $\tau _e$, $\tau _s$ are given independent Gamma(0.01, 0.01) priors. The joint posterior distribution can then be expressed as:

$$\begin{aligned} \pi (\mathbf {\beta }, \theta _2, \tau _s, \tau _e | \hat{\nu }(ct))&= \pi (\mathbf {\beta }, \theta _2 | \hat{\nu }(ct), \tau _s, \tau _e) \,\pi (\tau _s, \tau _e | \hat{\nu }(ct))\\&\quad \propto f(\hat{\nu }(ct) | \mathbf {\beta }, \theta _2, \tau _e)\, \pi (\mathbf {\beta })\, \pi ( \theta _2 | \tau _s)\, \pi (\tau _s)\, \pi (\tau _e). \end{aligned}$$

Note that the exponent of the expression above reduces to

$$\begin{aligned}&\tau _e(\hat{\nu }(ct) - \mathbf {X}^T \mathbf {\beta } - L^\prime \theta _2)^\prime \, (\hat{\nu }(ct) - \mathbf {X}^T \mathbf {\beta } - L^\prime \theta _2) + \tau _s \theta _2^{\prime } \widetilde{V}_{22} \theta _2\\&= \tau _e \mathbf {\beta }^\prime {\mathbf {X}^T}^\prime \mathbf {X}^T \mathbf {\beta } + \tau _e {\theta _2}^{\prime } L L^{\prime } \theta _2 + 2 \tau _e \mathbf {\beta }^\prime {\mathbf {X}^T}^\prime L^{\prime } \theta _2 - 2 \tau _e \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix}^{\prime } \begin{pmatrix} {\mathbf {X}^T}^{\prime } \\ L \end{pmatrix} \hat{\nu }(ct) \\&\qquad + \tau _e \hat{\nu }(ct)^{\prime } \hat{\nu }(ct) + \tau _s \theta _2^{\prime } \widetilde{V}_{22} \theta _2\\&= \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix}^\prime \begin{Bmatrix} \tau _e {\mathbf {X}^T}^{\prime } {\mathbf {X}^T}&0 \\ 0&\tau _e I_{k_1-r}+ \tau _s \widetilde{V}_{22} \end{Bmatrix} \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix} - 2 \tau _e \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix}^{\prime } \begin{pmatrix} {\mathbf {X}^T}^{\prime } \\ L \end{pmatrix} \hat{\nu }(ct) + \tau _e \hat{\nu }(ct)^{\prime } \hat{\nu }(ct)\\&= \begin{bmatrix} \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix} - \hat{\mu }_{\beta } \end{bmatrix}^\prime \Sigma \begin{bmatrix} \begin{pmatrix} \mathbf {\beta }\\ \theta _2 \end{pmatrix} - \hat{\mu }_{\beta } \end{bmatrix} - \hat{\mu }_{\beta }^{\prime }\Sigma \,\hat{\mu }_{\beta } + \tau _e \hat{\nu }(ct)^{\prime } \hat{\nu }(ct), \end{aligned}$$

where

$$\begin{aligned} \Sigma = \begin{Bmatrix} \tau _e {\mathbf {X}^T}^{\prime } {\mathbf {X}^T}&0 \\ 0&\tau _e I_{k_1-r}+ \tau _s \widetilde{V}_{22} \end{Bmatrix},\ \hat{\mu }_{\beta } = \tau _e \Sigma ^{-1} \begin{pmatrix} {\mathbf {X}^T}^{\prime } \\ L \end{pmatrix} \hat{\nu }(ct). \end{aligned}$$

From this, we have

$$\begin{aligned}&\pi (\beta , \theta _2, \tau _s, \tau _e | \hat{\nu }(ct)) \propto \tau _e^{k_1/2} \tau _s^{(k_1-r-G)/2} \exp \Big \{ -\frac{1}{2} \begin{bmatrix} \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix} - \hat{\mu }_{\beta } \end{bmatrix}^\prime \Sigma \begin{bmatrix} \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix} - \hat{\mu }_{\beta } \end{bmatrix} \Big \}\\&\times \exp \Big \{ -\frac{1}{2} \Big [ \tau _e \hat{\nu }(ct)^{\prime } \hat{\nu }(ct) - \hat{\mu }_{\beta }^{\prime }\Sigma \,\hat{\mu }_{\beta } \Big ] \Big \}\, \pi (\tau _s)\,\pi (\tau _e). \end{aligned}$$

Therefore, $( \mathbf {\beta }, \theta _2)\ | \ \hat{\nu }(ct), \tau _s, \tau _e \sim N_{k_1} ( \hat{\mu }_{\beta }, \Sigma )$ with density

$$\begin{aligned} \pi (\beta , \theta _2 |\, \hat{\nu }(ct), \tau _s, \tau _e) = \frac{|\Sigma |^{1/2}}{(\sqrt{2\pi })^{p}} \exp \Big \{ -\frac{1}{2} \begin{bmatrix} \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix} - \hat{\mu }_{\beta } \end{bmatrix}^\prime \Sigma \begin{bmatrix} \begin{pmatrix} \mathbf {\beta } \\ \theta _2 \end{pmatrix} - \hat{\mu }_{\beta } \end{bmatrix}\Big \}, \end{aligned}$$

and the posterior density of $(\tau _s, \tau _e)$ is

$$\begin{aligned}&\pi (\tau _s, \tau _e|\hat{\nu }(ct))\propto \pi (\tau _s)\,\pi (\tau _e)\, \tau _e^{k_1/2} \tau _s^{(k_1-r-G)/2} |\Sigma |^{-1/2} \, \\&\exp \Big \{ -\frac{1}{2} \Big [ \tau _e \hat{\nu }(ct)^{\prime } \hat{\nu }(ct) - \hat{\mu }_{\beta }^{\prime }\Sigma \,\hat{\mu }_{\beta } \Big ] \Big \}\\&= \pi (\tau _s)\,\pi (\tau _e) \, \tau _e^{k_1/2} \tau _s^{(k_1-r-G)/2} |\Sigma |^{-1/2} \, \exp \big \{ -\frac{1}{2} h(\hat{\nu }(ct), \tau _s, \tau _e) \big \}, \end{aligned}$$

where

$$\begin{aligned} h(\hat{\nu }(ct), \tau _s, \tau _e)= & {} \tau _e \hat{\nu }(ct)^{\prime } \hat{\nu }(ct) - \hat{\mu }_{\beta }^{\prime }\Sigma \, \hat{\mu }_\beta \\= & {} \tau _e \hat{\nu }(ct)^\prime \Big [ I_{k_1} - \tau _e \begin{pmatrix} {\mathbf {X}^T}^{\prime } \\ L \end{pmatrix}^{\prime } \Sigma ^{-1} \begin{pmatrix} {\mathbf {X}^T}^{\prime } \\ L \end{pmatrix} \Big ] \hat{\nu }(ct). \end{aligned}$$

This is not a standard density. For computations, we can simulate $(\tau _s, \tau _e)$ using the Metropolis-Hastings algorithm with the proposal distributions: $\tau _s^{cand}\, |\, \tau _s^{(i-1)} \sim \text { Log-normal}(\log \tau _s^{(i-1)}, \, \sigma ^2_s), \, \sigma ^2_s=0.1.$ and $\tau _e^{cand}\, |\, \tau _e^{(i-1)} \sim \text { Log-normal}(\log \tau _e^{(i-1)}$, $\sigma ^2_e),\, \sigma ^2_e=0.1.$

1.2 Prediction of Abundance Under the Constrained Model

We set $\theta _1=0$ in $\nu = \mathbf {X} \beta + K^\prime \theta _1 + L^\prime \theta _2$, $\theta = (\theta _1^\prime , \theta _2^\prime )^\prime |\tau _s \sim N(\mathbf {0}, \tau _s \widetilde{V} )$ where $\widetilde{V} = (K^\prime \ L^\prime )^\prime \, V \, (K^\prime \ L^\prime )$. Here K is an $r \times p$ matrix consisting of the eigenvectors of $B = X(X^\prime X )^{-1} X^\prime$ (corresponding to the non-zero eigenvalues) as its rows and L is $(p-r) \times p$ matrix with eigenvectors of $B^c = I_p - B$ (corresponding to the non-zero eigenvalues) as its rows. With $\theta _1=0$, the model becomes

$$\begin{aligned} \nu = \mathbf {X} \beta + L^\prime \theta _2, \theta _2|\tau _s \sim N(\mathbf {0}, \tau _s LVL^\prime ). \end{aligned}$$

(5.5)

From (5.5), the prior on $\nu$ is given by

$$\begin{aligned} \nu |\mathbf {\beta }, \tau _s \sim N_p(\mathbf {X}\mathbf {\beta }, U^{-1}), \end{aligned}$$

(5.6)

where $U=L^\prime (\tau _s LVL^\prime )^{-1}L$. Combining (5.4) and (5.6), we obtain

$$\begin{aligned} \hat{\nu }(ct) | \mathbf {\beta }, \tau _s, \tau _e \sim N_{k_1}\big (\mathbf {X}^T\mathbf {\beta }, (\tau _e^{-1} I_{k_1} + U_{11})^{-1}\big ), \end{aligned}$$

(5.7)

where $U_{11}={L^T}^\prime (\tau _s LVL^\prime )^{-1} L^T$ is the top $k_1\times k_1$ square block of U and $L^T$ is the first $k_1$ columns of L. Upon specifying a prior density $\pi ( \mathbf {\beta }, \tau _s, \tau _e)$, the corresponding posterior density $\pi ( \mathbf {\beta }, \tau _s, \tau _e |\hat{\nu }(ct))$ is obtained by combining it with the model density under (5.7).

1.2.1 Hierarchical Bayes and Empirical Bayes

Proposition 5.3

(i) The fully hierarchical Bayes estimate of $\nu ^S$ and its posterior covariance matrix are given by

$$\begin{aligned} E(\nu ^S|\hat{\nu }(ct))= & {} E^* \left( U_{21}(\tau _s)\bigl (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s)\bigr )^{-1}\right) \hat{\nu }(ct) \nonumber \\&+\, \mathbf {X}^S E^*(\mathbf {\beta }) - E^* \bigl ( U_{21}(\tau _s)\bigl (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s)\bigr )^{-1} \mathbf {X}^T \mathbf {\beta }\bigr ), \end{aligned}$$

(5.8)

$$\begin{aligned} Cov(\nu ^S| \hat{\nu }(ct))= & {} E^* \bigl (U_{22}(\tau _s) - U_{21}(\tau _s) \bigl (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s)\bigr )^{-1} U_{12}(\tau _s) \bigr )\nonumber \\&+\, Cov^* (E(\nu ^S | \hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e )), \end{aligned}$$

(5.9)

where $E^*$ and $Cov^*$ denote expectation and covariance with respect to $\pi (\mathbf {\beta }, \tau _s, \tau _e | \hat{\nu }(ct))$. (ii) An empirical Bayes estimate of $\nu ^S$ and an empirical Bayes estimate of its covariance matrix are given by

$$\begin{aligned} \hat{\nu }_{EB}^S= & {} U_{21}(\hat{\tau _s})\bigl (\hat{\tau _e}^{-1} I_{k_1} + U_{11}(\hat{\tau _s})\bigr )^{-1}\hat{\nu }(ct) \nonumber \\&+\, (\mathbf {X}^S - U_{21}(\hat{\tau _s})\bigl (\hat{\tau _e}^{-1} I_{k_1} + U_{11}(\hat{\tau _s})\bigr )^{-1} \mathbf {X}^T)\hat{\mathbf {\beta }}, \end{aligned}$$

(5.10)

$$\begin{aligned} \hat{Cov}_{EB}(\nu ^S)= & {} U_{22}(\hat{\tau _s}) - U_{21}(\hat{\tau _s}) \bigl (\hat{\tau _e}^{-1} I_{k_1} + U_{11}(\hat{\tau _s})\bigr )^{-1} U_{12}(\hat{\tau _s}), \end{aligned}$$

(5.11)

where $\hat{\mathbf {\beta }}, \hat{\tau _s}, \hat{\tau _e}$ are the empirical Bayes estimates of $\mathbf {\beta }, \tau _s, \tau _e$.

Proof

Since $\hat{\nu }(ct) = \nu ^T + \mathbf {\epsilon }$ where $\mathbf {\epsilon } \sim N(\mathbf {0}, \tau _e I_{k_1})$ (and is independent of $\nu ^T$), we have

$$\begin{aligned} \left( \begin{array}{c} \hat{\nu }(ct)\\ \nu ^T\\ \nu ^S\end{array}\right) \, | \, \mathbf {\beta }, \tau _s, \tau _e\sim & {} N_{p+k_1}\left( \left( \begin{array}{c} \mathbf {X}^T\mathbf {\beta }\\ \mathbf {X}^T\mathbf {\beta }\\ \mathbf {X}^S\mathbf {\beta } \end{array}\right) , \left( \begin{array}{ccc} \tau _e^{-1} I_{k_1} + U_{11}(\tau _s) &{} U_{11}(\tau _s) &{} U_{12}(\tau _s)\\ U_{11}(\tau _s) &{} U_{11}(\tau _s) &{} U_{12}(\tau _s)\\ U_{21}(\tau _s) &{} U_{21}(\tau _s) &{} U_{22}(\tau _s) \end{array}\right) ^{-1} \right) ,\nonumber \\ \end{aligned}$$

(5.12)

where $U_{11}$, $U_{22}$, $U_{12}$ and $U_{21} = U_{12}^\prime$ are as in

$$\begin{aligned} L^\prime (\tau _s LVL^\prime )^{-1}L = U(\tau _s) = \left( \begin{array}{cc} U_{11}(\tau _s) &{} U_{12}(\tau _s)\\ U_{21}(\tau _s) &{} U_{22}(\tau _s)\end{array}\right) . \end{aligned}$$

It then follows that

$$\begin{aligned}&\nu ^S | \hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e \sim N_{k_2}\Bigl ( \mathbf {X}^S\mathbf {\beta } + U_{21}\bigl (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s) \bigr )^{-1}(\hat{\nu }(ct) - \mathbf {X}^T\mathbf {\beta }),\nonumber \\&\bigl ( U_{22}(\tau _s) - U_{21}(\tau _s)\bigl (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s)\bigr )^{-1} U_{12}(\tau _s)\bigr )^{-1}\Bigr ), \end{aligned}$$

(5.13)

Now note that $E(\nu ^S | \hat{\nu }(ct)) = E[E(\nu ^S | \hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e)],$ where the outside expectation is with respect to $\pi ( \mathbf {\beta }, \tau _s, \tau _e |\hat{\nu }(ct))$. Further, $\nu ^S | \hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e$ is as given in ( 5.13) above. $\square$

1.2.2 Estimation of Total Abundance

In addition to the abundance levels across the region, we also desire an estimate of the total abundance in the region, $A(\mathbf {\lambda }) = \sum _{i=1}^{k_1+k_2} \lambda _i = \sum _{i=1}^{k_1+k_2} \exp (\nu _i)$. This estimate and its estimation error can be derived as follows. From (5.12), we have that

$$\begin{aligned} \nu |\hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e \sim N_p \left( \mathbf {\mu }(\mathbf {\beta }, \tau _s, \tau _e), P^{-1}(\mathbf {\beta }, \tau _s, \tau _e)\right) , \end{aligned}$$

(5.14)

where (suppressing the dependence on $\hat{\nu }(ct)$)

$$\begin{aligned} \mathbf {\mu }(\mathbf {\beta }, \tau _s, \tau _e)&= \mathbf {X}\mathbf {\beta } + (U_{11}(\tau _s), U_{12}(\tau _s))^\prime (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s))^{-1}(\hat{\nu }(ct)-\mathbf {X}^T\mathbf {\beta }), \nonumber \\ P(\mathbf {\beta }, \tau _s, \tau _e)&= U(\tau _s)-(U_{11}(\tau _s), U_{12}(\tau _s))^\prime (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s))^{-1} (U_{11}(\tau _s), U_{12}(\tau _s)). \end{aligned}$$

(5.15)

For later use, let $\mathbf {\mu }(\mathbf {\beta }, \tau _s, \tau _e) = (\mu _i)$ and $P(\mathbf {\beta }, \tau _s, \tau _e) = ((P_{ij}))$ so that $\mu _i$ denotes the ith element of the vector $\mathbf {\mu }$ and $P_{ij}$ denotes the (i, j)th element of the matrix P.

As before,

$$\begin{aligned} E(\exp (\nu _i)|\hat{\nu }(ct))&= E[E(\exp (\nu _i)|\hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e)]\\ Var(\exp (\nu _i)|\hat{\nu }(ct))&= E[Var(\exp (\nu _i)|\hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e)] + Var[E(\exp (\nu _i)|\hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e)]. \end{aligned}$$

Further, using normality,

$$\begin{aligned} E(\exp (\nu _i)|\hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e)&= \exp (\mu _i + P_{ii}/2),\\ E(\exp (\nu _i+\nu _j)|\hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e)&= \exp (\mu _i + \mu _j + (P_{ii}+P_{jj}+2P_{ij})/2). \end{aligned}$$

Therefore,

$$\begin{aligned} E(A(\mathbf {\lambda })|\hat{\nu }(ct),\mathbf {\beta }, \tau _s, \tau _e) = \sum _{i=1}^{k_1+k_2} \exp (\mu _i + P_{ii}/2), \end{aligned}$$

and

$$\begin{aligned}&Var(A(\mathbf {\lambda })|\hat{\nu }(ct),\mathbf {\beta }, \tau _s, \tau _e)\\&= \sum _{i=1}^{k_1+k_2} \exp (2\mu _i + 2P_{ii}) + \sum _{i\ne j} \exp (\mu _i + \mu _j + (P_{ii}+P_{jj}+2P_{ij})/2)\\&-\left( \sum _{i=1}^{k_1+k_2} \exp (\mu _i + P_{ii}/2)\right) ^2\\&= \sum _{i=1}^{k_1+k_2} \bigl (\exp (2\mu _i +2P_{ii}) - \exp (2\mu _i + P_{ii})\bigr ) + \sum _{i\ne j} \bigl (\exp (\mu _i + \mu _j + (P_{ii}+P_{jj}+2P_{ij})/2)\\&\quad - \exp (\mu _i + \mu _j + (P_{ii}+P_{jj})/2)\bigr )\\&= \sum _{i=1}^{k_1+k_2} \exp (2\mu _i +P_{ii})\bigl (\exp (P_{ii})-1)\bigr ) + \sum _{i\ne j} \exp (\mu _i + \mu _j + (P_{ii}+P_{jj})/2) \bigl (\exp (P_{ij})-1\bigr ). \end{aligned}$$

Using this, we have the following result.

Proposition 5.4

(i) The hierarchical Bayes estimate of total abundance and its posterior variance are, respectively,

$$\begin{aligned} \hat{A}_{HB}&= \sum _{i=1}^{k_1+k_2} E^* (\exp (\mu _i + P_{ii}/2)) \text { and }\\ \hat{Var}_{HB}(A)&= E^* \bigl (\sum _{i=1}^{k_1+k_2} \exp (2\mu _i +P_{ii}) \bigl (\exp (P_{ii})-1\bigr ) \bigr ) \\&\quad + E^* \bigl (\sum _{i\ne j} \exp (\mu _i + \mu _j + (P_{ii}+P_{jj})/2) \bigl (\exp (P_{ij})-1\bigr ) \bigr ) \\&\quad + Var^* \bigl ( \sum _{i=1}^{k_1+k_2} \exp (\mu _i + P_{ii}/2)\bigr ), \end{aligned}$$

where $E^*$ and $Var^*$ denote expectation and variance with respect to the posterior distribution $\pi (\mathbf {\beta }, \tau _s, \tau _e | \hat{\nu }(ct))$.

(ii) An empirical Bayes approximation for these are, respectively,

$$\begin{aligned} \hat{A}_{EB}&= \sum _{i=1}^{k_1+k_2} \exp (\hat{\mu }_i + \hat{P}_{ii}/2) \text { and }\\ \hat{Var}_{EB}(A)&= \sum _{i=1}^{k_1+k_2} \exp (2\hat{\mu }_i +\hat{P}_{ii}) \bigl (\exp (\hat{P}_{ii})-1\bigr ) \\&+ \sum _{i\ne j} \exp (\hat{\mu }_i + \hat{\mu }_j + (\hat{P}_{ii}+\hat{P}_{jj})/2) \bigl (\exp (\hat{P}_{ij})-1\bigr ), \end{aligned}$$

where $\hat{\mu }_i = \mu _i(\hat{\mathbf {\beta }}, \hat{\tau _s}, \hat{\tau _e}),\, \hat{P}_{ij} = P_{ij}(\hat{\mathbf {\beta }}, \hat{\tau _s}, \hat{\tau _e})$, $\hat{\mathbf {\beta }}, \hat{\tau _s}, \hat{\tau _e}$ are the empirical Bayes estimates of $\mathbf {\beta }, \tau _s, \tau _e$.

1.2.3 Expressions for the Model, Prior, Posterior and the Marginal Density

We have the model

$$\begin{aligned} \hat{\nu }(ct) = \nu ^T + \epsilon , where \epsilon \sim N_{k_1}(\mathbf {0}, \tau _e I_{k_1}), \end{aligned}$$

with the CAR prior distribution on $\nu$:

$$\begin{aligned} \nu |\mathbf {\beta },\tau _s \sim N_{p}(\mathbf {X}\mathbf {\beta }, U^{-1}), \end{aligned}$$

(5.16)

where $U=L^\prime (\tau _s LVL^\prime )^{-1}L$, $\mathbf {X}$ is the matrix of covariates. $\mathbf {\beta }$ is given a flat prior and $\tau _e$, $\tau _s$ are given independent Gamma(0.01, 0.01) priors.

Under this specification, the posterior distributions for the parameters derived below. Posterior distribution of $\nu$, obtained in (5.14) and (5.15), is

$$\begin{aligned} \nu |\hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e \sim N_p\left( \mathbf {\mu }(\mathbf {\beta }, \tau _s, \tau _e), P^{-1}(\mathbf {\beta }, \tau _s, \tau _e)\right) , \end{aligned}$$

where (suppressing the dependence on $\hat{\nu }(ct)$)

$$\begin{aligned} \mathbf {\mu }(\mathbf {\beta }, \tau _s, \tau _e)&= \mathbf {X}\mathbf {\beta } + (U_{11}(\tau _s), U_{12}(\tau _s))^\prime (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s))^{-1}(\hat{\nu }(ct)-\mathbf {X}^T\mathbf {\beta }),\\ P(\mathbf {\beta }, \tau _s, \tau _e)&= U(\tau _s)-(U_{11}(\tau _s), U_{12}(\tau _s))^\prime (\tau _e^{-1} I_{k_1} + U_{11}(\tau _s))^{-1} (U_{11}(\tau _s), U_{12}(\tau _s)). \end{aligned}$$

with the density

$$\begin{aligned} \pi (\nu \, |\, \hat{\nu }(ct), \mathbf {\beta }, \tau _s, \tau _e)=(\sqrt{2\pi })^{-p} |P|^{-1/2} \exp \Big [-\frac{1}{2} (\nu -\mu )^\prime P^{-1}(\nu -\mu )\Big ]. \end{aligned}$$

To obtain posterior of $\mathbf {\beta }$, note that

$$\begin{aligned}&\left( \left( \begin{array}{c} \hat{\nu }(ct)\\ \nu ^T\\ \nu ^S\end{array}\right) - \left( \begin{array}{c} \mathbf {X}^T\mathbf {\beta }\\ \mathbf {X}^T\mathbf {\beta }\\ \mathbf {X}^S\mathbf {\beta } \end{array}\right) \right) ^\prime \left( \begin{array}{ccc} \tau _e^{-1} I_{k_1} + U_{11}(\tau _s) &{} U_{11}(\tau _s) &{} U_{12}(\tau _s)\\ U_{11}(\tau _s) &{} U_{11}(\tau _s) &{} U_{12}(\tau _s)\\ U_{21}(\tau _s) &{} U_{21}(\tau _s) &{} U_{22}(\tau _s) \end{array}\right) ^{-1} \left( \left( \begin{array}{c} \hat{\nu }(ct)\\ \nu ^T\\ \nu ^S\end{array}\right) \right. \\&\left. \quad -\left( \begin{array}{c} \mathbf {X}^T\mathbf {\beta }\\ \mathbf {X}^T\mathbf {\beta }\\ \mathbf {X}^S\mathbf {\beta } \end{array}\right) \right) = (\nu -\mu )^\prime {P}^{-1} (\nu - \mu ) + (\hat{\nu }(ct) \\&\quad - \mathbf {X}^T \mathbf {\beta })^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1} (\hat{\nu }(ct) - \mathbf {X}^T \mathbf {\beta }), \end{aligned}$$

where $U_{11}$, $U_{22}$, $U_{12}$ and $U_{21} = U_{12}^\prime$ are as in

$$\begin{aligned} L^\prime (\tau _s LVL^\prime )^{-1}L = U(\tau _s) = \left( \begin{array}{cc} U_{11}(\tau _s) &{} U_{12}(\tau _s)\\ U_{21}(\tau _s) &{} U_{22}(\tau _s)\end{array}\right) . \end{aligned}$$

From this, we have that

$$\begin{aligned}&\pi (\beta , \tau _s, \tau _e|\hat{\nu }(ct))\\&\propto \frac{|P|^{1/2}\pi _3(\tau _s)\pi _4(\tau _e)}{(2\pi )^{k_1/2} |\Sigma |^{1/2}} \exp \Big [ -\frac{1}{2} \Big \{ (\hat{\nu }(ct)-X^T \beta )^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1} (\hat{\nu }(ct)-X^T \beta )\Big \}\Big ]\\&= \frac{\pi _3(\tau _s)\pi _4(\tau _e)}{(2\pi )^{k_1/2} | \tau _e^{-1} I_{k_1} + U_{11}|^{1/2}} \exp \Big [ -\frac{1}{2} (\beta -\hat{\beta }_0)^\prime \Sigma _{\beta }(\beta -\hat{\beta }_0) \Big ]\\&\times \exp \Big [ -\frac{1}{2} \Big \{ \hat{\nu }(ct)^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1} \hat{\nu }(ct) -{\hat{\beta }_0}^\prime \Sigma _{\beta } \hat{\beta }_0\Big \}\Big ], \end{aligned}$$

where

$$\begin{aligned} \Sigma= & {} \left( \begin{array}{ccc} \tau _e^{-1} I_{k_1} + U_{11}(\tau _s) &{} U_{11}(\tau _s) &{} U_{12}(\tau _s)\\ U_{11}(\tau _s) &{} U_{11}(\tau _s) &{} U_{12}(\tau _s)\\ U_{21}(\tau _s) &{} U_{21}(\tau _s) &{} U_{22}(\tau _s) \end{array}\right) ,\\ \Sigma _{\beta }= & {} {\mathbf {X}^T}^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1}\mathbf {X}^T,\, \hat{\mathbf {\beta }}_{0} = \Sigma _{\beta }^{-1} {\mathbf {X}^T}^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1} \hat{\nu }(ct). \end{aligned}$$

Therefore, $\beta | \hat{\nu }(ct), \tau _s, \tau _e \sim N_r(\hat{\beta }_0, \Sigma _{\beta })$ with density

$$\begin{aligned} \pi (\beta \, |\, \hat{\nu }(ct), \tau _s, \tau _e) = (\sqrt{2\pi })^{-r} |\Sigma _{\beta }|^{1/2} \exp \Big [ -\frac{1}{2} (\beta -\hat{\beta }_0)^\prime \Sigma _{\beta }(\beta -\hat{\beta }_0) \Big ]. \end{aligned}$$

Now to obtain the posterior of $(\tau _s, \tau _e)$, observe that $\pi (\beta , \tau _s, \tau _e|\hat{\nu }(ct)) = \pi (\beta \, |\, \hat{\nu }(ct), \tau _s, \tau _e)\, \pi (\tau _s, \tau _e \, |\, \hat{\nu }(ct))$. Therefore, the posterior density of $(\tau _s, \tau _e)$ is

$$\begin{aligned}&\pi (\tau _s, \tau _e|\hat{\nu }(ct))\\&\propto \frac{\pi _3(\tau _s)\, \pi _4( \tau _e) |\Sigma _{\beta }|^{-1/2}}{(2\pi )^{(k_1-r)/2} |\tau _e^{-1} I_{k_1} + U_{11}|^{1/2}} \, \exp \Big [ -\frac{1}{2} \Big \{ \hat{\nu }(ct)^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1} \hat{\nu }(ct) -{\hat{\beta }_0}^\prime \Sigma _{\beta } \hat{\beta }_0\Big \}\Big ]\\&=\frac{\pi _3(\tau _s)\, \pi _4( \tau _e) |\Sigma _{\beta }|^{-1/2}}{(2\pi )^{(k_1-r)/2} |\tau _e^{-1} I_{k_1} + U_{11}|^{1/2}} \, \exp \big \{ -\frac{1}{2} h(\hat{\nu }(ct), \tau _s, \tau _e) \big \}, \end{aligned}$$

where

$$\begin{aligned} h(\hat{\nu }(ct), \tau _s, \tau _e)&=\hat{\nu }(ct)^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1} \hat{\nu }(ct)-\hat{\mathbf {\beta }}_{0}^\prime \Sigma _{\beta } \hat{\mathbf {\beta }}_{0}\\&=\hat{\nu }(ct)^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1} \big [ I_{k_1} - \mathbf {X}^T \big ( {\mathbf {X}^T}^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1}\mathbf {X}_j^T\big )^{-1}\\&\quad {\mathbf {X}^T}^\prime (\tau _e^{-1} I_{k_1} + U_{11})^{-1} \big ] \hat{\nu }(ct). \end{aligned}$$

which is not a standard density. However, $(\tau _s, \tau _e)$ may be simulated using the Metropolis-Hastings algorithm with the proposal distributions: $\tau _s^{cand}\, |\, \tau _s^{(i-1)} \sim \text { Log-normal}(\log \tau _s^{(i-1)}, \sigma ^2_s)$, $\sigma ^2_s=0.1$ and $\tau _e^{cand}\, |\, \tau _e^{(i-1)} \sim \text { Log-normal}(\log \tau _e^{(i-1)}, \ \sigma ^2_e),\, \sigma ^2_e=0.1.$

1.3 Model Selection

Consider the model selection problem given in (2.12) in the presence of confounding spatial factors. Then (3.6) yields,

$$\begin{aligned} M_j:&\, \hat{\nu }(ct) = \nu ^T +\mathbf {\epsilon }_j,\, \nu ^T = \mathbf {X}_j^T \mathbf {\beta }_j+L_j^\prime \theta _{2j}, \end{aligned}$$

(5.17)

where $\mathbf {\epsilon }_j|\tau _e \sim N(\mathbf {0},\tau _e I_{k_1})$, $\theta _{2j}|\tau _s \sim N(\mathbf {0}, \tau _s \widetilde{V}_{22j})$, $\mathbf {\beta }_j$ has a flat prior, $\tau _e$, $\tau _s$ both have Gamma(a, b) prior distributions and they are all independent of each other.

Result

The marginal or predictive density $m_j$ of $\hat{\nu }(ct)$ under the model $M_j$ is given by:

$$\begin{aligned} m_j = \int f_j(\hat{\nu }(ct)| \tau _s, \tau _e) \pi _3(\tau _s) \pi _4( \tau _e)\,d\tau _s \,d\tau _e, \end{aligned}$$

(5.18)

where $f_j(\hat{\nu }(ct)|\tau _s, \tau _e) =\tau _s^{\frac{1}{2} (k_1-r-G)} \, \tau _e^{k_1/2} \, |\Sigma _j|^{-1/2} \,\exp \big \{ -\frac{1}{2} h(\hat{\nu }(ct), \tau _s, \tau _e)\big \}$ with $\Sigma _j = \begin{bmatrix} \tau _e\mathbf {X}^{T^\prime }_j\mathbf {X}^{T}_j&0\\ 0&\tau _e I_{k_1-r} + \tau _s \widetilde{V}_{22j} \end{bmatrix}$, $\hat{\mu }_j= \tau _e \Sigma ^{-1}_j \begin{pmatrix} \mathbf {X}^{T^\prime }_j \\ L_j \end{pmatrix}\hat{\nu }(ct)$, $h(\hat{\nu }(ct), \tau _s, \tau _e) = \tau _e \hat{\nu }(ct)^\prime \Big [I_{k_1} - \tau _e \begin{pmatrix} \mathbf {X}^{T^\prime }_j \\ L_j \end{pmatrix}^\prime \Sigma ^{-1}_j \begin{pmatrix} \mathbf {X}^{T^\prime }_j \\ L_j \end{pmatrix} \Big ] \hat{\nu }(ct)$.

Proof

The marginal is given by

$$\begin{aligned} m_j&= m(\hat{\nu }(ct)|M_j)\\&= \int f(\hat{\nu }(ct)|\beta _j, \theta _{2j},\tau _e) \pi _1(\mathbf {\beta }_j)\pi _2(\theta _{2j}|\tau _s)\pi _3(\tau _s) \pi _4(\tau _e) \,d\mathbf {\beta }_j\,d\theta _{2j}\,d\tau _s \,d\tau _e. \end{aligned}$$

Note from (5.17) that the exponent of the expression inside the above integral can be decomposed as shown below.

$$\begin{aligned}&\tau _e (\hat{\nu }(ct)- \mathbf {X}^T_j \beta _j - L_j^\prime \theta _{2j})^\prime (\hat{\nu }(ct)- \mathbf {X}^T_j \beta _j - L_j^\prime \theta _{2j}) + \tau _s \theta _{2j}^\prime \widetilde{V}_{22j} \theta _{2j} \\&= \Big [\begin{pmatrix} \beta _j \\ \theta _{2j} \end{pmatrix} - \hat{\mu }_j\Big ]^\prime \Sigma _j \Big [\begin{pmatrix}\beta _j \\ \theta _{2j} \end{pmatrix} - \hat{\mu }_j\Big ] + \tau _e \hat{\nu }(ct)^\prime \Big [I_{k_1} - \tau _e \begin{pmatrix} \mathbf {X}^{T^\prime }_j \\ L_j \end{pmatrix}^\prime \Sigma ^{-1}_j \begin{pmatrix} \mathbf {X}^{T^\prime }_j \\ L_j \end{pmatrix} \Big ] \hat{\nu }(ct) \\&= \Big [\begin{pmatrix} \beta _j \\ \theta _{2j} \end{pmatrix} - \hat{\mu }_j\Big ]^\prime \Sigma _j \Big [\begin{pmatrix}\beta _j \\ \theta _{2j} \end{pmatrix} - \hat{\mu }_j\Big ] + h(\hat{\nu }(ct), \tau _s, \tau _e), \end{aligned}$$

where $\Sigma _j = \begin{bmatrix} \tau _e\mathbf {X}^{T^\prime }_j\mathbf {X}^{T}_j&0\\ 0&\tau _e I_{k_1-r} + \tau _s \widetilde{V}_{22j} \end{bmatrix}$, $\hat{\mu }_j= \tau _e \Sigma ^{-1}_j \begin{pmatrix} \mathbf {X}^{T^\prime }_j \\ L_j \end{pmatrix}\hat{\nu }(ct)$,

$h(\hat{\nu }(ct), \tau _s, \tau _e) = \tau _e \hat{\nu }(ct)^\prime \Big [I_{k_1} - \tau _e \begin{pmatrix} \mathbf {X}^{T^\prime }_j \\ L_j \end{pmatrix}^\prime \Sigma ^{-1}_j \begin{pmatrix} \mathbf {X}^{T^\prime }_j \\ L_j \end{pmatrix} \Big ] \hat{\nu }(ct)$. Integrating out $\beta _j$ and $\theta _{2j}$, we obtain,

$$\begin{aligned} m_j&= m(\hat{\nu }(ct)|M_j)\\&= \int \tau _s^{\frac{1}{2} (k_1-r-G)} \, \tau _e^{k_1/2} \, |\Sigma _j|^{-1/2} \times \, \exp \big \{ -\frac{1}{2} h(\hat{\nu }(ct), \tau _s, \tau _e)\big \}\,\pi _3(\tau _s) \pi _4(\tau _e)\, d\tau _s \,d\tau _e\\&= b^{2a} (\Gamma (a))^{-2}\int \tau _s^{\frac{1}{2} (k_1-r-G)+a - 1} \, \tau _e^{k_1/2+a-1} \, |\Sigma _j|^{-1/2} \\&\quad \times \, \exp \big \{ -\frac{1}{2} h(\hat{\nu }(ct), \tau _s, \tau _e) - b(\tau _s + \tau _e)\big \}\, d\tau _s \,d\tau _e. \end{aligned}$$

$\square$