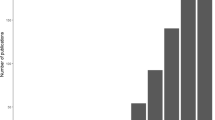
Abstract
Precise and accurate estimates of abundance and demographic rates are primary quantities of interest within wildlife conservation and management. Such quantities provide insight into population trends over time and the associated underlying ecological drivers of the systems. This information is fundamental in managing ecosystems, assessing species conservation status and developing and implementing effective conservation policy. Observational monitoring data are typically collected on wildlife populations using an array of different survey protocols, dependent on the primary questions of interest. For each of these survey designs, a range of advanced statistical techniques have been developed which are typically well understood. However, often multiple types of data may exist for the same population under study. Analyzing each data set separately implicitly discards the common information contained in the other data sets. An alternative approach that aims to optimize the shared information contained within multiple data sets is to use a “model-based data integration” approach, or more commonly referred to as an “integrated model.” This integrated modeling approach simultaneously analyzes all the available data within a single, and robust, statistical framework. This paper provides a statistical overview of ecological integrated models, with a focus on integrated population models (IPMs) which include abundance and demographic rates as quantities of interest. Four main challenges within this area are discussed, namely model specification, computational aspects, model assessment and forecasting. This should encourage researchers to explore further and develop new practical tools to ensure that full utility can be made of IPMs for future studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A key goal in the study of wildlife populations is often to estimate abundance and important demographic rates (e.g., recruitment and survival) of species and how these variables change over space and time. Accurate and precise estimates of such quantities lay the foundation of determining abundance trends and the ecological dynamics of species and thus are necessary for effective conservation planning and management in the face of ongoing global change [1]. For example, inferences demonstrating changes in a population’s abundance, and the mechanisms behind such change, can aid in decisions on how to halt declines or manage the invasion of deleterious species [2,3,4]. As inferences on wildlife population parameters need to take into account a variety of processes, including imperfect detection of species, extreme heterogeneity in and among environments, and the movement and clustering of individuals, a variety of data collection and analysis frameworks have been developed over the last century to provide the relevant and necessary metrics on wildlife populations [5,6,7].
A range of data are collected on wild populations with the specific biological questions, as well as logistical constraints, shaping the distinct types of data that are collected. Often, several types of data are collected on a single population or species within close proximity, as different researchers may be interested in multiple aspects of a particular study system. Historically, each data set would be analyzed separately, with perhaps estimates from one analysis being used in another or biological interpretations compared, again depending on the questions of interest and data types available. However, separate analyses of available data sources discard valuable information that could improve the estimation of the biological quantities of interest, for example, by increasing the precision of parameter estimates [8], permitting the estimation of confounded parameters [9], and/or correcting for sampling biases in one or more data sources [10].
An alternative approach, which optimizes the shared information contained within multiple data sets, is to use “model-based data integration.” Model-based data integration (or data integration, for short) is an umbrella term that refers to any modeling technique that simultaneously analyze all available data within a single, robust, statistical framework (e.g., data fusion, integrated data models). The development of data integration methods over the last three decades has grown almost exponentially [11,12,13], as these approaches can greatly reduce uncertainty of parameter estimates [14], make possible the estimation of parameters that are inestimable from a single data source (e.g., emigration and mortality [15]), and expand the spatiotemporal scope of inference [16]. Of note is that an individual data set may provide no additional information on the particular quantity of primary interest; however, by providing direct information on other model parameters, this can, in turn, lead to the ability to estimate a previously confounded parameter and/or an improved estimate of the quantity of interest [17].
In this paper, the ideas associated with integrated modeling are described and several associated outstanding statistical challenges discussed, with a specific focus on integrated population models (IPMs). While data integration approaches aim to estimate a variety of population processes (e.g., species distributions, abundances), IPMs specifically focus on the simultaneous estimation of both population abundance and demographic rates within a single analytical framework. IPMs may integrate across many types of data, typically including (but not limited to): 1) abundance, counts, and/or census data to inform temporally varying population sizes and/or trends, 2) productivity data to inform (annual) reproduction rates (e.g., nest records), and 3) capture-recapture-recovery-type data used to inform (seasonal, annual, and/or stage/age) survival.
[1, 18] provide an overview of common types of available data included in IPMs and associated component models that may be applied. Such models may be improved via the inclusion of environmental covariate data [19, 20]. IPMs have also recently been developed combining data sets (possibly the same type of data) across different species [21,22,23], although this work is fairly new and still under development.
The first use of integrated approaches within ecology were applied to stock assessments within the fisheries industry [12]. However, IPMs gained prominence in the wider ecological community over two decades ago [7, 19, 24] when the approaches were applied to terrestrial species, usually birds. This early work combines state-space modeling of census data with the analysis of capture-recapture-recovery-type data, exploiting the shared demographic parameters between the two modeling techniques. There has been substantial advancement over the last decade in particular expanding analyses to populations of birds, mammals, and amphibians [25]. However, widespread adoption of IPMs by the ecological community is hindered by technical statistical and implementation challenges. The aim of this paper is to provide a statistical overview of IPMs, including the identification of many outstanding statistical challenges within this area, which in turn will encourage researchers to investigate these issues and develop innovative and practical approaches to ensure that IPMs are able to reach their full potential within ecological studies.
2 Integrated Data
The fundamental concept of an integrated data approach is to estimate the ecological parameters of interest using all available information within a single and robust analysis. In particular, it is envisaged that there are multiple data sources that each provide information on the given ecological system/population of interest. For example, this may relate to multiple data sets collected on the same species but using different data collection survey techniques, or data sets relating to (potentially interacting) multiple species within the same geographical location, or even data sets that are separated geographically and/or temporally. In all cases, it is assumed that the different data sets provide information, either directly or indirectly, on some mechanism within the given ecosystem of interest.
Mathematically, suppose there are n distinct data collection surveys, leading to associated data sets \(\varvec{x}_i\), for \(i=1,\dots ,n\). Combining these data sets leads to the integrated data \(\varvec{x}= \{\varvec{x}_1,\dots ,\varvec{x}_n\}\). Given an associated model for these data, the associated global likelihood of the observed data is written as \(f_G(\varvec{x}; \varvec{\theta })\), here \(\varvec{\theta }\) denotes the set of all model parameters across the different data collection processes. The form of this likelihood is now considered in more detail, assuming different dependent structures for the observed data.
2.1 Conditionally Independent Data
Assuming that the different data sets are independent of each other, conditional on the associated model parameters, the global likelihood, \(f_G(\varvec{x}; \varvec{\theta })\) can simply be expressed as,
where \(f_i(\varvec{x}_i; \varvec{\theta })\) denotes the likelihood of the observed data \(\varvec{x}_i\), \(i=1,\dots ,n\). In general, this substantially simplifies the model specification, since each likelihood is constructed independently for each data set. In practice, it is assumed that there are some model parameters that are common across the different data sets, motivating an integrated data analysis approach. Conversely, if the model parameters are non-overlapping across the different data collection processes, so that \(\varvec{\theta }= \{\varvec{\theta }_1,\dots ,\varvec{\theta }_n\}\), where \(\varvec{\theta }_i \cap \varvec{\theta }_j = \emptyset \) for \(i \ne j\), the likelihood reduces to,
In this special case, analyzing the joint likelihood is equivalent to simply analyzing each data set independently of each other, and there is no benefit gained in considering an integrated approach. Thus, for the remainder of the paper it is assumed that the likelihood does not decompose into independent individual components, but the individual likelihoods for the different data sets share (at least) some parameters.
The conditional independence structure of the global likelihood also has an interesting interpretation within a Bayesian analysis. Without loss of generality suppose there are two independent data sets, so that \(n=2\). The posterior distribution can be expressed as,
In other words, the posterior distribution of the parameters given all the available data can be re-expressed as the posterior distribution of the parameters given data set \(\varvec{x}_1\), with an associated prior distribution equal to the posterior distribution of the parameters, given data set \(\varvec{x}_2\). This observation has practical model-fitting implications (see Sect. 3.2) and immediately extends to a more general number of data sets, \(n > 2\).
2.2 Dependent Data
In most cases, individual data sources are not independent of each other. Consequently, the joint likelihood of the dependent data sets, \(f_G(\varvec{x}; \varvec{\theta })\), cannot be simplified. In the presence of both dependent data sets (\(\varvec{x}_1,\dots ,\varvec{x}_k\)) and independent data sets (\(\varvec{x}_{k+1},\dots ,\varvec{x}_n)\), the joint likelihood of all available data can be expressed in the form,
where \(f_g(\varvec{x}_1,\dots ,\varvec{x}_k; \varvec{\theta })\) denotes the joint likelihood over the dependent data sets. Dependent data may arise due to the same individuals being studied in the given data collection surveys and hence resulting data sets. For example, this occurs in the case of capture-recapture and tag-recovery data. The same individuals appear in both the capture-recapture and tag-recovery data (e.g., following individuals being marked they may be observed at future periods both alive and dead), and the joint capture-recapture-recovery likelihood needs to be considered [26,27,28,29,30]. Alternatively, and particularly for populations that are geographically closed, census data combined with marked individuals (such as capture-recapture data) will often involve the same individuals in both sets of survey data [31]. As a final dependent data example, data may be collected on multiple interacting species within an area (and possibly data from different monitoring schemes) [21,22,23].
In practice, data sets may be assumed to be approximately (conditionally) independent within an analysis, even when it’s not strictly the case, as this dramatically simplifies the likelihood expression, i.e., the global likelihood can be decomposed into the product of the individual likelihoods for each data set. The impact of assuming independence between dependent data sets has been examined using simulation, see for example [32,33,34]. From their studies, which combined count data with demographic data, they concluded that the amount of information contained in the demographic data relative to the survey data influenced the magnitude of the effect of violating the independence assumption. In particular, the simplest and most immediate effect was an inflated level of precision on the model parameters, with biases also observed in some cases, albeit generally small. As described in [32], such explorations have typically focused on specific types of data being combined and the outcomes are often used as justification that dependence has little effect on parameter estimates. However, a more general exploration of this area is required, especially as the types of data being included in IPMs are rapidly expanding.
To avoid the issues of potential bias and/or over-confidence in the precision of the parameter estimates that may arise due to the same individuals appearing in multiple data sets (so that the data are non-independent), one approach has been to partition the individuals into the different data sets, so that they only belong to a single data set. This removes the dependence as individuals are no longer common to multiple data sets, but reduces the amount of information in each individual data set due to the reduced sample size. For example, [35] consider this approach for combining constant effort (mist-netting) count data and capture-recapture data, where the same individuals are recorded in both survey methods. The data were partitioned at the geographical site level, with approximately half the sites allocated to the constant effort data; and the other half for the capture-recapture data. Within their application, they concluded that the split data integrated analysis led to substantially improved precision of the parameter estimates compared to the analysis of only the constant effort data; and only marginally wider credible intervals compared to considering an integrated analysis assuming the data were independent. However, we note that in many situations, data may be limited, and the approach requires some knowledge relating to their overlap or dependence (e.g., individuals may be uniquely identifiable). In practice, there is a trade-off between the removal of potential dependence and the associated reduction of information with the data. A sensitivity analysis, using different data components, may help gain some insight into this trade-off. Further, and in general, the robustness of the results to splitting the data can be assessed by considering different data splits, which for [35] appeared to be minimal for their application.
3 Integrated Population Models
Ecological time-series data of species abundance are a very common input within IPMs, as they provide direct information on abundance as well as the (indirect) demographic processes. State-space models provide a structured way of describing such time series data and can be viewed as a special case of a wider class of models known as hidden process models [18, 36,37,38,39]. These models can be described via two separate processes: (i) the state process that describes the evolution of the true underlying (unobserved) state-vector corresponding to true abundance over time; and (ii) the observation equation that links the elements of the state vector to the observed data at each time point. Given the prominence of these data within IPMs, their general structure of them is briefly described.
Suppose observed data correspond to a multivariate time series over discrete time events, \(t=1,\dots ,T\), which are denoted by \(\varvec{y}=\{\varvec{y}_t:t=1,\dots ,T\}\), with each observation \(\varvec{y}_t\) a vector containing K elements. The observed data are related to an \(m \times 1\) vector, \(\varvec{\alpha }_t\), known as the state vector via the observation equation,
for \(t=1,\cdots ,T\), where \(\varvec{Z}_t\) denotes an \(K \times m\) matrix and \(\epsilon _t\) an \(K \times 1\) vector corresponding to the observation error. In general, the elements of \(\varvec{\alpha }_t\) are not observable, but are assumed to be first-order Markovian, such that the state equation can be expressed in the form,
where \(\varvec{\eta }_t\) denotes an \(m \times 1\) vector corresponding to the system process error.
For ecological applications, the state vector, \(\varvec{\alpha }_t\), often relates to the number of individuals in particular age (and/or state) classes. The matrix, \(\varvec{T}_t\), governs the evolution of the state-vector from occasion t to occasion \(t+1\), and is typically expressed as a function of demographic parameters, such as the survival probabilities, fecundity rates and/or migration rates. The formation of \(\varvec{T}_t\) can be fairly straightforward for state vectors of small dimension; however, it is often useful to decompose the formation of T into intermediate sub-processes, such as survival, aging, recruitment etc [37, 40].

A closedform likelihood for state-space models is only available when specifying either (i) a linear and Gaussian model, or (ii) where the state vector is discrete-valued, leading to a hidden Markov model (HMM). See [39] for further discussion. The information contained within the temporal abundance data alone may be relatively weak, in terms of the demographic parameters, which may be strongly correlated and/or even confounded. Thus, such abundance data are often integrated with additional forms of data that provide information on more of the demographic parameters. For example, capture-recapture-type data may be used to provide information on survival probabilities; or nest-record data for productivity rates. For such data, the associated likelihood functions may often be expressed in closed form. However, combining these different forms of data within an integrated modeling approach leads to a number of additional challenges and modeling considerations. Four practical challenges associated with the application of IPMs to ecological data are summarized in Table 1. Existing work that begins to address some of these challenges is discussed in Sects. 3.1–3.4 before discussing potential avenues for further research in Sect. 4.
3.1 Challenge 1: Model Specification
For any given data set, and specified ecological question or hypothesis, the first step in the data analysis pipeline involves specifying a statistical model to describe the observed data. This requires knowledge of both the data collection process and associated ecological system being studied. This information permits the construction of the statistical model, given appropriate assumptions, and the associated likelihood function to be derived [1, 42,43,44]. However, for IPMs, there are multiple observation processes, each associated with the different datasets, and typically either multiple system processes (which may interact with each other) and/or more complex system processes. Consequently, IPMs lead to additional considerations within the model specification. One such consideration has already been discussed in Sect. 2 in relation to the specification of the joint likelihood function of the data and whether the data sets can be regarded as independent, conditional on the associated model parameters. However, due to the combining of the different data sets, further care is needed in terms of the interpretation (or equivalence) of the parameters associated with the system process(es).
For multiple data sets, the relationship between the parameters associated with each data set needs to be considered with some care. In practice, there will be some parameters for which there is direct information from only one data set; and other parameters for which there is direct information from two (or more) data sets. For example, suppose that there are \(n=2\) data sets. The set of parameters can be decomposed as follows: \(\varvec{\theta }= \{\varvec{\theta }_1, \varvec{\theta }_2, \varvec{\theta }_{1,2}\}\), where \(\varvec{\theta }_j\) corresponds to the parameters uniquely associated with the model for data component \(j=1,2\); and \(\varvec{\theta }_{1,2}\) denotes the parameters for which there is direct information contained in both data sets. For simplicity, the parameters for which there is direct information from multiple data sets (i.e., \(\varvec{\theta }_{1,2}\) in this example) are referred to as the common parameters across the given data sets. For example, consider integrated count data with ring-recovery data (\(\varvec{x}_1\) = count data; \(\varvec{x}_2\) = ring-recovery data) with model parameters \(\varvec{\theta }\) corresponding to demographic survival probabilities, \(\varvec{\phi }\), and fecundity rates, \(\varvec{\rho }\); and associated observation process parameters corresponding to recovery rates, \(\varvec{\lambda }\) (for the ring-recovery data), and observation error variance, \(\sigma ^2\) (for the count data). Then, \(\varvec{\theta }_1 = \{\varvec{\rho }, \sigma ^2\}\); \(\varvec{\theta }_2 = \varvec{\lambda }\) and \(\varvec{\theta }_{1,2} = \varvec{\phi }\) (see, for example, [19] for further discussion in relation to this particular example). Note that for the special case of conditionally independent data sets, the joint likelihood (for \(n=2\)) can be written as,
with the immediate extension for \(n \ge 3\) data sets.
In considering the general model construction and parameter specification, there are two particular points to emphasize:
-
1.
The parameters that are common to different data sets must have the same interpretation across these different data sets; and
-
2.
Considering the joint likelihood of the integrated model may permit the estimation of previously confounded parameters.
The first point requires knowledge of the different data sets and associated modeling assumptions. In particular, parameters that appear to be common to multiple data sets may have slightly different (possibly nuanced) definitions. For example, consider two data sets which each provide information on the survival probabilities of the species of interest. However, there may still be assumed differences in relation to the interpretation of these survival parameters. For example, true survival (i.e., non-mortality) as opposed to apparent survival allowing for other departures from the study site, such as permanent migration [30]; or where the survival probabilities are specified over different geographical locations and/or temporal periods [45]. In practice, it may be of ecological interest whether given parameter(s) are equal across the different data sets, providing ecological insight into the systems, leading to potential model selection (or hypothesis testing) within the statistical analysis (see Sect. 3.3). Given the parameter is common across data sets, applying an integrated modeling approach typically leads to improved precision of the parameter, due to the increased information available on the parameter [45].
Note that, perhaps somewhat ironically, having “similar” but distinct parameters for the different data sets (as for true and apparent survival above), can be very useful in IPMs as this can lead to the estimation of parameters that are confounded when only considering the individual data sets. To illustrate this mathematically, return to the simple two data set example. Suppose the model processes for data set, \(\varvec{x}_1\), are a function of a true survival probability S, and for data set, \(\varvec{x}_2\), this is a function of apparent survival probability, \(\phi \), which is confounded with permanent migration from the study site. Let \(\gamma \) denote the probability of permanently migrating from the study site, so that \(\phi = (1-\gamma )S\). Then \(S \in \varvec{\theta }_{1,2}\) and \(\gamma \in \varvec{\theta }_2\), with \(\phi \) now a derived parameter, calculated as a function of these terms [15, 30, 46]. More generally, however, parameters that are confounded when considering a single data set, may be estimable when combined with additional, relevant information. For example, fledgling survival and first-year survival are confounded for ring-recovery data if rings are applied to chicks in the nest and rings are recorded at the (coarse) annual level. However, additional nest record data may provide direct information on the fledgling survival, which when combined with the ring-recovery data permits direct estimation of the first year (post-fledgling) survival [47]. Alternatively, count data is often focused on the number of (adult) breeding birds, often leading to the associated model with first year survival and productivity confounded. An IPM, incorporating additional capture-recapture/ring-recovery data, permits the estimation of first-year survival, and hence the estimation of productivity rates [7, 19, 48]; or additional nest-record data provides data on productivity rate, and in turn the first-year survival rates [49].
3.2 Challenge 2: Computational Aspects
To combine data sources together, as previously discussed, IPMs typically require a more indepth and/or complex model structure than the analysis of data sources individually. While each model component of an IPM taken independently may be easily fitted to data in a standard framework, their integration with abundance data expressed within a state-space modeling framework often leads to additional computational challenges [39]. This increased complexity leads to greater computational requirements in terms of algorithm complexity, run times and memory load. For example, standard MCMC (data augmentation) techniques that are widely used in practice can require days or even weeks to run IPMs on desktop computers using dedicated black-box software, such as JAGS [50]. The computational burden is such that it becomes difficult—if not impossible—to go through the usual modeling strategy of starting simple and adding complexity, or to fit several models and compare corresponding ecological hypotheses (see Sect. 3.3). Note that the most recent software like Nimble [51] allows choosing and customizing MCMC algorithms which may help optimizing time computation for specific components of IPMs. Here we describe two alternative strategies that are often applied to address the computational model-fitting challenges.
3.2.1 Consideration of Separate IPM Components
When building IPMs, for the case of conditionally independent data sets, it is common practice to go through building each data component separately before combining them [52]. This approach focuses on each individual component in turn and provides a natural approach to identifying the associated computational burden by identifying a possible bottleneck, and optimizing the fitting of the corresponding component. A bottleneck most naturally occurs when the model is specified via unobserved (latent) variables, such as state-space models for abundance/count data (with unobserved population sizes, possibly over several (st)ages); multi-state capture-recapture models (such that states are unknown when an individual is unobserved); or individual heterogeneity model (with unobserved random effect terms).
More generally, several approaches have been developed to improve computational times for individual model components. This often involves implementing strategies that lead to faster evaluations of the likelihood function. For example, [53] marginalize the likelihood, removing the latent states from the model, and hence decreases the number of parameters to be estimated. Similarly, for multi-state capture-recapture models [29, 54] marginalize the likelihood to provide closedform expressions via efficient sufficient statistics, further facilitating its efficient calculation. These marginalization approaches lead to more complex (observed-data) likelihood functions, compared to the augmented (complete-data) likelihood with additional latent variables. The marginal likelihood can be maximized directly within a frequentist framework; or needs to be evaluated substantially fewer times when using a Bayesian Markov chain Monte Carlo (MCMC) implementation leading to faster computational time and typically better mixing, compared to a latent variable data augmentation implementation.
Alternatively, approximate likelihood approaches may be applied to different modeling components. For example, state-space models, using linear and/or Gaussian approximations for the system and observation processes, permits the use of the fast and efficient Kalman filter algorithm [55] to evaluate the likelihood function. Alternatively, (at least for system processes of low dimension), a coarse discretization (or “binning” approach) may be applied to the system states, leading to an HMM approximation [56,57,58]. In particular, [59, 60] used binning to deal with the large number of possible states for the state vector of population abundance and showed that this numerical approximation performs well compared to the Kalman filter approximations and MCMC simulations. Further [60] proposed a semi-complete data likelihood approach [61] to improve computational efficiency of fitting more complex state-space models using a combined data augmentation and numerical integration scheme. They also demonstrated improved computational efficiency using a binning approach, with minimal impact on the estimation of the parameters. Overall, dealing with an intractable likelihood for general state-space models limits computational model-fitting tools, and more research is needed in that direction [39, 62].
3.2.2 Full IPM Likelihood Evaluation
An alternative to considering the separate IPM components is to optimize the evaluation of the full IPM likelihood. Note that this is, in general, necessary when the data are dependent, as the likelihood cannot be factored into the separate components, but can also be applied to the conditionally independent case. In general, this process may also involve optimizing the evaluation of each separate data component as well. One general approach for the likelihood specification is to formulate the IPM (possibly via a suitable approximation) as an HMM, with multiple observation processes, and potentially multiple system processes [63]. Formulating the IPM in this framework opens access to the available toolbox of efficient algorithms to fit HMMs that have been specifically developed to improve computational efficiency. See [64] for further discussion of pitfalls and opportunities of HMM approximation to general state-space population dynamics models.
Exploring another possibility, [65] proposed an efficient methodology for fitting IPMs in a Bayesian framework. In particular, they exploited the integrated model structure to reduce the computational cost of the algorithm by reducing the number of times the likelihood needed to be evaluated. More specifically, a delayed acceptance approach was implemented, where the computationally intensive part of the likelihood, corresponding to the state-space model for the count data, was only evaluated if the proposed parameter value in the MCMC algorithm was evaluated to be “good” in terms of the fast data likelihood component relating to the capture-recapture-recovery-type data.
For data sets that are conditionally independent, a further step-wise process can be applied when considering the full IPM likelihood. Recall that the joint posterior distribution of the parameters can be expressed as the product of the likelihood of a single data set, say \(\varvec{x}_1\), with prior equal to the posterior distribution of the parameters given the other data sets [Eq. (1). For this case, where the associated prior is of standard form, the model-fitting is simplified to consideration of data set \(\varvec{x}_1\), given the posterior distribution of the parameters given the other data sets. This approach has been adopted by, for example, [66] and [67] where \(\varvec{x}_1\) corresponded to multi-state capture-recapture-recovery data and \(\varvec{x}_2\) to multi-state radio-tagging data, with the common parameters between the data sets the survival and state-transition probabilities. However, in many cases, the posterior distribution \(\pi (\varvec{\theta }\, | \, \varvec{x}_2)\) may not be of standard distributional form. In this case, the posterior distribution may be approximated, for example, by specifying (independent) distributions with parameters determined using a moment-matching approach with the posterior summary statistics.
3.3 Challenge 3: Model Assessment
Assessment for ecological models, encompassing both relative goodness-of-fit using model selection/comparison strategies, and absolute goodness-of-fit are both well grounded with standard procedures available in a practitioner’s toolkit. However, model assessment for IPMs, combining multiple data sets within the same model-fitting process, is relatively underdeveloped.
3.3.1 Model Selection
The potential model space for integrated models can be very large. For example, demographic parameters may be time or state dependent and/or depend upon individual or time-varying covariates. In addition, error structures within a state-space model for longitudinal time series can vary over time and/or space. The combination of different parameter dependencies and/or error structures often leads to a large number of possible models that may be fitted to the data. Individually fitting all such possible models to data can be time-consuming or even simply infeasible, in practice. This typically leads to the use of a step-wise search algorithm over the model space [45]. Due to the lack of robust model selection approaches for IPMs, ad-hoc step-wise model selection approaches are often applied separately to the different modeling components, either at the parameter level or data set level. For example, the structure of an IPM may be investigated step-wise using the data set(s) which contains the most information about a parameter (in terms of precision). This approach is applied by [19] when combining ring-recovery and count data, with the model selected using the ring-recovery component for the survival component (common to both data sets); with subsequent parameter dependence for the productivity for the count model determined, conditional on the survival dependence already selected. Implementing such search algorithm strategies, however, can lead to different results when compared to model selection conducted on the global, integrated, model and a suboptimal model being selected [68].
For some forms of data, such as capture-recapture-recovery-type data, model selection using standard information criteria (or adaptations of information criteria to account for small sample sizes or overdispersion) generally appears to work well [69]. However, information criteria do not appear to perform as well for HMMs and/or state-space models, particularly where competing models differ in terms of the dimension of the (unobserved) state vector. For example, information criteria have been shown to overestimate the number of states within HMMs [70]. Information criteria within the Bayesian framework have also been applied to IPMs, such as the DIC [14, 71] and WAIC [72]. Although easy to compute, there has been no formal evaluation of the performance of these criteria for IPMs. Specific information criteria for state-space models have been proposed (see for example [73]); however, these are computationally intensive and their extension to state-space models when integrated with other models, as in an IPM, has not been investigated. As an alternative, [74] propose a step-wise approach to determine the dimension of the state vector (representing the age-structure of the population), and hence number of states required in the state vector, within an IPM framework and provides a starting-point for further research in this area.
Within the Bayesian framework, there are a number of standard model selection tools (see [75] and [76] for general guidance) which can be implemented in an IPM setting. Models can be quantitatively compared via posterior model probabilities, or Bayes Factors [77]. There are typically two particular challenges in their use relating to (i) their estimation; and (ii) their sensitivity to prior distributions specified on the model parameters. To estimate posterior model probabilities, reversible jump (RJ)MCMC has been applied in relation to the dependence structure of parameters, such as time and/or covariate dependence [48, 76]. One particular attraction of RJMCMC is that only a single MCMC chain needs to be run, as the MCMC chain is able to move over the model space. However, the RJMCMC algorithm can be difficult to implement in the general case and requires bespoke code, limiting its application in practice; although for the special case of variable selection, such as covariate selection for given demographic parameters, an indicator variable approach can be applied [51, 76, 78]. Alternatively, for state-space models, [65] considered an approach using sequential Monte Carlo samplers that permitted the calculation of posterior model probabilities across a set of different IPMs.
Approaching model selection separately for each component of an IPM is attractive for its simplicity since bespoke model selection approaches which have been optimized for a particular data type can be used. However, identifying a model as being the best from a candidate model set does not mean that the model actually fits the data well, and for IPMs in particular, even if individual components of the IPM fit well this does not necessarily mean that the overall IPM fits well. Therefore, assessment of fit of the overall IPM (as well as assessment of the appropriateness of any modeling assumptions made) is an essential step in an IPM analysis.
3.3.2 Absolute Goodness-of-Fit
Absolute goodness-of-fit tests for ecological models can be particularly useful for understanding disparities between the simplifying statistical model for a given system and the associated dynamics of the population under study. Gaining insight into potential lack of fit can provide ecological understanding and lead to improved ecological models. However, techniques for assessing absolute goodness-of-fit typically differ across the types of data (and models) available. For example, absolute goodness-of-fit techniques for capture-recapture-recovery-type models are fairly advanced, including diagnostic goodness-of-fit tests which link the detection of lack of fit with a determination of the likely biological underlying cause of the inadequacy of the model [79,80,81]. However, goodness-of-fit assessment for ecological state space models is substantially more limited. The appropriateness of the Gaussian assumptions made underlying the use of Kalman filter recursions can be investigated through diagnostic checks of normality of the prediction errors arising from the recursions, but are unlikely to help guide adaptation of the model to improve fit [19]. To date, where such goodness-of-fit tests do exist, they are considered separately for each type of data and not at the integrated level.
One approach, often referred to as posterior predictive checks, is to consider the evaluation of a discrepancy measure between the observed data and data simulated from the fitted model. For example, in a Bayesian framework, this leads to the idea of a Bayesian p-value, where multiple data sets are simulated from the posterior distribution of the model and compared to the observed data to see if these are “similar.” See [82] for further discussion, and additional Bayesian approaches. Similarly, in a frequentist setting, the idea of calibrated simulation has been proposed, which implements a parametric bootstrap to obtain simulated data sets which are subsequently compared to the observed data via a given discrepancy measure [83]. In general, Bayesian p-values and calibrated simulation rely on the specified discrepancy measure, and conclusions may vary dependent on the specific measure used. Further, for different types of data sets, one may wish to consider different discrepancy measures, which leads to further challenge when combined within an integrated framework.
3.4 Challenge 4: Forecasting
Forecasting ecological population sizes or trends is of particular interest within conservation management and, driven by the ecological incentive, there exist tools for forecasting across wide-ranging time scales. For instance, short-term forecasting tools are typically used in the regular management and conservation of a species, for example, in the fisheries industry to regulate annual harvest capacity of waters [84, 85]. In contrast, long-term forecasting tools are especially useful for prioritizing vulnerable species for conservation intervention [86], evaluating the viability of a population of a reintroduced species [87, 88], and in projecting the minimum effort needed to locally eradicate an invasive species [2]. Despite the rapid growth in technological tools for measuring, monitoring and analyzing species data, robust methods of ecological forecasting are still an underdeveloped area [84]. One of the biggest hindrances to forecasting the future trajectories of animal populations (regardless of time scale) is the limited amount of data available for precise inference on how environmental variables influence demographic parameters. High precision on estimates of covariate effects is critical for prediction, since forecast errors will magnify over time. Thus, when parameter precision is poor, forecasts will be rendered effectively useless ([89] demonstrate this point with climate predictions). However, by increasing the amount of data available for inference via integrated modeling techniques, it is possible to improve the precision of demographic parameters and their relationships to covariates and thus alleviate some uncertainty in species’ projections [3, 90].
Various time-series methods have been applied to ecological data to inform decision-making on short-term time scales (days to years), such as random-walk, autoregressive (AR-1) and moving average (MA-1) models [91,92,93]. However, such standard time-series techniques often require large datasets, which may be available for example for finance and climate, but rare in ecological settings and particularly so in newly established research or conservation initiatives.
Long-term forecasting is often used to assess the possible fates of populations. Such forecasts underpin population viability analysis (PVA), a procedure of estimating the probability that a species will persist for a certain amount of time [94,95,96]. By coupling IPMs with PVA, predictions of demographic parameters can be improved by specifically incorporating multiple sources of uncertainty in a unified framework. This may be particularly useful when forecasting populations of multiple interacting species with disparate data types. For example, this has been used to identify components of multi-species population cycles and evaluate the efficacy of different management strategies such as assessing how removals of one species may affect the population viability of the other [3]. Other work that has used IPMs within a PVA include, but are not limited to, forecasting future salmon populations in response to fishery exploitation [85], and predicting the population effects after environmental trauma such as large oil-spills [97].
An emerging area in ecological forecasting couples population models with climate projections to forecast populations over a number of decades [98, 99]. The main assumption behind such approaches is that species will respond to future climate conditions similarly to their responses in the past. This is particularly useful for providing evidence for practitioners of how populations may respond to certain climate scenarios and enables long-term risk assessment of species status. For example, [100] provided projections of the monarch butterfly population based on a range of climate change scenarios. However, while these environmental-based techniques provide useful insights into the future, they are not without their issues [101]. As the projection duration increases so does uncertainty in the parameter estimates and forecasts, especially if the future climate scenario is significantly different from the past and current [102]. Further, these forecasting methods simply involve iterating the process model for as long a time as needed past the observation period. However, when a population is rapidly changing and/or available retrospective data sets contain relatively short time frames of data, methods of iterating forward may not be very meaningful since the parameter estimates may be estimated from unstable or rapidly changing populations (for example, when reintroducing a species). Thus, there is a need for dynamic models that can incorporate statistical non-stationarity [103].
In general, one of the main reasons for inaccurate forecasting is a lack of available data and of methods accounting for multiple sources of uncertainty. IPMs may alleviate these issues, thus improving forecasts, by pooling information across data sources. In other words, the precision of parameter estimates in relatively data-poor sources can be improved by borrowing information from richer data sources [85].
4 Discussion
IPMs provide a statistically robust approach for integrating multiple sources of data, making use of all available information. Understanding the dependence between the multiple different forms of data sets and associated relationships will continue to lie at the interface of ecological data science. Close collaboration between ecologists and statisticians is essential in order to construct biologically meaningful and statistically robust models. Further, there are additional challenges in relation to interpreting meaningful results, including rigorous goodness-of-fit assessment, and use of the associated model outputs to inform conservation management, for example, via future predictions that include propagating the associated parameter uncertainties. Further, efficient computational algorithms and user-friendly software are critical for the models to be widely applied in practice. The outstanding challenges of the different aspects of applying and interpreting IPMs relating to: model specification; computational aspects; model assessment; and forecasting are discussed before final concluding remarks are provided.
4.1 Model Specification
A range of challenges arise in the different components of the model specification. In particular, the form of available data is continually evolving, particularly with advances in technology [104]. For example, citizen science data collection continues to grow in popularity [105, 106] and eDNA data collection is increasingly being used due to its capability to detect multiple species from water or air samples [107]. Remote sensing technology such as drones are providing finer-scale aerial survey data of animals [108], satellite earth observation data over fine scales of 30–50cm are becoming available across larger geographical areas and acoustic recording technology is enabling monitoring of elusive marine species [109], from which machine learning techniques can provide population count estimates [110]. The associated statistical models and tools are being developed for these new forms of data, but additional issues arise with incorporating such data into IPMs due to differences, for example, in relation to quality, quantity and scale [111, 112]. New challenges arise relating to how data of potentially very different geographical scales may be integrated. For example, where a large data set of “poor” quality (i.e., low information content) may be combined with small data set(s) of “high” quality within a robust and rigorous framework; and how the relative information can be computed across varying scales and levels of missing/incomplete data. Simple evaluation of the relative information in component data sets within an IPM has been proposed through evaluation of generalized variances [113]. However, there is a need for exploration of whether likelihood components could be weighted to reflect the varying quality of the available data.
Considering multi-species predator–prey models provides new insight into the dynamics of the wider ecosystem, as opposed to an individual single-species study [22, 23]. However, it is necessary for equilibrium conditions to be assessed for valid interpretation of output from such models [114]. Understanding how more complex models such as these can be incorporated within the general IPM framework will provide greater flexibility and potential for such data integration, with direct implications for wildlife management and conservation.
Further, as different forms of data are collected, and combined within IPMs, additional statistical models will be constructed. Even for relatively well-studied types of data and associated “standard” biologically sensible models, due to the specific observed data, this may lead to identifiability issues and confounded parameters that cannot be reliably estimated. Such issues are increasingly likely to arise with increasingly complex data. Analytic tools exist to determine if the model is parameter redundant and if so the estimable parameters of a model [115]. However, these typically only consider each individual (independent) model component associated with a particular type of data. Identifying parameter redundancy increases in complexity as the multiple types of data are combined within an IPM, so that analytic techniques may quickly become computationally infeasible and unable to scale to complex models. Formal determination of estimable parameters has been identified for the combination of count and ring-recovery data [9], but more practical exploration of identifiability, potentially with the use of numerical techniques [78, 116] may be required in practice.
4.2 Computational Aspects
Modern model-fitting to data typically reduces to a computational problem: either a numerical optimization problem to obtain the MLE of the parameters; or an MCMC sampling problem, in order to be able to obtain an estimate of the posterior distribution of interest. Additional issues arise, for example, when an associated likelihood component is not available in closed form (as for general state-space models or in the presence of missing data), or where the likelihood is computationally expensive to evaluate. Such computational challenges often lead to specialized algorithms being developed. However, in general, this requires additional coding experience and is bespoke to the particular problem being addressed. More general and easy-to-use computational solutions that can be applied to a wide suite of integrated models and applications are required for wider dissemination and impact.
Approximate likelihood approaches are an interesting alternative that can alleviate the computational expense of IPM components. For example, constructing capture-recapture-recovery-type likelihoods in terms of maximum-likelihood estimates and corresponding variance-covariance matrix using a multivariate normal approximation has been shown to work well in an IPM framework [117]. This provides a potential mechanism for specialized (optimized) computer packages to be applied to specific data types, which can then be combined with other data sets within an IPM framework. This has been extended further for an IPM combining census data with capture-recapture-type data. In this case, a further approximation was made, assuming independence between the estimated MLEs of the parameters from the capture-recapture data (i.e., assuming a diagonal variance–covariance matrix) within the multivariate model approximation [45]. This suggests that published model estimates may be more widely used within an integrated framework, to reduce the computational burden and widen the potential application of IPMs, and the Bayesian framework through informative priors seems like a natural solution to do so. However, the application of such approximations to date has been relatively limited, with further investigation required to more fully explore their potential and also associated limitations (see also additional model assessment challenges).
As data sets increase in size and/or models become more complex additional efficient computational optimization or sampling algorithms may be required. For example, by making use of structural properties of the likelihood function that may lead to improved optimization algorithms; or reducing the size of the data set by considering subsamples of the data and correcting the associated posterior estimates [118]. Further, it may be possible to take advantage of the flexibility of Bayesian black-box software such as Stan [119] and Nimble [120] which permit customization of the algorithms. This approach requires more intricate knowledge of the software, but the effort can substantially improve the model-fitting process [121, 122] and is usually more accessible than alternatives such as C(++) [123]. Understanding the relationship between the different components of an IPM may suggest potential techniques for efficient model-fitting [65]. Alternatively, general likelihood-free approaches have been developed for fitting complex models, such as approximate Bayesian computation (ABC; [124]) and synthetic likelihood [125]. Exploring how such techniques may be applied to IPMs is a potentially interesting avenue of future research.
4.3 Model Assessment
Various model selection approaches have been implemented for IPM analyses, including the use of standard information criteria [45], and model structure being determined by the most informative data set [19]. However, these approaches are limited since they have only compared models with the same length of state vector. [74] proposed an approach for selecting the appropriate age-structure for given model parameters in an IPM, which requires comparison of models with state vectors of different dimensions. However, this study was limited to selecting only age-structure and so extending the ideas to additional dependence structures such as time, state and/or covariate dependence is as yet largely untested.
Further, simultaneously considering the multiple types of dependencies (for example, age, time, covariate etc.) on the different model parameters is an additional challenge, both increasing the number of combinations of possible models that may be considered and also potentially the complexity of the models under consideration. Additionally, the performance of standard statistical approaches has not been fully explored for IPMs. This suggests potential avenues, including, for example, investigating regularization methods for model selection (such as Lasso), and the use of weakly informative priors [126]. Similarly, for absolute goodness-of-fit assessments, the calibrated simulation approach discussed in Sect. 3.3 may be applied for detecting a lack of fit within IPMs. [127] investigated the calibrated simulation approach and existing diagnostics goodness-of-fit tests for capture-recapture data to detect specific departures from the fitted model and the diagnostic tests performed well when under scenarios of substantial departure from model assumptions and large sample size (e.g., density-dependence, immigration, capture heterogeneity). However, where data are more sparse there was less power to detect mis-specified IPMs.
More generally, many ecological models, including longitudinal counts over time and demographic data such as capture-recapture-recovery-type data, can be expressed within an HMM framework [18]. Such models naturally extend to IPMs as demonstrated by [59]. Thus, model assessment techniques developed for HMMs may be considered more generally for such IPMs. In particular, [70] investigated different techniques for determining the number of latent states within HMMs which could assist model selection for IPMs, in relation to determining the age-dependence structures, for example. Alternatively, [128] developed a diagnostic goodness-of-fit test to determine whether the proposed latent structure in an HMM for partially-observed capture-recapture data was appropriate based on the observed data. The specification of components of IPMs all within the related state-space modeling framework also potentially suggests the use of forecast variance for goodness-of-fit assessment [129]. Developing these approaches, and in particular extending them to multiple observation and/or system processes, provide future directions for the associated model assessment challenges of IPMs.
Approximate likelihoods for different model components of IPMs may be used to deal with the computational challenges, or where the raw data may not be available. However, when using estimates and their associated variance-covariance matrix to approximate the likelihood function as a component within an IPM it is not possible to change the structure of the parameters within that approximate likelihood function. Therefore, the potential model space is restricted due to the use of the approximate likelihood and hence it would seem sensible that such a restriction should potentially be penalized for within the model selection of an IPM. However, no formal evaluation has yet been conducted to address what penalties should be imposed.
New statistical developments for model assessment of IPMs need to be practical, in terms of feasibility when the computational time for fitting an IPM is taken into account, and accessible to the wide user-community of IPMs. Thus, any new approaches developed need to be compatible with software that individuals are using to fit IPMs and users need to be aware of potential limitations of what the methods can be used to diagnose. Additionally, considerable effort needs to be made toward disseminating research and encouraging uptake from wider audiences.
4.4 Forecasting
One major avenue of future research within forecasting is the quantification and reduction of prediction uncertainty. Failure to account for uncertainty when making decisions in ecology can lead to poor management and policy decisions. In short-term forecasts, reduction in uncertainty may be possible by iteratively updating forecasts in light of new data by gaining feedback, assessing effectiveness, and adapting models [84, 130, 131]. Long-term forecasting tools which use climatic data to predict abundance [100, 132] can experience a nonlinear increase in uncertainty as the projection duration increases and their predictive skill can often vary because of the complex interactions between climate and population dynamics [133]. By decomposing the sources of uncertainty, [98] determined that the largest contributor was sampling variance. However, this can be easily reduced through larger sample sizes, or combining data sources, i.e., through the use of an IPM. In addition, [101] suggests that parameter uncertainty can be reduced, over the near and long term, by collecting targeted data to better understand mechanistic links. Another possibility, which is useful when resources are limited, is to optimize sampling design by investigating the cost-benefit of certain data collection methods, i.e., assessing whether the benefit of using more expensive monitoring methods are worth their possible reduction in uncertainty. Currently, there exists literature on optimizing sampling design of specific data types such capture-recapture [134] and occupancy studies [135]. However, optimizing sampling design in studies where multiple data types are integrated is a relatively unexplored area.
For multi-species systems, ensemble ecosystem modeling (EEM) [136, 137] provides a quantitative method for forecasting abundances in the future. EEM integrates species interaction networks and simulations of population models using the Lotka–Volterra equations as a standard predator–prey model. This technique is specifically designed for predicting the abundance of interacting species after a predator reintroduction and is useful for assessing whether there will likely be any significant change in species abundance between pre- and post-reintroduction estimates. While this allows for assessing large-scale species networks, it can be computationally challenging when a network exceeds 10 species. Long-term forecasting EEM can typically only provide suggestions of possible scenarios and future states of system with associated risk and it does so with uncertainty; however, EEM presents these uncertainties in a systematic way making it easier for end-users to make decisions [138]. One interesting possibility of future research could be to use the techniques of EEM within an IPM framework. For example, by using the species interaction networks of EEM within an IPM to forecast populations in multi-species systems. Conversely, it would also be worthwhile investigating whether the use of IPMs within an EEM framework helps to improve estimates.
Finally, emerging work combining integrated population models with integral projection models (referred to as \(\hbox {IPM}^2\)) allows individual heterogeneity in demographic rates to be included within an IPM [139]. This improves forecasting accuracy by allowing subtle individual-level mechanics to drive population dynamics. Further development and investigation of such approaches provide interesting avenues of research in this area.
4.5 Conclusion
With the recent advances in data collection technology, it is now possible to collect data at a range of spatial and/or temporal scales as well as from individual-based data collection toward community-level data collection. The IPM framework provides an adaptable and flexible approach that can accommodate the different scales and upscale to provide a community-level statistical modeling approach. Overcoming the different statistical challenges for IPMs presented within this paper will ensure that appropriate statistical methods are available for extracting intricate-level information from the available data sets. As data collection technology and ecological theory continues to evolve, it is essential that the associated statistical developments keep pace and, crucially, are made accessible to a wide range of users. Raising awareness and utility of such tools will permit rigorous data-driven conservation decision-making.
References
Williams B, Nichols J, Conroy M (2002) Analysis and management of animal populations. Academic Press, Cambridge, Massachusetts
Jardine SL, Sanchirico JN (2018) Estimating the cost of invasive species control. J Environ Econ Manag 87:242–257. https://doi.org/10.1016/j.jeem.2017.07.004
Saunders SP, Cuthbert FJ, Zipkin EF (2018) Evaluating population viability and efficacy of conservation management using integrated population models. J Appl Ecol 55:1380–1392. https://doi.org/10.1111/1365-2664.13080
DiRenzo GV, Zipkin EF, Grant EHC, Royle JA, Longo AV, Zamudio KR, Lips KR (2018) Eco-evolutionary rescue promotes host-pathogen coexistence. Ecol Appl 28:1948–1962
Royle JA, Dorazio RM (2009) Hierarchical Modeling and Inference in Ecology, Academic Press, San Diego https://doi.org/10.1016/B978-0-12-374097-7.50001-5
Kery M, Royle AJ (2020) Applied hierarchical modeling in ecology: analysis of distribution, abundance and species richness in R and BUGS vol. 2. Academic Press, Cambridge
Brooks SP, King R, Morgan BJT (2004) A Bayesian approach to combining animal abundance and demographic data. Anim Biodivers Conserv 27:525–529
Schaub M, Abadi F (2011) Integrated population models: a novel analysis framework for deeper insights into population dynamics. J Ornithol 152:227–237
Cole DJ, McCrea RS (2016) Parameter redundancy in discrete state-space and integrated models. Biom J 58:1071–1090
Dorazio RM (2014) Accounting for imperfect detection and survey bias in statistical analysis of presence-only data. Glob Ecol Biogeogr 23:1472–1484. https://doi.org/10.1111/geb.12216
Zipkin E, Zylstra E, Wright A, Saunders S, Finley A, Dietze M, Itter M, Tingley M (2021) Addressing data integration challenges to link ecological processes across scales. Front Ecol Environ 19:30–38. https://doi.org/10.1002/fee.2290
Maunder MN, Punt AE (2013) A review of integrated analysis in fisheries stock assessment. Fish Res 142:61–74. https://doi.org/10.1016/j.fishres.2012.07.025
Fournier D, Archibald CP (1982) A general theory for analyzing catch at age data. Can J Fish Aquat Sci 39:1195–1207. https://doi.org/10.1139/f82-157
Schaub M, Gimenez O, Sierro A, Arlettaz R (2007) Use of integrated modeling to enhance estimates of population dynamics obtained from limited data. Conserv Biol 21:945–955
Reynolds T, King R, Harwood J, Frederiksen M, Wanless S, Harris M (2009) Integrated data analyses in the presence of emigration and tag-loss. J Agric Biol Environ Stat 14:411–431
Saunders SP, Farr MT, Wright AD, Bahlai CA, Ribeiro JW Jr, Rossman S, Sussman AL, Arnold TW, Zipkin EF (2019) Disentangling data discrepancies with integrated population models. Ecology 100(6):e02714
Schaub M, Fletcher D (2015) Estimating immigration using a Bayesian integrated population model: choice of parameterization and priors. Environ Ecol Stat 22:535–549
King R (2014) Statistical ecology. Annu Rev Stat Appl 1:401–426
Besbeas P, Freeman SN, Morgan BJT, Catchpole EA (2002) Integrating mark-recapture-recovery and census data to estimate animal abundance and demographic parameters. Biometrics 58:540–547
Zhao Q, Heath-Acre K, Collins D, Conway W, Weegman MD (2021) Integrated population modelling reveals potential drivers of demography from partially aligned data: a case study of snowy plover declines under human stressors. PeerJ 9:12475
Lahoz-Monfort JJ, Harris MP, Wanless S, Freeman SN, Morgan BJT (2017) Bringing it all together: multi-species integrated population modelling of a breeding community. J Biol Agric Environ Stat 22:140–160
Barraquand F, Gimenez O (2019) Integrating multiple data sources to fit matrix population models for interacting species. Ecol Model 411:108713. https://doi.org/10.1016/j.ecolmodel.2019.06.001
Quéroué M, Barbraud C, Barraquand F, Turek D, Delord K, Pacoureau N, Gimenez O (2021) Multispecies integrated population model reveals bottom-up dynamics in a seabird predator-prey system. Ecol Monogr 91:01459. https://doi.org/10.1002/ecm.1459
Besbeas P, Freeman SN, Morgan BJT (2005) The potential of integrated population modelling. Aust N Z J Stat 47:35–48. https://doi.org/10.1111/j.1467-842X.2005.00370.x
Zipkin EF, Saunders SP (2018) Synthesizing multiple data types for biological conservation using integrated population models. Biol Cons 217:240–250. https://doi.org/10.1016/j.biocon.2017.10.017
Barker RJ (1997) Joint modeling of live-recapture, tag-resight, and tag-recovery data. Biometrics 53:666–677
Catchpole EA, Freeman SN, Morgan BJT, Harris MP (1998) Integrated recovery/recapture data analysis. Biometrics 54:33–46
King R, Brooks SP (2002) Model selection for integrated recovery/recapture data. Biometrics 58:841–851
King R, McCrea RS (2014) A generalised likelihood framework for partially observed capture-recapture-recovery models. Stat Methodol 17:30–45. https://doi.org/10.1016/j.stamet.2013.07.004
Sarzo B, King R, Conesa D, Hentati-Sundberg J (2021) Correcting bias in survival probabilities for partially monitored populations via integrated models. J Agric Biol Environ Stat 26:200–219. https://doi.org/10.1007/s13253-020-00423-1
Tavecchia G, Besbeas P, Coulson T, Morgan BJT, Clutton-Brock TH (2009) Estimating population size and hidden demographic parameters with state-space modeling. Am Nat 173:722–733
Besbeas P, Borysiewicz RS, Morgan BJT (2008) Completing the ecological jigsaw. In: Thomson D, Cooch EG, Conroy MJ (eds) Modeling demographic processes in marked populations, vol 3. Environmental and ecological statistics. Boston, MA, pp 513–540
Abadi F, Gimenez O, Aslettaz R, Schaub M (2010) An assessment of integrated population models: bias, accuracy, and violation of the assumption of independence. Ecology 91:7–14
Weegman MD, Arnold TW, Clark RG, Schaub M (2021) Partial and complete dependency among data sets has minimal consequence on estimates from integrated population models. Ecol Appl 31:2258
Cave VM, King R, Freeman SN (2010) Integrated population model from constant effort bird-ringing data. J Agric Biol Environ Stat 15:119–137
Newman KB, Buckland ST, Lindley ST, Thomas L, Fernandez C (2006) Hidden process models for animal population dynamics. Ecol Appl 16:74–86
Newman KB, Buckland ST, Morgan BJT, King R, Borchers DL, Cole DJ, Besbeas P, Gimenez O, Thomas L (2014) Modelling population dynamics: model formulation. Fitting and assessment using state-space methods. Springer, New York
Auger-Méthé M, Newman K, Cole D, Empacher F, Gryba R, King AA, Leos-Barajas V, Mills Flemming J, Nielsen A, Petris G, Thomas L (2021) A guide to state-space modeling of ecological time series. Ecol Monogr 91:1–38
Newman K, King R, Elvira V, de Valpine P, McCrea RS, Morgan BJT (2022) State-space models for ecological time series data: Practical model-fitting. Methods in Ecology and Evolution. In press
Buckland ST, Newman KB, Thomas L, Koesters NB (2004) State-space models for the dynamics of wild animal populations. Ecol Model 171:157–175
Caswell H (2020) The formal demography of kinship ii: Multistate models, parity, and sibship. Demogr Res 42:1097–1144
Hilborn R, Mangel M (1997) The ecological detective: confronting models with data. Princeton University Press, New Jersey
Clark JS (2007) Models for ecological data: an introduction. Princeton University Press, New Jersey
Bolker BM (2008) Ecological models and data in R. Princeton University Press, New Jersey
McCrea RS, Morgan BJT, Gimenez O, Besbeas P, Bregnballe T, Lebreton J-D (2010) Multi-site integrated population modelling. J Biol Agric Environ Stat 15:539–561
Burnham KP (1993) A theory for combined analyis of ring recovery and recapture data. In: Lebreton JD, North PM (eds) Marked individuals in the study of bird population. pp 199–213. Birkhäuser Verlag Basel, Switzerland
Thomson DL, Baillie SR, Peach WJ (1999) A method for studying post-fledging survival rates using data from ringing recoveries. Bird Study 46(sup1):104–111. https://doi.org/10.1080/00063659909477237
King R, Brooks S, Mazzetta C, Freeman S, Morgan B (2008) Identifying and diagnosing population declines: a Bayesian assessment of lapwings in the UK. J R Stat Soc Ser C 57:609–632. https://doi.org/10.1111/j.1467-9876.2008.00633.x
Robinson R, Baillie S, King R (2012) Population processes in European Blackbirds Turdus merula: A state-space approach. J Ornithol 152:419–433. https://doi.org/10.1007/s10336-010-0612-y
Plummer M (2003) JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. In: Proceedings of the 3rd international workshop on distributed statistical computing, vol 124, pp 1–9
de Valpine P, Turek D, Paciorek C, Anderson-Bergman C, Lang D, Bodik R (2017) Programming with models: writing statistical algorithms for general model structures with NIMBLE. J Comput Graph Stat 26:403–413
Schaub M, Kery M (2021) Integrated population models. Elsevier, Cambridge
Turek D, de Valpine P, Paciorek CJ (2016) Efficient Markov chain Monte Carlo sampling for hierarchical hidden Markov models. Environ Ecol Stat 23:549–564
King R, Brooks SP (2002) Closed-form likelihoods for Arnason-Schwarz models. Biometrika 90:435–444
Kalman RE (1960) A new approach to linear filtering and prediction problems. J Basic Eng Tran ASMA Ser D 82:35–45
Kitagawa G (1987) Non-Gaussian state-space modeling of nonstationary time series. J Am Stat Assoc 82:1032–1041
Langrock R (2011) Some applications of nonlinear and non-Gaussian state-space modelling by means of hidden Markov models. J Appl Stat 38:2955–2970
Langrock R, King R (2013) Maximum likelihood estimation of mark-recapture-recovery models in the presence of continuous covariates. Ann Appl Stat 7:1709–1732
Besbeas P, Morgan BJT (2019) Exact inference for integrated population modelling. Biometrics 75:475–484
Borowska A, King R (2022) Semi-complete data augmentation for efficient state-space model fitting. J Comput Graph Stat. In press
King R, McClintock B, Kidney D, Borchers DL (2016) Abundance estimation using a semi-complete data likelihood approach. Ann Appl Stat 10:264–285
Auger-Méthé M, Field C, Albertsen CM, Derocher AE, Lewis MA, Jonsen ID, Flemming JM (2016) State-space models’ dirty little secrets: even simple linear Gaussian models can have estimation problems. Sci Rep 6:1–10
Beliveau A (2016) Data integration methods for studying animal population dynamics. PhD thesis, Simon Fraser University
Glennie R, Adam T, Leos-Barajas V, Michelot T, Photopoulou T, McClintock BT (2022) Hidden markov models: pitfalls and opportunities in ecology. Methods in Ecology and Evolution. In press
Finke A, King R, Beskos A, Dellaportas P (2017) Efficient sequential monte carlo algorithms for integrated population models. J Agric Biol Environ Stat 24:204–224. https://doi.org/10.1007/s13253-018-00349-9
Dupuis J, Badia J, Maublanc M-L, Bon R (2002) Survival and spatial fidelity of mouflon (ovis gmelini): a bayesian analysis of an age-dependent capture-recapture model. J Agric Biol Environ Stat 7:277–298
King R, Brooks SP (2003) Survival and spatial fidelity of mouflons: the effect of location, age, and sex. J Agric Biol Environ Stat 8:486–513
McCrea RS, Morgan BJT (2011) Multistate mark-recapture model selection using score tests. Biometrics 67:234–241. https://doi.org/10.1111/j.1541-0420.2010.01421.x
Burnham KP, Anderson DR (2002) Model selection and multimodel inference. Springer, New York
Pohle J, Langrock R, van Beest FM, Schmidt NM (2017) Selecting the number of states in hidden Markov models: Pragmatic solutions illustrated using animal movement. J Agric Biol Environ Stat 22:270–293
Baillie SR, Brooks SP, King R, Thomas L (2009) Using a state-space model of the British Song Thrush Turdus philomelos population to diagnose the causes of a population decline. In: Thomson D, Cooch EG, Conroy MJ (eds) Modeling Demographic Processes in Marked Populations. Springer, Boston, MA, pp 541–561
Davis AJ, Hooten MB, Phillips ML, Doherty PF Jr (2014) An integrated modeling approach to estimating gunnison sage-grouse population dynamics: combining index and demographic data. Ecol Evol 4:4247–4257
Bengtsson T, Cavanaugh JE (2006) An improved akaike information criterion for state-space model selection. Comput Stat Data Anal 50:2635–2654
Besbeas P, McCrea RS, Morgan BJT (2022) Selecting survival age structure for integrated population models. Ecol Modell 473:110111
Hooten MB, Hobbs NT (2015) A guide to Bayesian model selection for ecologists. Ecol Monogr 85:3–28
King R, Morgan BJT, Gimenez O, Brooks SP (2009) Bayesian analysis for population ecology. CRC Press, Boca Raton
van de Schoot R, Depaoli S, King R, Kramer B, Märtens K, Tadesse MG, Vannucci M, Gelman A, Veen D, Willemsen J, Yau C (2021) Bayesian statistics and modelling. Nat Rev Methods Primers 1:1–26
Gimenez O, Morgan BJT, Brooks SP (2009) Weak identifiability in models for mark-recapture-recovery data. In: Thomson DL, Cooch EG, Conroy MJ (eds) Modeling demographic processes in marked populations, pp 1055–1067. Springer, Boston https://doi.org/10.1007/978-0-387-78151-8_48
McCrea RS, Morgan BJT, Pradel R (2014) Diagnostic goodness-of-fit tests for joint recapture and recovery models. J Agric Biol Environ Stat 19:338–356
McCrea RS, Morgan BJT, Gimenez O (2017) A new strategy for diagnostic model assessment in capture-recapture. J R Stat Soc Ser C (Appl Stat) 66:815–831
Jeyam A, McCrea R, Pradel R (2020) Assessing heterogeneity in transition propensity in multistate capture-recapture data. J Roy Stat Soc Ser C (Appl Stat) 69:413–427. https://doi.org/10.1111/rssc.12392
Conn PB, Johnson DS, Williams PJ, Melin SR, Hooten MB (2018) A guide to Bayesian model checking for ecologists. Ecol Monogr 88:526–542
Besbeas P, Morgan BJT (2014) Goodness-of-fit of integrated population models using calibrated simulation. Methods Ecol Evol 5:1373–1382. https://doi.org/10.1111/2041-210X.12279
Dietze MC, Fox A, Beck-Johnson LM, Betancourt JL, Hooten MB, Jarnevich CS, Keitt TH, Kenney MA, Laney CM, Larsen LG, Loescher HW, Lunch CK, Pijanowski BC, Randerson JT, Read EK, Tredennick AT, Vargas R, Weathers KC, White EP (2018) Iterative near-term ecological forecasting: needs, opportunities, and challenges. Proc Natl Acad Sci USA 115:1424–1432. https://doi.org/10.1073/pnas.1710231115
Buhle ER, Scheuerell MD, Cooney TD, Ford MJ, Zabel RW, Thorson JT (2018). Using integrated population models to evaluate fishery and environmental impacts on pacific salmon viability. https://doi.org/10.7289/V5/TM-NWFSC-140
The IUCN Red List: The IUCN Red List of Threatened Species. Version 2021-3. https://www.iucnredlist.org
Converse SJ, Moore CT, Armstrong DP (2013) Demographics of reintroduced populations: estimation, modeling, and decision analysis. J Wildl Manag 77:1081–1093. https://doi.org/10.1002/jwmg.590
Fischer JH, Wittmer HU, Kenup CF, Parker KA, Cole R, Debski I, Taylor GA, Ewen JG, Armstrong DP (2022) Predicting harvest impact and establishment success when translocating highly mobile and endangered species. J Appl Ecol. https://doi.org/10.1111/1365-2664.14219
Neupane N, Zipkin EF, Saunders SP, Ries L (2022) Grappling with uncertainty in ecological projections: a case study using the migratory monarch butterfly. Ecosphere 13:03874. https://doi.org/10.1002/ECS2.3874
DeFilippo LB, Buehrens TW, Scheuerell M, Kendall NW, Schindler DE (2021) Improving short-term recruitment forecasts for coho salmon using a spatiotemporal integrated population model. Fish Res. https://doi.org/10.1016/j.fishres.2021.106014
Johnson DS, Hoeting JA (2003) Autoregressive models for capture-recapture data: a bayesian approach. Biometrics 59:341–350
Codling EA, Plank MJ, Benhamou S (2008) Random walk models in biology. J R Soc Interface 5:813–834. https://doi.org/10.1098/RSIF.2008.0014
Ives AR, Abbott KC, Ziebarth NL (2010) Analysis of ecological time series with arma(p, q) models. Ecology 91:858–871. https://doi.org/10.1890/09-0442.1
Oppel S, Hilton G, Ratcliffe N, Fenton C, Daley J, Gray G, Vickery J, Gibbons D (2014) Assessing population viability while accounting for demographic and environmental uncertainty. Ecology 95(7):1809–1818
Boyce MS (1992) Population viability analysis. Annu Rev Ecol Syst 23:481–506. https://doi.org/10.1146/ANNUREV.ECOLSYS.23.1.481
Schaub M, Kéry M (2021) Integrated population models: theory and ecological applications with R and JAGS, p 622. Academic Press, Cambridge
Schwacke L, Thomas L, Wells R, McFee W, Hohn A, Mullin K, Zolman E, Quigley B, Rowles T, Schwacke J (2017) Quantifying injury to common bottlenose dolphins from the deepwater horizon oil spill using an age-, sex- and class-structured population model. Endanger Species Res 33:265–279. https://doi.org/10.3354/esr00777
Gauthier G, Péron G, Lebreton J-D, Grenier P, van Oudenhove L (2016) Partitioning prediction uncertainty in climate-dependent population models. Proc R Soc B Biol Sci 283:20162353
Iles D, Jenouvrier S (2019) Projected population consequences of climate change. Oxford University Press, Oxford, pp 147–164
Zylstra ER, Ries L, Neupane N, Saunders SP, Ramírez MI, Rendón-Salinas E, Oberhauser KS, Farr MT, Zipkin EF (2021) Changes in climate drive recent monarch butterfly dynamics. Nat Ecol Evol 5:1441–1452. https://doi.org/10.1038/s41559-021-01504-1
Zylstra ER, Zipkin EF (2021) Accounting for sources of uncertainty when forecasting population responses to climate change. J Anim Ecol 90:558–561. https://doi.org/10.1111/1365-2656.13443
Jenouvrier S, Holland M, Stroeve J, Barbraud C, Weimerskirch H, Serreze M, Caswell H (2012) Effects of climate change on an emperor penguin population: analysis of coupled demographic and climate models. Glob Change Biol 18:2756–2770. https://doi.org/10.1111/J.1365-2486.2012.02744.X
Rollinson CR, Finley AO, Alexander MR, Banerjee S, Hamil KAD, Koenig LE, Locke DH, Peterson M, Tingley MW, Wheeler K, Youngflesh C, Zipkin EF (2021) Working across space and time: nonstationarity in ecological research and application. Front Ecol Environ 19:66–72. https://doi.org/10.1002/fee.2298
Tuia D, Kellenberger B, Beery S, Costelloe BR, Zuffi S, Risse B, Mathis A, Mathis MW, van Langevelde F, Burghardt T, Kays R, Klinck H, Wikelski M, Couzin ID, van Horn G, Crofoot MC, Stewart CV, Berger-Wolf T (2022) Perspectives in machine learning for wildlife conservation. Nat Commun 13:1–15. https://doi.org/10.1038/s41467-022-27980-y
Robinson OJ, Ruiz-Gutierrez V, Fink D, Meese RJ, Holyoak M, Cooch EG (2018) Using citizen science data in integrated population models to inform conservation. Biol Cons 227:361–368
Johnston A, Matechou E, Dennis EB (2022) Outstanding challenges and future directions for biodiversity monitoring using citizen science data. Methods Ecol Evol. https://doi.org/10.1111/2041-210X.13834
Fukaya K, Kondo NI, Matsuzaki SIS, Kadoya T (2022) Multispecies site occupancy modelling and study design for spatially replicated environmental DNA metabarcoding. Methods Ecol Evol 13:183–193. https://doi.org/10.1111/2041-210X.13732
Hodgson JC, Baylis SM, Mott R, Herrod A, Clarke RH (2016) Precision wildlife monitoring using unmanned aerial vehicles. Sci Rep 6:1–7. https://doi.org/10.1038/srep22574
Marques TA, Thomas L, Martin SW, Mellinger DK, Ward JA, Moretti DJ, Harris D, Tyack PL (2013) Estimating animal population density using passive acoustics. Biol Rev 88:287–309. https://doi.org/10.1111/BRV.12001
Duporge I, Isupova O, Reece S, Macdonald DW, Wang T (2021) Using very-high-resolution satellite imagery and deep learning to detect and count african elephants in heterogeneous landscapes. Remote Sens Ecol Conserv 7:369–381. https://doi.org/10.1002/RSE2.195
Ross BE, Weegman MD (2022) Relative effects of sample size, detection probability, and study duration on estimation in integrated population models. Ecol Appl. https://doi.org/10.1002/EAP.2686
Zhao Q (2020) On the sampling design of spatially explicit integrated population models. Methods Ecol Evol 11:1207–1220. https://doi.org/10.1111/2041-210X.13457
Borysiewicz RS, Morgan BJT, Hénaux V, Bregnballe T, Lebreton J-D, Gimenez O (2009) An integrated analysis of multisite recruitment, mark-recapture-recovery and multisite census data. In: Thomson DL, Cooch EG, Conroy MJ (eds) Modeling demographic processes in marked populations, pp 579–591. Springer, Boston https://doi.org/10.1007/978-0-387-78151-8_25
Barraquand F, Gimenez O (2021) Fitting stochastic predator-prey models using both population density and kill rate data. Theor Popul Biol 138:1–27
Catchpole EA, Morgan BJT (1997) Detecting parameter redundancy. Biometrika 84:187–196. https://doi.org/10.1093/biomet/84.1.187
Choquet R, Cole DJ (2012) A hybrid symbolic-numerical method for determining model structure. Math Biosci 236:117–125. https://doi.org/10.1016/j.mbs.2012.02.002
Besbeas P, Lebreton J-D, Morgan BJT (2003) The efficient integration of abundance and demographic data. J R Stat Soc Ser C (Appl Stat) 52:95–102
King R, Sarzo B, Elvira V (2022) Large data and (not even very) complex ecological models: when worlds collide. arXiv:2205.07261
Carpenter B, Gelman A, Hoffman M, Lee D, Goodrich B, Betancourt M, Brubaker M, Guo J, Li P, Riddell A (2017) Stan: a probabilistic programming language. J Stat Softw 76
de Valpine P, Turek D, Paciorek CJ, Anderson-Bergman C, Lang DT, Bodik R (2017) Programming with models: writing statistical algorithms for general model structures with nimble. J Comput Graph Stat 26:403–413
Ponisio LC, de Valpine P, Michaud N, Turek D (2020) One size does not fit all: customizing MCMC methods for hierarchical models using NIMBLE. Ecol Evol 10:2385–2416
Turek D, Milleret C, Ergon T, Brøseth H, Dupont P, Bischof R, de Valpine P (2021) Efficient estimation of large-scale spatial capture-recapture models. Ecosphere 12:03385
ISO: ISO International Standard ISO/IEC 14882:2020(E) - Programming Language C++
Sisson SA, Fan Y, Beaumont M (2018) Handbook of approximate bayesian computation. CRC Press, Boca Raton
Wood SN (2010) Statistical inference for noisy nonlinear ecological dynamic systems. Nature 466:1102–1104
McElreath R (2016) Statistical rethinking: a bayesian course with examples in R and Stan. Chapman and Hall/CRC texts in statistical science series. CRC Press/Taylor and Francis Group, Boca Raton
Plard F, Turek D, Schaub M (2021) Consequences of violating assumptions of integrated population models on parameter estimates. Environ Ecol Stat 28:667–695
Jeyam A, McCrea RS, Pradel R (2021) A test for the underlying state-structure of hidden Markov models: partially observed capture-recapture data. Front Ecol Evol. https://doi.org/10.3389/fevo.2021.598325
Durbin J, Koopman SJ (2001) Time series analysis by state space methods. Oxford University Press, Oxford
Dietze MC (2017) Prediction in ecology: a first-principles framework. Ecol Appl 27:2048–2060. https://doi.org/10.1002/EAP.1589
Nichols JD, Runge MC, Johnson FA, Williams BK (2007) Adaptive harvest management of north american waterfowl populations: A brief history and future prospects. J Ornithol. https://doi.org/10.1007/s10336-007-0256-8
Zurell D, Graham CH, Gallien L, Thuiller W, Zimmermann NE (2018) Long-distance migratory birds threatened by multiple independent risks from global change. Nat Clim Chang 8:992–996. https://doi.org/10.1038/s41558-018-0312-9
Wainwright TC (2021) Ephemeral relationships in salmon forecasting: a cautionary tale. Progr Oceanogr. https://doi.org/10.1016/j.pocean.2021.102522
Lieury N, Devillard S, Besnard A, Gimenez O, Hameau O, Ponchon C, Millon A (2017) Designing cost-effective capture-recapture surveys for improving the monitoring of survival in bird populations. Biol Cons 214:233–241. https://doi.org/10.1016/j.biocon.2017.08.011
Guillera-Arroita G, Lahoz-Monfort JJ (2012) Designing studies to detect differences in species occupancy: power analysis under imperfect detection. Methods Ecol Evol 3(5):860–869. https://doi.org/10.1111/j.2041-210X.2012.00225.x
Baker CM, Gordon A, Bode M (2017) Ensemble ecosystem modeling for predicting ecosystem response to predator reintroduction. Conserv Biol 31:376–384. https://doi.org/10.1111/cobi.12798
Baker CM, Bode M, Dexter N, Lindenmayer DB, Foster C, MacGregor C, Plein M, McDonald-Madden E (2019) A novel approach to assessing the ecosystem-wide impacts of reintroductions. Ecol Appl. https://doi.org/10.1002/eap.1811
Spence MA, Blanchard JL, Rossberg AG, Heath MR, Heymans JJ, Mackinson S, Serpetti N, Speirs DC, Thorpe RB, Blackwell PG (2018) A general framework for combining ecosystem models. Fish Fish 19:1031–1042. https://doi.org/10.1111/FAF.12310
Plard F, Turek D, Grüebler MU, Schaub M (2019) Ipm2: toward better understanding and forecasting of population dynamics. Ecol Monogr 89:01364. https://doi.org/10.1002/ECM.1364
Acknowledgements
FF and RM were supported by EPSRC grant EP/S020470/1. RK was supported by the Leverhulme research fellowship RF-2019-299. EFZ was supported by the US National Science Foundation grant DBI-1954406. OG was supported by the French National Research Agency (grant ANR-16-CE02-0007). For the purpose of open access, the author has applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frost, F., McCrea, R., King, R. et al. Integrated Population Models: Achieving Their Potential. J Stat Theory Pract 17, 6 (2023). https://doi.org/10.1007/s42519-022-00302-7
Accepted:
Published:
DOI: https://doi.org/10.1007/s42519-022-00302-7