The Price Identity of Replicator(–Mutator) Dynamics on Graphs with Quantum Strategies in a Public Goods Game

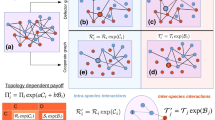
Abstract

Our research explores the influence of quantum strategies on the Price identity of replicator(–mutator) dynamics in networked systems. We specifically focus on potential solutions to social dilemmas through a quantum interpretation of the public goods game. The outcomes of our investigation defy the expected simplicity, suggesting that quantum strategies do not invariably induce cooperative behavior. Within the framework of replicator dynamics, based on a stratified interaction mechanism and a composite strategy update rule, complete entanglement could lead to super-cooperators dominating, given the cooperation and defection probabilities exceed zero. In replicator–mutator dynamics, super-cooperators reach their peak density when mutation leaning toward cooperation is certain. Numerical simulations corroborate our theoretical propositions, shedding light on the roles of various subpopulations as either complementary or substitutive entities. Our research underscores how quantum strategies accentuate observed patterns compared to non-entangled scenarios, and how the assuredness of mutation markedly impacts the behavior of super-cooperators.

Appendices

Appendix A

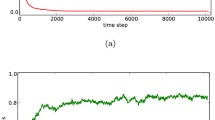
We conducted a stability analysis of the system by investigating its fixed points using computational tools in the Python programming language. It utilizes the fsolve function from the scipy.optimize library to find the fixed points of a given system and calculates the eigenvalues of the Jacobian matrix to determine the stability of each fixed point. It uses the odeint function from the scipy.integrate library to numerically solve a system of differential equations over time. The code then iterates over different combinations of these parameters to find the attractors of the system. We assumed a value of $\delta =0.5$ for the transition rate, which represents the probability of switching from a competitor to a cooperation state in a birth–death process on networks. This value implies that the system exhibits an equal likelihood of transitioning to either state, indicating a lack of preference or bias toward one particular state.

Proof of Proposition 5

We solved the differential equations $\{\dot{E}(p), \dot{E}(q), \dot{E}(1-p-q)\}=\{x_{i}, x_{j}, x_{k}\}$, that is, $\Sigma _{i} p x_{i} \left( 1+\delta - x_{i} \right) \pi _{i} - \Sigma _{i} p x_{i} (1-x_{i})(\pi _{j} + \pi _{k}) + \Sigma _{i} p x_{i} (x_{k}\pi _{j} + x_{j}\pi _{k} ) + \Sigma _{i}x_{i}\dot{p} = x_{i}$, $\Sigma _{j} q x_{j} \left( \delta + x_{i}+ x_{k}\right) \pi _{j} - \Sigma _{j}qx_{j} \left( x_{i}(\pi _{i}-\pi _{k})+(1-x_{j})\pi _{k} \right) + \Sigma _{j}x_{j}\dot{q}=x_{j}$ and $\Sigma _{k} (1-p-q) x_{k} \left( \delta + x_{i}+x_{j}\right) \pi _{k} - \Sigma _{k}(1-p-q)x_{k} \left( x_{i}(\pi _{i}-\pi _{j})+(1-x_{k})\pi _{j} \right) + \Sigma _{k}x_{k}\dot{(1-p-q)}=x_{k}$, which yielded the fixed point values $x_{i}^{\star }=\{0.00, \frac{p((1+\delta )\pi _{i} - (1-x_{k})\pi _{j} - (1-x_{j})\pi _{k}) - 1}{p (\pi _{i} - \pi _{j} - \pi _{k})}\}$, $x_{j}^{\star }=\{0.00, \frac{q(x_{i}(\pi _{i}-\pi _{j}-\pi _{k}) - (\delta + x_{k})\pi _{j} + \pi _{k}) + 1}{q \pi _{k}}\}$ and $x_{k}^{\star }=\{0.00, \frac{(1-p-q)(x_{i}(\pi _{i} - \pi _{j}-\pi _{k}) + \pi _{j} - (\delta + x_{j})\pi _{k}) + 1}{(1-p-q) \pi _{j}}\}$. We have thus discovered the existence of both corner equilibria and interior equilibria within the system. These equilibria represent points where the system’s dynamics remain constant over time. $\square$

Proof of Proposition 6

Upon investigating the stability of these fixed points, we have observed that they can possess different stability characteristics [21]. Our analysis has revealed two distinct types of fixed points: unstable points and points around which the system has both stable and chaotic behavior. The determination of stability relies on the eigenvalues of the associated Jacobian matrix for each fixed point. For unstable points, all eigenvalues of the Jacobian matrix have positive real parts. This indicates that trajectories in proximity to these points diverge away from them over time. Fixed points with unknown stability have been further analyzed through the study of the Lyapunov exponents. Here are the summarized findings. There are no stable fixed points. Fixed points with both finite positive and negative eigenvalues, along with positive Lyapunov exponents, indicate instability. In the specific configuration of $p=1$, $q=1$, and $\gamma =0$, the fixed points exhibit this instability. Fixed points with all zero eigenvalues and Lyapunov exponents of negative infinity are also likely to be unstable. These particular fixed points are identified by $p=(0,1)$, $q=0$ and $\gamma =0$. Fixed points with eigenvalues of mixed signs or Lyapunov exponents that include both finite values and negative infinity suggest unknown stability or the presence of neutral directions. These include all other fixed points with different combinations of p, q, and $\gamma$. $\square$

Proof of Proposition 7

After analyzing the stability of fixed points in the system, we now turn our attention to the presence of attractors. In a system of differential equations, an attractor is a set of states or trajectories that the system tends to converge toward over time, regardless of its initial conditions. Fixed points can also act as attractors in a system. We observe the following general rules for the values of p, q, and $\gamma$ in relation to the attractor states. When $p=0$, regardless of the values of q and $\gamma$, the coordinates of the attractor are $\{x_{i}, x_{j}, x_{k}\}=(0.1, 0.1, 0.1)$. When $p \in [0.25, 1]$, and $q=0$, the coordinates of the attractor are $\{x_{i}, x_{j}, x_{k}\}=(1, 0.1, 0.1)$. When $p \in [0.25, 1]$, $q \in [0.25, 1]$, and $\gamma =0$, the coordinates of the attractor are $\{x_{i}, x_{j}, x_{k}\}=(1, 0.1, 0.10)$. When $p \in [0.25, 1]$, $q \in [0.25, 1]$, and $\gamma$ is nonzero up to $\frac{\pi }{2}$, the coordinates of the attractor are $\{x_{i}, x_{j}, x_{k}\}=(1, 0.1, 1)$.

In summary, when the probability of encountering a cooperator is zero, the first coordinate ($x_{i}$) of the attractor is 0.1, indicating the extinction of the subpopulation of cooperators. When the probability of encountering a cooperator is non-zero, $x_{i} \rightarrow 1$, indicating that the subpopulation of cooperators reaches full density. Irrespective of the specific values of p, q, and $\gamma$, the second coordinate ($x_{j}$) of the attractor remains constant at 0.1, signifying the systematic convergence of the subpopulation of defectors toward extinction. The third coordinate ($x_k$) of the attractor depends on the values of p, q, and $\gamma$: When $p=0$ or $\gamma =0$, the third coordinate is 0.1, indicating the convergence to extinction of the subpopulation of super-cooperators. When $p \in [0.25, 1]$, $q \in [0.25, 1]$, and $\gamma$ is non-zero up to $\pi /2$, the third coordinate converges to 1, representing the attainment of full density by the subpopulation of super-cooperators. $\square$

Appendix B

We performed an analysis of the system by employing computational tools in the Python programming language. To examine the fixed points, we used the fsolve function from the scipy.optimize library to find the solutions for the given system of equations. Subsequently, we calculated the eigenvalues of the Jacobian matrix to determine the stability of each fixed point. For the dynamic analysis, we utilized the odeint function from the scipy.integrate library to numerically solve the system of differential equations over time. Through an iterative process, we explored different combinations of parameters to identify the attractors of the system. In our investigation, we assumed a transition rate of $\delta =0.5$, representing the probability of switching from a competitor to a cooperation state in a birth–death process on networks. This value implies that the system exhibits an equal likelihood of transitioning to either state, indicating a lack of preference or bias toward one particular state.

Proof of Proposition 8

We solved the differential equations $\{\dot{E}(\Delta , p), \dot{E}(\Delta , q), \dot{E}(\Delta , 1-p-q)\}=\{x_{i}, x_{j}, x_{k}\}$, that is, $\Sigma _{i}px_{i} \left( \left( \Sigma _{j}a_{ji} - x_{i} \right) \pi _{i} - (1-x_{i}-x_{k})\pi _{j} - (1-x_{i}-x_{j})\pi _{k} \right) + \Sigma _{j}p x_{j} \pi _{j} (1+\delta ) + \Sigma _{i}x_{i}\dot{p} = x_{i}$, $\Sigma _{k}(1-p-q)x_{k} \left( \left( \Sigma _{j}a_{jk} - (1-x_{i}-x_{j}) \right) \pi _{k} - x_{i}\pi _{i} \right. \left. - (1-x_{i}-x_{k})\pi _{j} \right) + \Sigma _{j}(1-p-q) x_{j} \pi _{j} (1+\delta ) + \Sigma _{k}x_{k}\dot{(1-p-q)}=x_{j}$ and $\Sigma _{k}(1-p-q)x_{k} \left( \left( \Sigma _{i}a_{ik} - (1-x_{i}-x_{j}) \right) \pi _{k} - x_{i}\pi _{i} - (1-x_{i}-x_{k})\pi _{j} \right) + \Sigma _{i}(1-p-q) x_{i} \pi _{i} (1+\delta ) + \Sigma _{k}x_{k}\dot{(1-p-q)}=x_{k}$, which yielded the fixed point values $x_{i}^{\star }=\{0.00, \frac{{\sqrt{{(\pi _{i} p a_{ji} {+} \pi _{j} p (x_{k} {-} 1) {+} \pi _{k} p (x_{j} {-} 1) {-} 1)^2 {-} 4 \pi _{j} (\delta {+} 1) p^2 x_{j} (-\pi _{i} {+} \pi _{j} {+} \pi _{k})}} {+} \pi _{i} p a_{ji} {+} \pi _{j} p (x_{k}-1) {+} \pi _{k} p (x_{j} - 1) {-} 1}}{{2 p (\pi _{i} {-} \pi _{j} {-} \pi _{k})}}\}$, $x_{j}^{\star }{=}\{\frac{ x_{k} (1-p-q) (-\pi _{i} x_{i} + \pi _{j} (x_{i} + x_{k} - 1) + \pi _{k} (a_{ji} + x_{i} - 1))}{ \pi _{j} (\delta + 1) (p + q - 1) + \pi _{k} x_{k} (p + q - 1) + 1}\}$ and $x_{k}^{\star }=\{0.00, \frac{\sqrt{((p+q-1)(\pi _{i} x_{i}- \pi _{j}(1- x_{i}))- \pi _{k}(a_{ik} + x_{i}+ x_{j}-1)(p+q-1)- 1)^2 + 4 (\pi _{j} (p+q-1)) -\pi _{i} x_{i}(p+q-1)(\delta -1)}}{2 \pi _{j} (p + q - 1)}\}$. We have discovered the existence of both corner equilibria and interior equilibria within the system. These equilibria represent points where the system’s dynamics remain constant over time. $\square$

Proof of Proposition 9

There are no stable fixed points observed in our study. Fixed points that possess both finite positive and negative eigenvalues, along with positive Lyapunov exponents, are indicative of instability. Specifically, when considering the specific configuration of $p=(0,1)$, $q=0$, $a_{ji}=(0,1)$, and $\gamma =0$, the fixed points demonstrate this instability. Additionally, fixed points characterized by all zero eigenvalues and Lyapunov exponents of negative infinity are also likely to be unstable. These particular fixed points align with the conditions where $p=(0,1)$, $q=0$, $a_{ji}=(0,1)$, and $\gamma =0$. Fixed points with eigenvalues of mixed signs or Lyapunov exponents that include both finite values and negative infinity suggest unknown stability or the presence of neutral directions. This pattern extends to all other fixed points encompassing different combinations of p, q, $a_{ji}$ and $\gamma$. $\square$

Proof of Proposition 10

We have observed the following general patterns concerning the values of p, q, and $\gamma$ in relation to the coordinates of the attractor states. When $p \le 0.5$, regardless of the values of q, $a_{ji}$, and $\gamma$, the coordinates of the attractor are $\{x_{i}, x_{j}, x_{k}\}=(0.1, 0.1, 0.1)$. When $p=0$ and $q=0$, irrespective of the values of $a_{ji}$ and $\gamma$, the coordinates of the attractor are $\{x_{i}, x_{j}, x_{k}\}=(0.1, 1, 0.1)$. When $p=1$, $q=0$, and $a_{ji} \ge 0.75$, regardless of the values of $\gamma$, the coordinates of the attractor are $\{x_{i}, x_{j}, x_{k}\}=(1, 0.1, 0.1)$. When $p=0$, $q=0$, regardless of the values of $a_{ji}$ and $\gamma$, the coordinates of the attractor are $\{x_{i}, x_{j}, x_{k}\}=(0.1, 1, 0.1)$. When $p=0$, $q>0$ and $a_{ji}>0.5$, we observe $\{x_{i}, x_{j}, x_{k}\}=(0.1, 1, 1)$

In summary, in scenarios where the likelihood of encountering a cooperator is low, the first coordinate ($x_{i}$) of the fixed point remains constant at 0.1, leading to the extinction of cooperators. Conversely, in situations where the presence of cooperators is certain, their population flourishes, causing $x_{i}$ to approach the value of 1. Additionally, when $a_{ji}=1$, cooperation prevails within the system. The second coordinate ($x_{j}$) remains fixed at 0.1, indicating a gradual decline of defectors toward extinction, except in cases where $p=0$, resulting in defectors reaching their maximum density. The third coordinate ($x_k$) is dependent on the values of p and q. In the absence of cooperation, $x_k$ remains at 0.1, signifying the extinction of super-cooperators. However, when $q>0$ or when $a_{ji}=1$, super-cooperators reach their maximum density. $\square$