Emission taxes and feed-in subsidies in the regulation of a polluting monopoly

Abstract

The paper studies the use of emission taxes and feed-in subsidies for the regulation of a monopoly that can produce the same good with a technology that employs a polluting input and a clean technology. In the first part of the paper, we show that the efficient solution can be implemented combining a tax on emissions and a subsidy on clean output. The tax is lower than the environmental damages, and the subsidy is equal to the difference between the price and the marginal revenue. In the second part of the paper, the second-best tax and subsidy are also calculated solving a two-stage policy game between the regulator and the monopoly with the regulator acting as the leader of the game. We find that the second-best tax rate can be the Pigouvian tax, but only if the marginal costs of the clean technology are constant. Using a linear–quadratic specification of the model, we show that the clean output is larger when a feed-in subsidy is used than when the tax is applied, but the dirty output can be larger or lower depending on the magnitude of marginal costs of the clean technology and marginal damages. The same occurs for the net social welfare, although we find that for low enough marginal costs of the clean technology, the net social welfare is larger when a feed-in subsidy is used to promote clean output regardless the importance of the marginal damages.

1 Introduction

Environmental regulation of a polluting monopoly is an interesting case of regulation since the market equilibrium can be inefficient because two market failures are operating at the same time but in an opposite direction. On the one hand, the firm’s market power leads to a contraction of output and emissions below their efficient levels. On the other hand, there is a negative externality that has the opposite effects. For this reason when the only way to adjust emissions is changing production, the first-best emission tax must be lower than the marginal damage and even it could be negative playing implicitly as a subsidy on production if the marginal damage is low enough as was shown by Misiolek (1980). However, if the firm can operate with an abatement technology that allows abate emissions without reducing production the first-best policy consistsof a combination of a subsidy on production and a Pigouvian tax on emissions. The tax corrects the distortion caused by the negative externality, and a subsidy equal to the difference between the price and the marginal revenue adjusts the distortion created by the power market of the firm.

The practical application of a subsidy on dirty output is problematic. However, notice that if the abatement technology is a clean technology and we can differentiate between clean and dirty outputs, it is possible to discriminate and subsidize only the clean output.

Thus, with a clean technology an alternative to a subsidy on total output is a feed-in subsidy that only applies to clean output, a policy instrument that, on the other hand, has become very popular, mainly in Europe, in the last twenty years for promoting renewable energy sources (RES) deployment.¹ The first aim of this paper is to investigate whether an emission tax/feed-in subsidy scheme could use to implement the efficient outcome in a monopolistic market. The model we propose to address this issue is that of a monopoly that operates with a technology that uses a polluting input, but that can also use a clean technology. A clear example is the production of electricity. A second issue we address in the paper is the analysis of the second-best policies; in particular, we characterize the second-best feed-in subsidy and investigate whether this subsidy generates a larger social welfare than the one that can be achieved applying only an emission tax.

Our results establish that the efficient solution can be implemented through the market mechanism using an emission tax/feed-in subsidy scheme. For this scheme, the subsidy is equal to the difference between the price and the marginal revenue, i.e., equal to the optimal subsidy to apply on total output. However, as the feed-in subsidy only applies on clean output, the tax must also contribute to compensate the distortion caused by the firm’s market power and is lower than the marginal damages. The Pigouvian tax is not the optimal tax in this case, but there exists an environmental policy scheme that can implement the first-best. This has a clear policy implication since we are able to define a proposal for a market regulation that replicates the efficient outcome without subsidizing the dirty output. This analysis is completed with a characterization of the second-best policies based on the primitive variables of the model. We develop this analysis because feed-in subsidies could be proposed as an alternative to the use of a tax and not as a complement to avoid the opposition to the use of taxes that can yield higher prices and lower production. We show that the optimal tax falls short of marginal damages as expected except if the marginal costs of the clean technology are constant. In this case, the second-best optimal tax is the Pigouvian tax. Both policy instruments decrease the dirty output and have a positive effect on the clean output, but the tax reduces the total output, whereas the subsidy increases it; this is the main difference between the two policy instruments. However, at a general level it is not possible to determine the sign of the comparison between the clean and dirty outputs under the two regulatory scenarios what hinders the comparison in terms of net social welfare.

To advance in the comparative analysis, we need to give more structure to the model. Using a linear–quadratic specification, we find out that the clean output is larger when a feed-in subsidy is applied than when a tax is used to control emissions, and that the dirty output can be lower if the marginal costs of the clean technology and the marginal damages are low enough, i.e., we cannot discard that the dirty output when a feed-in subsidy is used can be higher than when a tax is applied. This would be the effect of the positive effect that a subsidy has on total output. In terms of net social welfare, we find that for any level of marginal damages there exists always a threshold value for the marginal costs parameter of the clean technology such that if this parameter is lower than its threshold value the feed-in subsidy yields a larger net social welfare. When the marginal costs of the clean technology are low, a higher gross consumers’ surplus because of a larger total output is enough to achieve a higher net social welfare even in cases for which the dirty output is higher with the subsidy than with the tax. However, we should not expect this result when the marginal costs of the clean technology are not low enough. Then, the optimal policy would consist of applying a tax on emissions. In this case, we have that with the tax, consumers’ surplus is lower than with the subsidy, but the dirty output and environmental damages are also lower yielding a higher net social welfare. Thus, the subsidy can dominate in welfare terms the tax, but this is not a general result. There is a constellation of parameter values for which the tax yields a higher net social welfare. Nevertheless, our results support the idea that feed-in subsidies could contribute to improve the regulation of a polluting monopoly that is the main idea of this paper. On the one hand, the combination of an emissions tax and a feed-in subsidy leads the firm to implement the efficient solution. On the other hand, they could be a good alternative to taxation provided that the clean technology operates with low costs.

1.1 Literature review

Buchanan (1969) was the first in pointing out that if a Pigouvian tax equal to the optimal marginal damages is used to regulate a polluting monopoly, the result will be a reduction in welfare instead of implementing the efficient outcome. Later on, as we have already pointed out, Misiolek (1980) formalized this idea. The same year Barnett (1980) arrived to the same conclusion for a second-best emission tax when the monopolist can operate with an abatement technology. In the model proposed by Barnett (1980), it is easy to show that the first-best policy consists of a combination of a subsidy on production and a Pigouvian tax on emissions.²

Since the publication of these seminal papers, the analysis of the environmental regulation of a polluting monopoly has been extended in different directions. If we focus only on the papers that include the tax on the menu of policy instruments, we could mention the contributions by Katsoulacos and Xepapadeas (1995), Innes and Bial (2002), Petrakis and Xepapadeas (2003), Gersbach and Requate (2004), Puller (2006), Poyago-Theotoky (2007, (2010), Canton et al. (2008) and more recently by Moner-Colonques and Rubio (2016) and Martín-Herrán and Rubio (2018a, (2018b). In all these papers, following Barnett’s (1980) approach, emissions depend positively on output and negatively on a variable that can stand for both the resources devoted to abatement activities or a coefficient emissions/production that can be reduced at an increasing cost for the firm.³ The problem with this specification of the emission function is that it is not suitable for analyzing an environmental policy based on feed-in subsidies because it is not possible to discriminate between clean and dirty outputs. In fact, this literature focuses on the use of taxes, different types of standards or tradable permits, but no paper addresses the issue of feed-in subsidies on output as an instrument of the environmental policy.

More recently, different scholars have analyzed the environmental regulation in a context of imperfect competition considering that the same good can be produced with more than one technology and the regulator applies a feed-in subsidy to promote the use of the clean technology. The list includes the papers by Tamás et al. (2010), Reichenbach and Requate (2012), Sun and Nie (2015) and von der Fehr and Ropenus (2017).⁴ Tamás et al. (2010) study the use of feed-in subsidies and tradable green certificates to achieve a given quota of renewable resources in a oligopolistic market with clean and dirty firms.⁵ In our paper, we characterize the optimal policies using feed-in subsidies and emission taxes in a monopolistic market with clean and dirty technologies where the regulator decides on the optimal levels of the policy instruments. Reichenbach and Requate (2012) assume that the dirty firms form an oligopoly, whereas the clean firms constitute a competitive fringe. Furthermore, they consider an upstream competitive industry producing renewable energy equipment engaged in learning by doing. They show that a first-best policy requires two instruments, a tax on dirty output and a feed-in subsidy for renewable energy equipment producers. The tax, that is lower than the environmental damages, corrects for both the externality of pollution and the output contraction due to oligopoly power. The subsidy corrects for insufficient public learning. They also recognize that if emissions are not proportional to output, but firms have a separate clean technology, a Pigouvian tax will only correct for the pollution and a separate subsidy on dirty output would be necessary to correct for the distortion caused by the firms’ market power. Our paper shows that with a clean technology, the efficient outcome can be also implemented without using a subsidy on dirty output. Thus, the use of subsidies on dirty output can be avoided using instead feed-in subsidies on clean output, but then the Pigouvian tax is not the rule for a polluting firm with market power.

Sun and Nie (2015) work with a model very similar to the one used in this paper, but they focus in the numerical comparison of feed-in subsidies versus renewable portfolio standards assuming that the policy objective of the regulator is to achieve an exogenously given market share of the clean output as in Tamás et al. (2010). Instead, our focus is on the characterization of the first-best and second-best policies using feed-in subsidies and taxes. Finally, we could mention the paper by von der Fehr and Ropenus (2017) where they compare the market equilibrium with feed-in subsidies and with green certificates of an industry in which a dominant firm producing both dirty and clean output is facing a competitive fringe of clean firms. They demonstrate that markets for green certificate allow the dominant firm to squeeze the margins of its competitors, but that this does not occur when a system of feed-in subsidies is used. The main difference with our paper is not only that we consider the use of an emission tax, but also that we focus on the characterization of the optimal policies, whereas von der Fehr and Ropenus (2017) study how feed-in subsidies and green certificates influence the strategic price manipulation of the dominant firm yielding different market equilibria.

The paper is organized as follows. In Sect. 2, we present the model and characterize the market equilibrium and the efficient outcome. In Sect. 3, we characterize the first-best policy based on emission taxes and feed-in subsidies. Second-best policies are studied in Sect. 4, and a linear–quadratic case is used in Sect. 5 to compare the outcome of the second-best policies. Section 6 closes the paper with the conclusions and the presentation of different issues for future research.

2 The model

We consider a monopoly that faces a market demand represented by the decreasing inverse demand function p(q), where q is the firm’s output and $p^{\prime }<0$. Moreover, we assume that the marginal revenue is decreasing with the output what requires that $p^{\prime \prime }q+2p^{\prime }<0.\$The firm can produce the output using a dirty technology that employs a polluting factor given by $q_{d}=f(e)$, where e stands for the polluting input with $f(0)=0, f^{\prime }>0$, $\lim _{e\rightarrow 0}f^{\prime }=+\infty$ and $f^{\prime \prime }<0$. After an appropriate choice of measurement units, we can say that each unit of input generates one unit of pollution.⁶ According to this technology, the production cost of the dirty output is $C_{d}(q_{d})=p_{e}e(q_{d})$, where $p_{e}$ is the input market price for the polluting input. As $e^{\prime }=1/f^{\prime }>0$ and $e^{\prime \prime }=-1/f^{\prime }f^{\prime \prime }>0$, the marginal cost of the dirty output is zero when output is zero and increases with the quantity. Pollution generates environmental damages given by the function $D(e),\ D^{\prime }>0,\ D^{\prime \prime }\ge 0$. Alternatively, the firm can produce the same good using a clean technology that also operates with decreasing returns yielding a cost function, $C_{c}(q_{c})$, with the following properties $C_{c}^{\prime }(0)=0,\ C_{c}^{\prime }(q_{c})>0$ for $q_{c}>0$ and $C_{c}^{\prime \prime }(q_{c})>0$ for $q_{c}\ge 0$. Total output of the firm is given by $q=q_{c}+q_{d}$.

In this paper, we follow a strategic approach that supposes that the market regulation is analyzed as a policy game where the firm chooses the quantities to maximize its profits and the regulator selects the policy with the aim of maximizing net social welfare. Before studying the outcome of this game, we will characterize the monopoly equilibrium and the efficient allocation.

2.1 The monopoly equilibrium

The maximization problem faced by the monopolist is the following:

$$\begin{aligned} \max _{\{q_{c},q_{d}\}}\pi =p(q_{c}+q_{d})(q_{c}+q_{d})-C_{c}(q_{c})-p_{e}e(q_{d}). \end{aligned}$$

The first-order conditions (FOCs) can be summarized in one expression:

$$\begin{aligned} MR(q)=p^{\prime }(q)q+p(q)=C_{c}^{\prime }(q_{c})=p_{e}e^{\prime }(q_{d}), \end{aligned}$$

(1)

that establishes the well-known condition that the marginal revenue must be equal to the marginal costs what implies the equalization of marginal costs of both technologies. As we have assumed that the marginal costs are zero when the quantities are zero, the FOCs yield an interior solution for both the clean and dirty output.

By total differentiation of the FOCs, we obtain that

$$\begin{aligned} \frac{\partial q_{c}}{\partial p_{e}}= & {} -\frac{e^{\prime }MR^{\prime }}{ -MR^{\prime }p_{e}e^{\prime \prime }-C_{c}^{\prime \prime }MR^{\prime }+C_{c}^{\prime \prime }p_{e}e^{\prime \prime }}>0,\\ \frac{\partial q_{d}}{\partial p_{e}}= & {} \frac{(MR^{\prime }-C_{c}^{\prime \prime })e^{\prime }}{-MR^{\prime }p_{e}e^{\prime \prime }-C_{c}^{\prime \prime }MR^{\prime }+C_{c}^{\prime \prime }p_{e}e^{\prime \prime }}<0. \end{aligned}$$

Provided that the marginal revenue is decreasing and the marginal costs of both technologies are increasing, the effect on total input is

$$\begin{aligned} \frac{\partial q}{\partial p_{e}}=\frac{\partial q_{c}}{\partial p_{e}}+ \frac{\partial q_{d}}{\partial p_{e}}=\frac{-C_{c}^{\prime \prime }e^{\prime }}{-MR^{\prime }p_{e}e^{\prime \prime }-C_{c}^{\prime \prime }MR^{\prime }+C_{c}^{\prime \prime }p_{e}e^{\prime \prime }}<0, \end{aligned}$$

and we can conclude that an increase in the price of the polluting input augments the clean output, but has a negative effect on the dirty and total output.⁷ As a consequence, the production-mix used by the firm defined in this paper as the ratio between clean and total output will increase. We will represent this ratio by $\beta$.⁸

2.2 The efficient outcome

The efficient outcome is given by the quantities that maximize net social welfare defined as the sum of consumers’ surplus plus producer surplus minus environmental damages:

$$\begin{aligned} \max _{\{q_{c},q_{d}\}}NSW= \int _{0}^{q}p(y)\mathrm{d}y-C_{c}(q_{c})-p_{e}e(q_{d})-D(e(q_{d})). \end{aligned}$$

The solution to this optimization problem must satisfy the following condition for an interior solution:

$$\begin{aligned} p(q)=C_{c}^{\prime }(q_{c})=(p_{e}+D^{\prime }(e(q_{d})))e^{\prime }(q_{d}), \end{aligned}$$

(2)

where the last term stands for the full marginal costs of the dirty output that includes the marginal costs of production plus the marginal environmental damages caused by the production of the good with the dirty technology. The efficiency requires that the price be equal to the marginal costs and hence that the marginal costs of the clean production be equal to the full marginal costs of the dirty production.

As the marginal cost curve of the total output is equal to the horizontal sum of the marginal costs of the clean and dirty output, if we include the marginal damages in the sum, we obtain the standard result that establishes that the efficient level of total output can be lower or larger than the level of total output selected by the firm depending of the importance of the marginal damages. However, as the price corresponding to the efficient outcome is higher than the marginal revenue of the monopoly equilibrium, the efficient level of the clean output will be larger than the level of the clean output selected by the firm regardless of the importance of the marginal damages. But, the efficient level of the dirty output could be larger or lower than the monopoly dirty output depending on the importance of the marginal damages. Nevertheless, if the marginal damages are large enough as to yield an efficient level of the total output lower than the total output selected by the firm, the efficient level of the dirty output must be necessarily lower than the dirty production the firm takes to the market because as we have established above the efficient clean output is higher than the monopoly clean output. In this case, the production-mix efficient level is higher than the production-mix resulting for the monopoly equilibrium.

3 First-best policies: emission taxes with feed-in subsidies

In this section, we investigate whether an environmental policy that combines an emission tax with a feed-in subsidy can implement the efficient outcome. We follow a strategic approach solving a policy game where the regulator is the leader of the game and the firm the follower. Thus, in the first stage, the regulator selects the level of the policy instruments with the aim of maximizing the net social welfare, and in the second stage, the firm chooses the levels of clean and dirty output. Solving by backward induction, we begin analyzing the optimization problem of the firm given by

$$\begin{aligned} \max _{\{q_{c},q_{d}\}}\pi =p(q_{c}+q_{d})(q_{c}+q_{d})-C_{c}(q_{c})+sq_{c}-(p_{e}+t)e(q_{d}), \end{aligned}$$

where s stands for the feed-in subsidy and t is the emission tax.

The FOCs that maximize profits can be summarized in the following expression:

$$\begin{aligned} MR(q)=p^{\prime }(q)q+p(q)=C_{c}^{\prime }(q_{c})-s=(p_{e}+t)e^{\prime }(q_{d}). \end{aligned}$$

(3)

Total differentiation of the two conditions yields

$$\begin{aligned} MR^{\prime }(dq_{c}+dq_{d})= & {} C_{c}^{\prime \prime }dq_{c}-ds, \end{aligned}$$

(4)

$$\begin{aligned} MR^{\prime }(dq_{c}+dq_{d})= & {} e^{\prime }dt+(p_{e}+t)e^{\prime \prime }dq_{d}. \end{aligned}$$

(5)

Evaluating first the effects of a variation in the subsidy ($dt=0)$, we obtain that

$$\begin{aligned} \frac{\partial q_{c}}{\partial s}= & {} \frac{MR^{\prime }-(p_{e}+t)e^{\prime \prime }}{MR^{\prime }(p_{e}+t)e^{\prime \prime }+C_{c}^{\prime \prime }MR^{\prime }-C_{c}^{\prime \prime }(p_{e}+t)e^{\prime \prime }}>0. \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial q_{d}}{\partial s}= & {} -\frac{MR^{\prime }}{MR^{\prime }(p_{e}+t)e^{\prime \prime }+C_{c}^{\prime \prime }MR^{\prime }-C_{c}^{\prime \prime }(p_{e}+t)e^{\prime \prime }}<0, \end{aligned}$$

(7)

provided that the marginal revenue is decreasing and the marginal costs of both technologies are increasing.

Adding these two expressions, we can derive the effect on total output:

$$\begin{aligned} \frac{\partial q}{\partial s}=-\frac{(p_{e}+t)e^{\prime \prime }}{MR^{\prime }(p_{e}+t)e^{\prime \prime }+C_{c}^{\prime \prime }MR^{\prime }-C_{c}^{\prime \prime }(p_{e}+t)e^{\prime \prime }}>0. \end{aligned}$$

(8)

The subsidy increases the total output of the firm. The effect on the production-mix is ambiguous because although the clean production increases with the subsidy, the total output also does. However, calculating the following partial derivative

$$\begin{aligned} \frac{\partial \beta }{\partial s}=\frac{1}{q^{2}}\frac{qMR^{\prime }-q_{d}(p_{e}+t)e^{\prime \prime }}{MR^{\prime }(p_{e}+t)e^{\prime \prime }+C_{c}^{\prime \prime }MR^{\prime }-C_{c}^{\prime \prime }(p_{e}+t)e^{\prime \prime }}>0, \end{aligned}$$

we can conclude that the production-mix augments with an increase in the subsidy. The negative effect that the subsidy has on dirty output explains why the total output increases in a proportion lower than the proportion at which the clean output augments resulting in an increase in production-mix ratio.

Next, using again (4) and (5) we can evaluate the effect of a variation in the tax doing $ds=0$. Then, we obtain that

$$\begin{aligned} \frac{\partial q_{c}}{\partial t}= & {} \frac{e^{\prime }MR^{\prime }}{MR^{\prime }(p_{e}+t)e^{\prime \prime }+C_{c}^{\prime \prime }MR^{\prime }-C_{c}^{\prime \prime }(p_{e}+t)e^{\prime \prime }}>0, \end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial q_{d}}{\partial t}= & {} -\frac{(MR^{\prime }-C_{c}^{\prime \prime })e^{\prime }}{MR^{\prime }(p_{e}+t)e^{\prime \prime }+C_{c}^{\prime \prime }MR^{\prime }-C_{c}^{\prime \prime }(p_{e}+t)e^{\prime \prime }}<0. \end{aligned}$$

(10)

For the tax, we find the same kind of relationship between the policy instrument and the clean and dirty output. Adding these two expressions, the total effect on total output is given by

$$\begin{aligned} \frac{\partial q}{\partial t}=\frac{C_{c}^{\prime \prime }e^{\prime }}{ MR^{\prime }(p_{e}+t)e^{\prime \prime }+C_{c}^{\prime \prime }MR^{\prime }-C_{c}^{\prime \prime }(p_{e}+t)e^{\prime \prime }}<0. \end{aligned}$$

(11)

The tax reduces the firm’s total output.⁹ With a tax, the effect on the production-mix is straightforward because an increase in the tax rate increases the clean output, but has a negative effect on the total output.

Next, we move to the first stage. Substituting $q_{c}(s,t)$ and $q_{d}(s,t)$ in the net social welfare, we obtain an expression that depends on the policy instruments:

$$\begin{aligned} \max _{\{s,t\}}NSW= \int _{0}^{q(s,t)}p(y)\mathrm{d}y-C_{c}(q_{c}(s,t))-p_{e}e(q_{d}(s,t))-D(e(q_{d}(s,t))). \end{aligned}$$

The FOCs for this problem are

$$\begin{aligned} \frac{\partial NSW}{\partial s}= & {} (p-C_{c}^{\prime })\frac{\partial q_{c}}{ \partial s}+(p-(p_{e}+D^{\prime })e^{\prime })\frac{\partial q_{d}}{\partial s}=0, \end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial NSW}{\partial t}= & {} (p-C_{c}^{\prime })\frac{\partial q_{c}}{ \partial t}+(p-(p_{e}+D^{\prime })e^{\prime })\frac{\partial q_{d}}{\partial t}=0. \end{aligned}$$

(13)

Taking into account the FOCs for the maximization of profits, the condition (12) can be written as follows:

$$\begin{aligned} -(s+p^{\prime }q)\frac{\partial q_{c}}{\partial s}+((t-D^{\prime })e^{\prime }-p^{\prime }q)\frac{\partial q_{d}}{\partial s}=0. \end{aligned}$$

(14)

This condition is satisfied for¹⁰

$$\begin{aligned} s^{*}= & {} -p^{\prime }(q(s^{*},t^{*}))q(s^{*},t^{*}),\ \end{aligned}$$

(15)

$$\begin{aligned} \ t^{*}= & {} D^{\prime }(e(s^{*},t^{*}))+\frac{p^{\prime }(q(s^{*},t^{*}))q(s^{*},t^{*})}{e^{\prime }(q_{d}(s^{*},t^{*}))}, \end{aligned}$$

(16)

that implicitly defines the optimal values for the feed-in subsidy and the tax. It is easy to show that these values implement the efficient outcome. Substituting (15) and (16) in the FOCs for the maximization of profits given by (3), we obtain the FOCs that maximize net social welfare:

$$\begin{aligned} p(q(s^{*},t^{*}))=C_{c}^{\prime }(q_{c}(s^{*},t^{*}))=(p_{e}+D^{\prime }(e(s^{*},t^{*})))e^{\prime }(q_{d}(s^{*},t^{*})). \end{aligned}$$

The same result would be obtained using the FOC (13). Thus, we can conclude that

Proposition 1

The efficient solution can be implemented through the market mechanism using an emission tax lower than the marginal environmental damages and a feed-in subsidy equal to the difference between the price and the marginal revenue.

The optimal tax is lower than the environmental damages because the feed-in subsidy only applies to the clean output and then the tax must also compensate the distortion on the dirty output caused by the firm’s market power. If the subsidy applies to total output, we would have

$$\begin{aligned} MR(q)=p^{\prime }(q)q+p(q)=C_{c}^{\prime }(q_{c})-s=(p_{e}+t)e^{\prime }(q_{d})-s, \end{aligned}$$

and the condition (12) reads now as

$$\begin{aligned} -(s+p^{\prime }q)\frac{\partial q_{c}}{\partial s}+((t-D^{\prime })e^{\prime }-s-p^{\prime }q)\frac{\partial q_{d}}{\partial s}=0, \end{aligned}$$

then if $s=-p^{\prime }q$, we have that $t=D^{\prime }$. In this case, the first-best optimal tax is the Pigouvian tax. Thus, the use of a combination of a tax with a feed-in subsidy could be a more attractive environmental policy than the application of a tax along with a subsidy on total output that implies a subsidy on dirty output, provided that the marginal environmental damages are large enough as to avoid a “ negative” tax, i.e., a subsidy on emissions when the feed-in subsidies are used.

Summarizing, although both environmental policies implement the efficient outcome yielding the same level of net social welfare, the use of a feed-in subsidy would be less problematic from a political perspective since only the clean output must be subsidized.

4 Second-best policies: emission taxes versus feed-in subsidies

In this section, we focus on the study of the emission taxes and feed-in subsidies, but as alternative second-best policies. The issue we want to address now is the comparison of these two policy instruments to know which can be recommended if they are seen as alternative options. Following the strategic approach adopted in the previous section, we will begin with the analysis of the emission tax.

4.1 The emission tax

If only a tax is used to control pollution, the expression (3) that summarizes the FOCs for the maximization of profits in the second stage gives

$$\begin{aligned} p^{\prime }(q)q+p(q)=C_{c}^{^{\prime }}(q_{c})=(p_{e}+t)e^{\prime }(q_{d}), \end{aligned}$$

(17)

and then the condition for the maximization of net social welfare in the first stage (13) yields

$$\begin{aligned} -p^{\prime }q\frac{\partial q_{c}}{\partial t}+((t-D^{\prime })e^{\prime }-p^{\prime }q)\frac{\partial q_{d}}{\partial t}=0, \end{aligned}$$

that can be reorganized as follows:

$$\begin{aligned} -p^{\prime }q\frac{\partial q}{\partial t}+(t-D^{\prime })e^{\prime }\frac{ \partial q_{d}}{\partial t}=0, \end{aligned}$$

from where we obtain that

$$\begin{aligned} t^{*}=D^{\prime }+\frac{p^{\prime }q}{e^{\prime }}\frac{\partial q/\partial t}{\partial q_{d}/\partial t}=D^{\prime }-\frac{p}{\left| \eta \right| e^{\prime }}\frac{\partial q/\partial t}{\partial q_{d}/\partial t}, \end{aligned}$$

(18)

where $\left| \eta \right|$ is the price elasticity of demand. Using (10) and (11) to eliminate $\partial q_{d}/\partial t$ and $\partial q/\partial t$, respectively, the second-best emission tax must satisfy that

$$\begin{aligned} t^{*}=ED^{\prime }-\frac{p}{\left| \eta \right| e^{\prime }} \frac{C_{c}^{\prime \prime }}{C_{c}^{\prime \prime }-MR^{\prime }}. \end{aligned}$$

(19)

As is well known since Barnett’s (1980), the tax must be lower than the marginal damages if the firm can use an abatement technology. In this paper, we present a characterization of the tax in terms of the primitive functions of the model. Observe that if the marginal costs of the clean output are constant, the optimal emission tax would be the Pigouvian tax even in a second-best setting. Finally, we could point out that as has been established in the previous section, the tax will increase the clean output of the monopoly and will reduce its total output resulting in an increase for the ratio $\beta$.

4.2 The feed-in subsidy

If the firm faces a feed-in subsidy, the FOCs of the optimization problem that yields the quantities in the second stage are

$$\begin{aligned} p^{\prime }(q)q+p(q)=C_{c}^{\prime }(q_{c})-s=p_{e}e^{\prime }(q_{d}), \end{aligned}$$

(20)

and then the condition for the maximization of net social welfare in the first stage (12) gives

$$\begin{aligned} -(p^{\prime }q+s)\frac{\partial q_{c}}{\partial s}-(p^{\prime }q+D^{\prime }e^{\prime })\frac{\partial q_{d}}{\partial s}=0, \end{aligned}$$

that we can organize as follows:

$$\begin{aligned} p^{\prime }q\frac{\partial q}{\partial s}+s\frac{\partial q_{c}}{\partial s} +D^{\prime }e^{\prime }\frac{\partial q_{d}}{\partial s}=0, \end{aligned}$$

and the optimal subsidy must satisfy that

$$\begin{aligned} s^{*}=-\frac{1}{\frac{\partial q_{c}}{\partial s}}\left( p^{\prime }q \frac{\partial q}{\partial s}+D^{\prime }e^{\prime }\frac{\partial q_{d}}{ \partial s}\right) . \end{aligned}$$

Using (6)–(8) for eliminating $\partial q_{c}/\partial s,\partial q/\partial s$ and $\partial q_{d}/\partial s$, we obtain the following expression for the subsidy:

$$\begin{aligned} s^{*}=\frac{-\frac{p}{\left| \eta \right| }p_{e}e^{\prime \prime }+D^{\prime }e^{\prime }MR^{\prime }}{MR^{\prime }-p_{e}e^{\prime \prime }} >0. \end{aligned}$$

(21)

The subsidy presents two components. The first one reflects the distortion caused by the market power of the firm and is inversely related to the price elasticity of the demand function. The second component depends on the environmental damages and appears in the expression because of the distortion caused by the negative externality. Our model predicts that there is option for a negative subsidy as occurs with the tax.

The subsidy reduces the dirty output and increases the clean output as the tax does, but has a different effect on total output of the one caused by the tax. With the subsidy, the increase in clean output is larger than the decrease in dirty output resulting in an increase in total output. The subsidy reduces the marginal cost for the firm, and the monopoly produces more with the subsidy than with the tax. However, it is difficult to establish the relationship between the dirty and clean outputs. Nevertheless, as the total output is larger with a subsidy, the clean and dirty output selected by the firm when a tax is applied by the regulator cannot be larger than the levels chosen by the monopoly when a feed-in subsidy is applied because in this case the total output with the subsidy could not be larger than the total output with the tax. Given that it is not possible to determine the sign of the comparison between the clean and dirty outputs under the two regulatory scenarios, it is difficult to advance in the comparison of the net social welfare. With the subsidy, it is clear that consumers’ surplus is going to be larger than with a tax, but the comparison of the rest of components of the net social welfare function is not obvious. In the next section, we solve the policy game analyzed in this section for a linear–quadratic specification with the aim of deriving more clear conclusions, at least for this case, on the comparison of the two policy instruments.

5 The linear–quadratic case

In this section, we parametrize the model in the following way: The monopoly faces a linear demand function$\ p=A-q$, where q is the firm’s output. The dirty technology is given by $q_{d}=a_{s}e^{1/2}$ where $a_{d}$ is a positive parameter measuring factor productivity. According to this technology, the production cost of the dirty output is $C_{d}(q_{d})=(p_{e}/\alpha )=q_{d}^{2},~$where $a=a_{d}^{2}$. The damage function is $D(e)=dq_{d},\ d>0$, and the production costs of the clean output are $C_{c}(q_{c})=c_{c}q_{c}^{2}/2$.

For this specification of the model, the monopoly equilibrium quantities for the clean and dirty outputs are given by the following expressions:

$$\begin{aligned} q_{c}^{m}=\frac{Ap_{e}}{\alpha c+(2+c)p_{e}},\ \ q_{d}^{m}=\frac{\alpha Ac}{ 2(\alpha c+(2+c)p_{e})}, \end{aligned}$$

(22)

so that the total output is

$$\begin{aligned} q^{m}=\frac{A(2p_{e}+\alpha c)}{2(\alpha c+(2+c)p_{e})}. \end{aligned}$$

Moreover, using (22) we can obtain the production-mix used by the firm

$$\begin{aligned} \beta ^{m}=\frac{q_{c}^{m}}{q^{m}}=\frac{2p_{e}}{2p_{e}+\alpha c}. \end{aligned}$$

(23)

On the other hand, the quantities that maximize net social welfare are

$$\begin{aligned} q_{c}^{*}=\frac{2A(p_{e}+d)}{\alpha c+2(1+c)(p_{e}+d)},\ q_{d}^{*}= \frac{\alpha Ac}{\alpha c+2(1+c)(p_{e}+d)}. \end{aligned}$$

(24)

Adding these quantities, we obtain the total output:

$$\begin{aligned} q^{*}=\frac{A(\alpha c+2(p_{e}+d))}{\alpha c+2(1+c)(p_{e}+d)}. \end{aligned}$$

The production-mix corresponding to the efficient outcome is

$$\begin{aligned} \beta ^{*}=\frac{q_{c}^{*}}{q^{*}}=\frac{2(p_{e}+d)}{\alpha c+2(p_{e}+d)}. \end{aligned}$$

(25)

Comparing the clean and dirty outputs corresponding to the market equilibrium with those corresponding to the efficient solution, we obtain the following expressions:

$$\begin{aligned} q_{c}^{m}-q_{c}^{*}= & {} -\frac{A(2d(p_{e}+c\alpha )+2p_{e}^{2}+cp_{e}\alpha )}{(\alpha c+(2+c)p_{e})(\alpha c+2(1+c)(p_{e}+d))} <0, \end{aligned}$$

(26)

$$\begin{aligned} q_{d}^{m}-q_{d}^{*}= & {} \frac{\alpha Ac(2d(1+c)-(2p_{e}+\alpha c))}{ 2(\alpha c+(2+c)p_{e})(\alpha c+2(1+c)(p_{e}+d))}. \end{aligned}$$

(27)

Thus, the monopoly always selects a level of clean output below the efficient level. However, for the dirty output, the monopoly can produce below or above the efficient level. Nevertheless, looking at the numerator of the difference we can conclude that there exists a threshold value for d equal to $d_{1}=(2p_{e}+\alpha c)/2(1+c)$ such that

$$\begin{aligned} \text {if }d\left\{ \begin{array}{c}> \\ = \\< \end{array} \right\} d_{1}\text { then }q_{d}^{m}\left\{ \begin{array}{c} > \\ = \\ < \end{array} \right\} q_{d}^{*}. \end{aligned}$$

The comparison of the total output is given by

$$\begin{aligned} q^{m}-q^{*}=-\frac{A\left( \left( 2p_{e}+c\alpha \right) ^{2}-2(c^{2}\alpha -c\alpha -2p_{e})d\right) }{2(\alpha c+(2+c)p_{e})(\alpha c+2(1+c)(p_{e}+d))}. \end{aligned}$$

(28)

In this case, there exists a threshold value for c given by $c_{0}=(\alpha +(\alpha ^{2}+8\alpha p_{e})^{0.5})/2\alpha$ such that if $c\le c_{0}$ the numerator is negative and $q^{m}$ is lower than $q^{*}$ regardless of the importance of the environmental damages. However, if $c>c_{0}$ the sign of the numerator remains undetermined, but we can point out that there exists a threshold value for d defined by

$$\begin{aligned} d_{2}=\frac{\left( 2p_{e}+c\alpha \right) ^{2}}{2(c^{2}\alpha -c\alpha -2p_{e})}, \end{aligned}$$

such that if $d\le d_{2}$ then the numerator is negative and again $q^{m}$ is lower than $q^{*}$. Instead, if $d>d_{2}$ the numerator is positive and $q^{m}$ is larger than $q^{*}$. In other words, to have that $q^{m}$ is larger than $q^{*}$ we need not only a high value for marginal damages, but also a high enough value for the marginal costs of clean production, $c>c_{0}$.

Next, we compare the threshold values for d

$$\begin{aligned} d_{2}-d_{1}=\frac{\left( 2p+c\alpha +cp\right) \left( 2p+c\alpha \right) }{ (c^{2}\alpha -c\alpha -2p_{e})(1+c)}>0, \end{aligned}$$

provided that $c^{2}\alpha -c\alpha -2p_{e}>0.\$Given this relationship between the threshold values for d, we can conclude that

Proposition 2

If $c\le c_{0}$, then $q^{m}<q^{*}$ but $q_{d}^{m} < q_{d}^{*}$ only if $d <d_{1}$. For $d>d_{1}$, the relationship between the levels of the dirty output is reversed. If $c>c_{0}$, then we have that: (i) if $d<d_{1}$ then $q_{d}^{m}<q_{d}^{*}$ and $q^{m}<q^{*}$; (ii) if $d\in (d_{1},d_{2})$ then $q_{d}^{m}>q_{d}^{*}$ and $q^{m}<q^{*}$; (iii) if $d>d_{2}$ then $q_{d}^{m}>q_{d}^{*}$ and $q^{m}>q^{*}$.

Thus, we find that the relationship between the levels of dirty output depends on the importance of environmental damages, but the relationship between the levels of total output is also influenced by the marginal costs of the clean production. With low enough marginal costs, the monopoly total output is lower than the efficient level regardless of the severity of the damages.

Finally, we compare the production-mix

$$\begin{aligned} \beta ^{m}-\beta ^{*}=-\frac{2\alpha cd}{(\alpha c+2p_{e})(\alpha c+2(p_{e}+d))}<0. \end{aligned}$$

(29)

Taking into account this sign and the result obtained in the comparison of the clean outputs, we have that

Proposition 3

The monopoly clean production and its production-mix are lower than the efficient levels regardless of the importance of the environmental damages and marginal costs of clean output.

In the next subsection, we calculate the second-best emission tax.

5.1 The emission tax

In a second-best setting, the tax rate that maximizes the net social welfare is

$$\begin{aligned} t^{*}=\frac{2(2+c)d-(2p_{e}+c\alpha )}{2(3+c)}. \end{aligned}$$

(30)

Thus, we obtain that the optimal policy consists of setting up a subsidy on emissions that reduces the marginal costs of the dirty production if marginal damages are low enough, in particular if d is lower than $d_{3}=(2p_{e}+\alpha c)/2(2+c)$. We assume that d is larger than this lower bound and that consequently the optimal policy consists of taxing emissions.¹¹

The clean and dirty outputs when a tax is used to control emissions are¹²

$$\begin{aligned} q_{c}^{t}= & {} \frac{A(2(2+c)(p_{e}+d)-\alpha c)}{\alpha c(4+c)+2(2+c)^{2}(p_{e}+d)}>0, \end{aligned}$$

(31)

$$\begin{aligned} q_{d}^{t}= & {} \frac{\alpha Ac(3+c)}{\alpha c(4+c)+2(2+c)^{2}(p_{e}+d)}>0. \end{aligned}$$

(32)

Adding these two expressions, we obtain the total output

$$\begin{aligned} q^{t}=\frac{A(2+c)(\alpha c+2(p_{e}+d))}{\alpha c(4+c)+2(2+c)^{2}(p_{e}+d)} >0. \end{aligned}$$

(33)

These quantities give the following production-mix:

$$\begin{aligned} \beta ^{t}=\frac{q_{c}^{t}}{q^{t}}=\frac{2(2+c)(p_{e}+d)-\alpha c}{ (2+c)(\alpha c+2(p_{e}+d))}. \end{aligned}$$

(34)

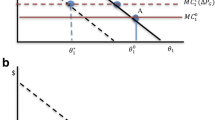
Figure 1 graphically illustrates the effects of the Pigouvian tax on the monopoly equilibrium.

Fig. 1

The emission tax

On the left panel, we have represented the marginal cost curves of both technologies and on the right panel the marginal cost of total output that is obtained adding horizontally the marginal cost curves of the clean and dirty output. The total output is given by the intersection of the marginal revenue curve with the marginal cost. Then, according to condition (1), the clean and dirty output are defined by the intersection of the level of the marginal revenue defined in the RHS panel with the marginal cost curves of the LHS panel: $MC_{d}$ for the dirty output and $MC_{c}$ for the clean output. The effect of the tax is to increase the marginal cost of dirty output for each level of production, but as in our model emissions are an input of the production function of dirty output, the effect of the tax is to increase the slope of this curve (red curve). This translates in higher marginal cost for total output and a new equilibrium with lower production but a higher marginal revenue. Then again according to condition (1), the production of clean and dirty adjusts to a higher marginal revenue. The effect is an increase in the clean output: $q_{c}^{t}>q_{c}^{m}$, where $q_{c}^{m}$ stands for the clean production of the monopoly equilibrium without taxation, a reduction in the dirty output because of the tax, where $q_{d}^{m}$ stands for the dirty output of the monopoly equilibrium without taxation. Summarizing, as was established in Sect. 3, the tax increases the clean output, reduces the dirty output and has a negative effect on total output.

Finally, we calculate the net social welfare obtained by applying a tax

$$\begin{aligned} NSW^{t}=\frac{A^{2}(c+3)\left( 2(d+p_{e})+c\alpha \right) }{2(\alpha c(4+c)+2(2+c)^{2}(p_{e}+d))}. \end{aligned}$$

(35)

5.2 The feed-in subsidy

The second-best feed-in subsidy reads

$$\begin{aligned} s^{*}=\frac{A(2p_{e}^{2}+(p_{e}+2d)c\alpha )}{2(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha )}. \end{aligned}$$

(36)

As was established in Sect. 4.2, this expression is positive.

The clean and dirty outputs when a feed-in subsidy is used are

$$\begin{aligned} q_{c}^{s}= & {} \frac{A\left( 2d\alpha +3p_{e}\alpha +2p_{e}^{2}\right) }{ 2(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha )}>0. \end{aligned}$$

(37)

$$\begin{aligned} q_{d}^{s}= & {} \frac{\alpha A\left( c(p_{e}+\alpha )-p_{e}\right) }{ 2(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha )}. \end{aligned}$$

(38)

Notice that a feed-in subsidy reduces the marginal cost of the clean output. As we assume that $C_{c}^{\prime }(0)=0$, the difference $C_{c}^{\prime }(q_{c})-s\$is negative for an initial interval of clean output values. Then, if the subsidy is high enough, the FOCs (20) could be satisfied for a negative value of the marginal costs of the dirty output and a negative value of the marginal revenue, yielding a positive clean production, but a negative dirty production. To avoid this type of solution, we assume that $c>c_{1}=p_{e}/(p_{e}+\alpha )$.

Using the two previous expressions, we can calculate the total output

$$\begin{aligned} q^{s}=\frac{A(2p_{e}^{2}+(2+c)p_{e}\alpha +(2d+c\alpha )\alpha )}{ 2(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha )}>0, \end{aligned}$$

(39)

and given the total output we obtain the production-mix of the firm

$$\begin{aligned} \beta ^{s}=\frac{q_{c}^{s}}{q^{s}}=\frac{2d\alpha +3p_{e}\alpha +2p_{e}^{2}}{ 2p_{e}^{2}+(2+c)p_{e}\alpha +(2d+c\alpha )\alpha }. \end{aligned}$$

Figure 2 graphically illustrates the effects of the feed-in subsidy on the monopoly equilibrium.

Fig. 2

The feed-in subsidy

The equilibrium quantities for the monopoly equilibrium without regulation are obtained as shown in Fig. 1. However, now as the subsidy applies to the clean output, we may see that the subsidy moves the marginal cost of the clean output down but with a clear difference with respect to the tax. There is no change in the slope of the curve but on the intersection point with the vertical axis. The red curve is $MC_{c}^{s}=MC_{c}-s$. Now, the intersection point with the vertical axis is negative and there will be a section of the curve with negatives values because the subsidy is higher than the marginal cost of clean production. Nevertheless, the effect of the subsidy implies a reduction in the marginal cost of total output and a new equilibrium where the total output is higher and the corresponding marginal revenue is lower. This reduction in the marginal revenue leads to a reduction in the dirty output: $q_{d}^{s}<q_{d}^{m}$, where $q_{d}^{m}$ represents the dirty output of the equilibrium without the subsidy, an increase in the clean output because of the subsidy, where $q_{c}^{m}$ represents the clean output of the monopoly equilibrium without the subsidy. Summarizing, as was established in Sect. 3, the subsidy increases the clean output, reduces the dirty output, but contrary to the tax has a positive effect on the total output.

Finally, we calculate the net social welfare

$$\begin{aligned} NSW^{s}=\frac{A^{2}(4p_{e}^{2}+2(3+c)p_{e}\alpha +2(3-c)d\alpha +3\alpha ^{2}c)}{8(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha )}. \end{aligned}$$

(40)

5.3 Comparing the outcome of both policies

In this section, we compare the regulated market equilibria with the aim of ranking them in welfare terms. We begin this comparative analysis comparing the outputs. The comparison of the total output is straightforward because the tax reduces the total output, whereas the subsidy increases it. The effects on clean and dirty output are not so easy to establish because both policy instruments increase the clean output and decrease the dirty output. Calculating the differences for these two variables, we obtain the following expressions:

$$\begin{aligned} q_{d}^{t}-q_{d}^{s}= & {} \frac{A\alpha (\left( 2p_{e}+c\alpha \right) \left( 4p_{e}+(2\alpha +3p_{e})c+(p_{e}+\alpha )c^{2}\right) )}{2(\alpha c(4+c)+2(2+c)^{2}(p_{e}+d))(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha ) } \nonumber \\&-\frac{2Ad\alpha \left( -4p_{e}-2c\alpha +(3p_{e}+2\alpha )c^{2}+(\alpha +p_{e})c^{3}\right) }{2(\alpha c(4+c)+2(2+c)^{2}(p_{e}+d))(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha )}. \end{aligned}$$

(41)

$$\begin{aligned} q_{c}^{t}-q_{c}^{s}= & {} -\frac{A(F_{0}c^{2}+F_{1}c+F_{2})}{2(\alpha c(4+c)+2(2+c)^{2}(p_{e}+d))(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha )}<0, \nonumber \\ \end{aligned}$$

(42)

where¹³

$$\begin{aligned} F_{0}= & {} \alpha \left( 4d^{2}+2(p_{e}-\alpha )d+3p_{e}\alpha +2\alpha ^{2}+2p_{e}^{2}\right)>0,\\ F_{1}= & {} 2(4d^{2}\alpha +2d\left( p_{e}+\alpha \right) ^{2}+p_{e}\left( 5p_{e}\alpha +4\alpha ^{2}+2p_{e}^{2}\right) )>0,\\ F_{2}= & {} 8p_{e}\left( p_{e}+\alpha \right) \left( d+p_{e}\right) >0. \end{aligned}$$

Thus, a first conclusion is

Proposition 4

The clean and total outputs are larger when a feed-in subsidy is applied than when a tax is applied.

The sign of (41) is undetermined, but there exists a threshold value for c given by the unique positive root of the equation¹⁴

$$\begin{aligned} -4p_{e}-2c\alpha +(3p_{e}+2\alpha )c^{2}+(\alpha +p_{e})c^{3}=0, \end{aligned}$$

(43)

that we call $c_{2}$ such that if $c\le c_{2}$ then $q_{d}^{t}$ is larger than $q_{d}^{s}$. It is easy to show by substitution on the LHS of the equation that $c_{1}<c_{2}$. Thus, if $c_{1}<c\le c_{2}$, the dirty production is larger under a regimen of taxation than when a feed-in subsidy is used regardless of the importance of the environmental damages. If $c>c_{2}$, then there exists a threshold value for d given by the following expression:

$$\begin{aligned} d_{4}=\frac{\left( 2p_{e}+c\alpha \right) \left( 4p_{e}+(2\alpha +3p_{e})c+(p_{e}+\alpha )c^{2}\right) }{2((3p_{e}+2\alpha )c^{2}+(\alpha +p_{e})c^{3}-2c\alpha -4p_{e})}, \end{aligned}$$

(44)

such that if $d<d_{4}$ then $q_{d}^{t}$ is still larger than $q_{d}^{s}$, but if $d>d_{4}$ the contrary occurs and $q_{d}^{s}$ is larger than $q_{d}^{t}$. In this case, both the clean and dirty outputs are higher when a subsidy is selected by the regulator. This result requires not only high damages, but also high marginal costs of the clean output. It can be checked that $d_{3}<$ $d_{4}$.¹⁵ Thus, the application of a tax is not a sufficient condition to get a lower level of dirty production, i.e., for $d\in (d_{3},d_{4})$ the optimal policy consists of applying a tax, but $q_{d}^{t}$ is larger than $q_{d}^{s}$. The results of this comparison can be summarized in the following proposition:

Proposition 5

If $c\le c_{2}$, then $q_{d}^{s}<q_{d}^{t}$. However, if $c>c_{2}$ then we have that if $d\in (d_{3,}d_{4})$ still $q_{d}^{s}<q_{d}^{t}$, but if $d>d_{4}$ the relationship is reversed and $q_{d}^{s}>q_{d}^{t}$.

Finally, we compare the production-mix

$$\begin{aligned} \beta ^{t}-\beta ^{s}=-\frac{\alpha (\left( 2p_{e}+c\alpha \right) \left( 2p_{e}+c\alpha +2cp_{e}\right) -2d\left( -2p_{e}-(\alpha -p_{e})c+c^{2}p_{e}\right) )}{(2+c)(\alpha c+2(p_{e}+d))(2p_{e}^{2}+(2+c)p_{e}\alpha +(2d+c\alpha )\alpha )}. \end{aligned}$$

(45)

Again, we find that the sign of the difference depends on parameters values. If c is equal to or lower than $c_{3}$, the unique positive root of equation $-2p_{e}-(\alpha -p_{e})c+c^{2}p_{e}=0$, that is defined from the second term of the numerator, the difference is negative and we have that $\beta ^{t} < \beta ^{s}$.¹⁶ With low marginal costs of clean production, the increase in clean output because of a subsidy is high enough as to yield a production-mix higher than the production-mix obtained when a tax is used though the tax reduces total output. If c is higher than the positive root of the equation, the sign of (45) depends on damages parameter. The threshold value for this parameter is given by

$$\begin{aligned} d_{5}=\frac{\left( 2p+c\alpha \right) \left( 2p+c\alpha +2cp\right) }{ c^{2}p+(p-\alpha )c-2p}, \end{aligned}$$

that is also larger than $d_{3}$ that guarantees that the tax is positive. Then, we obtain that if $d\in (d_{3},d_{5}),\ \beta ^{t}$ is still lower than $\beta ^{s}$, but if $d>d_{5}$ the contrary occurs and $\beta ^{t}$ is larger than $\beta ^{s}$. Now, the effect of the tax on total output is strong enough to lead to a larger production-mix. The problem is that the better performance of this indicator is not caused by an important increase in the clean output in comparison with what can be obtained through a subsidy, but for the reduction that the tax causes in total output.

Summarizing,

Proposition 6

If $c\le c_{3}$, then $\beta ^{t}<\beta ^{s}$. However, if $c>c_{3}$ then we have that if $d\in (d_{3},d_{5})$ still $\beta ^{t}<\beta ^{s}$, but if $d>d_{5}$ the relationship is reversed and $\beta ^{t}>\beta ^{s}$.

To conclude the comparison of the outcomes of both policies, we compare the net social welfare. The difference in terms of net social welfare reads

$$\begin{aligned} NSW^{t}-NSW^{s}=\frac{A^{2}N(c)}{8(\alpha c(4+c)+2(2+c)^{2}(p_{e}+d))(p_{e}^{2}+c(p_{e}+\alpha )^{2}+2(p_{e}+d)\alpha ) }, \end{aligned}$$

(46)

where

$$\begin{aligned} N(c)=\alpha \left( 2d-\alpha \right) ^{2}c^{3}+2\alpha (2d^{2}-(3\alpha +4p_{e})d+p_{e}\alpha )c^{2}-4c\alpha \left( 2d+p_{e}\right) ^{2}-8p_{e}^{2}\left( d+p_{e}\right) . \end{aligned}$$

(47)

This expression allows to conclude that

Proposition 7

For a given value of d, if c is lower than the positive root of the polynomial equation $N(c)=0$ then $NSW^{t}<NSW^{s}$. However, if the contrary occurs we have that $NSW^{t}>NSW^{s}$.

The proof of the proposition is straightforward if we notice that according to the Descartes’ rule of sign $N(c)=0$, regardless of the sign of the coefficient of $c^{2}$, can only have a positive root and moreover the independent term is negative. Then, for any value of c larger than the positive root, N(c) is positive and $NSW^{t}>NSW^{s}$.

When the marginal costs of clean output are low enough as to satisfy the threshold values defined by Propositions 5 and 7, the dirty output and consequently the emissions are low if the regulator applies a feed-in subsidy. Then, the application of the subsidy yields a larger gross consumers’ surplus because the total output is larger with the subsidy, lower costs of dirty production because the dirty production is lower with the subsidy, lower environmental damages because the emissions are also lower with the subsidy, and finally larger costs of clean output because the subsidy gives a larger level of clean output. But, if c is low enough, our analysis says that the increase in net social welfare because of the increase in the gross consumers’ surplus, the reduction in the costs of dirty production and the decrease in damages are larger than the decrease in net social welfare because of the increase in the costs of clean output. It is difficult to compare the threshold values for c defined by Propositions 5 and 7 which open the possibility, as the numerical example presented below shows, that we obtain a higher net social welfare with a subsidy even if the dirty output with the subsidy is larger than the dirty output associated with an emission tax. In this case, a larger gross consumers’ surplus because of a larger total output is enough as to yield a larger net social welfare. However, when the marginal costs of clean output are high enough this possibility disappears and the tax implements a higher level of net social welfare.

Finally, we illustrate the results of Propositions 5 and 7 with a numerical exercise graphically represented in Fig. 3. The aim of this example is to show for which combinations of (c, d) one policy instrument is superior to the other in terms of net social welfare. For $p_{e}=1$ and $\alpha =0.75$, we plot in Fig. 3 the curves defined by the conditions $q_{d}^{t}=q_{d}^{s}$ (in red) obtained from (41) and $NSW^{t}=NSW^{s}$ (in black) obtained from (46) in the space (c, d).¹⁷ Next, we explain how we obtain these curves. First, we should clarify that the origin of the axes is $d=0.5$ and $c=0.94$. For $d>0.5$, according to expression $d_{3}=(2p_{e}+\alpha c)/2(2+c)$, the optimal tax cannot be negative regardless of the value of parameter c. Notice that $d_{3}$ decreases with c so that the maximum value of $d_{3}$ is 0.5 for $c=0$. On the other hand, $c_{1}=p_{e}/(p_{e}+ \alpha )=0.57$ that is the lower bound that guarantees a positive dirty production and $c_{2}$ defined for the positive root of (43) is equal to 0.94. Below this threshold value, $q_{d}^{t}>q_{d}^{s}$ regardless of the values of environmental damages, so that assuming that $c>0.94$ we have that dirty production is positive because $c>c_{1},\$and the difference $q_{d}^{s}-q_{d}^{t}$ depends on marginal damages because $c>c_{2}$ as was established in Proposition 5.

Fig. 3

Comparing dirty outputs and net social welfare

The red curve represents the expression (44) that gives the combinations (c, d) for which $q_{d}^{t}=q_{d}^{s}$ when $p_{e}=1$ and $\alpha =0.75$. For these values, this expression is

$$\begin{aligned} d_{4}=\frac{(2+0.75c)(4+4.5c+1.75c^{2})}{2(4.5c^{2}+1.75c^{3}-1.5c-4)}. \end{aligned}$$

For$\ d=0.5,\ c=9.13$ and for $c=0.94,\ d$ is 604.74; thus, we have that if $d>0.5$ and $c>9.13$, and $c>0.94$ and $\ d>\ 604.74,\ q_{d}^{s}>q_{d}^{t}$ for all (c, d). For the rest of combinations, all combinations (c, d) above the red curve, $q_{d}^{s}>q_{d}^{t}$, whereas for all the combinations below the red curve the contrary occurs.¹⁸

The black curve represents the implicit function defined by $N(c;d)=0$ where N(c; d) is given by (47). Organizing terms, this condition can be rewritten as a second-degree equation for d:

$$\begin{aligned} 3cd^{2}(c^{2}+c-4)-\frac{1}{8} (3c+8)(6c^{2}+9c+8)d+0.42188c^{3}+1.125c^{2}-3c-8=0, \end{aligned}$$

where the first term is positive if $c>1.57$ and the independent term is positive if $c>2.77$. Then, $N(c;d)<0$ for all $d>0.5$ if $c<1.57$. Thus, assuming that $c>1.57,\ N(c;d)=0\$ has a solution and we can conclude that for all combinations (c, d) above the black curve $NSW^{t}>NSW^{s}$, but if the combinations are below the curve we have that $NSW^{t}<NSW^{s}$.¹⁹ Figure 3 shows that a feed-in subsidy yields a larger net social welfare if the marginal costs of clean output and marginal damages are low enough. However, for the values of $p_{e}$ and $\alpha$ selected for the example, the area for which the tax yields a higher net social welfare is larger than the area for which the subsidy leads to a higher net social welfare establishing that the range of parameter values for which the tax dominates in welfare terms the subsidy is wider. Finally, we could point out that the subsidy can yield a higher net social welfare even if the dirty output is larger when the subsidy is applied. For the combinations (c, d) between the red curve and the black curve, we have that $q_{d}^{t}<q_{d}^{s}$, but $NSW^{t}<NSW^{s}$. For these parameter values, a larger consumers’ surplus because of a larger output is enough to give a higher net social welfare when the subsidy is applied. When the tax dominates, the reduction in the consumers’ surplus is because a lower output is compensated by the reduction in the costs of the dirty output and environmental damages. However, this argument works only when the damages and costs of the dirty output are high enough since below the black curve and above the red curve, the subsidy yields a higher net social welfare even if the dirty output when the subsidy applies is higher than the dirty output when a tax is applied.

6 Conclusions

This paper studies the use of emission taxes and feed-in subsidies in the regulation of a polluting monopoly that can produce the same good with a technology that employs a polluting input and an alternative clean technology. Following a strategic approach, we assume that the regulator acts as the leader of a policy game where the firm chooses the levels of production to maximize net profits and the regulator the levels of the policy instruments to maximize net social welfare. In the first part of the paper, we characterize the market equilibrium and the efficient outcome and show that the efficient outcome can be implemented using an emission tax lower than the environmental damages and a feed-in subsidy equal to the difference between the price and the marginal revenue. We also calculate the second-best tax and subsidy. We find that the second-best tax rate is the Pigouvian tax, but only if the marginal costs of the clean output are constant. Both policies increase clean output and decrease dirty output, but the tax has a negative effect on total output, whereas the subsidy has a positive effect. However, it is difficult to compare the levels of the dirty and clean outputs for the two policy instruments analyzed in the paper. This leaves the comparison between the two equilibria of the policy game undetermined, except for the total output. To advance in the comparative analysis, we propose a linear–quadratic specification of the model. For this specification, we obtain that the clean output is larger when a feed-in subsidy is used than when a tax is charged on emissions. However, the dirty output can be larger or lower depending on the importance of marginal costs of the clean technology and marginal damages. The same occurs for the ratio of clean output over total output (production-mix) and the comparison of net social welfare. Nevertheless, we obtain that if the marginal costs of the clean technology are low enough the feed-in subsidy would lead to a larger net social welfare than the one achieved by applying a tax. Thus, the policy recommendation would be to use a subsidy on clean output, but only if the clean technology has reached a level of development that allows to produce the clean output with low costs. If this condition does not hold, it is better to use a tax on emissions. Thus, our findings support the idea that feed-in subsidies may help to improve the regulation of a polluting firm with market power. On the one hand, the combination of an emission tax and a feed-in subsidy induces the firm to implement the efficient outcome. On the other hand, they could be a good alternative to taxation if the clean technology operates with low costs.

The analysis developed in this paper could be extended in different directions. Our analysis has focused on the study of feed-in premiums, a policy that consists of setting up a subsidy (a premium) on clean output, discriminating between dirty and clean outputs. However, several countries in Europe instead have applied a feed-in tariff that implies a direct regulation of the price for the clean output. Thus, it would be interesting to extend the analysis to consider this alternative support scheme for the clean output. Another interesting extension in the line of Gersbach and Requate’s (2004) paper would be to consider public finance aspects assuming, for instance, that there is a limit to finance the subsidy, a limit that could be exogenous or could depend on the tax revenue. On the other hand, as the research has been confined to the case of a polluting monopoly, we could look at other market structures to check the robustness of the results obtained in the paper. We expect that the combination of an emission tax and a feed-in subsidy works for markets with imperfect competition as the results obtained by Reichenbach and Requate (2012) for a polluting oligopoly with a clean competitive fringe suggest. A first step in this direction could be to complete the analysis of the market equilibrium developed by von der Fehr and Ropenus (2017) for a dominant firm with a competitive fringe calculating the optimal policy. The study of the effects that other policy instruments have on green innovation is also in the research agenda for addressing in the future. Finally, the model could be extended to take into account the investment in innovation of the clean technology and analyze the time consistency of the environmental policy in this framework.