Introduction

The synthesis of binary chalcogenides of group II–VI semiconductor in a nanopowder form has been a rapidly growing area of research due to their unique chemical and physical properties, which are different from those of either the bulk materials or single atoms (Trindade et al. 2001). CdO is a degenerate, n-type semiconductor used in optoelectronic applications such as photovoltaic cells, solar cells, phototransistors, IR reflectors, transparent electrodes, gas sensors and a variety of other materials (Su et al. 1984; Kondo et al. 1971; Benko and Koffyberg 1986; Lide 1996/1997). These applications of CdO are based on its specific optical and electrical properties. The intensity of optical and electrical effects of CdO depends on the deviation from the ideal CdO stoichiometry, as well as on the size and shape of the particles (Ristic et al. 2004). CdO is attracting tremendous attention due to its interesting properties like direct band gap of 2.3 eV (Gurumurugan et al. 1995).

Various properties of CdO have been investigated by researchers (Zhang et al. 2005; Radi et al. 2006; Xiaochun et al. 1998; Reddy et al. 2010; Ghosh et al. 2005). Zhang et al. (2005) have synthesized cadmium hydroxide nanoflake and nanowisker by hydrothermal method. Radi et al. (2006) have characterized and studied the properties of CdO nanocrystals incorporated in polyacrylamide. Xiaochun et al. (1998) have studied the optical properties of nanometer-sized CdO organosol. Reddy et al. (2010), using cyclic voltammetry technique, have synthesized CdO nanoparticles and their modified carbon paste electrode for determination of dopamine and ascorbic acid.

Ghosh et al. (2005) have studied temperature-dependent structural and optical properties of nanocrystalline CdO thin films deposited by sol–gel process. But, no attention has ever been paid to the systematic study of the dielectric properties of CdO to the best of our knowledge.

The dielectric constant of a semiconductor is one among its most important properties. Its magnitude and temperature dependence are significant in both fundamental and technological considerations. Hence the knowledge of frequency-dependent dielectric constant of the nanomaterial is mandatory for its practical applications. Recently, we have investigated the dielectric relaxation of other II–VI semiconductor nanoparticles such as CdSe (Das et al. 2014) and ZnO (Tripathi et al. 2010). In the present work, we have synthesized CdO nanoparticles by soft chemical method and investigated its dielectric properties using impedance spectroscopy.

It is to be mentioned that the impedance spectroscopy is one of the powerful tools for the characterization of dielectric properties of materials. AC impedance spectroscopy allows measurement of the capacitance and loss tangent (tan δ) and/or conductance over a frequency range at various temperatures. From the measured capacitance and tan δ, following complex dielectric functions can be computed: impedance (Z*), electric modulus (M*) and permittivity (ε*). Studying dielectric data with the different functions allow one to find the features of dielectric relaxation process in different frequency regions.

Experiments

Experimental details were as follows: 1.33 g of cadmium acetate [Cd(OCOCH3)2] was put into 50 ml distilled water under stirring, thioglycerol solution of 0.043 ml (10−2 M) was mixed with constant stirring, and then 0.2 g NaOH was introduced into the aforementioned solution under stirring and, thus, a white aqueous solution was formed due to the formation of CdO precipitates. These precipitates were washed with distilled water and ethanol to remove any impurity present in the product. To obtain CdO in powder form, the washed precipitates were dried at room temperature and calcined at 300 °C.

The X-ray diffraction of the sample at room temperature was taken by a powder X-ray diffractometer (Rigaku Miniflex-II) with CuKα radiation of wavelength λ = 1.54 Å. The transmission electron micrograph (TEM) of the sample was taken by a transmission electron microscope (JEOL JEM-2010 microscope). Fourier-transformed infrared spectroscopy (FTIR-1000, Perkin-Elmer) was studied in the wave number range of 400–2000 cm−1. The absorption and luminescence spectra were recorded using UV–visible spectrophotometer (Lambda 35, Perkin Elmer) and fluorescence spectrofluorometer (FP-8500 JASCO), respectively. The dielectric measurement of the sample of thickness 2.06 mm and diameter 10.41 mm was carried out using gold electrodes by an LCR meter (3532-50, Hioki) in the frequency range from 100 Hz to 1 MHz and in the temperature range from 313 to 393 K. The temperature was controlled with a programmable oven. All the dielectric data were collected while heating at a rate of 1 °C min−1. Each measured temperature was kept constant with an accuracy of ±1 °C. The complex electric modulus M * (= 1/ε *) and impedance Z * (= M */iωC o) were obtained from the temperature dependence of the real (ε′) and imaginary (ε″) components of the dielectric permittivity ε * (= ε′−iε″).

Results and discussion

Structural study

Nanostructural studies and X-ray diffraction

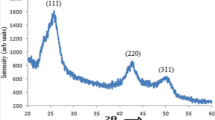
Figure 1 shows the X-ray diffraction pattern of the synthesized materials. The XRD pattern is well matched with the reported cubic structure of CdO with lattice constant a = 0.4695 nm (JCPDS No. 750594) having the diffraction pattern from (111), (200), (220), (311) and (222) planes (Cimino and Marezio 1960). There are no peaks ascribable to Cd(OCOCH3)2, and the results prove the complete transformation of Cd(OCOCH3)2 to CdO. We have calculated the crystallite size of CdO using Debye–Scherrer’s formula defined as:

Fig. 1
figure 1

The XRD patern of CdO nanoparticles. The TEM micrograph is shown in the inset

Full size image
$$L = \frac{0.94\,\lambda }{B\cos \theta }$$
(1)

where L is the average crystallite size of the particle, λ is the wavelength of X-ray radiation, B is the full width at half maximum (FWHM) and θ is the diffraction angle. From the XRD result, the average crystallite size of the material is found to be ~38 nm.

The low magnification TEM micrograph of CdO nanoparticles is shown in the inset of Fig. 1. The average particle size of the nanoclusters of CdO is found to be ~45 nm. The HRTEM micrograph of the particle as shown in Fig. 2a indicates the homogeneous orientation of the lattice planes with interplanar spacing of 0.274 nm. This correlates with the d spacing value of (111) plane of cubic CdO and confirms the crystallinity of CdO nanoparticles. The crystallinity and orientation of the nanoparticles are confirmed from the SAED patterns as shown in Fig. 2b. The SAED pattern (Fig. 2b) shows the bright spots for the crystalline nature of the particles.

Fig. 2
figure 2

HRTEM image (a) and SAED pattern (b) of CdO nanoparticles

Full size image

FT-IR and UV–visible spectra

FT-IR analysis of the sample at room temperature is presented in Fig. 3 which shows that the precursor nanoparticles exhibit the classical absorption bands assigned to symmetric (C–O) and asymmetric (C–O) vibrations of carbonate ions in the range from 1400 to 1600 cm−1 and at 1074, 1025, 859 and 727 cm−1 (Stoilova et al. 2002; Seguatni et al. 2005; Xu and Zeng 2001; Liu et al. 2005). The peaks are due to bond vibrational energy of Cd–O at 545 cm−1. The small hump at 620 cm−1 is also attributed to CdO (Gurumurugan et al. 1996). These characteristic absorption peaks, which are very similar to those of hydroxide carbonate salts, revealed that the as-synthesized precursor nanoparticles contain OH−, CO3 2− ions and Cd–O bond.

Fig. 3
figure 3

FT-IR spectrum of the CdO nanoparticles

Full size image

The fundamental absorption, which corresponds to electron excitation from the valance band to conduction band, can be used to determine the nature and value of the optical band gap. The UV–visible absorption spectrum of CdO nanoparticles is shown in Fig. 4. The band gap of CdO nanoparticles is determined by Tauc relation, αhν = A(hν−E g)n, where α is the absorption coefficient, E g is the absorption band gap, A is constant and n depends on the type of transition (n = 2 for indirect band gap and n = ½ for allowed direct band gap). To determine the possible transitions, (αhν)2 vs hν is plotted in the inset of Fig. 4 and corresponding band gap is obtained from extrapolating the straight portion of the graph near absorption edge to hν axis. The direct band gap value is found to be 2.36 eV which is larger than the bulk CdO. This blue shift of the band gap value could be a consequence of a size quantization effect in the sample. The size-induced widening of bandgap can be described based on two quantum confinement regimes, strong and weak (Brus 1984; Yoffe 1993). Strong quantum confinement occurs due to the independent confinement of electrons and holes when the sizes of nanostructures are much smaller than the size of Bohr radius (Brus 1984; Yoffe 1993; Rastogi et al. 2000). Whereas in the case of weak quantum confinement effect, the energy is dominated by the Coulomb term and quantum effects arise from quantization of exciton motion (Rastogi et al. 2000; May et al. 2007) and hence the bandgap shift is relatively smaller than the strong confinement. Since the particle sizes of our nanoparticles are much higher than the Bohr radius of CdO, we can consider that the weak quantum confinement is the origin of widening of bandgap in this material.

Fig. 4
figure 4

The UV–visible absorption spectrum of the CdO nanoparticles. Tauc plot of the system is shown in the inset to obtain the band gap

Full size image

Luminescence spectra

The PL spectra of CdO nanoparticles are shown in Fig. 5, which represents the shift of the emission peak by exciting the sample at different wavelengths. The sample exhibits broad emission bands at 405, 463, 531 and 600 nm at the excitation wavelengths of 300, 400, 450 and 500 nm, respectively. The emission peaks are blue to red shifted with the increase in the excitation wavelengths. The shift of the peak in the spectra towards the higher wavelengths with the increase in the excitation wavelength can be interpreted by the phonon bottleneck effect (Raymond et al. 1996). In the case of the phonon bottleneck, the transitions from the ground state to the excited states can be observed at various excitation wavelengths. In this type of transition, at a particular excitation wavelength, the excitation energy moves the electron to the higher state of conduction band from the valance band and when the excited electrons come down to the ground state of the conduction band, the energy is released giving a peak in the spectrum. Now for the lower excitation wavelength, the electron can move to higher states of conduction band which will release higher energy when coming down to the ground state of conduction band and one gets a peak in the lower wavelength side. Whereas for the higher excitation wavelength, the electron can move to lower state of conduction band which will release low energy while coming down to the ground state of the same and one gets a peak in the higher wavelength side. The intensity of the peaks also decreases with the change of the excitation wavelength because of the number of particles taking part in the luminescence process decreases with time.

Fig. 5
figure 5

Photoluminescence spectra at different excitation wavelength of CdO nanoparticles

Full size image

Electrical properties study

Impedance spectroscopy

Figure 6 shows the frequency (angular) dependence of impedance for CdO at various temperatures. It is evident from Fig. 6 that the position of the peak in the imaginary part of complex impedance, Z″ (centered at the dispersion region of the real part of complex impedance, Z′), shifts to higher frequencies with increasing temperature and that a strong dispersion of Z″ exists. The width of the peak in Z″ spectra points towards the possibility of a distribution of relaxation times. In such a situation, one can determine the most probable relaxation time τ m (= 1/ω m) from the position of the peak in the Z″ versus log ω plots. The most probable relaxation time follows the Arrhenius law, given by

Fig. 6
figure 6

Frequency dependence of the impedance (Z*) spectrum for CdO at various temperatures, where the symbols are the experimental data points and the solid lines represent the fitting of Cole–Cole expression. The inset shows the complex–plane impedance plots at various temperatures. The solid line is the best fit for CdO

Full size image
$$\omega_{\text{m}} = \omega_{ 0} \, \exp \, \left( { - E_{\text{a}} /k_{\text{B}} T} \right)$$
(2)

where ω 0 is the pre-exponential factor and E a is the activation energy. Plot of log ω m versus 103/T, where the symbols are the experimental data and the solid line is the least-squares straight-line fit, is shown in the inset of Fig. 7. The activation energy E a calculated from the least-squares fit to the points is 0.24 eV.

Fig. 7
figure 7

Scaling behavior of Z″ at various temperatures for CdO. The Arrhenius plot of the Z″ is shown in the inset for CdO

Full size image

The complex impedance spectra can be described by introducing a temperature-dependent factor m into the Debye expression, namely, the Cole–Cole expression (Cole and Cole 1941), as follows:

$$Z*(\omega ) = \frac{{R_{ 0} }}{{1 + (i\omega \tau_{ 0} )^{\text{m}} }}$$
(3)

where τ0 = 1/ω0, τ0 and ω0 are the characteristic relaxation time and the angular frequency, respectively.

In Fig. 6 we have fitted our experimental data with the Cole–Cole expression at 323, 363 and 383 K as shown by the solid lines. The values of m as obtained from the fitting vary from 0.8 to 0.85. The complex impedance plane plots are shown in the inset of Fig. 6. It is observed that the centers of the semi-circles at the measured temperatures lie below the real axis which indicates the non-Debye behavior of the relaxation process, also confirmed from the values of m (for Debye process m = 1).

If we plot the Z″(ω, T) data in scaled coordinates, i.e., Z″(ω, T)/Z″m and log(ω/ω m), where ω m corresponds to the frequency of the peak value of Z″ in the Z″ versus log ω plots, the entire data of imaginary part of impedance can collapse into one master curve, as shown in Fig. 7. The scaling behavior of Z″ clearly indicates that the relaxation mechanism in the sample is nearly temperature independent.

AC conductivity

If one assumes that all the loss in the dielectric material is due to conductivity, the frequency-dependent conductivity can be expressed as:

$$\sigma_{\text{AC}} = \varepsilon_{0} \varepsilon^{\prime}\omega \tan \delta$$
(4)

where ε 0 is the permittivity in free space, ε′ is the real part of the dielectric constant, tan δ is loss tangent and ω is the angular frequency.

Figure 8 shows the log–log plot of frequency-dependent conductivity spectra at various temperatures. A plateau is observed in the spectra, i.e., a region where σ AC is independent of frequency and the extrapolation of this part towards lower frequency gives the DC value of conductivity. The plateau region extends to higher frequencies with increasing temperatures. At low frequencies, random diffusion of charge carriers via hopping gives rise to a frequency-independent conductivity. At higher frequencies, σ AC exhibits dispersion, increasing in a power law fashion and eventually becoming almost linear. The real part of conductivity spectra can be explained by the power law defined as (Hairetdinov et al. 1994):

Fig. 8
figure 8

Frequency dependence of the conductivity (σ) for CdO at various temperatures, where the symbols are the experimental data points and the solid lines represent the fitting to Eq. (5). The Arrhenius plots of the DC conductivity (σ DC) are shown in the inset for CdO

Full size image
$$\;\sigma = \sigma_{\text{DC}} \left[ {1 + \left( {\frac{\omega }{{\omega_{\text{H}} }}} \right)^{\text{n}} } \right]$$
(5)

where σ DC is the DC conductivity, ω H is the hopping frequency of the charge carriers, and n is the dimensionless frequency exponent. The experimental conductivity spectra of CdO are fitted to Eq. (5) with σ DC and ω H as variable, keeping in mind that the value of parameter n is weakly temperature dependent. The best fit of the conductivity spectra is shown in Fig. 8 by solid lines. The values of σ DC obtained from low-frequency plateau follow Arrhenius law, given by

$$\sigma_{\text{DC}} = \sigma_{0} \exp \left( {\frac{{ - E_{\sigma } }}{{k_{\text{B}} T}}} \right)$$
(6)

where σ 0 is the pre-exponential factor. The activation energy of 0.23 eV extracted from the Arrhenius plot (inset of Fig. 8) indicates that the conduction mechanism may be primarily due to the hopping of the electrons in CdO.

Electric modulus

The frequency (angular) dependence of M′ (ω) and M″ (ω) for CdO as a function of temperature is shown in Fig. 9. M′ (ω) shows a dispersion tending towards M ∞ (the asymptotic value of M′ (ω) at higher frequencies), while M″ (ω) exhibits a maximum (M″m) centered at the dispersion region of M′ (ω). It may be noted from Fig. 9 that the position of the peak M″ m shifts to lower frequencies as the temperature is decreased. The frequency region below peak maximum M″m determines the range in which charge carriers are mobile on long distances. At frequency above peak maximum M″m, the carriers are confined to potential wells, being mobile on short distances. The frequency ω m (corresponding to M″m) gives the most probable relaxation time τ m from the condition ω m τ m = 1. The most probable relaxation time also obeys the Arrhenius relation as shown in the inset of Fig. 9 and the corresponding activation energy E τ = 0.2 eV which is found to be close to the activation energy E σ for DC conductivity (= 0.23 eV). Such a value of activation energy suggests a hopping type of conduction in CdO.

Fig. 9
figure 9

Frequency dependence of the M′ and M″ of CdO at various temperatures. The Arrhenius plots of M″ are shown in the inset for CdO

Full size image

Conclusions

The frequency-dependent dielectric dispersion of CdO nanoparticles synthesized by soft chemical method is investigated in the temperature range from 313 to 393 K for the first time. The average particle size analyzed by TEM is found to be ~45 nm. The band gap obtained from the UV–visible spectrum is found to be of 2.36 eV. The Cole–Cole model is used to describe the dielectric relaxation of the system. The most probable relaxation time follows the Arrhenius law with activation energy of 0.23 eV. The electrical data are also analyzed in the conductivity and electric modulus formalism. The frequency-dependent AC conductivity spectra follow the power law. The scaling behavior of the imaginary part of impedance spectra suggests that the relaxation describes the same mechanism at various temperatures.