Process modeling and evaluation of petroleum refinery wastewater treatment through response surface methodology and artificial neural network in a photocatalytic reactor using poly ethyleneimine (PEI)/titania (TiO₂) multilayer film on quartz tube

Abstract

In this study, poly ethyleneimine (PEI)/Titania (TiO₂) multilayer film on quartz tubes have been successfully fabricated via a layer-by-layer (LbL) self-assembly method. Scanning electron microscopy (SEM) and Brunauer-Emmett-Teller (BET) surface area analysis were carried out for characterization of the layers on quartz tube. The SEM pictures showed that the film surface is smooth and uniform. The BET characterization verified the formation of multilayer thin film. The photocatalytic activity of the PEI/TiO₂ multilayer deposited on the quartz tubes was evaluated in the treatment of raw petroleum refinery wastewater (PRW) under UV light irradiation in three annular photocatalytic reactors. This study examined the impact of initial chemical oxygen demand (COD) concentration, H₂O₂ concentration, pH and reaction time on the PRW treatment and the results were used to generate both a response surface methodology (RSM) model and an artificial neural network (ANN) model. Maximum COD removal (98 %) was achieved at the optimum conditions (initial COD concentration of 300 mg/l, hydrogen peroxide concentration of 8.8 mM, pH of 5 and reaction time of 120 min). A comparison between the model results and experimental data gave a high correlation coefficient (R ²_ANN  = 0.9632, R ²_RSM  = 0.943) and showed that two models were able to predict COD removal from PRW by PEI/TiO₂/UV process. However, ANN model was superior to RSM model with higher value of coefficient of determination (0.9632_ANN > 0.94_RSM) and the lower root mean square error (RMSE) (3.377_AAN < 3.569_RSM). The average percentage error for ANN and RSM models was 0.18 and 0.73, respectively, indicating the superiority of ANN in capturing the nonlinear behavior of the system. It was clear that the best networks were able to predict the experimental responses more accurately than the multiple regression analysis.

Introduction

The petroleum refinery and petrochemical industries are two of the largest industries in Iran [8]. Wastewater generated by petroleum industries is very complex, and includes several inorganic and organic components, such as emulsified oil, sulfides, ammonia, cyanides and especially phenol and phenolic derivatives [41]. Due to the nature of the pollutants included in petrochemical and oil refinery wastewater, its treatment is a challenging issue and several different physical–chemical, mechanical and even biological conventional treatment processes have been tested for its restoration in the past.

A wide diversity of procedures, such as API separators, specific biological systems, ultra-filtration, fenton and photo fenton processes [8], absorption [39] and other methods [34, 36] have been used for the reduction of chemical oxygen demand (COD), total petroleum hydrocarbon (TPHs), biochemical oxygen demand (BOD5) and many others in the effluent with some success.

Although these conventional techniques have been commonly used, there are several drawbacks [31]. The main drawback of these techniques relates to the disposal of the spent contaminated activated sludges, generation of toxic by-products, severe operation conditions (e.g., high temperature and high pressure) and the slow reaction rates, which mean higher energy consumption and expensive running cost.

In the last decade, advanced oxidation processes (AOPs) including heterogeneous (i.e., semiconductors such as TiO₂ and ZnO in the presence of UV light) and homogenous (i.e., Fenton’s reagent, H₂O₂ and ozone) processes have gained the interest of researchers for the elimination of dangerous organic pollutants from various wastewaters [19]. Among AOPs, TiO₂ has been widely used because of its various merits such as low toxigenicity, relative low cost, favorable band gap energy, high chemical stability and activity [37].

In previous studies, the majority of experiments to date have used small TiO₂ particles suspended in the discontinuous slurry photoreactors. However, these reactors have many practical and economical disadvantages related to the filtration and reuse of the catalyst and also the inefficient illumination of the particles, resulting in an actually higher operating cost and lower reactivity, respectively. Moreover, recent studies have raised concerns about the potential toxicity of titanium dioxide nanoparticles. Consequently, many research efforts have been dedicated to the development of immobilized systems following different approaches, synthesis routes and support materials [1, 26]. Catalyst can be immobilized with various procedures such as, sputtering, dip coating, sol–gel synthesis, and chemical vapor deposition method, spin coating, etc. Among these techniques, the layer-by-layer self-assembling (LBL-SA) method that was pioneered by Decher [24], is a simple and effective method for constructing organic/inorganic films via alternate deposition of components (polyelectrolytes or nanoparticles) with opposite electrical surface charge or hydrogen-bonding groups from dilute solutions [10].

The conventional “one-factor-at-a-time” approach is laborious and time consuming. Moreover, it seldom guarantees the determination of optimal conditions. These limitations of a single factor optimization process can be overcome by using empirical methods. Recently, response surface methodology (RSM) and artificial neural network (ANN) methods have been used jointly for both modeling and optimization purposes in environmental studies.

Response surface methodology is a series of experimental design, analysis, and optimization techniques that originated in the work by Box and Wilson in 1951 [6]. The main idea of response surface methodology is to optimize an unknown and noisy function by means of simpler approximating functions that are valid over a small region using designed experiments. By moving the operating conditions of a process using a sequence of experimental designs, process improvement is achieved. Response surface methodology has important applications in industrial designing, developing, and improving existing product. It also can be useful for the formulation of new products. It defines the effect of the controlling or independent variables, alone and in combination on the response, in the processes [3, 7, 20, 21, 23, 27, 33, 40].

With the interdisciplinary development of modern computational technologies, artificial neural networks (ANNs), as typical artificial intelligence (AI) algorithms, have become an attractive approach for modeling highly complicated and nonlinear system [12, 38, 43]. The ANN can be described as a group of simple processing elements called neurons arranged in parallel layers that are fully interconnected by weighted connections. One of the most important characteristics of neural networks is learning. Artificial neural networks have two operation modes, training mode and normal mode [30]. In training mode, adjustable parameters of the networks are modified. In normal mode, the trained networks are applied for simulating the outputs [30].

An ANN attempts to learn the relationships between the input and output data sets in the following way: during the training phase, input/output data pairs, called training data, are introduced into the neural network. The difference between the actual output values of the network and the training output values is then calculated. The difference is an error value which is decreased during the training by modifying the weight values of the connections. Training is continued iteratively until the error value has reached the predetermined training goal [22].

It is believed that ANN would require much more number of experiments (number of patterns) than RSM to build an efficient model. But in fact, the ANN can also work well even with relatively less data, if the data are statistically well distributed in the input domain, which is the case with DOE. This experimental data of RSM should be sufficient to build effective ANN model. There are few case studies available in the literature where models were developed by RSM and ANN using same DOE; and ANN models have consistently worked better than RSM [5, 12, 17].

The major advantages of ANN compared to RSM are (1) it does not need a prior specification of appropriate fitting function and (2) ANN is capable of universal estimation, i.e., ANN can estimate nearly all types of nonlinear functions such as quadratic functions, where RSM is suitable only for quadratic estimations [9].

In this study, poly (ethyleneimine) (PEI)/titania (TiO₂) multilayer film on quartz tubes was assembled through the layer-by layer (LbL) self-assembly method and were applied in PRW treatment and characterization methods were carried out for determination of the morphology and roughness of the prepared thin films on quartz tube. Then ANN and RSM have been used to compare the performances of the statistical- and artificial intelligence-based optimization techniques. The predictive models given by RSM and ANN have also been compared for their experimental and predicted response factor values, lower root mean square error (RMSE), average error percentage (Er  %), and coefficients of determination (R²).

Experimental

Materials

The chosen catalyst of TiO₂, mainly anatase (90 % anatase and 10 % rutile, Degussa P 25) with a particle size of 30 nm and Cationic poly (ethyleneimine) (PIA, MW = 7.5 × 10⁵ g/mol) were both purchased from Aldrich and used as-received (Sigma, St. Loius, MO, USA). Hydrogen peroxide (30 %, v/v) was obtained from Merck Co. (Darmstadt, Germany). Sulfuric acid and sodium hydroxide (Merck Co. Darmstadt, Germany) solutions were used to adjust the pH of wastewater samples. For dipping solutions of the LBL-SA method,PIA polymers were dissolved in DI water to the concentration of 0.01 M. The pH of the solution was also adjusted with HCl and NaOH to the required pH.

Preparation of multilayered film by the LbL technique

Quartz tubes were cleaned by immersing them in the mixture of methanol and concentrated HCl (1:1) for 30 min and then in the piranha solution (70/30 v/v of concentrated H₂SO₄ and 30 % H₂O₂) to create negatively charged surfaces for 24 h. The substrate was finally rinsed several times with DI water and then dried with N₂ flushing. To make a doping solution for the LBL-SA process, TiO₂ nanoparticles were dispersed in DI water (pH 8) to yield a 0.1 % wt. transparent solution in which TiO₂ nanoparticles had a negatively charged surface [31].

Layer-by-layer self-assembled thin films were fabricated by sequential deposition of oppositely charged polymer and TiO₂ nanoparticles at room temperature. For a single nanoparticle layer in the film, for example, a negatively charged substrate was sequentially dipped in a cationic PEI (0.01 M) and then in ananionic TiO₂ solution (0.1 wt.  %), yielding a (PEI/TiO₂) thin film. By controlling this dipping sequence, LBL-SA thin films of PEI/TiO₂ (PEI/TiO₂) n−1 were fabricated with a desired number of TiO₂ nanoparticle layers (n). For each layer, the substrate was dipped into the solution for 15 min, and washed by distilled water, and then dried in the temperature of 100 °C.

Photoreactor configuration

Figure 1 shows the experimental setup of the photoreactor for the treatment of PR Win continuous mode operation. This photoreactor was equipped with three thin gap annular photocatalytic reactors in series with the working volume of 2,850 ml [total liquid volume of each of photoreactor was 950 ml excluding volume of the quartz tube (40 tubes in each of the reactor) inside the photoreactor]. The UV lamps (22 cm body length and 16 cm arc length) were mercury 400 W (200–550 nm) lamps. The UV lamp was installed in the inner quartz tube of each reactor and was totally immersed in the reactor. Therefore, the maximum light utilization was achieved. At first, PRW flow flowed sequentially through each annular reactor one by one by means of peristaltic pump from the wastewater reservoir and subsequently discharged to the settling tank. Hydrogen peroxide was added to the first reactor at a certain concentration. This photoreactor was operated under room temperature (22 ± 2 °C). The air was introduced into the each reactor with a bubble air diffuser at the bottom of the each reactor, and the air flow rate was controlled with an air flow-meter connected to blower (aeration rate, 4 l/min). The laboratory tests were accomplished using the pre-treated refinery wastewater samples (after flotation and coagulation). PRW was randomly collected from an oil refinery plant located in the city of Kermanshah, Iran. The COD and BOD5 of the PRW sample were about 750 ± 60 and 300 ± 26 mg/l, respectively, and it was diluted to the required initial concentrations. Other specifications were pH: 6.7, turbidity: 115 NTU, phenol concentration: 96 mg/l and total dissolved solids: 645 mg/l. The concentrations of chemical oxygen demand (COD) and BOD were determined by using standard methods [4].

Fig. 1

Photoreactor set up

Characterization of the PEI/TiO₂ multilayer film

A surface morphology of PEI/TiO₂ thin films was studied by scanning electron microscopy using a Philips XL30 microscope at an accelerating voltage of 20 kV. After oven-drying of the thin film for 12 h, the sample was coated with a platinum layer using an SCDOOS sputter coater (BAL-TEC, Sweden) in an argon atmosphere. Subsequently, the sample was scanned and photomicrographs were obtained. Also the surface properties of PEI/TiO₂ thin films were visualized using an atomic force microscope (Mobile S, Nanosurf, Switzerland). Explorer atomic force microscopy was in the noncontact mode, using high resonant frequency (F0 170 kHz) pyramidal cantilevers with silicon probes having dynamic force.

N₂ adsorption/desorption isotherms (BET) at 77 K were measured on Belsorp mini II (Bel Japan). Samples were placed in a tube under N₂ atmosphere and then outgassed for 2 h at 80 °C prior to the measurements. X-ray diffraction (XRD) patterns of samples were recorded using EQUINOX diffractometer (Inel Company) operating with a Cu anode and a sealed X-ray tube. The 2θ scans were recorded at several resolutions using CuKα radiation of wavelength 1.548 Å in the range of 20–80 with 0.05 step size.

Predictive modeling and optimization methods

Artificial neural network

A typical neural network structure used in this study is shown in Fig. 2. As shown in the figure, the ANN structure consists of an input layer (independent variables), hidden layer (hidden) and output layer (dependent variables), so that these layers are connected together by connections with different weights.

Fig. 2

The ANN optimized structure in three layered feed—forward back propagation neural network for COD removal modeling

The task of the hidden layer makes a connection between input and output layer. One or more neurons can be putted in the hidden layers. Network with a hidden layer is capable of deriving the nonlinear equations from presented data belong to that.

The topology of an artificial neural network is determined by the number of its layers, number of nodes in each layer and the nature of transfer functions. The most important step in the development of the model probably is optimization of ANN topology. We used three layered feed-forward back propagation neural network (4:5:1) for modeling of COD removal (Fig. 2).

In this study, input variables to the feed-forward neural network were as follows: initial COD conc. (mg/l), hydrogen peroxide (mM), pH and reaction time (min). The percentage of COD removal was chosen as an experimental response or output variable. The training parameters and the range of the data used for ANN in this investigation are listed in Tables 1 and 2, respectively.

Table 1 ANN training parameters

Table 2 Model variables and their ranges. (the range of the data used for ANN)

In this work, we tested different numbers of neurons, from 2 to 10, in the hidden layer. Each topology was repeated three times to avoid random correlation due to the random initialization of the weights. Table 3 demonstrates the relation between the network error and the number of neurons in the hidden layer. The root mean square error (RMSE) and the sum of squared error (SSE) were used as the error function. RMSE and SSE measure the efficiency of the network according to the following equation:

Table 3 Effect of the number of neurons in the hidden layer on the performance of the neural network

$$\text{RMSE}=\sqrt{\frac{{\sum }_{i=1}^n{\left(y_{i,\text{predic}}-y_{i,exp}\right)}^2}{n}}$$

(1)

$$\text{SSE}=\sum _{i=1}^n{\left(y_{i,\text{predic}}-y_{i,exp}\right)}^2$$

(2)

Also in Table 3, we see the correlation coefficient which represents the ratio between the data predicted by the neural network and real data:

$$R^2=1-\frac{{\sum }_{i=1}^{i=n}{\left(y_{i,\text{predic}}-y_{i,exp}\right)}^2}{{\sum }_{i=1}^{i=n}{\left(y_{i,exp}-y_{\text{m}}\right)}^2}$$

(3)

where n is the number of data point, $y_{i,\text{predict}}$ the network prediction, $y_{i,exp}$ experimental response, $y_{\text{m}}$ average actual and i is an index of data. We can see that the performance of the network stabilized after inclusion of an enough number of hidden units just about eleven. As can be seen from Table 3, the root mean square error and the sum of squared error are minimum just about five neurons. The highest correlation coefficient for the network was five hidden neurons, which was 0.9632 with the RMSE of 0.03377 and SEE of 0.03144. The R² value is in reasonable agreement with the “R ²_adj ” values of 0.9619, showing a very good agreement between the predicted and actual data.

Response surface methodology

RSM is an empirical statistical modeling technique employed for multiple regression analysis using quantitative data obtained from properly designed experiments to solve multivariate equations simultaneously [23, 28, 29].

A central composite experimental design (CCD) for independent variables involving four numerical factors: initial COD concentration (a), initial H₂O₂ concentration (b), pH (c) and reaction time (d) were used. The independent variable selected for the optimization was COD removal. Regression analysis was performed on the data obtained from the experiments. After conducting the experiments, the relationship between the dependent and independent variables was calculated using the following equation [2, 15, 18, 19, 44]:

$$Y={\mathit{\beta }}_0+{\mathit{\beta }}_i{X}_i+{\mathit{\beta }}_j{X}_j+{\mathit{\beta }}_{ii}{X}_i^2+{\mathit{\beta }}_{jj}{X}_j^2+{\mathit{\beta }}_{ij}{X}_i{X}_j+\dots$$

(4)

where, Y, i, j, β, X are chosen process response, linear coefficient, quadratic coefficient, regression coefficient and coded independent variables, respectively. Model terms are chosen or neglected based on the probability of error (P) value with 95 % confidence level. The results obtained from CCD were entirely examined by means of analysis of variance (ANOVA) by Design Expert software Table 4.

Table 4 Estimated regression coefficients and corresponding to ANOVA results from the data of central composite design experiments before elimination of insignificant model terms

Data preparation

ANN model is good as interpolating data, but not extrapolating. Therefore, to achieve a valid ANN model, the data selected for training should cover the full range of input random variables. However, selection of appropriate algorithms and transfer functions is essential to design a suitable ANN model; otherwise, the output results will be unreliable. Transition function of Tausig has been used in the hidden layer and transition function of linear has been used in output layer.

Since the sigmoidal transfer function was used in the hidden layer, before the training, it is better that inputs and targets are scaled to always be in a specified range. Therefore, all data input (Y _i ) in the area of 0.1–0.9 is normalized as follows (Y_norm):

$$Y_{\text{norm}}=0.8\left(\frac{Y_i-Y_{i,\text{min}}}{Y_{i,\text{max}}-Y_{i,\text{min}}}\right)+0.1$$

(5)

where Y_i,min and Y_i,max are extreme values of Y _i [42]. After the training of the network, all output reverted to its original scale and then the response predicted by the empirical results were compared to experimental design.

Results and discussion

PEI/TiO₂ multilayer film characterization

The LbL-TiO₂ thin films were characterized by SEM and AFM to evaluate the surface morphology and the effectiveness of the multilayer assembly technique.

Figure 3a, b shows the top view surface morphology of PEI/TiO₂ thin films that were examined by scanning electron microscope. A close view surface of the film shows a flat and dense surface morphology of polyelectrolytes and distributed TiO₂ nanoparticles embedded in the film.

Fig. 3

SEM images: a 20 kV, ×20 K, b 20 kV, ×50 K, c N₂ adsorption/desorption isotherms for the PEI/TiO2 multilayers thin film, d X-ray diffraction patterns of samples and e AFM image

Figure 3c showed the N₂ adsorption/desorption isotherms for thin film. This adsorption isotherm is apparently classified as the type III isotherm [14]. On the other hand, for this kind of isotherm the gradient once decreased around 0.1–0.3 of P/P₀ and then increased from 0.7 to 1.0 of P/P₀. These results suggest the presence of at least two steps of pore filling, one at very low P/P₀ associated with the pores of molecular dimensions for effectively trapping the light into the inner layers and the other at a 0.7–1.0 of P/P₀ associated with pores involving quasi-multilayer formation that proved the formation of PEI/TiO₂ thin films which was our purpose [35]. The XRD results of coated TiO₂ before and after coating did not show any significant changes in the structure of photocatalysts as a consequence of the coating and calcination processes (Fig. 3d).

The PEI/TiO₂ multilayer thin films were further examined by AFM to determine the surface roughness. Figure 3e shows the image for a thin film sample. It was from topography scan forward that the roughness of the film was around 120 nm. With an increase in the number of multilayers, the roughness of some parts of the surface amplified because of farther deposition of TiO₂ in these sites, which is due to the increase in the amount of TiO₂ deposited per each layer.

Predictive modeling with ANN

The design of experiments, which is used for training the network and respective experimental removal percentages is given in Table 5.

Table 5 Central composite design (CCD) matrix of independent variables and their corresponding experimental and predicted values

ANN-based process model was developed using the most popular feed-forward ANN architecture namely, multi-layer perceptron (MLP) with logistic sigmoidal function. The MLP network has four input nodes representing independent variables and one output node representing the COD removal (%). The data partitioning as training set and test had been done to avoid over training and over parameterization. The training cycle was performed for varying numbers of neurons in the hidden layer and also for various combinations of ANN-specific parameter like learning rate, random initialization. The generalization capacity of the model was ensured by selecting the weights resulting in the least test set RMSE.

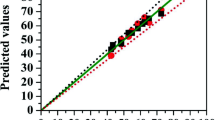
Figure 3 shows a comparison between calculated and experimental values of the output variable for data set by using neural network model. Plot in this figure has correlation coefficient of 0.951 and indicates the reliability of the model.

The generalization and predictive capabilities of both RSM and ANN were compared. ANN model was superior to RSM mode with higher value of coefficient of determination (0.9632_ANN > 0.94_RSM) and lower root mean square error (RMSE) (3.377_AAN < 3.569_RSM). Desai et al. [9] have also reported the average percentage error for ANN and RSM models and the CC after employing ANN with genetic algorithm approach for optimization of fermentation process parameters, the results indicating the superiority of ANN in capturing the nonlinear behavior of the system.

Response surface methodology

To examine the combined effect of four different independent variables, on COD removal, a central composite factorial design of 2⁴ = 16 plus 6 centre points and (2 × 4 = 8) star points leading to a total of 30 experiments were performed. Second-order polynomial equation was used to correlate the independent process variables, with COD removal. The second-order polynomial coefficient for each term of the equation determined through multiple regression analysis using the Design Expert. The same DoE, which used in ANN-based model development, was also used to build the RSM model. The results were analyzed by using ANOVA, i.e., analysis of variance suitable for the experimental design. The results are shown in Table 4. The Model F-value of 66.28 implies that the model is significant. Model F-value is calculated as ratio of mean square regression and mean square residual. Model P value (Prob > F) is very low (0.0001). This resignifies the significance of the model [9].

The P values were used as a tool to check the significance of each of the coefficients, which, in turn, are necessary to understand the pattern of the mutual interactions between the test variables. The corresponding P values, along with the coefficient estimate, are given in Table 4.

Comparison of RSM and ANN

Predictive capabilities

The ANN and RSM model were compared for DoE, using which the both models were prepared. The comparison was made on the basis of various parameters such as average percentage error, RMSE and R². Korany et al. [16] compared experimental and predicted response factor values, mean of squares error (MSE), average error percentage (Er %) and squared coefficients of correlation (r²). Their results showed that the best networks were able to predict the experimental responses more accurately than the multiple regression analysis. The predicted values by ANN as well RSM model are tabulated in Table 5.

Figure 4 shows the comparative parity plot for ANN and RSM predictions for DoE. The MLP-based model had fitted the experimental data with an excellent accuracy. This higher predictive accuracy of ANN can be attributed to its universal ability to approximate non-linearity of the system, whereas RSM only restricted to second-order polynomial. The comparative values average percentage error, RMSE and R² were given in Table 6.

Fig. 4

RSM and ANN predicted vs. experimental data

Table 6 Comparison of predictive capacity of RSM and ANN

Sensitivity analysis

As shown in Table 4, the model term of (A) has the largest coefficient (9.03) which indicates that COD concentration is the most dominating factor. This model term has significant effect on the system compared to other interactions. ANN being a black box model, it does not give such insights of the system directly. Black-box neural network model are allowed to acquire the relationships that exist between important variables and was used to predict the system variables. Except for a small network, it is almost impossible that the models describe the equations in the short-term and easily. Subsequently, the practical implementation of artificial neural networks is difficult. Desai et al. [9] found that ANN is equally efficient in sensitivity analysis and interestingly quite comparable to the coefficient of first-order terms in the quadratic RSM equation.

However, the nature of the black-box for ANN, one can perform sensitivity analysis for neural networks with different input variables on the results obtained from the model [32]. But there are numerous methods available which give the sensitivity analysis of the system using the inherent nature of ANN. Using Eq. 5, the effect of each input variable on the output variable modeling matrix was obtained by the network weight [11].

$$I_j=\frac{{\sum }_{m=1}^{m=N_h}\left(\left(\left|W_{jm}^{jh}\right|/{\sum }_{k=1}^{N_i}\left|W_{km}^{ih}\right|\right)\times \left|W_{mn}^{ho}\right|\right)}{{\sum }_{k=1}^{k=N_h}\left\{{\sum }_{m=1}^{m=N_h}\left(\left|W_{km}^{ih}\right|/{\sum }_{k=1}^{N_i}\left|w_{km}^{ih}\right|\right)\times \left|W_{mn}^{ho}\right|\right\}}$$

(6)

where I _j is the relative importance of the jth input variable on the output variable, N _i and N _h are the numbers of input and hidden neurons, respectively; W’s are connection weights, the superscripts ‘i’, ‘h’ and ‘o’ refer to input, hidden and output layers, respectively; and subscripts ‘k’, ‘m’ and ‘n’ refer to input, hidden and output neurons, respectively.

Effect of the variables studied

To gain a better understanding of the interaction effects of variables on COD removal efficiency, two and three dimensional contour plots for the measured response were formed based on the model (Eq. 4). Figure 5a shows the plots of the model for variation in COD removal as a function of initial COD concentration and reaction time for H₂O₂ concentration of 8.8 mM and initial pH of 6. It can be seen from Fig. 5a that the percentage of COD removal decreases as the initial concentration of the COD increases. The percentage removal was gradually decreased from 101.64 % (with standard deviation of 4.92) to 71.8 % as the COD concentration increased from 300 to 700 mg/l. This can be explained in terms of either saturation of the limited number of accessible active sites on the photocatalyst surface that leads to a decrease in degradation efficiency, or poisoning (deactivation) of the active sites of the catalyst.

Fig. 5

3D and counter plots of COD removal efficiency (%) as the function of a initial COD concentration and reaction time (min), b H₂O₂ (mg/l) and reaction time(min) and c pH and reaction time (min)

Three dimensional (3D) response surface and contour plots for COD removal as a function of initial H₂O₂ concentration and reaction time are presented in Fig. 5b. Such plots present the function of two variables, maintaining all others at the fixed levels (usually X _i  = 0). It could be seen from the figure that the degradation efficiency has increased by increasing the H₂O₂ concentration up to 8.8 mM and then declined as H₂O₂ loading increased.

The effects of the pH and reaction time on the COD removal are shown in Fig. 5c. The examination of the figure shows that the pH of the emulsion has a crucial effect on performance. A reverse impact of the pH on COD removal was observed as the variable increased (Fig. 5c). As shown in this figure, an increase in pH (from 3 to 6) increases COD removal, while further increment in the variable (from 6 to 9) decreased the response. So, the optimum pH for COD removal was found to be in the range of 4.5–6. The pH-effect is related to the point of zero charge (pzc) of TiO₂ at pH 6.2 and charge of organic maters in different pH [25]. In acidic media (pH <6.2), the surface of TiO₂ is positively charged, whereas it is negatively charged under alkaline conditions (pH >6.2).

Since the majority of organic maters in PRW are phenol and phenolic derivatives being negatively charged due to the OH groups which are ionized in water, their electrostatic attraction to the TiO₂ surface is favorable in acidic solution and forbidden in alkaline media due to the columbic repulsion between the negatively charged surface of TiO₂ and the organic molecules. From Fig. 5a–c, it can be seen that the most desirable operating conditions were initial COD concentration of 300 mg/l, H₂O₂ concentration of 8 mM, pH of 5 and reaction time of 120 min.

Conclusion

Poly ethyleneimine (PEI))/titania (TiO₂) multilayers films deposited on quartz tubes with smooth and uniform morphology were fabricated by LbL electrostatic self-assembly method. The LbL TiO₂ thin film was characterized by SEM and BET analyses. SEM images indicated that the film surface is smooth and uniform. The BET characterization method proved the multi-layer preparation. In continuation, the advantages of artificial neural network in comparison with response surface methodology were shown. By using central composite design, the number of required experiments was obtained. The predictive and generalization capabilities of both RSM and ANN were compared using separate dataset. The correlation coefficients for ANN and RSM were 0.96 and 0.94, respectively. The modeling capability of ANN has shown its superiority over RSM with comparative less value of RMSE and average percentage error.