Performance of multistage-fractured horizontal wells with secondary discrete fractures in heterogeneous tight reservoirs

Abstract

A significant portion of tight sandstone reservoirs commonly displays intricate fluvial channels or fault systems. Despite various attempts at analytical/semi-analytical modeling of multistage-fractured horizontal wells (MFHWs) in unconventional reservoirs, the majority of studies have focused on scenarios with homogeneous original physical properties, neglecting cases where MFHWs traverse multiple regions in channelized heterogeneous reservoirs. Comprehending the influence of heterogeneous and leaky faults on the performance of MFHWs is essential for efficient development. This study presents an innovative semi-analytical model to analyze the pressure transient behavior of MFHWs with secondary fractures as they traverse multiple regions in banded channel heterogeneous reservoirs, particularly considering the presence of partially-communicating faults. The approach combines the source method and Green’s function method to obtain solutions, introducing a novel technique for discretizing fractures without discretizing interfaces. The effects of the reservoir heterogeneity, partially-communicating faults and fractures system on pressure behavior are analyzed. The results indicate that the pressure behavior of MFHWs passing through regions with different physical properties exhibits distinctive characteristics, differing from both the homogeneous case and the heterogeneous cases where the well does not traverse distinct regions. Permeability heterogeneity influences the curves of all other flow regimes, except the early and late flow regimes. Faults affect transient pressure behavior only when not positioned in the middle of each two primary fractures. Region area heterogeneity primarily influences the medium flow regimes. This work provides valuable insights into the performance of MFHWs in channelized heterogeneous reservoirs, offering technical support for well testing in these reservoirs.

Introduction

Unconventional tight oil/gas reservoirs have significantly contributed to the global hydrocarbon supply over the past decade. MFHWs are commonly employed for developing these reservoirs due to their extremely low permeability. It has been postulated that fractures do not have an ideal bi-wing shape but instead exhibit induced secondary fractures during the fracturing process. (Daneshy 2003; Weng et al. 2014; Murillo and Salguero 2016; Xiao et al. 2023). Additionally, a substantial portion of the tight reservoirs displays complex fluvial channels, which are highly heterogeneous and often characterized by laterally discontinuous reservoir units (Cuba et al. 2013; Ramirez et al. 2012; McDowell and Plink-Björklund 2013). Moreover, complex fault distributions are also a common characteristic of tight sandstone reservoirs (Kuchuk and Habashy 1997; Dijk et al. 2020; Cui et al. 2021). Consequently, the MFHWs in these reservoirs may intersect various partial hydrologic barriers (e.g., partially communicating faults), and the properties of the formation and generated secondary fractures may also respond differently at different fracturing stages.

Pressure transient analysis is an effective method for characterizing the properties of both hydraulic fractures and the reservoir matrix. Numerous analytical and semi-analytical models have been previously proposed in the literature to extensively investigate the behavior of MFHWs in unconventional reservoirs. In the early 1990s, several semi-analytical models based on the source method were proposed for MFHWs in homogeneous reservoirs. In these models, fractures were considered as simplified bi-wing uniform flux or infinite-conductivity fractures. (Guo et al. 1994; Horne and Temeng 1995; Wan and Aziz 1999; Raghavan et al. 1997). Subsequently, these semi-analytical models were expanded to simulate a more complex bi-wing fractures system, encompassing fractures with various conductivity, inclined angles, intervals, and lengths, in both infinite and closed box-shaped reservoirs (Zerzar et al. Zerzar and Bettam 2003; Al Rbeawi and Tiab 2012; Jia et al. 2014; Yao et al. 2013; Wang 2014; Ren and Guo 2015).

Analytical models were proposed based on various forms of one-dimensional linear flow concerning MFHWs with stimulated reservoir volume (SRV). Brown et al. (2011) firstly established an analytical tri-linear flow model for MFHWs with SRV. In this model, the MFHWs-reservoir system is divided into three rectangular regions: the finite-conductivity hydraulic fractures region, SRV region, and USRV region, with linear flow assumed in all these regions. Based on Brown’s tri-linear flow model, several linear flow models have been developed to capture a broader range of reservoir/fracture properties, and flow regime sequences, such as five-region model (Stalgorova and Mattar 2013), enhanced five-region model (Deng et al. 2015; Heidari Sureshjani and Clarkson 2015; Tao et al. 2018; Wang et al. 2023), and seven-region model (Zeng et al. 2017, 2018, 2019; Guo et al. 2023). While these linear flow models demonstrate high computing efficiency and have been proven accurate for simulating some simple MFHWs-reservoir systems, they fall short in capturing the intricacies of real fracture networks, including irregular spatial distribution and complex interconnected scenarios of fractures. Additionally, these linear flow models are unable to fully characterize the entire pressure behavior and flow regimes, such as the pseudo-radial regime, of the MFHWs-reservoir system.

Unlike the one-dimensional linear flow modelling method, the source method can explicitly simulate the complex fracture systems and capture the entire pressure behavior and flow regimes of the MFHWs- reservoirs system. Lin and Zhu (2012) and Hwang et al. (2013) established semi-analytical models to investigate the behavior of MFHWs, considering infinite- conductivity secondary fractures. Zhou et al. (2014) introduced a semi-analytical approach that combines numerical fracture solutions with analytical reservoir solutions for transient-behavior analysis. Chen et al. (2016a, 2016b, 2018) developed a semi-analytical model for MFHWs, considering orthogonal finite-conductivity secondary fractures by discretizing the fracture networks into multiple cells. They also analyzed the flow regimes and pressure behaviors of such fracture networks. Jia et al. (2016) and Cheng et al. (2017) introduced semi-analytical models for the transient behaviors of MFHWs with complex secondary fracture networks. In their models, fracture solutions were obtained using the finite-difference method, leading to a significant increase in computation cost. Chen et al. (2019) introduced a semi-analytical method to investigate the transient behaviors in fractured reservoirs, considering discrete natural-fracture and hydraulic-fracture networks simultaneously. In their subsequent work (Chen and Yu 2022), they further developed a discrete semi-analytical model to account for more complex fracture distribution cases, including wellbore-isolating/wellbore-connecting fracture networks, wellbore-isolating/wellbore-connecting fractures, and matrix domains. Several authors have also conducted research on semi-analytical models for MFHWs with simplified SRV by considering the SRV as a circular shape enhanced region (Zhao et al. 2014; Xu et al. 2020), a rectangular enhanced region (Medeiros et al. 2008; Zhao 2012; Zhao et al. 2018; Wu et al. 2020) or an arbitrary shape enhanced region (Zhang and Yang 2021; Chu et al. 2022). These works, employing the source method and boundary element method, primarily focused on continuous homogeneous reservoirs.

While numerous analytical or semi-analytical models have been proposed for MFHWs, they have primarily focused on scenarios where the original physical properties of the reservoir are homogeneous. Few studies have explored models for MFHWs in tight heterogeneous reservoirs characterized by channelized or fault systems with linear discontinuity characteristics.

Wang et al. (2017) introduced a semi-analytical model for MFHWs in banded channel heterogeneous reservoirs using the boundary element method. In their approach, the reservoir was divided into several sub-systems, represented as linear assemblies of distinct homogeneous regions. Flow interactions between these regions were resolved by discretizing the interfaces. However, the model did not account for partially communicating faults, a typical characteristic of such heterogeneous tight reservoirs. Additionally, the model only considered orthogonal bi-wing fracture geometry, limiting its effectiveness in capturing complex fracture systems. Moreover, the semi-analytical solutions were obtained through the boundary element method, necessitating interface discretization and increasing computational demands.

Recently, Deng et al. (2022) presented an analytical solution for fluid flows in rectangular bounded anisotropic multi-region linear composite reservoirs, considering partially communicating faults. However, only the case of vertical fractured wells is investigated.

Considering that horizontal wells in heterogeneous reservoirs may intersect numerous partial hydrologic barriers, Shi et al. (2023) proposed a semi-analytical model for a horizontal well intercepting multiple faults in karst carbonate reservoirs. However, the model did not account for hydraulic fractures and flow in the matrix, making it specifically suitable for carbonate reservoirs.

To fill this gap, a semi-analytical model is presented for fluid flows to MFHWs with secondary fractures passing through banded channel heterogeneous reservoirs, particularly considering the presence of partially-communicating faults. The reservoir is a multi-region linear composite system that considers different formation properties in each individual region and partially-communicating faults between regions. Secondary discrete fractures can interconnect the primary hydraulic fractures with different inclinations and lengths, while accounting for the effects of wellbore storage and skin. The solution, an extension of our previous analytical solution for fluid flows in a vertically fractured well in bounded multi-region linear composite reservoirs (Deng et al. 2022), is obtained by applying the source method and Green’s function method, eliminating the need for discretizing the interfaces to reduce computational costs. The performance and relative sensitivity of the solution are finally analyzed using type curves.

Conceptual model

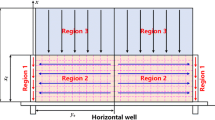
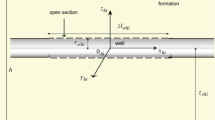
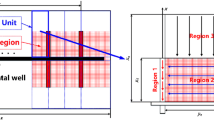
Figure 1 depicts the schematics of the two-dimensional top view of the conceptual model for a multistage-fractured horizontal well with secondary fractures in a banded channel heterogeneous reservoir. The banded channel heterogeneous reservoir is divided into multiple cubical regions along the lateral direction by vertical faults. Each individual region is assumed to be homogeneous and isotropic with uniform thickness, while the physical properties of each region differ from the others. The faults are assumed to be partially communicating with a fault skin. The external boundaries at the top and bottom are closed. A multistage-fractured horizontal well with arbitrarily distributed secondary fractures is positioned in all regions. The primary fractures (PFs) and secondary fractures (SFs) are assumed to have a rectangular shape with constant fracture length, width, and permeability. The system can be treated as a two-dimensional system since both types of fractures are assumed to be fully penetrating.

Fig. 1

Schematic of the two-dimensional top view of the multi-region linear composite model for a multistage-fractured horizontal well with secondary fractures

Other assumptions of the conceptual model include the following:

• 1. Fluids are in single-phase, slightly compressible, with a constant compressibility.

• 2. Isothermal Darcy's law is followed.

• 3. The effects of the gravity and capillary pressure are ignored.

• 4. The initial formation pressure throughout the reservoir is equal to p_i.

• 5. A constant production rate is expected at the MFHWs.

Mathematical model

The multi-region composite matrix systems

The governing differential equations for the two-dimensional pressure distribution in the composite systems with partially-communicating faults are written as

$$\left( {\frac{k}{\mu }} \right)_{j} \frac{{\partial^{2} p_{j} }}{{\partial x^{2} }} + \left( {\frac{k}{\mu }} \right)_{j} \frac{{\partial^{2} p_{j} }}{{\partial y^{2} }} = \left( {\phi C_{{\text{t}}} } \right)_{j} \frac{{\partial p_{j} }}{\partial t}$$

(1)

The initial condition is expressed as

$$p_{j} |_{t = 0} = p_{{\text{i}}}$$

(2)

The connecting conditions between regions with the partially-communicating faults (Abbaszadeh and Cinco-Ley 1995; Rahman et al. 2003; Deng et al. 2022) are

$$\left. {\left( {\frac{kh}{\mu }} \right)_{j} \frac{{\partial p_{j} }}{\partial x}} \right|_{{x = x_{j} }} { = }\left. {\left( {\frac{kh}{\mu }} \right)_{{j{ + }1}} \frac{{\partial p_{{j{ + }1}} }}{\partial x}} \right|_{{x = x_{j} }}$$

(3)

$$\left( {p_{{j{ + }1}} - p_{j} } \right)_{{x = x_{j} }} = \left[ {\frac{{2\mu w_{a} }}{{k_{a} h}}} \right]_{j} \left. {\left( {\frac{kh}{\mu }} \right)_{j} \frac{{\partial p_{j} }}{\partial x}} \right|_{{x = x_{j} }}$$

(4)

The external boundary conditions in x and y direction are

$$\left. {\frac{{\partial p_{1} }}{\partial x}} \right|_{x = 0} = \left. {\frac{{\partial p_{N} }}{\partial x}} \right|_{{x = x_{N} }} { = }0{\kern 1pt} {\kern 1pt}$$

(5)

$$\left. {\frac{{\partial p_{j} }}{\partial x}} \right|_{y = 0} = \left. {\frac{{\partial p_{j} }}{\partial x}} \right|_{{y = y_{{\text{e}}} }} { = }0$$

(6)

Note: $x_{N} { = }x_{{\text{e}}}$where p is the pressure, MPa; p_i is the initial reservoir pressure, MPa; μ is fluid viscosity, mPa·s; k is the reservoir permeability, mD; ϕ is the rock porosity, %; C_t is the total compressibility, MPa^–1; h is the reservoir thickness, m; x and y are the Cartesian coordinates, m; x_j is the distance from the fault j to the original point of the coordinate; x_e is the length of the reservoir, m; y_e is the width of the reservoir, m; k_a and w_a are the permeability and half-width of a fault, respectively. The subscript j represents the region number, j = 1,…, N.

Using the dimensionless variables defined in Table 1, the aforementioned transient flow equations (i.e., Eqs. 1–6) for the matrix flow can be rewritten in a dimensionless form as:

$$\frac{{\partial^{2} p_{{j{\text{D}}}} }}{{\partial x_{{\text{D}}}^{2} }} + \frac{{\partial^{2} p_{{j{\text{D}}}} }}{{\partial y_{{\text{D}}}^{2} }} = \eta_{\min ,j} \frac{{\partial p_{{j{\text{D}}}} }}{{\partial t_{{\text{D}}} }}$$

(7)

$$p_{{j{\text{D}}}} |_{{t_{{\text{D}}} = 0}} = 0$$

(8)

$$\left. {\frac{{\partial p_{{j{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }} { = }\left. {\lambda_{{j{ + }1,j}} \frac{{\partial p_{{j{ + }1{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }}$$

(9)

$$\left( {p_{{j{ + }1{\text{D}}}} - p_{{j{\text{D}}}} } \right)_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }} = \left. {S_{aj} \frac{{\partial p_{{j{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x = x_{{j{\text{D}}}} }}$$

(10)

$$\left. {\frac{{\partial p_{{1{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{x = 0} = \left. {\frac{{\partial p_{{N{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{N{\text{D}}}} }} { = }0{\kern 1pt} {\kern 1pt}$$

(11)

$$\left. {\frac{{\partial p_{{j{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{y_{{\text{D}}} = 0}} = \left. {\frac{{\partial p_{{j{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{y_{{\text{D}}} = y_{{{\text{eD}}}} }} { = }0$$

(12)

Table 1 Definitions of the dimensionless variables

Fractures systems

In view of the asymmetrical distribution of fractures system, the left wing and right wing of one primary fracture are regarded as individual primary fracture, respectively. Hence, there are 2N_PF primary fracture parts considered in the model.

The governing differential equations for one-dimensional pressure distribution in l-th fracture are given by (Cinco-Ley and Meng 1988; Chen et al. 2016a)

$$\left( {\frac{k}{\mu }} \right)_{{_{fl} }} \frac{{\partial^{2} p_{fl} }}{{\partial \hat{x}_{fl}^{2} }} + \frac{{q_{fl} }}{{hw_{fl} }} = 0$$

(13)

The initial condition is

$$\left. {p_{fl} } \right|_{t = 0} = p_{{\text{i}}}$$

(14)

The inner boundary condition is

$$\left( {\frac{k}{\mu }} \right)_{fl} w_{fl} h\left. {\frac{{\partial p_{fl} }}{{\partial \hat{x}_{fl} }}} \right|_{{\hat{x}_{fl} = 0}} = q_{{{\text{w}}fl}}$$

(15)

The external boundary condition is

$$\left. {\frac{{\partial p_{fl} }}{{\partial \hat{x}_{fl} }}} \right|_{{\hat{x}_{fl} = L_{fl} }} = 0$$

(16)

where subscript f can represent primary fracture (PF) or secondary fracture (SF); subscript l represents the fracture number, l = 1,…, N_PF for PF and l = 1,…, N_SF for SF; $\hat{x}_{fl}$ is the local Cartesian coordinate system associated with the l-th fracture; w_fl is the width of the l-th fracture;

L_PFl is the fracture length for the l-th primary fracture part (it is equal to the primary fracture half-length if the primary fracture is symmetric about the horizontal well); L_SFl is the fracture length for the l-th secondary fracture; q_fl is the flow rate of the l-th fracture face; q_wPFl is the flow rate from the l-th primary fracture to wellbore; and q_wSFl is the flow rate from the l-th secondary fracture to the primary fracture connected it.

The transient flow equations (Eqs. 13–16) for the fractures flow can be given by following dimensionless form using dimensionless variables defined in Table 1:

$$\frac{{\partial^{2} p_{{fl{\text{D}}}} }}{{\partial \hat{x}_{{fl{\text{D}}}}^{2} }} - \frac{2\pi }{{F_{{fl{\text{CD}}}} }}q_{{fl{\text{D}}}} = 0$$

(17)

$$p_{{fl{\text{D}}}} (t_{{\text{D}}} = 0) = 0$$

(18)

$$\left. {\frac{{\partial p_{{fl{\text{D}}}} }}{{\partial \hat{x}_{{fl{\text{D}}}} }}} \right|_{{\hat{x}_{{fl{\text{D}}}} = 0}} = \frac{2\pi }{{F_{{fl{\text{CD}}}} }}q_{{wfl{\text{D}}}} {\kern 1pt}$$

(19)

$$\left. {\frac{{\partial p_{{fl{\text{D}}}} }}{{\partial \hat{x}_{{fl{\text{D}}}} }}} \right|_{{\hat{x}_{{fl{\text{D}}}} = L_{{fl{\text{D}}}} }} = 0$$

(20)

Model solutions

Firstly, each primary fracture and secondary fracture is divided into M_PF and M_SF discrete segments respectively to obtain the solution for this system consisting of N_PF primary fractures (2N_PF primary fractures part) and N_SF secondary fractures, as shown in Fig. 2. The flow rate is assumed to be uniform in each discrete segment. The pressure responses caused by these fracture segments are calculated.

Fig. 2

Schematic of the discretization of a primary fracture with secondary fractures

Solution for Fluid flow in multi-region composite matrix systems

Taking the Laplace transformation with respect to t_D in Eqs. 7–12 yields,

$$\frac{{\partial^{2} \overline{p}_{{j{\text{D}}}} }}{{\partial x_{{\text{D}}}^{2} }} + \frac{{\partial^{2} \overline{p}_{{j{\text{D}}}} }}{{\partial y_{{\text{D}}}^{2} }} = \eta_{\min ,j} u_{j} \overline{p}_{{j{\text{D}}}} {\kern 1pt}$$

(21)

$$\left. {\frac{{\partial \overline{p}_{{j{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }} { = }\left. {\lambda_{{j{ + }1,j}} \frac{{\partial \overline{p}_{{j{ + }1{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }}$$

(22)

$$\left. {\left( {\overline{p}_{{j{ + }1{\text{D}}}} - \overline{p}_{{j{\text{D}}}} } \right)} \right|_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }} = \left. {S_{aj} \frac{{\partial \overline{p}_{{j{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }}$$

(23)

$$\left. {\frac{{\partial \overline{p}_{{1{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = 0}} = \left. {\frac{{\partial \overline{p}_{{N{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{N{\text{D}}}} }} { = }0{\kern 1pt} {\kern 1pt}$$

(24)

$$\left. {\frac{{\partial \overline{p}_{{j{\text{D}}}} }}{{\partial y_{{\text{D}}} }}} \right|_{{y_{{\text{D}}} = 0}} = \left. {\frac{{\partial \overline{p}_{{j{\text{D}}}} }}{{\partial y_{{\text{D}}} }}} \right|_{{y_{{\text{D}}} = y_{{{\text{eD}}}} }} { = }0$$

(25)

In Eq. 21, u_j = sf_j(s) is a parameter to extend the solution into dual-porosity idealization of naturally fractured reservoirs (Ozkan and Raghavan 1991a, 1991b). s is the Laplace transform variable based on t_D and f_j(s) is given by

$$f_{j} \left( s \right){\text{ = }}\left\{ {\begin{array}{*{20}c} 1 & {{\text{for}}\,{\text{homogeneous}}\,{\text{reservoir}}} \\ {\frac{{\omega _{{{\text{NF}}j}} s\left( {1 - \omega _{{{\text{NF}}j}} } \right) + \chi _{{{\text{mNF}}j}} }}{{s\left( {1 - \omega _{{{\text{NF}}j}} } \right) + \chi _{{{\text{mNF}}j}} }}} & {{\text{for}}{\kern 1pt} \,{\text{pseudosteady}}\,{\kern 1pt} {\text{dual - porosity}}\,{\text{reservoir}}} \\ \end{array} } \right.$$

(26)

where χ_mNFj is the inter-porosity flow coefficient in region j, ω_NFj is the storage ratio between naturally fractures and matrix in region j.

We first consider the pressure response caused by a fracture segment in the multi-region composite matrix system. Using the Green’s function method (Raghavan 2010; Deng et al. 2017, 2022), the Laplace domain solution for a fracture segment in the multi-region composite matrix system, $\overline{p}_{{f{\text{s}}j,l,k{\text{D}}}}$, can be expressed as:

$$\overline{p}_{{f{\text{s}}j,l,k{\text{D}}}} = \overline{p}_{{{\text{h}}fj,l,k{\text{D}}}} { + }\overline{p}_{{{\text{ns}}fj,l,k{\text{D}}}} \,{\text{for }}\,{\text{the }}\,{\text{source }}\,{\text{region, }}\,{\text{where }}\,{\text{segment }}\,{\text{located}}$$

(27)

$$\overline{p}_{{f{\text{s}}j,l,k{\text{D}}}} = \overline{p}_{{{\text{ns}}fj,l,k{\text{D}}}} \,{\text{for }}\,{\text{the}}\,{\text{ no - source}}\,{\text{ region}}$$

(28)

where $\overline{p}_{{{\text{h}}fj,l,k{\text{D}}}}$ is the solution for the k-th segment of the l-th fracture in a homogeneous rectangular banded system with the properties of the j-th region and $\overline{p}_{{{\text{ns}}fj,l,k{\text{D}}}}$,which satisfies the Eq. 21, is the no-source solution to a rectangular banded linear composite system for the j-th region.

Considering the azimuth of fracture segment, $\overline{p}_{{{\text{h}}fj,l,k{\text{D}}}}$ is given by:

$$\overline{p}_{{{\text{h}}fj,l,k{\text{D}}}} \left( {x_{{\text{D}}} ,y_{{\text{D}}} } \right) = \frac{{\pi \overline{q}_{{l,k{\text{D}}}} }}{{2y_{{{\text{eD}}}} \lambda_{j,\min } }}\int\limits_{{x_{{fl,k{\text{D}}}} }}^{{x_{{fl,k + 1{\text{D}}}} }} {\left[ \begin{gathered} G\left( {x_{{\text{D}}} ,y_{{\text{D}}} ,x^{\prime}_{{\text{D}}} ,\tan \left( {\theta_{fl} } \right)\left( {x^{\prime}_{{\text{D}}} - x_{{{\text{w}}fl{\text{D}}}} } \right){ + }y_{{{\text{w}}fl{\text{D}}}} } \right) \hfill \\ \times \sqrt {1 + \left( {\tan \theta_{fl} } \right)^{2} } \hfill \\ \end{gathered} \right]} {\text{d}}x^{\prime}_{{\text{D}}}$$

(29)

$$G\left( {x_{{\text{D}}} ,y_{{\text{D}}} ,x^{\prime}_{{\text{D}}} ,y^{\prime}_{{\text{D}}} } \right){ = }\sum\limits_{m = 0}^{\infty } {\varepsilon_{m} \cos \left( {\frac{{m\pi y_{{\text{D}}} }}{{y_{{{\text{eD}}}} }}} \right)\cos \left( {\frac{{m\pi y^{\prime}_{{\text{D}}} }}{{y_{{{\text{eD}}}} }}} \right)\frac{{\cosh \left( {\gamma_{m,j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{{{\text{D}}1}} } \right) + \cosh \left( {\gamma_{m,j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{{{\text{D}}2}} } \right)}}{{\gamma_{m,j} \times \sinh \left( {\gamma_{m,j} x_{{{\text{eD}}}} } \right)}}}$$

(30)

where $\overline{q}_{{l,k{\text{D}}}}$ is the dimensionless flow rate from matrix from a fracture segment in Laplace domain, x_fl,kD and x_fl,k+1D are the value of starting and ending x coordinates of the k-th segment of the l-th fracture, respectively, θ_fl is the azimuth between the l-th fracture segment and x axis, x_wflD and y_wflD are the value of starting coordinates of the starting l-th fracture, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x}_{{{\text{D}}1}} = x_{{{\text{eD}}}} - \left| {x_{{\text{D}}} - x^{\prime}_{{\text{D}}} } \right|$,$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{x}_{{{\text{D2}}}} = x_{{{\text{eD}}}} - \left| {x_{{\text{D}}} + x^{\prime}_{{\text{D}}} } \right|$,$\gamma_{m,j} = \sqrt {\left( {m\pi /y_{{{\text{eD}}}} } \right)^{2} + \eta_{{{\text{min, }}j}} u}$ and $\varepsilon_{m} = \left\{ \begin{gathered} 1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} m = 0 \hfill \\ 2{\kern 1pt} {\kern 1pt} {\kern 1pt} m \ge 1 \hfill \\ \end{gathered} \right.$

Next, by applying the method of finite Fourier cosine transform and its inverse transform to Eqs. 21–25, the no-source solution to a rectangular banded linear composite system for the j-th region, $\overline{p}_{{{\text{ns}}fj,l,k{\text{D}}}}$, can be obtained. The detailed derivation of the Laplace domain solution is provided in Appendix A, and the resulting expression is as follows:

$$\overline{p}_{{{\text{ns}}fj,l,k{\text{D}}}} { = }\frac{1}{2}\frac{\pi }{{y_{{{\text{eD}}}} }}\overline{q}_{{l,k{\text{D}}}} \sum\limits_{m = 0}^{\infty } {\left\{ \begin{gathered} \varepsilon_{m} \cos (\frac{{m\pi y_{{\text{D}}} }}{{y_{{{\text{eD}}}} }}) \hfill \\ \times \left( {c_{m,j,l,k} e^{{\gamma_{m,j} \left( {x_{{\text{D}}} - x_{{j{\text{D}}}} } \right)}} + d_{m,j,l,k} e^{{\gamma_{m,j} \left( {x_{{j - 1{\text{D}}}} - x_{{\text{D}}} } \right)}} } \right) \hfill \\ \end{gathered} \right\}}$$

(31)

where c_m,j,l,k and d _mj,l,k are coefficient matrix.

Utilizing the superposition principle to all fracture segments in all regions, the dimensionless Laplace domain solution in the multi-region composite matrix system can be written as

$$\overline{p}_{{j{\text{D}}}} = \sum\limits_{l = 1}^{{2N_{{{\text{PF}}}} }} {\sum\limits_{k = 1}^{{M_{{{\text{PF}}}} }} {\overline{p}_{{{\text{PF}}sj,l,k{\text{D}}}} } } + \sum\limits_{{l^{\prime} = 1}}^{{N_{{{\text{SF}}}} }} {\sum\limits_{{k^{\prime} = 1}}^{{M_{{{\text{SF}}}} }} {\overline{p}_{{{\text{SF}}sj,l,k{\text{D}}}} } }$$

(32)

According to Eqs. 29–30, Eq. 32 can be rewritten as

$$\overline{p}_{{j{\text{D}}}} = \sum\limits_{l = 1}^{{2N_{{{\text{PF}}}} }} {\sum\limits_{k = 1}^{{M_{{{\text{PF}}}} }} {\overline{q}_{{l,k{\text{D}}}} S_{{f{\text{s}}j,l,k{\text{D}}}} } } + \sum\limits_{{l^{\prime} = 1}}^{{N_{{{\text{SF}}}} }} {\sum\limits_{{k^{\prime} = 1}}^{{M_{{{\text{SF}}}} }} {\overline{q}_{{l,k{\text{D}}}} S_{{f{\text{s}}j,l,k{\text{D}}}} } }$$

(33)

where

$$S_{{f{\text{s}}j,l,k{\text{D}}}} = \frac{\pi }{{2y_{{{\text{eD}}}} }}\left\{ \begin{gathered} \int\limits_{{x_{{fl,k{\text{D}}}} }}^{{x_{{fl,k + 1{\text{D}}}} }} {\left[ \begin{gathered} G\left( {x_{{\text{D}}} ,y_{{\text{D}}} ,x^{\prime}_{{\text{D}}} ,\tan \left( {\theta_{fl} } \right)\left( {x^{\prime}_{{\text{D}}} - x_{{{\text{w}}fl{\text{D}}}} } \right){ + }y_{{{\text{w}}fl{\text{D}}}} } \right) \hfill \\ \times \sqrt {1 + \left( {\tan \theta_{fl} } \right)^{2} } \hfill \\ \end{gathered} \right]} dx^{\prime}_{{\text{D}}} \hfill \\ { + }\sum\limits_{m = 0}^{\infty } {\left\{ \begin{gathered} \varepsilon_{m} \cos (\frac{{m\pi y_{{\text{D}}} }}{{y_{{{\text{eD}}}} }}) \hfill \\ \times \left( {c_{m,j,l,k} e^{{\gamma_{m,j} \left( {x_{{\text{D}}} - x_{{j{\text{D}}}} } \right)}} + d_{m,j,l,k} e^{{\gamma_{m,j} \left( {x_{{j - 1{\text{D}}}} - x_{{\text{D}}} } \right)}} } \right) \hfill \\ \end{gathered} \right\}} \hfill \\ \end{gathered} \right\}$$

(34)

Hence, the dimensionless pressure on the k-th segment of l-th fracture can be rewritten as

$$\overline{p}_{{fj,l,k{\text{D}}}} = \sum\limits_{l = 1}^{{2N_{{{\text{PF}}}} }} {\sum\limits_{k = 1}^{{M_{{{\text{PF}}}} }} {\overline{q}_{{{\text{PF}}l,k{\text{D}}}} S_{{{\text{PFs}}j,l,k{\text{D}}}} } } + \sum\limits_{{l^{\prime} = 1}}^{{N_{{{\text{SF}}}} }} {\sum\limits_{{k^{\prime} = 1}}^{{M_{{{\text{SF}}}} }} {\overline{q}_{{{\text{SF}}l,k{\text{D}}}} S_{{{\text{SFs}}j,l,k{\text{D}}}} } }$$

(35)

Solution of fluid flow in the fracture system

The dimensionless pressure in the l-th primary fracture in the Laplace domain, according to Eqs. 17–20 is expressed as (Cinco-Ley et al. 1988)

$$\overline{p}_{{{\text{wD}}}} - \overline{p}_{{{\text{PF}}l{\text{D}}}} = \frac{{{\uppi }\hat{x}_{{{\text{PF}}l{\text{D}}}} }}{{F_{{{\text{PFCD}}l}} }}\overline{q}_{{{\text{wPF}}l{\text{D}}}} - \frac{{\uppi }}{{F_{{{\text{PFCD}}l}} }}\int\limits_{0}^{{\hat{x}_{{{\text{PF}}l{\text{D}}}} }} {\int\limits_{0}^{v} {\overline{q}_{{{\text{PF}}l{\text{D}}}} d\hat{x}_{{{\text{PF}}l{\text{D}}}} {\text{d}}v} }$$

(36)

The dimensionless pressure in the l-th secondary fracture in the Laplace domain, according to Eqs. 17–20 is expressed as (Chen et al. 2016a)

$$\overline{p}_{{{\text{int}} {\text{erSF}}l{\text{D}}}} - \overline{p}_{{{\text{SF}}l{\text{D}}}} = \frac{{{\uppi }\hat{x}_{{{\text{SF}}l{\text{D}}}} }}{{F_{{{\text{SFCD}}l}} }}\overline{q}_{{{\text{wSF}}l{\text{D}}}} - \frac{{\uppi }}{{F_{{{\text{SFCD}}l}} }}\int\limits_{0}^{{\hat{x}_{{{\text{SF}}l{\text{D}}}} }} {\int\limits_{0}^{v} {\overline{q}_{{{\text{SF}}l{\text{D}}}} d\hat{x}_{{{\text{SF}}l{\text{D}}}} {\text{d}}v} }$$

(37)

where $\overline{p}_{{{\text{wD}}}}$ is the dimensionless wellbore pressure in the Laplace domain, $\overline{p}_{{{\text{int}} {\text{erSF}}l{\text{D}}}}$ is the dimensionless pressure of intersectional segment in the l-th secondary fracture in the Laplace domain.

Equations 36 and37 can be discretized respectively as follows:

For the primary fracture

$$\overline{p}_{{{\text{wD}}}} - \overline{p}_{{{\text{PF}}l{\text{D}}}} \left( {\hat{x}_{{{\text{PFm}}l,k{\text{D}}}} } \right) = \left\{ \begin{gathered} \frac{{{\uppi }\hat{x}_{{{\text{PFm}}l,k{\text{D}}}} }}{{F_{{{\text{PFCD}}l}} }}\sum\limits_{i = 1}^{{M_{{{\text{PF}}}} }} {\overline{q}_{{{\text{PF}}l,i{\text{D}}}} } \hfill \\ - \frac{{\uppi }}{{F_{{{\text{PFCD}}l}} }}\sum\limits_{i = 1}^{k - 1} {\left[ \begin{gathered} \overline{q}_{{{\text{PF}}l,i{\text{D}}}} \left( \begin{gathered} \frac{1}{2}\Delta \hat{x}_{{{\text{PF}}l{\text{D}}}}^{2} \hfill \\ + \Delta \hat{x}_{{{\text{PF}}l{\text{D}}}} \left( {\hat{x}_{{{\text{PFm}}l,k{\text{D}}}} - i\Delta \hat{x}_{{{\text{PF}}l{\text{D}}}} } \right) \hfill \\ \end{gathered} \right) \hfill \\ + \overline{q}_{{{\text{PF}}l,k{\text{D}}}} \frac{{\Delta \hat{x}_{{{\text{PF}}l{\text{D}}}}^{2} }}{8} \hfill \\ \end{gathered} \right]} \hfill \\ \end{gathered} \right\}$$

(38)

For the secondary fracture

$$\overline{p}_{{{\text{int}} {\text{erSF}}l{\text{D}}}} - \overline{p}_{{{\text{SF}}l{\text{D}}}} \left( {\hat{x}_{{{\text{SFm}}l,k{\text{D}}}} } \right) = \left\{ \begin{gathered} \frac{{{\uppi }\hat{x}_{{{\text{SFm}}l,k{\text{D}}}} }}{{F_{{{\text{SFCD}}l}} }}\sum\limits_{i = 1}^{{M_{{{\text{SF}}}} }} {\overline{q}_{{{\text{SF}}l,i{\text{D}}}} } \hfill \\ - \frac{{\uppi }}{{F_{{{\text{SFCD}}l}} }}\sum\limits_{i = 1}^{k - 1} {\left[ \begin{gathered} \overline{q}_{{{\text{SF}}l,i{\text{D}}}} \left( \begin{gathered} \frac{1}{2}\Delta \hat{x}_{{{\text{SF}}l{\text{D}}}}^{2} \hfill \\ + \Delta \hat{x}_{{{\text{SF}}l{\text{D}}}} \left( {\hat{x}_{{{\text{SFm}}l,k{\text{D}}}} - i\Delta \hat{x}_{{{\text{SF}}l{\text{D}}}} } \right) \hfill \\ \end{gathered} \right) \hfill \\ + \overline{q}_{{{\text{SF}}l,k{\text{D}}}} \frac{{\Delta \hat{x}_{{{\text{SF}}l{\text{D}}}}^{2} }}{8} \hfill \\ \end{gathered} \right]} \hfill \\ \end{gathered} \right\}$$

(39)

where $\hat{x}_{{{\text{PFm}}l,k{\text{D}}}}$ and $\hat{x}_{{{\text{SFm}}l,k{\text{D}}}}$ is the dimensionless distance of the midpoint of the k-th segment in the l-th primary fracture and the l-th secondary fracture respectively; $\Delta \hat{x}_{{{\text{PF}}l{\text{D}}}}$ and $\Delta \hat{x}_{{{\text{SF}}l{\text{D}}}}$ is the dimensionless length of each segment of the l-th primary fracture and the l-th secondary fracture respectively, and $\Delta \hat{x}_{{{\text{PF}}l{\text{D}}}} = \frac{{L_{{{\text{PF}}l{\text{D}}}} }}{{M_{{{\text{PF}}}} }}$,$\Delta \hat{x}_{{{\text{SF}}l{\text{D}}}} = \frac{{L_{{{\text{SF}}l{\text{D}}}} }}{{M_{{{\text{SF}}}} }}$.

Solution of transient pressure in the complex systems

Considering the continuity condition in the intersectional segments between primary fractures and secondary fractures, the pressure and flow rate should satisfy

$$\overline{p}_{{{\text{int}} {\text{erPF}}l{\text{D}}}} = \overline{p}_{{{\text{int}} {\text{erSF}}l{\text{D}}}}$$

(40)

$$\sum\limits_{k = 1}^{{M_{{{\text{SF}}}} }} {\overline{q}_{{{\text{SF}}l,k{\text{D}}}} } { + }\overline{q}_{{{\text{int}} {\text{erPF}}l{\text{D}}}} = \overline{q}^{*}_{{{\text{int}} {\text{erPF}}l{\text{D}}}}$$

(41)

where $\overline{p}_{{{\text{int}} {\text{erPF}}l{\text{D}}}}$ is the dimensionless pressure of intersectional segment in primary fracture connected to the l-th secondary fracture in the Laplace domain; $\overline{q}_{{{\text{int}} {\text{erPF}}l{\text{D}}}}$ is the dimensionless flow rate caused by the intersectional segment in primary fracture connected to the l-th secondary fracture in the Laplace domain; $\overline{q}^{*}_{{{\text{int}} {\text{erPF}}l{\text{D}}}}$ is the total dimensionless flow rate of intersectional segment in primary fracture connected to the l-th secondary fracture in the Laplace domain.

The total flow rate is described as the summation of the flow rate from each primary fracture segment. Thus,

$$\sum\limits_{l = 1}^{{N_{{{\text{PF}}}} }} {\sum\limits_{k = 1}^{{2M_{{{\text{PF}}}} }} {\overline{q}^{*}_{{{\text{PF}}l,k{\text{D}}}} \Delta \hat{x}_{{{\text{PF}}l{\text{D}}}} } } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{s}$$

(42)

Substituting Eq. 41 into Eq. 42, and notice that $\overline{q}^{*}_{{{\text{PF}}l,k{\text{D}}}} { = }\overline{q}_{{{\text{PF}}l,k{\text{D}}}}$ for all segments except intersectional segments we have

$$\sum\limits_{l = 1}^{{N_{{{\text{PF}}}} }} {\sum\limits_{k = 1}^{{M_{{{\text{PF}}}} }} {\overline{q}_{{{\text{PF}},l,k{\text{D}}}} \Delta \hat{x}_{{{\text{PF}}l{\text{D}}}} } } {\kern 1pt} {\kern 1pt} + \sum\limits_{l = 1}^{{N_{{{\text{SF}}}} }} {\sum\limits_{k = 1}^{{M_{{{\text{SF}}}} }} {\overline{q}_{{{\text{SF}},l,k{\text{D}}}} \Delta \hat{x}_{{{\text{SF}}l{\text{D}}}} } } {\kern 1pt} = \frac{1}{s}$$

(43)

Then writing Eqs. 38 and 39 for each segment of each fracture and combining Eqs. 40 and 43 creates a system of 2N_PF × M_PF + N_SF × M_SF + 1 equations with 2N_PF × M_PF + N_SF × M_SF + 1 unknowns($\overline{q}_{{{\text{PF}}l,k{\text{D}}}}$,$\overline{q}_{{{\text{SF}}l^{\prime},k^{\prime}{\text{D}}}}$, $\overline{p}_{{{\text{wD}}}}$). The unknown numbers can also be easily obtained using linear algebra.

Considering the effect of wellbore storage and the skin, the dimensionless wellbore pressure in Laplace domain can be obtained by the following:

$$\overline{p}_{{{\text{wD}}}} = \frac{{s\overline{p}_{{{\text{wD}}}} + S}}{{s + C_{{\text{D}}} s^{2} \left( {s\overline{p}_{{{\text{wD}}}} + S} \right)}}$$

(44)

where C_D is the dimensionless wellbore storage coefficient, and $S$ is the skin factor.

Noticed that we can also obtain the rate solution under constant pressure by using Duhamel principle (Everdingen and Hurst 1949), and its form is given as follows:

$$\overline{q}_{{{\text{wD}}}} = \frac{1}{{s^{2} }}\overline{p}_{{{\text{wD}}}}$$

(45)

The dimensionless wellbore pressure (p_wD) can be obtained using the Stehfest numerical inversion to convert the Laplace domain solution $\overline{p}_{{{\text{wD}}}}$ to p_wD (Stehfest 1970).

Model validation

The results of the newly developed model are compared with those from the two widely used models in the literature, one is the model of a MFHW with secondary fractures in an infinite homogeneous reservoir (Chen et al. 2016a) and the other is the model of MFHWs in a banded channel heterogeneous reservoir (Wang et al. 2017). Figure 3 illustrates the comparison between Chen et al.’ s model and the newly developed model in the pressure derivative curve (p_wD’ vs t_D) under four sets of the number of secondary fractures (N_SF = 0, 8, 12, 24). It should be noted that, the four values of N_SF are set to 0, 4, 6, 12, respectively in, Chen et al.’ s curves for consistency due to different definition of the number of secondary fractures between the two models. By setting an approximate infinite boundary (i.e., x_eD = 2 × 10⁶, y_eD = 2 × 10⁶) and N = 1(i.e., homogeneous reservoir), the newly developed model converges to a homogeneous model (Chen et al. 2016a). The other parameters used in Fig. 3 are as follow: N_PF = 2, △x_wPF1D = 250 (△x_wPF1D = x_wPF2D- x_wPF1D), x_PFD = 7.5, l_SFD/ x_PFD = 2, F_PFCD = 80, F_SFCD = 20, χ_mNF = 1 × 10^–8, ω_NF = 0.2.

Fig. 3

Performance comparison between the newly developed model and the homogeneous model (Chen et al. 2016a)

Figure 4 shows the comparison between Wang et al.’ s model and the newly developed model in the rate curve (q_wD vs t_D) under a four-region heterogeneous case. By setting N_SF = 0 (no secondary fractures) and S_aj = 0 (no fault skin) the newly developed model converges to the no- secondary fractures model (Wang et al. 2017). The other parameters used in Fig. 4 are as follow: N_PF = 4, N = 4, x_eD = 30, y_eD = 7, λ_2,1 = 3, λ_3,2 = 2, λ_4,3 = 1.5, △x_wPFD = 6.67, F_PFCD = 35.

Fig. 4

Performance comparison between the newly developed model and the no- secondary fractures model (Wang et al. 2017)

The good match between Figs. 3 and 4 shows that the newly developed model, in their simplified cases, converge to the existing models, and it also proves that the newly developed model is correct.

Type curve construction and sensitivity analysis

Solutions of the newly-developed models are calculated to obtain the standard log–log type curves, including the dimensionless pressure and its derivative with respect to the t_D/C_D of the transient pressure response. The main flow regimes are identified, and the effects of the relevant parameters on the pressure transient behavior are analyzed by analyzing the type curves. The default values of the parameters used in this section are shown in Table 2.

Table 2 Default parameter values

Flow regimes recognition and effect of the characteristic parameters of reservoir heterogeneity

Setting three values of λ_2,1 (①λ_2,1 = 1; ②λ_2,1 = 2; ③λ_2,1 = 5), with the other relevant parameters as presented in Table 2, three types of pressure transient behavior are obtained. Because the dimensionless pressure and time are based on the parameter of the minimum conductivity region in our work, one can consider that the well is traversing many interfaces and draining higher permeability regions in the heterogeneous case.

Figure 5 shows the main flow regimes and the effect of permeability heterogeneity on the type curves related to pressure behavior characteristics of a MFHW with two primary fractures and four secondary fractures passing through two- region banded channel heterogeneous reservoir. It can be seen that there are nine main flow regimes in the type curves:

• I. Wellbore storage regime During this regime, the production is dominated by the fluids stored in the wellbore. The shape of the dimensionless wellbore pressure and its derivative curve is an upward straight line with a unit slope.

• II. Skin effect regime In this regime, the shape of the dimensionless wellbore derivative curve resembles a "hump".

• III. Bilinear flow regime During this regime, two linear flows occur simultaneously. One flows from the hydraulic fractures to the wellbore, while the other flows from the reservoir of region 1 to the hydraulic fracture. The derivative curve of bilinear flow regime is an upward straight line with a slope of 1/4.

• IV. Fluid-feed regime During this regime, fluid start to flow from the secondary fractures to the primary fractures. The derivative curve of the fluid-feed regime resembles a “dip”.

• V. First linear flow regime The dimensionless wellbore pressure derivative curve is an upward straight line with a slope of 0.5. The fluids mainly experience linear flow from the reservoir to the primary fractures during the first linear flow regime.

• VI. Early pseudo-radial flow regime During this regime, the slope of the dimensionless wellbore pressure derivative curves is zero, indicating a pseudo-radial flow from the reservoir to each of the primary fractures.

• VII. Second linear flow regime During this regime, the dimensionless wellbore pressure derivative curve is an upward straight line. This behavior is attributed to the interference of pressure waves from adjacent fractures during fracture production.

• VIII. The second pseudo-radial flow regime During this regime, the slope of the dimensionless wellbore pressure derivative curves is zero. This behavior indicates that the fluids experience radial flow from the reservoir to the MFHW, and this regime persists until the reservoir boundary is reached.

• IX. Boundary-dominated flow regime During this regime, the pressure front interacts with all closed boundaries. The curves of dimensionless wellbore pressure and its derivative follow unit-slope lines, indicating a pseudo-steady-state flow of fluids.

Fig. 5

Flow regimes of MFHWs with secondary fractures in heterogeneity reservoirs and effect of the permeability heterogeneity in type curves

The contrast with the homogeneous case, as been seen from Fig. 5 reveals that permeability heterogeneity does not introduce a new, unique flow regime. However, it significantly influences the curves of all other flow regimes, except the wellbore storage and skin effect and boundary-dominated flow regimes. The vertical position of II–VIII flow regimes on curves gradually decreases in the heterogeneous case compared to that in the homogeneous case. A higher value of mobility ratio λ_2,1 leads to a smaller pressure drop in the wellbore, and thus a greater difference from the homogeneous case. This is because the average permeability in the heterogeneous case is higher than that in the homogeneous case. Owing to the higher average permeability in the heterogeneous case, VI–VIII flow regimes appear earlier in the curves. This distinction is also notable when comparison to the pressure characteristics observed in heterogeneous cases where the well does not traverse distinct regions (Zhao et al. 2014; Deng et al. 2022). In such cases, permeability heterogeneity primarily influences the later radial/ pseudo-radial flow regime.

Effect of the storativity heterogeneity

The effect of storativity ratio, ω_2,1, on the pressure transient behavior is illustrated in Fig. 6 It can be observed that ω_1,2 mainly influences the time of occurrence of all flow regimes except the wellbore storage flow regime. A higher value of ω_2,1 results in a higher average storativity in the reservoir, consequently causing the II–IX flow regimes to appear later.

Fig. 6

Effect of the storativity ratio, ω_1,2

Effect of the fault skin (S _a)

Two scenarios of S_a are discussed: one is that the fault is located in the middle of two prime fractures (x_wPFD1 = 1850, x_1D = 2000, x_wPFD2 = 2150) and the other is that the fault is located close to one of prime fractures (x_wPFD1 = 1990, x_1D = 2000, x_wPFD2 = 2290). Three types of pressure transient behavior are obtained in two cases by setting three values of S_a (①S_a = 0; ②S_a = 100; ③S_a = 1000). Figure 7 illustrates the impact of S_a on the pressure transient behavior in the first scenario. It is apparent that S_a exerts no discernible effect on the type curves in this instance. This lack of influence is attributed to the fault being positioned in the middle of each two primary fractures, where the pressure wave of two fractures interferes with each other. Essentially, the interference between the pressure waves in the middle of the two fractures creates an equivalent "sealed fault." Consequently, the influence of S_a is masked by the presence of this equivalent "sealed fault" on the curves in this particular case.

Fig. 7

Effect of the fault skin, S_a, in the first scenario

Figure 8 illustrates the effect of S_a on the pressure transient behavior in the second scenario. Notably, S_a influences both the early pseudo-radial flow regime and the second linear flow regime on the type curves. Due to the asymmetric position of fault, the effect of S_a is not masked by the influence of the equivalent “sealed fault”. As S_a increases, a greater additional drawdown is required in the fault, resulting in an upward shift in the vertical position of the early pseudo-radial flow regime on the curves and a delayed appearance of the second linear flow regime.

Fig. 8

Effect of the fault skin, S_a, in the second scenario

Effect of the region area heterogeneity

Figures 9 and 10 illustrate the effect of region area heterogeneity on the pressure transient behavior for a no-fault skin case (s_aj = 0, j = 1 ~ 5) and a fault skin case (s_aj = 10, j = 1 ~ 5) respectively. The horizontal well with five primary fractures and ten secondary fractures is positioned in a relatively small (x_eD = 200, y_eD = 200) five-region composite reservoir. The mobility decreases with the increase in distance from the center (λ_1,1 = 1, λ_2,1 = 3, λ_3,1 = 5, λ_4,1 = 3, λ_5,1 = 1), and a uniform distribution of fractures (△x_wPFD = 40) is considered in the system. Similarly, three types of pressure transient behavior are observed in the small and large secondary fracture cases, by setting three sets of the length of region,△x_jD, (①△x_jD = 40, j = 1 ~ 5;②△x_1D = △x_5D = 25, △x_2D = △x_4D = 40, △x_3D = 70; ③△x_1D = △x_5D = 55, △x_2D = △x_4D = 40, △x_3D = 10).

Fig. 9

Effect of the region area heterogeneity in no-fault skin case

Fig. 10

Effect of the region area heterogeneity in fault skin case

It is evident that the early pseudo-radial flow regime and the second pseudo-radial flow regime are obscured by the second linear flow regime in the case of a relatively small reservoir and a small interval between fractures. This is because the impact of pressure interference between fractures and the effect of closed boundaries manifests early in this case. In addition, region area heterogeneity mainly influences the second linear flow regime in the type curves, as seen from Fig. 9. The I–V flow regime remain unchanged with variations in △x_jD because the pressure response of three cases reflects the part of reservoir with same average permeability before the interference among fractures occurs. During the second linear flow regime, the pressure front reaches the entire reservoir. Therefore, the larger the region with higher permeability, the higher the average permeability of reservoir will be. Consequently, the lower the vertical position of second linear flow regime in the type curves appears.

Figure 10 indicates that the impact of region area heterogeneity in the fault skin case differs from that in the no-fault skin case. Since the faults are asymmetrically positioned among the primary fractures (see Fig. 10, case ② and ③), the effect of fault skin is not obscured by the equivalent “sealed fault” effect in this case. Consequently, the vertical position of second linear flow regime increases in cases with region area heterogeneity (case ② and ③) in the curves. It is noteworthy that the pressure drop in the wellbore is smaller in case ② compared to case ③, attributed to the higher average permeability of the reservoir.

Effect of the characteristic parameters of fractures system

Effect of the primary fracture-conductivity (FPFCD)

Figure 11 illustrates the impact of F_PFCD on the pressure transient behavior. It is evident that F_PFCD influences the skin effect regime, bilinear flow regime, fluid-feed regime and first linear flow regime in the type curves. With an increase in the F_PFCD, a smaller pressure drop is needed in the primary fractures. Consequently, the vertical position of the II–V flow regimes decreases, and the duration of the bilinear flow regime and fluid-feed regime decreases.

Fig. 11

Effect of the primary fracture conductivity, F_PFCD

Effect of the secondary fracture-conductivity (FSFCD)

Figure 12 depicts the impact of F_SFCD on the pressure transient behavior. It is evident that F_SFCD influences the bilinear flow regime and fluid-feed regime in the type curves. With an increase in F_SFCD, a smaller pressure drop is required in the secondary fractures. Consequently, the duration of the bilinear flow regime decreases and the fluid-feed regime appears earlier.

Fig. 12

Effect of the secondary fracture conductivity, F_SFCD

Effect of the fracture-length ratio (the ratio of the length of the primary fracture to the secondary fracture, l_SFD/ x_PFD)

Figure 13 illustrates the impact of l_SFD/x_PFD on the pressure transient behavior. l_SFD/x_PFD influences the fluid-feed regime and first linear flow regime in the type curves. As l_SFD/x_PFD increases, indicating relatively more reserves in the secondary fractures, the duration of the fluid-feed regime increases, and the vertical position of the first linear flow regime decreases.

Fig. 13

Effect of the fracture-length ratio, l_SFD/ x_PFD

Effect of secondary-fracture number (NSF)

Figure 14 illustrates the impact of N_SF on the pressure transient behavior. N_SF influences the bilinear flow regime, fluid-feed regime and first linear flow regime in the type curves. An increase in the number of secondary fractures, for the same number of primary fractures, is equal to an increase in effective formation permeability around primary fractures. Consequently, in the case of a large N_SF, a smaller pressure drop is needed in the primary fractures. Thus, the vertical position of the fluid-feed regime decreases, the duration of the fluid-feed regime increases, and the duration of the bilinear flow regime decreases.

Fig. 14

Effect of the secondary-fracture number, N_SF

Effect of azimuth angle between secondary-fracture and primary-fracture (θ _SPF)

Figures 15 and 16 depict the effect of θ_SPF on the pressure transient behavior for small secondary fractures case (l_SFD/ x_PFD = 0.2; F_SFCD/ F_PFCD = 0.1) and large secondary fractures case (l_SFD/x_PFD = 1; F_SFCD/ F_PFCD = 1) respectively. Six types of pressure transient behavior are observed for a small secondary fractures case and a large secondary fractures case by setting five values of θ_SPF (①θ_SPF = 10;②θ_SPF = 30; ③θ_SPF = 45; ④θ_SPF = 60; ⑤θ_SPF = 90) and a no-secondary fractures case (N_SF = 0).

Fig. 15

Effect of the azimuth angle between SF and PF, θ_SPF, in small secondary fractures case

Fig. 16

Effect of the azimuth angle between SF and PF, θ_SPF, in large secondary fractures case

It can be seen from Fig. 15 that θ_SPF mainly influences the fluid-feed regime and first linear flow regime in the type curves. As the θ_SPF approaches 90°, indicating a larger extent of the fractures system, a smaller pressure drop is required in the wellbore. Consequently, the vertical position of fluid-feed regime in type curves is decreases, and the appearance of the first linear flow regime is delayed.

Figure 16 illustrates the notable impact of θ_SPF on the fluid-feed regime in the type curves for the large secondary fractures case. In this case, the first linear flow regime is gradually obscured as θ_SPF approaches 90°, and the trend in the type curves resembles that observed in the case of small secondary fractures, albeit more pronounced.

Conclusions

In this study, we developed a novel semi-analytical model to investigate the pressure transient behavior of multistage-fractured horizontal wells (MFHWs) with secondary fractures passing through banded channel heterogeneous reservoirs. The proposed approach integrates the source method and Green’s function method, introducing an innovative technique for discretizing fractures without necessitating the discretization of interfaces. The model verification is performed through a comparative analysis with two established models from the existing literature. Subsequently, we analyze the influences of reservoir heterogeneity, partially-communicating faults and fracture systems on transient behaviors. The following conclusions have been drawn from the study:

• (1) The pressure behavior of MFHWs passing through regions with different physical properties exhibits distinctive characteristics. In contrast to the homogeneous case, permeability heterogeneity does not introduce a new, unique flow regime. However, it significantly influences the curves of all other flow regimes, except the wellbore storage and skin effect and boundary-dominated flow regimes. This distinction is also notable in comparison to the pressure characteristics observed in heterogeneous cases where the well does not traverse distinct regions.

• (2) The fault skin influences the medium flow regimes when the fault is not positioned in the middle of each two primary fractures in the case of MFHWs passing through regions and faults. In the opposite case, the effect of the fault skin is masked by the equivalent “sealed fault” on the curves, and the pressure response characteristics of that case cannot reflect the connectivity of the fault.

• (3) Heterogeneity in region areas mainly influences the middle and late stages of flow regimes in the case of MFHWs passing through regions and faults, particularly when the connectivity of the fault is poor.

• (4) Fracture properties can influence the early flow regimes. A distinctive flow regime, identified by a 'dip' in derivative curves, emerges due to the secondary fractures connected to primary fractures, and this behavior strengthens and lengthens with higher fracture-length ratio, secondary fracture conductivity, and the number of secondary fractures.

Appendix A

Applying the finite Fourier cosine transform with respect to y_D to Eqs. (21–25) and considering the case of a fracture segment, we obtain the following:

$$\frac{{\partial^{2} \tilde{\overline{p}}_{{fsj,l,k{\text{D}}}} }}{{\partial x_{{\text{D}}}^{2} }} - \gamma_{m,j} \tilde{\overline{p}}_{{fsj,l,k{\text{D}}}} = {\kern 1pt} 0$$

(A1)

$$\left. {\frac{{\partial \tilde{\overline{p}}_{{fsj,l,k{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }} { = }\left. {\lambda_{{j{ + }1,j}} \frac{{\partial \tilde{\overline{p}}_{{fsj + 1,l,k{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }}$$

(A2)

$$\left( {\tilde{\overline{p}}_{{fsj + 1,l,k{\text{D}}}} - \tilde{\overline{p}}_{{fsj,l,k{\text{D}}}} } \right)_{{x_{{\text{D}}} = x_{{j{\text{D}}}} }} = \left. {S_{aj} \frac{{\partial \tilde{\overline{p}}_{{fsj,l,k{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x = x_{{j{\text{D}}}} }}$$

(A3)

$$\left. {\frac{{\partial \tilde{\overline{p}}_{{fs1,l,k{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = 0}} = \left. {\frac{{\partial \tilde{\overline{p}}_{{fsN,l,k{\text{D}}}} }}{{\partial x_{{\text{D}}} }}} \right|_{{x_{{\text{D}}} = x_{{N{\text{D}}}} }} { = }0{\kern 1pt} {\kern 1pt}$$

(A4)

According to Eq. (27), the general form of the solution for Eq. (A1) can be given as.

For the source region,

$$\tilde{\overline{p}}_{{fsj,l,k{\text{D}}}} = \tilde{\overline{p}}_{{{\text{h}}fj,l,k{\text{D}}}} { + }a_{m,j,l,k} e^{{\gamma_{{m{,}j}} x_{{\text{D}}} }} + b_{m,j,l,k} e^{{ - \gamma_{{m{,}j}} x_{{\text{D}}} }}$$

(A5)

For the no-source region,

$$\tilde{\overline{p}}_{{fsj,l,k{\text{D}}}} = a_{m,j,l,k} e^{{\gamma_{{m{,}j}} x_{{\text{D}}} }} + b_{m,j,l,k} e^{{ - \gamma_{{m{,}j}} x_{{\text{D}}} }}$$

(A6)

where $\tilde{\overline{p}}_{{{\text{h}}fj,l,k{\text{D}}}}$ can be obtained by using finite Fourier cosine transform to Eq. 29, and its form is as follow:

$$\tilde{\overline{p}}_{{{\text{h}}fj,l,k{\text{D}}}} { = }\overline{q}_{{l,k{\text{D}}}} O_{sj,l,k}$$

(A7)

$$O_{f{\rm s}j,l,k} = \frac{\pi }{2}\int\limits_{{x_{{fl,k{\text{D}}}} }}^{{x_{{fl,k + 1{\text{D}}}} }} {\left[ \begin{gathered} \cos \left( {\frac{{m\pi \left( {\tan \left( {\theta_{fl} } \right)\left( {x^{\prime}_{{\text{D}}} - x_{{{\text{w}}fl{\text{D}}}} } \right){ + }y_{{{\text{w}}fl{\text{D}}}} } \right)}}{{y_{{{\text{eD}}}} }}} \right) \hfill \\ \times \frac{{\cosh \left( {\gamma_{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{{{\text{D}}1}} } \right) + \cosh \left( {\gamma_{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{{{\text{D}}2}} } \right)}}{{\gamma_{m} \times \sinh \left( {\gamma_{m} x_{{{\text{eD}}}} } \right)}}\sqrt {1 + \left( {\tan \theta_{fl} } \right)^{2} } \hfill \\ \end{gathered} \right]} dx^{\prime}_{{\text{D}}}$$

(A8)

For ease of calculation, a transformation of the constants, a _mj,l,k and b _mj,l,k, are given as follows:

$$c_{m,j,l,k} = \frac{{a_{m,j,l,k} }}{{\overline{q}_{{l,k{\text{D}}}} e^{{ - \gamma_{m,j} x_{{j{\text{D}}}} }} }}$$

(A9)

$$d_{m,j,l,k} = \frac{{b_{m,j,l,k} }}{{\overline{q}_{{l,k{\text{D}}}} e^{{\gamma_{m,j} x_{{j - 1{\text{D}}}} }} }}$$

(A10)

Substituting Eqs. (A7–A10) into Eqs. (A5) and (A6), the general forms of the solution in in Laplace- Fourier domain are obtained:

For the source region,

$${\tilde{\overline{p}}_{f{\rm s}j,l,k{\text{D}}}} = {\bar q_{l,k{\text{D}}}}\left[ {{O_{f{\rm s}j,l,k}}{\text{ + }}\left( {{c_{m,j,l,k}}{e^{{\gamma _{m,j}}\left( {{x_{\text{D}}} - {x_{j{\text{D}}}}} \right)}} + {d_{m,j,l,k}}{e^{{\gamma _{m,j}}\left( {{x_{j - 1{\text{D}}}} - {x_{\text{D}}}} \right)}}} \right)} \right]$$

(A11)

For the no-source region,

$${\tilde{\overline{p}}_{f{\rm s}j,l,k{\text{D}}}} = {\bar q_{l,k{\text{D}}}}\left( {{c_{m,j,l,k}}{e^{{\gamma _{m,j}}\left( {{x_{\text{D}}} - {x_{j{\text{D}}}}} \right)}} + {d_{m,j,l,k}}{e^{{\gamma _{m,j}}\left( {{x_{j - 1{\text{D}}}} - {x_{\text{D}}}} \right)}}} \right)$$

(A12)

All constants, c_m,j,l,k and d_m,j,l,k, can be obtained by substituting Eqs. (A11) and (A12) into the interface connecting conditions of each region (Eqs. (A2) and (A3)) and boundary condition (Eq. (A4)).

Then we apply the finite Fourier inverse transform to Eq. (A11) results in Eq. (31).