Analytical model for pressure and rate analysis of multi-fractured horizontal wells in tight gas reservoirs

Abstract

Multi-fractured horizontal wells (MFHWs) are effective for developing unconventional reservoirs. A complex fracture network around the well and hydraulic fractures form during fracturing. Hydraulic fractures and fracture network are sensitive to the effective stress. However, most existing models do not consider the effects of stress sensitivity. In this study, a new analytical model was established for an MFHW in tight gas reservoirs based on the trilinear flow model. Fractal porosity and permeability were employed to describe the heterogeneous distribution of the complex fracture network. The stress sensitivity of fractures was also considered in the model. Pedrosa substitution and perturbation method were applied to eliminate the nonlinearity of the model. Analytical solutions in the Laplace domain were obtained using Laplace transformation. The model was then validated and applied. Finally, sensitivity analyses of pressure and rate were discussed. The presented model provides a new approach to estimate the effect of fracturing. It can also be utilized to recognize formation properties and forecast the dynamics of pressure and the production of tight gas reservoirs.

Introduction

With the continuous decrease in conventional oil and gas reserves, the development of unconventional resources, such as tight gas and shale gas, has attracted increasing attention. Tight gas reservoir features low permeability and low porosity (Huang et al. 2018), which lead to a quick decline of production for a single well. Multi-fractured horizontal wells (MFHWs) are effective for developing tight gas reservoirs. Multistage fracturing leads to the formation of a complex multi-scale coupling medium, which has complicated seepage characteristics and is composed of matrix, natural and induced fractures (fracture network), and artificial fractures.

A complex analytical model must be established to accurately characterize the complex seepage of MFHWs. Such a model can be established using two methods. One is to divide the fracture into many segments and then use the Green’s function and the point source function to solve the problem. The other one is to establish a linear flow model by simplifying the seepage process as a combination of linear flow. The advantage of the linear flow model approach is that it considers a finite conductivity of the fracture without dividing the fracture into many units. Hence, the linear flow method is more convenient and is a significant alternative for simulating the behavior in MFHW (Wang et al. 2016a). The bilinear flow model was first proposed by Cinco-Ley (1981) for studying the transient pressure behavior of a vertical fractured well with infinite conductivity in an infinite reservoir. Basing on the bilinear flow model, Wong et al. (1986) studied the pressure characteristic of a vertical well with a finite conductivity fracture. Similarly, Lee and Brockenbrough (1986) first proposed a trilinear flow model for a vertical well. The trilinear flow model was introduced into a fractured horizontal well by Brown et al. (2009). They established a multi-fractured horizontal well model by treating the simulated area around hydraulic fracture stages as a dual-porosity medium. The correctness of the model was verified by comparing it with the semi-analytical solutions obtained by Medeiros et al. (2007). Thereafter, the trilinear flow model has been widely used to investigative the dynamic characteristics of MFHWs in unconventional reservoirs (Ozcan et al. 2014; Gao 2014; Wei et al. 2015; Wang et al. 2015; Chen et al. 2016; Wang et al. 2016a, 2016b). Aside from the trilinear flow model, other multi-linear models such as five- (Zhang et al. 2016) and seven-region flow models (Yuan et al. 2015) have been proposed by some scholars. However, the accuracy of these models is not significantly improved compared with that of the trilinear flow model. Moreover, the boundaries between different regions are not easy to divide, and the parameters of each region are difficult to obtain, thereby limiting the practical applications of these models.

Due to the presence of natural fractures and induced fractures generated by hydraulic fracturing, dual-porosity assumption (Barenblatt et al. 1960; Warren and Root 1963; Kazemi et al. 1976) is generally used in the stimulated area around the hydraulic fracture. However, considering the large variations of scale in tight formation, dual-porosity assumption, which is only a first-order approximation, would inevitably lead to a deviation between simulation and actuality (Ozcan et al. 2014). Studies have shown that natural fractures obey fractal distribution in fractured reservoirs. Chang and Yortsos (1990) obtained the power law expression of permeability and porosity of fractures by introducing fractal theory. Subsequently, many scholars have applied the theory of Chang and Yortsos (1990) to seepage models of various types of fractured reservoirs (Tong and Ge 1998; Tong and Zhou 1999; Tong and Liu 2003; Tong et al. 2003; Velazquez et al. 2008; Zhao and Zhang 2011). Cossio et al. (2013) first applied this theory to the trilinear flow model and obtained a semi-analytical solution for a vertically fractured well. Wang et al. (2015) further established a fractal trilinear flow model for MFHWs in tight oil reservoirs.

The effectiveness of the complex fracture network considerably affects yield, drainage area, and final recovery (Mayerhofer et al. 2008; Warpinski et al. 2008). The pressure in the fracture drops rapidly because of the greater conductivity compared with the matrix, which will lead to a production reduction caused by fracture closure. However, previous trilinear flow models do not consider the effect of the stress sensitivity of fractures.

Based on the trilinear flow model proposed by Brown et al. (2009), a new model was established to analyze the pressure and rate responses of MFHWs in tight gas reservoirs by considering the effect of stress sensitivity of fracture. Fractal theory and dual-porosity model were considered in this model to accurately describe the complex fracture network. To obtain an analytical solution of the model, we assumed the permeability modulus of natural and induced fractures and hydraulic fracture to be equal. Although this assumption is inappropriate to some degree, some scholars (Chen et al. 2015, 2016; Teng et al. 2016; Ji et al. 2017) have already proven that this method is acceptable. With Pedrosa substitution, perturbation method, and Laplace transformation method, the analytical solution of the model in the Laplace domain was obtained. Finally, a sensitivity analysis of pressure and rate was conducted.

Mathematical model

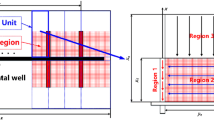
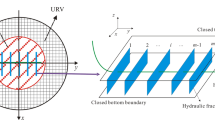
Figure 1 shows the schematic of the trilinear flow model for a MFHW. Regions 1–3 represent the flow in the hydraulic fracture, the stimulated reservoir, and the outer reservoir, respectively. Other assumptions of the presented mathematical model are as follows:

Fig. 1

Schematic of the trilinear flow model for MFHW in tight gas reservoirs

• 1. The outer boundary of the rectangular tight gas reservoir is impermeable, and the length and width of the reservoir are $L_{\text{R}}$ and $W_{\text{R}}$, respectively.

• 2. The height of each fracture is equal to the formation thickness. The hydraulic fractures are the same in feature and are equally spaced. The yield of each fracture is the same. No gas flow is observed at the end of the fracture, as well as at the region at the parallel fracture direction in the center of the fracture spacing.

• 3. Region 3 is considered a single medium, and the effect of gas slippage is considered. Region 2 is considered a dual-porosity medium, and the fractal porosity and permeability coupling with stress sensitivity are employed. In region 1, the effect of stress sensitivity is considered.

• 4. The gas flow in the reservoir is isothermal, and the effects of gravity and capillary pressure are negligible.

The viscosity and compression coefficient of gas are functions of pressure. Therefore, a pseudo-pressure function (Russell et al. 1966) was introduced to eliminate the nonlinearity of the model. The definitions of dimensionless variables are shown in Table 1.

Table 1 Definitions of dimensionless variables

Mathematical model in outer reservoir (region 3)

According to the apparent permeability derived by Ozkan et al. (2010), the apparent permeability considering the effect of gas slippage in region 3 is as follows:

$$k_{{3{\text{a}}}} = b_{3} k_{3}$$

(1)

where $b_{3} = 1 + {{\left( {\mu c_{{{\text{g}}3}} D_{{{\text{g}}3}} } \right)} \mathord{\left/ {\vphantom {{\left( {\mu c_{{{\text{g}}3}} D_{{{\text{g}}3}} } \right)} {k_{3} }}} \right. \kern-0pt} {k_{3} }}$. Therefore, the seepage velocity of matrix in region 3 is as follows:

$$v_{3} = - \frac{{3.6k_{{3{\text{a}}}} }}{\mu }\frac{{\partial p_{3} }}{\partial x}.$$

(2)

Governing equations in region 3 are obtained by combining the movement equation with the continuity equation. By introducing pseudo-functions and dimensionless variables into governing equations, we describe the mathematical model in region 3 as follows:

$$\frac{{\partial^{2} m_{{3{\text{D}}}} }}{{\partial x_{\text{D}}^{2} }} = \frac{1}{{\eta_{{3{\text{D}}}} }}\frac{{\partial m_{{3{\text{D}}}} }}{{\partial t_{\text{D}} }}$$

(3)

$${\text{Initial condition}}:\;\left. {m_{{3{\text{D}}}} } \right|_{{t_{\text{D}} = 0}} = 0$$

(4)

$${\text{Inner boundary condition}}:\;\left. {m_{{3{\text{D}}}} } \right|_{{x_{\text{D}} = x_{\text{fD}} }} = \left. {m_{{2{\text{fD}}}} } \right|_{{x_{\text{D}} = x_{\text{fD}} }}$$

(5)

$${\text{Outer boundary condition}}:\left. {\frac{{\partial m_{{3{\text{D}}}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = x_{{e{\text{D}}}} }} = 0.$$

(6)

Mathematical model in stimulated reservoir (region 2)

The dual-porosity model was used to model the stimulated area. Moreover, the power law expression of permeability and porosity of natural and induced fractures considering the effect of stress sensitivity (Tong and Zhou 1999) was employed. The permeability and porosity are given by:

$$k_{2f} = k_{{2{\text{fref}}}} \,{\text{e}}^{{ - \gamma \left( {p_{i} - p_{2f} } \right)}} \left( {\frac{y}{{b_{\text{f}} }}} \right)^{{D_{\text{f}} - \theta - 2}}$$

(7)

$$\phi_{2f} = \phi_{{2{\text{fref}}}}\, {\text{e}}^{{ - c_{\phi 2f} \left( {p_{i} - p_{2f} } \right)}} \left( {\frac{y}{{b_{\text{f}} }}} \right)^{{D_{\text{f}} - 2}} .$$

(8)

Similarly, governing equations in region 2 were obtained. The mathematical model in region 2 can be described as follows:

Fracture network:

$$\begin{aligned} \frac{{\partial^{2} m_{{2{\text{fD}}}} }}{{\partial y_{\text{D}}^{2} }} + \frac{{D_{\text{f}} - \theta - 2}}{{y_{\text{D}} }}\frac{{\partial m_{{2{\text{fD}}}} }}{{\partial y_{\text{D}} }} - \gamma_{\text{D}} \left( {\frac{{\partial m_{{2{\text{fD}}}} }}{{\partial y_{\text{D}} }}} \right)^{2} + {\text{e}}^{{\gamma_{\text{D}} m_{{2{\text{fD}}}} }} \lambda \frac{1}{{b_{\text{fD}}^{\theta } }}y_{\text{D}}^{\theta } \left( {m_{2mD} - m_{2fD} } \right) \hfill \\ \left. { + \,{\text{e}}^{{\gamma_{\text{D}} m_{{ 2 {\text{fD}}}} }} y_{\text{D}}^{\theta } \frac{1}{{F_{{2{\text{D}}}} }}\frac{1}{{b_{\text{fD}}^{\theta } }}\frac{{\partial m_{{3{\text{D}}}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = x_{\text{fD}} }} = {\text{e}}^{{\gamma_{\text{D}} m_{{2{\text{fD}}}} }} \frac{{y_{\text{D}}^{\theta } }}{{b_{\text{fD}}^{\theta } }}\omega \frac{{\partial m_{{2{\text{fD}}}} }}{{\partial t_{\text{D}} }} \hfill \\ \end{aligned}$$

(9)

$${\text{Matrix}}:\;\;\left( {1 - \omega } \right)\frac{{\partial m_{{2m{\text{D}}}} }}{{\partial t_{\text{D}} }} + \lambda \left( {m_{{2m{\text{D}}}} - m_{{2{\text{fD}}}} } \right) = 0$$

(10)

$${\text{Initial condition}}:\left. {m_{{2{\text{fD}}}} } \right|_{{t_{\text{D}} = 0}} = \left. {m_{{2m{\text{D}}}} } \right|_{{t_{\text{D}} = 0}} = 0$$

(11)

$${\text{Inner boundary condition}}:\left. {m_{{2{\text{fD}}}} } \right|_{{y_{\text{D}} = b_{\text{fD}} }} = \left. {m_{{1{\text{D}}}} } \right|_{{y_{\text{D}} = b_{\text{fD}} }}$$

(12)

$${\text{Outer boundary condition}}:\left. {\frac{{\partial m_{{2{\text{fD}}}} }}{{\partial y_{\text{D}} }}} \right|_{{y_{\text{D}} = y_{{e{\text{D}}}} }} = 0.$$

(13)

Mathematical model in hydraulic fracture (region 1)

To consider the effect of stress sensitivity on hydraulic fracture, we adopted a stress-dependent permeability.

$$k_{1} = k_{{1{\text{ref}}}}\, {\text{e}}^{{ - \gamma \left( {p_{i} - p_{1} } \right)}} .$$

(14)

Similarly, governing equations in region 1 were obtained. The mathematical model in region 1 can be described as follows:

$$\frac{{\partial^{2} m_{{1{\text{D}}}} }}{{\partial x_{\text{D}}^{2} }} - \gamma_{D} \left( {\frac{{\partial m_{{1{\text{D}}}} }}{{\partial x_{\text{D}} }}} \right)^{2} - {\text{e}}^{{\gamma_{D} m_{1D} }} \frac{1}{{\eta_{{1{\text{D}}}} }}\frac{{\partial m_{{1{\text{D}}}} }}{{\partial t_{\text{D}} }} + \frac{1}{{F_{{1{\text{D}}}} }}\left. {\frac{{\partial m_{{2{\text{fD}}}} }}{{\partial y_{\text{D}} }}} \right|_{{y_{\text{D}} = b_{\text{fD}} }} = 0$$

(15)

$${\text{Initial condition}}:\;\left. {m_{1D} } \right|_{{t_{D} = 0}} = 0$$

(16)

$$\begin{aligned} {\text{Inner boundary condition}}:\left\{ {\begin{array}{*{20}l} {\left. {{\text{e}}^{{ - \gamma_{\text{D}} m_{{1{\text{D}}}} }} \frac{{\partial m_{{1{\text{D}}}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = 0}} = - \frac{1}{{2F_{{ 1 {\text{D}}}} }}} \hfill & \quad {\left( {\text{Constant gas rate}} \right)} \hfill \\ {\left. {m_{{1{\text{D}}}} } \right|_{{x_{\text{D}} = 0}} = 1} \hfill & \quad { \left( {{\text{Constant bottom}}\;{\text{hole pressure}}} \right)} \hfill \\ \end{array} } \right. \hfill \\ \hfill \\ \end{aligned}$$

(17)

$${\text{Outer boundary condition}}:\left. {\frac{{\partial m_{{1{\text{D}}}} }}{{\partial x_{\text{D}} }}} \right|_{{x_{\text{D}} = x_{\text{fD}} }} = 0.$$

(18)

Solutions

To obtain the pressure and rate solution, we performed Laplace transformation of the equations and boundary conditions. Moreover, Pedrosa substitution and perturbation method were applied to linearize the equations. Finally, analytical solutions of dimensionless bottom hole pressure and dimensionless gas rate in Laplace domain were obtained. Detailed derivation of the solution can be found in Appendix 1.

Bottom hole pressure

The dimensionless bottom hole pressure in Laplace domain is as follows:

$$\bar{\xi }_{0wD} = \frac{1}{{2\sqrt {a_{1} } F_{{ 1 {\text{D}}}} s}}\frac{1}{{\tanh \left( {\sqrt {a_{1} } x_{\text{fD}} } \right)}}.$$

(19)

According to the Duhamel principle, the dimensionless bottom hole pressure incorporating the wellbore storage effect in the Laplace domain can be obtained as follows (Zhao et al. 2015):

$$\bar{\xi }_{{0wD,{\text{storage}}}} = \frac{{\bar{\xi }_{0wD} }}{{1 + s^{2} C_{D} \bar{\xi }_{0wD} }}$$

(20)

Using the Stehfest algorithm (Stehfest 1970a, b) and inverse substitution, the dimensionless pseudo-pressure at bottom hole in the time domain was obtained as follows:

$$m_{wD} = - \frac{1}{{\gamma_{D} }}\ln \left( {1 - \gamma_{D} \xi_{{0wD,{\text{storage}}}} } \right).$$

(21)

Gas rate

The dimensionless gas rate is as follows:

$$\bar{q}_{D} = 2F_{1D} \sqrt {a_{1} } \frac{{1 - e^{{ - \gamma_{D} }} }}{{\gamma_{D} s}}\tanh \left( {\sqrt {a_{1} } x_{fD} } \right).$$

(22)

The gas rate in the time domain can be also obtained by using the Stehfest algorithm. $q_{D}$ is the rate for a single symmetry element. To obtain the total rate of horizontal well, we employed Meyer’s method (Meyer et al. 2010).

Figure 2 illustrates the system configuration of $N_{\text{F}}$, number of equally spaced fractures in closed rectangular reservoir with aspect ratio ($\varPi$). The individual fractured reservoir aspect ratios for the in-between fractures ($\varPi_{c}$) and extreme fractures ($\varPi_{e}$) are given by:

Fig. 2

Schematic of multiple stage fractures in closed reservoir

$$\varPi_{c} = \frac{{W_{R} }}{{2y_{e} }},\varPi_{e} = \frac{{W_{R} }}{{2y_{o} }}.$$

(23)

The total flow rate $Q_{D}$ of horizontal well is given by:

$$Q_{D} = q_{D} \left( {\varPi_{c} } \right) \cdot \left( {N_{F} - 1} \right) + q_{D} \left( {\varPi_{e} } \right).$$

(24)

Validation and application

To validate the bottom hole pressure solution, we compared the solution with the classic dual-porosity trilinear flow model obtained from Brown et al. (2009) for the special case of $D_{f} = 2$,$\theta { = }0$,$\gamma { = }0$. The input data used for the comparison are listed in Fig. 3. As can be seen from Fig. 3, there is a good agreement between the two solutions for both dimensionless pressure and pressure derivative. We further verified the solution by applying the model to match with actual data of Well 314 (Al-Ahmadi and Wattenbarger 2011). Some of the reservoir parameters are collected from the paper SPE149054 as shown in Table 2. After matching the rate data, other reservoir parameters, especially the parameters of the complex fracture network (such as fracture permeability, inter-porosity coefficient, fractal dimension, connectivity index and permeability modulus) are obtained. The parameters obtained from the matching are given in Table 2 and marked with an asterisk. As shown in Fig. 4, the new model matches the gas rate quite well. Therefore, our model could be a useful tool for pressure and rate analysis of tight gas wells.

Fig. 3

Comparison between the new model and the classic dual-porosity trilinear flow model

Table 2 Relevant parameters in a real tight gas reservoir

Fig. 4

Matching result of gas rate for Well 314

Pressure and rate behavior analyses

The pressure and rate responses for MFHW in tight gas reservoir were calculated with the well testing model proposed above. The transient pressure and rate type curves are plotted in Fig. 5. An MFHW in tight gas reservoirs has five possible flow stages as follows:

Fig. 5

Transient pressure type curves of MFHW in tight gas reservoir

(1) Wellbore storage stage. The pseudo-pressure curve and the pseudo-pressure derivative curve coincide at this stage, and the slopes of the two curves are 1. (2) Transitional flow. (3) Inter-porosity flow. The derivative curve of this stage is characterized by a “dip.” At this stage, the rate of decline in gas rate slows down because of inter-porosity flow. (4) Compound linear flow. The derivative curves of this stage are characterized by a slope of 1/2. At this stage, gas in outer region begins to flow linearly, and gas rate begins to decline rapidly. (5) Boundary dominated flow. The pseudo-pressure curve and the pseudo-pressure derivative curve coincide again at this stage, and the slope of the two curves is 1. The quick depletion of the formation pressure leads to a closure of the natural and induced fractures. As a result, gas rate rapidly decreases until the well stops production.

Then, the effects of relevant parameters on the type curves were analyzed. The effects of inter-porosity flow coefficient $\lambda$ on pressure and rate are shown in Fig. 6. $\lambda$ determines the location and size of the “dip” in the pseudo-pressure derivative curve. The larger the value of $\lambda$, the more left and more down the location of the “dip.” Besides, the larger the value of $\lambda$, the higher the gas rate at the middle stage, which leads to an earlier decline at the later stage. This is because $\lambda$ is related to shape factor $\sigma$. When the value of $\sigma$ is small, the characteristic length of the matrix is large, which leads to a small density of the fracture network. The inter-porosity flow now has a slim chance of occurrence, and the quantity of the flow is small. As a result, the inter-porosity flow stage is delayed. On the contrary, a larger value of $\lambda$ means a higher density of the fracture network; thus, the gas rate increases at the middle stage.

Fig. 6

Effect of inter-porosity flow coefficient on pseudo-pressure and rate curves. a Dimensionless pseudo-pressure and pseudo-pressure derivative curve, b dimensionless rate curve

The effects of storativity ratio $\omega$ on pressure and rate are shown in Fig. 7. The storativity ratio mainly affects the width and depth of the “dip” in the pseudo-pressure derivative curve. The smaller the value of $\omega$, the deeper and wider the “dip” in the derivative curve. This is because $\omega$ reflects the gas capacity in the fracture network. A smaller value of $\omega$ means less gas in the fracture network; thus, the gas in the matrix must transfer into the fracture network earlier. The smaller the value of $\omega$ is, the smaller the gas rate at the early stage.

Fig. 7

Effect of storativity ratio on pseudo-pressure and rate curves. a Dimensionless pseudo-pressure and pseudo-pressure derivative curve, b dimensionless rate curve

The effects of fractal dimension $D_{\text{f}}$ on pressure and rate are shown in Fig. 8. The fractal dimension significantly affects the curves throughout entire stages, except for the early stage when wellbore storage is the predominant mechanism. $D_{\text{f}}$ reflects the development of the fracture network. The greater the value of $D_{\text{f}}$, the more the induced fractures produced by the fracturing process. The fractal permeability of the fracture network reduces slowly further away from the hydraulic fracture, which leads to a lower seepage resistance. Therefore, the position of pseudo-pressure and pseudo-pressure derivative curves becomes lower, and the value of gas rate becomes higher. Therefore, $D_{\text{f}}$ is a satisfactory parameter that can be used to describe and evaluate the effects of multistage fracturing.

Fig. 8

Effect of fractal dimension on pseudo-pressure and rate curves. a Dimensionless pseudo-pressure and pseudo-pressure derivative curve, b dimensionless rate curve

The effects of conductivity index $\theta$ on pressure and rate are shown in Fig. 9. The positions of the pseudo-pressure and pseudo-pressure derivative curves are lower when the value of $\theta$ is smaller. The gas rate decreases as the value of $\theta$ increases. This is because $\theta$ is related to the topology of the fracture network and reflects the connectivity of the fractal fracture network. In general, the more complex the fracture network is, the worse the connectivity of the fracture network, and the larger the value of $\theta$. Therefore, $\theta$ can be also used to evaluate the quality of the fracture network.

Fig. 9

Effect of conductivity index on pseudo-pressure and rate curves. a Dimensionless pseudo-pressure and pseudo-pressure derivative curve, b dimensionless rate curve

The effects of fracture conductivity $w_{f} k_{{1{\text{ref}}}}$ on pressure and rate are shown in Fig. 10. The fracture conductivity mainly affects the pressure and rate at the early and middle stages. The larger the value of $w_{f} k_{{1{\text{ref}}}}$, the easier the gas flow in the hydraulic fracture. Therefore, the position of the pseudo-pressure and pseudo-pressure derivative becomes lower, and the position of gas rate becomes higher. However, the larger the fracture conductivity, the earlier the gas rate begins to decrease. Hence, fracture conductivity for a specific tight gas reservoir has an optimal value.

Fig. 10

Effect of fracture conductivity on pseudo-pressure and rate curves. a Dimensionless pseudo-pressure and pseudo-pressure derivative curve, b dimensionless rate curve

The effects of dimensionless permeability modulus $\gamma_{\text{D}}$ on pressure and rate are shown in Fig. 11. The definition of dimensionless permeability modulus varies under different working systems. Therefore, the values of $\gamma_{\text{D}}$ in Fig. 11a and b are different. The stress sensitivity of fractures also significantly affects the curves throughout the different stages, except for the early time when wellbore storage is the predominant mechanism. The larger the value of $\gamma_{\text{D}}$, the faster the decrease in fracture permeability, which leads to a higher position of pseudo-pressure and pseudo-pressure derivative curves and a lower gas rate. When the gas rate is constant, a large pressure drop is required to maintain the constant rate as the value of $\gamma_{\text{D}}$ is large, which leads to a short seepage period.

Fig. 11

Effect of dimensionless permeability modulus on pseudo-pressure and rate curves. a Dimensionless pseudo-pressure and pseudo-pressure derivative curve, b dimensionless rate curve

Conclusions

In this paper, we established an analytical model for an MFHW in tight gas reservoirs based on the trilinear flow model. Fractal porosity and permeability were applied to consider the heterogeneous distribution of the complex fracture network. Moreover, the stress sensitivity of fractures was considered in the model. Pedrosa substitution, perturbation method, and Laplace transformation were employed to solve this model. The transient pressure and rate type curves were obtained, and a sensitivity analysis was performed. The following conclusions can be obtained:

• 1. The transient pressure and rate type curves contain five flow regimes, including the wellbore storage stage, transitional flow, inter-porosity flow, compound linear flow, and boundary dominated flow.

• 2. Inter-porosity flow coefficient is related to the density of the fracture network. The larger the inter-porosity flow coefficient is, the lower the position of pressure curves and the larger the gas rate at the inter-porosity flow stage. Storativity ratio reflects the storage capacity of the fracture network. The larger the storativity ratio is, the lower the position of pressure curves and the larger the gas rate at the early stage.

• 3. Fractal dimension and conductivity index can fully reflect the development and connectivity of the complex fracture network. When the fractal dimension is larger and the connectivity index is smaller, more fractures are produced by fracturing process, and the connectivity between fractures is better, which leads to a lower position of pressure curves and a larger gas rate.

• 4. Fracture conductivity considerably affects the pressure and rate at the early and middle stages. A larger fracture conductivity leads to a lower position of the pressure curves and a larger gas rate at early and middle stages.

• 5. The effect of the stress sensitivity of the fracture is obvious and cannot be neglected. The larger the dimensionless permeability modulus, the higher the position of pressure curves and the lower the gas rate.

• 6. The model presented here can be utilized to recognize formation properties and forecast the pressure and rate dynamics of tight gas reservoirs. In addition, the new model is recommended as an evaluation model for screening attractive tight gas reservoirs and evaluating the effect of fracturing.

Appendix 1: Analytical solutions in the Laplace domain

Outer reservoir (region 3)

By taking the Laplace transformation, the model of region 3 in Laplace domain can be obtained:

$$\begin{aligned} \left\{ {\begin{array}{*{20}l} {\frac{{\partial^{2} \bar{m}_{3D} }}{{\partial x_{D}^{2} }} - \frac{1}{{\eta_{3D} }}s\bar{m}_{3D} = 0} \hfill \\ {\left. {\bar{m}_{3D} } \right|_{{x_{D} = x_{fD} }} = \left. {\bar{m}_{2fD} } \right|_{{x_{D} = x_{fD} }} } \hfill \\ {\left. {\frac{{\partial \bar{m}_{3D} }}{{\partial x_{D} }}} \right|_{{x_{D} = x_{eD} }} = 0} \hfill \\ \end{array} } \right.. \hfill \\ \hfill \\ \end{aligned}$$

(A.1)

The general solution of the model in the Laplace domain is as follows:

$$\bar{m}_{3D} = A_{3} {\text{e}}^{{\sqrt {\frac{1}{{\eta_{3D} }}s} x_{D} }} + B_{3} {\text{e}}^{{ - \sqrt {\frac{1}{{\eta_{3D} }}s} x_{D} }} .$$

(A.2)

By taking the derivative of Eq. (A.2) with respect to $x_{D}$, we obtain:

$$\frac{{\partial \bar{m}_{3D} }}{{\partial x_{D} }} = A_{3} \sqrt {\frac{1}{{\eta_{3D} }}s} {\text{e}}^{{\sqrt {\frac{1}{{\eta_{3D} }}s} x_{D} }} - B_{3} \sqrt {\frac{1}{{\eta_{3D} }}s} {\text{e}}^{{ - \sqrt {\frac{1}{{\eta_{3D} }}s} x_{D} }} .$$

(A.3)

Substituting inner and outer boundary conditions into Eqs. (A.2) and (A.3), we can obtain:

$$\left\{ \begin{aligned} A_{3} = \frac{{{\text{e}}^{{ - 2\sqrt {\frac{1}{{\eta_{3D} }}s} x_{eD} }} }}{{{\text{e}}^{{ - 2\sqrt {\frac{1}{{\eta_{3D} }}s} x_{eD} + \sqrt {\frac{1}{{\eta_{3D} }}s} x_{fD} }} + {\text{e}}^{{ - \sqrt {\frac{1}{{\eta_{3D} }}s} x_{fD} }} }}\left. {\bar{m}_{2fD} } \right|_{{x_{D} = x_{fD} }} \hfill \\ B_{3} = \frac{1}{{{\text{e}}^{{ - 2\sqrt {\frac{1}{{\eta_{3D} }}s} x_{eD} + \sqrt {\frac{1}{{\eta_{3D} }}s} x_{fD} }} + {\text{e}}^{{ - \sqrt {\frac{1}{{\eta_{3D} }}s} x_{fD} }} }}\left. {\bar{m}_{2fD} } \right|_{{x_{D} = x_{fD} }} . \hfill \\ \end{aligned} \right.$$

(A.4)

Substituting Eq. (A.4) into Eq. (A.3), we obtain:

$$\left. {\frac{{\partial \bar{m}_{3D} }}{{\partial x_{D} }}} \right|_{{x_{D} = x_{fD} }} = a_{3} \left. {\bar{m}_{2fD} } \right|_{{x_{D} = x_{fD} }}$$

(A.5)

where $a_{3} = \sqrt {\frac{1}{{\eta_{3D} }}s} \tanh \left[ {\sqrt {\frac{1}{{\eta_{3D} }}s} \left( {x_{fD} - x_{eD} } \right)} \right].$

Stimulated reservoir (region 2)

Obviously, there is a strong nonlinearity in the model of region 2. Hence, the Pedrosa substitution and the perturbation method are applied to linearize the equations (Pedrosa 1986; Wang 2014):

$$m_{2fD} = - \frac{1}{{\gamma_{\text{D}} }}\ln \left( {1 - \gamma_{\text{D}} \zeta } \right).$$

(A.6)

Similarly, dimensionless pseudo-pressure of region 1 can be also substituted to the following form:

$$m_{1D} = - \frac{1}{{\gamma_{D} }}\ln \left( {1 - \gamma_{D} \xi } \right).$$

(A.7)

Performing a parameter perturbation in $\gamma_{\text{D}}$ by defining the following series: (Kikani and Pedrosa 1991; Chen et al. 2016):

$$\zeta = \zeta_{0} + \gamma_{\text{D}} \zeta_{1} + \gamma_{\text{D}}^{2} \zeta_{2} + \gamma_{\text{D}}^{3} \zeta_{3} + \cdots$$

(A.8)

$$\frac{1}{{1 - \gamma_{\text{D}} \zeta }} = 1 + \gamma_{\text{D}} \zeta + \gamma_{\text{D}}^{2} \zeta^{2} + \gamma_{\text{D}}^{3} \zeta^{3} + \cdots$$

(A.9)

$$- \frac{1}{{\gamma_{D} }}\ln \left( {1 - \gamma_{D} \zeta } \right) = \zeta + \frac{1}{2}\gamma_{D} \zeta^{2} + \frac{1}{3}\gamma_{D} \zeta^{3} + \cdots$$

(A.10)

Considering that the value of $\gamma_{D}$ is always small, usually $\gamma_{D} \zeta \text{ < }1$. The zero-order perturbation solution can satisfy accuracy requirement. Therefore, the model of region 2 can be transformed to the following form:

$$\left\{ \begin{gathered} \frac{{\partial^{2} \zeta_{0} }}{{\partial y_{D}^{2} }} + \frac{{D_{f} - \theta - 2}}{{y_{D} }}\frac{{\partial \zeta_{0} }}{{\partial y_{D} }} + \lambda \frac{1}{{b_{fD}^{\theta } }}y_{D}^{\theta } \left( {m_{2mD} - \zeta_{0} } \right)\left. { +\, y_{D}^{\theta } \frac{1}{{F_{2D} }}\frac{1}{{b_{fD}^{\theta } }}\frac{{\partial m_{3D} }}{{\partial x_{D} }}} \right|_{{x_{D} = x_{fD} }} = \frac{{y_{D}^{\theta } }}{{b_{fD}^{\theta } }}\omega \frac{{\partial \zeta_{0} }}{{\partial t_{D} }} \hfill \\ \left( {1 - \omega } \right)\frac{{\partial m_{2mD} }}{{\partial t_{D} }} + \lambda \left( {m_{2mD} - \zeta_{0} } \right) = 0 \hfill \\ \left. {\zeta_{0} } \right|_{{t_{D} = 0}} = \left. {m_{2mD} } \right|_{{t_{D} = 0}} = 0 \hfill \\ \left. {\zeta_{0} } \right|_{{y_{D} = b_{fD} }} = \left. {\xi_{0} } \right|_{{y_{D} = b_{fD} }} \hfill \\ \left. {\frac{{\partial \zeta_{0} }}{{\partial y_{D} }}} \right|_{{y_{D} = y_{eD} }} = 0. \hfill \\ \end{gathered} \right.$$

(A.11)

By taking the Laplace transformation, the model of region 2 in Laplace domain can be obtained:

$$\frac{{\partial^{2} \bar{\zeta }_{0} }}{{\partial y_{D}^{2} }} + \frac{{D_{f} - \theta - 2}}{{y_{D} }}\frac{{\partial \bar{\zeta }_{0} }}{{\partial y_{D} }} + \lambda \frac{1}{{b_{fD}^{\theta } }}y_{D}^{\theta } \left( {\bar{m}_{2mD} - \bar{\zeta }_{0} } \right) + \left. {y_{D}^{\theta } \frac{1}{{F_{2D} }}\frac{1}{{b_{fD}^{\theta } }}\frac{{\partial \bar{m}_{3D} }}{{\partial x_{D} }}} \right|_{{x_{D} = x_{fD} }} = \frac{{y_{D}^{\theta } }}{{b_{fD}^{\theta } }}\omega s\bar{\zeta }_{0}$$

(A.12)

$$\left( {1 - \omega } \right)s\bar{m}_{2mD} + \lambda \left( {\bar{m}_{2mD} - \bar{\zeta }_{0} } \right) = 0.$$

(A.13)

Equation (A.13) can be transformed to the following form:

$$\bar{m}_{2mD} = f\left( s \right)\bar{\zeta }_{0} .$$

(A.14)

Here, $f\left( s \right) = \frac{\lambda }{{\left( {1 - \omega } \right)s + \lambda }}.$

Substituting Eqs. (A.5) and (A.14) into Eq. (A.12), we obtain:

$$\frac{{\partial^{2} \bar{\zeta }_{0} }}{{\partial y_{D}^{2} }} + \frac{{D_{f} - \theta - 2}}{{y_{D} }}\frac{{\partial \bar{\zeta }_{0} }}{{\partial y_{D} }} = a_{2} y_{D}^{\theta } \bar{\zeta }_{0} .$$

(A.15)

Here, $a_{2} = \frac{1}{{b_{fD}^{\theta } }}\omega s - \frac{{\lambda \left[ {f\left( s \right) - 1} \right]}}{{b_{fD}^{\theta } }} - \frac{1}{{b_{fD}^{\theta } F_{2D} }}a_{1} .$.

Therefore, the final equations of the model are as follows:

$$\left\{ \begin{gathered} \frac{{\partial^{2} \bar{\zeta }_{0} }}{{\partial y_{D}^{2} }} + \frac{{D_{f} - \theta - 2}}{{y_{D} }}\frac{{\partial \bar{\zeta }_{0} }}{{\partial y_{D} }} = a_{2} y_{D}^{\theta } \bar{\zeta }_{0} \hfill \\ \left. {\bar{\zeta }_{0} } \right|_{{y_{D} = b_{fD} }} = \left. {\bar{\xi }_{0} } \right|_{{y_{D} = b_{fD} }} \hfill \\ \left. {\frac{{\partial \bar{\zeta }_{0} }}{{\partial y_{D} }}} \right|_{{y_{D} = y_{eD} }} = 0. \hfill \\ \end{gathered} \right.$$

(A.16)

The generalized Bessel function can be described as follows:

$$\frac{{{\text{d}}^{2} R}}{{{\text{d}}r^{2} }} + \frac{n}{r}\frac{{{\text{d}}R}}{{{\text{d}}r}} - sr^{m - n} R = 0.$$

(A.17)

When $2 + m - n\text{ > }0$, the general solution of the function is as follows:

$$R(r,s) = r^{{\frac{1 - n}{2}}} \left[ {A_{2} I_{\nu } \left( {\frac{2\sqrt s }{2 + m - n}r^{{\frac{2 + m - n}{2}}} } \right) + B_{2} K_{\nu } \left( {\frac{2\sqrt s }{2 + m - n}r^{{\frac{2 + m - n}{2}}} } \right)} \right].$$

(A.18)

Here, $\nu = \frac{1 - n}{2 + m - n} = \frac{{3 - D_{f} + \theta }}{2 + \theta }.$

By comparing Eq. (A.16) and Eq. (A.17), we obtain:

$$\left\{ \begin{array}{l} m - n = \theta \\ n = D_{f} - \theta - 2. \end{array} \right.$$

(A.19)

Obviously, $2 + m - n = \theta + 2\text{ > }0$. Therefore, the general solution of the model is as follows:

$$\bar{\zeta }_{0} = y_{D}^{\alpha } \left[ {A_{2} I_{\nu } \left( {\beta y_{D}^{\chi } } \right) + B_{2} K_{\nu } \left( {\beta y_{D}^{\chi } } \right)} \right].$$

(A.20)

Here, $\alpha = \frac{{3 - D_{f} + \theta }}{2}$, $\beta = \frac{{2\sqrt {a_{2} } }}{\theta + 2}$, $\chi = \frac{\theta + 2}{2}.$.

By taking the derivative of Eq. (A.20) with respect to $y_{D}$, we obtain:

$$\frac{{\partial \bar{\zeta }_{0} }}{{\partial y_{D} }} = y_{D}^{\alpha - 1 + \chi } \beta \chi \left[ {A_{2} I_{\nu - 1} \left( {\beta y_{D}^{\chi } } \right) - B_{2} K_{\nu - 1} \left( {\beta y_{D}^{\chi } } \right)} \right].$$

(A.21)

Substituting inner and outer boundary conditions into Eqs. (A.20) and (A.21), we can obtain:

$$\left\{ \begin{aligned} A_{2} = \frac{1}{{b_{fD}^{\alpha } }}\frac{{K_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right)}}{{I_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right)K_{\nu } \left( {\beta b_{fD}^{\chi } } \right) + I_{\nu } \left( {\beta b_{fD}^{\chi } } \right)K_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right)}}\left. {\bar{\xi }_{0} } \right|_{{y_{D} = b_{fD} }} \hfill \\ B_{2} = \frac{1}{{b_{fD}^{\alpha } }}\frac{{I_{\nu - 1} \left( {\beta y_{eD}^{\gamma } } \right)}}{{I_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right)K_{\nu } \left( {\beta b_{fD}^{\chi } } \right) + I_{\nu } \left( {\beta b_{fD}^{\chi } } \right)K_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right)}}\left. {\bar{\xi }_{0} } \right|_{{y_{D} = b_{fD} }} \hfill \\ \end{aligned} \right.$$

(A.22)

Substituting Eq. (A.22) into Eq. (A.21), we obtain:

$$\left. {\frac{{\partial \bar{\zeta }_{0} }}{{\partial y_{D} }}} \right|_{{y_{D} = b_{fD} }} = a_{2}^{\prime } \left. {\bar{\xi }_{0} } \right|_{{y_{D} = b_{fD} }} .$$

(A.23)

Here, $a_{2}^{\prime } = \sqrt {a_{2} } \frac{{I_{\nu - 1} \left( {\beta b_{fD}^{\chi } } \right)K_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right) - I_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right)K_{\nu - 1} \left( {\beta b_{fD}^{\chi } } \right)}}{{I_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right)K_{\nu } \left( {\beta b_{fD}^{\chi } } \right) + I_{\nu } \left( {\beta b_{fD}^{\chi } } \right)K_{\nu - 1} \left( {\beta y_{eD}^{\chi } } \right)}}b_{fD}^{ - 1 + \chi }.$

Hydraulic fracture (region 1)

Similarly, the model of region 1 in Laplace domain is as follows:

$$\left\{ \begin{gathered} \frac{{\partial ^{2} \bar{\xi }_{0} }}{{\partial x_{D} ^{2} }} - a_{1} \bar{\xi }_{0} = 0 \hfill \\ \left. {\frac{{\partial \bar{\xi }_{0} }}{{\partial x_{D} }}} \right|_{{x_{D} = 0}} = - \frac{1}{{2F_{{1D}} s}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {CGR} \right) \hfill \\ \left. {\bar{\xi }_{0} } \right|_{{x_{D} = 0}} = \frac{{1 - e^{{ - \gamma _{D} }} }}{{\gamma _{D} s}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {CBP} \right) \hfill \\ \left. {\frac{{\partial \bar{\xi }_{0} }}{{\partial x_{D} }}} \right|_{{x_{D} = x_{{fD}} }} = 0 \hfill \\ \end{gathered} \right.$$

(A.24)

where $a_{1} = \frac{1}{{\eta_{1D} }}s - \frac{1}{{F_{1D} }}a_{2}^{\prime }$.

The general solution of the governing equation is as follows:

$$\bar{\xi }_{0} = A_{1} {\text{e}}^{{\sqrt {a_{1} } x_{D} }} + B_{1} {\text{e}}^{{ - \sqrt {a_{1} } x_{D} }} .$$

(A.25)

By taking the derivative of Eq. (A.25) with respect to $x_{D}$, we obtain:

$$\frac{{\partial \bar{\xi }_{0} }}{{\partial x_{D} }} = A_{1} \sqrt {a_{1} } {\text{e}}^{{\sqrt {a_{1} } x_{D} }} - B_{1} \sqrt {a_{1} } {\text{e}}^{{ - \sqrt {a_{1} } x_{D} }} .$$

(A.26)

• 1. Constant gas rate

Substituting constant gas rate inner boundary condition and the outer boundary condition into Eqs. (A.25) and (A.26), we can obtain:

$$\left\{ \begin{aligned} A_{1} = \frac{{{\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} }}{{2\sqrt {a_{1} } F_{1D} \left( {{\text{e}}^{{\sqrt {a_{1} } x_{fD} }} - {\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} } \right)s}} \hfill \\ B_{1} = \frac{{{\text{e}}^{{\sqrt {a_{1} } x_{fD} }} }}{{2\sqrt {a_{1} } F_{1D} \left( {{\text{e}}^{{\sqrt {a_{1} } x_{fD} }} - {\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} } \right)s}}. \hfill \\ \end{aligned} \right.$$

(A.27)

Substituting Eq. (A.27) into Eq. (A.25), the solution of hydraulic fracture can be obtained as follows:

$$\bar{\xi }_{0} = \frac{1}{{2\sqrt {a_{1} } F_{1D} s}}\frac{{{\text{e}}^{{\sqrt {a_{1} } x_{fD} }} {\text{e}}^{{ - \sqrt {a_{1} } x_{D} }} + {\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} {\text{e}}^{{\sqrt {a_{1} } x_{D} }} }}{{{\text{e}}^{{\sqrt {a_{1} } x_{fD} }} - {\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} }}.$$

(A.28)

By setting $x_{D} = 0$ in Eq. (A.28), we can obtain the bottom hole pressure of the fractured horizontal well in Laplace domain as follows:

$$\bar{\xi }_{0wD} = \left. {\bar{\xi }_{0} } \right|_{{x_{D} = 0}} = \frac{1}{{2\sqrt {a_{1} } F_{1D} s}}\frac{{{\text{e}}^{{\sqrt {a_{1} } x_{fD} }} + {\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} }}{{{\text{e}}^{{\sqrt {a_{1} } x_{fD} }} - {\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} }} = \frac{1}{{2\sqrt {a_{1} } F_{1D} s}}\frac{1}{{\tanh \left( {\sqrt {a_{1} } x_{fD} } \right)}}.$$

(A.29)

• 2. Constant bottom hole pressure

Substituting the constant bottom hole pressure inner boundary condition and the outer boundary condition into Eq. (A.25) and Eq. (A.26), we can obtain:

$$\left\{ \begin{aligned} A_{1} = \frac{{1 - {\text{e}}^{{ - \gamma_{D} }} }}{{\gamma_{D} s}}\frac{{{\text{e}}^{{ - 2\sqrt {a_{1} } x_{fD} }} }}{{{\text{e}}^{{ - 2\sqrt {a_{1} } x_{fD} }} + 1}} \hfill \\ B_{1} = \frac{{1 - {\text{e}}^{{ - \gamma_{D} }} }}{{\gamma_{D} s}}\frac{1}{{{\text{e}}^{{ - 2\sqrt {a_{1} } x_{fD} }} + 1}}. \hfill \\ \end{aligned} \right.$$

(A.30)

Substituting Eq. (A.30) into Eq. (A.26), and setting $x_{D} = 0$, we can obtain:

$$\left. {\frac{{\partial \bar{\xi }_{0} }}{{\partial x_{D} }}} \right|_{{x_{D} = 0}} = \frac{{1 - {\text{e}}^{{ - \gamma_{D} }} }}{{\gamma_{D} s}}\sqrt {a_{1} } \frac{{{\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} - {\text{e}}^{{\sqrt {a_{1} } x_{fD} }} }}{{{\text{e}}^{{ - \sqrt {a_{1} } x_{fD} }} + {\text{e}}^{{\sqrt {a_{1} } x_{fD} }} }} = - \frac{{1 - {\text{e}}^{{ - \gamma_{D} }} }}{{\gamma_{D} s}}\sqrt {a_{1} } \tanh \left( {\sqrt {a_{1} } x_{fD} } \right).$$

(A.31)

Finally, the dimensionless gas rate in Laplace domain can be obtained:

$$\bar{q}_{D} = - 2F_{1D} \left. {\frac{{\partial \bar{\xi }_{0} }}{{\partial x_{D} }}} \right|_{{x_{D} = 0}} = 2\sqrt {a_{1} } F_{1D} \frac{{1 - {\text{e}}^{{ - \gamma_{D} }} }}{{\gamma_{D} s}}\tanh \left( {\sqrt {a_{1} } x_{fD} } \right).$$

(A.32)