Performance forecasting of hydraulically fractured horizontal wells using dynamic-drainage-area concept with correct distance of investigation

Abstract

Performance forecasting of multi-fractured horizontal wells (MFHWs) completed in tight/shale oil or gas reservoirs is of great significance in the development of unconventional resources. Dynamic drainage area (DDA) concept has emerged as a production forecasting methodology for unconventional reservoirs. This paper investigated the DDA method and derived correct expressions of distance of investigation (DOI) for both constant production rate and constant bottom-hole pressure cases by integrating material balance and deliverability equation within the range of DOI. The modified DDA method with correct DOI coefficients provided in this paper permits direct calculation of dynamic performance at arbitrary time steps before the end of transient linear flow. At the same time smooth production forecasting of MFHWs from transient linear to boundary-dominated flow is realized without modification by extra coefficient. Hybrid models such as DDA plus dual-exponential and DDA plus hyperbolic are presented, which can be applied quickly and easily to MFHWs in unconventional reservoirs as alternatives to complex numerical simulation. Meanwhile, average pressure in the range of DDA can be readily obtained with correct DOI coefficients, avoiding complex iterative calculations. The reliability and practicability of this solution have been demonstrated by synthetic and field cases in this work.

Introduction

Over the past two decades of years, multi-fractured horizontal wells have become the primary and fundamental recovery technology for tight/shale oil and gas reservoirs. Besides complex numerical simulation, different analytical, semi-analytical, and empirical methods (Clarkson 2013, 2014) have been developed for history matching and production forecasting of MFHWs completed in these unconventional resources.

Due to the ultra-low permeability associated with unconventional reservoirs, the major flow regime usually exhibits a very long transient linear flow with or without boundary-dominated flow depending on the property of the reservoir and characteristics of fractures. The rigorous reservoir numerical simulation technique usually cannot be applied to every well due to a lack of supporting data and time–cost problems. Empirical methods, such as power-law exponential (PLE) (Ilk et al. 2008), stretched exponential production diagnostic (SEPD) (Valko and Lee 2010), and the Duong model (Duong Anh 2014), even though remain popular, do not rigorously account for flow regime and fracture geometries.

Shahamat et al. (2014) introduced a concept of continuous succession of pseudo-steady states (SPSS), in which the flow regime in the region of investigation is assumed to be pseudo-steady state. He used this method to predict reservoir performance by combining material balance equation, boundary-dominated flow and distance of investigation. A capacitance–resistance methodology (CRM) was presented, in which the capacitance is expressed as the product of the total system compressibility and the reservoir volume of DOI and resistance is equivalent to the inverse of productivity index in deliverability equation.

Clarkson et al. (2016) extended the idea of SPSS and introduced dynamic drainage area (DDA) concept, which is actually a continuous succession of steady state. As a production-forecasting method, the DDA concept has attracted much more attention because of its simplicity and physical-model-based nature of application. The DDA method has been extended to cases of multi-wells and multi-phases with complex fracture geometry (Clarkson and Qanbari 2015, 2016a, b; Qanbari and Clarkson 2016; Shahamat and Clarkson 2018; Ahmadi et al. 2021). The DDA method combines the deliverability equation, material balance equation and distance of investigation together and requires an iterative calculation procedure to determine the average pressure.

The calculation of DOI is critical in determining the end of linear flow, as well as the flow continuity in the linear-to-boundary (LTB) model. Some “hybrid” approach has been used for modeling the LTB system (Nobakht and Clarkson 2011; Nobakht and Clarkson 2011, 2012), in which different models are adopted separately for transient-linear-flow and boundary-dominated flow periods, such as square-root-of-time plot and hyperbolic decline model. The key problem here is how to determine the end of linear flow (${t}_{elf}$).

In this work, we modified and developed the DDA method by introducing a derived DOI equation, avoiding the iterative calculation and maintaining a good continuity between transient linear and boundary-dominated flow. Average pressure in the range of DOI can be directly calculated without iteration as previously required. This new method is robust and flexible enough for performance forecasting of MFHWs under various conditions. The new modified DDA approach has been validated using synthetic simulation and field examples, showing reasonable match both in transient and boundary dominated flow periods.

In the following, the detailed development of the new method is presented for constant production rate and constant bottom-hole pressure cases. Applications on performance forecasting of MFHWs and comparisons with numerical simulation case are also provided to demonstrate the practical applicability of this solution.

Theory and model development

The calculation of distance of investigation is essentially required in both SPSS and DDA methods. The following equation is generally used.

$$y_{{{\text{inv}}}} = \alpha \sqrt {\frac{kt}{{\phi \mu c_{t} }}}$$

(1)

The coefficient α must be carefully selected, which covers a large range depending on the criterion used for defining the DOI. Many values of α have been suggested based on the type of production (constant-rate or constant-pressure) or selective criteria (gauge resolution, rate ratio and cut-off values). Both Shahamat et al. (2014) and Clarkson (2015), Clarkson et al. (2016) adopted the empirical values suggested by Wattenbarger et al. (1998), which are α = 0.113 for the case of constant production rate and α = 0.159 for constant production pressure. When expressed in dimensionless form, Eq. (1) becomes

$$y_{{{\text{invD}}}} = D\sqrt {t_{D} }$$

(2)

The constant 0.159 of α is equivalent to D = 2 in Eq. (2). When DOI reaches the boundaries of formation or fractures inferences start, the value of ${y}_{inv}$ equals to ${y}_{e}$, marking the start of pseudo steady state (PSS) and the time equals to the start of boundary-dominated flow (${t}_{BDF}$). In the iterative calculation of DDA method, an estimated value of ${t}_{BDF}$ must be provided in advance based on DOI equation. There is no supporting proof provided by Nobakht and Clarkson (2012), Shahamat et al. (2014) and Clarkson (2015), Clarkson et al. (2016) for the selection of 0.159. On the other hand, because of the inappropriate value of coefficient D in DOI equation as Eq. (2), an extra coefficient α_o was forcibly incorporated to keep continuity of production rate at the end of transient linear flow and start of boundary-dominated flow (Clarkson and Qanbari 2015).

In this work, we reinvestigated and simplified the DDA method using a derived value of coefficient D, which can avoid the complex iterative algorithm for average pressure and remove the artificial continuity coefficient α_o. We demonstrated that in DDA concept the 0.159 value is just suitable for constant production rate transient radial flow case (Appendix B). The correct D values for transient linear flow at different production-control conditions are derived in the following sections.

Basic model

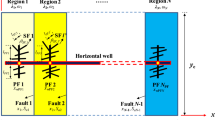
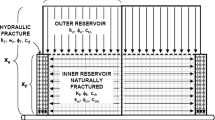
The basic physical model of MFHW is depicted in Fig. 1. For simplicity we just select one element of MFHW as shown in Fig. 1b, similar to that of Wattenbarger et al. (1998) and Nobakht and Clarkson (2012), in which a hydraulic fracture lies in the center traversing the reservoir. For the model in Fig. 1b, the reservoir exhibits transient linear flow until the investigated distance equals to the element length in y-direction and thereafter boundary-dominated flow prevails (and fractures interference starts).

Fig. 1

Schematic of basic physical model: a MFHW in unconventional reservoir; b representative element of MFHW with transvers hydraulic fracture

In the next two sections, we derived the expressions of DOI for DDA method at constant production rate and constant bottom-hole pressure cases. Even though the performance study of MFHWs involves transient linear flow only, we still incorporated the derivation of D-value in transient radial flow (which is shown in Appendix B). This is for theoretical completeness and to prove that the D-value of 2 (and the corresponding α = 0.159) is only suitable for transient radial flow. The DOI equation for transient radial flow cannot be used for transient linear flow.

Constant production rate case

The key algorithm of DDA is to find an average pressure to calculate oil and gas rate using an iterative algorithm. Assuming $\overline{p }\left({y}_{inv},t\right)$ is the average pressure in the drainage area within the distance of investigation. The following expression holds unconditionally.

$$p_{i} - p_{{{\text{wf}}}} = p_{i} - \overline{p}\left( {y_{{{\text{inv}}}} ,t} \right) + \overline{p}\left( {y_{inv} ,t} \right) - p_{{{\text{wf}}}}$$

(3)

The right side of Eq. (3) implies that the total pressure drop of the well can be separated into two terms. The first pressure drop from initial pressure to average pressure accounts for reservoir depletion, described by material balance equation. The second pressure drop is due to the flow from reservoir into the well. For constant-production-rate case in transient linear flow, we can give the following material balance equation for the model described in Fig. 1b.

$$5.615\;qBt = 4x_{f} y_{{{\text{inv}}}} h\phi c_{t} \left( {p_{i} - \overline{p}\left( {y_{{{\text{inv}}}} ,t} \right)} \right)$$

(4)

Define a dimensionless material-balance pressure at constant-rate production,

$$p_{mbD,q} \left( {t_{D} } \right) = \frac{{kh\left( {p_{i} - \overline{p}\left( {y_{{{\text{inv}}}} ,t} \right)} \right)}}{141.2\;q\mu B}$$

(5)

Rearranging Eq. (4) and substituting Eq. (2) yields

$$p_{mbD,q} \left( {t_{D} } \right) = \frac{\pi }{2} \times \frac{0.00633\;kt}{{\phi \mu c_{t} x_{f}^{2} }}\frac{{x_{f} }}{{y_{{{\text{inv}}}} }} = \frac{\pi }{2D}\sqrt {t_{D} }$$

(6)

As previously mentioned, the DDA method assumes a succession of steady state flow. The productivity equation (suggested by Clarkson and Qanbari 2015, and revised here) is

$$q = \frac{{kh\left( {\overline{p}\left( {y_{{{\text{inv}}}} ,t_{D} } \right) - p_{{{\text{wf}}}} } \right)}}{{141.2\;\mu B\left( {\frac{\pi }{2}\left( {\frac{{y_{{{\text{inv}}}} }}{{x_{f} }}} \right)} \right)}}$$

(7)

Based on Eq. (7), we define a steady-state dimensionless pressure for constant production rate case as implied in DDA concept.

$$p_{ssD,q} \left( {t_{D} } \right) = \frac{{kh\left( {\overline{p}\left( {y_{{{\text{inv}}}} ,t} \right) - p_{{{\text{wf}}}} } \right)}}{141.2\;q\mu B} = \frac{\pi D}{2}\sqrt {t_{D} }$$

(8)

Multiplying ${{kh} \mathord{\left/ {\vphantom {{kh} {\left( {141.2q\mu B} \right)}}} \right. \kern-0pt} {\left( {141.2q\mu B} \right)}}$ on both sides of Eq. (3), we have

$$p_{wD,q} = p_{mbD,q} + p_{ssD,q}$$

(9)

In which.$p_{wD,a} = \frac{{kh\left( {p_{i} - p_{wf} } \right)}}{141.2q\mu B}$, indicates the dimensionless bottom-hole pressure.

From solution of transient linear diffusivity equation (Wattenbarger et al. 1998), we have

$$p_{wD,q} \left( {t_{D} } \right) = 2\sqrt {\pi t_{D} }$$

(10)

Substituting Eq. (6), Eq. (8), and Eq. (10) into Eq. (9), we obtain

$$2\sqrt {\pi t_{D} } = \frac{\pi }{2D}\sqrt {t_{D} } + \frac{\pi }{2}D\sqrt {t_{D} }$$

(11)

Solving Eq. (11) yields the value of D, which is 1.651. This value of D is corresponding to α value of 0.131 in DOI equation of Eq. (1). This value of α is greater than 0.113 from unit impulse method and less than 0.141 from method of intersection suggested by Behmanesh et al. (2015). This derived D value implies that the average pressures in material balance and deliverability equation are equivalent to each other. Most importantly, this D value avoids the iterative calculation of average pressure suggested by Clarkson et al. (Clarkson and Qanbari 20152016a, b; Qanbari and Clarkson 2016). Another significant application is that we can estimate the end of linear flow or the start of boundary-dominated flow correctly based on the equation of DOI. The match of dimensionless pressure under different D values is illustrated in Fig. 2. It is noted that the dimensionless pressure ${p}_{D}$ under D = 1.651 is in excellent agreement with the theoretical solution. Lower value of D than 1.651 will underestimate the pressure drop, while high D value than 1.651 will overestimate pressure drop.

Fig. 2

Match of ${p}_{D}$ for constant-production-rate case under different D values

For constant-production-rate case, different D values are corresponding to different dimensionless front-bottomhole rate ratio (FBRR, which defines the pressure front for constant-production-rate case),${Q}_{Dr}$. According to the definition of FBRR (Fan 2021), the D value of 1.651 is corresponding to a FBRR of 0.243. Comparison of ${Q}_{Dr}$ for different D values is listed in Table 1.

Table 1 Comparison of ${Q}_{Dr}$ for different D values under constant rate case

Constant production pressure case

In constant-production-pressure situation, the production rate varies with time. Dividing ${(p}_{i}-{p}_{wf})$ on both sides of Eq. (3) gives

$$1 = \frac{{p_{i} - \overline{p}\left( {y_{{{\text{inv}}}} ,t} \right)}}{{p_{i} - p_{{{\text{wf}}}} }} + \frac{{\overline{p}\left( {y_{{{\text{inv}}}} ,t} \right) - p_{{{\text{wf}}}} }}{{p_{i} - p_{{{\text{wf}}}} }}$$

(12)

Like constant-production-rate case, the first term on the right side of Eq. (12) is material balance contribution due to reservoir pressure depletion. The second term can be treated as dimensionless pressure drop caused by fluid flow toward the hydraulic fracture.

Because production rate varies with time in this case, we modify Eq. (4) as

$$5.615\;N_{p} = 4x_{f} y_{{{\text{inv}}}} h\phi c_{t} \left( {p_{i} - \overline{p}\left( {y_{{{\text{inv}}}} ,t} \right)} \right)$$

(13)

Define dimensionless cumulative production and dimensionless material-balance-pressure at constant-production-pressure case, as Eq. 14 and Eq. 15

$$N_{pD} = \frac{{0.8938\;N_{p} }}{{x_{f}^{2} \phi hc_{t} \left( {p_{i} - p_{{{\text{wf}}}} } \right)}}$$

(14)

$$p_{mbD,p} = \frac{{p_{i} - \overline{p}\left( {y_{{{\text{inv}}}} ,t} \right)}}{{p_{i} - p_{{{\text{wf}}}} }}$$

(15)

From Eq. (13), we have

$$p_{mbD,p} = \frac{\pi }{2}\frac{{N_{pD} }}{{y_{{{\text{invD}}}} }}$$

(16)

The production rate in transient linear flow is given by

$$\frac{1}{{q_{D} }} = \pi \sqrt {\pi t_{D} }$$

(17)

We note that dimensionless cumulative production can be alternatively derived from the integration of dimensionless production rate.

$$N_{pD} = \int_{0}^{{t_{D} }} {q_{D} \left( \xi \right)d\xi } = \frac{2}{\pi \sqrt \pi }\sqrt {t_{D} }$$

(18)

Substitute Eq. (18) into Eq. (16) yields

$$p_{mbD,p} = \frac{1}{D\sqrt \pi }$$

(19)

Define a dimensionless flow pressure at constant-production-pressure case.

$$p_{ssD,p} = \frac{{\overline{p}\left( {y_{{{\text{inv}}}} ,t_{D} } \right) - p_{{{\text{wf}}}} }}{{\left( {p_{i} - p_{{{\text{wf}}}} } \right)}}$$

(20)

Equation (12) becomes

$$1 = p_{mbD,p} + p_{ssD,p}$$

(21)

From the definition of dimensionless production rate and the deliverability equation of Eq. (7) in DDA method, we can obtain

$$p_{ssD,p} = \frac{\pi }{2}y_{{{\text{invD}}}} q_{ssD} = \frac{D}{2\sqrt \pi }$$

(22)

Substituting Eq. (19) and Eq. (22) into Eq. (21) yields

$$1 = \frac{1}{D\sqrt \pi } + \frac{D}{2\sqrt \pi }$$

(23)

Solving Eq. (23) yields D value as 2.84. This value of D is corresponding to α value of 0.226 in DOI equation as Eq. (1), which is greater than 0.194 from unit impulse method and 0.180 from method of intersection suggested by Behmanesh et al. (2015). This value of D for constant-production-pressure case also implies that we can avoid the iterative algorithm to calculate the average pressure in material balance and deliverability equation. Meanwhile, this derived value of D makes it easier to estimate the end of linear flow or the start of boundary-dominated flow based on equation of DOI. The match of dimensionless production rate under different D values is illustrated in Fig. 3. It is noted that dimensionless production rate ${q}_{D}$ under D = 2.84 is in excellent agreement with the theoretical solution. Lower value of D than 2.84 will overestimate production rate, while higher D value than 2.84 will underestimate production rate.

Fig. 3

Match of ${q}_{D}$ for constant BHP case under different D values

Both flow regime and production condition can affect the selection of correct DOI coefficient. For constant-production-pressure case, different values of D are corresponding to different dimensionless front-bottomhole pressure ratio (FBPR, which define the pressure front for constant BHP case), ${p}_{Dr}$. According to the definition of FBPR (Fan 2021), the D value of 2.84 is related to a FBPR of 0.045. Comparison of ${p}_{Dr}$ for different D values is listed in Table 2.

Table 2 Comparison of ${p}_{Dr}$ for different D values under constant BHP case

Average pressure calculation

Average reservoir pressure (p_av) is one of the fundamental parameters in reservoir engineering calculations. It is essential to evaluate fluid properties in material balance applications and to calculate pseudo-time for pressure-sensitive reservoirs. Traditionally the direct method of estimating p_av is based on the relation of flowing bottom-hole pressure and average reservoir pressure during pseudo-steady-state (PSS) of a constant production rate system. However, in unconventional reservoirs, it usually takes very long time to reach PSS flow and it is almost impossible to reach PSS for constant bottom-hole pressure case.

Anderson and Mattar (2007) proposed that during transient flow the pseudo-time should be evaluated at the average pressure of the region of influence rather than the average reservoir pressure. For DDA and SPSS methods, the average pressure within the area of distance of investigation (DOI) is an essential parameter that can only be solved by iterative methods. Alternatively, the average pressure can also be evaluated by the volumetric average method, which is highly dependent on the definition of distance of investigation. For transient linear flow of MFHWs, the dimensionless average pressure in the influence region can be expressed by

$$\overline{p}_{D} = \frac{1}{{y_{{{\text{invD}}}} }}\int_{0}^{{y_{{{\text{invD}}}} }} {p_{D} \left( {y_{D} ,t_{D} } \right)dy_{D} }$$

(24)

From the transient linear flow solution of constant-production-rate case (Wattenbarger et al. 1998; Behmanesh et al. 2015), it has

$$\overline{p}_{D,q} \left( {t_{D} } \right) = \frac{\pi }{{y_{{{\text{invD}}}} }}\int_{0}^{{y_{{{\text{invD}}}} }} {\left[ {2\sqrt {\frac{{t_{D} }}{\pi }} \cdot \exp \left( { - \frac{{y_{D}^{2} }}{{4t_{D} }}} \right) - y_{D} \cdot {\text{erfc}} \left( {\frac{{y_{D} }}{{2\sqrt {t_{D} } }}} \right)} \right]dy_{D} }$$

(25)

Substituting Eq. (2) into the integration result yields

$$\overline{p}_{D,q} \left( {t_{D} } \right) = \pi \left\{ {\frac{1}{D} - \left( {\frac{1}{D} + \frac{D}{2}} \right){\text{erfc}}\left( \frac{D}{2} \right) + \frac{1}{\sqrt \pi }\exp \left( { - \frac{{D^{2} }}{4}} \right)} \right\}\sqrt {t_{D} }$$

(26)

Based on the derived value of D = 1.651 in this work, we can have

$$\overline{p}_{D,q} \left( {t_{D} } \right) = 1.707\;\sqrt {t_{D} }$$

(27)

Comparing Eq. (10) with Eq. (27), we can derive a direct calculation method of average pressure from initial pressure and bottom-hole pressure in dimensional form.

$$\overline{p} = 0.518p_{i} + 0.482p_{{{\text{wf}}}}$$

(28)

Similarly, from the solution of transient linear flow at constant production pressure case (Wattenbarger et al. 1998; Behmanesh et al. 2015), the dimensionless average pressure in the region of influence for constant BHP is

$$\overline{p}_{D,p} \left( {t_{D} } \right) = erfc\left( \frac{D}{2} \right) - \frac{2}{D\sqrt \pi }e^{{ - \left( \frac{D}{2} \right)^{2} }} + \frac{2}{D\sqrt \pi }$$

(29)

Based on the derived value of D = 2.84 for constant production pressure, it gives

$$\overline{p}_{D,p} = 0.389$$

(30)

From the definition of dimensionless pressure in constant BHP case, we can obtain another direct calculation method of average pressure from initial pressure and bottom-hole pressure in dimensional form.

$$\overline{p} = 0.611p_{i} + 0.389p_{{{\text{wf}}}}$$

(31)

We note that the average pressure for constant production rate is a function of square-root-of-time, while the average pressure for constant production pressure case is a constant value, as shown in Fig. 4 and Fig. 5. Coefficients of these two relations depend on the selection of DOI equation. Equation (28) and Eq. (31) indicate that average pressure in the drainage area is a unique function of initial pressure and flowing wellbore pressure, which allows for a direct calculation of pseudo-time and avoids an iterative process in current practice.

Fig. 4

Pressure profile and average pressure at constant-rate case

Fig. 5

Pressure profile and average pressure at constant BHP case

Roadifer (2015) derived different average pressure expressions for the above two cases, which are $\overline{p }=0.6\sqrt{{t}_{D}}$ and $\overline{p }=0.4411$, respectively. The reason for the differences is that he used the DOI equations from Behmanesh (2015), which are D =$\surd 2$ for constant production rate and D=$\surd 6$ for constant production pressure case. In fact, these two values are not suitable for DDA concepts. For instance, if we use D=$\surd 6$ for constant pressure case, we can derive ${p}_{mbD,p}=0.23$ and ${p}_{ssD,p}=0.69$, which makes the equation ${p}_{mbD,p}+{p}_{ssD,p}=1$ not hold. The derived coefficients in this work actually synchronize the change of average pressure in material balance and deliverability equations within the dynamic drainage area, leading to a direct calculation of dynamic performance at arbitrary time step before the end of transient linear flow.

After the end of linear flow, we can derive the expression of average pressure from material balance equation (Roadifer and Kalaei 2015).

$$\begin{array}{*{20}c} {\overline{p} = \overline{p}_{{{\text{elf}}}} - \left( {p_{i} - \overline{p}_{{{\text{elf}}}} } \right)\left( {\frac{t}{{t_{{{\text{elf}}}} }} - 1} \right)} & {\left( {{\text{for}}\;{\text{constant}}\;{\text{rate}}} \right)} \\ \end{array}$$

(32)

$$\begin{array}{*{20}c} {\overline{p} = \overline{p}_{{{\text{elf}}}} - \left( {p_{i} - \overline{p}_{{{\text{elf}}}} } \right)\left( {\frac{{N_{p} }}{{N_{{p,{\text{elf}}}} }} - 1} \right)} & {\left( {{\text{for}}\;{\text{constant}}\;{\text{BHP}}} \right)} \\ \end{array}$$

(33)

In which, ${t}_{elf}$ is the time at end of linear flow, ${\overline{p} }_{elf}$ is the average pressure at end of linear flow and N_pelf is the cumulative production at end of linear flow.

Production forecasting

Wattenbarger et al. (1998) presented the analytical solution to hydraulically fractured wells under constant bottom-hole condition, as in Eq. (34). However, the use of such an infinite-series function is not necessarily desirable for production data analysis. Using DDA method, we can simplify the production forecasting procedure. As previously described, under correct DOI the iterative calculation of average pressure can be avoided. We can determine the time at the end of linear flow or start of boundary-dominated flow under correct value of D coefficient. This is crucial for selection of predicting equations.

$$\frac{1}{{q_{D} }} = \frac{{\frac{\pi }{2}\left( {\frac{{y_{e} }}{{x_{f} }}} \right)}}{{\sum\limits_{{n_{{{\text{odd}}}} }}^{\infty } {\exp \left[ { - \frac{{n^{2} \pi^{2} }}{4}\left( {\frac{{x_{f} }}{{y_{e} }}} \right)t_{D} } \right]} }}$$

(34)

Substituting Eq. (18) and Eq. (2) into material balance Eq. (13) yields

$$p_{i} - \overline{p}\left( {y_{{{\text{inv}}}} ,t_{D} } \right) = \frac{{5.615\;N_{p} }}{{4x_{f} y_{{{\text{inv}}}} h\phi c_{t} }} = \frac{{\pi q_{D} }}{D}\sqrt {t_{D} } \left( {p_{i} - p_{{{\text{wf}}}} } \right)$$

(35)

From deliverability equation Eq. (7) and the definition of dimensionless production rate, we can obtain

$$\overline{p}\left( {y_{{{\text{inv}}}} ,t_{D} } \right) - p_{{{\text{wf}}}} = q_{D} \left( {\frac{\pi D}{2}\sqrt {t_{D} } } \right)\left( {p_{i} - p_{{{\text{wf}}}} } \right)$$

(36)

From the summation of the above two equations, we can derive an expression of dimensionless production rate, as in Eq. (37).

$$\frac{1}{{q_{D} }} = \pi \left( {\frac{1}{D} + \frac{D}{2}} \right)\sqrt {t_{D} }$$

(37)

This equation is equivalent to the linear approximation of Eq. (34), which can be used to forecast production before the boundary is reached or the fractures interference starts. The time at end of linear flow or the start of boundary-dominated flow is easy to derive from Eq. (2).

$$t_{{{\text{Delf}}}} = \left( {\frac{{y_{{{\text{eD}}}} }}{D}} \right)^{2}$$

(38)

When fracture half-length is not known explicitly, the slope of the inverse of production rate vs. square-root-of-time plot ${m}_{L}$ can be used to estimate its value.

$$x_{f} = \frac{6.59\;B}{{m_{L} h\Delta p}}\sqrt {\frac{\mu }{{k\phi c_{t} }}}$$

(39)

After the end of linear flow, the long-term exponential approximation is generally suggested for pressure or flow rate dynamic analysis. However, we adopt a dual-exponential model here, which is derived by taking the first two terms of the infinite-summation series in Wattenbarger’s solution.

$$\frac{1}{{q_{D} }} = \frac{{\frac{\pi }{2}\left( {\frac{{y_{e} }}{{x_{f} }}} \right)}}{{\exp \left[ { - \frac{{\pi^{2} }}{4}\left( {\frac{{x_{f} }}{{y_{e} }}} \right)t_{D} } \right] + \exp \left[ { - \frac{{9\pi^{2} }}{4}\left( {\frac{{x_{f} }}{{y_{e} }}} \right)t_{D} } \right]}}$$

(40)

The advantage of this dual-exponential model is that a smooth continuity of flow rate is obtained, without introducing a connecting coefficient suggested by Clarkson. This is illustrated in Fig. 6. The blue circle series (DDA + EXP D = 2) is from DDA method suggested by Clarkson (Clarkson and Qanbari 2015, 2016a, b, Qanbari and Clarkson 2016; Ahmadi et al. 2021), which is not continuous between transient linear flow and boundary-dominated flow without introducing additional connecting coefficient. The reason of this discontinuity is due to inappropriate D-value in DOI equation.

Fig. 6

Match of ${q}_{D}$ under different D coefficients and b values of LTB models

It is obvious that late-time data will eventually deviate from early straight line and marks the end of transient linear flow. In many cases, however, late-time data does not follow a strict theoretical exponential decline. The reasons may include, properties change due to pressure drop, contribution of unstimulated region, heterogeneities of fracture and reservoir properties, or transitional flow regimes (elliptical/radial) before a complete boundary-dominated flow regime is reached. From reservoir practices, hyperbolic model (Nobakht and Clarkson 2012) or SEPD model (Valko and Lee 2010) are suggested after the end of linear flow.

The hyperbolic model is (Nobahkt et al. 2010)

$$q_{D} = \frac{{q_{{{\text{Delf}}}} }}{{\left[ {1 + bD_{{{\text{elf}}}} \left( {t_{D} - t_{{{\text{Delf}}}} } \right)} \right]^{{{1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0pt} b}}} }}$$

(41)

In which, q_Delf and D_elf are the production rate and decline rate at the end of linear flow, respectively, which can be derived based on Eq. (37). The constant b is the decline exponent, which varies from 0 to 1.

The SEPD model is (Valko and Lee 2010)

$$q_{D} = q_{{{\text{Delf}}}} \exp \left[ { - \left( {\frac{{t_{D} }}{{\tau_{D} }}} \right)^{n} } \right]$$

(42)

In which, n and ${\tau }_{D}$ are constants, which can be determined from group average or statistical experience.

Validation

Synthetic case

To demonstrate the applicability of the modified DDA method in this paper, we generated synthetic production data using reservoir simulation software. The model is an element (as shown in Fig. 1b) of hydraulically fractured well from a tight oil reservoir. The bottom-hole pressure is set to ensure pure single-phase linear flow and the producing time is set long enough to generate both transient and boundary-dominated flow. The parameters are listed in Table 3.

Table 3 Reservoir geometry and properties used for synthetic model

The reservoir starts with a transient linear flow and the pressure distribution after two months is shown in Fig. 7. After outer boundary is reached, the production does not follow a strict exponential decline, as illustrated in Fig. 8. Before the end of transient linear flow, DDA method is used to match the production rate. After the end of linear flow, both hyperbolic model and SEPD can match the simulation results. It shows that the SEPD model can provide a much better match than hyperbolic decline.

Fig. 7

Reservoir pressure distribution after 2 months in simulation model

Fig. 8

Production match to simulation result from different models

Field case

The field case is a multi-fractured horizontal well completed in DL tight oil reservoir of Shengli oilfield, East China. The number of hydraulic fractures is 10 and the average fracture spacing is 300ft. The oil production is shown in Fig. 9. From the log–log plot of production rate versus time, a transient linear flow period is observed. The late-time data exhibits a deviation from early straight line, indicating fracture interference and boundary effect. The fracture half-length is 256ft, determined from the slope of the early straight line. The modified DDA method is used to match the early transient linear flow period. After the end of linear flow, a hyperbolic decline is adopted to match the production decline, in which D_elf is 1.79 and the value of b equals to 1.

Fig. 9

Production match of field case based on modified DDA method

Conclusions

• 1. This paper investigated and developed dynamic drainage area (DDA) method for performance forecasting of multi-fractured horizontal wells (MFHWs) completed in unconventional reservoirs. Correct expressions of distance of investigation (DOI) for DDA method are derived for both constant production rate and constant bottom-hole pressure cases. The DOI coefficients of D-value are 1.651 and 2.84, respectively.

• 2. Simple and direct expressions of average pressure for performance forecasting of MFHWs are presented to avoid complex iterative calculation in DDA method.

• 3. Hybrid models, such as DDA plus dual-exponential, DDA plus stretched exponential production diagnostic model, and DDA plus hyperbolic model are presented for performance forecasting of MFHWs in unconventional reservoirs as alternatives to complex numerical simulation, bridging the gap between analytical and empirical methods.

• 4. This modified DDA method can be extended to MFHWs in unconventional gas reservoirs by adopting pseudo-pressure. Reliable forecasts can be obtained without using pseudo-time, reducing complexities and iterative procedures.

• 5. Even though the results in this work are aimed at performance forecasting of MFHWs, the introduced technique is readily adaptable for transient radial flow and other geometries. This study will be of interest to those petroleum engineers who desire to find a simple tool for performance forecasting of MFHWs in unconventional reservoirs.

Appendices

Appendix A: Definitions of dimensionless variables

The dimensionless parameters used in this work are defined as follows.

Dimensionless distance of investigation

$$y_{{{\text{invD}}}} = \frac{{y_{{{\text{inv}}}} }}{{x_{f} }}$$

(43)

Dimensionless time

$$t_{D} = \frac{0.00633\;kt}{{\phi \mu c_{t} x_{f}^{2} }}$$

(44)

Dimensionless pressure

$$p_{D} = \frac{{kh\left( {p_{i} - p_{wf} } \right)}}{141.2\;q\mu B}$$

(45)

Dimensionless production rate

$$q_{D} = \frac{141.2\;q\mu B}{{kh\left( {p_{i} - p_{{{\text{wf}}}} } \right)}}$$

(46)

Dimensionless pressure for constant production rate case

$$p_{D,q} = \frac{{kh\left( {p_{i} - p\left( {y,t} \right)} \right)}}{141.2\;q\mu B}$$

(47)

Dimensionless pressure for constant production pressure case

$$p_{D,p} = \frac{{p_{i} - p\left( {y,t} \right)}}{{p_{i} - p_{{{\text{wf}}}} }}$$

(48)

Appendix B: Derivation of D coefficient in transient radial flow under DDA concept

for transient radial flow, the following expression holds unconditionally.

$$p_{i} - p_{{{\text{wf}}}} = p_{i} - \overline{p}\left( {r_{{{\text{inv}}}} ,t} \right) + \left( {\overline{p}\left( {r_{{{\text{inv}}}} ,t} \right) - p_{{{\text{wf}}}} } \right)$$

(49)

In which,$\overline{p}\left( {r_{inv} ,t} \right)$ is the average pressure within the radius of investigation (ROI). Multiplying ${{kh} \mathord{\left/ {\vphantom {{kh} {\left( {141.2q\mu B} \right)}}} \right. \kern-0pt} {\left( {141.2q\mu B} \right)}}$ on both sides of Eq. (49) yields

$$p_{D} = p_{mbD} + p_{pssD}$$

(50)

In which, $p_{mbD} \left( {t_{D} } \right) = \frac{{kh\left( {p_{i} - \overline{p}\left( {r_{{{\text{inv}}}} ,t} \right)} \right)}}{141.2\;q\mu B}$, $p_{{{\text{pssD}}}} = \frac{{kh\left( {\overline{p}\left( {r_{{{\text{inv}}}} ,t} \right) - p_{{{\text{wf}}}} (t)} \right)}}{141.2\;q\mu B}$. For constant-production-rate radial flow, the material balance equation is

$$5.615\;qBt = \pi r_{{{\text{inv}}}}^{2} h\phi c_{t} \left( {p_{i} - \overline{p}\left( {r_{{{\text{inv}}}} ,t} \right)} \right)$$

(51)

For transient radial flow, $r_{{{\text{invD}}}} = {{r_{{{\text{inv}}}} } \mathord{\left/ {\vphantom {{r_{{{\text{inv}}}} } {r_{w} }}} \right. \kern-0pt} {r_{w} }} = D\sqrt {t_{D} }$, it gives

$$p_{mbD} \left( {t_{D} } \right) = 2 \times \frac{0.00633\;kt}{{\phi \mu c_{t} r_{w}^{2} }}\frac{{r_{w}^{2} }}{{r_{{{\text{inv}}}}^{2} }} = 2t_{D} \frac{1}{{r_{{{\text{invD}}}}^{2} }} = \frac{2}{{D^{2} }}$$

(52)

Based on the assumption of continuous succession of pseudo-steady states, the relation between average pressure and bottom-hole pressure within the drainage area can be given as:

$$\overline{p}\left( {r_{{{\text{inv}}}} ,t} \right) = p_{{{\text{wf}}}} (t) + \frac{141.2\;q\mu B}{{kh}}\left( {\ln \frac{{r_{{{\text{inv}}}} }}{{r_{w} }} - \frac{3}{4}} \right)$$

(53)

Dimensionless form of Eq. (53) is

$$p_{{{\text{pssD}}}} = \ln r_{{{\text{invD}}}} - \frac{3}{4}$$

(54)

Ignoring skin factor, the dimensionless bottomhole pressure of transient radial flow is

$$p_{D} = \frac{1}{2}\ln \frac{{4t_{D} }}{\gamma }$$

(55)

Substituting Eq. (52), Eq. (54) and Eq. (55) into Eq. (50), we obtain

$$\frac{1}{2}\ln \frac{{4t_{D} }}{\gamma } = \frac{2}{{D^{2} }} + ln\left( {D\sqrt {t_{D} } } \right) - \frac{3}{4}$$

(56)

Solving Eq. (56) yields D = 2. This value is consistent with the traditional value of D in ROI expression (Muskat 1937; Lee 1982), which is corresponding to a dimensionless pressure front cut-off value of 0.11. It should be noted that the ROI equation for transient radial flow cannot be used for transient linear flow.