Introduction

While horizontal drilling and hydraulic fracturing can produce significant amounts of shale gas, a better knowledge of basic fluid transport mechanisms might improve efficiency and reduce environmental impacts. Hydraulic fracturing uses a massive amount of water in shale gas reservoirs. When gas wells are produced, only a small portion of the fracturing water is recovered as fluid flowback ( Abdulelah et al. 2018b; Alzanam et al. 2021; Makhanov et al. 2014; Mojid et al. 2021).

Shale rocks possess tight pores and extremely low permeability and include a considerable amount of clay minerals (Shen et al. 2018a, b; Shen et al. 2015), which are often susceptible to hydration, swelling, and instability (Chen et al. 2003; Lomba et al. 2000). Water gets adsorbed on clay minerals and free surfaces in shale rocks, forming a water layer that is mostly surface-hydrated. In some cases, swelling and damage might result from water adsorption by shale clays Scott et al. (2007). Capillary and osmotic hydration occurs when the water film expands (Roshan et al. 2016) and gas production is hindered by water in the matrix. Understanding how water saturation of shale pores varies on water vapor pressure is crucial for anticipating water blocks in gas recovery. Because of this, understanding water vapor adsorption and equilibrium in shales is crucial for gas production estimation. Usually, an isotherm model describes adsorption equilibrium, providing useful information on pore structure and capacity (Shen et al. 2018a, b). Many studies have focused on methane adsorption isotherms in shale in recent years (Abdulelah 2018; Abdulelah et al. 2021; Al-Mutarreb et al. 2018; Chen et al. 2019a, b; Meng et al. 2020; Pang et al. 2021; Rexer et al. 2020). However, little research has been done on water vapor adsorption on shale rocks and the feasibility of isotherm models. Adsorption isotherms for water on shales should be determined to improve shale gas reservoir recovery. Commonly, gas adsorption isotherms such as N2 or CO2 are used to obtain the quantitative parameters of pores in shales, including fractal dimension (Abdulelah et al. 2018a; Wang et al. 2015). However, such gases provide quantification for smaller pores, which are not accessible by water. Therefore, using water adsorption isotherm provides better insights into fractal characteristics of shales to assess water–shale interaction.

It is well known that the capillarity induced by the retained water in shale causes blockage of gas flow from the shale (Agrawal and Sharma 2013; Ge et al. 2015; Holditch, 1979). Finding precise measurement of capillary pressure datasets for modeling the flow behaviors is needed in petroleum reservoirs; therefore, it has been tracked by researchers for many years (Melrose, 1990; Morrow and Mason 2001; Slobod et al. 1951). Commonly, the assessment of imbibition and drainage curves of capillary pressure (Pc) – saturation (S), Pc–S relationship, in porous media is carried out in laboratory using porous plate method and centrifuge method. Such methods were developed to assess capillary pressure in conventional resources such as sandstone reservoirs, where capillary pressure ranged up to ~ 3 MPa. However, the capillary pressure in unconventional reservoirs, including gas shales, ranges up to ~ 500 MPa. Therefore, the traditional methods such as porous plate and centrifuge are incapable of measuring capillary pressure – saturation relationship for gas shales due to the high capillary pressures associated with its small pores (Donnelly et al. 2016; Tokunaga et al. 2017).

There are limited number of studies that have been carried out to explore alternative methods to generate Pc–S curve on shales, which adopted a modified form of Kelvin equation (Eq. 1) (Thomson 1871) to compute the capillary pressure at varying volumetric water content.

$$P_{{\text{C}}} = \ln \left( {a_{{\text{w}}} } \right)\frac{{{\text{RT}}}}{{V_{{\text{m}}} }}$$
(1a)
$$a_{{\text{w}}} = {\text{RH}}$$
(1b)

where \(P_{{\text{C}}}\) is capillary pressure (MPa), \(a_{{\text{w}}}\) is a dimensionless parameter called water activity, and \(\mathrm{RH}\) is the relative humidity (%); the ratio of the vapor pressure of water within a porous medium to the vapor pressure of pure free water at the same temperature, \(R\) is the universal gas constant (8.314 j/mol.k), \({T}\) is the absolute temperature (K), and \({V}_{\mathrm{m}}\) is the molar volume of water (g mol−1) (Newsham et al. 2004). However, the existing studies used crushed shale sample are susceptible to mass loss hence influencing the calculation of water content (Donnelly et al. 2016; Tokunaga et al. 2017).

In this study, the measurements of water vapor adsorption isotherm and capillary pressure for intact shale samples from Marcellus, Eagle Ford, Wolfcamp and Mancos formations were performed using relative humidity chamber at 90 °C. Shale fractal dimensions were obtained from water adsorption isotherms. The capillary pressure curves of all shale samples were also developed and then parametrized using Brooks & Corey and van Genuchten capillary pressure models.

Materials and methods

Shale samples

Figure 1 displays the four shale samples used in this study. One shale sample was collected from Chattanooga shale member of Marcellus shale formation. It is black shales and has some gray interbedding layers. Three other samples, Eagle Ford shale, Mancos shale and Wolfcamp shale, were commercially obtained from Kocurek Industries inc.

Fig. 1
figure 1

The examined shale samples. a Marcellus shales, b Eagle Ford shales, c Mancos shale and d Wolfcamp shale

Full size image

Shale samples preparation and characterization

A total of four shale samples were examined in this study. Thin slabs of shale samples (Figure 1) were prepared using a slim taper saw file. The cutting process utilized no fluid to eliminate shale swelling also the post-cutting dust was removed; then, shale samples were dried in an oven at 105 °C for 24 hr to establish the dry mass. An X-ray diffractometer analyzed the mineral content of shale samples (model XPert3, PANalytical). To eliminate inorganic carbon, pulverized shale was first treated with 37% HCL. The surplus carbon was measured by introducing 0.60 g crushed shale into Multi N/C 3100. The TOC measurements procedures adopted from (Abdulelah et al. 2018a). Each shale sample's porosity was measured using a helium porosimeter (Model: HEP-E, Vinci Technologies).

Measurement of water adsorption and capillary pressure

A benchtop humidity and temperature chamber (Model SH-242, ESPEC) that is shown in Figure 2 was utilized for obtaining the imbibition/adsorption and drainage/desorption datasets. Figure 2a shows the three major parts; (1) test area, (2) 5 L water tank, and (3) controlling and monitoring panel; (b) is an enlarged image of the control and monitoring panel showing the digital gauges of humidity and temperature; (c) details the components of the test area; (4) fan, (5) sample shelf, (6) dry-bulb and wet-bulb thermometers, and (7) built-in water pan.

Fig. 2
figure 2

The main components of the benchtop humidity and temperature chamber (SH-242)

Full size image

The test began by setting the required RH value and temperature in the control panel. Following the psychrometric approach, the wet-bulb thermometer temperature is automatically adjusted to achieve the required RH at that temperature. At any given temperature, including at 90 °C, the relative humidity (RH) is the ratio of the actual to the saturation vapor pressure. The actual vapor pressure quantifies the amount of water vapor in a volume of air. Saturation vapor pressure is attained when the water molecules evaporating into the air are condensing from the air back into the water. The used relative humidity chamber works automatically to maintain a certain level of RH.

According to the SH-242 manual, the accuracies of the temperature sensor and relative humidity sensor are 2.5 °C and ± 3.0% RH, respectively. To ensure that relative humidity remains unaffected by the humidity in laboratory, the chamber was placed in a controlled area in the laboratory and was surrounded by long PVC strip curtain. Air blower was also installed in the controlled area to minimize air exchange with surroundings.

To establish the dry mass of shale samples, the measurements were started by drying them in an oven at 105 °C for 24 hr and then cool down to room temperature in a vacuum desiccator following the protocol established by Tokunaga et al. (2017). The dry mass was obtained by weighing the oven-dried samples using a digital weight balance. The accuracy of the weight balance used is ± 0.0001 g. The oven-dried shale samples were placed on a shelf (Figure 2c) suspended inside the test area of the humidity and temperature chamber.

First set of measurements were carried out to obtain the imbibition/adsorption datasets for the shale samples. The relative humidity (RH) was set, starting with 10%. The mass of each shale sample was taken every 2 hr until a constant mass was achieved. The measurements were repeated in an increasing order at RH of 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% and 100% following the same procedures. All measurements were conducted at a temperature of 90 °C. The capillary pressure (Pc) at each water saturation was then calculated using the Kelvin equations (Eqs. 1a and 1b).

Once imbibition/adsorption measurements were completed, the drainage/desorption process was started. The drainage/desorption data set of shale samples was obtained by progressively decreasing relative humidity inside the chamber from 100% to 10%. Like imbibition/adsorption, the mass of each shale sample was taken every 2 hr, and mass gain was noted until a constant mass was achieved. Generally, mass equilibrium was achieved in 12–20 hr at each relative humidity level during imbibition and drainage. The equilibrium time was achieved faster than previous spontaneous vapor desorption methods (Donnelly et al. 2016) due to having the fan, which forced the vapor to penetrate the shale samples.

During both imbibition/adsorption and drainage/desorption, the wetting phase is water in form of vapor, and the non-wetting phase is the air. The gravimetric water saturation (\(S_{{\text{w}}}\)) at each relative humidity level was determined at equilibrium by calculating the difference between the equilibrated mass (\(m_{{{\text{wet}}}}\)) and the oven-dried mass (\(m_{{{\text{dry}}}}\)) using Eq. 2:

$$S_{{\text{g}}} = \frac{{m_{{{\text{wet}}}} - m_{{{\text{dry}}}} }}{{m_{{{\text{dry}}}} }}$$
(2)

The gravimetric water saturation was used to present water adsorption and desorption isotherms as a function of relative humidity. For presenting the capillary pressure curves, the volumetric water saturation (\(S_{{\text{v}}}\)) corresponding to each relative humidity level is then calculated using Eq. 3:

$$S_{{\text{v}}} = \frac{{S_{{\text{g}}} \rho_{{\text{b}}} }}{{\rho_{{\text{w}}} }}$$
(3)

where \(\rho_{{\text{b}}}\) is the bulk density of oven-dried sample, and \(\rho_{{\text{w}}}\) is water density, taken as 1.0 g/cc. The procedures for calculating the gravimetric water saturation (\(S_{{\text{g}}}\)) and volumetric water saturation (\(S_{{\text{w}}}\)) were adopted from Donnelly et al. (2016) and Newsham et al. (2004). The capillary pressure (Pc) at each saturation point was then computed applying Kelvin equations (Eq. 1a and 1b), and imbibition and drainage curves were then constructed.

Capillary pressure curve fittings and parametrization

The measured imbibition and drainage data of all shale samples were separately fitted to Brooks & Corey (BC) and van Genuchten (VG) capillary pressure models. The goodness of the fits was assessed based on the value of the coefficient of determination (R2). Equation 4a and b shows a mathematical form of Brooks and Corey equation that is widely used in the oil and gas industry to describe the capillary pressure curve on reservoir rocks (Donnelly et al. 2016; Xu et al. 2016).

$$S_{{\text{v}}} = \varphi [ 0 < P_{{\text{c}}} < P_{{\text{e}}} ]$$
(4a)
$$S_{{\text{v}}} = S_{{\text{r}}} + \left( {\varphi - S_{{\text{r}}} } \right)\left( {\frac{{P_{{\text{e}}} }}{{P_{{\text{c}}} }}} \right)^{\lambda } \;\;[ P_{{\text{c}}} > P_{{\text{e}}} ]$$
(4b)

where \(S_{{\text{v}}}\) is the volumetric wetting phase saturation, \(S_{{\text{r}}}\) is the volumetric residual wetting phase saturation, \(\varphi\) is the porosity, \(P_{{\text{e}}}\) is the entry pressure, which is the capillary pressure required to access the largest pores, and \({\uplambda }\) is the pore size distribution index that indicates the range of existing pore sizes. The parameters of Brooks and Corey model, \(S_{{\text{r}}}\), \(P_{{\text{e}}}\) and \({\lambda }\), were obtained through nonlinear regression fitting using high-performance computer.

van Genuchten capillary pressure model was also fitted to the imbibition and drainage datasets of shale samples. Equation 5 shows a form of van Genuchten capillary pressure model. It is a well-established model that is used to parametrize the capillary pressure curves of reservoir rocks (Xu et al. 2016).

$$S_{{\text{v}}} = S_{{\text{r}}} + \left( {\varphi - S_{{\text{r}}} } \right)\left( {\frac{1}{{1 + (\alpha P_{{\text{c}}} )^{n} }}} \right) ^{m}$$
(5)

where \(S_{{\text{v}}}\) is the volumetric wetting phase saturation, \(S_{{\text{r}}}\) is the volumetric residual wetting phase saturation, \(\varphi\) is the porosity, \(n\), \(m,\) and \(\alpha\) are van Genuchten fitting parameters, which depend on the shape of the Pc– S curve. It is commonly assumed that \(m = 1 - 1/n\), leaving only three unknown parameters:\(S_{{\text{r}}}\), \(n,\) and \(m\). The unknown parameters were determined by nonlinear fitting of the collected data to the model.

BC model parameters (\(P_{c} ,\lambda\) and \({\text{S}}_{{\text{r}}}\)) and VG model parameters were (\(n,\alpha\) and \(S_{{\text{r}}}\)) obtained by fitting the two models (Eqs. (6) and (7)) to the imbibition and drainage curves separately using nonlinear regression. In fitting both models, BC and VG, the measured porosities (Table 1) for a given shale were used as known inputs, while the model’s parameters were treated as unknowns. A bound statement of \(0{\le {S}}_{\mathrm{r}}\le \mathrm{\varphi }\) was used to prevent the regression from estimating a negative water content or exceeding the maximum expected water saturation.

Table 1 Shale characteristics
Full size table

Results and discussion

Sample characteristics

Table 1 shows the porosity, matrix density, and mass loss for the four shale samples. The Mancos (MC) and Eagle Ford shale (EF-2) samples have higher matrix density (2.72 and 2.66 g/cc) than other shale samples, whereas the matrix density of Wolfcamp shale sample (2.45 g/cc) is the lowest among all shales.

The percentage of mass loss for shale samples has varied between 0.020 and 0.450%. The highest mass loss was seen on the Marcellus shale (0.450%). Lower mass loss allows a more accurate calculation of the gravimetric and volumetric water saturation (content). As explained by Donnelly et al. (2016), the loss mass could be attributed to the breakage or slacking of shale during the imbibition measurements. In this study, the use of Benchtop humidity and temperature chamber for imbibition and drainage of the shale samples allowed achieving a lower mass.

Water adsorption isotherms

Figure 3 shows water vapor adsorption and desorption measured in Marcellus, Eagle Ford, Wolfcamp and Mancos shales. The isotherms were measured at relative humidity (RH) 10% to 99% at 90 °C. The total amount of adsorbed water was 0.019 mg/g in Mancos shale, 0.012 mg/g in Marcellus shale, 0.010 mg/g in Eagle Ford shale and 0.00098 mg/g in Wolfcamp shale. Mancos shale has more adsorbed water due to its high clay content and low TOC. However, Wolfcamp shale has the lowest TOC and clay content, adsorbing the least water. Rich in clay, clayey shales adsorb more water than organic-rich shales (Abdulelah et al. 2018b).

Fig. 3
figure 3

Water sorption isotherms in Marcellus, Eagle Ford, Wolfcamp and Mancos shale

Full size image

A minimal hysteresis exists between adsorption and desorption isotherms. (Adsorption and desorption curves do not coincide.) This explains why water retention in some shales occurs due to capillary condensation (Abdulelah et al. 2018b).

Fractal analysis

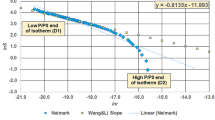
The solid surface's geometric and structural properties can be described by fractal analysis (Avnir and Jaroniec 1989; Pfeifer and Avnir 1983). The fractal dimension D is used to quantify the surface roughness or structural irregularity of a solid (Pfeifer and Avnir 1983). D value ranges from 2 to 3, with 3 representing a completely irregular or rough surface and 2 representing a perfectly smooth surface (Pfeifer and Avnir 1983). Frenkel–Halsey–Hill (FHH) model, described in equation 6 and 7 (Chen et al. 2019a, b; Hill, 1952), was used to calculate fractal dimension according to the data from water adsorption isotherms as follow:

$$\ln q = K\ln \left[ {\ln \left( {\frac{{p_{0} }}{p}} \right)} \right] + C$$
(6)
$$D = K + 3$$
(7)

where q represents the amount of adsorbed water (mg/g), \(\frac{{p_{0} }}{p}\) is the inverse of relative humidity (RH), C is constant, which represent the intercept, and K is the constant related to adsorption mechanism and fractal dimension D. The fractal dimension D was obtained by first plotting \(\ln q\) versus \(\ln \left[ {\ln \left( {\frac{{p_{0} }}{p}} \right)} \right]\), and the slope K was determined and used to calculate D using Eq. 7.

The FHH plots in Figure 4 present water vapor adsorption isotherms of (a) Marcellus shale, (b) Eagle Ford shale, (c) Wolfcamp shale and (d) Mancos shale. The plots are divided into two groups (two straight lines), one for RH less than 0.5 and the other for RH from 0.5 to 1. Each behavior indicates a different water adsorption mechanisms. Thus, two fractal dimensions (D1 and D2) were obtained from plots. Table 2 shows the fractal dimensions calculated from water adsorption (D1 and D2). The values of D1 are in the range of 0.8406–2.6968 and average of 1.6058, while D2 values ranged between 2.4527 and 2.7634 and average of 2.5647. All fractal dimensions D1 are less than 2, with the exception of Wolfcamp shale, and thus deviate from the definition of fractal dimension (Pfeifer and Avnir 1983). A previous study reported the same deviation for D1 values obtained for shale samples from N2 adsorption isotherm (Liu et al. 2015). However, fractal dimension values D2 are more realistic and within the definition range. Hence, the fractal dimensions D2 can describe fractal characteristics of shale samples, such as irregular pore surface and complex pore structure.

Fig. 4
figure 4

Plots of ln (q) vs ln (ln(P0/P)) reconstructed from water vapor adsorption isotherms of a Marcellus shale, b Eagle Ford shale, c Wolfcamp shale and d Mancos shale

Full size image
Table 2 Shale fractal dimensions calculated from water adsorption isotherms
Full size table

Capillary pressure curves

The plot of capillary pressure (Pc) versus volumetric water saturation (Sv) relationship for shale samples during imbibition and drainage is shown in Figure 5. The measurements were reported at varying levels of saturation and a constant temperature of 90 °C. As shown in Figure 5, shale samples have different capillary pressure–water saturation relationships. Another essential feature in Figure 5 is that the majority of the data fall in the low volumetric saturation range or high capillary pressure range for both imbibition and drainage measurements.

Fig. 5
figure 5

Measured imbibition and drainage curves for: a Marcellus shale, b Eagle Ford shale, c Wolfcamp shale and d Mancos shale

Full size image

Figures 6 and 7 show the fittings of BC and VG models to the measured imbibition and drainage data, respectively, of the four shale samples. As shown in Figs. 4 and 5, the results of this study are matching the BC and VG models; therefore, we believe that the proposed method can be considered as one of the accurate approaches to assess Pc – S relationship for shales. Table 3 summarizes the fitting parameters for BC and VG capillary pressure models as well as the goodness of fit (R2) for the imbibition and drainage branches of Pc – SV curves of our four shale samples.

Fig. 6
figure 6

Brooks and Corey (BC) and van Genuchten (VG) capillary pressure models fitted to the experimental imbibition data for: a Marcellus shale, b Eagle Ford shale, c Wolfcamp shale and d Mancos shale

Full size image
Fig. 7
figure 7

Brooks and Corey (BC) and van Genuchten (VG) capillary pressure models fitted to the drainage data for: a Marcellus shale, b Eagle Ford shale, c Wolfcamp shale and d Mancos shale

Full size image
Table 3 BC and VG model fitting parameters and goodness of fit (R2) from nonlinear regression analyses for the imbibition and drainage branches of Pc – S curves of four shale samples
Full size table

BC model fitting parameters, shown in Table 2, suggest that there are differences between the shale samples. Estimates of \({{P}}_{\mathrm{e}}\) parameter varied between 0.00 and 0.299 MPa for the imbibition branch and between 0.00094 and 0.30 for drainage. Marcellus shale sample has the highest \({{P}}_{\mathrm{e}}\) parameter, whereas Mancos shale sample has the lowest values of this parameter irrespective of imbibition or drainage branch. By definition, \({{P}}_{\mathrm{e}}\) is the entry pressure require to access the largest existing pores. Therefore, the values of \({{P}}_{\mathrm{e}}\) indicate that the largest accessible pores in Marcellus shale are smaller in size than the largest pores in Mancos shale. Regarding the dimensionless \(\uplambda\) parameter, it varied between 0.43 and 1.14 for imbibition and between 0.31 and 1.11 for drainage. Wolfcamp shale sample has the highest values in both imbibition and drainage branches. Higher values of the \(\uplambda\) parameter of Wolfcamp suggest a narrow range of pore size distribution as compared to the other shale samples. Table 3 also shows that the fitting BC model resulted in residual water saturation (\({{S}}_{\mathrm{r}}\)) of zero in all of the tested shale samples. Similar findings were reported in the literature where zero residual water saturation was found at high capillary pressures (Melrose et al. 1994).

Similarly, the variation of VG model fitting parameters shown in Table 3 indicates that there are differences between the shale samples. The \({\alpha }\) parameter varied between 3.01 and MPa−1 for imbibition and between 2.97 and 996.70 MPa−1 for drainage. In both imbibition and drainage branches, Eagle Ford shale has the highest \({\alpha }\) parameter, whereas Marcellus shale has the lowest value of this parameter. The \({\alpha }\) parameter in the VG model determines the location of entry pressure in the capillary curve, which is controlled by the diameter of the largest pores. The values of the \({\alpha }\) parameter suggest that the largest pores of Eagle Ford shale are smaller than that of the Marcellus shale sample. Estimates of the dimensionless \({n}\) parameter varied between 1.41 and 1.90 for imbibition and between 1.32 and 1.58 for drainage. The highest values of the \({n}\) parameter were seen in Mancos shale, while the lowest estimates of this parameter were found on Eagle Ford shale. The \({n}\) parameter controls the steepness of the capillary Pc – S curve. The larger the value of the \({n}\) parameter, the steeper the curve and narrower is the breadth of pore size distribution. Table 2 also shows that the fitting VG model resulted in a residual water saturation (\({{S}}_{\mathrm{r}}\)) of zero in all of the tested shale samples.

Comparison with previous studies

Compared Brooks and Corey model parameter of the pore size distribution (\(\uplambda\)) from this study was compared with parameters obtained in Donnelly et al. (2016) for two samples. \(\uplambda\) is the pore size distribution index that indicates the range of existing pore sizes and it is an intrinsic property that is not expected to vary much for samples from the same formation or fabric. Table 4 compares between the values of \(\uplambda\) obtained in this study with those obtained by Donnelly et al. (2016) for the same shale formation, it can be seen that the values are quite close.

Table 4 Comparison between λ parameter from this study with previous study for two samples
Full size table

The slight difference is attributed to the fact that Donnelly et al. (2016) used crushed sample, while this study used intact samples. It was not possible to compare the other samples due to unavailability of published data.

Conclusions

A benchtop humidity and temperature chamber (SH-242) was used to assess water sorption, fractal properties and capillary pressure in four shale samples at 90 °C. Water adsorption isotherms were obtained, and FHH model was utilized to quantify fractal properties of shale samples. Volumetric water saturations were then calculated, and capillary pressure curves of the four shale samples were obtained and parametrized using Brooks & Corey (BC) and van Genuchten (VG) capillary pressure models. The key findings are summarized as follow:

  1. 1.

    Water adsorption isotherms were measured at 10% to 99% RH at 90 °C. Shale samples from Mancos, Marcellus, Eagle Ford, and Wolfcamp were all found to have adsorbed water of various concentrations. Mancos shale contains more absorbed water due to its high clay concentration and low TOC. However, Wolfcamp shale has the lowest TOC and clay concentration, adsorbing the least water. Clay-shales absorb more water than organic-rich shales.

  2. 2.

    There is little hysteresis between adsorption and desorption isotherms. (Adsorption and desorption curves do not coincide.) Capillary condensation causes water retention in some shales.

  3. 3.

    The fractal dimensions D2 can describe fractal characteristics of shale samples, such as irregular pore surface and complex pore structure.

  4. 4.

    The proposed method yielded different capillary pressure curves or relationships for the different shale samples, which is attributed to the difference in petrophysical properties.

  5. 5.

    Both imbibition and drainage data sets of all the samples were successfully fitted. The values of R2 for BC fits varied between 0.90 and 0.97 for imbibition and between 0.85 and 0.98 for drainage. The fits of the VG model resulted in R2 values that ranged between 0.94 and 0.99 for imbibition and between 0.84 and 0.99 for drainage.

  6. 6.

    The difference in the values of the BC model fitting; entry pressure parameter \(({{P}}_{\mathrm{e}}\)) and pore size distribution parameter (\(\uplambda\)); were found between the US shale samples of different locations.

  7. 7.

    Similarly, the values of the entry pressure parameter (\({\alpha }\)) and pore size distribution parameter (\({n}\)) for the VG model varied between the several shale samples.

  8. 8.

    The findings also indicate that there is a negligible hysteresis when comparing imbibition and drainage data sets.

  9. 9.

    This study represents a new significant benchmark for the benchtop humidity and temperature chamber method to be used for evaluation capillary pressure relationships in gas shales at reservoir temperature.