Introduction

Prediction of short-term and long-term deliverability of gas wells is important for reservoir management, designing production facilities, planning field development, estimating payout time and setting allowable (Al-Attar and Al-Zuhair 2009; Chase 2002; Xiao et al. 2017)). Generally, it is preferred to perform conventional four-point tests (backpressure or flow after flow, isochronal and modified isochronal tests) to get coefficients of deliverability equation(s). In this case, a well is typically produced at four different flow rates, and the pressure–rate–time response is recorded. Equation (1) presents the general form of the conventional empirical equation of the stabilized well deliverability which is widely used to determine AOF and well deliverability curves when multi-point tests are conducted (Rawlins and Schellhardt 1935; Lee and Wattenbarger 1996; Ahmed 2006).

$$q = C\left( {m\left( {p_{r} } \right) - m\left( {p_{wf} } \right)} \right)^{n}$$
(1)

where q is current gas flow rate, Pr and Pwf are current average reservoir pressure and bottom hole flowing pressure, respectively, m(p) represents gas pseudopressure, and C and n are constants to be determined from multi-point test data. For reservoir pressure less than 2000 psi, m(p) can be simply replaced by pressure squared (p2) (Al-Attar and Al-Zuhair 2009).

As mentioned, it is preferred to calculate gas well deliverability from conventional multi-point test data. However, in some cases it may not be feasible due to operational, technical or economical limitations, especially for low permeable formations or where offshore rig time is considered (Chase 2002). Thus, industry practice may sometimes shortcut these conventional methods utilizing just three, two and sometimes just one flow test (Chase 2002; Lee and Wattenbarger 1996). As an alternative, several Vogel-type dimensionless inflow performance relationships (IPR) have been proposed to mitigate the need to perform conventional multi-point tests and obtain well deliverability with just a single-point buildup or drawdown test (Mishra and Caudle 1984; Chase and Alkandari 1993; Billiter and Lee 2000; Chase 2002; Al-Attar and Al-Zuhair 2009).

Mishra and Caudle (1984) used a broad range of reservoir rock and fluid properties to generate a Vogel-type dimensionless IPR correlation (Eq. 2) for prediction of current gas well deliverability under pseudosteady-state conditions. Equation (2) shows current dimensionless rate (ratio of gas flow rate to AOF, q/qmax) as a function of dimensionless pseudopressure (m(pwf)/m(pr)).

$$\frac{q}{{q_{\max } }} = \frac{5}{4}\left( {1 - 5^{{\left( {\frac{{m\left( {p_{wf} } \right)}}{{m\left( {p_{r} } \right)}} - 1} \right)}} } \right)$$
(2)

where q is the stabilized flow rate and qmax is the current AOF. Equation (2) allows obtaining gas well deliverability equation (relation of q and pwf) with known maximum theoretical flow rate (qmax) at current reservoir pressure. Thus, having average reservoir pressure (pr) and a single-point test data (stabilized q and pwf), then AOF (qmax) and well IPR can be obtained. They also proposed another equation to predict future performance of gas wells based on current AOF and average reservoir pressure as follows:

$$\frac{{q_{\max ,\,f} }}{{q_{\max ,\,c} }} = \frac{5}{3}\left( {1 - 5^{{\left( {\frac{{m\left( {p_{r,f} } \right)}}{{m\left( {p_{r,c} } \right)}} - 1} \right)}} } \right)$$
(3)

where subscripts f and c correspond to the future and current reservoir conditions, respectively. With the known current AOF (qmax,c), Eq. (3) is used to estimate the future AOF (qmax,f) of a gas well at a given average reservoir pressure (pr,f) and future deliverability analysis.

Based on concepts proposed by Mishra and Caudle (1984), Chase and Alkandari (1993) developed a single-point test method that uses dimensionless IPR curves for predicting the inflow performance of fractured gas wells producing under stabilized or pseudosteady-state flow conditions.

Chase and Anthony (1988) studied current dimensionless IPR correlation presented by Mishra and Caudle (1984) and showed that it could also be applied to predict the performance of a fractured gas wells. They also showed that for average reservoir pressure or static bottom hole pressure less than about 2000 psi (13.8 MPa), pressure-squared values could be substituted for pseudopressures (Chase et al. 1988).

Billiter and Lee (2000) extended the work of Mishra and Caudle (1984) using numerical simulator and developed permeability-dependent dimensionless IPR for gas wells. The reader is referred to the original papers for detailed formulations.

Chase (2002) applied a model developed for fractured gas wells for unfractured gas wells using apparent skin factor. From analysis of data from 25 Canadian gas wells and 5 simulated wells, it was concluded that the dimensionless IPR curve model offers a reasonably accurate and economical method for predicting current and future gas well IPR from a single-point test data.

Trick et al. (2002) compared three dimensionless IPRs (Mishra and Caudle (1984), Billiter and Lee (2000) and Chase and Alkandari (1993)) for 31 Alberta gas wells and found that the dimensionless IPRs from Mishra and Caudle (1984) and Chase and Alkandari (1993) closely match the predictions from measured inflow performance coefficients.

Al-attar and Al-Zuhair (2009) extended the work of Mishra and Caudle (1984) and included parameters that were ignored by Mishra and Caudle (1984) such as formation porosity, skin factor and reservoir thickness and developed a new empirical correlations for current gas well deliverability calculations (Eq. 4).

$$\begin{aligned} Y = & - 0.7193X^{6} + 0.6221X^{5} + 0.3037X^{4} - 0.6108X^{3} \\ & + 0.0756X^{2} - 0.6712X + 1.006 \\ \end{aligned}$$
(4)

where

$$X = \frac{{m\left( {p_{wf} } \right)}}{{m\left( {p_{r} } \right)}},\;Y = \frac{q}{{q_{\max } }}$$
(5)

In addition, they proposed another polynomial dimensionless correlation for future gas well performance prediction from current single-point test data (Eq. 6).

$$\begin{aligned} Y = & 10.436X^{6} - 31.143X^{5} + 33.867X^{4} - 15.374X^{3} \\ & + 1.4779X^{2} + 1.7044X + 0.0234 \\ \end{aligned}$$
(6)

where

$$X = \frac{{m\left( {p_{r,f} } \right)}}{{m\left( {p_{r,c} } \right)}},\;Y = \frac{{q_{\max ,f} }}{{q_{\max ,c} }}$$
(7)

Mohammed et al. (2010) compared AOF of different methods using numerical simulation studies and found that stabilized flow condition is the main factor which influences the AOF.

Kalantariasl et al. (2013) applied Mishra and Caudle (1984) and Al-Attar and Al-Zuhair (2009) methods to compare their results with multi-point test of several gas wells from different Middle East fields and found significant errors from both correlations for high rate gas wells. They found that both correlations has almost accurate results for low rate gas wells. However, these correlations had unacceptable results for high rate gas wells. Absolute error up to 300% was found for high rate gas wells. In addition, both correlation were evaluated up to AOF of 184 MMSCF. Here, a more comprehensive correlation is needed to cover a wider range of operational conditions which is developed in this paper.

Shi et al. (2015) developed a method for considering wellbore flow effect on well deliverability of ultra-thick gas reservoirs. Mu et al. (2016) proposed a method for calculation of AOF with steady single-point test based on iterative calculation of permeability.

In addition to the mentioned works, many studies applied data-driven approaches and artificial intelligence to investigate well deliverability and prediction of production performance in coal bed methane gas, underground gas storage and tight carbonate reservoirs (Akhondzadeh et al. 2018; Ali 2021; Ali and Guo 2019, 2020, 2021; Li et al. 2021; Zhang et al. 2021).

To the best of our knowledge, a comprehensive dimensionless IPR that can be used for wide range of reservoir conditions does not exist in the literature. In addition, as mentioned, previous correlations lose their accuracy for high rate gas reservoirs and there is a lack for a more comprehensive correlation to be used for a wide range of reservoir properties. This paper develops a new comprehensive dimensionless IPR correlations for prediction of gas well deliverability which allows more accurate prediction than previous studies for a wide range of well and reservoir conditions.

Comparison of predicted values of AOF from the proposed correlation with results of AOF calculation from multi-point tests of 61 different wells and error analysis showed very good agreement. In addition, error analysis confirmed superiority of the new proposed dimensionless IPR correlation to previous works by Mishra and Caudle (1984) and Al-Attar and Al-Zuhair (2009).

Objectives

The objectives of the current paper are as follows:

  • 1 To develop a Vogel type dimensionless IPR correlation between dimensionless rate \(\frac{q}{{q_{\max } }}\) and dimensionless pseudo pressure \(\frac{{m(p_{wf} )}}{{m(p_{r} )}}\) for gas wells to be used with stabilized single point test data.

  • 2. To make sensitivity analysis of the developed correlation to reservoir rock and fluid parameters (reservoir pressure and temperature, gas gravity, reservoir permeability, wellbore radius, drainage shape and drainage area).

  • 3. To compare predicted AOF and IPR of the new dimensionless correlation with result of multi-point test data and existing dimensionless IPR correlations based on a comprehensive bank of field data.

  • 4. To develop a new dimensionless correlation for predicting future deliverability from current flow test data, i.e. to seek a correlation between \(\frac{{q_{\max ,f} }}{{q_{\max ,c} }}\) and \(\frac{{m(p_{r,f} )}}{{m(p_{r,c} )}}\)

The structure of the paper is as follows: Section two describes methods used for development, sensitivity analysis and validation of a new correlation proposed in this paper. Discussion of results and comparison with existing models are presented in Section three. Section four concludes the paper.

Materials and methods

Development of new comprehensive dimensionless IPR curves for gas wells

Assumptions

  1. I.

    Homogeneous, isotropic reservoir with a closed outer boundary.

  2. II.

    Fully penetrating single well;

  3. III.

    Stabilized conditions (i.e., pseudosteady-state equations can be used to describe gas flow in the reservoir).

  4. IV.

    Turbulent flow effects are considered and characterized by a constant turbulence factor D and a rate-dependent skin Dq.

Theoretical approach

Considering the above assumptions, Eq. (8) describes fluid flow in gas reservoirs (field units)

$$\frac{{m\left( {p_{r} } \right) - m\left( {p_{wf} } \right)}}{{1422\frac{qT}{{kh}}}} = \frac{1}{2}\ln \left( {\frac{A}{{r_{w}^{2} }}} \right) + \frac{2.2458}{{CA}} + s + Dq$$
(8)

Quadratic form of Eq. (8) is as follows:

$$m(p_{r} ) - m(p_{wf} ) = aq + bq^{2}$$
(9)
$$a = 1637\frac{T}{kh}\left[ {\log (\frac{A}{{r_{w}^{2} }}) + \log (\frac{2.2458}{{CA}}) + 0.87s} \right]$$
(10)
$$b = 1422\frac{T}{kh}D$$
(11)

Here, k is reservoir permeability, T is reservoir temperature, h is net formation thickness, A is well drainage area, rw is wellbore radius, CA is reservoir shape factor, S is skin factor and D is turbulent flow factor assumed for extra pressure drop due to deviation from Darcy's law assumption. There are several correlations for calculation of turbulent flow factor in the literature (Economides et al. 2013)). In this study, Eqs. (12 & 13) have been used to consider extra pressure drop and turbulent flow factor.

$$D = 2.715 \times \frac{{10^{ - 15} \beta kMP_{sc} }}{{h\mu_{@Pwf} }}$$
(12)
$$\beta = 1.88 \times 10^{10} k^{ - 1.47} \phi^{ - 0.53}$$
(13)

where M is gas molecular weight, Psc is standard pressure, μ @Pwf is gas viscosity measured at bottom hole flowing pressure (Pwf), Tsc is temperature at standard conditions and φ is reservoir porosity.

In order to develop a functional relation between dimensionless rate and dimensionless pseudopressure for current well deliverability, let us start from Eq. (9). The positive root of Eq. (9) is given by

$$q = \frac{{ - a + \sqrt {a^{2} + 4b\left[ {m(p_{r} ) - m(p_{wf} )} \right]} }}{2b}$$
(14)

The Absolute Open Flow (AOF) of a gas well shows the theoretical maximum flow rate of a well at zero sandface pressure (pwf = 0)

$$q_{\max } = q(p_{wf} = 0) = \frac{{ - a + \sqrt {a^{2} + 4b\left[ {m(p_{r} )} \right]} }}{2b}$$
(15)

The ratio of the gas flow rate, q, (Eq. (14)) to AOF, \({q}_{max}\), (Eq. (15)) is defined as

$$\frac{q}{{q_{\max } }} = \frac{{ - a + \sqrt {a^{2} + 4b\left[ {m(p_{r} ) - m(p_{wf} )} \right]} }}{{ - a + \sqrt {a^{2} + 4b\left[ {m(p_{r} )} \right]} }}$$
(16)

Equation (16) can be rewritten as the form of

$$\frac{q}{{q_{\max } }} = F\left[ {\frac{{m(p_{wf} )}}{{m(p_{r} )}}} \right]$$
(17)

where F is some functional form.

Thus, the objective is to generate dimensionless groups \(\left( {\frac{q}{{q_{\max } }}\;{\text{and}}\;\frac{{m\left( {p_{wf} } \right)}}{{m\left( {p_{r} } \right)}}} \right)\) from numerous cases to develop a new empirical IPR correlation for current gas well deliverability in the form of Eq. (17). The relation between dimensionless groups \(\left( {\frac{q}{{q_{\max } }}\;{\text{and}}\;\frac{{m\left( {p_{wf} } \right)}}{{m\left( {p_{r} } \right)}}} \right)\), results in the calculation of q as a function of bottomhole flowing pressure for current reservoir conditions using a single flow test (q and pwf).where F is some functional form.

The equation for predicting AOF at future reservoir pressures can be expressed as follows:

$$q_{\max f} = \frac{{ - a + \sqrt {a^{2} + 4b\left[ {m\left( {p_{rf} } \right)} \right]} }}{2b}$$
(18)

where qmax, f is AOF of the gas well at future reservoir pressure prf. Dividing Eq. (18) to Eq. (15), gives new functional form for prediction of future performance of a gas well with known current AOF and reservoir pressure (pr),

$$\frac{{q_{\max ,f} }}{{q_{\max ,c} }} = \frac{{ - a + \sqrt {a^{2} + 4b\left[ {m\left( {p_{rf} } \right)} \right]} }}{{ - a + \sqrt {a^{2} + 4b\left[ {m\left( {p_{rc} } \right)} \right]} }}$$
(19)

Equation (19) can be rearranged in the form of Eq. (20) which is similar to Eq. (17).

$$\frac{{{q_{\max ,\;f}}}}{{{q_{\max ,\;c}}}} = G\left[ {\frac{{m\left( {{p_{rf}}} \right)}}{{m\left( {{p_{rc}}} \right)}}} \right]$$
(20)

Here, the objective is to generate dimensionless groups \(\frac{{q_{\max ,f} }}{{q_{\max ,c} }}\) and \(\frac{{m\left( {p_{r,f} } \right)}}{{m\left( {p_{r,c} } \right)}}\) using numerous cases and develop a second new dimensionless correlation for prediction of gas well performance at future reservoir pressures with known current AOF and reservoir pressure.

Programming methodology

To develop new IPR correlations for current and future reservoir conditions (Eqs. (17 and 20)), a computer based program (MATLAB R2018) was developed to consider a variety of reservoir rock and fluid properties scenarios with the following steps:

  • (a) Generate a database for calculation of gas pseudopressure as a function of pressure for different reservoir temperatures and gas properties, using correlations available in the literature (Ahmed 2006; Economides et al. 2013).

  • (b) Generate a data base of dimensionless groups \(\left( {\frac{q}{{q_{\max } }}\;{\text{and}}\;\frac{{m\left( {p_{wf} } \right)}}{{m\left( {p_{r} } \right)}}} \right)\) for a wide range of reservoir rock, fluid, geometry and well properties (Table 1).

  • (c) Evaluate the effects of changing reservoir rock, fluid, geometry and well properties, over the range given in Table 1, on a dimensionless IPR generated for a base case. The properties of the base case are shown in Table 1.

  • (d) Using the same parameters as listed in Table 1, generate a data base of \(\left( {\frac{{m\left( {p_{r,f} } \right)}}{{m\left( {p_{r,c} } \right)}}\;{\text{and}}\;\frac{{q_{\max ,f} }}{{q_{\max ,c} }}} \right)\).

Table 1 Rock and fluid properties used in developing correlations
Full size table

New dimensionless IPR correlations

A total number of 30,240,000 (30,240 scenarios from Table 1 with 1000 pressure intervals) pairs of \(\frac{q}{{q_{\max } }}\) and \(\frac{{m\left( {p_{wf} } \right)}}{{m\left( {p_{r} } \right)}}\) were obtained using various reservoir rock, fluid, geometry and well properties for all combinations of the variables listed in Table 1. Figure 1 shows the plot of data points. Previous studies used much lower number of data for generation of dimensionless IPR correlations (25,344 and 10,206 for Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984), respectively).

Fig. 1
figure 1

Generated data and fitted new dimensionless IPR for current conditions (Eq. 21)

Full size image

Employing MATLAB curve fitting tool (R2018), different curves were fitted to the generated set of data. The best curve was found to be the 7th degree polynomial with R2 value of 0.9995 given in Eq. (21).

$$Y = p_{1} X^{7} + p_{2} X^{6} + p_{3} X^{5} + p_{4} X^{4} + p_{5} X^{3} + p_{6} X^{2} + p_{7} X + p_{8}$$
(21)

where \(Y = \frac{q}{{q_{\max } }},X = \frac{{m\left( {p_{wf} } \right)}}{{m\left( {p_{r} } \right)}}\)

$$\begin{gathered} p_{1} = - 24.7712,p_{2} = 75.1463,p_{3} = - 89.5387,p_{4} = 52.5531,p_{5} = - 15.8089,p_{6} = 2.0926, \hfill \\ p_{7} = - 0.6320,p_{8} = 1.0010 \hfill \\ \end{gathered}$$

Equation (21) is a new dimensionless IPR curve to estimate the current gas wells deliverability with a single pair of stabilized flow rate and bottom hole pressure and known average reservoir pressure. Figures 2, 3, 4, 5, 6, 7, 8, 9, 10 present sensitivity analysis of different parameters compared to base case in Table 1.

Fig. 2
figure 2

Sensitivity analysis—effect of drainage area shape factor

Full size image
Fig. 3
figure 3

Sensitivity analysis—effect of drainage area

Full size image
Fig. 4
figure 4

Sensitivity analysis—effect of gas specific gravity

Full size image
Fig. 5
figure 5

Sensitivity analysis—effect of net reservoir thickness

Full size image
Fig. 6
figure 6

Sensitivity analysis—effect of reservoir permeability

Full size image
Fig. 7
figure 7

Sensitivity analysis—effect of reservoir pressure

Full size image
Fig. 8
figure 8

Sensitivity analysis—effect of skin factor

Full size image
Fig. 9
figure 9

Sensitivity analysis—effect of wellbore radius

Full size image
Fig. 10
figure 10

Sensitivity analysis—effect of reservoir temperature

Full size image

Similar method for current well deliverability was used to develop a second dimensionless correlation for prediction of future well performance. In total, 30,240,000 points (30,240 scenarios with 1000 pressure intervals) were generated for \(\left( {\frac{{m\left( {p_{r,f} } \right)}}{{m\left( {p_{r,c} } \right)}}\;{\text{and}}\;\frac{{q_{\max ,f} }}{{q_{\max ,c} }}} \right)\) to develop an equation for predicting the future gas wells deliverability with known current AOF and pressure (see Fig. 11). The best seventh order polynomial that fit the curve is given in Eq. (22)

$$Y = p_{1} X^{7} + p_{2} X^{6} + p_{3} X^{5} + p_{4} X^{4} + p_{5} X^{3} + p_{6} X^{2} + p_{7} X + p_{8}$$
(22)
Fig. 11
figure 11

New dimensionless IPR for Future conditions (Eq. 22)

Full size image

where \(Y = \frac{q}{{q_{\max } }},X = \frac{{m\left( {p_{wf} } \right)}}{{m\left( {p_{r} } \right)}}\)

$$\begin{gathered} p_{1} = 57.76,p_{2} = - 216.3649,p_{3} = 327.1399,p_{4} = - 256.1986,p_{5} = 111.3743,p_{6} = - 27.3358, \hfill \\ p_{7} = 4.6068,p_{8} = 0.0273 \hfill \\ \end{gathered}$$

Validation with field data

Both Eq. (1) and/or Eq. (9) can be used to obtain deliverability parameters for well deliverability calculations with multi-point test data (c,n in Eq. 1 or a,b in Eq. 9). Known deliverability parameters allow calculation of AOF and construction of IPR curve. In this study, Eq. 9 is used as benchmark for error analysis and validation of dimensionless IPR models against measured field data.

Well test data from more than 60 wells with both multi-point test and stabilized pressure drawdown data from Middle East reservoirs were collected (Kalantariasl et al. 2013). Among them, 50 wells with valid data were selected (see Table 2, wells# 1–50). In addition, 11 data were collected from other references (wells# 51, 52 from Sung et al. (2001), well# 53 from Shumakov et al. (2006) and wells# 54–61 from Brar and Aziz (1978)).

Table 2 Summary of error analysis
Full size table

The selected field data for validation of the proposed correlation were from 61 wells of 15 fields. The current absolute open flow potential (AOF) using pseudopressure was set as an objective to evaluate its prediction ability against multi-point flow test results. Equation (9) was used as benchmark for calculation of AOF from multi-point test data and results are presented in 2nd column of Table 2. In addition, AOF were calculated using previously developed correlations by Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) in 3rd and 4th columns of Table 2, respectively. AOF calculated from Eq. 21 is presented in 5th column. Error analysis was used to compare the results obtained by the new proposed correlation in this paper with other models.

Relative and absolute error values (Eqs. 23 and 24) were calculated to evaluate and compare of three correlations (Ali 2020). These values were used for analysis of accuracy in terms of standard deviation, overperdition and underprediction of different models.

$$\% {\text{Relative}}\;{\text{Error}} = 100 \times \left[ {\frac{{{\text{AOF}}_{{{\text{Predicted}}\;{\text{IPR}} }} - {\text{AOF}}_{{{\text{multi - point }}\;{\text{est}}}} }}{{{\text{AOF}}_{{{\text{multi - point}}\;{\text{test}}}} }}} \right]$$
(23)
$${\text{\% Absolute}}\;{\text{Error}} = \left| {100 \times \left[ {\frac{{{\text{AOF}}_{{{\text{Predicted}}\;{\text{IPR}}}} - {\text{AOF}}_{{\text{multi - point test}}} }}{{{\text{AOF}}_{{\text{multi - point test}}} }}} \right]} \right|$$
(24)

Columns six to eight show relative error as calculated from Eq. 21. Absolute error for each method is presented in columns nine to eleven of Table 2.

These dimensionless IPRs were selected for comparison, since other correlations need additional data such as permeability and skin factor and rock permeability that was not available.

Discussion of results

Figure 1 shows the IPR curve of the new dimensionless correlation derived in this work as expressed in Eq. (21). Table 1 indicates parameters and variation of each parameter for development of the proposed correlation. It also shows the benchmark case properties used for sensitivity analysis of different parameters. To evaluate the effects of variance of different parameters on the new IPR curve, each parameter was varied over two values: high and low cases. Figures 2, 3, 4, 5, 6, 7, 8, 9, 10 illustrate the sensitivity analysis results. The results of sensitivity analysis demonstrate that among all identified variables, reservoir pressure, formation permeability and mechanical skin factor have significant impact on IPR curve. Similar results were reported by Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984). The variation in IPR curve due to reservoir pressure and permeability is because of their effect on available reservoir energy and turbulence factor, respectively. The higher negative value of skin factor improves the conductivity of reservoir near the wellbore and hence the deliverability, thus affects the IPR curve.

Figure 2 demonstrate that reservoir shape factor has minimum effect on IPR correlation as expected from Eqs. 8 and 10. In addition, the range of variations of this parameter is low and has low effect. Well drainage area has also minimum effect as shown in Fig. 3 and Eq. 8 (Ln (A)). Gas specific gravity with low variation only affects turbulent coefficient and pseudopressure; thus, its effect on final correlation is minimal as demonstrated in Fig. 4. Equation 16 suggests that reservoir thickness, which appears in both a and b, has very small effect on dimensionless parameters as indicated in Fig. 5. According to Darcy’s law, reservoir permeability directly affects well deliverability. In addition variation of permeability can be orders of magnitude. Here, one can expect considerable share for permeability variation. Figure 6 shows that with increasing permeability, for a given value of m(pwf)/m(pr), q/qmax increase and vice versa. Reservoir pressure is one of the main factors that affect the well deliverability. Reservoirs with higher pressure allow higher production for a given well flowing pressure according to Eq. 8; thus, Fig. 7 indicates high variation of IPR with pressure. Positive skin factor decreases well production rate for a given pressure conditions. On the other hand, negative skin corresponds to higher permeability in the near wellbore area and higher rate can be obtained as shown in Fig. 8. Figure 9 shows that wellbore radius has low effect with low range of variation and according to Eq. 8. Temperature appears in a and b coefficients in Eqs. 10 and 11. Despite its hidden effects on gas viscosity and pseudopressure, according to Eq. 16 and low range of variation its effect is minimal as indicated in Fig. 10.

The validity of the new proposed dimensionless IPR curve method was evaluated by calculating the relative and absolute percentage error described in Eqs. 23 and 24 between the AOF obtained from conventional multi-point analysis method (Eq. 9), and the AOF determined with single-point flow data from the same well using the dimensionless IPR curve models (Eqs. 2,4and21). In addition to the new dimensionless IPR model, Mishra and Caudle (1984) and Al-Attar and Al-Zuhair (2009)models are also examined against multi-point test results of all wells.

Table 2 summarizes the AOF values of the 61 wells calculated from multi-point tests and predicted values from the new proposed dimensionless correlation and previous correlations. It also shows associated relative error values for three dimensionless IPR correlations. Column 2 shows AOF calculated from multi-point test data (Eq. 9). Columns 3, 4 and 5 present AOF calculated from single-point dimensionless IPR correlations proposed by Al-Attar and Al-Zuhair (2009) (Eq. (4)), Mishra and Caudle (1984) (Eq. (2)) and the new one in this paper (Eq. (21)), respectively. Associated relative and absolute error percent are presented in columns 6 to 11.

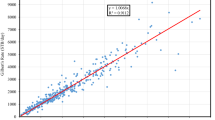
Figure 12 compares AOF predicted by new dimensionless IPR model (Eq. (21)) against results of multi-point test data analysis. It shows very good agreement between predicted AOF and AOF calculated by multi-point test. In addition, Fig. 13 presents AOF calculated from multi-point test data and AOF predicted by dimensionless correlations developed by Al-Attar and Al-Zuhair (2009) (Eq. (4)), Mishra and Caudle (1984) (Eqs. (2) and (21). Deviation from 45 angle linear trend is clear for Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) models in several wells. Figure 14 shows absolute error values against AOF calculated from multi-point test data for all three dimensionless IPR models (Eqs. 2, 4and21) on log–log paper. One can see the more generality of the new proposed model (Eq. 21) from Figs. 12, 13, 14. It should be noted that previous dimensionless IPR models can be used with acceptable accuracy for many cases particularly for wells with AOF less than 100 MMSCF/D. Error analysis shows that both Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984)models predict unacceptable AOFs for 13 wells with error percentages more than 100% (Table 2).

Fig. 12
figure 12

Comparison of AOF calculated from multi-point test data and AOF predicted by new dimensionless IPR (Eq. (21))

Full size image
Fig. 13
figure 13

Comparison of AOF calculated from multi-point test data and AOF predicted by dimensionless IPR correlations (log–log plot)

Full size image
Fig. 14
figure 14

Absolute error% versus multi-point AOF of all wells (log–log plot)

Full size image

Errors associated with Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) predictions were between 40 and 100% for 5 and 6 wells, respectively. Mishra and Caudle (1984) and Al-Attar and Al-Zuhair (2009) models underpredict for 29 and 19 wells out of 61, respectively, while new correlation (Eq. 21) underpredicts for 47 wells. The new proposed dimensionless IPR (Eq. 21) overpredicts for 14 wells out of 61.

Maximum absolute error for Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) and new proposed (Eq. (21)) models are 466%, 623% and 32.7%, respectively. Minimum absolute error for Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) and new proposed (Eq. (21)) models are 0.27%, 2.12% and 0.26%, respectively.

The average absolute error for new model (Eq. 21) is 11.6% (standard deviation of 8.5%) while the average absolute error values for Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) are 85.9% (standard deviation: 148.1%) and 68.6% (standard deviation:115.3%), respectively. It should be noted that previous models lose their accuracy for high rate wells more than low rate wells and weight of high error values affects average error values in the presented data bank.

For new proposed dimensionless IPR model, all 61 wells have AOF absolute errors less than 32.7% (maximum error), 52 of which have errors less than 20%. In fact, absolute error associated with AOF of 27 wells is less than 10% (22 wells for both Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984).

In addition, as an example, comparison between predicted IPR from Eq. (21), Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984)models with IPR calculated from multi-point test data for wells #3 and 42 is shown in Figs. 15 and 16, respectively. Both Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) models fail to predict acceptable IPR for well#3 (Fig. 15) while prediction of three models for well#42 is more accurate and very close to what calculated from multi-point well test data (Fig. 16).

Fig. 15
figure 15

Well#3: Comparison of IPR from multi-point test data and dimensionless IPR correlations

Full size image
Fig. 16
figure 16

Well#42: Comparison of IPR from multi-point test data and dimensionless IPR correlations

Full size image

Generally, results show the superiority of the new model to the previous models for field data presented in this paper. However, for low rate high drawdown gas wells both Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) models work fair and can be used for analysis of single-point test data.

The data evaluated in this work are more comprehensive than previously published works. In addition, wide range of reservoir pressure and AOF were used for evaluation of the proposed model. To the best of our knowledge, maximum multi-point AOF tested for dimensionless IPR models was less than 200 MMSCFD. The presented data bank covers wide ranges of AOF (2.1–1411.3 MMSCFD) and reservoir pressure (1500–7500 psi). Additional measured well data are required to check the validity of the proposed model in different conditions rather than wells presented in this study.

If skin data are available from analysis of transient single-point test pressure data, dimensionless IPR model developed by Chase (2002) can be evaluated against multi-point test results and compared with other dimensionless IPR models including the proposed model in this study specifically for high rate gas wells.

The proposed dimensionless IPR correlation along with previous models (Al-Attar and Al-Zuhair 2009; Mishra and Caudle (1984); Billiter and Lee 2000; Chase 2002) can be used in estimation of AOF and well deliverability instead of assuming n = 1 (see Eq. (1)) in some commercial software packages due to unacceptable error associated with assumption of n = 1 (Trick et al. (2002)). Additional well test data are needed to evaluate the accuracy of future IPR model presented in this paper (Eq. 22).

Conclusions

The following conclusions can be drawn from the present study:

  • A new simple dimensionless IPR correlation is developed for calculation of current deliverability of gas wells with a wide range of reservoir properties.

  • The mean absolute value of errors between the AOFs predicted using multi-point test analysis method and the proposed dimensionless IPR from single-point test for 61 wells was 11.6%.

  • The superiority of this model against previous proposed correlations by Al-Attar and Al-Zuhair (2009) and Mishra and Caudle (1984) is clearly supported by the current field data analysis of 61 wells.

  • The results of this study indicate that the proposed dimensionless correlations in this study are applicable for high rate low drawdown gas wells as well as low rate wells with reasonable accuracy.

  • The present study provides additional evidence of using dimensionless IPR curve as a reasonably accurate and cost-effective method for prediction of gas well inflow performance from just a single-point flow test.

  • A new dimensionless IPR correlation was developed for future well deliverability analysis.