Introduction

Geostatistic presents tools to analyze geological information for constructing 3D numerical models which are used to predict reservoir performance (Pyrcz and Deutsch 2014). The estimation methods (kriging-based) provide a reasonable porosity estimation by analyzing porosity from well log data with given trends (Ketteb et al. 2019). Kriging and simulation require the use of either the covariance or the variogram. Kriging equations minimize and give a detailed description of the estimation variance (Armstrong 1984; Omre 1985; Srivastava and Parker 1989). Thus for complex reservoirs, the kriging may not present a realistic level of heterogeneities while the simulation methods have been derived increasingly to generate detailed models (Sahin and Al-Salem 2001). Estimation tends to generate a smooth distribution of the variables (White and Willis 2000). To overcome the limitations of estimation methods, approximate algorithms can be applied, allowing dealing with large numbers of data on unstructured grids. Multigaussian kriging allows generalizing the traditional approach to account for local stationarity. Also, it was mentioned by Emery (2005) that the multigaussian kriging no longer relies on the mean value of the normal score data. It is an important solution for the old problem of non-stationarity. Pyrcz and Deutsch (2014) expressed that the p-field simulation is a novel method that divorces the calculation of the local distribution of uncertainty and simulation with the correct spatial continuity and global distribution. In the early nineties, Gómez-Hernández and Journel (1993) declared that the random function is a statistical model of distributed variables like porosity that is defined by a multivariate probability distribution. As Emery and Peláez (2011) mentioned, sequential simulation in an area with scattered data relies on the global distribution which must be representative of all areas being simulated. Random function models can recognize geological complexity features that are difficult or impossible to characterize (Zaytsev et al. 2015). A comparison between Sequential Gaussian Simulation (SGS) and turning bands method was investigated by (Paravarzar et al. 2015) which showed that the turning bands method reproduces a global correlation by cross-variograms of the regionalized variables, while sequential simulation produces some biases. Furthermore, a study by (Daly et al. 2010) expressed that the conditional simulation like Gaussian Random Function Simulation (GRFS) has a better performance in global porosity modeling compared with SGS. The SGS method is a common method for continuous property modeling and it follows a multivariate technique that calculates the local distribution of uncertainty from simple kriging (Nazarpour et al. 2014). A conditional simulation like SGS and GRFS is proper to generate the global distribution (Goovaerts 1997). The SGS method is efficient to describe the reservoir heterogeneity and provides the proper spatial distribution of petrophysical properties (Rahimi and Riahi 2020). Statistical testing is useful to illustrate the effect of different neighborhood performances on the simulation (SGS) results (Safikhani et al. 2017). The goal of this study is to assess the accuracy of simple kriging and simulation methods (SGS and GRFS) by evaluating the local and global distribution.

Case study and theory of methods

Case study

This study deals with a sandstone reservoir that is related to Jurassic to early cretaceous times with regional tectonic movements. The initial structure was built by 116 layers including follow base, proportional, fractions and follow top zoning subsections. The fault data sets were imported and modeled into the initial structure. Fifteen well were entered into the structure, and the porosity range of this reservoir is from 2.5 to 30%.

Geostatistical methods

Kriging

The kriging method was developed by Matheron (1963). The base of kriging is the local estimation which is clustered to the single and secondary attribute values for estimating at unsampled locations. Kriging is the best linear unbiased estimator (Goovaerts 1997). The main idea of kriging is to predict a reservoir property of a function at a located point by computing a weighted average of the known values in the neighborhood of the point (Matheron 1963). This estimator is defined as follows:

$$Z_{K}^{*} = \mathop \sum \limits_{i = 1}^{n} \lambda_{i} z_{xi}$$
(1)

where \(z_{xi}\) and \(\lambda_{i}\) are the value of the sample and the weighting factor at point i, respectively, and \(Z_{K}^{*}\) is kriged estimator. The first step in kriging is to estimate the semi-variogram and model it. For any given separation h the semi-variance can be estimated by (Cressie and Hawkins 1980):

$$\gamma \left( h \right) = \frac{1}{2m\left( h \right)}\mathop \sum \limits_{i = 1}^{m\left( h \right)} \left\{ {Z\left( {X_{i} } \right) - Z\left( {X_{i} + h} \right)} \right\}^{2}$$
(2)

where \(m\left( h \right)\) is the number of pairs of points separated by lag h. This method generates the best unbiased estimates and minimizes the estimation variance. Several kriging types are common including linear kriging such as simple kriging (SK), ordinary kriging (OK), universal kriging (UN) and co-kriging (CK) (Journel 1983; Goovaerts 1997). The purpose of conventional mapping like kriging is not to depict the full distribution of variability of the property (Pyrcz and Deutsch 2014). All the kriging estimators are the variants of the basic Eq. (3), as follows:

$${{Z}}^{*} \left( {\text{u}} \right) - m\left( u \right) = \mathop \sum \limits_{\alpha = 1}^{n\left( u \right)} \lambda_{\alpha } .[z\left( {u_{\alpha } } \right) - m\left( {u_{\alpha } } \right)]$$
(3)

In equation \({{Z}}^{*} \left( {\text{u}} \right)\) is the estimate at unsampled location u, \({\text{m}}\left( {\text{u}} \right)\) is the prior mean value at unsampled location u, α = 1……n in \({\lambda }_{{\alpha }}\) are weights applied to the n data, \({{z}}\left( {{{u}}_{{\alpha }} } \right),\) α = 1……n, are the n data values, and \({{ m}}\left( {{{u}}_{{\alpha }} } \right)\), α = 1……n, are the n prior mean values at the data locations. In simple kriging, the modeling of the trend component \({{m}}\left( {{u}} \right){ }\) is assumed as a stationary mean. The parameter \({\text{m}}\left( {\text{u}} \right)\) is assumed constant over the whole domain and calculated as the average of the data. SK is used to estimate residuals from this reference value \(m\left( u \right)\) given a priori and is therefore sometimes referred to as “kriging with known mean” (Goovaerts 1997). The local distribution of uncertainty can be reached from simple kriging and variance which can increase the spatial correlation (Rossi and Deutsch 2014). Figure 1 shows the procedure of the kriging method in this study.

Fig. 1
figure 1

Flowchart of the procedure of the kriging method in this study

Full size image

Sequential gaussian simulation

Sequential Gaussian simulation is a widely used method for the reservoir characterization of properties (here porosity) from various earth science disciplines (Manchuk and Deutsch 2012). The SGS method is a conditional simulation that follows a sequential principle under the multigaussian random function model (Emery and Peláez 2011; Goovaerts 1997). The popularity of this method is because of its simplicity and effectiveness for generating numerical models with correct spatial statistics. The multivariate Gaussian distribution can help for the calculation of local distributions of uncertainty from simple kriging. Global distribution can be reproduced by these conditional distributions (Goovaerts 1997). The simple kriging forces the covariance between the data and the kriging estimate to be correct; however, the variance is too small, and the covariance is incorrect. This covariance can be fixed by proceeding sequentially that is, to use previously predicted values in subsequent predictions (Hu and Ravalec-Dupin 2005). The modeling stage consists of the following steps:

  • The original data sets are forced to a normal distribution by the normal scores method; then, the transformed data is assigned into the simulation grid.

  • The random path is generated from grid nodes, and a random node is estimated by simple kriging (Eq. 3).

  • A random value is selected from the equation which was calculated by estimated mean and standard deviation where the local conditional probability distribution is defined.

  • A random value is selected from the local conditional probability distribution to set the node value to the first unknown variable (porosity), and this process is repeated sequentially.

This algorithm represents the global distribution of continuous variables (Kavousi and Gao 2013). Another interesting property of kriging is that the variance of the kriged estimate is known:

$${\text{Var}}\{ {\text{Y}}^{*} \left( {\text{u}} \right)\} \, = {\text{ C}}\left( 0 \right) \, {-}{\upsigma }_{{{\text{sk}}}}^{2} \left( {\text{u}} \right)$$
(4)

where C(0) is the covariance value at separation vector h = 0. This equation tells us how much variance is missing: the kriging variance \({\upsigma }_{{{\text{sk}}}}^{2}\)(u). This missing variance must be added back in without changing the covariance reproduction properties of kriging (Emery and Peláez 2011). An independent component with zero mean and the correct variance can be added to the kriged estimate:

$${\text{Y}}_{{\text{s}}} \left( {\text{u}} \right) = {\text{Y}}^{*} \left( {\text{u}} \right) + {\text{R}}({\text{u}})$$
(5)

The expected value of the residual, E{R(u)}, is 0; therefore, E{R(u)·\({\text{Y}}\left( {{\text{u}}_{{\upalpha }} } \right)\)} = 0. Thus, the covariance between the simulated value and all data values is correct.

Gaussian random function simulation

GRFS is a conditional simulation, and the base of estimation in this method is the parallel kriging. Parallel kriging provides estimates with high accuracy and can be applied to various extension of kriging and other gaussian methods (Zhuo et al. 2011). The parallel algorithm reduces the execution time of the kriging process with the high quality of the model results (Pesquer et al. 2011). The other section of GRFS is an unconditional simulation which is based on the fast Fourier transform (FFT). Fourier integral method is an efficient method to generate realizations of random functions in multidimension sections. Moreover, in this method the nugget effect in zonal and geometric anisotropy is straightforward (Pardo-Iguzquiza and Chica-Olmo 1993). In this method, the standard search for variogram correlation tends to find highly correlated neighbors along with the vertical wells (Daly et al. 2010).

Parallel kriging

Parallel kriging is designed to deal with rather equally spaced data. This method tries to distribute the task of predicting at the points of the prediction grid to some computing cluster. This process has to investigate the distribution of data sets from clustered cells. Each clustered cell is then assigned to a single CPU which computes the value of the parameter (here porosity) using the kriging algorithm (the equation is present in the previous part). Finally, the results are gathered from all CPUs to create realization from estimated values (Strzelczyk and Porzycka 2010).

Fourier integral method (FIM)

The Fourier Integral Method (FIM) was presented to generate realizations of a random function in one, two or three dimensions. It is an efficient technique of non-conditional sequences with imposed covariance. This method can generate the realization with nested structures and anisotropic covariance (geometric, zonal or both) (Pardo-Iguzquiza and Chica-Olmo 1993).

By calculating the inverse Fourier transform of the complex coefficients A (j), the discrete finite realization {z(k), k = 0 ….. N—1} is obtained with the specified covariance model:

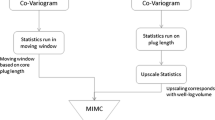
$${\text{z}}\left( {\text{K}} \right) = \mathop \sum \limits_{j = 0}^{N - 1} A\left( j \right)e^{i2\pi jk/N}$$
(6)

k = 0 ….. N—1. If the number of points N is to the power of two, the inverse discrete Fourier transform can be rapidly and efficiently computed with the fast Fourier transform (FFT) (Pardo-Iguzquiza and Chica-Olmo 1993). Figure 2 shows the flowchart of the procedure of the SGS and GRFS methods in this study.

Fig. 2
figure 2

Flowchart of the procedure of the simulation methods in this study

Full size image

Procedure and implementation

Porosity is estimated and simulated using three methods. At first, porosity is estimated using simple kriging. In the second step, due to the dependency of multivariate analysis to porosity, SGS and GRFS are used to simulate porosity. In the third step, the local and global distribution is investigated for each method. All of the statistical and geostatistical analysis is done using GSLIB (version 1.5) and PETREL (Version 2017.4) software. Details about the procedure will be being discussed in the following sections.

Data preparation and stratigraphic coordinate

The horizontal variograms are sensitive to stratigraphic transform (Zrel). For spatial correlation, the coordinate transform is needed when the structure is folded by faults, unconformities, etc. (Rossi and Deutsch 2014). Therefore, this problem was corrected before fitting the variogram. The vertical coordinate was defined between the top and base grid. Transforming the vertical coordinate in two-dimensional modeling presents the following equation:

$${\text{Z}}_{{{\text{relative}}}} = \frac{{{\text{Z}}_{{\text{i}}} \_{\text{Z}}_{{{\text{bottom}}}} }}{{{\text{Z}}_{{{\text{top}}}} \_{\text{Z}}_{{{\text{bottom}}}} }} \cdot {\text{T}}_{{{\text{average}}}}$$
(7)

In equation, \({\text{Z}}_{{{\text{top}}}} ,\) is the correlation top and \({\text{Z}}_{{{\text{bottom}}}}\) is the correction base. \({\text{T}}_{{{\text{average}}}}\) is the average thickness of layers. In this study, vertical coordinate was performed and also the data sets were normalized by Normal Scores (NS) transformation. This process is shown in Fig. 3.

Fig. 3
figure 3

a Histogram of porosity data after normalization process. b Porosity scatter plot for vertical coordinate

Full size image

Experimental variogram computation

In this section, the variograms for the porosity in horizontal and vertical directions were calculated considering the depositional directions. Statistical parameters like azimuth, dip, the number of lags, search radius, bandwidth, tolerance angle and lag tolerance were analyzed and calculated to fit the model of the primary variogram. Moreover, the main section of variograms like sill, nugget effect, major, minor and vertical ranges was extracted as the inputs for the estimation and simulation process. Azimuth is an angle measured from the north to the major direction which varies from 0° to 360°, and the main azimuth is 173.8˚. The dip is measured 0, between the horizontal plane and specified direction. The minimum distance between the wells was 1100 m which was used in computing the lag distance. After computing the parameters, the best correlation between pairs and regression plot was fitted. Figures 4, 5 and 6 are shown as the fitted variograms in major, minor and vertical directions. Table 1 shows the variogram parameters that were used as the input data for the modeling process.

Fig. 4
figure 4

The model of fitted variogram and experimental parameters in major direction

Full size image
Fig. 5
figure 5

The model of fitted variogram and experimental parameters in minor direction

Full size image
Fig. 6
figure 6

The model of fitted variogram and experimental parameters in vertical direction

Full size image
Table 1 Experimental parameters as the input data for estimation and simulation process
Full size table

Q-Q plots for kriging and simulation methods

In this study, the Q-Q plot is a refined graphical tool for comparing two distributions (Target Porosity Distribution versus Porosity realization) for each method. After fitting the model of variograms, the modeling process was performed by kriging estimator and conditional simulation methods (SGS and GRFS). The Q-Q plots were built to check the distribution procedure. The plots showed both sets of quintiles, the target porosity (upscaled porosity) distribution versus estimated and simulated porosity had a normal distribution in all methods. Any departure was not seen above or below 45˚ line so that the center or mean of the distribution is normal. Moreover, after calculating the equations, it was observed that the simple kriging had a slightly better correlation coefficient which shows the simple kriging is more locally accurate. Figures 7, 8 and 9 show the Q-Q cross plots for the applied methods. Table 2 denotes the linear equation, correlation factor and covariance which were presented by plots.

Fig. 7
figure 7

Q-Q Cross plot between target porosity and GRFS-based modeled data

Full size image
Fig. 8
figure 8

Q-Q Cross plot between target porosity and SGS-based modeled data

Full size image
Fig. 9
figure 9

Q-Q Cross plot between target porosity and kriging-based modeled data

Full size image
Table 2 The linear equation and correlation coefficient calculated by Q-Q plots related to methods
Full size table

The generated model of variograms for estimation and simulation methods

For some validation, final variograms were extracted from each realization. In this study, 10 different seed numbers were chosen for the conditional simulations; then, 10 horizontal variograms were generated by each conditional method (SGS and GRFS). For the kriging method, a main horizontal variogram was extracted from the estimated realization. The purpose of this study was to investigate the variogram reproduction by checking the global distribution for the estimate and conditional methods. The sill and nugget effect were compared for each method. Finally, it was observed that the conditional simulations could reproduce the variograms globally with proper sill and nugget effect (with a normal distribution) as well as original data (upscaled porosity). Moreover, horizontal variogram of the kriging showed that this method minimized the variance (0.63). It shows that the SGS and GRFS methods are practical than kriging for the geostatistical reservoir modeling, where the sill is the equal-weighted variance of the data entering variogram calculation (1.0 if the data are normal scores). Figures 10, 11 and 12 are the horizontal variograms. Table 3 denotes the sill ranges and nugget effects which are calculated by the conditional simulations. The sill range varies from 0.98 to 1, and the nugget effect varies from 0.25 to 0.33 for GRFS in 10 realizations and also for SGS, the sill range was between 0.97 and 1, and the nugget effect was between 0.34 and 0.45. Table 4 presents the variogram statistics for the kriging.

Fig. 10
figure 10

Raw model of horizontal variogram (black) and extracted horizontal variograms based on the GRFS realizations

Full size image
Fig. 11
figure 11

Raw model of horizontal variogram (black) and extracted horizontal variograms based on the SGS realizations

Full size image
Fig. 12
figure 12

Raw model of horizontal variogram (black) and extracted horizontal variogram (yellow) based on the kriging realizations

Full size image
Table 3 The calculated statistics by raw and extracted variograms based on SGS and GRFS
Full size table
Table 4 The calculated statistics by raw and extracted variograms based on kriging
Full size table

Cross-validation

The basic idea of this step is to estimate the property (here porosity) at locations where we know the true value. This step was implemented to validate the models locally. In this procedure, three wells as the actual data were deleted one at a time and re-estimated from the remaining neighboring data. It was assured that the wells were far away from each other to improve the quality of validation. Wells B2, C4 and C7 were chosen with the following depths: 762.8, 490 and 606.3 m, respectively. Moreover, the fraction of porosity was investigated through the well sections window where the reproduced porosity by kriging, SGS and GRFS methods was compared with the original well data. To check the result of distributions of uncertainty, the percent error was calculated in all sections which show the difference between the original well log and the simulated porosity. The mean error between estimated and measured porosity in 15 cored points is 3.4, 3.6 and 1.9 for GRFS, SGS method and kriging method, respectively. It was observed that the kriging method had a better performance than the SGS and GRFS to reproduce the porosity locally. Thus, the kriging method is more reliable to prove the optimality of a given estimation at specific locations (locally accurate). Figures 13, 14 and 15 represent the well sections of the original porosity (solid line) and the simulated porosity (showed in colors) in three wells. Table 5 denotes the percent error for each method.

Fig.13
figure 13

Well section of porosity log (solid lines) and simulated porosity (colors) related to well B2

Full size image
Fig.14
figure 14

The well section of porosity log (solid lines) and simulated porosity (colors) related to well C4

Full size image
Fig.15
figure 15

Well section of porosity log (solid lines) and simulated porosity (colors) related to well C7

Full size image
Table 5 The percent error of simulated porosity for chosen wells
Full size table

Cross-sectional models

In this part, the last realizations were showed in cross-sectional models. Two realizations with the same seed number were chosen for simulation methods and also a sectional model was depicted which was made by kriging algorithm. The result showed that the kriging tried to smooth the model by omitting the global distribution of porosity. On the other hand, the simulation methods (SGS and GRFS) tried to generate more detailed models as well as results in horizontal variograms. Figure 16 shows the cross-sectional models for each method.

Fig. 16
figure 16

Cross-sectional models related to GRFS, SGS and kriging realizations with the location of upscaled well logs

Full size image

Discussions and results

As discussed earlier, the Q-Q plots were generated to validate the distribution of porosity of three methods in Fig. 7, 8 and 9. The linear functions and correlation coefficient are calculated and presented in Table 2. As it can be seen it was not any sign of systematic departure above or below the 45˚ line which means that the center or mean of the distribution in all methods is normal but after the calculation of equations, it was observed that the simple kriging had a slightly better correlation coefficient which shows the simple kriging is more locally accurate.

An alternative method based on parallel kriging and Fourier integral is used. This method uses parallel kriging instead of simple kriging for local estimation. This conditional simulation shows highly reliable results as well as the sequential simulation for generating highly detailed models with correct covariance while the simple kriging represents the incorrect covariance.

As shown in Figs. 10, 11 and 12, the horizontal variograms were extracted from simulation and estimation realizations to peruse porosity as the global distribution. The evaluation of parameters in Tables 3 and 4 showed that the alternative simulation methods (SGS and GRFS) were able to reproduce the sill as well as the initial experimental variogram, while the kriging method minimized the variance of the model.

Furthermore, as seen in Fig. 13, 14 and 15, the cross-validation was implemented to validate the local distribution of porosity by removing three wells to check the reproduction of porosity. The percent error was estimated for each method. As shown in Table 5, the mean error between estimated and measured porosity in 15 cored points is 3.4, 3.6 and 1.9 based on GRFS, SGS and kriging methods, respectively. Therefore, the kriging could regenerate the porosity with minimum error.

Finally, cross-sectional models in Fig. 16 were depicted and the results confirmed that the simple kriging tries to produce smoother distribution, whereas the conditional simulations try to represent more global-detailed sections.

Conclusion

There are different methods for porosity estimate that can be categorized into two groups: conditional simulations and estimation methods. This research aimed at assessing the performance of three popular algorithms (Kriging, SGS and GRFS) by considering the local and global distribution for simulating regionalized variables through a real case study. The GRFS method was used as an alternative method that uses different kriging from the other methods. At the first step of validation, the Q-Q plots were checked and the linear equations were calculated. The Q-Q plots had a normal distribution in both sets of quintiles (target porosity distribution versus estimated porosity). The calculated correlation coefficients (0.93, 0.94 and 0.97 related to GRFS, SGS and kriging, respectively) denoted that the kriging method had a slightly better performance in local distribution compared with simulation methods. The extracted horizontal variograms were calculated for investigating the global distribution. Results showed that the kriging method tried to minimize the variance of the variogram. This problem is more severe in multivariate cases where the global distribution is so important for the reservoir characterization. The cross-validation was applied to validate the porosity distribution locally. In this process, the percent error was calculated for each method which showed that the kriging had the minimum error by estimating the porosity at well locations. Therefore, kriging makes the best possible estimate at the unsampled location by minimizing the error. Finally, cross-sectional models were depicted in which the kriging method tried to smooth the porosity through the layers while the simulation method could represent a more detailed visualization. Therefore, it is recommended to apply the kriging for estimation of a single realization of random field (local concentration), while the simulation methods can be applied for the complicated reservoirs to analyze its accuracy on different spatial environments for multiple observations of a multivariate data set.