Introduction

The hydraulic jump constitutes one of the most complex phenomena in hydraulic engineering (Hager 1992). Its chaotic nature, involving important turbulence, intense air entrainment and significant fluctuations in the velocity and pressure fields, places the current knowledge far from a full understanding of the phenomenon (Macián-Pérez et al. 2020a, b, c). In spite of its complexity, the turbulent nature of the hydraulic jump holds great interest for energy dissipation purposes in certain hydraulic works. More specifically, stilling basins are the preferred energy dissipation structure in large dams (Hager 1992). In such structures, a hydraulic jump dissipates the excess energy of the flow, in order to guarantee the discharge into the river in appropriate conditions.

Large dams can be considered as one of the most relevant civil engineering constructions, given their social and economic importance. In their design and building process, the stilling basin often constitutes the most challenging part (Fernández-Bono and Vallés-Morán 2006). In addition to this, spillways and energy dissipation structures are in the spotlight due to climate change effects and increasing demands regarding flood protection (Carrillo et al. 2020; Macián-Pérez et al. 2020b). The need for adaptation in existing dams to larger discharges than those originally considered arises under these new conditions. This adaptation requires a deep knowledge of the hydraulic jump and of how it is influenced by the stilling basin design.

The study of the hydraulic jump dates back almost two centuries, in which different features have been analyzed, mainly from an experimental perspective. First studies focused on the hydraulic jump basic dimensions such as the free surface profile, the sequent depths ratio or the jump length (Bakhmeteff and Matzke 1936; Bélanger 1841). Later, the velocity and pressure fields were approached through extensive experimental campaigns (Mossa 1999; Rajaratnam 1965; Toso and Bowers 1988). In the last decades, multiple researchers focused on the air entrainment process (Chanson and Brattberg 2000; Murzyn et al. 2005) and the fluctuating characteristics of the phenomenon (Montano et al. 2018; Wang and Chanson 2015a, b; Wang and Murzyn 2017). It is also important to highlight recent studies bringing together some of the aforementioned hydraulic jump features under one unique research (Kramer and Valero 2020; Montano and Felder 2020).

Despite the extensive experimental research devoted to the hydraulic jump study, the complex interaction between all the physical processes involved hinders a complete characterization of the phenomenon (Macián-Pérez et al. 2020a, b, c). In particular, some experimental studies either use intrusive instrumentation or focus on external macroscopic features (Bayón and López-Jiménez 2015). Moreover, the study of hydraulic jumps for energy dissipation purposes in large dams by means of a physical model often implies dealing with significant scale effects (Heller 2011). On these terms, numerical modeling techniques such as computational fluid dynamics (CFD) represent powerful tools providing a useful complementary perspective (Aydin and Ulu 2023; Viti et al. 2019), since they provide straightforward information, without intrusive measuring and, moreover, they allow developing prototype scale models. These techniques have already shown their ability to successfully model hydraulic jumps (Bayón et al. 2016; Chippada et al. 1994; Macián-Pérez et al. 2020a, b, c; Mortazavi et al. 2016). It is also important to remark the potential of CFD techniques in the hydraulic engineering field. Benchmarking between different codes, together with the development of optimized meshing strategies and new sub-grid and turbulence models, is helping to solve the shortcomings of numerical modeling, mainly derived from the available computational capacity (Viti et al. 2019).

In terms of the approach used to numerically model hydraulic phenomena such as the hydraulic jump, it is important to distinguish between the Eulerian and the Lagrangian approach (Bayón and López-Jiménez 2015; De Padova et al. 2017, 2018a). According to the literature, modeling a hydraulic jump with the first of the approaches can reduce the accuracy of the free surface representation due to the difficulties to capture the propagation of short breaking waves. On the other hand, the meshless Lagrangian approach can overcome these issues and achieve a better representation of the highly unsteady free surface profile of the hydraulic jump (De Padova et al. 2017). Nevertheless, some three-dimensional hydraulic jump models could require using a large number of particles, making the Lagrangian approach very demanding in computational terms (Bayón and López-Jiménez 2015). In this context, Eulerian methods proved their efficiency since they only need to use a single variable value in every mesh element to model the free surface (Bayón et al. 2016). Furthermore, regarding the air entrainment modeling, Eulerian approaches are able to consider buoyancy, drag and lift forces, despite requiring longer computation times (Bayón and López-Jiménez 2015). Nevertheless, it is important to highlight that successful three-dimensional hydraulic jump models have been achieved under both approaches (Bayon et al. 2016; De Padova et al. 2013).

Developing the potential of numerical models in the hydraulic engineering field requires an extensive data base for contrast and comparison purposes. As previously mentioned, there are several numerical studies focusing on the hydraulic jump phenomenon. However, they usually deal with the Classical Hydraulic Jump (CHJ), which is referred to a horizontal, rectangular, prismatic, smooth channel. On the other hand, relatively less attention has been paid to hydraulic jumps developed in stilling basins, in spite of their undeniable engineering interest (Macián-Pérez et al. 2020a, b, c; Valero et al. 2019).

The negative step or abrupt drop constitutes an important feature in the stilling basin design (Hager 1985; Hager and Bretz 1986). Thus, the analysis of the hydraulic jump in a prismatic, rectangular channel, with an abrupt drop of the channel bottom has been undertaken by several authors. Hager and Bretz (1986) conducted an experimental research comparing the performance of positive and negative steps in stilling basins. These authors analyzed different types of hydraulic jumps, focusing on the energy dissipation efficiency and dimensions such as the sequent depths ratio or the roller length. Other experimental studies dealt with the pressure fluctuations (Armenio et al. 2000) or the tailwater effect (Mossa et al. 2005) at hydraulic jumps with negative step. There are also recent investigations using numerical models to approach the characteristics of oscillating hydraulic jumps at an abrupt drop (De Padova et al. 2017, 2018b, 2023; Jiang et al. 2022). Hence, the research conducted up to date highlights the contribution of the negative step in the stabilization of hydraulic jumps in the stilling basin, but it also points out to a shortcoming of systematic studies regarding this subject. On this basis, the present research employed a validated three-dimensional numerical model to assess the performance and characteristics of a hydraulic jump with negative step under six different configurations. It is important to highlight that these configurations were carefully chosen to test inflow Froude numbers and step sizes with interest in the design of a stilling basin. Consequently, this research seeks to enhance the knowledge on the hydraulic jumps at negative steps and its study using numerical techniques.

Numerical model

The simulations for this research were performed using CFD techniques. In particular, version 11 of the commercial code FLOW-3D® was employed. This software, which has been widely employed in hydraulic engineering, provides a description of the flow through the resolution of the flow governing equations. Firstly, the continuity equation can be obtained from the application of the mass conservation law to the flow:

$$\frac{\partial \rho }{{\partial t}} + {{\varvec{u}}} \cdot \nabla \rho + \rho \cdot \nabla {{\varvec{u}}} = 0$$
(1)

where ρ is the fluid density, t is the time, and u is the velocity field. As the fluid is incompressible for the present research, Eq. (1) can be expressed as:

$$\nabla {{\varvec{u}}} = 0$$
(2)

Furthermore, the application of the momentum conservation principle to a Newtonian incompressible fluid like the one under study leads to the following expression of the Navier–Stokes (N–S) equations:

$$\frac{{\partial {{\varvec{u}}}}}{\partial t} + {{\varvec{u}}} \cdot \nabla {{\varvec{u}}} = - \frac{1}{\rho } \cdot \nabla p + \nu \cdot \nabla^2 {{\varvec{u}}} + {{\varvec{f}}}_{{\varvec{b}}}$$
(3)

where p is the pressure, ν the kinematic viscosity of the fluid, and fb refers to the body forces, namely gravity and surface tension. Regarding the numerical resolution of these equations, FLOW-3D® employs the Finite Volume Method (McDonald 1971) for the discretization of the conservation laws in the spatial domain. On the other hand, for time discretization, the time-step is automatically adjusted by the code using a Courant-type stability criterion. This improves the simulation efficiency by minimizing numerical divergence risks and saving calculation time.

Numerical resolution and turbulence modeling

The numerical resolution of the N–S equations was carried out through the time-averaging of velocity and pressure. This approach, known as the Reynolds Averaging of the N–S equations (RANS), overcomes the limitations of the direct resolution of the equations, which requires extremely refined meshes and short time-steps. Thus, the RANS approach enables the application of CFD techniques to practical hydraulic engineering problems with the existing computational capacity. Nevertheless, the nonlinear character of the N–S equations leads to the appearance of new unknown terms in the averaging process. This closure problem is solved by using a turbulence model that considers the effects of turbulence in the mean flow characteristics. Turbulence models solve the closure problem by adding new transport equations for variables related to the turbulent viscosity. Among them, the two-equation models are the most frequent option, as they are able to reproduce a wide range of flows (Pope 2001). In particular, the renormalization-group (RNG) k–ε was the two-equation turbulence model employed in this research. This model introduces additional transport equations for the turbulent kinetic energy (k) and its dissipation rate (ε) and has proven its efficiency to successfully simulate phenomena like the hydraulic jump (Bayón et al. 2016; Macián-Pérez et al. 2020a, b, c). The transport equations associated with the RNG k-ε turbulence model are:

$$\frac{\partial }{\partial t}\left( {\rho k} \right) + \frac{\partial }{\partial x_i }\left( {\rho ku_i } \right) = \frac{\partial }{\partial x_j }\left[ {\left( {\mu + \frac{\mu_t }{{\sigma_k }}} \right)\frac{\partial k}{{\partial x_j }}} \right] + P_k - \rho \varepsilon$$
(4)
$$\frac{\partial }{\partial t}\left( {\rho \varepsilon } \right) + \frac{\partial }{\partial x_i }\left( {\rho \varepsilon u_i } \right) = \frac{\partial }{\partial x_j }\left[ {\left( {\mu + \frac{\mu_t }{{\sigma_\varepsilon }}} \right)\frac{\partial \varepsilon }{{\partial x_j }}} \right] + C_{1\varepsilon } \frac{\varepsilon }{k}P_k - C_{2\varepsilon } \rho \frac{\varepsilon^2 }{k}$$
(5)

where xi and xj are the coordinates in different axes, μ is the dynamic viscosity of the fluid, μt is the turbulent dynamic viscosity, Pk is the production of k, and the terms σk, σε, C1ε and C2ε represent model parameters whose values are reported in the literature (Yakhot et al. 1992).

Free surface modeling

Free surface problems like the one here presented are treated in FLOW-3D® with a one-fluid approach. Accordingly, the inertia of the air adjacent to the water was neglected and the volume occupied by the gas was replaced with an empty space represented only by uniform pressure and temperature, which allows significantly reducing the computational efforts (Bombardelli et al. 2011). The reason behind this approach is that the inertia of the air phase has a negligible effect on the water motion. As a result of this, boundary conditions were directly applied to the free surface.

Under the described approach, the volume of fluid (VOF) technique (Hirt and Nichols 1981) constitutes the basis for the free surface modeling and tracking. This technique uses a variable named fraction of fluid (F) to represent the fractional volume of water contained in every cell of the meshed domain. To do so, the variable F ranges from 0 to 1 so that its value is 1 when the corresponding cell is completely filled with water. The evolution of F throughout the domain was computed with the following equation:

$$\frac{\partial F}{{\partial t}} + \nabla \left( {{{\varvec{u}}}F} \right) = 0$$
(6)

Finally, a series of routines were applied to enhance the free surface modeling and tracking. Thus, a mechanism that creates small divergences in internal fluid cells to help close up partial voids and sharpen the interface was used for the free surface refinement.

Air entrainment modeling

Air entrainment in the hydraulic jump was modeled by establishing a balance between instabilities at the free surface caused by turbulence and stabilizing forces originating from gravity and surface tension. This balance can be expressed through the following equations:

$$\delta V = \left\{ {\begin{array}{*{20}l} {k_{{\text{air}}} A_S \left[ {\frac{{2\left( {P_t - P_d } \right)}}{\rho }} \right]^{1 / 2} } \hfill & {{\text{if}}\,P_t > P_d } \hfill \\ 0 \hfill & {{\text{if}}\,P_t < P_d } \hfill \\ \end{array} } \right\}$$
(7)
$$P_t = \rho k$$
(8)
$$P_d = \rho gL_T + \frac{\sigma }{L_T }$$
(9)

where δV is the volume rate at which air enters the flow. Pd and Pt are the stabilizing and destabilizing forces, respectively. Moreover, kair is a coefficient of proportionality that needs to be calibrated for the particular case under analysis and AS is the free surface area for each cell. For the stabilizing forces (Pd) in Eq. (9), g is the gravity component normal to the free surface, σ is the surface tension coefficient, and LT is the turbulent length scale, defined as:

$$L_T = \frac{{C_\mu^{3 / 4} k^{3 / 2} }}{\varepsilon }$$
(10)

where the parameter Cμ has a value of 0.085 for the RNG k–ε turbulence model (Bayon et al. 2016). It can be observed from Eq. (7) that air enters the flow when turbulent instabilities overcome the stabilizing forces. Air entrainment leads to variations in the flow density resulting in a mixture density (ρm) that can be expressed as:

$$\rho_m = F\rho_w + (1 - F)\rho_a$$
(11)

where ρw and ρa are the water and the air densities, respectively. Finally, the air bubbles movement within the fluid was also captured by the model in order to account for the interaction between phases. To do so, the drag per unit volume (Kp) was defined as:

$$K_p = \frac{1}{2}A_p \rho \left( {C_D u_r + 12\frac{\mu }{\rho R_p }} \right)$$
(12)

where Ap is the cross-sectional area of the air bubble, CD is a drag coefficient with a default value of 0.5 for spheres, ur is the magnitude of the relative velocity, and Rp is the average bubble radius. Further information on how FLOW-3D® models the interaction between phases in simulations involving air entrainment into water can be found in the literature (Brethour and Hirt 2009).

Meshing procedure and convergence analysis

The spatial discretization of the domain was done using a three-dimensional structured mesh formed by cubic cells. The use of a structured mesh was favored by the simplicity of the analyzed geometry, consisting in a prismatic horizontal channel, whose dimensions were 10.0 m long, 1.0 m high and 0.3 m wide. Structured rectangular meshes present multiple benefits regarding their generation and storage. Moreover, they contribute to the stability of the numerical solution (Bayón and López-Jiménez 2015). As to the cell size, two different mesh blocks were employed. On the one hand, a refined block was used to mesh the upstream part of the domain, where the hydraulic jump roller was enclosed and, consequently, higher flow gradients were expected. On the other hand, the downstream part of the channel, where the subcritical flow takes place, was meshed with a coarser block, with cells doubling the size of those forming the refined one. This meshing strategy allowed saving computational resources without jeopardizing the simulation results.

Furthermore, the actual cell size was chosen by performing a convergence analysis on the refined mesh block. To do so, the procedure described by the American Society of Mechanical Engineers (ASME) (Celik et al. 2008) was applied. This procedure has been successfully applied in similar research (Aydin and Ulu 2021, 2023). Accordingly, three different cell sizes were tested considering the recommended minimum refinement ratio of 1.3 (Table 1). Simulations were run for each of these cell sizes, obtaining velocity values for 10 different positions along the hydraulic jump longitudinal axis. The use of these basic variables as indicators provided the grid convergence index and the mesh apparent order. Thus, the resulting model apparent order was 2.02, very close to the numerical model formal order, which means a feasible signal of the grids being in the asymptotic range (Celik et al. 2008). Besides, the grid convergence index resulting from the analysis was 12.94%, which can be considered an acceptable value for hydraulic jump numerical simulations (Bayón et al. 2016; Macián-Pérez et al. 2020a, b, c). These results supported the use of the finest mesh (labeled as 3 in Table 1) in the models developed for this research.

Table 1 Cell sizes tested in the mesh convergence analysis
Full size table

The boundary conditions in the meshed domain were set to place the hydraulic jump in the desired position. Thus, a supercritical flow was imposed upstream the hydraulic jump, with the corresponding discharge and flow elevation. Moreover, the inlet variables k and ε were set to its default FLOW-3D® value to ensure that they developed as the simulations progress. This is the procedure recommended by the code when the initial value for these variables is unknown (Bayón et al. 2016; Macián-Pérez et al. 2020a, b, c). The downstream condition was set to allow the flow leaving the domain. The fluid elevation in the downstream end was adjusted by running successive simulations to stabilize the hydraulic jump. In addition to this, atmospheric pressure was applied to the free surface, whereas a wall non-slip boundary condition was imposed for the solid contours. A high Reynolds number wall function with a law-of-the-wall velocity profile was assumed in the vicinities of these contours.

Stability of the solution

Considering the nature of the flow under study, the variables in the analysis were averaged in time windows long enough to ensure stationarity. To do so, a series of subsequent simulations were run for each particular case, until the desired hydraulic jump position was reached. Then, a 10-s simulation was performed. These simulations were considered as representative of a quasi-stationary state if the variation of the fluid fraction in the domain was below 5%. Finally, these simulations were used to average the variables describing the phenomenon, and the results were included in the analysis. It is important to highlight that this is usually a long process in which numerous simulations must be performed to reach stable results. In addition to this, the multiple features included in the three-dimensional CFD model here presented led to quite detailed, but also time-consuming simulations. The average computing time needed to reach the final 10-s simulation for the 6 cases that will be presented was around 3 days.

Fig. 1
figure 1

Experimental channel in the Hydraulics Laboratory at Universitat Politècnica de València (UPV, Spain)

Full size image

Model validation

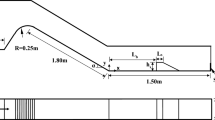
The numerical model was developed reproducing the geometry of the experimental device available in the Hydraulics Laboratory at Universitat Politècnica de València (UPV, Spain) (Fig. 1), as recommended for validation purposes (Valero et al. 2019). The case configuration chosen to validate the model consisted in a CHJ with an inflow Froude number (F1) of 6.0, achieved through a unit discharge (q) of 0.21 m2/s and a supercritical flow depth (y1) of 0.05 m.

The experimental channel (10.0 m long, 1.0 m high and 0.3 m wide) was built with glass walls and PVC streambed. The upstream flow entered the channel through a jetbox that allowed regulating the supercritical flow depth, whereas the subcritical flow depth downstream of the hydraulic jump was controlled with a sluice gate. The discharge in the device was measured using an electromagnetic flow meter (SITRANS MAG 5100 W, Siemens, Munich, Germany) with an uncertainty below 0.1%. The dimensions of the device and the hydraulic conditions of the CHJ led to an inflow Reynolds number (Re1) of 210,000. This value of Re1 is high enough to accomplish the recommendations to avoid significant scale effects when modeling hydraulic jumps (Heller 2011).

The validation process was focused on the comparison of the mean free surface profile and the averaged velocity distribution between the physical and the numerical model. The free surface profile was measured in the experimental device using Digital Image Processing (DIP) techniques (Macián-Pérez et al. 2020a, b, c). Figure 2a shows the normalized mean profile obtained in both models using the following variables:

$$X = \frac{x}{L_r }$$
(13)
$$Z = \frac{y - y_1 }{{y_2 - y_1 }}$$
(14)

where x is the position along the hydraulic jump longitudinal axis, Lr is the roller length, y is the free surface elevation, and y1 and y2 are, respectively, the supercritical and subcritical flow depths. Furthermore, a Pitot tube (General flow sensor, PASCO, Washington, USA) was used to measure streamwise velocities (ux) in three different positions along the hydraulic jump longitudinal axis. These measurements were compared with the corresponding streamwise averaged velocity vertical profiles obtained in the numerical model, where z is the vertical coordinate (Fig. 2b–d).

Fig. 2
figure 2

Numerical model validation: a normalized mean free surface profiles, b–d streamwise averaged velocity vertical profiles for positions b x = 0.75 m, c x = 1.00 m and d x = 1.20 m

Full size image

Figure 2a shows that the hydraulic jump free surface profiles for the physical and the numerical models follow similar patterns, with an initial increase that tends to stabilize for positions further from the jump toe. There are some differences that can be explained by the unstable nature of the phenomenon. Actually, the biggest discrepancies occur in the roller area, where the most intense turbulence is enclosed. Besides, experimental techniques such as the DIP still present some limitations that could have contributed to the differences in the presented results (Macián-Pérez et al. 2020a, b, c). These limitations are derived from the intense aeration of the hydraulic jump that leads to bubbles and droplets being continuously expelled. This causes changes of light intensity that introduce bias in the image treatment. In addition, it is important to consider that FLOW-3D® provides the free surface profile along the longitudinal axis of the jump, whereas, in DIP techniques, images are taken from the side of the experimental device. Nevertheless, the numerical model was able to reproduce the profile observed in the experimental device with a value above 0.95 for the R2 coefficient. As to the streamwise velocity results, there was also a high level of agreement between the numerical and the experimental model (Fig. 2b–d). The measurements made with the Pitot tube did not provide a complete vertical profile, since the reliability of this device is affected in certain flow areas such as the highly aerated region close to the free surface, where negative velocities take place (Wang 2014). However, the general contrast between models showed an adequate performance of the numerical simulations developed and the resulting validated model was employed.

Once the model was validated a series of cases were analyzed, focusing on the effect of the negative step in the hydraulic jump. It is important to highlight that numerical models can be used to test modifications in the hydraulic phenomenon under study, if the resulting design is close enough to the experimental background (Schulz et al. 2015).

Case study

The analysis of how a negative step can improve the energy dissipation performance of hydraulic jumps involves different questions (Jiang et al. 2022): Not only the shape and size of the step must be considered, but also the inflow conditions and jump toe position of the hydraulic jump. On these terms, several authors point out to the B-jump, in which the jump toe is located right over the drop, as the more stable and efficient jump type with negative step (Bakhti and Hazzab 2010; Hager 1985; Hager and Bretz 1986). As to the inflow conditions, the United States Bureau of Reclamation (USBR) establishes that hydraulic jumps with inflow Froude numbers ranging from 4.5 to 9.0 provide an optimal energy dissipation performance (Peterka 1978). Regarding the step, rounded shapes have been analyzed (Armenio et al. 2000). However, the influence of the step shape on the flow seems to be negligible (Hager and Bretz 1986) and the straight step geometry is the most widely spread. Finally, the size of the step has been studied too. The relative step height (S) can be defined as:

$$S = \frac{s}{y_1 }$$
(15)

where s is the step height. Some authors highlighted the influence of the relative step height on the subcritical flow depth (Mossa et al. 2005) or the pressures at the bottom of the jump (Armenio et al. 2000). Besides, a value of 2.5 for this relative height was found to provide the maximum energy dissipation, even though the effect of the step size seemed to lose relevance for F1 > 8 (Hager 1985). On this basis, the present research analyzed a series of B-jumps with a negative straight step. Up to six different cases were studied (Table 2), resulting from the combination of two different step heights and three different F1 values covering the range recommended by the USBR.

Table 2 Analyzed configurations of hydraulic jump with negative step
Full size table

Figure 3 illustrates the variables involved in the analysis, with particular values used in one of the mentioned simulated cases.

Fig. 3
figure 3

Hydraulic jump (B-jump type) with negative step. Case study 1: y1 = 0.05 m, q = 0.175 m.2/s, F1 = 5, S = 1

Full size image

Results and discussion

In the design of a stilling basin, the priority is to minimize the hydraulic jump dimensions and still ensure its stability and the energy dissipation performance (Hager 1985). Therefore, a series of variables describing the hydraulic jump dimensions such as the sequent depths ratio and the roller length were analyzed for all the cases under study. Besides, the energy dissipation was approached through the hydraulic jump efficiency provided by each particular case. Finally, the streambed pressures were also discussed as a key factor to guarantee the stilling basin security (Armenio et al. 2000).

Hydraulic jump dimensions

Sequent depths ratio

The sequent depths ratio (Y) can be defined as the ratio between the subcritical flow depth downstream (y2) and the supercritical flow depth upstream (y1) of the hydraulic jump. This ratio was obtained for each of the analyzed cases (Fig. 4). As all the cases shared the same value for the supercritical flow depth, the sequent depths ratio provides a measure of how F1 and S influence the subcritical flow depth and, consequently, the stilling basin dimensions. For comparison purposes, the following bibliographic expression for B-jumps with negative step (Hager 1985) was also considered:

$$\text{F}_{\rm{1}}^2 = \frac{{Y\left( {Y^2 - S^2 - 1} \right)}}{{2\left( {Y - 1} \right)}}$$
(16)
Fig. 4
figure 4

Sequent depths ratio for the simulated cases and literature results

Full size image

For the particular case of the CHJ, a value of zero for the relative step height (S) in Eq. (16) leads to the well-known Bélanger’s relation for the sequent depths ratio (Bélanger 1841).

Figure 4 shows that, for a fixed step height, increasing inflow Froude numbers provide higher values of the sequent depths ratio. The results also show that, for a fixed inflow Froude number, the subcritical flow depth downstream of the hydraulic jump generally increases with increasing step height, in good agreement with previous experimental and numerical research (Mossa et al. 2003; De Padova et al. 2023). It is important to remark that the results of the simulations performed for S = 2.5 do not exactly follow the straight trend shown by the simulations for S = 1 and the literature results, which possibly means a higher variability associated to higher relative step height. In this regard, some bibliographic information suggests a relationship between the increase of the relative step height and the splashing effect on the flow field becoming significant (Mossa et al. 2003).

The sequent depths ratio values obtained in the cases analyzed for this research are systematically lower than the literature results, both for the CHJ (Bélanger 1841) and for hydraulic jumps at negative steps (Hager 1985; Mossa et al. 2003). The comparison between the simulations performed and the CHJ information suggests that the use of negative steps in stilling basins provides lower values of Y, which would lead to smaller training walls in the basin.

Roller length

The hydraulic jump roller can be defined as the recirculating region that extends from the jump toe. The roller region boundary separates the area with negative longitudinal velocity component from the flow with positive velocity (Bai et al. 2021). Thus, the roller length (Lr), as seen in Fig. 3, can be obtained by means of the stagnation point criterion (Hager et al. 1990). The stagnation point is identified as the point in which velocity tends to zero. The line joining the stagnation point of a series of longitudinal velocity vertical profiles along the hydraulic jump provides the roller boundary. The intersection of this boundary with the free surface profile indicates the end of the roller region, whose length can be then measured. Figure 5 shows the roller length obtained for each of the cases under study. The following bibliographic expressions for CHJ (Hager et al. 1990; Wang and Chanson 2015a, b) were also included in the analysis to assess the effect of the negative step:

$$L_r = y_1 \left[ { - 12 + 100\tanh \left( {\frac{{{\rm{F}}_{\rm{1}} }}{12.5}} \right)} \right]{\text{for }}{{0.10 < y_1 } / {b < 0.70}}$$
(17)
$$L_r = y_1 \left[ {6\left( {{\rm{F}}_{\rm{1}} - 1} \right)} \right]{\text{for 1}}{.5 < }{\rm{F}}_{\rm{1}} < 8.5$$
(18)

where b is the hydraulic jump width. In terms of hydraulic jumps at negative steps, previous research pointed out to an approximate value of \(L_r = 4.25\cdot y_2\) for minimum B-jumps (Hager and Bretz 1986). These authors also provide the following expression for minimum B-jumps, based on an extensive experimental campaign:

$$L_r = 4.25y_1 \left( {\sqrt {2} {\rm{F}}_{\rm{1}} - \frac{1}{2}} \right)$$
(19)
Fig. 5
figure 5

Roller length values after the simulated cases and previous literature results

Full size image

The results from Fig. 5 show that, although there are no large differences, negative steps tend to increase the roller length of the hydraulic jump when compared to a CHJ. These differences seem to increase with higher values of the inflow Froude number. Moreover, the comparison between the FLOW-3D® simulations and the results for minimum B-jumps (Hager and Bretz 1986) suggests that the B-jump typology provides slightly larger values of the roller length. As to the stilling basin dimensions, larger roller lengths implies a larger extension of the area where the highest turbulence is enclosed, which must be accounted in the basin design.

Regarding the relative step height, the results are quite similar. However, a small influence of the inflow Froude number can be observed. Hence, for low values of F1, smaller values of the relative step height seem to provide larger roller lengths, whereas these changes for F1 > 7.5.

Free surface profile

After the discussion of the sequent depths ratio and the roller length as crucial parameters to assess the hydraulic jump dimensions, the free surface longitudinal profile was analyzed for a general perspective of the hydraulic jump shape. Figure 6 shows this averaged profile for each of the simulations performed, whereas in Fig. 7 these same profiles are normalized following Eqs. 13 and 14.

Fig. 6
figure 6

Mean free surface profile for the analyzed cases

Full size image
Fig. 7
figure 7

Normalized mean free surface profile for the analyzed cases

Full size image

Firstly, the influence of the inflow Froude number in the hydraulic jump profile can be clearly observed as higher values of F1 lead to larger hydraulic jumps, both in length and height, as shown in Fig. 6. With regard to the step height, this figure also shows that higher values of S bring higher flow depths in positions close to the hydraulic jump toe, in good agreement with bibliographic results (Jiang et al. 2022). As the distance to the jump toe increases, these differences tend to disappear and there is not a significant influence of the step height on the downstream flow depth or the jump length.

Furthermore, Fig. 7 shows that there are no big differences for the normalized mean free surface profiles of the six cases under analysis. Hence, the shape for all of them is quite similar and they reach the subcritical flow depth at approximately the same position (X ~ 2.5). In spite of these similarities, cases 4 and 5 clearly show higher values of the normalized flow depth (Z) in the vicinities of the hydraulic jump toe, as a result of the combination between low F1 values and large step height. The normalized profile for case 4 joins the rest of the cases shortly downstream of the jump toe, whereas for case 5, the higher values of Z persist along the whole roller region (from X = 0 to X = 1). Downstream of the roller region (X > 1), the influence of the step height seems to disappear and the slight differences observed suggest that higher F1 lead to higher Z values until the downstream flow depth is reached.

Hydraulic jump efficiency

The hydraulic jump efficiency measures the amount of energy dissipated in the phenomenon. This parameter is usually based on the relative hydraulic head loss in the jump. However, the height drop caused by the negative step obviously affects the hydraulic head. Therefore, the following formulation was proposed for the relative energy dissipation (η) (Hager 1985):

$$\eta = \frac{\Delta H}{{H_1 + s}} = 1 - \frac{{Y + \frac{{{\rm{F}}_{\rm{1}}^2 }}{2Y^2 }}}{{1 + S + \frac{{{\rm{F}}_{\rm{1}}^2 }}{2}}}$$
(20)

where ΔH is the energy loss and H1 the hydraulic head upstream of the hydraulic jump. Figure 8 shows the results of relative energy dissipation for each of the hydraulic jumps analyzed.

Fig. 8
figure 8

Hydraulic jump efficiency for the analyzed cases and previous literature results

Full size image

The information reported in the bibliography (Hager 1985; Hager and Bretz 1986) shows that the relative energy dissipation is always larger with a negative step when compared to the CHJ. This affirmation is in good agreement with the results of this research presented in Fig. 8, in which the values of η for all of the analyzed cases involving a negative step are above the results for the CHJ. This figure also shows experimental results for hydraulic jumps at abrupt channel drops with S values ranging from 1.25 to 5.7 (Rajaratnam et al. 1977). These data seems to fall within the results provided by the simulations and those derived from Eq. (20).

The previously mentioned bibliographic studies also pointed out to a value of S = 2.5 as the one that provides the maximum energy dissipation, even though the effect of the step size seemed to lose relevance for F1 > 8. The results of the CFD simulations in the present research are in line with this statement, since the energy dissipation for case 5 (F1 = 7 and S = 2.5) is clearly higher than the one for case 2 (F1 = 7 and S = 1), whereas the η value is very similar for cases 6 (F1 = 9 and S = 2.5) and 3 (F1 = 9 and S = 1). These simulations also provided similar values of η for cases 4 (F1 = 5 and S = 2.5) and 1 (F1 = 5 and S = 1). On this basis, the influence of the step height seems to gain relevance only for F1 values between 5 and 8 for the simulations performed. It is also important to highlight that previous literature on the topic describes the influence of the step height on the energy dissipation efficiency as limited (Jiang et al. 2022).

Finally, the comparison between the CFD simulations results and the values obtained using Eq. (20) by Hager (Hager 1985) shows that, although the trends of the results are similar, especially for a relative step height of 1, this bibliographic expression generally underestimates the energy dissipation values obtained in the simulations. It is important to highlight that Eq. (20) is an expression derived from the application of the energy theorem between sections upstream and downstream of the hydraulic jump (Hager 1985). The deviation between the modeled results and the aforementioned expression must be put in perspective, given the complexity of the hydraulic jump phenomenon. Furthermore, these discrepancies between theoretical expressions and model results regarding the hydraulic jump efficiency can also be observed in previous bibliographic results on the topic (Jiang et al. 2022; Macián-Pérez et al. 2020b; Padulano et al 2017).

Streambed pressure

The analysis of the streambed pressures is crucial in the structural design of the stilling basin. The influence of the negative step was discussed through the streambed pressure magnitudes (p) and their fluctuations. Figure 9 shows the average relative pressures along the hydraulic jump longitudinal axis for all the modeled cases, together with bibliographic results (Toso and Bowers 1988) for a CHJ with a F1 value of 6.

Fig. 9
figure 9

Average streambed relative pressures for the analyzed cases and literature results

Full size image

Two different regions can be clearly distinguished in Fig. 9. There is a first area, immediately downstream of the jump toe and the negative step presenting a significant variability of the streambed pressure values, including negative pressures for three of the simulations. Then, for x/y1 > 15, the streambed pressure results follow a similar trend to the one obtained for a CHJ, even though the pressure values seem to be lower as a result of the influence of the step. This is a remarkable result regarding the stilling basin security and, more specifically, the protection of the energy dissipation structure.

For the vicinities of the hydraulic jump toe, the large variability of the pressure results can be explained by the influence of the negative step. This step originates a jet that directly impacts downstream of the jump toe, causing a relative maximum for the streambed pressure values. The position where the jet impacts the basin (impingement point (Yang 2021)) depends on the step height (x/y1 ~ 5 for cases 1 to 3 and x/y1 ~ 10 for cases 4 to 6). Upstream of the impingement point, a reattachment region is created underneath the jet. According to the literature, this reattachment region is characterized by low pressures. As expected, its extension increases with the increase in the step height (Jiang et al. 2022), in good agreement with the results of the simulations performed in this research.

The identification of the jet impingement point can be interesting, not only to locate the relative maximum of the streambed pressure values, but also to establish the end of the reattachment region. Regarding the design of the stilling basin, the location of the impingement point marks the place where special protection may be needed to face large pressure values. Furthermore, this point limits the reattachment region, where the potential development of negative pressures must be accounted for in the design.

Precise location of the jet impingement point can be addressed through the analysis of the horizontal velocity (vx) vertical profiles along the hydraulic jump axis (Fig. 10).

Fig. 10
figure 10

Horizontal velocity vertical profiles: a Case 2 upstream of the impingement point, b Case 2 downstream of the impingement point, c Case 4 upstream of the impingement point and d Case 4 downstream of the impingement point

Full size image

Figure 10 shows that, immediately upstream of the point where the maximum pressures where located, there are negative velocities in the lower part of the profile. These negative velocities are bounded to the reattachment region upstream of the jet impingement point. On the other hand, for the profile immediately downstream of the maximum pressures point, there are no negative velocities in the lower part, as this profile is not under the influence of the reattachment region. Figure 10 depicts two of the six simulated cases. The first one (Fig. 10a and b) corresponds to a relative step height of 1, in which the relative maximum of the streambed pressures is at x/y1 ~ 5, whereas Fig. 10c and d shows a case with relative step height of 2.5 and location of the relative maximum of the streambed pressures at x/y1 ~ 10.

In addition, streambed pressure fluctuations were analyzed as a characteristic closely related to the turbulent nature of the hydraulic jump (Fig. 11). According to the literature, these pressure fluctuations are the main cause of structural fatigue in negative step stilling basins (Yang 2021). To approach the analysis, the bibliographic definition of the coefficient of pressures fluctuations intensity (cp’) (Abdul Khader and Elango 1974; Armenio et al. 2000) was employed:

$$c_p^{\prime} = \frac{{{{\sigma_p } / \gamma }}}{{{{u_1^2 } / {\left( {2g} \right)}}}}$$
(21)

where σp is the standard deviation of the pressure, γ is the fluid specific weight, u1 is the average supercritical velocity upstream the hydraulic jump, and g is the gravity acceleration.

Fig. 11
figure 11

Streambed pressure fluctuations for the analyzed cases

Full size image

According to experimental results found in the literature (Armenio et al. 2000; Yang 2021), for stilling basins with a negative step and a B-jump, cp’ reaches its maximum value in the vicinities of the step, more precisely, in the reattachment region. From this maximum values, the coefficient decreases rapidly, followed by a gradual and slow decrease. Figure 11 shows that the flow pattern described in the literature is generally followed by the simulations performed in this research.

The comparison between different cases shows that larger step heights lead to lower maximum values of cp’, as pointed out by previous studies (Armenio et al. 2000; Yang 2021). Moreover, for positions further from the jump toe, increasing step heights generally provide lower streambed pressure fluctuations. In addition, even though the maximum cp’ value is enclosed in the reattachment area for all the simulated cases, it is located further downstream as the step height increases. Finally, the magnitude of the cp’ coefficient is lower when compared to previous research conducted for a CHJ (Macián-Pérez et al. 2020a, b, c). These results support the idea that the addition of a negative step at the entrance of a standard stilling basin reduces the fluctuating pressure, as a result of the increase of water in the basin that participates in the energy dissipation process (Yang 2021).

To further explore the pressure fluctuations concerning the mean value of the data, the skewness coefficient was calculated for each of the cases under analysis. In particular, cases 1 and 3 showed some relevant similarities with bibliographic results that analyze B-jumps (De Padova et al. 2023). Figure 12 shows a comparison between the skewness coefficient for cases 1 and 3 and the information found in the literature, arranged by similar inflow Froude numbers.

Fig. 12
figure 12

Skewness coefficient and literature results: a Case 1, b Case 3

Full size image

The patterns of the skewness coefficient for the presented cases seem to be in good agreement with the bibliographic results. Nevertheless, some differences can be observed. The results found in the literature show a good agreement between the maximum skewness coefficient and the region of maximum turbulence intensity (De Padova et al. 2023). On the other hand, cases 1 and 3 seem to achieve the maximum skewness coefficient in positions downstream this region of maximum values of cp’. Finally, the progressive decrease in the skewness coefficient from its maximum as the distance from the jump toe increases can be observed for both, the cases under analysis and the bibliographic results. It is important to note that some of the differences found in Fig. 12 can be related to the particularities of the cases, such as the inflow Froude number, the supercritical flow depth or the negative step size.

Conclusions

The research presented herein is focused on the performance of stilling basin designs including a negative step or abrupt drop. Results address the effect of the negative drop on the energy dissipation efficiency, dimensions and structural properties of the hydraulic jump, streambed pressures and pressure fluctuations.

Six simulated cases have been analyzed in detail, considering two possible relative heights for the negative step and three possible inflow Froude numbers. The simulations were carried out using a CFD three-dimensional numerical model previously validated with a physical model specifically developed for this purpose. The results obtained have been compared to previous research in the topic.

The sequent depths ratio values obtained after the simulations were found to be lower than those reported in previous literature results. The negative step yields to lower subcritical depths, allowing smaller basin dimensions. Nevertheless, it tends to slightly increase the roller length of the hydraulic jump.

No significant differences were found regarding the normalized mean free surface profiles of the hydraulic jump, after the numerical simulations performed.

Concerning the relative energy dissipation, results clearly confirm the improvement derived from the negative step presence, when compared to the CHJ.

The internal flow occurring in the jump was analyzed in this research, and more specifically the subzones generated upstream and downstream the impingement point. Both, horizontal component of velocity and pressure fluctuations were studied. It has been proved the beneficial contribution of the negative step in the stabilization of hydraulic jumps in the stilling basin. In particular, the pressure values seem to be lower downstream of the impingement point as a result of the influence of the step. This is a remarkable result regarding the stilling basin security and, more specifically, the protection of the energy dissipation structure. In addition to this, pressure fluctuations in the streambed are significantly reduced due to the negative step size influence on the hydraulic jump.

Overall, the research shows the effectiveness of the CFD techniques to adequately characterize and quantify every relevant value of the hydraulic jump flow affecting the hydraulic performance of the stilling basin. As shown in the results obtained, these techniques significantly contribute to an important improvement of the basis for optimal design of such hydraulic devices.