Introduction

Siphon spillways are used to pass more discharges at lower crest head than free napped spillways through its siphonic sub-atmospheric pressures. Siphon spillways have the advantage of a great sensitivity at the rise of the water upstream level and the great discharge per length of sill (Houichi et al. 2009). On the other hand, shaft spillways can be preferred especially in arch and embankment dams in order to avoid some problems such as vibration and leakage in the body. Siphon-shaft spillway as a hybrid type combines the advantages of siphon and shaft spillways. Since the velocities in the cross section are higher due to the siphon effect, the same flow discharge can be transferred with smaller sections in siphon-shaft spillways compared to the shaft spillways. The weir discharge is not affected by the water level in the reservoir as much as free over-flow spillways. A small crest head is sufficient for it to operate at maximum capacity. Vortex effects are less than free surface shaft weirs, as the siphon head prevents the free vortex. Additionally, the inlet mouth can absorb the accumulated sediment closer to the reservoir base. In siphon-shaft spillway, it is recommended to make it vertical, as large vacuums may occur if the shaft is inclined (Binie, 1938). Besides its advantages, there are some disadvantages such as limited capacity, so it is recommended to plan it with an auxiliary spillway to be used when necessary (Agiralioglu, 1977).

There are limited studies on siphon-shaft spillways in the literature. Davis and Strickney (1914), Stickney (1922) and Lawaczeck (1930) patented different types of siphon spillways. The studies and practices intensified in the 1970s and have continued until today. For example, Head (1971), Charlton (1971), Ackers and Thomas (1975), Head (1975), Unser (1975), Ali and Pateman (1980), Ervine and Oliver (1980), Bollrich (1994) conducted various theoretical and experimental studies on the design and performance of siphon spillways. In the recent years, Houichi et al. (2006), Yucel (2008), Jourabloo (2010), Ghafourian et al. (2011) experimentally studied on the hydraulic performance of the siphon spillways. Babaeyan-Koopaei et al. (2002) and Petaccia and Fenocchi (2015) conducted case studies to solve the problems in siphon spillways of some dams in the operation. Musavi-Jahromi (2011), Ghafourian et al. (2011), Tadayon and Ramamurthy (2013), Aydin et al. (2015), Ahmed and Ramamurthy (2019) and Ramezani et al. (2020) applied numerical models to determine hydraulic characteristics of the different types of siphon spillways. Ghafourian et al. (2011) examined the hydraulic performance of a siphon spillway experimentally and numerically and found a good agreement between the two methods in terms of the spillway discharge and pressures. Tadayon and Ramamurthy (2013) focused on the discharge coefficients of siphon spillways based on experimental and numerical model with k-ε turbulence model. Aydın et al. (2015) used a numerical model to examine the hydrodynamics of a siphon side weir used as a side weir structure in a main channel. Modeling results using three-dimensional computational fluid dynamics (CFD) indicated a good agreement with experimental measurements. Prasanna and Suresh Kumar (2018) compared the physical and numerical results of flows over air-regulated siphon spillways and declared that numerical model could be used in the absence of physical modeling.

When the vacuum pressures in the siphon drop below the vapor pressure of the water, water begins to evaporate. The formed vapor bubbles change phase with sudden explosions in the regions where the pressure is high. This event called as cavitation can severely damage or cause technical problems through the spillways. Agiralioglu (1977) and Agiralioglu and Muftuoglu (1989) recommended the use of air-regulating devices to reduce undesirable sub-atmospheric pressure, especially for high operating heads, but they did not perform any study on the aeration devices for siphon-shaft spillways. Agiralioglu (1977) carried out a comprehensive study on the siphon-shaft spillways. However, no other study on the subject has been encountered so far. In this study, a series of numerical model studies were conducted to investigate the effects of aerators placed in the hood on the siphon-shaft spillway.

Method

Computational fluid dynamics (CFD) is an advanced technique, which solves the governing equations of fluid motion using some discretization methods such as finite-volume method. This method needs, besides main fluid motion equations, some additional equations for turbulence and multiphase flow. In the numerical models, Reynolds-averaged Navier–Stokes (RANS) equations and standard continuity equations are implemented three-dimensionally as momentum and mass transport equations. Since the flow is viscous and turbulent, realizable k-ε turbulence model applied in the solutions. The standard k-ε model with two equations is based on transport equations for turbulent kinetic energy (k) and its dissipation rate (ε). The realizable k-ε model, on the other hand, contains an alternative turbulent viscosity formulation, unlike the standard k-ε model, and uses a modified convection equation for the dissipation rate (ε). The VOF method was also used to determine the volume fractions between phases (air and water) in the flow and to track the free surface. The VOF method solves a single set of momentum equations (Eq. 1) for two immiscible fluids and calculates the volume fraction of each fluid in a cell (ANSYS-Fluent, 2012; Aydin and Isik, 2015):

$$\frac{\partial }{\partial t}\left( {\rho u_{i} } \right) + \frac{\partial }{{\partial x_{i} }}\left( {\rho u_{i} u_{j} } \right) = - \frac{{\partial P_{s} }}{{\partial x_{j} }} + \frac{\partial }{{\partial x_{i} }}\mu \left( {\frac{{\partial u_{i} }}{{\partial x_{i} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) + \rho g_{i} + F_{j}$$
(1)

where ρ is fluid density, μ is dynamic viscosity of fluid, u is velocity vectors, Ps is pressure, g is gravitational acceleration, and F is a body force. The interface between the phases is traced by solving the following continuity equation for the volume fraction of the phases (ANSYS-Fluent, 2012):

$$\frac{1}{{\rho_{q} }}\left[ {\frac{\partial }{\partial t}\left( {\alpha_{q} \rho_{q} } \right) + \nabla \cdot \left( {\alpha_{q} \rho_{q} \vec{\nu }_{q} } \right) = S_{\alpha q} + \sum\limits_{p = 1}^{n} {\left( {\dot{m}_{pq} - \dot{m}_{qp} } \right)} } \right]$$
(2)

in which \(\dot{m}_{qp}\) and \(\dot{m}_{pq}\) are the mass transfers between phases, and αq is volume fraction of qth fluid in a cell. \(S_{{\alpha_{q} }}\) is source term by default zero. The value of αq depends on whether the cell is empty or full and takes a value from 0 to 1.

The below equations were given for the turbulent kinetic energy and the dissipation rate (Ansys-Fluent, 2012).

$$\frac{{\partial \left( {\rho k} \right)}}{\partial t} + \frac{{\partial \left( {\rho ku_{i} } \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\frac{{\mu_{t} }}{{\sigma_{k} }}\frac{\partial k}{{\partial x_{j} }}} \right] + 2\mu_{t} E_{ij} E_{ij} - \rho \varepsilon$$
(3)
$$\frac{{\partial \left( {\rho \varepsilon } \right)}}{\partial t} + \frac{{\partial \left( {\rho \varepsilon u_{i} } \right)}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\frac{{\mu_{t} }}{{\sigma_{\varepsilon } }}\frac{\partial \varepsilon }{{\partial x_{j} }}} \right] + C_{1\varepsilon } \frac{\smallint }{k}2\mu_{t} E_{ij} E_{ij} - C_{2\varepsilon } \rho \frac{{\varepsilon^{2} }}{k}$$
(4)

in which ui: velocity components, Eij: component of deformation rates, μt: turbulent viscosity (\({\mu }_{t}=\rho {C}_{\mu }{k}^{2}/\epsilon\)), the constants of models as default based on experiences: Cμ = 0.09, σk = 1.00, σε = 1.30, C1ε = 1.44, C2ε = 1.92 (Versteeg and Malalaseker, 2007). Solution methods were performed in second order accurate in space. The CFD analyses in this study were carried out using ANSYS-Fluent software package.

Model geometry and mesh structure

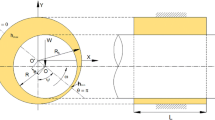
The 3D geometry on the numerical model with the boundary conditions is illustrated in Fig. 1. Four-air inlet was installed on the siphon hood for aeration. Vertical shaft gallery was connected to horizontal outlet gallery with a large curve. A sufficiently large reservoir is defined around the siphon to allow free water inlet at the specified levels. Three different diameters of aeration hole (Da = 100 mm, 125 mm and 150 mm) were used for aeration. The inner diameter of the shaft (D) is 4.00 m, the diameter at the crest (Ds) is 7.18 m, and the hood height (Hb) is 9.10 m, and the inner diameter (Db) of the hood is 10.18 m. Numerical simulations were performed for three different operating heads (H = 10.5 m, 13.5 m and 16.5 m). Wagner (1956) profile used for free shaft spillways was also applied at the shaft inlet, according to the Bureau of Reclamation (1987) criteria.

Fig. 1
figure 1

3D geometry and boundary conditions of the numerical model

Full size image

The mesh structure of the CFD models is given in Fig. 2. A procedure based on the ASME Journal of Fluids Engineering publication policies was performed for the control of numerical accuracy (Roache et al. 1986; Celik et al. 2008). Before any discretization error estimation was calculated, it is shown in Fig. 3a that iterative convergence was achieved with at least three orders of magnitude decrease in the normalized residuals for each equation solved. From the residual-iteration plot, it is observed that there is no problem with the vector velocities and the equations being solved during the process. Additionally, Fig. 3b shows that iterative convergence was ensured in terms of outlet water discharges, which is one of the important parameters for the study.

Fig. 2
figure 2

Mesh structure of the numerical model

Full size image
Fig. 3
figure 3

Iterative convergences of the solutions. a Normalized residuals for each equation solved, b convergence of outlet water discharge

Full size image

The Grid Convergence Index (GCI) method based on method Richardson extrapolation method was used herein to calculate discretization errors, which is an acceptable method by many CFD users (Celik et al. 2008). According to the method, the representative mesh size (h) is defined for three-dimensional calculation as

$$h = \left[ {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} (\Delta V_{i} )} \right]^{1/3}$$
(5)

where Vi is the volume of the ith cell, and N is the total number of cells in the calculation domain. The summations were run for three mesh sizes, i.e., fine, medium and coarse mesh (h1 < h2 < h3), and some key parameters such as pressure and velocity were used for describing discretization errors. To calculate the apparent order, p, of the method the following expressions were used.

$$p = \frac{1}{{\ln r_{21} }}\left| {\ln \left| {\frac{{\varepsilon_{32} }}{{\varepsilon_{21} }}} \right| + q\left( p \right)} \right|$$
(6)

in which ε32 = ϕ3–ϕ3, ε21 = ϕ2–ϕ1, ϕk denoting the solution on the kth grid denoting the solution on the kth grid, considering r = h3/h2 = h2/h1 = 1.3 as a constant because of q(p) = 0. Calculate the extrapolated values from

$$\phi_{ext}^{21} = \left( {r_{21}^{p} \phi_{1} - \phi_{2} } \right)/\left( {r_{21}^{p} - 1} \right)$$
(7)

Similarly, calculate \({\phi }_{ext}^{32}\). Then, calculate approximate relative error and extrapolated relative error:

$$e_{a}^{21} = \left| {\frac{{\phi_{1} - \phi_{2} }}{{\phi_{1} }}} \right|$$
(8)

Based on the above formulations the Grid Convergence Index:

$$GCI_{fine}^{21} = \frac{{1.25e_{a}^{21} }}{{r_{21}^{p} - 1}}$$
(9)

Figure 4a and c presents velocity and pressure profiles along centerline of the shaft from Z = 0 (crest level) to − 12 m for a turbulent three-dimensional flow. The three sets of grids have 899,170, 2,035,429 and 4,082,602 tetrahedral unstructured cells, respectively, as given in Table 1. The local order of accuracy p ranged from 0.96 to 9.30, with a average pave of 3.96 for velocity profiles; and 1.31 to 7.80, with an average pave of 4.67 for pressure profiles, which are a good indication of the hybrid method applied for that calculation. The GCI values in Eq. (9) were plotted in the form of error bars on the fine grid solution, as shown in Fig. 4b and d. The maximum discretization uncertainty is 10% for the velocity which corresponds to \(\pm\) 0.66 m/s and 7% for pressure which corresponds to \(\pm\) 4300 Pa. Additionally, the parameters of the mesh quality for the worst elements are given in Table 1.

Fig. 4
figure 4

Different grid solutions with discretization error bars

Full size image
Table 1 Mesh quality parameters
Full size table

Results and discussion

CFD analyses were carried out for three different water loads and three different diameters of aeration hole. Figure 5 shows the air mixing drawn into the siphon for these nine cases. The figures from left to right show the change of water levels from maximum to minimum, and top to bottom figures show the change of aeration diameters from minimum to maximum, in Fig. 5. When the water level is at the maximum of the top of the siphon hood, siphon pressures do not occur, but due to the low pressure caused by the flow velocities in the siphon, even a little air entrainment occurs (Fig. 5a). In this case, there is no risk of cavitation, therefore there is no need for air entrainment, and at the same time the discharge capacity does not reduce due to air intake. However, as the falling water level increases the negative siphon (vacuum) pressures, the amount of air drawn into the siphon through the aerators increases with increasing pressure differences. On the other hand, the amount of air entering the siphon increases with increasing the diameter of the aerator for constant water levels. However, the amount of air entering after a certain aerator diameter will seriously affect the discharge capacity and even disrupt the siphon flow (Fig. 5i). This situation can cause irregular flows and large vibrations in the siphon. It is essential to determine an optimal diameter of the aeration diameter that can supply sufficient air without disturbing the siphon flow.

Fig. 5
figure 5

Air–water mixing for different aeration diameters and operating heads

Full size image

As similarly in Fig. 6, velocity contours in the siphon-shaft spillway were presented for different aeration diameters and operating heads. While the flow velocity in the siphon shaft is greatest for the maximum water level, it decreases with the water level (Fig. 6a). It is seen that the flow velocity in the shaft slightly decreases as the diameter of the aeration holes increases. In other words, the air entering the siphon slightly reduces the flow rate. These figures also show stagnant velocity regions within the flow. Especially in the area between the aerator inlets located under the hood, stagnant velocity zones are formed where the flow velocity decreases, and air accumulation occurs. These stagnant zones can be closed to flow to improve the hydrodynamics of the flow and thus the discharge efficiency of the siphon-shaft spillway.

Fig. 6
figure 6

Velocity contours of the siphon flow for different aeration diameters and operating heads

Full size image

In order to observe the effects of the aerations diameter on the flow characteristics, the pressure distributions at the maximum and minimum water levels are plotted in Fig. 7. At the maximum water level (H = 16.5 m), while the pressure graphs given for the edge and centerline (Figs. 7a and c) do not have a significant effect on the pressure distribution of the aeration diameter, it is seen that the aeration diameter at the minimum water level has significant effects on the pressure distribution (Figs. 7b and d). At the minimum water level, the pressure distributions for the small aeration diameter (Da = 100 mm) are almost the same as the siphon flow without aerator. However, for larger diameters (Da = 125 mm and 150 mm) it is seen that the aeration diameter increases the pressure values along the siphon shaft significantly. Similarly, in Fig. 8, the effect of the aeration diameters on the velocity is insignificant at the maximum water level, but a significant decrease in the velocity values was observed at the minimum water level, especially for the large aeration diameter (Fig. 8b and d for Da = 150 mm). The results show that the air mixture supplied by the aerator holes will have positive effects on cavitation prevention, as it reduces both the sub-pressure and the flow velocity. On the other hand, except for large aeration diameters, the low effect of aeration on velocities means that it will not affect the discharge performance too much. It is also known that air bubbles mixed in the flow can prevent cavitational erosions by damping vapor explosions during cavitation event.

Fig. 7
figure 7

Comparison pressure distributions along the edge of spillway profile and centerline of the shaft at maximum (H = 16.5 m) and min (H = 10.5 m) operating heads for different aeration diameters

Full size image
Fig. 8
figure 8

Comparison velocity distributions along the edge of spillway profile and centerline of the shaft at maximum (H = 16.5 m) and min (H = 10.5 m) operating heads for different aeration diameters

Full size image

Aeration and discharge performance

The effects of the aerator holes on the discharge coefficient and aerator performance are given in Table 2. In the table, nDa/H is the relative aeration diameter, and n(Da/D)2 is the relative aeration area. Here n indicates the number of aerators, where n = 4, Qw is water discharge, Aa is total cross section of aeration holes, Va(avg) is average velocity in the aeration holes, Qa is air discharge, β (= Qa/Qw) is air entrainment rate, and Ca is average air concentration. The discharge coefficient of the siphon-shaft spillways can be calculated from the following equation.

$$Q = C_{o} A_{o} \sqrt {2gH}$$
(10)

in which Ao is cross-sectional area of the shaft outlet, and g is gravitational acceleration. Based on the air entrainment rate (β) the average air concentration can be estimated by Ca = β/(1 + β). It is seen in Table 2 that air entrainment from the aeration holes has significant negative effects on water discharge coefficients (Co). This effect is in the range of 2% to 7% for Da = 100 mm and 125 mm, while the reduction in discharge coefficient is up to 30% at the minimum water level for Da = 150 mm. It is seen in Fig. 9a that the discharge coefficient significantly decreases in cases where the relative aeration diameter (nDa/H) is greater than about 0.05. For nDa/H < 0.045 the decrease in the water discharge performance is less than 10%, which is an acceptable value. However, it was observed that at larger values, the amount of entraining air severely reduces the siphon efficiency due to an irregular siphon flow; even further, the siphon flow can be disrupted.

Table 2 Effects of aerators on spillway discharge and aeration performance
Full size table
Fig. 9
figure 9

Variations of discharge performance and air entrainment rates with relative aeration diameter

Full size image

In last five columns of Table 2, the aeration parameters obtained from the numerical simulations are given. For constant aeration diameters, the average air concentrations increase due to the decreasing siphon pressures with the decrease in water level (operating head). On the other hand, an extension in aeration diameters increases the aeration performance. In order to monitor the effect of these two parameters (Da and H) on the aeration performance, the change of the air entrainment coefficient with the relative aeration diameter is plotted in Fig. 9b. As seen from the figure, a nonlinear relationship with R2 = 0.98 was achieved between two dimensionless parameters. The graph shows convexly increasing the aeration performance with the relative aeration diameter. Air entrainment rates are between 0.8 and 3% for the maximum operating heads, in which case cavitation risk does not occur due to high pressures in siphon. Also, for high water levels where aeration is not important, low aeration will not affect the discharge capacity too much. On the other hand, for low water level that negative siphon pressures are effective, the amount of aeration is important, since the risk of cavitation will be high, especially in the low-pressure region inside the siphon. The amount of the entraining air reduces the sub-pressures and is very effective in preventing cavitation damage. When seen the air entrainment rates at the minimum water level in Table 2, it is 3.9% for Da = 100 mm, 7.5% for Da = 125 mm and 14.1% for Da = 150 mm. Based on a comprehensive literature review (i.e., Kells and Smith, 1991; Rutschmann and Volkart, 1988), Aydin (2016) reported that the air entrainment rate (β) should be above 7% to avoid cavitation. Accordingly, if it is remembered that the 100 mm diameter is insufficient and the 150 mm diameter reduces the performance of the siphon weir, it can be said that 125 mm diameter is an optimum diameter in terms of cavitation and discharge efficiency for this study. According to the data obtained in this study, the relative aeration area corresponding to the optimal diameter is approximately n(Da/D)2 = 0.004, and the optimum relative diameter can be accepted as nDa/H = 0.45.

Conclusions

One of the most effective ways to protect hydraulic systems from cavitation damage is to aerate the flow. In this study, the performances of the aerators placed on the siphon hood to reduce the sub-pressure inside the siphon shaft and reduce the risk of cavitation were analyzed by the reliable CFD models. For this purpose, three different aeration diameters for three different operating heads were considered. The analyses results show that the air entrainment rate increases with the decrease in pressures in siphon with water level, while the discharge performance decreases slightly. Considering that siphon pressures decrease at low water levels (operating heads) and the risk of cavitation will increase accordingly, an increase in air entrainment will reduce the risk of cavitation. Moreover, it is also observed that the aeration diameters have a significant effect on air entrainment for a constant water level. However, since too much air entering in the siphon will affect the siphon flow negatively and even disrupt the siphon flow, the aeration diameter should be determined carefully. Based on the study results, it can be assumed that the optimum relative aeration area n(Da/D)2 = 0.004, and the relative aeration diameter nDa/H = 0.45. This value provided sufficient air entrainment to protect from cavitation (Ca = 7.5%) and did not decrease the discharge performance too much (Co = 0.96 ~ 1.00).

This study also showed that correctly constructed numerical models provide great convenience in the design of such hydraulic structures. Although this study shows that the aeration devices have significant effects on the pressures and cavitation at high operating heads, the subject needs to be scrutinized with further studies in terms of applicability.