Introduction

Numerical and analytical models play an important role in scientific research in engineering. Therefore, researchers have been doing research on new techniques to solve differential equations. In the recent years, many computational methods have been proposed and developed for analyses of engineering problems (Avazzadeh et al. 2020; Nikan and Avazzadeh 2021; Nikan et al. 2022; Rasoulizadeh et al. 2021).

Analytical models have proposed in fluid mechanics subjects for analyses of engineering problems. For example, an accurate prediction of the behavior of the groundwater flow in aquifers in response to changes in surface water is of considerable importance in obtaining solutions for groundwater flow problems. Therefore, prediction of groundwater head in porous media is among the most important topics in the study of groundwater–surface water systems. Groundwater and surface water should be treated as an integrated system. Numerical and analytical models play an important role in assessing the future behavior of water table fluctuations in the groundwater-surface water systems. Although the numerical methods can easily deal with complex geometries as well as heterogeneity and anisotropy, the analytical methods are preferred because they consume rather less time to compute the problem than numerical methods. Moreover, analytical solutions are useful tools for analyzing the sensitivity of aquifer parameters.

Many analytical models have been developed to estimate groundwater head variations in response to recharge or pumping from wells (Zlotnik and Tartakovsky 2008; Lu et al. 2015), surface recharge (Rai and Manglik 1999; Teloglou et al. 2008), tidal fluctuations (Sun 1997; Tang and Jiao 2001; Huang et al. 2015) and stage changes in adjacent water bodies (Singh 2004a, b; Jiang and Tang 2015). The aforementioned studies assumed that the aquifer was isotropic. In fact, many soils exhibit a certain degree of anisotropy due to stratification associated with soil forming processes such as sedimentation, illuviation, compaction and particle orientation (Assouline and Or 2006). There are also several analytical attempts that take into account the anisotropy of the aquifer (Park and Zhan 2002; Intaraprasong and Zhan 2009; Fen and Yeh 2012; Wang et al. 2015).

The effects of anisotropy on the nature of groundwater variation have been investigated by several researchers. For example, Chang and Yeh (2007) presented an analytical solution to describe the hydraulic head distribution and flow system in an anisotropic unconfined aquifer with a sloping bed and arbitrarily located multiwells under transient recharge. They demonstrated that the water table is steeper in y-direction than in x-direction as the ratio of hydraulic conductivity in x-direction to y-direction increases. Manglik et al. (2013) presented an analytical solution of groundwater flow equation for unconfined, anisotropic, two-dimensional rectangular aquifer to predict water table variations in the aquifer in response to general time-varying intermittent recharge from multiple basins. They assumed that the aquifer is bounded with four constant head boundaries. The solution is obtained by using extended finite Fourier sine transform. The results showed a significant effect of anisotropy in hydraulic conductivity on the pattern and magnitude of the water table variations. It was found that the growth of the water table for isotropic aquifer always maintains higher elevation than the level of water table for anisotropic aquifer. Singh (2010) presented some generalized analytical solutions for groundwater head in a horizontal aquifer in the presence of subsurface drains. The aquifer is homogeneous and anisotropic and interacts with four surrounding streams of constant head. It was found that the isotropic case is overall characterized with higher water levels as compared to the anisotropic one. Manglik and Rai (2015) developed an analytical model to predict water table variations in an anisotropic aquifer in response to intermittently applied time-varying recharge from multiple heterogeneous basins and pumping from multiple wells. They considered no-flow boundary conditions and solved the equations by using the finite Fourier transform. In the process of investigation of the effects of anisotropy on water table, it was found that the growth of water table below the recharge basin and its surrounding region is more for the isotropic aquifer than that for the anisotropic aquifer. However, in the region away from the boundaries of the recharge basin, growth of the water table for anisotropic aquifer is more than that for the isotropic aquifer.

Huang et al. (2011) presented an analytical solution for describing the head distribution in an anisotropic unconfined aquifer with a single pumping horizontal well parallel to a fully penetrating stream. They assumed the anisotropic aquifer has smaller vertical hydraulic conductivity than horizontal one. Given that the stream has a constant stage during the pumping period, they indicated that the anisotropic aquifer has larger stream depletion rate than the isotropic one.

In the present work, an effort is being made to investigate the effects of anisotropy on hydraulic head and flow rate in a rectangular confined aquifer adjoining to time-varying streams. In this paper, an anisotropic aquifer generally refers to an aquifer in which the hydraulic conductivity of the aquifer along x-direction is more than that along y-direction. Hence, the novelty of this paper is evaluating the anisotropy effects on groundwater hydraulic head as well as flow rate in a confined aquifer in contact with varying level boundaries. Therefore, a set of new analytical expressions are obtained by means of the Laplace and Fourier transforms and the solutions applicability is shown by the help of hypothetical examples. The results show that the presented new analytical solutions are accurate, robust and efficient. Therefore, the results indicate that the presented new analytical solutions are very effective in the simulation of the groundwater flow in river-aquifer systems. Furthermore, one of the advantages of the new analytical solutions is to investigate the sensitivity analysis of aquifer parameters, which has been carried out in this paper. Also, some other new analytical solutions for steady-state conditions and sudden fall in streams level are provided as well. The main applicability of the new analytical solutions is to investigate interactions between stream and aquifer. These new analytical solutions can also be used to evaluate aquifer response to gradual and sudden drop in stream stage. Also, the derived new analytical solutions could be used inversely to find the aquifer parameters. It can be mentioned that the presented new analytical solutions could further be used in many practical problems in stream-aquifer systems. Furthermore, it could be utilized for the validation of experimental and numerical models. Also, the results of the present new analytical solutions obtained will enable a better understanding regarding the modeling of the interaction between the river and the aquifer. Therefore, this research is a contribution to a better understanding of the fluxes between the river and the aquifer. Finally, the current study contributes to overcome common weaknesses of model applications, fulfills gaps in the existing literature and highlights the importance of the modeling process in planning sustainable management of groundwater resources.

The remainder of this paper is structured as follows: At first, new analytical solutions based on integral transforms to calculate and simulate the hydraulics of groundwater flow in river–aquifer systems are presented. Then, results and discussion are provided. Finally, in the last section conclusions are drawn.

Methodology

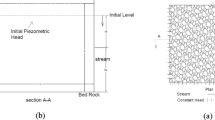
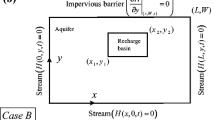
The geometry of the stream–aquifer system considered for study is shown in Fig. 1. A finite confined, anisotropic, incompressible and homogeneous aquifer is assumed to be surrounded with four streams of varying levels. The partial differential equation governing hydraulic head in a two-dimensional confined aquifer is taken to be:

$$K_{x} \frac{{\partial^{2} h}}{{\partial x^{2} }} + K_{y} \frac{{\partial^{2} h}}{{\partial y^{2} }} = S_{{\text{s}}} \frac{\partial h}{{\partial t}}.$$
(1)
Fig. 1
figure 1

A confined aquifer bounded with four streams

Full size image

The initial and boundary conditions of the problem are:

$$h(x,\;y,\;0) = h_{{\text{L}}} + h_{0} ,$$
(2)
$$h(x,\;y_{{\text{L}}} ,\;t) = h_{{\text{L}}} + h_{0} \;e^{{ - \varphi_{1} \,{\kern 1pt} t}} ,$$
(3)
$$h(x_{{\text{L}}} ,y,t) = h_{{\text{L}}} + h_{0} \;e^{{ - \varphi_{2} {\kern 1pt} {\kern 1pt} t}} ,$$
(4)
$$h(x,\;0,\;t) = h_{{\text{L}}} + h_{0} \;e^{{ - \varphi_{3} \;t}} ,$$
(5)
$$h(0,\;y,\;t) = h_{{\text{L}}} + h_{0} \;e^{{ - \varphi_{4} \;t}} ,$$
(6)

where h is the hydraulic head,\(S_{{\text{s}}}\) is the specific storage and \(K_{x}\) and \(K_{y}\) are the hydraulic conductivity of the aquifer along x-axis and y-axis, respectively.\(x_{{\text{L}}}\) and \(y_{{\text{L}}}\) are the length and width of the aquifer, respectively.\(\varphi_{1} ,\,\,\varphi_{2} ,\,\,\varphi_{3}\) and \(\varphi_{4}\) are the positive constants signifying change rate of the streams at the north, east, south and west of the aquifer, respectively (thereafter called the rates of streams), \(h_{L} + h_{0}\) is the initial head of the system and \(h_{{\text{L}}}\) is the final level of the streams.

Defining \(h^{\prime } = h - h_{{\text{L}}} - h_{0}\), Eqs. (2)–(6) may be rewritten as follows:

$$h^{\prime } (x,y,0) = 0,$$
(7)
$$h^{\prime } (x,\;y_{{\text{L}}} ,\;t) = h_{0} \;e^{{ - \varphi_{1} \;{\kern 1pt} t}} - h_{0} ,$$
(8)
$$h^{\prime } (x_{L} ,y,t) = h_{0} \;e^{{ - \varphi_{2} \;t}} - h_{0} ,$$
(9)
$$h^{\prime } (x,\;0,\;t) = h_{0} \;e^{{ - \varphi_{3} \;t}} - h_{0} ,$$
(10)
$$h^{\prime } (0,\;y,\;t) = h_{0} \;e^{{ - \varphi_{4} \;t}} - h_{0} .$$
(11)

Dimensionless variables can be introduced as follows:

$$\begin{aligned} & X = \frac{x}{b},\quad Y = \frac{y}{b}\sqrt \alpha ,\quad \eta = \frac{{K_{x} }}{{S_{{\text{S}}} {\kern 1pt} b^{2} }}t,\quad H = \frac{{h^{\prime } }}{{h_{0} }},\quad \lambda_{1} = \frac{{S_{{\text{S}}} b^{2} }}{{K_{x} }}\varphi_{1} ,\quad \\ & \lambda_{2} = \frac{{S_{{\text{S}}} b^{2} }}{{K_{x} }}\varphi_{2} ,\quad \lambda_{3} = \frac{{S_{{\text{S}}} b^{2} }}{{K_{x} }}\varphi_{3} ,\quad \lambda_{4} = \frac{{S_{{\text{S}}} b^{2} }}{{K_{x} }}\varphi_{4} \quad , \\ & X_{{\text{L}}} = \frac{{x_{{\text{L}}} }}{b},\quad Y_{{\text{L}}} = \frac{{y_{{\text{L}}} }}{b}\sqrt \alpha ,\quad \alpha = \frac{{K_{x} }}{{K_{y} }}, \\ \end{aligned}$$
(12)

where \(\alpha\) is the anisotropy ratio. Using Eq. (12), the governing equation with boundary conditions can be rewritten as follows:

$$\frac{{\partial^{2} H}}{{\partial X^{2} }} + \frac{{\partial^{2} H}}{{\partial Y^{2} }} = \frac{\partial H}{{\partial \eta }},$$
(13)
$$H(X,\;Y,\;0) = 0,$$
(14)
$$H(X,\;Y_{{\text{L}}} ,\;\eta ) = e^{{ - \lambda_{1} \;\eta }} - 1,$$
(15)
$$H(X_{{\text{L}}} ,\;Y,\;\eta ) = e^{{ - \lambda_{2} \;\eta }} - 1,$$
(16)
$$H(X,\;0,\;\eta ) = e^{{ - \lambda_{3} \;\eta }} - 1,$$
(17)
$$H(0,\;Y,\;\eta ) = e^{{ - \lambda_{4} \;\eta }} - 1.$$
(18)

The problem is decomposed into four parts, each of which has a three constant level boundaries and one varying level boundary, as shown in Fig. 2. Accordingly, the function \(H{\kern 1pt} {\kern 1pt} (X,Y,\eta )\) can be divided into four parts:

$$H{\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = H_{1} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) + H_{2} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) + H_{3} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) + H_{4} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ).$$
(19)
Fig. 2
figure 2

Decomposition of the problem into four parts

Full size image

Details of derivations of the solution for \(H_{1} (X,\;Y,\;\eta )\) are as follows:

Part 1

The governing equation with boundary conditions for \(H_{1} (X,\;Y,\;\eta )\) is:

$$\frac{{\partial^{2} H_{1} }}{{\partial X^{2} }} + \frac{{\partial^{2} H_{1} }}{{\partial Y^{2} }} = \frac{{\partial H_{1} }}{\partial \eta },$$
(20)
$$H_{1} (X,\;Y,\;\eta ) = 0,$$
(21)
$$H_{1} (X,\;Y_{{\text{L}}} ,\;\eta ) = e^{{ - \lambda_{1} \;\eta }} - 1,$$
(22)
$$H_{1} (X_{{\text{L}}} ,\;Y,\;\eta ) = 0,$$
(23)
$$H_{1} (X,\;0,\;\eta ) = 0,$$
(24)
$$H_{1} (0,\;Y,\;\eta ) = 0.$$
(25)

The Laplace transform can be defined as:

$$\Lambda {\kern 1pt} (X,\;Y,{\kern 1pt} \;p) = \int\limits_{0}^{\infty } {e^{ - p\tau } } H(X,\;Y,\;\eta )d\eta ,$$
(26)

where \(\Lambda {\kern 1pt}\) denotes the Laplace transform of H and p is the Laplace variable. Taking the Laplace transform of Eq. (20) results in:

$$\frac{{\partial^{2} }}{{\partial X^{2} }}{\kern 1pt} \Lambda_{1} (X,\;Y,{\kern 1pt} p) + \frac{{\partial^{2} }}{{\partial Y^{2} }}{\kern 1pt} \Lambda_{1} (X,Y,{\kern 1pt} p) = p{\kern 1pt} \Lambda_{1} (X,\;Y,{\kern 1pt} \;p) - H_{1} (X,\;Y,\;\eta = 0),$$
(27)

and the associated Laplace-transformed initial and boundary conditions are as follows:

$$\Lambda_{1} (X,\;Y,\;0) = 0,$$
(28)
$$\Lambda_{1} (X,\;Y_{{\text{L}}} ,\;p) = \frac{1}{{\lambda_{1} + p}} - \frac{1}{p},$$
(29)
$$\Lambda_{1} (X_{{\text{L}}} ,\;Y,\;p) = 0,$$
(30)
$$\Lambda_{1} (X,0,p) = 0,$$
(31)
$$\Lambda_{1} (0,\;Y,\;p) = 0.$$
(32)

The finite Fourier sine transform with respect to \(X\) can be defined as:

$$F_{{\text{s}}} \left\{ {\Lambda (X,\;Y,{\kern 1pt} p)} \right\} = \frac{\pi }{{X_{{\text{L}}} }}\int\limits_{0}^{{X_{L} }} {\Lambda (X,\;Y,{\kern 1pt} p){\kern 1pt} \sin (\frac{n\pi X}{{X_{{\text{L}}} }})\,{\text{d}}X} = \theta (n,\;Y,{\kern 1pt} p),$$
(33)

where \(\theta\) is the finite Fourier sine transform of \(\Lambda\) and n is the transform parameter. Applying the finite Fourier sine transform with respect to \(X\) in Eqs. (27)–(32) results in:

$$\frac{{{\text{d}}^{2} }}{{{\text{d}}Y^{2} }}{\kern 1pt} \theta_{1} (n,\;Y,{\kern 1pt} \;p) - \psi^{2} \theta_{1} (n,\;Y,{\kern 1pt} p) = 0,$$
(34)

where \(\psi^{2} = p + {{n^{2} \pi^{2} } \mathord{\left/ {\vphantom {{n^{2} \pi^{2} } {X_{{\text{L}}}^{2} }}} \right. \kern-0pt} {X_{{\text{L}}}^{2} }}\),and the associated Fourier-transformed initial and boundary conditions are as follows:

$$\theta_{1} (n,\;Y,\;0) = 0,$$
(35)
$$\theta_{1} (n,\;Y_{{\text{L}}} ,\;p) = \frac{{\lambda_{1} }}{{p(\lambda_{1} + p)}}\left[ {\frac{\cos (n\pi ) - 1}{n}} \right],$$
(36)
$$\theta_{1} (X_{{\text{L}}} ,\;Y,\;p) = 0,$$
(37)
$$\theta_{1} (n,\;0,\;p) = 0,$$
(38)
$$\theta_{1} (0,\;Y,\;p) = 0.$$
(39)

Equation (34) is an ordinary differential equation. The solution of this equation with boundary conditions is:

$${\kern 1pt} \theta (n,\;Y,{\kern 1pt} p) = C\cosh (\psi Y) + D\sinh (\psi Y),$$
(40)

where C and D are constants that can be determined by substituting Eqs. (36) and (38) in Eq. (40):

$$C = 0,\quad D = \frac{{\lambda_{1} }}{{p(\lambda_{1} + p)\sinh (\psi Y_{{\text{L}}} )}}\left[ {\frac{\cos (n\pi ) - 1}{n}} \right].$$
(41)

Therefore, transient hydraulic head in the Laplace–Fourier domain is:

$$\theta_{1} (n,\;Y,{\kern 1pt} p) = \frac{\lambda }{{p(\lambda + p)\sinh (\psi Y_{{\text{L}}} )}}\left[ {\frac{\cos (n\pi ) - 1}{n}} \right]\sinh (\psi Y).$$
(42)

Taking inverse finite Fourier sine transform of Eq. (42) results in:

$$\Lambda_{1} (X,\;Y,{\kern 1pt} p) = \frac{2}{\pi }\sum\limits_{n = 1}^{\infty } {\frac{{\lambda_{1} }}{{p(\lambda_{1} + p)\sinh (\psi Y_{{\text{L}}} )}}\left[ {\frac{\cos (n\pi ) - 1}{n}} \right]\sinh (\psi Y)\,\sin (\frac{n\pi X}{{X_{{\text{L}}} }})} .$$
(43)

The following equation can be used to invert the Laplace-domain solutions into time-domain solutions:

$$H(X,\;Y,\;\eta ) = \sum\limits_{n = 1}^{\infty } {\mathop {{\text{Re}} s}\limits_{{p = p_{n} }} \left[ {e^{pt} \Lambda (X,\;Y,\;p)} \right]} .$$
(44)

Finally, the time-domain solution is obtained after the application of Laplace inversion procedures:

$$\begin{aligned} H_{1} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{n = 1}^{\infty } {\left[ {\frac{2(\cos (n\pi ) - 1)}{{n\pi }}\sin (\frac{n\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{n\pi Y}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{n\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}} - e^{{ - \lambda_{1} \eta }} \frac{{\sinh (\sqrt {\frac{{n^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{1} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y)}}{{\sinh (\sqrt {\frac{{n^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{1} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y_{{\text{L}}} )}}} \right)} \right]} \\ & \quad + \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{m\lambda_{1} (\cos (n\pi ) - 1)\sin (\frac{m\pi Y}{{Y_{{\text{L}}} }})\sin (\frac{n\pi X}{{X_{{\text{L}}} }})( - 1)^{m} }}{{Y_{L}^{2} n\left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \left( {\lambda_{1} - \left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(45)

Equation (45) provides the transient hydraulic head of a confined aquifer with a varying level boundary at the north end and three constant level boundaries at the other ends.

Dimensionless flow rate through the two-dimensional aquifer with a unit cross-sectional area can be stated as:

$$Q = Q_{x} i + Q_{y} j,$$
(46)

in which

$$Q_{X} = \frac{\partial H}{{\partial X}} = - \frac{b}{{K_{x} h_{0} }}q_{x} \quad \& \quad q_{x} = - K_{x} \frac{{\partial h^{\prime } }}{\partial x} = - K_{x} \frac{\partial h}{{\partial x}},$$
(47)
$$Q_{Y} = \frac{\partial H}{{\partial Y}} = - \frac{b}{{\sqrt {K_{x} K_{y} } h_{0} }}q_{y} \quad \& \quad q_{y} = - K_{y} \frac{{\partial h^{\prime } }}{\partial y} = - K_{y} \frac{\partial h}{{\partial y}},$$
(48)

Hence, the dimensionless flow rate along x-axis and y-axis for part 1 can be stated as follows:

$$\begin{aligned} Q_{X1} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{n = 1}^{\infty } {\left[ {\frac{2(\cos (n\pi ) - 1)}{{X_{{\text{L}}} }}\cos (\frac{n\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{n\pi Y}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{n\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}} - e^{{ - \lambda_{1} \eta }} \frac{{\sinh (\sqrt {\frac{{n^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{1} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y)}}{{\sinh (\sqrt {\frac{{n^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{1} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y_{{\text{L}}} )}}} \right)} \right]} \\ & \quad + \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{m\lambda_{1} (\cos (n\pi ) - 1)\sin (\frac{m\pi Y}{{Y_{{\text{L}}} }})\cos (\frac{n\pi X}{{X_{{\text{L}}} }})( - 1)^{m} }}{{X_{L} Y_{L}^{2} \left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi \left( {\lambda_{1} - \left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(49)
$$\begin{aligned} Q_{Y1} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{n = 1}^{\infty } {\left[ {\frac{2(\cos (n\pi ) - 1)}{{n\pi }}\sin (\frac{n\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\frac{n\pi }{{X_{{\text{L}}} }}\cosh (\frac{n\pi Y}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{n\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}} - e^{{ - \lambda_{1} \eta }} \frac{{\sqrt {\frac{{n^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{1} } {\kern 1pt} {\kern 1pt} {\kern 1pt} \cosh (\sqrt {\frac{{n^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{1} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y)}}{{\sinh (\sqrt {\frac{{n^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{1} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y_{{\text{L}}} )}}} \right)} \right]} \\ & \quad + \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{m^{2} \lambda_{1} (\cos (n\pi ) - 1)\cos (\frac{m\pi Y}{{Y_{L} }})\sin (\frac{n\pi X}{{X_{{\text{L}}} }})( - 1)^{m} }}{{Y_{L}^{3} n\left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi \left( {\lambda_{1} - \left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(50)

Similarly, the procedures to get the solutions of transient hydraulic head and flow rate for parts 2–4 can be summarized as follows:

Part 2

The governing equation with boundary conditions for \(H_{2} (X,\;Y,\;\eta )\) is:

$$\frac{{\partial^{2} H_{2} }}{{\partial X^{2} }} + \frac{{\partial^{2} H_{2} }}{{\partial Y^{2} }} = \frac{{\partial H_{2} }}{\partial \eta },$$
(51)
$$H_{2} (X,\;Y,\;0) = 0,$$
(52)
$$H_{2} (X,\;Y_{{\text{L}}} ,\;\eta ) = 0,$$
(53)
$$H_{2} (X_{{\text{L}}} ,\;Y,\;\eta ) = e^{{ - \lambda_{2} \;\eta }} - 1,$$
(54)
$$H_{2} (X,\;0,\;\eta ) = 0,$$
(55)
$$H_{2} (0,\;Y,\;\eta ) = 0.$$
(56)

In this part, the Laplace transform is applied with respect to \(\eta\) and the finite Fourier sine transform is applied with respect to Y. Finally, the solution for \(H_{2} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta )\) is obtained as follows:

$$\begin{aligned} H_{2} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{k = 1}^{\infty } {\left[ {\frac{2(\cos (k\pi ) - 1)}{{k\pi }}\sin (\frac{k\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{k\pi X}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{k\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}} - e^{{ - \lambda_{2} \eta }} \frac{{\sinh (\sqrt {\frac{{k^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{2} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X)}}{{\sinh (\sqrt {\frac{{k^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{2} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X_{{\text{L}}} )}}} \right)} \right]} \\ & \quad + \sum\limits_{u = 1}^{\infty } {\sum\limits_{k = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{u\lambda_{2} (\cos (k\pi ) - 1)\sin (\frac{u\pi X}{{X_{{\text{L}}} }})\sin (\frac{k\pi Y}{{Y_{{\text{L}}} }})( - 1)^{u} }}{{X_{L}^{2} k\left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \left( {\lambda_{2} - \left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(57)

And the components of dimensionless flow rate are as follows:

$$\begin{aligned} Q_{X2} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{k = 1}^{\infty } {\left[ {\frac{2(\cos (k\pi ) - 1)}{{k\pi }}\sin (\frac{k\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\frac{k\pi }{{Y_{{\text{L}}} }}\cosh (\frac{k\pi X}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{k\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}} - e^{{ - \lambda_{2} \eta }} \frac{{\sqrt {\frac{{k^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{2} } {\kern 1pt} {\kern 1pt} {\kern 1pt} \cosh (\sqrt {\frac{{k^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{2} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X)}}{{\sinh (\sqrt {\frac{{k^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{2} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X_{{\text{L}}} )}}} \right)} \right]} \\ & \quad + \sum\limits_{u = 1}^{\infty } {\sum\limits_{k = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{u^{2} \lambda_{2} (\cos (k\pi ) - 1)\cos (\frac{u\pi X}{{X_{{\text{L}}} }})\sin (\frac{k\pi Y}{{Y_{{\text{L}}} }})( - 1)^{u} }}{{X_{{\text{L}}}^{3} k\left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi \left( {\lambda_{2} - \left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(58)
$$\begin{aligned} Q_{Y2} {\kern 1pt} {\kern 1pt} (X,Y,\eta ) = & \sum\limits_{k = 1}^{\infty } {\left[ {\frac{2(\cos (k\pi ) - 1)}{{Y_{{\text{L}}} }}\cos (\frac{k\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{k\pi X}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{k\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}} - e^{{ - \lambda_{2} \eta }} \frac{{\sinh (\sqrt {\frac{{k^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{2} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X)}}{{\sinh (\sqrt {\frac{{k^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{2} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X_{{\text{L}}} )}}} \right)} \right]} \\ & \quad + \sum\limits_{u = 1}^{\infty } {\sum\limits_{k = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{u\lambda_{2} (\cos (k\pi ) - 1)\sin (\frac{u\pi X}{{X_{{\text{L}}} }})\cos (\frac{k\pi Y}{{Y_{{\text{L}}} }})( - 1)^{u} }}{{X_{{\text{L}}}^{2} Y_{{\text{L}}} \left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi \left( {\lambda_{2} - \left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(59)

Equations (57), (58) and (59) provide the transient hydraulic head, flow rate along x-axis and flow rate along y-axis, respectively, for a confined aquifer with a varying level boundary at the east end and three constant level boundaries at the other ends.

Part 3

The governing equation with boundary conditions for \(H_{3} (X,\;Y,\;\eta )\) is:

$$\frac{{\partial^{2} H_{3} }}{{\partial X^{2} }} + \frac{{\partial^{2} H_{3} }}{{\partial Y^{2} }} = \frac{{\partial H_{3} }}{\partial \eta },$$
(60)
$$H_{3} (X,\;Y,\;0) = 0,$$
(61)
$$H_{3} (X,Y_{{\text{L}}} ,\eta ) = 0,$$
(62)
$$H_{3} (X_{{\text{L}}} ,\;Y,\;\eta ) = 0,$$
(63)
$$H_{3} (X,\;0,\;\eta ) = e^{{ - \lambda_{3} \;\eta }} - 1,$$
(64)
$$H_{3} (0,\;Y,\;\eta ) = 0.$$
(65)

In this part, the Laplace transform is applied with respect to \(\eta\) and the finite Fourier sine transform is applied with respect X. Finally, the solution for \(H_{3} (X,\;Y,\;\eta )\) is obtained as follows:

$$\begin{aligned} H_{3} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{a = 1}^{\infty } {\left[ {\frac{2(\cos (a\pi ) - 1)}{{a\pi }}\sin (\frac{a\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{{a\pi (Y_{{\text{L}}} - Y)}}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{a\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}} - e^{{ - \lambda_{3} \eta }} \frac{{\sinh (\sqrt {\frac{{a^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{3} } {\kern 1pt} {\kern 1pt} {\kern 1pt} (Y_{{\text{L}}} - Y))}}{{\sinh (\sqrt {\frac{{a^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{3} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y_{{\text{L}}} )}}} \right)} \right]} \\ & \quad + \sum\limits_{b = 1}^{\infty } {\sum\limits_{a = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{b\lambda_{3} (\cos (a\pi ) - 1)\sin (\frac{{b\pi (Y_{{\text{L}}} - Y)}}{{Y_{{\text{L}}} }})\sin (\frac{a\pi X}{{X_{{\text{L}}} }})( - 1)^{b} }}{{Y_{{\text{L}}}^{2} a\left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \left( {\lambda_{3} - \left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } \quad . \\ \end{aligned}$$
(66)

and the components of dimensionless flow rate are as follows:

$$\begin{aligned} Q_{X3} {\kern 1pt} {\kern 1pt} (X,Y,\eta ) = & \sum\limits_{a = 1}^{\infty } {\left[ {\frac{2(\cos (a\pi ) - 1)}{{X_{{\text{L}}} }}cos(\frac{a\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{{a\pi (Y_{{\text{L}}} - Y)}}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{a\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}} - e^{{ - \lambda_{3} \eta }} \frac{{\sinh (\sqrt {\frac{{a^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{3} } {\kern 1pt} {\kern 1pt} {\kern 1pt} (Y_{{\text{L}}} - Y))}}{{\sinh (\sqrt {\frac{{a^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{3} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y_{{\text{L}}} )}}} \right)} \right]} \\ & \quad + \sum\limits_{b = 1}^{\infty } {\sum\limits_{a = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{b\lambda_{3} (\cos (a\pi ) - 1)\sin (\frac{{b\pi (Y_{L} - Y)}}{{Y_{L} }})cos(\frac{a\pi X}{{X_{{\text{L}}} }})( - 1)^{b} }}{{X_{{\text{L}}} Y_{{\text{L}}}^{2} \left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi \left( {\lambda_{3} - \left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(67)
$$\begin{aligned} Q_{Y3} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{a = 1}^{\infty } {\left[ {\frac{2(\cos (a\pi ) - 1)}{{a\pi }}\sin (\frac{a\pi X}{{X_{{\text{L}}} }}) \times \left( \begin{gathered} \frac{{\frac{ - a\pi }{{X_{{\text{L}}} }}cosh(\frac{{a\pi (Y_{{\text{L}}} - Y)}}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{a\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}} \hfill \\ - e^{{ - \lambda_{3} \eta }} \frac{{ - \sqrt {\frac{{a^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{3} } \sinh (\sqrt {\frac{{a^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{3} } {\kern 1pt} {\kern 1pt} {\kern 1pt} (Y_{{\text{L}}} - Y))}}{{\sinh (\sqrt {\frac{{a^{2} \pi^{2} }}{{X_{{\text{L}}}^{2} }} - \lambda_{3} } {\kern 1pt} {\kern 1pt} {\kern 1pt} Y_{{\text{L}}} )}} \hfill \\ \end{gathered} \right)} \right]} \\ & \quad - \sum\limits_{b = 1}^{\infty } {\sum\limits_{a = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{b^{2} \lambda_{3} (\cos (a\pi ) - 1)\sin (\frac{{b\pi (Y_{{\text{L}}} - Y)}}{{Y_{{\text{L}}} }})\sin (\frac{a\pi X}{{X_{{\text{L}}} }})( - 1)^{b} }}{{Y_{{\text{L}}}^{3} a\left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi \left( {\lambda_{3} - \left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(68)

Equations (66), (67) and (68) provide the transient hydraulic head, flow rate along x-axis and flow rate along y-axis, respectively, for a confined aquifer with a varying level boundary at the south end and three constant level boundaries at the other ends.

Part 4

The governing equation with boundary conditions for \(H_{4} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta )\) is:

$$\frac{{\partial^{2} H_{4} }}{{\partial X^{2} }} + \frac{{\partial^{2} H_{4} }}{{\partial Y^{2} }} = \frac{{\partial H_{4} }}{\partial \eta },$$
(69)
$$H_{4} (X,\;Y,\;0) = 0,$$
(70)
$$H_{4} (X,\;Y_{{\text{L}}} ,\;\eta ) = 0,$$
(71)
$$H_{4} (X_{{\text{L}}} ,\;Y,\;\eta ) = 0,$$
(72)
$$H_{4} (X,\;0,\;\eta ) = 0,$$
(73)
$$H_{4} (0,\;Y,\;\eta ) = e^{{ - \lambda_{4} \;\eta }} - 1.$$
(74)

In this part, the Laplace transform is applied with respect to \(\eta\) and the finite Fourier sine transform is applied with respect Y. Finally, the solution for \(H_{4} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta )\) is obtained as follows:

$$\begin{aligned} H_{4} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{f = 1}^{\infty } {\left[ {\frac{2(\cos (f\pi ) - 1)}{{f\pi }}\sin (\frac{f\pi Y}{{Y_{{\text{L}}} }}) \times \left( \begin{gathered} \frac{{\sinh (\frac{{f\pi \left( {X_{{\text{L}}} - X} \right)}}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{f\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}} \hfill \\ - e^{{ - \lambda_{4} \eta }} \frac{{\sinh (\sqrt {\frac{{f^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{4} } {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {X_{{\text{L}}} - X} \right))}}{{\sinh (\sqrt {\frac{{f^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{4} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X_{{\text{L}}} )}} \hfill \\ \end{gathered} \right)} \right]} \\ & \quad + \sum\limits_{d = 1}^{\infty } {\sum\limits_{f = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{d\lambda_{4} (\cos (f\pi ) - 1)\sin (\frac{{d\pi \left( {X_{{\text{L}}} - X} \right)}}{{X_{{\text{L}}} }})\sin (\frac{f\pi Y}{{Y_{{\text{L}}} }})( - 1)^{d} }}{{X_{{\text{L}}}^{2} f\left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \left( {\lambda_{4} - \left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } , \\ \end{aligned}$$
(75)

and the components of dimensionless flow rate are as follows:

$$\begin{aligned} Q_{X4} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{f = 1}^{\infty } {\left[ {\frac{2(\cos (f\pi ) - 1)}{{f\pi }}\sin (\frac{f\pi Y}{{Y_{{\text{L}}} }}) \times \left( \begin{gathered} \frac{{\frac{ - f\pi }{{Y_{{\text{L}}} }}\cosh (\frac{{f\pi \left( {X_{{\text{L}}} - X} \right)}}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{f\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}} \hfill \\ - e^{{ - \lambda_{4} \eta }} \frac{{ - \sqrt {\frac{{f^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{4} } {\kern 1pt} {\kern 1pt} {\kern 1pt} \cosh (\sqrt {\frac{{f^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{4} } {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {X_{{\text{L}}} - X} \right))}}{{\sinh (\sqrt {\frac{{f^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{4} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X_{{\text{L}}} )}} \hfill \\ \end{gathered} \right)} \right]} \\ & \quad - \sum\limits_{d = 1}^{\infty } {\sum\limits_{f = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{d^{2} \lambda_{4} (\cos (f\pi ) - 1)\cos (\frac{{d\pi \left( {X_{{\text{L}}} - X} \right)}}{{X_{{\text{L}}} }})\sin (\frac{f\pi Y}{{Y_{{\text{L}}} }})( - 1)^{d} }}{{X_{L}^{3} f\left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi \left( {\lambda_{4} - \left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(76)
$$\begin{aligned} Q_{Y4} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{f = 1}^{\infty } {\left[ {\frac{2(\cos (f\pi ) - 1)}{{Y_{{\text{L}}} }}cos(\frac{f\pi Y}{{Y_{{\text{L}}} }}) \times \left( \begin{gathered} \frac{{\sinh (\frac{{f\pi \left( {X_{{\text{L}}} - X} \right)}}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{f\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}} \hfill \\ - e^{{ - \lambda_{4} \eta }} \frac{{\sinh (\sqrt {\frac{{f^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{4} } {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {X_{{\text{L}}} - X} \right))}}{{\sinh (\sqrt {\frac{{f^{2} \pi^{2} }}{{Y_{{\text{L}}}^{2} }} - \lambda_{4} } {\kern 1pt} {\kern 1pt} {\kern 1pt} X_{{\text{L}}} )}} \hfill \\ \end{gathered} \right)} \right]} \\ & \quad + \sum\limits_{d = 1}^{\infty } {\sum\limits_{f = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{d\lambda_{4} (\cos (f\pi ) - 1)\sin (\frac{{d\pi \left( {X_{{\text{L}}} - X} \right)}}{{X_{{\text{L}}} }})cos(\frac{f\pi Y}{{Y_{{\text{L}}} }})( - 1)^{d} }}{{Y_{L} X_{L}^{2} \left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi \left( {\lambda_{4} - \left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} } \right)}}} \right]} } . \\ \end{aligned}$$
(77)

Equations (75), (76) and (77) provide the transient hydraulic head, flow rate along x-axis and flow rate along y-axis, respectively, for a confined aquifer with a varying level boundary at the west end and three constant level boundaries at the other ends.

Comparison of the new analytical solutions with numerical model of MODFLOW

In order to demonstrate the capability of the proposed new analytical solutions in the estimation of groundwater hydraulic head in an anisotropic aquifer, another hypothetical aquifer is simulated in numerical model of MODFLOW. The rates of streams are: \(\varphi_{1} = 0.05\,\,{\text{day}}^{ - 1}\), \(\varphi_{2} = 0\), \(\varphi_{3} = 0.1\,\,{\text{day}}^{ - 1}\) and \(\varphi_{4} = 0.2\,\,{\text{day}}^{ - 1}\). The anisotropy ratio is \(\alpha = 3\) (\(K_{x} = 30\;{\text{m}}/{\text{day}}\), \(K_{y} = 10\;{\text{m}}/{\text{day}}\)). The length and width of the aquifer are selected as: \(x_{{\text{L}}} = 100\,{\text{m}}\) and \(y_{{\text{L}}} = 50\,{\text{m}}\). The other parameters are given in Table 1. For the numerical model of MODFLOW, the domain is discretized into \(500 \times 250\) rectangular cells with \(\Delta x = \Delta y = 0.2\,{\text{m}}\). The computational time interval for numerical model of MODFLOW is 12 h. The type of boundary conditions is considered as specified hydraulic head. The solver and flow packages are PCG2 and LPF, respectively. LPF has the ability to enter horizontal anisotropy values on a cell-by-cell basis. The values of hydraulic head at \(t = 10\,{\text{days}}\) and at \(y = 25\,{\text{m}}\) are shown in Fig. 3. Figure 3 shows that the results of the new analytical solutions are in good agreement with those results obtained from numerical model of MODFLOW.

Table 1 The values of hypothetical aquifer parameters
Full size table
Fig. 3
figure 3

Comparison of the new analytical solutions with numerical model of MODFLOW

Full size image

Results and discussion

The configuration of the personal computer used to perform the simulation results is that the CPU is Intel(R)/Core(TM)4/i7-8550U, CPU@4.000 GHz. As mentioned earlier, Eq. (19) presents the new analytical solution of an aquifer bounded with four time-varying level boundaries, which is sum of Eqs. (45), (57), (66) and (75). Notice that setting \(\varphi_{i} = 0\;(i = 1,2,3,4)\) gives constant level boundaries. Therefore, the new analytical expressions for other types of boundary configurations with both constant and time-varying levels can readily be obtained. Table 2 presents the new analytical expressions for 15 different boundary configurations.

Table 2 The new analytical expressions of 15 possible bounded aquifers formed by constant and varying level boundaries
Full size table

Thereafter, BC stands for boundary configuration and the following number indicates the type of boundary configuration given in Table 2. For example, BC5 refers to the boundary configuration number 5 in Table 2.

Steady state condition

Setting \(\eta \to \infty\) in Eqs. (45), (57), (66) and (75) provides the steady-state condition of these solutions.

Steady state of Eq. (45) is:

$$H_{{{\text{s}}{\kern 1pt} t1}} {\kern 1pt} {\kern 1pt} (X,Y,\eta \to \infty ) = \sum\limits_{n = 1}^{\infty } {\frac{2(\cos (n\pi ) - 1)}{{n\pi }}\sin (\frac{n\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{n\pi Y}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{n\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}}} \right)} .$$
(78)

And the associated flow rates can be expressed as follows:

$$Q_{{s{\kern 1pt} t1X}} {\kern 1pt} {\kern 1pt} (X,Y,\eta \to \infty ) = \sum\limits_{n = 1}^{\infty } {\frac{2(\cos (n\pi ) - 1)}{{X_{{\text{L}}} }}\cos (\frac{n\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{n\pi Y}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{n\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}}} \right)} .$$
(79)
$$Q_{{s{\kern 1pt} t1Y}} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = \sum\limits_{n = 1}^{\infty } {\frac{2(\cos (n\pi ) - 1)}{{X_{{\text{L}}} }}\sin (\frac{n\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\cosh (\frac{n\pi Y}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{n\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}}} \right)} .$$
(80)

Steady state of Eq. (57) is:

$$H_{{s{\kern 1pt} t2}} {\kern 1pt} {\kern 1pt} (X,Y,\eta \to \infty ) = \sum\limits_{k = 1}^{\infty } {\frac{2(\cos (k\pi ) - 1)}{{k\pi }}\sin (\frac{k\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{k\pi X}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{k\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}}} \right)} .$$
(81)

And the associated flow rates can be expressed as follows:

$$Q_{{s{\kern 1pt} t2X}} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = \sum\limits_{k = 1}^{\infty } {\frac{2(\cos (k\pi ) - 1)}{{Y_{{\text{L}}} }}\sin (\frac{k\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\cosh (\frac{k\pi X}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{k\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}}} \right)} .$$
(82)
$$Q_{{s{\kern 1pt} t2Y}} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = \sum\limits_{k = 1}^{\infty } {\frac{2(\cos (k\pi ) - 1)}{{Y_{{\text{L}}} }}\cos (\frac{k\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{k\pi X}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{k\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}}} \right)} .$$
(83)

Steady state of Eq. (66) is:

$$H_{{s{\kern 1pt} t3}} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = \sum\limits_{a = 1}^{\infty } {\frac{2(\cos (a\pi ) - 1)}{{a\pi }}\sin (\frac{a\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{{a\pi (Y_{{\text{L}}} - Y)}}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{a\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}}} \right)} \quad .$$
(84)

And the associated flow rates can be expressed as follows:

$$Q_{{s{\kern 1pt} t3X}} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = \sum\limits_{a = 1}^{\infty } {\frac{2(\cos (a\pi ) - 1)}{{X_{{\text{L}}} }}\cos (\frac{a\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{{a\pi (Y_{{\text{L}}} - Y)}}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{a\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}}} \right)} .$$
(85)
$$Q_{{s{\kern 1pt} t3Y}} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = - \sum\limits_{a = 1}^{\infty } {\frac{2(\cos (a\pi ) - 1)}{{X_{{\text{L}}} }}\sin (\frac{a\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\cosh (\frac{{a\pi (Y_{{\text{L}}} - Y)}}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{a\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}}} \right)} .$$
(86)

Steady state of Eq. (75) is:

$$H_{{s{\kern 1pt} t4}} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = \sum\limits_{f = 1}^{\infty } {\frac{2(\cos (f\pi ) - 1)}{{f\pi }}\sin (\frac{f\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{{f\pi \left( {X_{{\text{L}}} - X} \right)}}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{f\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}}} \right)} \quad .$$
(87)

And the associated flow rates can be expressed as follows:

$$Q_{{s{\kern 1pt} t4}} X{\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = - \sum\limits_{f = 1}^{\infty } {\frac{2(\cos (f\pi ) - 1)}{{Y_{{\text{L}}} }}\sin (\frac{f\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{cosh(\frac{{f\pi \left( {X_{{\text{L}}} - X} \right)}}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{f\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}}} \right)} \quad .$$
(88)
$$Q_{{s{\kern 1pt} t4Y}} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta \to \infty ) = \sum\limits_{f = 1}^{\infty } {\frac{2(\cos (f\pi ) - 1)}{{Y_{{\text{L}}} }}cos(\frac{f\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{{f\pi \left( {X_{{\text{L}}} - X} \right)}}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{f\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}}} \right)} .$$
(89)

Equations (78), (81), (84) and (87) are very useful new exact expressions describing the groundwater hydraulic head distribution in an anisotropic 2D aquifer in steady-state conditions. In a one-dimensional aquifer connected to two streams with different stages, the initial groundwater head can be assumed to vary linearly between the streams. However, estimation of the initial groundwater hydraulic head in a two-dimensional aquifer connected to four streams with different stages is more complicated. Equations (78), (81), (84) and (87) can be used for such these conditions.

Sudden fall in streams level

For the case of sudden fall in streams level \(\lambda_{i} \;(i = 1,\;2,\;3,\;4)\) goes to infinity in Eqs. (45), (57), (66) and (75).

Sudden fall in level of the north stream is:

$$\begin{aligned} H_{Su1} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{n = 1}^{\infty } {\left[ {\frac{2(\cos (n\pi ) - 1)}{{n\pi }}\sin (\frac{n\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{n\pi Y}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{n\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}}} \right)} \right]} \\ & \quad + \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{m(\cos (n\pi ) - 1)\sin (\frac{m\pi Y}{{Y_{{\text{L}}} }})\sin (\frac{n\pi X}{{X_{{\text{L}}} }})( - 1)^{m} }}{{Y_{L}^{2} n\left( {\frac{{n^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{m^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} }}} \right]} } . \\ \end{aligned}$$
(90)

Sudden fall in level of the east stream is:

$$\begin{aligned} H_{Su2} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{k = 1}^{\infty } {\left[ {\frac{2(\cos (k\pi ) - 1)}{{k\pi }}\sin (\frac{k\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{k\pi X}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{k\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}}} \right)} \right]} \\ & \quad + \sum\limits_{u = 1}^{\infty } {\sum\limits_{k = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{u(\cos (k\pi ) - 1)\sin (\frac{u\pi X}{{X_{{\text{L}}} }})\sin (\frac{k\pi Y}{{Y_{{\text{L}}} }})( - 1)^{u} }}{{X_{{\text{L}}}^{2} k\left( {\frac{{k^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{u^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} }}} \right]} } . \\ \end{aligned}$$
(91)

Sudden fall in level of the south stream is:

$$\begin{aligned} H_{Su3} {\kern 1pt} {\kern 1pt} (X,\;Y,\;\eta ) = & \sum\limits_{a = 1}^{\infty } {\left[ {\frac{2(\cos (a\pi ) - 1)}{{a\pi }}\sin (\frac{a\pi X}{{X_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{{a\pi (Y_{{\text{L}}} - Y)}}{{X_{{\text{L}}} }})}}{{\sinh (\frac{{a\pi Y_{{\text{L}}} }}{{X_{{\text{L}}} }})}}} \right)} \right]} \\ & \quad + \sum\limits_{b = 1}^{\infty } {\sum\limits_{a = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{b(\cos (a\pi ) - 1)\sin (\frac{{b\pi (Y_{{\text{L}}} - Y)}}{{Y_{{\text{L}}} }})\sin (\frac{a\pi X}{{X_{{\text{L}}} }})( - 1)^{b} }}{{Y_{{\text{L}}}^{2} a\left( {\frac{{a^{2} }}{{X_{{\text{L}}}^{2} }} + \frac{{b^{2} }}{{Y_{{\text{L}}}^{2} }}} \right)\pi^{2} }}} \right]} } . \\ \end{aligned}$$
(92)

Sudden fall in level of the west stream is:

$$\begin{aligned} H_{Su4} {\kern 1pt} {\kern 1pt} (X,Y,\eta ) = & \sum\limits_{f = 1}^{\infty } {\left[ {\frac{2(\cos (f\pi ) - 1)}{{f\pi }}\sin (\frac{f\pi Y}{{Y_{{\text{L}}} }}) \times \left( {\frac{{\sinh (\frac{{f\pi \left( {X_{{\text{L}}} - X} \right)}}{{Y_{{\text{L}}} }})}}{{\sinh (\frac{{f\pi X_{{\text{L}}} }}{{Y_{{\text{L}}} }})}}} \right)} \right]} \\ & \quad + \sum\limits_{d = 1}^{\infty } {\sum\limits_{f = 1}^{\infty } {\left[ {4e^{{ - \left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} \eta }} \frac{{d(\cos (f\pi ) - 1)\sin (\frac{{d\pi \left( {X_{{\text{L}}} - X} \right)}}{{X_{{\text{L}}} }})\sin (\frac{f\pi Y}{{Y_{{\text{L}}} }})( - 1)^{d} }}{{X_{{\text{L}}}^{2} f\left( {\frac{{f^{2} }}{{Y_{{\text{L}}}^{2} }} + \frac{{d^{2} }}{{X_{{\text{L}}}^{2} }}} \right)\pi^{2} }}} \right]} } . \\ \end{aligned}$$
(93)

Groundwater hydraulic head distribution for three scenarios of sudden fall in streams level at \(t = 1\,{\text{s}}\) is illustrated in Fig. 4. The figures are plotted for three different BCs. Scenario 1: Fig. 4a shows groundwater hydraulic head distribution for sudden changes in streams level of BC1. In this scenario, the water level falls suddenly at the north stream and is constant at the other streams. Thus, the results can be obtained by using Eq. (90). Figure 4b shows groundwater hydraulic head distribution for sudden changes in streams level of BC5. Scenario 2: In this scenario, the water level falls suddenly at the north and east streams and is constant at the other streams. Here, the results can be obtained by sum of Eqs. (90) and (91). Scenario 3: Fig. 4c shows groundwater hydraulic head distribution for sudden changes in streams level of BC14. In this scenario, the water level falls suddenly at the east, south and west streams and is constant at the north stream. Here, the results can be obtained by sum of Eqs. (91), (92) and (93). The anisotropy ratio is \(\alpha = 3\) (\(K_{x} = 30\;{\text{m}}/{\text{day}}\),\(K_{y} = 10\;{\text{m}}/{\text{day}}\)), and the other parameters are as before.

Fig. 4
figure 4

Groundwater hydraulic head distribution for sudden fall in streams level at \(t = 1\,{\text{s}}\) a scenario 1, b scenario 2 and c scenario 3

Full size image

Figure 5a, b and c shows the groundwater hydraulic head variations with time at different points of the aquifer for scenarios 1, 2 and 3, respectively. Five different points are considered, namely P1:\(x = 20\), \(y = 30\;{\text{m}}\), P2:\(x = 80\), \(y = 20\;{\text{m}}\), P3:\(x = 50\), \(y = 50\;{\text{m}}\), P4:\(x = 30\), \(y = 80\;{\text{m}}\) and P5:\(x = 70\), \(y = 60\;{\text{m}}\). It can be seen that the groundwater hydraulic head stabilizes about less than 0.01 s.

Fig. 5
figure 5

Groundwater hydraulic head variations at different points of the aquifer for sudden fall in streams level a scenario 1, b scenario 2 and c scenario 3

Full size image

Effects of anisotropy on aquifer response

In this section, several examples are conducted to investigate the effects of anisotropy on hydraulic head and flow rate. Here, four cases are defined. The rates of streams for these cases are given in Table 3, the anisotropy ratio is \(\alpha = 3\) and the other parameters are kept as before.

Table 3 Rates of streams for cases 1–4
Full size table

Effects of anisotropy on hydraulic head

Figure 6 shows the values of hydraulic head over distance at 10th day for both isotropic and anisotropic aquifer and for cases 1–4. It can be observed from Fig. 6 that with increases in \(K_{y}\) the hydraulic head increases in cases 1 and 3 but decreases in cases 2 and 4. This phenomenon is valid for any arbitrary time, which is also found in Fig. 7. Figure 7 shows the hydraulic head variations with time at a point located at \(x = 50\,{\text{m}}\), \(y = 25\,{\text{m}}\). This phenomenon is because that a higher hydraulic conductivity along y-direction deviates the groundwater flow direction along this direction. On the other hand, in cases 2 and 4 the streams level at the south and north boundaries are falling rather faster than the other streams. This causes the groundwater direction to also deviate along y-axis. Therefore, an isotropic aquifer \(K_{y} = 30\;({\text{m}}/{\text{day}})\) allows the water to flow faster in y-direction, and as a result, the groundwater hydraulic head decreases. This is exactly vice versa in cases 1 and 3 in which the groundwater hydraulic head is deviated along x-direction due to the available gradient as well as a smaller \(K_{y}\). Therefore, in the presence of anisotropy the groundwater hydraulic head decreases in cases 1 and 3.

Fig. 6
figure 6

Effects of anisotropy on transient hydraulic head at \(t = 10\,{\text{days}}\) and \(y = 25\,{\text{m}}\) for a case 1, b case 2, c case 3, d case 4

Full size image
Fig. 7
figure 7

Variations of hydraulic head at \(x = 50\,{\text{m}}\), \(y = 25\,{\text{m}}\) for a case 1, b case 2, c case 3, d case 4

Full size image

Figures 8, 9, 10 and 11 show the sensitivity of hydraulic head to changes in rates of the streams in the isotropic (\(\alpha = 1:\,\;K_{y} = K_{x} = 30\;{\text{m}}/{\text{day}}\)) and anisotropic (\(\alpha = 3:\,\;K_{y} = 10\,\,{\text{m}}/{\text{day}},\;K_{x} = 30\;{\text{m}}/{\text{day}}\)) aquifers for \(t = 10\,{\text{days}}\) and at a point located at \(x = 70\,{\text{m}}\), \(y = 40\,{\text{m}}\). These figures are plotted for different rates \(\varphi_{1}\), \(\varphi_{2}\), \(\varphi_{3}\) and \(\varphi_{4}\), keeping the other parameters as before.

Fig. 8
figure 8

Sensitivity of hydraulic head to changes in \(\varphi_{1}\). Here, \(\varphi_{2} = 0.06\), \(\varphi_{3} = 0.09\) and \(\varphi_{4} = 0.12\)

Full size image
Fig. 9
figure 9

Sensitivity of hydraulic head to changes in \(\varphi_{2}\). Here, \(\varphi_{1} = 0.03\), \(\varphi_{3} = 0.09\) and \(\varphi_{4} = 0.12\)

Full size image
Fig. 10
figure 10

Sensitivity of hydraulic head to changes in \(\varphi_{3}\). Here,\(\varphi_{1} = 0.03\), \(\varphi_{2} = 0.06\) and \(\varphi_{4} = 0.12\)

Full size image
Fig. 11
figure 11

Sensitivity of hydraulic head to changes in \(\varphi_{4}\). Here, \(\varphi_{1} = 0.03\), \(\varphi_{2} = 0.06\) and \(\varphi_{3} = 0.12\)

Full size image

Figure 7 shows that the magnitude of difference between corresponding hydraulic head for \(\varphi_{1} = 0.01\) and \(\varphi_{1} = 1\) \(day^{ - 1}\) is about 0.52 m for the isotropic aquifer and it is about 0.14 m for the anisotropic aquifer. Also, Fig. 8 shows that the magnitude of difference between corresponding hydraulic head for \(\varphi_{2} = 0.01\) and \(\varphi_{2} = 1\) \(day^{ - 1}\) is about 1.64 m for the isotropic aquifer and it is about 2.24 m for the anisotropic aquifer. Moreover, Fig. 9 shows that the magnitude of difference between corresponding hydraulic head for \(\varphi_{3} = 0.01\) and \(\varphi_{3} = 1\) \(day^{ - 1}\) is about 1.05 m for the isotropic aquifer and it is about 0.42 m for the anisotropic aquifer. In addition, Fig. 10 shows that the magnitude of difference between corresponding hydraulic head for \(\varphi_{4} = 0.01\) and \(\varphi_{4} = 1\) \(day^{ - 1}\) is about 0.41 m for the isotropic aquifer and it is about 0.82 m for the anisotropic aquifer.

In summary, it can be concluded from Figs. 7, 8, 9 and 10 that the hydraulic head in an anisotropic aquifer is more sensitive to changes in \(\varphi_{2}\) and \(\varphi_{4}\) and less sensitive to changes in \(\varphi_{1}\) and \(\varphi_{3}\) than that in an isotropic aquifer. This is because a large value of hydraulic conductivity along y-direction raises the groundwater flow velocity along this direction. Hence, with increases in \(K_{y}\) the groundwater flow tends to move toward either the north or south streams and consequently the hydraulic head gets more sensitive to variations of \(\varphi_{1}\) and \(\varphi_{3}\) in isotropic aquifer.

Effects of anisotropy on flow rate

Table 4 gives the values of flow rate and the direction of the flow (\(\beta\)) at different points of the aquifer.\(\beta\) is the angle between vector \(q\) and positive axis. To investigate the effects of anisotropy on flow rate and its direction, two values of hydraulic conductivity are considered, namely \(K_{y} = 30\) and \(K_{y} = 10\;({\text{m}}/{\text{day}})\). Here, \(\varphi_{1} = \varphi_{2} = \varphi_{3} = \varphi_{4} = 0.02\,({\text{day}}^{ - 1} )\) and the other parameters are given in Table 1. As expected, Table 4 shows that as \(K_{y}\) increases, the groundwater flow tends to deviate along y-axis and vice versa. This is because the higher hydraulic conductivity allows the water to flow easier in aquifer. Tables 5, 6, 7 and 8 provide the dimensionless flow rate at the left, right, north and south interfaces for different values of \(K_{y}\), respectively.

Table 4 Values of flow rate and the direction of the flow at different points of the aquifer at \(t = 10\) days
Full size table
Table 5 Values of dimensionless flow rate at the left interface at \(t = 10\) days
Full size table
Table 6 Values of dimensionless flow rate at the right interface at \(t = 10\) days
Full size table
Table 7 Values of dimensionless flow rate at the north interface at \(t = 10\) days
Full size table
Table 8 Values of dimensionless flow rate at the south interface at \(t = 10\) days
Full size table

Table 5 shows that at the left interface, the average difference between corresponding dimensionless flow rate (\(Q\)) of \(K_{y} = 30\) and \(K_{y} = 10\;({\text{m}}/{\text{day}})\) is 0.73, 0.1, 0.13 and 0.1 for cases 1 to 4, respectively.

Table 6 shows that at the right interface, the average difference between corresponding dimensionless flow rate (\(Q\)) of \(K_{y} = 30\) and \(K_{y} = 10\;({\text{m}}/{\text{day}})\) is 0.13, 0.1, 0.73 and 0.1 for cases 1–4, respectively.

Table 7 shows that at the north interface, the average difference between corresponding dimensionless flow rate (\(Q\)) of \(K_{y} = 30\) and \(K_{y} = 10\;({\text{m}}/{\text{day}})\) is 0.42, 0.12, 0.42 and 0.04 for cases 1 to 4, respectively.

Table 8 shows that at the south interface, the average difference between corresponding dimensionless flow rate (\(Q\)) of \(K_{y} = 30\) and \(K_{y} = 10\;({\text{m}}/{\text{day}})\) is 0.42, 0.04, 0.42 and 0.12 for cases 1–4, respectively.

Tables 5, 6, 7 and 8 show that with rises in \(K_{y}\), values of flow rate at different points of interfaces may increase or decrease. However, it can be seen that the average dimensionless flow rate at interfaces increases with increasing \(K_{y}\). The average of the dimensionless flow rate of interfaces in cases 1 to 4 is increased about \(0.425\), \(0.09\), \(0.425\) and \(0.09\), respectively, in the isotropic aquifer. It can be highlighted that in case 1 (when the rate of the left stream is more than that of the other streams), the dimensionless flow rate by a change in \(K_{y}\) is more influenced at the left boundary than that at the other boundaries. Similarly, in case 3 (when the rate of the right stream is more than that of the other streams) the dimensionless flow rate by a change in \(K_{y}\) is more influenced at the right boundary than that at the other boundaries. However, this phenomenon is vice versa in cases 2 and 4. In case 2 (when the rate of the south stream is more than that of the other streams), the dimensionless flow rate by a change in \(K_{y}\) is less influenced at the south boundary than that at the other boundaries. Moreover, in case 4 (when the rate of the north stream is more than that of the other streams) the dimensionless flow rate by a change in \(K_{y}\) is less influenced at the north boundary than that at the other boundaries.

Conclusions

A set of dimensionless new analytical solutions are proposed to describe transient hydraulic head and flow rate in a finite confined, anisotropic, incompressible and homogeneous aquifer with four time-varying streams located at its ends. Using superposition principle, the problem is decomposed into four parts and the final solution is obtained by the sum of the solutions. In part one, a new analytical solution describing the hydraulic head for an aquifer with a time-varying stream at the north boundary and three constant streams at the other boundaries is derived. The associated new analytical expression for this case is Eq. (45). Part 2 deals with an aquifer with a time-varying stream at the east boundary and three constant streams at the other boundaries. The associated new analytical expression for part 2 is given in Eq. (57). Part 3 provides a new analytical solution (Eq. (66)) of an aquifer with a time-varying stream at the south boundary and three constant streams at the other boundaries. Also, in part 4, Eq. (75) is the new analytical expression of an aquifer with a time-varying stream at the west boundary and three constant streams at the other boundaries. These equations can be summed with each other to calculate the hydraulic head of aquifers with different types of boundary configurations. Hence, the new analytical expressions of the some other boundary configurations are also given. The new analytical solutions are obtained with Laplace and Fourier transforms and a numerical comparison of the model is also carried out using numerical model of MODFLOW. The results of the presented new analytical solutions were in good agreement with the results of MODFLOW. The results show that the presented new analytical solutions are accurate, robust and efficient. Therefore, the results indicate that the presented new analytical solutions are very effective in the simulation of the groundwater flow in river–aquifer systems. Furthermore, one of the advantages of the new analytical solutions is to investigate the sensitivity analysis of aquifer parameters, which has been carried out in this paper. Also, some other new analytical solutions for steady-state conditions and sudden fall in streams level are provided as well.

Some significant new analytical expressions describing the sudden fall in streams level as well as steady-state conditions are derived. The associated new analytical expressions of steady-state conditions for parts 1 to 4 are given in Eqs. (78)–(89). Equations (78), (81), (84) and (87) are very important new exact expressions and can be used to calculate the initial groundwater hydraulic head in an anisotropic aquifer when the initial levels of the surrounding streams are different. Moreover, the new analytical expressions of sudden fall in streams level for parts 1 to 4 are given in Eqs. (90)–(93). Using these equations, the groundwater hydraulic head distribution for three scenarios of sudden fall in streams level is presented as well.

Several examples are provided to investigate the effects of anisotropy (\(K_{y} < K_{x}\)) on hydraulic head and flow rate. The following pertinent conclusions are drawn:

  • It is shown when the rates of the north and south streams are more than those of the other streams, the hydraulic head for isotropic aquifer is less than that for anisotropic aquifer and when the rates of the west and east streams are more than that of the other streams, the hydraulic head for isotropic aquifer is more than that for anisotropic aquifer.

  • The hydraulic head in an anisotropic aquifer is more sensitive to changes in rates of the east and west streams and less sensitive to changes in rates of the north and south streams than that in an isotropic aquifer.

  • Furthermore, it is demonstrated that an isotropic aquifer provides more water exchange at the interfaces than an anisotropic aquifer. An anisotropy ratio of \(\alpha = 3\) reduced the average of the dimensionless values of flow rate at boundaries about 0.425, 0.09, 0.425 and 0.09 for cases 1 to 4, respectively. In other words, neglecting anisotropy of the aquifer leads to overestimate the flow rate at interfaces.

In this research, we showed the significance of consideration of the rates of the streams when dealing with anisotropic aquifers. Actually, the hydraulic conductivity is a controlling parameter in determination of flow direction in the aquifer. This parameter shows that the aquifer is how and how much sensitive to each stream. Finally, it can be stated that neglecting the effects of anisotropy causes to wrongly predict the flow path line, and as a result, the researchers will be misled in estimation of travel time and contaminant distribution in the aquifer.

The main applicability of the new analytical solutions is to investigate interactions between stream and aquifer. These new analytical solutions can also be used to evaluate aquifer response to gradual and sudden drop in stream stage. Also, the derived new analytical solutions could be used inversely to find the aquifer parameters. It can be mentioned that the presented new analytical solutions could further be used in many practical problems in stream–aquifer systems. Furthermore, it could be utilized for the validation of experimental and numerical models. Also, the results of the present new analytical solutions obtained will enable a better understanding regarding the modeling of the interaction between the river and the aquifer. Therefore, this research is a contribution to a better understanding of the fluxes between the river and the aquifer. Finally, the current study contributes to overcome common weaknesses of model applications, fulfills gaps in the existing literature and highlights the importance of the modeling process in planning sustainable management of groundwater resources.

The novelty of this paper is evaluating the anisotropy effects on groundwater hydraulic head as well as flow rate in a confined aquifer in contact with varying level boundaries. Therefore, a set of new analytical expressions are obtained by means of the Laplace and Fourier transforms and the solutions applicability is shown by the help of hypothetical examples.