Introduction

The presence of toxic non-degradable heavy metals in the ecosystem, even at trace levels, presents a serious environmental health hazard (Khani et al. 2010; Gupta and Nayak 2012). Chromium may exist in several oxidation states in the environment. The hexavalent and trivalent oxidation states are the most stable in the environment. Trivalent chromium [Cr(III)] is an essential micronutrient found naturally in rocks, plants and soil, while hexavalent chromium [Cr(VI)] is rarely found in nature and is toxic (Gardea-Torresdey et al. 2000). The main sources of Cr(VI) in drinking water are of anthropogenic origin including discharges or leakages from steel and pulp mills, and from a number of industries including: paint and pigments, textile, electroplating, canning, chrome plating, leather tanning, cement dyeing and erosion of natural deposits of chromium (III) (Parvathi and Nagendran 2007).

Conventional methods including adsorption by various sorbents (Gupta et al. 2015), biosorption (Moussavi and Barikbin 2010), reduction (An et al. 2014), solvent extraction (Pagilla and Canter 1999), reverse osmosis (Lin et al. 2014) and ion exchange (Pehlivan and Cetin 2009) have been reported for chromium removal. Reduction–precipitation is the most commonly used technique for removal of Cr(VI), particularly at the industrial scale (Gupta et al. 2010). However, it is expensive as it requires large amounts of chemicals, a large piece of land and produces large quantities of chemical sludge that require skilled operators to deal with it (Gupta et al. 2010). Ion exchange is considered as an alternative; however, it too is expensive and is characterized by poor selectivity for Cr(VI) ions (Altun and Pehlivan 2012).

Biomaterials derived from agricultural waste have received much attention by researchers seeking to develop low-cost and efficient materials for adsorption of pollutants (Miretzky and Cirelli 2010; Gupta et al. 2015). Biomaterials have been used for the removal of various pollutants (Gupta et al. 2015) including dyes (Mittal et al. 2010; Dawood and Sen 2012), lead (Pholosi et al. 2013), zinc (Paduraru et al. 2015), cadmium (Gupta and Nayak 2012). Such waste materials are basically made up of lignin, cellulose and hemicellulose which usually account for exchange and complexation properties of this class of adsorbents (Ofomaja and Ho 2007). Although these adsorbents have shown promising results for the removal of pollutants from wastewater, there are still limitations encountered in their use including their low uptake capacity when used in the raw form and the release of organic components leading to a high chemical and biological oxygen demand and total organic carbon (Abdolali et al. 2014). To overcome these limitations, lignocellulosic materials are usually chemically activated to improve their properties and performance using several types of chemical reagents including basic solutions such as sodium hydroxide, calcium hydroxide and sodium carbonate and inorganic acid solutions such as hydrochloric acid, nitric acid, sulfuric acid, tartaric acid, citric acid and thioglycollic acid (Ngah and Hanafiah 2008).

Chemical treatment of biomaterials does not only aid the extraction of soluble organic compounds from lignocellulosic materials thereby enhancing chelating efficiency, but also modifies the surface chemical properties of the final product. Djilali et al. (2012) observed that NaOH treatment of timber sawdust not only permitted the extraction of hemicelluloses and most of the lignin but also allowed the conversion of the polyol structure into a negatively charged cellulose-based material. Dawood and Sen (2012) treated pine cone biomass with HCl and observed that while the surface area increased, the mean particle size decreased when compared to the untreated samples. Therefore, treatment of lignocellulosic materials with an acid or basic solution will not only modify the chemical composition of the material but also lead to the formation of new functional groups via hydrolysis or saponification of existing chemical compounds (Marshall and Johns 1996; Dhakal et al. 2005; Lu et al. 2009).

South Africa is the fourth largest producer of chromium in the world. It has a chromium reserve of over 200,000 tonnes and produced 11,000 tonnes in 2011 (Dhal et al. 2013). Chromium(VI) is known for its toxicity and carcinogenicity and has a tolerance concentration limit of below 0.1 mg L−1 for discharge into land surface water and 0.05 mg L−1 for potable water (WHO 1993). Chromium mining operations lead to the discharge of large volumes of effluent water containing chromium ions on a daily basis. Among the several methods that can be used for the removal of pollutants in effluents, adsorption methods using agricultural waste materials have gained popularity (Ofomaja and Ho 2007; Miretzky and Cirelli 2010; Gupta and Nayak 2012; Abdolali et al. 2014). However, there is a need to develop cheaper and more effective adsorbent materials for the removal of chromium from our water sources.

South Africa is the third largest producer of Macadamia in the world after Australia and Hawaii (Mogala 2014). As the growth rate of Macadamia plantations steadily increases so also is the accumulation of Macadamia shells (Moodley et al. 2007; Mogala 2014). There appears to be no real use for waste Macadamia shells except for road compaction in farms and as a source of heat.

This paper explores the application of Macadamia shells for producing a cheaper and more effective adsorbent for removal of Cr(VI) ions from aqueous solutions. In addition, this study will also determine the effect of an acid and base treatment on the adsorption properties of Macadamia shells and how these treatments affect its ability to remove Cr(VI) from solution.

Materials and methods

Chemicals and materials

Sodium hydrogen carbonate, sodium carbonate, sodium hydroxide, hydrochloric acid, sulfuric acid, potassium nitrate and potassium dichromate were purchased from Merck Chemical Co. (Johannesburg, South Africa). All the solutions were prepared with ultrapure water from LaboStar equipment by Siemens (Warrendale, PA). All chemical reagents used were of high purity analytical grade. 1,5′-Diphenylcarbazide was purchased from Sigma-Aldrich (Johannesburg, South Africa). Dried K2Cr2O7 was used to prepare a Cr(VI) stock solution of 1000 mg L−1 in ultrapure water. Working solutions were prepared from serial dilutions of the stock solution. Macadamia nutshells were supplied by Eastern Produce Estates—SA (Pty) Ltd (Louis Trichardt, South Africa).

Characterization of Macadamia nutshells

The elemental composition of the raw and modified Macadamia nutshells was performed with a Thermo Flash 2000 series CHNS/O Organic Elemental Analyzer. The morphological evaluation of raw and modified Macadamia nutshells was done with a scanning electron microscope and energy-dispersive X-Ray spectrometer (SEM–EDS) from FEI Nova NanoLab FIB/SEM (Milpitas, CA). Thermogravimetric analysis (TGA) was performed with a PerkinElmer STA 600 Simultaneous Thermal Analyzer (Waltham, USA). The infrared absorption spectra were obtained with a PerkinElmer Spectrum 400 FT-IR/FT-NIR spectrometer (Waltham, USA). Batch adsorptions of Cr(VI) onto adsorbents were performed on a Multichannel stirrer MS-53 M model Jeio Tech (Seoul, Korea).

Experimental methods

Macadamia homogenization (sample preparation)

Macadamia nutshells were washed thoroughly with deionized water to remove the dirt and then dried in the vacuum oven at 105 °C overnight. The shells were crushed and ground to a fine powder and then sieved through a pore size of between 90 and 150 µm. This sample was labeled as the raw Macadamia nutshells (RMN). Part of RMN sample was divided into two parts: One part was treated with 0.1 M HCl (stirred for 3 h) to remove all the nutrients from the shells and labeled acid-treated Macadamia nutshells (ATMN). The other part was treated with 0.1 M NaOH (stirred for 3 h) and was labeled base-treated Macadamia nutshells (BTMN). ATMN and BTMN were washed with deionized water through a funnel until the water coming out of funnel was neutral. The samples were then dried in a vacuum oven at 105 °C overnight.

Bulk density determination and surface area measurement

The bulk densities of the RMN, ATMN and BTMN powdered samples were determined by slowly transferring quantities of the samples into pre-weighed empty 25 cm3 density bottles. During transfer of the samples, the bottles were tapped gently to ensure that the particles settled at the bottom and that void spaces were eliminated. The surface area measurements were obtained from a Micromeritics Flow Prep 060 from Tristar instrument employing nitrogen adsorption/desorption isotherms at −196 °C.

Determination of surface negative charge using Boehm method

The total negative charge on the surface of the Macadamia powder was determined by using the modified Boehm (1994) method. Pholosi et al. (2013) stated that the ‘total’ negative charge could only be determined accurately on samples with a pH <3. Subsequently, samples of RMN, ATMN and BTMN were soaked in 0.1 M HCl to bring the pH of the materials to below pH 3. The acidified samples were filtered and dried in an oven. One and half grams of Macadamia powder (RMN, ATMN or BTMN) was transferred into separate stoppered Erlenmeyer flasks, and 25 mL of 0.10 M NaOH was added and the contents were stirred at 300 rpm for 16–20 h. The contents of the flasks were filtered under vacuum through a Whatman #4 filter paper. Thereafter, 10 mL of the filtrate was added to 15 mL of 0.10 M HCl solution in the flask. The addition of excess HCl to the filtrate was done to prevent possible adsorption of carbon dioxide by the base and was necessary since the solutions were required to stand for extended time periods before analysis (Pholosi et al. 2013). Few drops of phenolphthalein indicator were added to each flask, and the solutions were titrated with 0.1 M NaOH until an endpoint was achieved. The results were expressed in mmoles H+ neutralized by excess OH− per gram of Macadamia powder.

Optimization of adsorption parameters

Parameters influencing Cr(VI) adsorption onto RMN, ATMN and BTMN were investigated. The parameters studied were the effect of initial solution pH (2–9), initial concentration (25–300 mg L−1), stirring time (10–600 min) and sorbent dosage (0.05–0.5 g). All the experiments were conducted in duplicate. After adsorption, the Macadamia nutshell powder was removed from the solution by filtration through a Whatman #4 filter paper and the un-extracted (un-adsorbed) concentration of Cr(VI) was measured at a wavelength of 540 nm with a UV–visible spectrometer (T80+, PG Instruments) with 1,5′-diphenylcarbazide as a complexing agent in acidic medium (Greenberg et al. 1992). In an acidic medium, diphenylcarbazide reacts with Cr(VI) to produce a Cr(III)–diphenylcarbazone complex as indicated by the expression below (Pehlivan and Cetin 2009). Total chromium was measured using an atomic absorption spectrophotometer AA-7000 from Shimadzu (Kyoto, Japan).

$$2{\text{Cr}}_{2} {\text{O}}_{4}^{2 - } + 3{\text{H}}_{4} {\text{L}} + 8{\text{H}}^{ + } \to {\text{Cr}}\left( {\text{HL}} \right)_{2}^{ + } + 3{\text{Cr}}^{3 + } + {\text{H}}_{2} {\text{L}} + 8{\text{H}}_{2}$$

where H4L is 1,5-diphenylcarbazide and H2L is diphenylcarbazone.

The removal efficiency of Cr(VI) (% removal) and the maximum binding capacity (q e , mg g−1) of the sorbents were calculated using Eqs. 1 and 2, respectively.

$$R \left( \% \right) = \frac{{\left( {C_{o} - C_{e} } \right)}}{{C_{o} }} \times 100$$
(1)
$$q_{e} = \frac{{V\left( {C_{o} - C_{e} } \right)}}{m}$$
(2)

where C o is the initial concentration of Cr(VI) in (mg L−1) and C e is the concentration of Cr(VI) in solution after adsorption (mg L−1), q e is the adsorbed Cr(VI) (mg g−1 adsorbent) on the sorbent, m is the weight of sorbent (g) and V is the volume of metal solution (L).

Adsorption isotherms and kinetic modeling

In order to relate the concentration of the adsorbate in the liquid and the amount adsorbed on the sorbent surface, several models are used to describe the phenomena (Langmuir 1918; Freundlich and Helle 1939; Redlich and Peterson 1959). In this study, four models Langmuir, Freundlich, Redlich–Peterson and Sips were used in their nonlinear forms. The Langmuir model assumes a monolayer coverage of a homogenous adsorbent surface by the adsorbate (Langmuir 1918), and Langmuir isotherm equation is given below.

$$q_{e} = \frac{{q_{\text{m}} bC_{e} }}{{(1 + bC_{e} )}}$$
(3)

where b the Langmuir isotherm constant (L mg−1), q m is the maximum metal uptake (mg g−1), q e and C e as previously described. The dimensionless parameter, R L , also known as the equilibrium parameter or separation factor given by Eq. 4 (Webber and Chakkravorti 1974) was calculated and used to interpret adsorption conditions from the Langmuir isotherm.

$$R_{L} = \frac{1}{{\left( {1 + bC_{o} } \right)}}$$
(4)

The R L parameter gives information on the nature of adsorption, where 0 < R L  < 1 is regarded as favorable adsorption, R L  > 1 is unfavorable, R L  = 0 is irreversible and R L  = 1 implies linear adsorption (Webber and Chakkravorti 1974). The Freundlich model relates the sorption of an adsorbate to heterogeneous surfaces, and it assumes a multilayer adsorption (Freundlich and Helle 1939). The equation is given below.

$$Q_{e} = K_{\text{F}} C_{e}^{1/n}$$
(5)

where K F is the Freundlich constant [(mg g−1)/(mg L−1)1/n] and n F the Freundlich exponent describing biosorption capacity and biosorption intensity, respectively.

The Redlich–Peterson model is a three-parameter Langmuir–Freundlich hybrid isotherm with linear dependence on the concentration in the numerator and exponential function in the denominator (Ng et al. 2002). The nonlinear form equation is supplied below (Redlich and Peterson 1959).

$$q_{e} = \frac{{K_{\text{rp}} C_{e} }}{{(1 + a_{\text{rp}} C_{e}^{g} )}}$$
(6)

where k rp (L g−1) and a rp (L mg−1)g are equilibrium constants and g is the Redlich–Peterson model exponent. As g tends to zero, the model describes Freundlich, and as g gets closer to 1, the model describes Langmuir isotherm.

Sips is a combined form of Freundlich and Langmuir isotherm equations and can be expressed as in Eq. 7

$$q_{e} = \frac{{q_{\text{ms}} \cdot K_{\text{s}} \cdot C_{e}^{\text{ms}} }}{{(1 + K_{\text{s}} \cdot C_{e}^{\text{ms}} )}}$$
(7)

where q ms (mg g−1) and k s (L mg−1)ms are Sips adsorption capacity and equilibrium constant, respectively. The Sips model translates to Langmuir when ms = 1 and to Freundlich when ms approaches zero.

Several kinetic models are used to investigate the processes controlling biosorption of adsorbate as well as the rate of mass transfer. Pseudo-first order (PFO), pseudo-second order (PSO) and Elovich models were employed to fit the experimental data. The equations for the models in their nonlinearized form are supplied below.

The PFO rate equation (also, known as Lagergren equation) and the PSO kinetic model (Ho and McKay 1999) are represented in Eqs. 8 and 9.

$$q_{t} = \, q_{e} \left( {1 - \exp_{1}^{ - kt} } \right)$$
(8)
$$q_{t} = \frac{{tk_{2} \cdot q_{e}^{2} }}{{(1 + k_{2} tq_{e} )}}$$
(9)

where q t (mg g−1) is the metal ion uptake at time t, k 1 (min−1) is the PFO rate constant of biosorption and k 2 [g (mg min)−1] is the PSO rate constant of biosorption.

The Elovich kinetic model represented by Eq. 10 describes the chemisorption of adsorbates on solid surface without desorption of products.

$$q_{t} = \frac{1}{\beta } \left( {{\text{Ln}}\left( {\alpha \beta } \right) + {\text{Ln}}t} \right)$$
(10)

where α (mg g−1 min−1) and β (g mg−1) are the initial adsorption rate and the desorption constant, respectively.

Results and discussion

Material characterization

Plant materials contain, among other components, pigments, resin acids, lignin, sugars, alkaloids and water soluble tannins (Wartelle and Marshall 2000). During treatment of plant materials with aqueous basic or acidic solutions, parts of the components are extracted from the plant material leaving behind void spaces (Ofomaja et al. 2010). In addition, hydrolysis of condensed functionalities may occur, particularly in the case of a base extraction, and this process may result in the formation of a more negatively charged surface (Lu et al. 2009; Dawood and Sen 2012). The void spaces act as channels for metal uptake. Therefore, as more components are extracted, the larger the void spaces and the lower is the bulk density. However, this process also decreases the number of available adsorption sites on the material and therefore the reactions must be controlled. Treatment of Macadamia nutshell sorbents with HCl and NaOH produced different results on the amount of cellulose and hemicellulose extracted. NaOH led to the extraction of most hemicellulose components (Table 1).

Table 1 Characteristics of adsorbents used in this study
Full size table

The bulk densities for RMN, ATMN and BTMN obtained were 0.612, 0.584 and 0.574 g cm−3, respectively (Table 1). RMN had a higher bulk density than ATMN and BTMN. The percentage decrease in bulk density after treatment with 0.1 M NaOH and 0.1 M HCl was 6.2 and 4.6 %, respectively. More extractives were removed by treatment with NaOH, implying that Macadamia contains more base-soluble extractives (hemicellulose fraction) than those that are acid soluble. A much higher percentage decrease of 31.0, 36.4 and 60.1 % in bulk density has been reported when corn cob, soybean hull and almond hull were treated, respectively, with 0.1 M NaOH for 1 h (Wartelle and Marshall 2000). The lower values obtained with Macadamia could be due to inefficient extraction process or that Macadamia does not contain a high percentage of extractives that could be removed by either acid or basic treatment. The surface area of RMN, ATMN and BTMN was 0.018, 0.065 and 0.546 m2 g−1, respectively. These values were comparable to other waste materials as reported in the literature (Basal et al. 2009).

Determination of the surface negative charge (e.g., carboxylic groups) is important to ascertain the potential suitability of natural materials for adsorption of metal ions. The surface negative charge values for RMN, ATMN and BTMN were 2.39, 2.35 and 6.67 mmol g−1, respectively. These results suggest that Macadamia has a low carboxylic content. No major difference between the RMN and ATMN surface negative charge values was observed. BTMN exhibited the highest surface negative charge of 6.67 mmol g−1 which can be attributed to the formation of ionic groups during hydrolysis (Lu et al. 2009; Dawood and Sen 2012) and the higher percent of hemicellulose extracted leading to the formation of negatively charged cellulose-based materials (Table 1).

Elemental analysis of RMN, ATMN and BTMN

Table 1 also shows the percent of C, H, N, O and ratio of O/C (atomic) for RMN, ATMN and BTMN. The percentage of oxygen was obtained by difference. The results of the elemental analysis showed that RMN, ATMN and BTMN were mainly composed of carbon, hydrogen and oxygen. A similar composition was reported for other lignocellulosic compounds such as walnut shells (Altun and Pehlivan 2012). The O/C ratio was lowest for ATMN and could imply that acid treatment had a high affinity for oxygen-containing groups.

Fourier transform infrared (FTIR) spectra and thermogravimetric analysis (TGA)

Figure 1a–c displays the FTIR spectra of RMN, ATMN and BTMN before and after adsorption of Cr(VI). The RMN, ATMN and BTMN spectra before adsorption showed similar characteristics except for differences caused by the treatments. The notable differences (deformations, intensities and shifts) in RMN, ATMN and BTMN before adsorption were observed at the following wavenumbers, 3339, 2925, 1740, 1452, 1241 and 1026 cm−1. These could be attributed to the presence of hydrogen-bonded hydroxyl (OH) groups due to the cellulose structure (Zhao et al. 2013), aliphatic (C–H), carboxyl group (C=O), methoxyl (C–O–CH3), hydroxyl (C–OH) bending of phenolic structure in lignin (Yang et al. 2007) and –C–O functional groups, respectively. The band intensity at 2925 cm−1 decreased in the order RMN > ATMN > BTMN suggesting that the base extraction removed more aliphatic compounds from the lignin structure. Lu et al. (2009) also observed that alkaline pretreatment of orange peel caused a degradation of cellular compounds. The spectra of RMN, ATMN and BTMN before adsorption were further characterized by an asymmetric broad band at 1637 cm−1 ascribed to the presence of carboxylate groups (Yang and Chen 2008; Bermudez et al. 2012). The broad band at 1637 cm−1 decreased in intensity and split into two bands after Cr(VI) loading signifying its involvement in Cr(VI) removal in all three sorbents. The shape of the splits in RMN and ATMN were similar but different to that of BTMN, an indication that the latter has slightly different surface characteristics. In addition, the decrease in intensities and shapes of the band at 1455 cm−1 in all three materials implied that the methoxyl group was also involved in Cr(VI) removal. Similar observations were reported in the literature where the changes in intensities and shifts of absorption bands at 1637, 1454 and 1244 cm−1 were attributed to oxidation of lignin when contacted by Cr(VI) ions (Yang et al. 2007; Albadarin et al. 2011), resulting in reduction of Cr(VI) to Cr(III). The differences observed in FTIR spectra of RMN, ATMN and BTMN before and after adsorption of Cr(VI) confirm participation of functional groups in the removal of Cr(VI) by the materials.

Fig. 1
figure 1

FTIR spectra of RMN (a), ATMN (b) and BTMN (c) before and after Cr(VI) biosorption

Full size image

Thermogravimetric analysis (TGA) of RMN, ATMN and BTMN was conducted to evaluate the change in percentage weight as a function of temperature (Fig. 2). Thermal degradation of plant biomass can be categorized into four successive individual stages, namely moisture evolution, and the decomposition of hemicelluloses, cellulose and lignin (Paduraru et al. 2015). The first stage of percentage weight loss occurred at about 120 °C estimated at 12, 2 and 3 % for RMN, ATMN and BTMN, respectively, was ascribed to evaporation of absorbed water. The higher %weight loss for RMN can be attributed to the hemicellulose content of the material. The amount of adsorbed water in plant material is a measure of the hydrophilic components in its structure. The hydroxyl groups of the hemicellulose can associate with water molecules via hydrogen bonding, thereby leading to higher water content (Azwa and Yousif 2013). On treatment of the RMN with acid and base solutions, leaching out of plant components occurred, releasing part of the hemicellulose components into the extracting solvents, thereby reducing the ability of the materials to associate with water molecules. This will account for the lower moisture loss of the treated samples over the RMN sample. The second stage which took place at about 120–310 °C quantified at 16 % (RMN) and 13 % (ATMN) and 24 % (BTMN) was due to loss of volatile compounds (such as CH4, CO2, CO, H2) and hemicellulose degradation (Rangabhashiyam and Selvaraju 2015a). The third stage due to cellulose degradation was observed at about 310–380 °C for RMN (29 %) and ATMN (35 %), but come earlier for BTMN (22 %) at 310–365 °C. The derivative spectra for RMN, ATMN and BTMN are shown in Fig. 2b. ATMN and BTMN showed two distinct decomposition peaks, while RMN had two decomposition peaks (370 °C) and a shoulder. The difference in decomposition peak shapes and decomposition temperatures further emphasized that chemical modification affected the chemical makeup of sorbents (Dhakal et al. 2005). It can then be concluded that chemical extraction produced major changes in the chemical composition of RMN.

Fig. 2
figure 2

Thermogravimetric analysis (a) and derivative weight percent (b), for RMN, ATMN and BTMN

Full size image

The morphology and structure of RMN, ATMN and BTMN were characterized with scanning electron microscope (SEM). The SEM images revealed that the materials consisted of flaky long fold-like structures (Fig. 3a–c), which are typical of plant materials (Zhao et al. 2013). The structural backbone of the materials was not greatly altered since they all retained their flakiness, suggesting that the treatment methods were not excessively harsh to completely destroy the materials. SEM–EDS images confirm that the Macadamia shells consist of C and O as the main elements with no traces of heavy metals except for Au and Pd that originated from the coating used for SEM sample preparation.

Fig. 3
figure 3

Scanning electron microscope and EDS images of RMN (a), ATMN (b) and BTMN (c)

Full size image

Adsorption results

Effect of pH

The uptake of Cr(VI) ion by the RMN, ATMN and BTMN was evaluated at different pH values ranging from 2 to 9, while keeping other parameters constant. The sorption of Cr(VI) by RMN, ATMN and BTMN was favored at acidic conditions and showed a strong dependence on pH as it decreased with increase in pH from 2 to 9 (Fig. 4a). Similar observations have been made in the literature (Deng and Ting 2005; Yang and Chen 2008; Liu and Huang 2011; Ramrakhiani et al. 2011). The percent removal of total chromium at pH 2 was 65, 62 and 50 % for ATMN, RMN and BTMN, respectively. Figure 4b–d shows that at pH 2 some of the Cr(VI) was not adsorbed by the sorbents, but converted to Cr(III). As the pH was raised from 3 to 9, the amount of Cr(III) present in solution decreased, implying that there was less reduction at these pHs. The percent Cr(VI) removal at pH 3–9 also decreased due to electrostatic repulsion by negatively charged hydroxyl ions. Yang and Chen (2008) stated that at strongly acidic conditions and in the presence of materials with electron-donating groups, Cr(VI) can be reduced to Cr(III). Therefore, it can be concluded that Macadamia adsorbents used in this study contained electron-donating groups which were capable of reducing Cr(VI) to Cr(III) in acidic conditions. Cr(VI) is an anionic species which may exist as HCrO4 −, Cr2O7 2−, Cr3O10 2−, Cr4O13 2− or CrO4 − at different pHs and concentrations (Garg et al. 2007). HCrO4 − is the dominant species in acidic conditions due to the hydrolysis reaction of the dichromate ion (Cr2O7 2−) (Basal et al. 2009) and as the pH increases HCrO4 − shifts to Cr2O7 2− and CrO4 2− species (Basal et al. 2009). HCrO4 − was the dominant species at pH 2, and pH 2 was used in subsequent experiments.

Fig. 4
figure 4

Effect of pH on chromium removal by RMN, ATMN and BTMN (a), RMN (b), ATMN (c), and BTMN (d) (conditions: amount of adsorbent 0.2 g; solution volume 25 mL; contact time 2 h; concentration of solution 100 mg L−1)

Full size image

According to Saha and Orvig (2010), there are four mechanisms with which biomaterials may sequestrate Cr(VI) from aqueous solutions, viz., (1) adsorption resulting from electrostatic attraction of anionic Cr(VI) by the biomaterial; (2) adsorption of Cr(VI) followed by complete reduction of Cr(VI) on the surface to Cr(III); (3) anionic Cr(VI) is adsorbed, and other fraction of Cr(VI) is reduced to Cr(III) and subsequently adsorbed on the surface of the biomaterial; (4) part of Cr(VI) is adsorbed, and the other fraction is reduced and released back into solution. Therefore, the mode of removal of Cr(VI) by RMN, ATMN and BTMN can be classified under category 4 (reduction–biosorption process). The amount of Cr(III) released back into solution at pH 2 decreased in the order BTMN > RMN > ATMN. The final pH after adsorption of Cr(VI) by RMN, ATMN, and BTMN was also recorded. The change in pH (pHf − pHi) was plotted versus initial pHi and the point where the graph intersect the X-axis was reported as the pHpzc. The pHpzc values obtained for RMN, ATMN and BTMN were 6.25, 6.42 and 6.70, respectively. For all three materials, the final pH was higher than the initial pH when the initial concentration was lower than 6.25, 6.42 and 6.70 for RMN, ATMN and BTMN, respectively, and this was attributed to exhaustion of H+ during oxidation process (Sun et al. 2013). Adsorbents that can effectively reduce Cr(VI) to Cr(III) followed by immobilization of Cr(III) onto the sorbents are sought after and development of such adsorbents could be a breakthrough in dealing with Cr(VI) contamination (Deng and Ting 2005). However, the intrinsic complexity of biomaterials still makes it difficult to fully understand the reaction parameters affecting the reduction-sorption process (Deng and Ting 2005) even though some complexing groups (for Cr(III)) and redox active centers for Cr(VI) reduction could be deduced (Liu and Huang 2011).

Effect of concentration

Figure 5 shows the effect of concentration on the adsorption of Cr(VI) by Macadamia nutshell powder. The calculations revealed that almost 100 % of Cr(VI) removal was achieved at low concentrations (25–100 mg L−1) for all three sorbents (data not shown). When the concentration was increased from 100 to 300 mg L−1, the percent removal of Cr(VI) decreased to about 40 % for all materials, while adsorption capacities increased with increase in concentration. The decrease in sorption of Cr(VI) at high concentration was due to the saturation of active binding sites (Basal et al. 2009; Gupta and Rastogi 2009). The results of adsorption capacity (mg g−1) versus initial concentration are plotted in Fig. 5. The maximum calculated binding capacities (q e ) obtained at 200 mg L−1 for RMN, ATMN and BTMN were 42.53, 40.60 and 37.49 mg g−1, respectively. Equilibrium concentration and adsorption capacity results were fitted in different sorption isotherms.

Fig. 5
figure 5

Effect of initial concentration (condition: solution concentration 100 mg L−1; amount of adsorbent 0.2 g; solution volume 25 mL; pH 2; contact time 10 h)

Full size image

Biosorption equilibrium studies

Table 2 shows Langmuir, Freundlich, Sips and Redlich–Peterson isotherm constants obtained after fitting equilibrium concentration and adsorption capacity values into the models. Nonlinear forms of the models equations were used to plot the data using KyPlot 2.0 software (quasi-Newton algorithm). The Langmuir model biosorption capacities (q m ) were 45.23, 44.83 and 42.44 mg g−1 for RMN, ATMN and BTMN, respectively. The Langmuir equilibrium constant increased from 0.109 to 0.235 L mg−1 in the order ATMN < BTMN < RMN, implying that Cr(VI) formed stronger bonds with RMN and BTMN.

Table 2 Parameters of adsorption isotherm models for Cr(VI) sorption
Full size table

The Freundlich K F values obtained for RMN, ATMN and BTMN were 13.86, 10.48 and 9.71, respectively (Table 2). The calculated n F values were larger than unity, giving 1/n F values between 0 and 1, indicating favorable biosorption in this order RMN > ATMN > BTMN.

The Redlich–Peterson model which best describes the biosorption process over a wide range of concentrations was evaluated and showed that the Redlich–Peterson constants k rp and a g increased in the order RMN, BTMN and ATMN. This is different from what has been observed with previous models. The exponent g values were closer to 1, which implied a homogenous coverage consistent with the Langmuir model. The adsorption capacities obtained from the Sips model were 43.69, 40.42 and 39.77 mg g−1 for RMN, ATMN and BTMN, respectively. This trend is consistent with the Langmuir model capacities. The Sips adsorption capacities were closer to the experimental values. The Sips exponent (ms) values were 1.215, 1.908 and 1.345 for RMN, ATMN and BTMN, respectively. Two of these values are close to one which showed that Sips approached Langmuir for RMN and BTMN. This could be supported by the differences in the respective adsorption capacities from the Langmuir and Sips model observed for the corresponding samples, 1.54, 2.67 and 4.41 for RMN, BTMN and ATMN, respectively. The bigger the difference in q m , the lesser the models converge. In this case, the Sips result of the RMN and BTMN described Langmuir better than ATMN. Since the data in Table 2 could not be described perfectly by any model studied, the overall mechanism for Cr(VI) removal by Macadamia could be described as a complex involving complexation, ion exchange, reduction and/or electrostatic interaction. Similar deductions were made in the literature (Ramrakhiani et al. 2011). Treatment with NaOH and HCl in this case led to a decreased efficiency due to the removal of active functional groups.

Table 3 shows the actual R L values obtained from Eq. 5. All the values are between 0 and 1, implying favorable adsorption of Cr(VI) by RMN, ATMN and BTMN. The R L values for RMN were closer to zero, which further indicated that the adsorption was likely irreversible (implying stronger bonds between adsorbate and adsorbent or that Cr(VI) was changed to a different form (Cr(III) by reduction), while those of ATMN and BTMN were closer to 1 which implied a linear adsorption. The Chi-square, χ 2, statistic test described by Eq. 12 measures the sum of the squares of the difference between the experimental adsorption capacity (q e ) and q m predicted using models, each divided by the corresponding q m .

$$X^{2} = \sum {\frac{{q_{e} - q_{\text{m}} }}{{q_{\text{m}} }}}$$
(12)
Table 3 Langmuir separation factor for biosorption of Cr(VI) onto RMN, ATMN and BTMN
Full size table

If χ 2 is small, it implies that the experimental data were closer to the model results and if χ 2 is large, the results are far apart. According to this explanation, the models did fit the experimental results in the order Redlich–Peterson > Sips > Langmuir > Freundlich.

Table 4 shows the comparison of adsorption capacities from different biosorbents. A direct comparison of sorbents is not totally possible due to different treatment methods and experimental conditions used. The Macadamia nutshell powdered materials investigated here had comparable biosorption capacities to other sorbents used for Cr(VI) removal. The Langmuir model biosorption capacities (q m ) were 45.23, 44.83 and 42.44 mg g−1 for RMN, ATMN and BTMN, respectively.

Table 4 Comparison of binding capacities
Full size table

Effect of contact time

Figure 6 shows the adsorption capacity of RMN, ATMN and BTMN as a function of time. Contact time was varied from 10 to 600 min. It was observed that between 10 and 200 min the uptake of Cr(VI) was almost linear, implying faster removal kinetics due to the concentration gradient created by the large number of available adsorption sites (Albadarin et al. 2011). From 200 to 600 min, the uptake slowed down, as shown by the curvelinear part of the graph. After 600 min, all three materials reached equilibrium for adsorption, suggesting that optimum removal was achieved at 600 min for all three materials. Therefore, 600 min was used in subsequent experiments. The longer equilibration time (600 min) attained was attributable to the materials having deeper embedded adsorption sites that were not easily accessible or that the surface of the materials was slightly hydrophobic causing repulsion of Cr(VI).

Fig. 6
figure 6

Effect of contact time on RMN, ATMN and BTMN (conditions: amount of material 0.2 g; solution volume 25.0 mL; solution time 10–600 min; initial concentration of solution 100 mg L−1)

Full size image

The PFO, PSO rate models and Elovich model were utilized to study the time dependence of Cr(VI) sorption onto Macadamia particles. Table 5 shows the results obtained by fitting the experimental values to the different models. The qe values for the PSO model were closer to the q t values for RMN, ATMN and BTMN than PFO q e and q t values. Using R 2, χ 2 and MSq, one can conclude that the chemisorption process was better defined in ATMN, BTMN and RMN in that order. The Elovich adsorption rate α (mg g−1 min−1) and desorption constant β (g mg−1) decreased from 3.318 to 1.060 mg g−1 min−1 and 0.280–0.240 g mg−1, respectively. It can be deduced that RMN had a higher driving capacity for adsorption of Cr(VI). This may be due to the presence of reduction groups on the surface or the crystalline cellulose which increased water retention capacity of RMN. The observations from Elovich were consistent with what was predicted by adsorption models, supporting the RMN > ATMN > BTMN order for the removal efficiency of Cr(VI).

Table 5 Comparison of kinetic models
Full size table

Sorbent mass

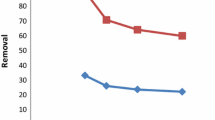
Figure 7 shows the adsorption capacity as a function of adsorbent mass. Cr(VI) removal efficiency for all three sorbents increased rapidly while increasing the mass from 0.05 to 0.50 g. The higher the dose of adsorbent, the greater is the surface area and greater is the number of available adsorption and/or reduction sites present for metal ion uptake (Azwa and Yousif 2013). Thereafter, all sorbents seem to attain saturation at about 95 % removal efficiency (0.2–0.5 g) as the number of active sites decreases. Hence, optimum Cr(VI) removal (95 %) was achieved with 0.2 g sorbent mass and this was used for subsequent studies.

Fig. 7
figure 7

Effect of dosage (conditions: solution concentration 100 mg L−1; initial pH 2; solution volume 25 mL; contact time 10 h)

Full size image

Reusability studies

Natural adsorbents based on agricultural waste are advocated as cost-effective sorbents. Therefore, it is important to investigate their reusability over cycles of adsorption–regeneration process. In this case, RMN, ATMN or BTMN (0.2 g) were placed in separate reaction vessels containing a Cr(VI) solution (100 mg L−1) and stirred for 10 h. Particles were removed by centrifugation and desorbed with a 0.1 M NaOH solution (10 mL). Figure 8 shows that all three sorbents investigated could be used more than once with recoveries of greater than 80 %. The decreased recoveries especially with RMN could be attributed to modification of the surface during Cr(VI) leaching by NaOH solution.

Fig. 8
figure 8

Adsorption–desorption cycles (conditions: solution concentration 100 mg L−1; initial pH 2; solution volume 25 mL; contact time 10 h)

Full size image

Conclusions

Three forms of Macadamia nutshell biosorbents viz., raw, acid-treated and base-treated were evaluated for adsorption of Cr(VI) from aqueous solution in batch mode. NaOH treatment (BTMN) gave a higher percent extraction of hemicellulose fraction that affects its Cr(VI) removal efficiency. The adsorbent materials were characterized by FTIR, SEM and TGA. The FTIR spectra before and after adsorption of Cr(VI) revealed significant changes in the region of 1637 and 1455 cm−1 which were attributed to the participation of carboxylate and methoxyl groups, respectively, in the removal of Cr(VI). SEM images revealed that ATMN and BTMN had retained the flaky structural backbone observed in raw Macadamia, implying that the treatment procedures were not excessively harsh to destroy the structure of materials. The optimal operating conditions for removal of Cr(VI) were found to be at pH 2, concentration 100 mg L−1, adsorbent mass 0.2 g and initial contact time of 10 h, indicating that adsorption is strongly dependent on the mentioned parameters. The maximum binding capacities obtained for RMN, ATMN and BTMN were 45.2, 44.8 and 42.4 mg g−1, respectively. It was also demonstrated that the prepared materials can be recycled more than once with removal efficiencies greater than 80 %. The presence of electron-donating groups on RMN, ATMN and BTMN facilitated the anionic adsorption–reduction mechanism. The mode of adsorption for all three sorbents investigated could not be described by a single model due to complex processes involved. It was found that the acid and base treatments of Macadamia adsorbents decreased the percent removal of Cr(VI) due to extraction of electron donor groups from RMN. However, when comparing the adsorption capacities in Table 4 with other biomaterials, it can be concluded that Macadamia nutshells are good sorbents for the removal of Cr(VI) from aqueous solutions.