Abstract
In 1966 Richard Levins argued that applications of mathematics to population biology faced various constraints which forced mathematical modelers to trade-off at least one of realism, precision, or generality in their approach. Much traditional mathematical modeling in biology has prioritized generality and precision in the place of realism through strategies of idealization and simplification. This has at times created tensions with experimental biologists. The past 20 years however has seen an explosion in mathematical modeling of biological systems with the rise of modern computational systems biology and many new collaborations between modelers and experimenters. In this paper I argue that many of these collaborations revolve around detail-driven modeling practices which in Levins’ terms trade-off generality for realism and precision. These practices apply mathematics by working from detailed accounts of biological systems, rather than from initially idealized or simplified representations. This is possible by virtue of modern computation. The form these practices take today suggest however Levins’ constraints on mathematical application no longer apply, transforming our understanding of what is possible with mathematics in biology. Further the engagement with realism and the ability to push realistic models in new directions aligns well with the epistemological and methodological views of experimenters, which helps explain their increased enthusiasm for biological modeling.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In a paper titled ‘‘The Strategy of Model Building in Population Biology’’ Levins (1966) famously characterized mathematical applications to mathematical ecology and population biology as bound by several unavoidable constraints given biological complexity. No approach could maximize generality, precision and realism simultaneously. Levins’ theory can be used to characterize mathematical applications to biology historically. Many theoretical and mathematical biologists for instance have aspired to generality (often in the form of say fundamental theory) at the expense of realism through practices of idealization and simplification. As Keller (2003) documents such practices have often conflicted with the methodological and epistemological preferences of experimenters and created obstacles to interaction.
However the past 20 years has seen a rapid increase in the mathematical modeling of biological systems through the advent of modern computational systems biology with an uptake in engagement by molecular and other biologists in interdisciplinary modeling with mathematically trained specialists. In the paper I pursue two claims. Firstly, while there are certain continuities within modern systems biology with previous more traditional practices, certain practices are novel. Some of these practices, which I call detail-driven, use computation to facilitate a more brute force replication of biological systems over more subtle idealized or simplified representations of biological phenomena. Levins’ criteria help situate these practices relative to traditional ones in modern systems biology, and in fact can help us attribute divides amongst systems biologists to more basic preferences regarding mathematical application. However detail-driven systems biologists leverage realism into methods which produce potentially novel applications of mathematics some of which, if they work out, would suggest that Levins’ constraints no longer hold on mathematical application. Generality, precision and realism can be obtainable conjointly with respect to particular generalizations, and preferably so. Secondly these detail-driven practices align better with the methodological and epistemological preferences of experimenters and what experimenters generally consider useful and viable goals for modeling. This helps explain to some extent their relative engagement of experimenters with these practices, compared to those of systems biologists working with a more traditional approach.
To achieve these aims in the next section of the paper I give a brief introduction to the structure of contemporary systems biology. In the third section I outline Levins’ criteria on mathematical application, and its use in characterizing various practices in mathematical biology including contemporary systems biology, particularly traditional idealization and simplification-driven practices, and the reactions of experimenters to these both historically and today. In the fourth section we look at detail-driven practices closely; how these are both captured by Levins’ criteria but also potentially move beyond them. I build our understanding here partially by relying on the results of a 4 year ethnographic study of collaborative model-building practices in the fieldFootnote 1 plus systems biologists’ own philosophical reflections on their practices. This ethnographic study of two labs, provided us a first-hand insight into the nature of these practices and how participants in the modeling process rationalize their activity and their involvement.
2 The structure of modern systems biology
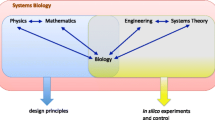
Modern systems biology is remarkably eclectic trying to marry under the common label of “systems biologist” theoretical biologists, (often formally trained in mathematics) committed to more traditional theoretical positions on the purpose and need for a well-developed biological theory, with technology-driven computer scientists and engineers who see an opportunity to enter biology and make substantial new discoveries using new data sources. At the same time practices are diverse with respect to the role and scale of modeling, the role of computation and the role of collaboration and experiment. The field resists any easy demarcations. O’Malley and Dupré however describe modern systems biology as composed of two broad distinct streams – a systems theoretic stream and a pragmatic stream. What unites these two streams is a general commitment to the need to treat a biological systems as fundamental units of analysis and explanation rather than their individual parts. Beyond that however the distances can be substantial. The systems-theoretic stream is characterized by historical relations to a long tradition of theoretical biology which has promoted various systems ideas and concepts as a means to a theoretical account of biological systems, as opposed to a more reductionistic account. Progenitors of these ideas include the cyberneticists, Bertalanffy’s general systems theory, Waddington’s epigenetic landscape theory, and Rashevsky and his student Rosen’s relational biology. Pragmatic systems biologists however do not necessarily harbor any commitment to the theoretical projects of the systems-theoretical systems biologists. Their involvement has been precipitated by the scaling up of data generation (see genomics), and the affordance of modern computation, which allow this information to be processed into large scale models of systems.
At the same time modeling in systems biology is often divided into two general practices; top-down and bottom-up. Bottom-up practices work to assemble models of systems from the component biological parts such as metabolites or genes and by virtue predict and control or explain various functions of those systems. Pragmatists generally work in this stream. Top-down systems biology on O’Malley and Dupre’s view aims for a “higher” account of biological systems at the outset in terms of the basic laws and principles governing biological systems. Systems-theoretical biologists predominantly practice top-down systems biology. Alternatively however top-down is also used to describe practices of reverse-engineering system structure from high-density data sets. Thus top-down/bottom-up is often just used to distinguish practices within the more pragmatic stream, and ignore somewhat the more traditional stream.
These bottom-up/top-down and theoretic/pragmatic categorizations are neither perfect nor exhaustive. For instance certain systems biologists working within the more pragmatic mode do have an historical and theoretical legacy to draw from, for instance those following Savageau’s approach to metabolic modeling which is grounded in a something like a basic theoretical account of biological systems, one which can be used to guide bottom-up modeling (see e.g. Biochemical Systems Theory; Voit, 2000). But these distinctions do I believe track basic contrasting views on how mathematics can be applied to the modeling of biological systems. Levins’ criteria helps locate these differences with respect to what modelers see as productive trade-offs to make given their goals, at least initially, in the modeling of biological systems.
3 Traditional notions of mathematical applicability in systems biology
Levins’ Framework
Levins’ oft-cited paper on strategies of model building in population ecology is one of the more influential attempts to position and compare mathematical practices. Levins’ concern is the problem of how to approach a complex problem in population biology involving simultaneously “genetic, physiological, and age heterogeneity within species of multispecies systems changing demographically and evolving under the fluctuating influences of other species in a heterogeneous environment.” (421) He argues that in such circumstances no model can maximize generality, precision and reality simultaneously. Hence if the goal is to achieve general mathematical accounts (for the purposes of theory) then one of either precision or realism must be sacrificed in order to handle the complexity of such phenomena. The principal approach in this regard sacrifices realism in favour of precision and generality, through the use of unrealistic equations and assumptions, by setting up initially general equations from which precise (meaning numerically exact) results follow. Modelers working in this tradition never try to represent their phenomena in detail. Rather they start from simplified and idealized representations based on certain theoretical presuppositions and mathematical concepts in which only the most relevant aspects are represented, elements which generally have the capacity to represent multiple similar phenomena. In mathematical ecology the extensive work on Lotka-Volterra equations falls in this category. This methodology, Levins asserts, derives from physics. “These workers hope that their model is analogous to assumptions of frictionless systems or perfect gases. They expect that many of the unrealistic assumptions will cancel each other, that small deviations from realism result in small deviations in the conclusions, and that, in any case, the way in which nature departs from theory will suggest where further complications will be useful. Starting with precision they hope to increase realism. (422)”.
Levins’ own preferred approach is to sacrifice precision to realism and generality, accepting that idealized mathematics is an appropriate approach but favouring representations that can qualitatively represent general trends, rather than starting from simplified models which capture idealized general behaviours in exact terms. Levin’s puts emphasis on models which thus facilitate visual analysis or can be understood in terms of basic inequalities. Understanding derives from tracking the general qualitative properties of systems, rather than mathematical manipulation or formal analysis.Footnote 2
Levins also briefly mentions a third strategy, in which generality is sacrificed for realism and precision, which he ascribes to mathematical ecologists Holling and Watt. Such models are capable of short term predictions of complex ecological system, employing models with numerous precise parameters fed into computers. However Levin’s expresses the view that analytically insoluble equations—ones insoluble in terms of readily interpretable equations—are of little use to scientists since they have “no meaning for us”. This would seem to suggest that Levins held that idealized or simplified approaches should be preferred on grounds of explanation and understanding, against say expanding the Holling and Watt type- approach.Footnote 3 Normatively the most fruitful and preferable applications of mathematics, on the basis of these constraints, should be through working from simplified and idealized representations.
It is possible to associate Levins’ first strand, in which generality is strived for at a cost to realism through idealization and simplification, with many researchers in mathematical biology historically who have often had strong theoretical goals, including those who have played an historical role in the development of the modern systems theoretic stream of systems biology. Keller for instance places much historical importance on Rashevsky and Turing in the history of mathematical biology. Levins ascribes the development of this strand of mathematical application in population biology to physicists moving into the field. Keller likewise thinks Rashevsky and Turing’s approaches largely took the inspiration from the success of using idealization to obtain generality in mathematical approaches in physics. Rashevsky’s practice can be described broadly as follows, to begin from certain theoretical or mathematical hypotheses (including say a principle of parsimony; Hoffman, 2013) which licensed or motivated simplified or idealized representations in place of having to account for, or represent, enormous amounts of detail. In one of his early moves he treated cells as idealized spheres, in another neurons as simple excitatory and inhibitory elements, thus putting to the side an otherwise great deal of complexity at the outset of the investigation. In the former case, as Keller reports, Rashevsky perceived that cell division might be explained in terms of ordinary physical forces involved in cell metabolism, licensing a reductionistic and idealized account of cells as spheres. Confirmation of such a mathematical account would on Rashevsky’s view confirm the original hypotheses and facilitate the identification of the “simplest possible laws of interaction” to explain a system’s behaviour (Shmailov, 2016; 67).
Historically the motivation for this approach may have come from physics but it has not been tied to physical explanations or physics-based explanations. Much of mathematical ecology for instance, such as Lotka-Volterra modeling, which Levins cites, does not operate with physics or chemistry as a starting point, but rather with its own basic hypotheses on population dynamics. Rashevsky himself moved away from physics later in his career without abandoning a strategy of idealization and simplification in his hunt for a theoretical basis for biology (Hoffman, 2013). Historically some systems biologists have explicitly rejected physics based accounts of biological systems in favour of their own systems concepts (see Rosen for instance). But they share the basic approach by preferencing generality (in the form of theory) over realism and pursuing idealized and simplified representations as the starting point for the mathematical investigation of biological systems. Rosen’s relational biology for instance operates on the basis that highly abstract mathematical concepts -in this case categories- can provide a fundamental account of the principles governing biological organization and physiological function independent of any particular physical mechanism or material realization. As such Levins’ framework provides a rough way at least to group a broad range of mathematical approaches historically in the life sciences as sharing a basic approach to mathematical application, even if they differ sometimes substantially in their theoretical presuppositions.
In modern systems biology
For many contemporary systems biologists – those working in O’Malley and Dupre’s systems-theoretic stream –the historical relationships to past mathematical biologists are often direct, and modelers continue practices of trading-off realism for generality by employing idealized and simplified representations as the starting point for mathematical work. There are obvious links to the inheritors of relational biology for instance, as well as others Green labels as taking a “global” approach (Green, 2017). These approaches draw on dynamical systems theory-based landscape accounts of biological systems in order to conceptualize and map biological processes to mathematical features of these landscapes. Fagan (2016) documents for instance the use of dynamical systems modeling in stem cell biology by Huang and others. The models she describes in those cases model simplified basic dynamic interactions between genes (using ordinary differential equations) producing a complicated theoretical account in terms of developmental landscapes. These landscapes map developmental trajectories which represent different pluripotent states of a stem cell. The approach proceeds on the basis that these landscapes, defined by a minimal set of interacting agents, are instructive for the general behavior of stem cells without requiring full representations of entire genetic networks.
Various other topological, graph-theoretic or network accounts of biological organization in modern systems biology might in some cases be similarly understood insofar as they aim at representing general properties or feature of systems by working from initially idealized and simplified representations of their component parts or structure. Krohs and Callebaut (2007) refer to a stream of cybernetic modeling which they call top-down, in which researchers pursue a minimal modeling strategy, searching for, and basing their analysis on the “a model of the lowest possible mathematical complexity which can explain a system’s behavior” (p190). These models apply theories or principles from cybernetics and electrical engineering to do so. As in historical cases such models are constructed largely independently of detailed physical properties of the systems at issue, but can be enriched once such models are developed through closer investigation of the system at hand. They give the Hodgkin-Huxley equations as historical examples. As such while the landscape models and these cybernetic models vary substantially in terms of their mathematical formalisms and principles, they do share a similar approach in their strategy of applying mathematics. Such a strategy would arguably fail if systems were not simplified at the outset, particularly in terms of the ability to recognize and apply the relevant theoretical principles. There is an argument too that topological accounts can also be seen as pursuing something similar, insofar as such approaches pare away details and apply otherwise simplified representations of general systems properties (see Jones, 2014). Similarly systems biologists working on design principles who also operate from basic minimal model accounts, based on an expectation that there is underlying simplicity (parsimony) in biological organization (see Gross, 2019). However in the next section I will suggest however that some of this work does not fit entirely well with the systems-theoretic stream on this analysis given the extent to which such accounts are actually derived from rich accounts and detailed models, and do not trade-off realism in any substantial way. Either way our analysis here, using Levins’ framework, provides some means here of deepening our account of the approach to mathematical application otherwise varied researchers within the systems-theoretic tradition share, despite quite different theoretical backgrounds and motivations.
Relations to experimentation
However regardless of how many modelers could be said both historically and today to fit this generality/precision tradition, it in particular seems to have inspired negative reactions from experimenters and other non-mathematical biologists. The objections Keller identifies to have characterized relations between molecular biologists and mathematicians for much of the 20th can be understood as specific objections the trading off of realism for generality in particular. For example in response to some of Rashevsky’s earlier work, which modeled cells as spheres, Keller documents how biologists rejected explicitly the value of fictional or idealized nature of the models. The experimenters felt essentially that the motivating theory behind Rashevsky’s models was too speculative given both the overwhelming complexity of biology and the limited current state of biological knowledge. Experimenters were not willing to grant any special license to mathematicians to hit upon the right theoretical principles certainly if the only evidence was the ability of a simplified representations to reproduce some general biological behaviors or patterns. They were not happy to accept that broadly accounting for a phenomena was any indication of the truth of the mathematical account. On a deeper level, Keller argues, these concerns also reflect disagreement over what constitutes a good biological explanation. Mathematical biologists have often proposed higher level mathematical properties of mathematical representations, based on for instance stability points, limit cycles or topological structures, as general accounts, in contrast to the experimenter’s preference for causal mechanical explanations based on the discovery of specific causal biological elements and their interactions (Bechtel & Abrahamsen, 2010). From this perspective higher-level general mathematical claims about biological phenomena are unlikely to be considered particularly compelling until they can be extrapolated in terms of particular molecular elements and interactions. As such Turing’s, 1952 account of morphogenesis or pattern generation in terms of a generic reaction–diffusion process lacked a connection to any explicit mechanism biologists were familiar with, and was easy to dismiss as highly speculative.
Fagan (2016) points similarly to explanatory and evidential conflicts in interactions between experimenters and modern systems biologists working in stem cell biology. She documents for instance the lack of uptake of stem cell landscape modeling within the experimental stem cell community, giving three potential reasons for it. Firstly that the full biology of stem cells is not understood, which makes it hard for biologists to consider these results compelling even if the mathematicians feel that the mathematical result is nonetheless profound. Secondly modelers fail to engage with the full richness of experimental work on these systems. Thirdly the idealization of stem cells as gene regulatory networks is advocated for by modelers more or less on the basis that it produces a compelling mathematical explanation. Fagan believes that each of these serve as obstacles to the reception of such models within the experimental stem cell community and help explain why these mathematical approaches are more or less ignored even when the mathematicians themselves explicitly address their work to experimenters.
These responses amongst biologists historically and today bear much in character to historical responses to mathematical ecology, Levins’ principal subject matter. Ecologists have objected to practices trading off realism for generality – such Lotka-Volterra based theory -citing particularly their methodological basis in physics, and predominant concern with just a small set of analytical mathematical formalisms, instead producing models which try to capture details of particular situations (Hall, 1988; Simberloff, 1981). As such the responses of molecular biologists to these traditional approaches in mathematical biology and elsewhere are not limited to them alone, and are more deeply shared than might be suggested by the limited cases I have presented. And while we certainly cannot say based on these few cases above that philosophical disagreement have been precise cause of historical lack of interaction between biologists and experimenters- there are many other historical factors at play – it does set a framework for understanding why experimenters are engaging with certain practices now in systems biology more readily.
4 Detail-Driven Modeling and Levins’ Framework
In Levins’ characterization, as mentioned, the third category of modelers pursuing realism at a cost to generality is treated rather brusquely, and conflicts somewhat with constraints on understanding as Levins sees them. Here I want to argue that in the modern computational age practices pursuing realism upfront, at least at an initial cost to generality, have developed and expanded in novel ways Levins could not necessarily have anticipated, providing means to enrich and extend this category, and explore in depth how far apart the more traditional systems-theoretic methods and modern computational practices are in modern systems biology in terms of their mathematical approaches. The development of this space of mathematical application has two important consequences. Firstly, Levins’ constraints on achieving generality, precision and realism simultaneously may no longer hold, opening the way to much more powerful applications of mathematics but ones which may render the traditional approach redundant. Secondly, in this new environment the objections of experimenters, that modelers trade-off realism too willingly, no longer holds to the same degree. In fact the practices I want to bring attention to here put a priority on detail and rich experimental data. These practices I call detail-driven modeling practices.
These practices start from the position that effective application of mathematics for various purposes requires working from detailed accounts of systems (detail that often runs up against computational constraints). In this respect the label detail-driven modeling can cover a number of practices in systems biology, including top-down processes deriving from ‘omics which use rich data sets to reverse engineer system structure and also whole cell or whole systems modeling. These practices may well share a similar philosophy to that guiding the practices I describe here. Mainly I restrict the focus here though to a set of bottom-up modeling processes which often involve collaboration with experimenters. These were the target of ethnographic investigation, the results of which I rely on here. These practices seek to apply mathematics to prediction, theory generation but also to the production of novel information on system structure.
Detail-driven modeling
The overarching goal which motivates many detail-driven practices and helps explain the original motivations for such modeling, is prediction, which was true also of Levins’ ecological examples. Modelers modeling biochemical networks in computational systems biology aim to provide precise mathematical predictions of large scale systems suitable for say clinical purposes in medical contexts (Hood et al., 2004). Systems biologists pursuing these predictive goals take as a starting point the belief that only from initially detailed accurate representation of whole systems can the variabilities and nonlinearities of biological systems be captured sufficiently for drawing reliable predictions particularly for the high-stakes purpose of medical intervention (see Voit, 2013). In this respect systems biologists are certainly motivated by a systems theoretical account of biological systems. Biological systems are too nonlinear or chaotic for abstract, idealized or linearized accounts of systems to properly account for (Voit, 2013). They are also motivated by the affordances of modern computation and its capacities for detailed representation. Models will be effective for predictive and control purposes if they can substantially replicate a system rather than just represent it.
To achieve this most mathematical models within the field, and certainly all the models we investigated in our ethnographic study, are straightforward and concentrate on interactions between specific biological elements by trying at least initially to account widely for those interactions. Modelers generally work with large numbers of coupled ordinary differential equations which track the concentrations or states of certain biochemicals and genes within a cell and how these change dynamically due to reactions between them. The sequences of reactions are represented in terms of a pathway diagram. Based on our intensive study of practices modelers almost always begin by assembling such a pathway, often themselves, out of available information from molecular biologists. This requires their own initiative pulling different bits of published information together, given that molecular biologists are not necessarily interested in studying whole systems as opposed to local sets of interactions. Once a complete (or complete as possible) pathway is assembled, the modeler chooses how to represent the interactions amongst biochemical elements and there are different options available with various strengths and limits, such as using a fairly well accepted but not particularly mathematically analyzable Michaelis–Menten model in the case metabolic modeling.Footnote 4 Subsequently the modeler must acquire information on the parameters governing the interactions, which is usually a difficult incomplete process. Unknown parameters need to be calculated through a fitting process such as simulated annealing. Once fit the model should be in theory capable of replicating the operations of its target biological networks, particularly in response to perturbations. With such a model in hand calculations can be made on how to best harness or control that network towards given ends.
Whereas mathematicians such as Rashevsky others might have been comfortable drawing on theoretical perspectives and mathematical hypotheses to limit the level of biological detail (or degree of biological realism) required upfront, the modelers we studied operate with large degrees of biological information and base their confidence as much as possible on the completeness of that information. As one modeler described it, his modeling was governed by “a sense that its… large stuff coming together and there’s something influencing the other and the other thing keeping a check like this and unless you have everything these things are not going to work properly.” Systems biologists with these predictive goals do not perceive their ability to capture the phenomena as generally indicative that their models have captured any fundamental or underlying aspect of reality. Indeed systems biologists are often pragmatic with respect to the fact that models with so many degrees of freedom as theirs can always be made to fit a data set with enough trial and error (MacLeod & Nersessian, 2015). Much importance is thus placed on predictive testing and experimental confirmation as result, to demonstrate that their models have some degree of robustness. “You do experiments in the lab and try to collect a lot of data. Then you go to the computer and try and make sense of this data using computer models. See if you can describe the system mathematically and if you are able to predict something. Otherwise this cycle where you have experimentation, data collection and computer modeling. Go back and get more data.” As systems biologists would see it, the elements of their models are strictly guided by the molecular record which documents the parts and their relations of the systems they wish to model. As one modelers put it to us, “ We aren’t theoretical modelers. We don’t just come up with ideas and then just shoot them out there and wait for people to do them.”
This preference for realism should not be interpreted in the sense that these models encompass no abstraction or idealizations. As with any model idealizations or simplifications are unavoidable and indeed modelers must represent interactions between biochemical elements in terms of a simplified accounts of their relationship of which Michaelis–Menten representations are an option. The modelers we studied in general shy away from including mathematical complexity in the form of partial differential equations – thus assuming biochemicals in cells are well mixed—or multiscale relationships (see cardiac models as one counter-example; Gross & Green, 2017; Carusi, 2014). Their representations of systems leave out much information. But the basic philosophical approach is that details should be included to the greatest extent possible according to computational, mathematical or other constraints. In this respect modeling should start from an exhaustive pathway account, and choose representations which are as complex or accurate as the modeling will allow. Once assembled computational and data issues will almost invariably demand further simplifications. Importantly however most modelers use the modeling process or general experience with that process to make decisions on how to simplify the models further without losing reliability or accuracy. For example modelers often apply sensitivity analysis to an initially too complex model to identify the most important variables in a network for a given function. The model can then be for simplified to focus on representing these alone. As such initial detailed representations often guide later simplification decisions.
Indeed in our ethnographic studies modelers often bristled at the suggestion by experimenters that the need to simplify their models or use idealized or abstract representation of interactions somehow demonstrated less commitment to detail than experimenters themselves held. As one modeler argued to us they were not making decisions that experimenters themselves did not themselves make. “For example, there's a very famous equation that's just called the Michaelis–menten equation. It's supposed to represent… kinetics. But that is an approximation. Most biologists, you know, do not realize that.” [a modeler]. Systems biologists are happy to acknowledge the limitations they need to build into their models, but not that they are working at a different level of detail or making different decisions than experimenters themselves make.
Finally detail-driven modeling is largely incompatible with the use of analytic or closed form equations, and does not restrict itself to equations or formulations which are considered to be analytically tractable. This would be at odds with the goal of replicating these complex systems in detail. As such no notion of understanding generally attaches to the ability to solve the equations in a limited or reduced form. Accordingly while systems biologists are fairly narrow in their preference for ODE equations they tend to be quite flexible and pragmatic in how they construct those equations interchanging and experimenting with different interaction terms with no obligation to ensure that these formulations adhere to a well-known mathematical functional form or be generally solvable. It should not be a surprise to learn that many systems biologists building these models come from engineering rather than applied mathematics or physics. Engineers are appreciated for their more pragmatic perspective.
As such detail-driven modeling in this sense that I have explored it here, represents a starkly different and novel approach towards the application of mathematics than that which can be ascribed to traditional generality-focused practices in the modeling of biological systems. Principally detailed representations of specific systems guide mathematical practices as opposed to general theoretical presuppositions, where replication of systems is favored as a means of achieving predictively reliable models.
Detail-driven modeling, understanding and theoretical goals
That said given the direction some systems biologists are trying to push detail-driven modeling it is possible Levins’ schema and the constraints he places on mathematical applications may no longer in fact hold. There are a few aspects of detail-driven practices which might warrant this claim.
Firstly as noted Levins suggests, albeit briefly, that “understanding” is unavailable to highly detailed models because the models are too complex and not reducible to easily interpretable mathematical forms. He asserts in fact that to provide understanding models need to be “general”, which he characterizes in terms of certain simplifications which can capture general features (430). While detail-driven modeling is driven primarily by prediction and control goals, modelers do believe nonetheless they are building up certain kinds of understanding, and indeed that understanding contributes to their ability to refine their models and contribute to their ability to control systems. One modeler reported her lab PI telling her that building a successful predictive model “means you understood the system. And then you…you could make changes to it and that’s the whole purpose of the whole process.” This kind of understanding is, as might be imagined, governed by a strongly mechanistic philosophy (Green et al., 2018), based on the idea that understanding consists in understanding cause and effect relations within the system through the agency of mathematics which helps identify those relations, with the caveat that as systems biologists these modellers reject monocausal linear accounts or explanations (Westerhoff & Kell, 2007). In fact understanding the properties which systems exhibit requires both mathematical language and analysis to comprehend. Importantly, as Brigandt (2013) shows, working from a causal-mechanical perspective does not preclude the use of mathematical explanations which cite say the existence of stability points or other dynamical systems properties, which modelers in our study consistently do. However in contrast with the more traditional use of such explanations these are considered reliable and useful by detail-driven modelers because they emerge out of a detailed representation rather than from a simplified account. In other words a detail-driven mathematical representation can be a source of relevant mathematical properties and mathematical explanations. These observations suggest that more brute force modeling is not simply instrumental, as Levins suggests it is.
Secondly, if understanding and explanation are possible through these detail-driven practices modeling then there are conceivable pathways to more general claims and indeed theoretical claims. Theoretical goals are not a principal concerns of many of those working on detailed models for the purposes of prediction and control, certainly not in the labs we studied. However, certain systems biologists nonetheless see pathways to theoretical generalisations based on detail-driven modeling. These pathways do not abide by the constraint that realism or detail must be traded away at the start of investigation in order to identify or hypothesize say fundamental and interpretable mathematical principles. Rather, more inductively, analysis of families of detailed models can be the source of general claims. For instance variability in either parameter measurement or even system structure within a population can be represented in terms of families or ensembles of models allowing more robust generalizations to be drawn on say disease effective treatments (see Kuepfer et al., 2007). But more importantly it is possible to argue that detail-driven modeling is both capable of theory-generation and in fact is a preferable pathway to the generation of theory. Westerhoff and Kell advocate that a principal function of systems biology is to produce a general mathematical theory of biological systems based on mathematical laws of structure and organization that tie biological, biochemical and physical principles together (Westerhoff & Kell, 2007, 48). Kitano (2002) presents a similar viewpoint using the BCS theory of superconductivity from physics as an analogy for what such laws will look like. Such laws or theories will not be fundamental however in the physics sense, they will be “structural”. They will define the specific constraints that allow specific biological phenomena to manifest themselves given background fundamental laws and theories (see Green, 2015). These may take the form of design or organizational principles which themselves help explain aspects of system function and organization. Importantly these principles can be derived from network models and analysis of network structures, which hold generally across different types of systems. Topological accounts of network structure on this basis are reliably identifiable as significant because a class of detailed representations of systems exhibit the same structure. These structural theories, laws and principles can thus emerge from accurate large-scale computational simulation models, through the ability of computers themselves to recognize generalizations across models. Such a perspective reverses the traditional mathematical approach of working from theoretical insights and hypotheses. Instead theory is inferred by virtue of the exhaustiveness of complex models.
This approach is essentially advocated by Bromig et al. (2020). They present a framework for identifying design principles which relies on generating families of models across a parameter space, identifying ones that meet good biological and performance criteria, and then comparing those resulting models in order to extract information on optimal biological design. Parameter choices, which can represent different background aspects such cell architecture or protein sequences, influence the kinds of processes or mechanisms a network will rely on to perform a given function effectively. This research represents a strain of investigation of design principles which has been operating in this vein over at least the past 10 years, applying computation to the wide exploration of design spaces (see Lim et al. 2013). Outside of design principle research Westerhoff and Kell give their own example of summation theorems (related to metabolic control analysis), which according to a personal communication they received from their discoverers was derived initially from numerical experiments on models (2007; 63).
As such mathematical understanding, generality and theory may not in fact lie outside the scope of what is possible with detailed-driven modeling, implying that Levins’ constraints on generalization and theory may no longer necessarily hold. Further one can argue that detail-driven approaches render in fact traditional practices of obtaining generalizations inferior, insofar as theoretical claims inferred directly from detailed predictively validated models are more reliable than starting from simplified or idealized representations of specific systems. Even assumptions such as parsimony are not strictly necessary, if computation is capable of identifying shared structures at any level of complexity. Indeed Westerhoff and Kell argue that although older mathematical biologists such as Turing and Prigogine were able through the use of “phenomenological” model with “oversimplified and unrealistic rate equations” to demonstrate particular emergent properties the results were not robust to variations in parameters or the equations. Instead, to demonstrate an emergent function reliably in the function of a particular process, precision and realism are required through the computational replication of networks (62).
In any case, while there is potential here to challenge Levins’ conceptions on the limits on mathematical applicability with respect to biology, it is not necessarily clear at this point that either predictive goals and in turn these theoretical aims are generally achievable at least in the short term. One of our own lab PIs was highly skeptical. There are genuine question marks over whether or not mathematics can be effectively employed to either of these ends given the complexity and nonlinearity of the systems being modeled. For one thing the complexity of highly detailed nonlinear models renders them highly sensitive to even small amounts data-uncertainty, yet uncertainty is pervasive and somewhat intrinsic to biological data given noise and variability (see MacLeod, 2016). Certainly current models are rarely effective for predictive goals (Voit, 2014). If such models are not rigorously validated for such purposes, these structural theories derived from these models cannot necessarily claim a stronger empirical basis. However if it is the case that detail-driven modeling can produce better supported generalizations and theories, then Levins’ theory of trade-offs and constraints may need to be put aside. And that outcome should challenge traditional conceptions of how mathematical theory can and should be developed in biology.
Novel inferential practices
Even if these claims about the potential novelty of mathematical application in systems biology do not hold, detail-driven modeling in systems biology allow other novel uses of models which create a strong contrast with applications possible using traditional approaches and arguably beyond what Levins had in mind as possible for modelers pursuing realism. These practices involve the use of detailed mathematical models to infer elements of biological networks which were not previously known. These uses may in fact be dominant ones amongst modelers in the field given the limits mentioned above on the uses of current models for predictive and theoretical goals. Certainly these are a dominant use of models made by members of the labs we studied and similar practices can be found across the field (e.g. Kuepfer et al., 2007).
Principally detailed and precise models allow modelers to identify differences or errors between their models and the data, and use this to infer missing information in an account of a system. For example in one of the cases I examined the modeler was tasked with producing a model of a system for which experimenters had produced a pathway (MacLeod & Nersessian, 2018). However when a model of that system was put together it proved incapable of accounting for particular dynamics of the system. Through computational manipulation he discovered that various pathways were over and underregulated (producing too little and too much output respectively). Then by experimenting computationally with different structural changes he was able to pose the existence of an unknown biochemical element operating in the network to provide that regulation. This element was later identified by experiment.
In another case a modeler faced uncertainty about the structure of the system she was attempting to model (MacLeod, 2016). The system was otherwise complex and it was difficult to find a unique parameter fit. Regardless she was able to hypothesize the right structure by exploring structural alternatives across a number of increasingly tighter biological conditions and a wide set of potential parameters sets using Monte Carlo simulation. Since only one structural alternative could meet all these conditions for at least some parameter sets, she hypothesized this must be the correct structure. As such even without producing an accurate model of the system she was able to use her ability to explore a wide-landscape of possibilities to reach a conclusion on the biological system. These techniques provide novel applicability for mathematics as means through which inferences about missing elements of our knowledge can be derived by exploring a landscape of possibilities. Large scale realistic and precise mathematical representation makes these possibilities accessible and comparable.
These uses apply the affordance of computation to explore a vastly wider set of detailed model possibilities than would be possible without either, rendering mathematical representations useful as discovery tools. The rigor and exhaustiveness of these models give them power to localize errors and identify solutions. Such uses are certainly novel in the context of biology, and could not easily have been anticipated by Levins. Arguably they represent a new understanding of what mathematics can achieve, which lies outside previous characterizations. Knowledge of these practices helps enrich our understanding of the contrast and divide between systems-theoretic researchers and more pragmatic researchers in systems biology. These practices speak to just how remote such modelers can be from any relying on any pretense to generality or theory to motivate their practice (those described above excepted) and how close their motivations can align to those of basic empirical investigators, by employing mathematics principally to improve and fix the information record.
To summarize then four aspects of modern detail driven practices stand-out. Firstly that such modelers generally begin their analysis from detailed accounts, and use this detail to inform decisions, often on mathematical grounds, regarding simplification. This is in contrast with the more traditional practice of working from initial mathematical hypotheses and mathematical concepts which can be expressed at the outset in terms of idealized and simplified representations. Secondly detail-driven modelers share a basic mechanistic philosophy which itself underwrites and supports modelers’ detail-driven approaches. Thirdly, some modelers think that detailed models are a source of generalizations and theory about biological systems, if not a more effective one. Fourthly many modelers extend these practices to encompass inferential practices which improve and develop network details. Overall these descriptions provide a rich account of the motivations and practices governing those pursuing mathematical approaches within Levins third strand – practices trading-off generality, at the outset, in favor of realism and precision—certainly to a greater degree than Levins does himself, and in the process helps further our understanding of the different attitudes and preferences guiding both groups of systems biologists with respect to mathematical application.
5 Detail-driven approaches and experimentation
The second claim of this paper is that detail-driven uses promote better relations and connections between experimenters and modelers. Systems biologists have and are cultivating substantial collaborations with experimenters as part now of routine work (Calvert & Fujimura, 2011). As one experimenter put it to us, including modelers on a grant application is now almost an expected practice and one funders certainly favor. In the labs we studied almost all the modelers had active experimental collaborations. I want to claim here part of the reason why experimenters are engaging now is that detail-driven practices (particularly inferential uses) provide a more methodologically sound application of mathematics from an experimenter’s point of view. Here I turn back again to the ethnographic investigation in order to bolster this claim through experimenters’ and modelers’ own comments on their relationships and motivations.
Firstly and perhaps most importantly both experimenters and detail-driven modelers agree that details matter, and must form a starting point for any modeling process. If there is no thorough well-validated understanding of a pathway to begin with then mathematical inferences cannot be easily trusted according to experimenters, as we saw in responses to Rashevsky’s attempt to model systems yet to be well-understood or investigated. We see this also in the motivations Fagan ascribes to experimenters who ignore or reject stem-cell modeling. These detail-driven models can be seen as closely tied to experimental evidence and the data record, indeed to depend on them, and in turn to motivate a need for collaboration between experimenters and modelers. With respect to biological variability, modelers, as mentioned, often make efforts to incorporate it in their models through ensemble modeling. Both groups accept that models require predictive validation to be taken seriously, and expressed that importance in interviews. In fact one modelers highlighted to us a tendency of experimenters to interpret detailed models as simply a summary or record of current experimental knowledge, rather than as a device for generating novel prediction or understanding, a view which can be interpreted by modelers as putting limits on the value of models. “They [experimenters] think of [models] as something that's… just hooked up to – to, you know, match figures…. “. Putting these potentially negative issues to the side, experimenters do recognize the fact that these models do operate at least at the start from a substantial record of current information.
Secondly both modelers and experimenters engaged in these detail-driven practices and experimenters share a basic-mechanistic philosophy and a causal-mechanistic concept of explanation, which is not necessarily shared with modelers that have strong mathematical notions of explanation (Green, 2017). This shared philosophy facilitates a basic shared understanding of what these detail-driven models represent. Many modelers are using models primarily to track cause and effect relationships, as molecular biologists are usually characterized as doing. Some experimenters at least—certainly those that engage full heartedly in modeling—often recognize their own cognitive limitations in this respect and understand that detail-driven models can produce insight on causal relationships they simply could not perceive on their own. As such there is a demonstrable power in models to bring together and represent information that is otherwise cognitively inaccessible. According to one experimenter.
“…. so if you were just looking at one protein that is changing one way or the other, in such an adaptive environment, you may actually find something that changes but in the overall global picture as far as disease pathology goes it might not be that relevant because there may be something else in the system that is changing to compensate for that. And so it has become sort of important for us to call on people like G4 [a modeler]…… to try to understand what are what’s happening system wide and in that way find changes that occur that aren’t compensated for that would be significant in terms of pathology.” (experimenter).
Experimenters holding these views can accept that detailed models can do things they simply cannot. Further because these modelers model the mechanisms using relatively non-abstract non-opaque mathematical formalisms it is easier for experimenters to perceive the content of models and how biological information is represented (as a mechanism) within them, e.g., in metabolic modeling every term in a pathway is represented in the model in terms of its cellular concentration. On Fagan’s account the complexity of stem-cell landscape modeling was one reason why experimenters were not engaging with such landscape models (2016). Sophisticated mathematical concepts and ideas do not play a strong role in these representations (although they might in various say parameter fitting processes). And while experimenters certainly do not claim to understand what modelers are doing to get the result the structure of the model is otherwise relatively transparent to experimenters in the way that other more idealized or theoretical mathematical formulations based on more sophisticated mathematical concepts may not be (consider categories in Rosen’s theory as an example). Each side can communicate on the molecular elements involved and the nature of their interactions.
“G4 likes to look at data… and I think ….he doesn’t like to look at data very differently from the way I like to look at data. I fill it in with biochemical information and he fills it in with boxes that he gets from models or papers. I become the person that provides them with this box to this box and there as a result we see an increase in inflammation. And then he takes that and puts it into a model and says ok this is what happens and then inserts information about what he knows about what he knows about how these boxes talk to some other things that talk to inflammation.” (experimenter).
As such it is possible to identify a much better alignment between a detail-driven modeling approach and experimenter’s own methodological and epistemological preconceptions about how molecular phenomena can be reliably and fruitfully represented. Having said that the relationships between modelers working on detail-driven models and experimenters are far from seamless. As mentioned while recognizing the close connection of these data-driven models to the data experimenters can tend to see models principally as means for accounting for information or drawing it together in one place and illustrating relations that may not have been visible rather than as predictive engines capable of handling significant perturbations. Indeed modelers who push the predictive capacity of their models while making assumptions and simplifications in the process can alienate their experimental collaborators. As one modeler put it. “…so, for them, it's just like, you're using your data and then, you know, you're plugging in some numbers to fit the output of your model to that. And then they would not pose a lot of faith in those models or what they predict.” (A modeler) Experimenters have an acute sense of fragility of models beyond the available data and the ability of a model to fit that data. They anticipate new information might easily come along at any point. “we know how complicated the system is… one change in experimental condition can totally change the result” (An experimenter). In this respect experimenters attitudes towards the predictive goals of modelers is often skeptical.
Nonetheless experimenters do not reject that models built in this way cannot provide them reliable insights into the systems they study. In this regard the more inferential use of models to generate hypotheses about the structure of networks and their parameters fits very well to the kinds of objectives experimenters expressed to us for engaging with modelers. “…the usefulness of what she [a modeler] does is to see connections that we might not predict based on kind of guessing what kind of signaling molecules are connected to another. In reading in the literature that this might have an influence on this pathway but she sees an entire set of pathways regulate that that’s useful information.” Modelers that tend to aim at this kind of information are appreciated. These inferential uses are helped by the fact that the generation of an hypothesis does not require certainty. Such hypotheses can be speculative. Experiments, as experimenters maintain, are always required in any case to confirm any model-based result and they will generate their own belief about a result from experiment alone, not from any particular claims the modelers might make. As such while experimenters do not necessarily have deep insight into how modelers are producing good hypotheses, using models to generate them is perceived as an effective and meaningful use of mathematics.
On this basis detail-driven modeling helps facilitate interaction and engagement between modelers and experimenters, and in turn helps explain why more experimenters are engaging in deep collaborations currently with certain systems biologists, and not others. Detail-driven modelers and experimenters share a more compatible outlook on what fruitful and reliable applications of mathematics in biology can consist in, and how to produce them, compared to systems-theoretic biologists. On this view there is a deep agreement on the necessity of trading off generality in favour of realism and precision as a basic approach to biological investigation, and while such applications of mathematics have traditionally lacked sufficient power to be of interest or use to experimenters, the situation now has substantially changed.
6 Conclusion
In this paper, using the results of an ethnographic study,I have applied Levins’ analysis of mathematical application in order to further understand and explore the relations between different groups of moderns systems biologists in terms of their mathematical practices and preferences. The result is hopefully a deeper account of the potential divisions between such groups and one which locates these divisions with respect to views on what are the most meaningful and useful ways to apply mathematics to complex systems. From this analysis I have argued here for two claims; 1) that Levins constraints may no longer apply opening up mathematical modeling to more powerful applications than Levins could countenance; and 2), that delving deeper into the realism-strand, and asking questions with respect to how “realism” is applied, reveals deeper commonalities and philosophical attitudes between experimental practices and then mathematical ones than many would expect. Hence greater relationships between experimenters and these kinds of modelers, despite a lack of shared education, is not unexpected. Having said all this systems biology is far from unique for applying the power of modern computation towards for purposes of prediction, drawing inferences or indeed generating theory. Things are changing fast. As such I take it to be one implication of this paper that our understanding of the effect of modern large scale computation on modern mathematical applications and their governing philosophies, and on our understanding of the constraints governing mathematics, still requires much further investigation.
Notes
This NSF project was led by Professor Nancy Nersessian. The two labs were studied over 4 years, through lab observations and interviews specifically on modeling practices. Over 100 interviews were performed.
See Weisberg for an analysis of how Levins characterizes and limits “understanding” in this context.
Although Odenbaugh argues here that Levin’s was factoring in at least the limited scope of contemporary computation rather than simply ruling out this approach (Odenbaugh, 2006).
Michaelis–Menten kinetics is a model describing the rate of enzymatic interactions – an enzyme facilitates the transformation of one biochemical compound into another (catalyzation).
References
Bechtel, W., & Abrahamsen, A. (2010). Dynamic mechanistic explanation: Computational modeling of circadian rhythms as an exemplar for cognitive science. Studies in History and Philosophy of Science Part A, 41(3), 321–333.
Brigandt, I. (2013). Systems biology and the integration of mechanistic explanation and mathematical explanation. Studies in History and Philosophy of Science Part c: Studies in History and Philosophy of Biological and Biomedical Sciences, 44(4), 477–492.
Bromig, L., Kremling, A., & Marin-Sanguino, A. (2020). Understanding biochemical design principles with ensembles of canonical non-linear models. PloS one, 15(4), e0230599.
Calvert, J., & Fujimura, J. H. (2011). Calculating life? Duelling discourses in interdisciplinary systems biology. Studies in History and Philosophy of Science Part c: Studies in History and Philosophy of Biological and Biomedical Sciences, 42(2), 155–163.
Carusi, A. (2014). Validation and variability: Dual challenges on the path from systems biology to systems medicine. Studies in History and Philosophy of Science Part c: Studies in History and Philosophy of Biological and Biomedical Sciences, 48, 28–37.
Fagan, M. B. (2016). Stem cells and systems models: Clashing views of explanation. Synthese, 193(3), 873–907.
Green, S. (2015). Revisiting generality in biology: Systems biology and the quest for design principles. Biology & Philosophy, 30(5), 629–652.
Green, S. (2017). Philosophy of systems and synthetic biology. In E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/win2019/entries/systems-synthetic-biology/. Accessed 27 Feb 2021.
Green, S., Şerban, M., Scholl, R., et al. (2018). Network analyses in systems biology: New strategies for dealing with biological complexity. Synthese, 195, 1751–1777.
Gross, F. (2019). Occam’s razor in molecular and systems biology. Philosophy of Science, 86(5), 1134–1145.
Gross, F., & Green, S. (2017). The sum of the parts: Large-scale modeling in systems biology. Philosophy, Theory and Practice in Biology, 9(10).
Hall, C. A. (1988). An assessment of several of the historically most influential theoretical models used in ecology and of the data provided in their support. Ecological Modelling, 43(1–2), 5–31.
Hoffman, D. S. (2013). The Dawn of Mathematical Biology. Controvérsia, 9(2), 53–61.
Hood, L., Heath, J. R., Phelps, M. E., & Lin, B. (2004). Systems biology and new technologies enable predictive and preventative medicine. Science, 306(5696), 640–643.
Jones, N. (2014). Bowtie structures, pathway diagrams, and topological explanation. Erkenntnis, 79(5), 1135–1155.
Keller, E. F. (2003). Making sense of life: Explaining biological development with models, metaphors, and machines. Harvard University Press.
Kitano, H. (2002). Computational systems biology. Nature, 420(6912), 206–210.
Krohs, U., & Callebaut, W. (2007). Data without models merging with models without data. In F. Boogerd, F. J. Bruggeman, J.-H. S. Hofmeyer, & H. V. Westerhoff (Eds.), Systems biology: Philosophical foundations (pp. 181–283). Elsevier.
Kuepfer, L., Peter, M., Sauer, U., & Stelling, J. (2007). Ensemble modeling for analysis of cell signaling dynamics. Nature Biotechnology, 25(9), 1001–1006.
Levins, R. (1966). The strategy of model building in population biology. American Scientist, 54(4), 421–431.
Lim, W. A., Lee, C. M., & Tang, C. (2013). Design principles of regulatory networks: Searching for the molecular algorithms of the cell. Molecular Cell, 49(2), 202–212.
MacLeod, M. (2016). Heuristic approaches to models and modeling in systems biology. Biology and Philosophy, 31(3), 353–372. https://doi.org/10.1007/s10539-015-9491-1
MacLeod, M., & Nersessian, N. J. (2015). Modeling systems-level dynamics: Understanding without mechanistic explanation in integrative systems biology. Part c: Studies in History and Philosophy of Biological and Biomedical Sciences, 49(1), 1–11.
MacLeod, M., & Nersessian, N. J. (2018). Modeling complexity: cognitive constraints and computational model-building in integrative systems biology. History and Philosophy of the Life Sciences, 40, 17. https://doi.org/10.1007/s40656-017-0183-9
Odenbaugh, J. (2006). The strategy of “The strategy of model building in population biology”. Biology and Philosophy, 21, 607–621.
Shmailov, M. M. (2016). Intellectual Pursuits of Nicolas Rashevsky. Springer International Publishing Switzerland.
Simberloff, D. (1981). The sick science of ecology: Symptoms, diagnosis, and prescription. Eidema, 1, 49–54.
Turing, A. M. (1952). The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society London B, 237, 37–94.
Voit, E. O. (2000). Computational analysis of biochemical systems: A practical guide for biochemists and molecular biologists. Cambridge University Press.
Voit, E. O. (2013). A first course in systems biology. Garland Science.
Voit, E. O. (2014). Mesoscopic modeling as a starting point for computational analyses of cystic fibrosis as a systemic disease. Biochimica et Biophysica Acta (BBA)-Proteins and Proteomics, 1844(1), 258–270.
Westerhoff, H. V., & Kell, D. B. (2007). The methodologies of systems biology. In F. Boogerd, F. J. Bruggeman, J.-H. S. Hofmeyer, & H. V. Westerhoff (Eds.), Systems biology: Philosophical foundations (pp. 23–70). Elsevier.
Acknowledgements
Many thanks to the three reviewers and to the editors of this special issue for their advice and guidance on the development of this paper.
Funding
The ethnographic study reported in publication work was funded by a grant of the National Science Foundations (USA) – DRL097394084.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Ethical approval
The ethnographic study cited in this paper was funded by the National Science Foundation (NSF) and performed in accordance with the ethical standards as laid down in the 1964 Declaration of Helsinki and its later amendments. In alignment with these standards ethical approval was granted by the Institutional Review Board (Georgia Institute of Technology). Data collection and data management plans were subject to IRB approval. All personal references were anonymized during data collection, data analysis and publication. All participants were required to give written informed consent to participation and publication.
Informed consent
All participants in the ethnographic study gave explicit informed consent on the basis that any identifying information is omitted from any output of project. No identifying information is revealed in this publication.
Conflict of Interest
There are no conflicts of interest in this study.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article belongs to the Topical Collection: Dimensions of Applied Mathematic
Guest Editors: Matthew W. Parker, Davide Rizza
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
MacLeod, M. The applicability of mathematics in computational systems biology and its experimental relations. Euro Jnl Phil Sci 11, 84 (2021). https://doi.org/10.1007/s13194-021-00403-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13194-021-00403-3