Creeping effect across a buried, inclined, finite strike-slip fault in an elastic-layer overlying an elastic half-space

Abstract

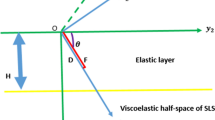
The process of stress-strain accumulation near earthquake faults during the aseismic period has become a subject of research during the last few decades. It is noted that seismic waves, generated by an earthquake, result in a considerable disturbance in a seismic region causing a movement of the free surface. Such ground movements are not observed during the aseismic period. But a slow quasi-static aseismic surface displacement of the order of few cms. per year or less can be observed during the aseismic period which indicates a slow sub-surface process of stress-strain accumulation. Keeping this in view we here consider an aseismically creeping, buried, finite strike-slip fault inclined to the vertical at an arbitrary angle. The fault is situated in an elastic layer over an elastic half-space representing the lithosphere-asthenosphere system. An analytical study for displacement, stress and strain due to creeping effect has been carried out for a buried, finite, inclined fault. The solutions for displacement, stress and strain are then found before the onset of fault slip and then superpose the effect of fault slip using Laplace transform and suitable mathematical techniques of Green’s function. The analytical results and the graphical presentations show that the inclination of the fault and the velocities of the fault movement has noticeable effect on displacements, stresses and strains.

Appendix

1.1 Appendix-I (Solutions of displacement, stress and strain in the absence of fault movements)

Let

$$\begin{aligned} \left. \begin{array}{ll} \bar{u_1} =&{} \frac{(u_1)_0}{p} + F_1(y_1, y_2,y_3,p) + A_1 y_1 + A_2 y_2\\ \bar{u_2} =&{} \frac{(u_2)_0}{p} + F_2(y_1, y_2,y_3,p) + B_1 y_1 + B_2 y_2\\ \bar{u_3} =&{} \frac{(u_3)_0}{p} + F_3(y_1, y_2,y_3,p) + C_1 y_1 + C_2 y_2\\ \bar{u_1}' =&{} \frac{(u'_1)_0}{p} + F'_1(y_1, y_2, y_3, p) + A_1 y_1 + A_2 y_2\\ \bar{u_2}' =&{} \frac{(u'_2)_0}{p} + F'_2(y_1, y_2, y_3, p) + B_1 y_1 + B_2 y_2\\ \bar{u_3}' =&{} \frac{(u'_3)_0}{p} + F'_3(y_1, y_2, y_3, p) + C_1 y_1 + C_2 y_2\\ \end{array}\right\} \end{aligned}$$

(25)

where $A_i,~ B_i,~ C_i (i = 1,2),~ F_i ~\text {and} ~F'_i~ (i= 1,2,3)$ are to be determined.

Now

$$\begin{aligned} \bar{e_{12}}= & {} \frac{1}{2} \left( \frac{\bar{\partial u_1}}{\partial y_2}+\frac{\bar{\partial u_2}}{\partial y_1}\right) \nonumber \\= & {} \frac{1}{p}(e_{12})_0 + \frac{1}{2}\left( \frac{\partial F_1}{\partial y_2}+ \frac{\partial F_2}{\partial y_1}\right) + \frac{1}{2}(A_2 + B_1) ~[~\text {for}~ |y_2|\rightarrow \infty ~]\end{aligned}$$

(26)

$$\begin{aligned} \bar{e_{12}}'= & {} \frac{1}{2} \left( \frac{\bar{\partial u'_1}}{\partial y_2}+\frac{\bar{\partial u'_2}}{\partial y_1}\right) \nonumber \\= & {} \frac{1}{p}(e'_{12})_0 + \frac{1}{2}\left( \frac{\partial F'_1}{\partial y_2}+ \frac{\partial F'_2}{\partial y_1}\right) + \frac{1}{2}(A_2 + B_1) ~[~\text {for}~ |y_2|\rightarrow \infty ~] \end{aligned}$$

(27)

Taking Laplace transformation of Eq. (12) we get

$$\begin{aligned} \bar{e_{12}}\rightarrow \frac{1}{p}(e_{12})_{0, \infty } + g(p) + h(p) \end{aligned}$$

(28)

$$\begin{aligned} \bar{e_{12}}' \rightarrow \frac{1}{p}(e'_{12})_{0, \infty } + g(p) + h(p) \end{aligned}$$

(29)

Now comparing Eqs. (26) with (28) and (27) with (29) we get

$$\begin{aligned}&\frac{1}{2}(A_2 + B_1) = g(p) + h(p)\nonumber \\&\quad \text {Let}~~~ A_2 = 2h(p) \end{aligned}$$

(30)

$$\begin{aligned}&\quad \text {and} ~~B_1 = 2g(p) \end{aligned}$$

(31)

Since $F_1$, $F_2$, $F'_1$ and $F'_2$ are functions of $y_1,~ y_2,~ y_3 ~\text {and}~ p$, $(\frac{\partial F_1}{\partial y_2}+ \frac{\partial F_2}{\partial y_1})$ and $(\frac{\partial F'_1}{\partial y_2}+ \frac{\partial F'_2}{\partial y_1})$ can not be in general equal to g(p) and h(p) except for some particular cases.

Then $(\frac{\partial F_1}{\partial y_2}+ \frac{\partial F_2}{\partial y_1})_{|y_2|\rightarrow \infty } =(\frac{\partial F'_1}{\partial y_2}+ \frac{\partial F'_2}{\partial y_1})_{|y_2|\rightarrow \infty } =0$

On $y_3 = 0$

$$\begin{aligned} \frac{\partial F_1}{\partial y_3} = \frac{\partial F_2}{\partial y_3} = \frac{\partial F_3}{\partial y_3} = 0 \end{aligned}$$

(32)

At $y_3 = h_1$

$$\begin{aligned} F_1 = F'_1,~ F_2 = F'_2,~ F_3 = F'_3 ~[\text {since the two media are in welded contact}] \end{aligned}$$

(33)

and

$$\begin{aligned} \frac{\partial F'_1}{\partial y_3} = \frac{\partial F'_2}{\partial y_3} = \frac{\partial F'_3}{\partial y_3} \rightarrow 0 ~\text {as}~ y_3 \rightarrow \infty \end{aligned}$$

(34)

Taking Laplace transform on expression of $\tau _{13}$ and $\tau '_{13}$ given in Eqs. (2) and (3) and putting the value of $\bar{u_1}, \bar{u_3}, \bar{u_1}', \bar{u_3}'$ from Eq. (25) we get

$$\begin{aligned} \bar{\tau _{13}} = \frac{1}{p}(\tau _{13})_0 + \mu _1(\frac{\partial F_1}{\partial y_3} + \frac{\partial F_3}{\partial y_1}) + \mu _1 c_1 \end{aligned}$$

Similarly

$$\begin{aligned} \bar{\tau _{13}}' = \frac{1}{p}(\tau '_{13})_0 + \mu _2\left( \frac{\partial F'_1}{\partial y_3} + \frac{\partial F'_3}{\partial y_1}\right) + \mu _2 c_1 \end{aligned}$$

and also

$$\begin{aligned} \bar{\tau _{13}} = \bar{\tau _{13}}'~\text {at} ~y_3 = h_1 \end{aligned}$$

(35)

Let ${(\tau _{13})_0} = {(\tau '_{13})_0} = \tau _{h_1}$ at $y_3 = h_1$

Then putting the value of $\bar{\tau _{13}} ~\text {and} ~\bar{\tau _{13}}'$ in Eq. (35) and since at $y_3 = h_1$

$F_1 = F'_1~ \text {and}~ F_3 = F'_3$ then we get

$$\begin{aligned} \left( \frac{\partial F_3}{\partial y_1} + \frac{\partial F_1}{\partial y_3}\right) = - c_1 \end{aligned}$$

In our model, we consider the case where $\tau _{h_1} = 0$. Then an obvious solution for $F_1, F_3, F'_1, F'_3~$ is

$$\begin{aligned} F_1 = F_3 = F'_1 = F'_3 = 0 \end{aligned}$$

(36)

So $c_1 = 0$

Then Eq. (25) becomes

$$\begin{aligned} \left. \begin{array}{ll} \bar{u_1} =&{} \frac{(u_1)_0}{p} + A_1 y_1 + 2 h(p) y_2\\ \bar{u_2} =&{} \frac{(u_2)_0}{p} + F_2 + 2 g(p) y_1 + B_2 y_2\\ \bar{u_3} =&{} \frac{(u_3)_0}{p} + c_2 y_2\\ \bar{u_1}' =&{} \frac{(u'_1)_0}{p} + A_1 y_1 + 2 h(p) y_2\\ \bar{u_2}' =&{} \frac{(u'_2)_0}{p} + F'_2 + 2 g(p) y_1 + B_2 y_2\\ \bar{u_3}' =&{} \frac{(u'_3)_0}{p} + c_2 y_2 \end{array}\right\} \end{aligned}$$

(37)

Taking Laplace transform on Eqs. (2) and (3) except on $\tau _{13}$ and $\tau '_{13}$ and using equation (37) we get in elastic layer

$$\begin{aligned}&\bar{\tau _{11}} = \frac{1}{p} (\tau _{11})_0 + 2A_1 \mu _1 \end{aligned}$$

(38)

$$\begin{aligned}&\quad \bar{\tau _{12}} = \frac{1}{p} (\tau _{12})_0 + \mu _1 \frac{\partial F_2}{\partial y_1} + 2\mu _1 [h(p) + g(p)] \end{aligned}$$

(39)

$$\begin{aligned}&\quad \bar{\tau _{23}} = \frac{1}{p}(\tau _{23})_0 + \mu _1\frac{\partial F_2}{\partial y_3} + \mu _1 c_2 \end{aligned}$$

(40)

$$\begin{aligned}&\quad \bar{\tau _{22}} = \frac{1}{p}(\tau _{22})_0 + 2\mu _1 \frac{\partial F_2}{\partial y_2} + 2B_2 \mu _1 \end{aligned}$$

(41)

$$\begin{aligned}&\quad \bar{\tau _{33}} = \frac{1}{p}(\tau _{33})_0 \end{aligned}$$

(42)

and in elastic half-space

$$\begin{aligned}&\bar{\tau _{11}}' = \frac{1}{p} (\tau '_{11})_0 + 2A_1 \mu _2 \end{aligned}$$

(43)

$$\begin{aligned}&\quad \bar{\tau _{12}}' = \frac{1}{p} (\tau '_{12})_0 + \mu _2 \frac{\partial F'_2}{\partial y_1} +2 \mu _2 [h(p) + g(p)] \end{aligned}$$

(44)

$$\begin{aligned}&\quad \bar{\tau _{23}}' = \frac{1}{p}(\tau '_{23})_0 + \mu _2\frac{\partial F'_2}{\partial y_3} + \mu _2c_2 \end{aligned}$$

(45)

$$\begin{aligned}&\quad \bar{\tau _{22}}' = \frac{1}{p}(\tau '_{22})_0 + 2\mu _2 \frac{\partial F'_2}{\partial y_2} + 2B_2 \mu _2 \end{aligned}$$

(46)

$$\begin{aligned}&\quad \bar{\tau _{33}}' = \frac{1}{p}(\tau '_{33})_0 \end{aligned}$$

(47)

Taking Laplace transform on boundary conditions (6) and (7) we get

$$\begin{aligned} \lim _{y'_1\rightarrow \ L-} \bar{\tau _{11}}(y_1,y_2,y_3,p) = \lim _{y'_1\rightarrow \ L+} \bar{\tau _{11}}(y_1,y_2,y_3,p) = \frac{\tau _L}{p}, \end{aligned}$$

($y'_2 = 0,~ 0 \le y'_3 \le D,~ t \ge 0$) and

$$\begin{aligned} \lim _{y_1\rightarrow \ (-L)-} \bar{\tau _{11}}(y_1,y_2,y_3,p) = \lim _{y_1\rightarrow \ (-L)+} \bar{\tau _{11}}(y_1,y_2,y_3,p) = \frac{\tau _{L}}{p} \end{aligned}$$

($y'_2 = 0,~ 0 \le y'_3 \le D,~ t \ge 0$)

From Eq. (38) as $-L \le y'_1 \le L$,  $y'_2 = 0$ and $0 \le y'_3 \le D$

$$\begin{aligned}&\bar{\tau _{11}} = \frac{1}{p} (\tau _{11})_0 + 2A_1 \mu _1 \\&\frac{\tau _L}{p} = \frac{\tau _L}{p} + 2A_1 \mu _1 \end{aligned}$$

Therefore

$$\begin{aligned} A_1 = 0 \end{aligned}$$

Taking Laplace transform on boundary condition (8) we get

$$\begin{aligned} \bar{\tau _{12}}\rightarrow \tau _{\infty }(p)~ \text {as}~ |y_2| \rightarrow \infty \end{aligned}$$

Then form Eq. (39)

$$\begin{aligned} \frac{\partial F_2}{\partial y_1} = \frac{1}{\mu _1}[\tau _{\infty }(p) - \frac{1}{p}\tau _{\infty }(0)]- 2[h(p) + g(p)] ~\text {as}~ |y_2| \rightarrow \infty \end{aligned}$$

Also at $y_3 = 0$

$$\begin{aligned} \bar{\tau _{23}} = \bar{\tau _{22}} = 0 \end{aligned}$$

From Eq. (40)

$$\begin{aligned} \frac{\partial F_2}{\partial y_3} + c_2 = 0 \end{aligned}$$

So $c_2 = 0$[Since from (32) $\frac{\partial F_2}{\partial y_3} = 0]$

From Eq. (41)

$$\begin{aligned} \frac{\partial F_2}{\partial y_2} + B_2 = 0 \end{aligned}$$

Since $B_2$ is a function of p and $F_2$ is a function of $y_1$, $y_2$, $y_3$, p, so in general $\frac{\partial F_2}{\partial y_2}$ can not equal to $B_2$ except particular cases.

Therefore

$$\begin{aligned} \frac{\partial F_2}{\partial y_2} = B_2 = 0 \end{aligned}$$

Taking Laplace transform on boundary condition (10) we get

$$\begin{aligned} \bar{\tau _{22}}' = 0 \end{aligned}$$

From Eq. (46)

$$\begin{aligned} \frac{\partial F'_2}{\partial y_2} + B_2 = 0 \end{aligned}$$

Therefore

$$\begin{aligned} \frac{\partial F'_2}{\partial y_2} = 0 ~[~\text {Since}~ B_2 = 0] \end{aligned}$$

So, $F_2 = {\frac{1}{\mu _1}([\tau _{\infty }(p) - \frac{1}{p}\tau _{\infty }(0)]- 2[h(p) + g(p)])}y_1$

Therefore $\bar{u_1} = \frac{(u_1)_0}{p} + 2 h(p) y_2$

$$\begin{aligned}&\bar{u_2} = \frac{(u_2)_0}{p} + \frac{1}{\mu _1}[\tau _{\infty }(p) -\frac{1}{p}\tau _{\infty }(0)]y_1 - 2 h(p)y_1\\&\bar{u_3} = \frac{(u_3)_0}{p}\\&\bar{u_1}' = \frac{(u'_1)_0}{p} + 2 h(p) y_2\\&\bar{u_2}' = \frac{(u'_2)_0}{p} + \frac{1}{\mu _2}[\tau _{\infty }(p) -\frac{1}{p}\tau _{\infty }(0)] - 2 h(p)y_1\\&\bar{u_3}' = \frac{(u'_3)_0}{p} \end{aligned}$$

Taking inverse Laplace Transform we get

For elastic layer

$$\begin{aligned} \left. \begin{array}{ll} u_1 =&{} (u_1)_0 + 2 h(t) y_2\\ u_2 =&{} (u_2)_0 + \frac{1}{\mu _1}[\tau _{\infty }(t) - \tau _{\infty }(0)]y_1 - 2 h(t) y_1\\ u_3 =&{} (u_3)_0\\ \end{array}\right\} \end{aligned}$$

(48)

and for elastic half-space

$$\begin{aligned} \left. \begin{array}{ll} u'_1 =&{} (u'_1)_0 + 2 h(t) y_2\\ u'_2 =&{} (u'_2)_0 + \frac{1}{\mu _2}[\tau _{\infty }(t) - \tau _{\infty }(0)]y_1 - 2 h(t) y_1\\ u'_3 =&{} (u'_3)_0 \end{array}\right\} \end{aligned}$$

(49)

Now for elastic layer $(0 \le y_3 \le h_1,~ |y_2| < \infty )$

$$\begin{aligned} \left. \begin{array}{ll} \tau _{11} =&{} (\tau _{11})_0\\ \tau _{12} =&{} (\tau _{12})_0 + [\tau _{\infty }(t) - \tau _{\infty }(0)]\\ \tau _{13} =&{} (\tau _{13})_0\\ \tau _{23} =&{} (\tau _{23})_0\\ \tau _{22} =&{} (\tau _{22})_0\\ \tau _{33} =&{} (\tau _{33})_0\\ e_{12} =&{} (e_{12})_0 + \frac{1}{2\mu _1} [\tau _{\infty }(t) - \tau _{\infty }(0)]\\ e_{13}=&{} (e_{13})_0 \end{array}\right\} \end{aligned}$$

(50)

and similarly for elastic half-space $(y_3 \ge h_1,~|y_2| < \infty )$

$$\begin{aligned} \left. \begin{array}{ll} \tau '_{11} =&{} (\tau '_{11})_0\\ \tau '_{12} =&{} (\tau '_{12})_0 + [\tau _{\infty }(t) - \tau _{\infty }(0)]\\ \tau '_{13} =&{} (\tau '_{13})_0\\ \tau '_{23} =&{} (\tau '_{23})_0\\ \tau '_{22} =&{} (\tau '_{22})_0\\ \tau '_{33} =&{} (\tau '_{33})_0\\ e'_{12} =&{} (e'_{12})_0 + \frac{1}{2\mu _2} [\tau _{\infty }(t) - \tau _{\infty }(0)]\\ e'_{13} =&{} (e'_{13})_0 \end{array}\right\} \end{aligned}$$

(51)

We assume $u_i$ = $(u_i)_1$, $\tau _{ij}=(\tau _{ij})_1$ (i, = 1,2,3), $e_{12} = (e_{12})_1$ and $e_{13} = (e_{13})_1$ for elastic layer and $u'_i$ = $(u'_i)_1$, $\tau '_{ij}=(\tau '_{ij})_1$ (i, = 1,2,3), $e'_{12} = (e'_{12})_1$ and $e'_{13} = (e'_{13})_1$ for elastic half-space in the absence of fault movement.

1.2 Appendix-II (Solution of displacements, stresses and strains after the commencement of fault creep)

The displacements, stresses and strains after the commencement of fault creep have been found in the form given in equation (18) and (19), where $(u_i)_1,~ (u'_i)_1 (i = 1,2,3),~ (\tau _{ij})_1, ~(\tau '_{ij})_1, (e_{12})_1,~(e_{13})_1,~ (e'_{12})_1,~(e'_{13})_1$ $(i, j = 1, 2, 3)$ are given by equation (48), (49), (50) and (51) and $(u_i)_2,~ (u'_i)_2 ~(i = 1,2,3),~ (\tau _{ij})_2,~ (\tau '_{ij})_2 ~(i, j = 1, 2, 3),~ (e_{12})_2,~(e_{13})_2,~ (e'_{12})_2,~(e'_{13})_2$ satisfy Eq. (2) to (11), (16), (17). This boundary value problem involving $(u_i)_2,~ (u'_i)_2~ (i = 1,2,3),~ (\tau _{ij})_2, ~(\tau '_{ij})_2, ~ (i, j = 1, 2, 3,~(e_{12})_2,~(e_{13})_2,~ (e'_{12})_2,~(e'_{13})_2$ can be solved by using modified Green’s function technique developed by Maruyama (1966) and Rybicki (1971) and correspondence principle. According to them we get,

$$\begin{aligned} \bar{(u_1)}_2 (Q_1)= & {} \iint _{F}[(\bar{u_1})_2(p)]~G(P, Q_1) \,dx_3 \,dx_1~\text { in the layer} \nonumber \\ \end{aligned}$$

(52)

$$\begin{aligned} (\bar{u_1}')_2 (Q_2)= & {} \iint _{F}[(\bar{u_1})_2(p)]~G'(P, Q_2) \,dx_3 \,dx_1~ \text {in the half-space} \nonumber \\ \end{aligned}$$

(53)

where $Q_1(y_1, y_2, y_3),~ Q_2(y_1, y_2, y_3)$ are field points in the layer and half-space respectively and $P(x_1, x_2, x_3)$ is any point on the fault F and $[(u_1)_2(p)]$ is the magnitude of discontinuity of $u_1$ across F and G and $G'$ are Green’s function.

where

$$\begin{aligned}&G(P, Q_1) = \frac{\partial }{\partial x_2}[G_{12(1)}(P,Q_1) -G_{13(1)}(P, Q_1)]\\&G'(P, Q_2) = \frac{\partial }{\partial x_2}[G_{12(2)}(P,Q_2) -G_{13(2)}(P, Q_2)] \end{aligned}$$

Here

$$\begin{aligned} G_{12(1)}(P,Q_1)= & {} \int _0^{\infty }[A_1(\lambda )e^{-\lambda (y_3 - y_1)} + B_1(\lambda )e^{\lambda (y_3 - y_1)}]sin[{\lambda (x_2 - y_2)}]d\lambda \nonumber \\&-\frac{1}{[(y_1 - x_1)^2 + (y_2 - x_2)^2 + (y_3 - x_3)^2]^{(\frac{1}{2})}} \end{aligned}$$

(54)

$$\begin{aligned} G_{13(1)}(P, Q_1)= & {} \int _0^{\infty }[C_1(\lambda )e^{-\lambda (y_3 - y_1)} + D_1(\lambda )e^{\lambda (y_3 - y_1)}]cos[{\lambda (x_2 - y_2)}]d\lambda \nonumber \\&-\frac{1}{[(y_1 + x_1)^2 + (y_2 - x_2)^2 + (y_3 - x_3)^2]^{(\frac{1}{2})}}\end{aligned}$$

(55)

$$\begin{aligned} G_{12(2)}(P,Q_2)= & {} \int _0^{\infty }A_2(\lambda )e^{-\lambda (y_3 - y_1)}sin[{\lambda (x_2 - y_2)}]d\lambda \nonumber \\ G_{13(2)}(P, Q_2)= & {} \int _0^{\infty }C_2(\lambda )e^{-\lambda (y_3 - y_1)}cos[{\lambda (x_2 - y_2)}]d\lambda \frac{\partial }{\partial x_2}G_{12(1)}(P,Q_1)\nonumber \\= & {} \lambda \int _0^{\infty }[A_1(\lambda )e^{-\lambda (y_3 - y_1)} \nonumber \\&+B_1(\lambda )e^{\lambda (y_3 - y_1)}]cos[{\lambda (x_2 - y_2)}]d\lambda \nonumber \\&-\frac{y_2 - x_2}{[(y_1 - x_1)^2 + (y_2 - x_2)^2 + (y_3 - x_3)^2]^{(\frac{3}{2})}}\end{aligned}$$

(56)

$$\begin{aligned}&\frac{\partial }{\partial x_2} G_{13(1)}(P, Q_1) = (-\lambda )\int _0^{\infty }[C_1(\lambda )e^{-\lambda (y_3 - y_1)} \nonumber \\&-\ + D_1(\lambda )e^{\lambda (y_3 - y_1)}]sin[{\lambda (x_2 - y_2)}]d\lambda \nonumber \\&-\frac{y_2 - x_2}{[(y_1 + x_1)^2 + (y_2 - x_2)^2 + (y_3 - x_3)^2]^{(\frac{3}{2})}}\nonumber \\&\frac{\partial }{\partial x_2}G_{12(2)}(P,Q_2) = \lambda \int _0^{\infty }A_2(\lambda )e^{-\lambda (y_3 - y_1)}cos[{\lambda (x_2 - y_2)}]d\lambda \nonumber \\&\frac{\partial }{\partial x_2}G_{13(2)}(P, Q_2)= (-\lambda )\int _0^{\infty }C_2(\lambda )e^{-\lambda (y_3 - y_1)}sin[{\lambda (x_2 - y_2)}]d\lambda \nonumber \\ \end{aligned}$$

(57)

where

$$\begin{aligned}&A_1 = -\frac{1}{2\pi \Delta _1}\left[ e^{-\lambda (x_3 + x_1)} + \frac{1-{\gamma _1}}{1 + {\gamma _1}} e^{-\lambda (2 h_1 - x_3 + x_1)}\right] \\&B_1 = \frac{1}{2\pi \Delta _1}\frac{\gamma _1 - 1}{\gamma _1 + 1}\left[ e^{-\lambda (2 h_1+x_3 - x_1)} + e^{-\lambda (2 h_1 - x_3 - x_1)}\right] \\&C_1 = -\frac{1}{2\pi \Delta _1}\left[ e^{-\lambda (x_3 - x_1)} - \frac{1-{\gamma _1}}{1 + {\gamma _1}} e^{-\lambda (2 h_1 - x_3 - x_1)}\right] \\&D_1 = \frac{1}{2\pi \Delta _1}\frac{\gamma _1 - 1}{\gamma _1 + 1}\left[ e^{-\lambda (2 h_1+x_3 + x_1)} - e^{-\lambda (2 h_1 - x_3 + x_1)}\right] \\&A_2 = - \frac{1}{\pi (\gamma _1 + 1)\Delta _1}\left[ e^{\lambda (x_3 - x_1)} + e^{-\lambda (x_3 + x_1)}\right] \\&C_2 = \frac{1}{\pi (\gamma _1 + 1)\Delta _1}\left[ e^{\lambda (x_3 + x_1)} - e^{-\lambda (x_3 - x_1)}\right] \end{aligned}$$

where $\gamma _1 =\frac{\mu _2}{\mu _1}~\text {and} ~ \mu _1, ~\mu _2$ are rigidity of elastic layer and elastic half-space respectively and $\lambda$ is Lame’s constant, $h_1$ is the thickness of elastic layer.

$$\begin{aligned} \Delta _1 = 1 - \frac{1 - \gamma _1}{1+ \gamma _1} e^{-2\lambda h_1} \end{aligned}$$

Now assume $d = x_3 + y_3,~ d_1 = x_2 - y_2,~ d_2 = x_3 - y_3,~ d_3 = x_1 - y_1$ and $d_4 = x_1 + y_1$

Then

$$\begin{aligned}&\frac{\partial }{\partial x_2}G_{12(1)}(P,Q_1) = \frac{\lambda }{2\pi \Delta _1} \left[ - \frac{(d + d_3)}{(d + d_3)^2 + d^2_1}\right. \nonumber \\&\quad - \frac{1 - \gamma _1}{1 + \gamma _1}\frac{(2 h_1 - d_2 + d_3)}{(2 h_1 - d_2 + d_3)^2 + (d^2_1)} +\nonumber \\&\frac{\gamma _1 - 1}{\gamma _1 + 1} \frac{(2 h_1 + d_2 - d_3)}{((2 h_1 + d_2 - d_3))^2 + (d^2_1)}+ \frac{\gamma _1 - 1}{\gamma _1 + 1}\nonumber \\&\quad \left. \frac{(2 h_1 - d - d_3)}{((2 h_1 - d - d_3))^2 + (d^2_1)} \right] + \frac{d_1}{[d^2_1 + d^2_2 + d^2_3]^\frac{3}{2}} \end{aligned}$$

(58)

$$\begin{aligned}&\frac{\partial }{\partial x_2}G_{13(1)}(P,Q_1) = \frac{-\lambda }{2\pi \Delta _1}\left[ - \frac{d_1}{(d - d_4)^2 + d^2_1} - \frac{ \gamma _1 - 1}{ \gamma _1 + 1}\frac{d_1}{(2 h_1 - d_2 - d_4)^2 + (d^2_1)}\right. \nonumber \\&+ \frac{\gamma _1 - 1}{\gamma _1 + 1} \frac{d_1}{(2 h_1 + d_2 + d_4)^2 + (d^2_1)}\nonumber \\&\left. + \frac{\gamma _1 - 1}{\gamma _1 + 1} \frac{d_1}{(2 h_1 - d + d_4)^2 + (d^2_1)}\right] + \frac{d_1}{[d^2_1 + d^2_2 + d^2_4]^\frac{3}{2}}\nonumber \\&\frac{\partial }{\partial x_2}G_{12(2)}(P, Q_2) = - \frac{\lambda }{\pi (\gamma _1 + 1)\Delta _1}\left[ \frac{(d_3 - d_2)}{(d_3 - d_2)^2 + d^2_1} + \frac{(d_3 + d)}{(d_3 + d)^2 + d^2_1}\right] \nonumber \\&\frac{\partial }{\partial x_2}G_{13(2)}(P, Q_2) = - \frac{\lambda }{\pi (\gamma _1 + 1)\Delta _1}\left[ \frac{d_1}{(d_2 + d_4)^2 + d^2_1} - \frac{(d_1)}{(d - d_4)^2 + d^2_1}\right] \nonumber \\ \end{aligned}$$

(59)

Therefore $G(P, Q_1) = \frac{\partial }{\partial x_2} G_{12(1)}(P, Q_1) - \frac{\partial }{\partial x_2} G_{13(1)}(P, Q_1)$

$$\begin{aligned}&= \frac{\lambda }{2\pi \Delta _1}\left[ - \frac{(d + d_3)}{(d + d_3)^2 + d^2_1} - \frac{1 - \gamma _1}{1 + \gamma _1}\frac{(2 h_1 - d_2 + d_3)}{(2 h_1 - d_2 + d_3)^2 + (d^2_1)} \right. \\&\quad + \frac{\gamma _1 - 1}{\gamma _1 + 1} \frac{(2 h_1 + d_2 - d_3)}{((2 h_1 + d_2 - d_3))^2 + (d^2_1)}\\&\quad \left. + \frac{\gamma _1 - 1}{\gamma _1 + 1} \frac{(2 h_1 - d - d_3)}{((2 h_1 - d - d_3))^2 + (d^2_1)}\right] \\&\quad + \frac{d_1}{[d^2_1 + d^2_2 + d^2_3]^\frac{3}{2}} + \frac{\lambda }{2\pi \Delta _1}[- \frac{d_1}{(d - d_4)^2 + d^2_1} \\&\quad - \frac{ \gamma _1 - 1}{\gamma _1 + 1}\frac{d_1}{(2 h_1 - d_2 - d_4)^2 + (d^2_1)} \\&\quad + \frac{\gamma _1 - 1}{\gamma _1 + 1} \frac{d_1}{((2 h_1 + d_2 + d_4))^2 + (d^2_1)}- \frac{\gamma _1 - 1}{\gamma _1 + 1} \frac{d_1}{((2 h_1 - d + d_4))^2 + (d^2_1)}]\\&\quad -\frac{d_1}{[d^2_1 + d^2_2 + d^2_4]^\frac{3}{2}} \end{aligned}$$

and

$$\begin{aligned}&G'(P, Q_2) = \frac{\partial }{\partial x_2} G_{12(2)}(P, Q_2) - \frac{\partial }{\partial x_2} G_{13(2)}(P, Q_2)\\&\quad = - \frac{\lambda }{\pi (\gamma _1 + 1)\Delta _1}[\frac{(d_3 - d_2)}{(d_3 - d_2)^2 + d^2_1} \\&\quad + \frac{(d_3 + d)}{(d_3 + d)^2 + d^2_1} - \frac{d_1}{(d_2 + d_4)^2 + d^2_1} + \frac{(d_1)}{(d - d_4)^2 + d^2_1}] \end{aligned}$$

$P(x_1, x_2, x_3)$ being a point on the fault F. Since the fault inclined at an angle $\theta$ and depth is $r_1$ from the free surface , then $0 \le x_2 \le D \cos \theta , ~0 \le x_3 \le D \sin \theta ~\text {and}~ x_2 = x_3~ \cot \theta$. A change in co-ordinate from $(x_1, x_2, x_3)$ to $(x'_1, x'_2, x'_3)$ connected by the relations :

$$\begin{aligned} x_1 = x'_1,~ x_2 = x'_2 \sin \theta + x'_3 \cos \theta ,~ x_3 = -x'_2 \cos \theta + x'_3 \sin \theta + r_1 , \end{aligned}$$

From $x_2 = x_3 ~\cot \theta$ we get $x'_2 = 0$

Then $x_1 = x'_1,$  $x_2 = x'_3 \cos \theta$,  $x_3 = x'_3 \sin \theta + r_1$ and $d x_1 = d x'_1$, $d x'_2 = 0$, $d x_3 = \sin \theta ~d x'_3$

$$\begin{aligned} \bar{(u_1)_2}(Q_1) = \iint _{F} [\bar{(u_1)}_2(p)] G(P, Q_1) ~dx_3 dx_1 \end{aligned}$$

Since the co-ordinate of the end points of the fault are taken w.r.t prime co-ordinate system as A $(-L, 0, 0)$ and B (L, 0, 0) respectively then the limit of the integration of $x'_1$ is $-L$ to L. Also w.r.t prime co-ordinate system the width of the fault is D then the limit of $x'_3$ is taken as 0 to D.

Then $\bar{(u_1)_2}(Q_1)= \int _{-L}^{L} \int _{0}^{D} U_1 (p)f(x'_1, x'_3)G(P, Q_1) \sin \theta ~dx'_3 dx'_1$

$$\begin{aligned} = U_1(p) \phi (y_1, y_2, y_3) \end{aligned}$$

Taking inverse Laplace transform we get,

$$\begin{aligned}&=(u_1)_2(Q_1) = \frac{U_1(t_1)}{2 \pi }\phi (y_1, y_2, y_3) \\&\quad H(t_1) , \end{aligned}$$

where $H(t_1)$ is the Heaviside step function, $t_1 = t - T_1$ and

$$\begin{aligned}&\phi (y_1, y_2, y_3 ) = \int _{-L}^{L} \int _{0}^{D}f(x'_1, x'_3)G(P, Q_1)\sin \theta ~ dx'_3 dx'_1 \\&\quad = \int _{-L}^{L} \int _0^{D} f(x'_1, x'_3)(\frac{\lambda }{2 \pi \Delta _1}\left[ -A_{11} - \frac{1 - \gamma _1}{1 + \gamma _1} A_{12}\right. \\&\qquad \quad +\frac{\gamma _1 - 1}{\gamma _1 + 1} A_{13} + \frac{\gamma _1 - 1}{\gamma _1 + 1} A_{14} - B_{11} - \frac{\gamma _1 - 1}{\gamma _1 + 1} B_{12} \\&\qquad \quad \left. + \frac{\gamma _1 - 1}{\gamma _1 + 1} B_{13} - \frac{\gamma _1 - 1}{\gamma _1 + 1} B_{14}\right] + A_{15} - B_{15})~\sin \theta ~ dx'_3 ~dx'_1 \end{aligned}$$

where

$$\begin{aligned}&A_{11}= \frac{d + d_3}{(d + d_3)^2 +d^2_1}\\&\qquad \qquad = \frac{(y_3 - y_1 + x_3 + x_1)}{(y_3 - y_1 + x_3 + x_1)^2 + (x_2 - y_2)^2} \\&\qquad \qquad =\frac{(y_3 - y_1 + x'_3 \sin \theta + r_1 + x'_1)}{(y_3 - y_1 + x'_3 \sin \theta + r_1 + x'_1)^2 + (x'_3 \cos \theta - y_2)^2} \\&\quad A_{12} = \frac{2 h_1 - d_2 + d_3}{(2 h_1 - d_2 + d_3)^2 + d_1^2}\\&\qquad \qquad = \frac{(2 h_1 - x_3 + y_3 + x_1 - y_1)}{(2 h_1 - x_3 + y_3 + x_1 - y_1)^2 + (x_2 - y_2)^2}\\&\qquad \qquad = \frac{(2 h_1 + y_3 - y_1 + x'_1 - x'_3 \sin \theta - r_1)}{(2 h_1 + y_3 - y_1 + x'_1 - x'_3 \sin \theta - r_1)^2 + (x'_3 \cos \theta - y_2)^2}\\&\quad A_{13} = \frac{2 h_1 + d_2 - d_3}{(2 h_1 + d_2 - d_3)^2 + d_1^2}\\&\qquad \qquad = \frac{(2 h_1 + x_3 - y_3 - x_1 + y_1)}{(2 h_1 + x_3 - y_3 - x_1 + y_1)^2 + (x_2 - y_2)^2}\\&\qquad \qquad = \frac{(2 h_1 + y_1 - y_3 + x'_3 \sin \theta + r_1 - x'_1)}{(2 h_1 + y_1 - y_3 + x'_3 \sin \theta + r_1 - x'_1)^2 + (x'_3 \cos \theta -y_2)^2}\\&\quad A_{14} = \frac{2 h_1 - d - d_3}{(2 h_1 - d - d_3)^2 + d_1^2}\\&\qquad \qquad = \frac{(2 h_1 -x_3 - y_3 - x_1 + y_1)}{(2 h_1 -x_3 - y_3 - x_1 + y_1)^2 + (x_2 - y_2)^2}\\&\qquad \qquad = \frac{(2 h_1 - y_3 + y_1 - x'_3 \sin \theta - r_1 - x'_1)}{(2 h_1 - y_3 + y_1 - x'_3 \sin \theta - r_1 - x'_1)^2 + (x'_3 \cos \theta - y_2)^2}\\&\quad A_{15} = \frac{d_1}{(d^2_1 + d^2_2 + d^2_3)^\frac{3}{2}}\\&\qquad \qquad = \frac{x_2 - y_2}{[(x_1 - y_1)^2 + (x_2 - y_2)^2 + (x_3 - y_3)^2]^\frac{3}{2}}\\&\qquad \qquad = \frac{x'_3 \cos \theta - y_2}{[(x'_1 - y_1)^2 + (x'_3 \cos \theta - y_2)^2 + (x'_3 \sin \theta + r_1 - y_3)^2]^\frac{3}{2}}\\&\quad B_{11} = \frac{d_1}{(d - d_4)^2 + d^2_1}\\&\qquad \qquad = \frac{(x_2 - y_2)}{(x_2 - y_2)^2 + (x_3 + y_3 - x_1 - y_1)^2}\\&\qquad \qquad = \frac{(x'_3 \cos \theta - y_2)}{(x'_3 \cos \theta - y_2)^2 +(x'_3 \sin \theta + r_1 + y_3 - x'_1 - y_1)^2}\\&\quad B_{12} = \frac{d_1}{(2 h_1 - d_2 - d_4)^2 + d^2_1}\\&\qquad \qquad = \frac{(x_2 - y_2)}{(x_2 - y_2)^2 + (2 h_1 - x_3 + y_3 - x_1 - y_1)^2}\\&\qquad \qquad = \frac{(x'_3 \cos \theta - y_2)}{(x'_3 \cos \theta - y_2)^2 +(2 h_1 - x'_3 \sin \theta - r_1 + y_3 - x'_1 - y_1)^2}\\&\quad B_{13} = \frac{d_1}{(2 h_1 + d_2 + d_4)^2 + d^2_1}\\&\qquad \qquad = \frac{(x_2 - y_2)}{(x_2 - y_2)^2 + (2 h_1 + x_3 - y_3 + x_1 + y_1)^2}\\&\qquad \qquad = \frac{(x'_3 \cos \theta - y_2)}{(x'_3 \cos \theta - y_2)^2 + (2 h_1 + x'_3 \sin \theta + r_1 - y_3 + x'_1 + y_1)^2}\\&\quad B_{14} = \frac{d_1}{(2 h_1 - d + d_4)^2 + d^2_1}\\&\qquad \qquad = \frac{(x_2 - y_2)}{(x_2 - y_2)^2 + (2 h_1 - x_3 - y_3 + x_1 +y_1)^2}\\&\qquad \qquad = \frac{(x'_3 \cos \theta - y_2)}{(x'_3 \cos \theta - y_2)^2 +(2 h_1 - x'_3 \sin \theta - r_1 - y_3 + x'_1 + y_1)^2} \\&B_{15} = \frac{d_1}{(d^2_1 + d^2_2 + d^2_4)^\frac{3}{2}}\\&\qquad \qquad = \frac{x_2 - y_2}{[(x_1 + y_1)^2 + (x_2 - y_2)^2 + (x_3 - y_3)^2]^\frac{3}{2}}\\&\qquad \qquad = \frac{x'_3 \cos \theta - y_2}{[(x'_1 + y_1)^2 + (x'_3 \cos \theta -y_2)^2 + (x'_3 \sin \theta + r_1 - y_3)^2]^\frac{3}{2}}\\&\qquad \qquad \bar{(u'_1)_2}(Q_2) = \iint _F [\bar{(u_1)}_2(p)] G'(P, Q_2) dx_3 dx_1\\&\qquad \qquad = \int _{-L}^{L} \int _{0}^{D} U_1 (p)f(x'_1, x'_3)G'(P, Q_2)~\sin \theta ~ dx'_3 dx'_1\\&\qquad \qquad = U_1(p) ~\psi (y_1, y_2, y_3)\\ \end{aligned}$$

Taking inverse Laplace transform we get,

$$\begin{aligned}(u'_1)_2(Q_2) = \frac{U_1(t_1)}{2 \pi }\psi (y_1, y_2, y_3) H(t_1),\end{aligned}$$

where $H(t_1)$ is the Heaviside step function and $t_1 = t - T_1$

and $\psi (y_1, y_2, y_3 ) = \int _{-L}^{L} \int _{0}^{D} f(x'_1, x'_3)G'(P, Q_2) ~\sin \theta ~ dx'_3~ dx'_1$

$$\begin{aligned}&= \int _{-L}^{L} \int _{0}^{D} f(x'_1, x'_3)\left( -\frac{\lambda }{\pi (\gamma _1 + 1) \Delta _1}[\frac{d_3 - d_2}{(d_3 - d_2)^2 + d^2_1} + \frac{d + d_3}{(d + d_3)^2 + (d_1)^2} \right. \nonumber \\&\quad \left. -\frac{d_1}{(d_4 + d_2)^2 + (d_1)^2} + \frac{d_1}{(d - d_4)^2 +d^2_1}]\right) ~\sin \theta ~ dx'_3~ dx'_1 \\&\quad = \int _{-L}^{L} \int _{0}^{D} f(x'_1, x'_3)\left( \frac{\lambda }{\pi (\gamma _1 + 1) \Delta _1}\right) \left[ - A'_{11} - A'_{12} + B'_{11} - B'_{12} \right] ~\sin \theta ~ dx'_3~ dx'_1 \end{aligned}$$

where

$$\begin{aligned}&A'_{11} = \frac{d_3 - d_2}{(d_3 - d_2)^2 + d^2_1}\\&\qquad \qquad = \frac{(x_1 - y_1 - x_3 + y_3)}{(x_1 - y_1 - x_3 + y_3)^2 + (x_2 - y_2)^2}\\&\qquad \qquad = \frac{(x'_1 - x'_3 \sin \theta - r_1 + y_3 - y_1)}{(x'_1 - x'_3 \sin \theta - r_1 + y_3 - y_1)^2 + (x'_3 \cos \theta - y_2)^2}\\&\quad A'_{12} = \frac{d + d_3}{(d + d_3)^2 + (d_1)^2}\\&\qquad \qquad = \frac{(x_1 - y_1 + x_3 + y_3)}{(x_1 - y_1 + x_3 + y_3)^2 + (x_2 - y_2)^2}\\&\qquad \qquad = \frac{(x'_1 + x'_3 \sin \theta + r_1 + y_3 - y_1)}{(x'_1 + x'_3 \sin \theta + r_1 + y_3 - y_1)^2 + (x'_3 \cos \theta - y_2)^2}\\&\quad B'_{11} = \frac{d_1}{(d_4 + d_2)^2 + (d_1)^2} \\&\qquad \qquad = \frac{(x_2 - y_2)}{(x_1 + y_1 + x_3 - y_3)^2 + (x_2 - y_2)^2}\\&\qquad \qquad = \frac{(x'_3 \cos \theta - y_2)}{(x'_3 \cos \theta - y_2)^2 + (x'_1 + y_1 + x'_3 \sin \theta + r_1 - y_3)^2} \\&\quad B'_{12} = \frac{d_1}{(d - d_4)^2 + d^2_1} \\&\qquad \qquad = \frac{(x_2 - y_2)}{(x_3 + y_3 - x_1 - y_1)^2 + (x_2 - y_2)^2} \\&\qquad \qquad = \frac{(x'_3 \cos \theta - y_2)}{(x'_3 \cos \theta - y_2)^2 + ( x'_3 \sin \theta + r_1 + y_3 -x'_1 - y_1 )^2} \end{aligned}$$