Comparison of ground deformation due to movement of a fault for different types of crack surface

Abstract

An analytical solution of deformation of a homogeneous, isotropic elastic layer of uniform thickness overlying a homogeneous, isotropic viscoelastic half-space of Burger medium due to movement of an infinite fault for different types of crack surface has been studied. The deformation by this fault has been compared with the deformation by an infinite fault situated in viscoelastic half-space of Burger medium. The expressions of displacement, stress and strain have been obtained in aseismic period (period in between two major seismic events) by using Green’s function technique and Laplace transform by applying suitable boundary conditions and initial conditions. Finally these displacement, stress and strain components are numerically computed with suitable values of the model parameters and the results thus obtained are presented graphically. A detailed study of these expressions may give some idea about the amount of displacement due to different types of fault movement and the nature of stress-strain accumulation across the earthquake fault. A Comparison of these results has also been analysed and the effect of change of inclinations and velocities of the fault movement has been studied. Such theoretical models may be used for obtaining greater insight into the earthquake processes in seismically active region.

Appendices

Appendix-I

1.1 For the fault situated in an elastic layer overlying viscoelastic half-space of Burger medium

Since $\bar{u_1}$ and $\bar{u'_1}$ are linear (from 11 and 12) and independent on $y_1$ and dependent on $y_2$ and $y_3$ then for solving the boundary value problem, we assume that $\bar{u_1}$ and ${\bar{u}}'_1$ is of the form

$$\begin{aligned} \bar{u_1}(y_2, y_3, s)= & {} \frac{(u_1)_0}{s} + A_1 y_2 + A_2 y_3 \end{aligned}$$

(33)

$$\begin{aligned} {\bar{u}}'_1(y_2, y_3, s)= & {} \frac{(u'_1)_0}{s} + A'_1 y_2 + A'_2 y_3 \end{aligned}$$

(34)

Now taking Laplace transform on all constitutive equations and boundary conditions, we get

For elastic layer

$$\begin{aligned} \bar{\tau _{12}}= & {} \mu _1 \frac{\partial \bar{u_1}}{\partial y_2} = \mu _1 \left[ \frac{1}{s}(\frac{\partial u_1}{\partial y_2})_0 + A_1\right] = \frac{1}{s} (\tau _{12})_0 + \mu _1 A_1 \end{aligned}$$

(35)

Similarly

$$\begin{aligned} \bar{\tau _{13}}= & {} \frac{1}{s} (\tau _{13})_0 + \mu _1 A_2 \end{aligned}$$

(36)

Now $\bar{e_{12}} = \frac{1}{2}\left[ \frac{\partial \bar{u_1}}{\partial y_2} + \frac{\partial \bar{u_2}}{\partial y_1}\right]$

            =$\frac{1}{2} \left[ \frac{1}{s} (\frac{\partial u_1}{\partial y_2})_0 + A_1\right]$

$(e_{12})_0 + g(s) = (e_{12})_0 + \frac{1}{2} A_1$

Therefore $A_1 = g(s)$

Now $\bar{\tau _{12}} = \frac{1}{s} (\tau _{12})_0 + g(s) \mu _1$

Taking inverse Laplace transform we get, $\tau _{12} = (\tau _{12})_0 + g(t) \mu _1$

Taking Laplace transform on boundary condition we get $\bar{\tau _{13}} =0$

Then from Eq. (36) it is found that $A_2 =0$

Therefore $\bar{u_1} = \frac{(u_1)_0}{s} + g(s) y_2$

Taking inverse Laplace transform we get $u_1 = (u_1)_0 + g(t)y_2$

Substituting the value of $A_1$ and $A_2$ in Eqs. (35) and (36) and by inverse Laplace transform we get

$\tau _{12} = (\tau _{12})_0 + g(t) \mu _1$ and $\tau _{13} = (\tau _{13})_0$

Therefore $e_{12} = (e_{12})_0 + g(t)$ and $e_{13} = (e_{13})_0$

For viscoelastic half-space

$$\begin{aligned} {\bar{\tau }}'_{12} = (\tau '_{12})_0 \frac{(p_1 + p_2 s)}{(1+p_1s+p_2 s^2)} + 2 A'_1 \frac{(q_1 s + q_2 s^2)}{(1+ p_1 s + p_2 s^2)} \end{aligned}$$

(37)

and

$$\begin{aligned} {\bar{\tau }}'_{13} = (\tau '_{13})_0 \frac{(p_1 + p_2 s)}{(1+p_1s+p_2 s^2)} + 2 A'_2 \frac{(q_1 s + q_2 s^2)}{(1+ p_1 s + p_2 s^2)} \end{aligned}$$

(38)

By using boundary conditions we get $A'_1 = g(s)$ and $A'_2 =0$

Therefore ${\bar{u}}'_1 = \frac{(u'_1)_0}{s} + g(s) y_2$

By taking inverse Laplace transform we get

$u'_1 = (u'_1)_0 + g(t) y_2$

From Eqs. (37) and (38) it is found that

$$\begin{aligned} \tau '_{12}= & {} \frac{(\tau '_{12})_0}{A} [(p_1 - p_2 r_1) e^{-r_1t} - (p_1 - p_2 r_2)e^{-r_2 t}] + \frac{q_2}{p_2} g(t) \\&+ \frac{q_1 m- p_1 q_2}{p_2 A} \int ^t_0 [(p_1 - p_2 r_1)e^{-r_2 (t-u)} \\&-(p_1 - p_2 r_2) e^{-r_1 (t-u)}] g(u) du + \frac{q_2}{p_2 A} \int ^t_0 [e^{-r_1 (t-u)} - e^{-r_2 (t-u)}] g(u) du \end{aligned}$$

and

$$\begin{aligned} \tau '_{13}= & {} \frac{(\tau '_{13})_0}{A} \left[ (p_1 - p_2 r_1) e^{-r_1 t} - (p_1 - p_2 r_2) e^{- r_2 t}\right] \\ \hbox {Now }{\bar{e}}'_{12}= & {} \frac{1}{2}\left[ \frac{\partial \bar{u'_1}}{\partial y_2} + \frac{\partial \bar{u'_2}}{\partial y_1}\right] \\= & {} \frac{1}{2} \left[ \frac{1}{s} (\frac{\partial u'_1}{\partial y_2})_0 + A'_1\right] \\= & {} \frac{1}{s} (e'_{12})_0 + g(s) \end{aligned}$$

Taking inverse Laplace transform

$e'_{12} = (e'_{12})_0 + g(t)$

Similarly

$e'_{13} = (e'_{13})_0$

To solve the boundary value problem after the fault movement a suitable modified form of Green’s function technique has been developed by Maruyama (1966) and Rybicki (1971) and following them we get,

For elastic layer

$$\begin{aligned} \bar{(u_1)}_2 (Q_1)= & {} \int _{F_1}[(\bar{u_1})_2(P_1)]~~[G_{13}(Q_1,~P_1) dx_2 - G_{12}(Q_1,~P_1) ~dx_3] \end{aligned}$$

(39)

where $Q_1(y_1,~y_2,~y_3)$ is the field point in the layer and $P_1(x_1, ~ x_2,~ x_3)$ is any point on the fault $F_1$ and $[(\bar{u_1})_2 (P_1)]$ is the magnitude of discontinuity in $(\bar{u_1})_2$ across $F_1$ at $P_1$.

For viscoelastic half-space

$$\begin{aligned} \bar{(u}'_1)_2 (Q'_1)= & {} \int _{F_1}[({\bar{u}}'_1)_2(P_1)]~~[G'_{13}(Q'_1,~P_1) dx_2 - G'_{12}(Q'_1,~P_1) ~dx_3] \end{aligned}$$

(40)

where $Q'_1(y_1,~y_2,~y_3)$ is any point in the half-space.

In Eq. (39), $G_{13} (Q_1, P_1) = \mu _1 \frac{\partial }{\partial x_3} G_1 (Q_1, P_1)$

                 and $G_{12} (Q_1, P_1) = \mu _1 \frac{\partial }{\partial x_2} G_1 (Q_1, P_1)$

where

$G_1 (Q_1, P_1){=}-\frac{1}{2\pi \mu _1} [\ln \sqrt{(x_2 {-} y_2)^2 {+} (x_3 {-} y_3)^2} {+} \ln \sqrt{(x_2 - y_2)^2 + (x_3{+}y_3)^2}{+} \sum _{m=1}^{\infty } (\frac{\mu _1 - \mu _2}{\mu _1{-}\mu _2})^m \{ln \sqrt{(x_2{-}y_2)^2{+}(x_3{-}2mH-y_3)^2}{+}\ln \sqrt{(x_2{-}y_2)^2{+} (x_3 -2mH+y_3)^2}{+} \ln \sqrt{(x_2{-}y_2)^2{+} (x_3{+}2mH-y_3)^2}{+} \ln \sqrt{(x_2 - y_2)^2 + (x_3 + 2mH+ y_3)^2} \} ]$

For half-space

$$\begin{aligned} G'_{13} (Q'_1, P_1) = \mu _1 \frac{\partial }{\partial x_3} G'_1 (Q'_1, P_1) \end{aligned}$$

and

$$\begin{aligned} G'_{12} (Q'_1, P_1) = \mu _1 \frac{\partial }{\partial x_2} G'_1 (Q'_1, P_1) \end{aligned}$$

where

$G'_1 (Q'_1, P_1)=-\frac{1}{\pi (\mu _1 + \mu _2)}[\ln \sqrt{(x_2 - y_2)^2 + (x_3 - y_3)^2} + \ln \sqrt{(x_2{-}y_2)^2{+} (x_3{+}y_3)^2} {+} \sum _{m=1}^{\infty } (\frac{\mu _1 - \mu _2}{\mu _1 - \mu _2})^m \{\ln \sqrt{(x_2 - y_2)^2 + (x_3 +2mH-y_3)^2} + \ln \sqrt{(x_2 - y_2)^2 + (x_3 +2mH+y_3)^2} \} ]$

Fig. 17

Rotation of axes $(x_1, x_2, x_3)$ to $(x'_1, x'_2, x'_3)$ through an angle $\theta$ with field point Q and fault point P

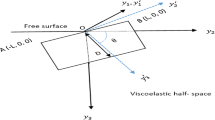
Now $P(x_1, x_2, x_3)$ being a point on the fault $F_1$. Since the fault inclined at an angle $\theta _1=\theta$ then $0 \le x_2 \le D \cos \theta , ~0 \le x_3 \le D \sin \theta ~\text {and}~ x_2 = x_3~ \cot \theta$. To perform the integration along the fault plane, a change in co-ordinate from $(x_1, x_2, x_3)$ to $(x'_1, x'_2, x'_3)$ is introduced which is shown in Fig. 17.

By Fig. 17b, using projection technique

$$\begin{aligned} x_1= & {} x'_1,\\ x_2= & {} \hbox {projection of }x'_2\hbox { on }x_2 +\hbox { projection of }x'_3\hbox { on }x_2\\= & {} x'_2 \cos (90^\circ -\theta ) + x'_3 \cos \theta \\= & {} x'_2 \sin \theta + x'_3 \cos \theta ,\\ x_3= & {} \hbox {projection of }x'_2\hbox { on }x_3 + \hbox {projection of }x'_3\hbox { on }x_3\\= & {} -x'_2 \cos (180^\circ -\theta ) +x'_3 \cos (90^\circ -\theta ) \\= & {} -x'_2 \cos \theta + x'_3 \sin \theta , \end{aligned}$$

From Fig. 17c, $\frac{x_2}{h}=\sin (90^\circ -\theta )=\cos \theta$ and $\frac{x_3}{h}=\sin \theta$

We get $x_2 = x_3 \cot \theta$

Then $x'_2 = 0$ and $0 \le x'_3 \le D$ on the fault $F_1$.

A change in co-ordinate axes from $(x_1,~x_2,~x_3)$ to $(x'_1,~x'_2,~x'_3)$ connected by the relations

$$\begin{aligned} \left. \begin{aligned} x_1=&x'_1 \\ x_2 =&x'_2 \sin \theta + x'_3 \cos \theta \\ x_3 =&-x'_2 \cos \theta + x'_3 \sin \theta \end{aligned}\right\} \end{aligned}$$

(41)

From $x_2 = x_3 \cot \theta$ we get $x'_2 = 0$

Then for elastic layer ($0 \le y_3 \le H$)

$(\bar{u_1})_2(Q_1) = \frac{U_1(s)}{2 \pi } \frac{1}{s} \int _0^D f(x'_3)[\frac{y_2 \sin \theta - y_3 \cos \theta }{A_1} + \frac{y_2 \sin \theta + y_3 \cos \theta }{A_2}] d x'_3 + \sum _{m=1}^{\infty } (\frac{\alpha }{\beta })^m A_m(t_1) \int _0^D f(x'_3) [\frac{y_2 \sin \theta - y_3 \cos \theta - 2mH \cos \theta }{A_3} + \frac{y_2 \sin \theta + y_3 \cos \theta - 2mH \cos \theta }{A_4} + \frac{y_2 \sin \theta - y_3 \cos \theta + 2mH \cos \theta }{A_5} + \frac{y_2 \sin \theta + y_3 \cos \theta + 2mH \cos \theta }{A_3}] dx'_3$

Taking inverse Laplace transform we get,

$(u_1)_2 = \frac{U_1(t_1)}{2 \pi } H(t_1) \psi (y_2, y_3, t)$

where $\psi {=} \int _0^D f(x'_3)[\frac{y_2 \sin \theta - y_3 \cos \theta }{A_1} + \frac{y_2 \sin \theta + y_3 \cos \theta }{A_2}] d x'_3 + \sum _{m{=}1}^{\infty } (\frac{\alpha }{\beta })^m A_m(t_1) \int _0^D f(x'_3) [\frac{y_2 \sin \theta - y_3 \cos \theta - 2mH \cos \theta }{A_3} + \frac{y_2 \sin \theta + y_3 \cos \theta - 2mH \cos \theta }{A_4} + \frac{y_2 \sin \theta - y_3 \cos \theta + 2mH \cos \theta }{A_5} +\frac{y_2 \sin \theta + y_3 \cos \theta + 2mH \cos \theta }{A_3}] dx'_3$

For viscoelastic half-space ($y_3 >H$)

$({\bar{u}}'_1)_2 (Q'_1) = \frac{\mu _1}{(\mu _1 + \mu _2)} \frac{U_1(s)}{\pi } [\int _0^D f(x'_3)[\frac{y_2 \sin \theta - y_3 \cos \theta }{A_1} + \frac{y_2 \sin \theta + y_3 \cos \theta }{A_2} dx'_3 + \sum _{m = 1}^{\infty } (\frac{\mu _1 - \mu _2}{\mu _1 + \mu _2})^m \int _0^D f(x'_3) \{\frac{y_2 \sin \theta + 2mH \cos \theta - y_3 \cos \theta }{A_5} + \frac{y_2 \sin \theta + 2mH\cos \theta + y_3 \cos \theta }{A_6}\} dx'_3]$

$=\frac{U_1(s)}{\pi } \phi$

Taking inverse Laplace transform we get,

$(u'_1)_2 = \frac{U_1(t_1)}{\pi } H(t_1) \phi$

where $\phi {=} \frac{\mu _1}{\pi (\mu _1 {+} \mu _2)}[\int _0^D f(x'_3)[\frac{y_2 \sin \theta - y_3 \cos \theta }{A_1} + \frac{y_2 \sin \theta + y_3 \cos \theta }{A_2} dx'_3 + \sum _{m = 1}^{\infty } (\frac{\mu _1 - \mu _2}{\mu _1 + \mu _2})^m \int _0^D f(x'_3) \{\frac{y_2 \sin \theta + 2mH \cos \theta - y_3 \cos \theta }{A_5} + \frac{y_2 \sin \theta + 2mH\cos \theta + y_3 \cos \theta }{A_6}\} dx'_3]$

and

$$\begin{aligned} A_1= & {} {x'_3}^2 - 2 x'_3 (y_2 \cos \theta + y_3 \sin \theta ) + {y_2}^2+{y_3}^2 \\ A_2= & {} {x'_3}^2 - 2 x'_3 (y_2 \cos \theta - y_3 \sin \theta ) + {y_2}^2+{y_3}^2 \\ A_3= & {} {x'_3}^2 - 2x'_3 (y_2 \cos \theta + y_3 \sin \theta + 2mH \sin \theta ) + {y_2}^2 + {y_3}^2 + 4y_3mH + 4m^2H^2 \\ A_4= & {} {x'_3}^2 - 2x'_3 (y_2 \cos \theta - y_3 \sin \theta + 2mH \sin \theta ) + {y_2}^2 + {y_3}^2 - 4y_3mH + 4m^2H^2 \\ A_5= & {} {x'_3}^2 - 2x'_3 (y_2 \cos \theta + y_3 \sin \theta - 2mH \sin \theta ) + {y_2}^2 + {y_3}^2 - 4y_3mH + 4m^2H^2 \\ A_6= & {} {x'_3}^2 - 2x'_3 (y_2 \cos \theta - y_3 \sin \theta - 2mH \sin \theta ) + {y_2}^2 + {y_3}^2 + 4y_3mH + 4m^2H^2 \\ \hbox {s}= & {} \frac{\mu _2}{\mu _1}, \alpha = \frac{\mu _1}{\mu _2} - 1, \beta = \frac{\mu _1}{\mu _2} + 1 \\ a_1= & {} \frac{mu_1 \mu _2}{\eta (\mu _1 + \mu _2)}, b_1 = \frac{2 \mu _1 {\mu _2}^2}{\eta ({\mu _1}^2 - {\mu _2}^2)} \\ A_m (t_1)= & {} U(t_1) + \sum _{r = 1}^m {^m}c_r (b_1)^r \int _0^{t_1} U(\tau ) \frac{(t_1 - \tau )^{r-1}}{(r-1)!} e^{- a_1 (t_1 - \tau )} d\tau \\ \psi _2= & {} \frac{\partial \psi }{\partial y_2}\hbox { and } \psi _3 = \frac{\partial \psi }{\partial y_3} \\ \phi _2= & {} \frac{\partial \phi }{\partial y_2}\hbox { and }\phi _3 = \frac{\partial \phi }{\partial y_3} \end{aligned}$$

Appendix-II

1.1 For the fault situated in viscoelastic half-space of Burger medium

We are found from 24 that $\bar{V_1}$ is linear and independent on $z_1$ and dependent on $z_2$ and $z_3$ then for solving the boundary value problem before the fault movement, it is customary to assume that

$$\begin{aligned} \bar{v_1} = \frac{(v_1)_0}{s} + B_1 z_2 + B_2 z_3 \end{aligned}$$

(42)

Taking Laplace transform on all constitutive equations and then by using Eq. (42) we get,

$$\begin{aligned} \bar{\chi _{12}}= & {} \frac{(p'_1 + p'_2s) (\chi _{12})_0 + (q'_1 s + q'_2 s^2)(B_1)}{(1+p'_1s + p'_2 s^2)} \end{aligned}$$

(43)

$$\begin{aligned} \bar{\chi _{13}}= & {} \frac{(p'_1 + p'_2s) (\chi _{13})_0 + (q'_1 s + q'_2 s^2)(B_2)}{(1+p'_1s + p'_2 s^2)} \end{aligned}$$

(44)

Taking Laplace transform on boundary conditions we get,

$\bar{\chi _{12}} \rightarrow \chi _{\infty } (s) = \chi _{\infty }(0) (\frac{1}{s} + \frac{k}{s^2})~ \text {as} |z_2| \rightarrow 0$

$\bar{\chi _{13}} = 0$ on $z_3 =0$ and $\bar{\chi _{13}} \rightarrow 0$ as $z_3 \rightarrow \infty$

Using boundary conditions and then from Eqs. (43)and (44) we get,

$B_1 = \frac{(1+p'_1s + p'_2s^2)}{2s (q'_1 + q'_2 s)} \left[ \chi _{\infty }(s) - \frac{(p'_1 + p'_2 s) \chi _{\infty } (0)}{(1 + p'_1 s + p'_2 s^2)}\right]$ and $B_2 = 0$

Therefore Eq. (42) becomes

$\bar{v_1} = \frac{(v_1)_0}{s} + \frac{(1+p'_1s + p'_2s^2)}{2s (q'_1 + q'_2 s)} \left[ \chi _{\infty }(s) - \frac{(p'_1 + p'_2 s) \chi _{\infty } (0)}{(1 + p'_1 s + p'_2 s^2)}\right] z_2$

whose inverse Laplace transform results in the following:

$$\begin{aligned} v_1= & {} (v_1)_0 + \frac{\chi _{\infty }(0)}{q'_1}\left[ t-\frac{q'_2}{q'_1}(1-e^{-\frac{q'_1 t}{q'_2}}) + k\left\{ \frac{t^2}{2} + \frac{q'_2}{q'_1}\left( \frac{q'_2}{q'_1}\left( 1-e^{-\frac{q'_1 t}{q'_2}}\right) -t\right) \right. \right. \\&\left. \left. + p'_1\left( t-\frac{q'_2}{q'_1}\left( 1-e^{-\frac{q'_1 t}{q'_2}}\right) \right) + p'_2 \left( 1-e^{-\frac{q'_1 t}{q'_2}}\right) \right\} \right] z_2 \end{aligned}$$

From Eqs. (43) and (44) it is found that

$$\begin{aligned} \chi _{12}= & {} \frac{(\chi _{12})_0}{A'}[(p'_1 - p'_2 r'_1)e^{-r'_1 t} - (p'_1 - p'_2 r'_2) e^{-r'_2 t}] \\&+ \left[ \chi _{\infty }(t) - \frac{\chi _{\infty }(0)}{A'}\{(p'_1 - p'_2 r'_1)e^{-r'_1 t} - (p'_1 - p'_2 r'_2) e^{-r'_2 t}\}\right] \end{aligned}$$

and

$\chi _{13} = \frac{(\chi _{13})_0}{A'}\left[ (p'_1 - p'_2 r'_1)e^{-r'_1 t} - (p'_1 - p'_2 r'_2) e^{-r'_2 t}\right]$

$$\begin{aligned} \hbox {Therefore }\omega _{12}= & {} \frac{(\omega _{12})_0}{2} + \frac{\chi _{\infty }(0)}{2 q'_1}\left[ t-\frac{q'_2}{q'_1}\left( 1-e^{-\frac{q'_1 t}{q'_2}}\right) \right. \\&+ k\left\{ \frac{t^2}{2} + \frac{q'_2}{q'_1}\left( \frac{q'_2}{q'_1}\left( 1-e^{-\frac{q'_1 t}{q'_2}}\right) -t\right) \right. \\&\left. \left. + p'_1\left( t-\frac{q'_2}{q'_1}\left( 1-e^{-\frac{q'_1 t}{q'_2}}\right) \right) + p'_2 (1-e^{-\frac{q'_1 t}{q'_2}})\right\} \right] \end{aligned}$$

and $\omega _{13} = \frac{(\omega _{13})_0}{2}$

To solve the boundary value problem after the fault movement a suitable modified form of Green’s function technique has been developed by Maruyama (1966) and Rybicki (1971). From this Greens function technique,

Let $Q_2 (z_1, z_2, z_3)$ be the observational point in the medium and $P_1$ be dislocation point on the fault $F_2$.

$$\begin{aligned} \bar{(v_1)}_2 (Q_2)= & {} \int _{F_2}[({\bar{v}}_1)_2(P_1)]~~[G''_{13}(Q_2,~P_1) dx_2 - G''_{12}(Q_2,~P_1) ~dx_3] \nonumber \\ \hbox {where} ~~~~G''_{12}(Q_2, P_1)= & {} \frac{1}{2 \pi } \left[ \frac{z_2 - x_2}{L^2} + \frac{z_2 - x_2}{M^2}\right] \nonumber \\ G''_{13}(Q_2, P_1)= & {} \frac{1}{2 \pi } \left[ \frac{z_3 - x_3}{L^2} - \frac{z_3 + x_3}{M^2}\right] \nonumber \\ L^2= & {} (z_2 - x_2)^2 + (z_3 - x_3)^2\nonumber \\ M^2= & {} (z_2 - x_2)^2 + (z_3 + x_3)^2 \end{aligned}$$

(45)

Fig. 18

Rotation of axes $(x_1, x_2, x_3)$ to $(x'_1, x'_2, x'_3)$ through an angle $\theta$ with field point Q and fault point P

Now $P(x_1, x_2, x_3)$ being a point on the fault $F_2$. Since the fault inclined at an angle $\theta _2=\theta$ then $0 \le x_2 \le D \cos \theta , ~0 \le x_3 \le D \sin \theta ~\text {and}~ x_2 = x_3~ \cot \theta$. To perform the integration along the fault plane, a change in co-ordinate from $(x_1, x_2, x_3)$ to $(x'_1, x'_2, x'_3)$ is introduced which is shown in Fig. 18.

By Fig. 18b, using projection technique

$$\begin{aligned} x_1= & {} x'_1,\\ x_2= & {} \hbox {projection of }x'_2\hbox { on }x_2 +\hbox { projection of }x'_3\hbox { on }x_2\\= & {} x'_2 \cos (90^\circ -\theta ) + x'_3 \cos \theta \\= & {} x'_2 \sin \theta + x'_3 \cos \theta ,\\ x_3= & {} \hbox {projection of }x'_2\hbox { on }x_3 +\hbox { projection of }x'_3\hbox { on }x_3\\= & {} -x'_2 \cos (180^\circ -\theta ) +x'_3 \cos (90^\circ -\theta ) \\= & {} -x'_2 \cos \theta + x'_3 \sin \theta , \end{aligned}$$

From Fig. 18c, $\frac{x_2}{h}=\sin (90^\circ -\theta )=\cos \theta$ and $\frac{x_3}{h}=\sin \theta$

We get $x_2 = x_3 \cot \theta$

Then $x'_2 = 0$ and $0 \le x'_3 \le D$ on the fault $F_2$. A change in co-ordinate axes from $(x_1,~x_2,~x_3)$ to $(x'_1,~x'_2,~x'_3)$ connected by the relations

$$\begin{aligned} \left. \begin{aligned} x_1=&x'_1 \\ x_2 =&x'_2 \sin \theta + x'_3 \cos \theta \\ x_3 =&-x'_2 \cos \theta + x'_3 \sin \theta \end{aligned}\right\} \end{aligned}$$

(46)

From $x_2 = x_3 \cot \theta$ we get $x'_2 = 0$

Then $\bar{(v_1)}_2 (Q_2)= \frac{V'_1(s)}{2 \pi } \int _0^D \left[ \frac{z_2 \sin \theta - z_3 \cos \theta }{L^2} + \frac{z_2 \sin \theta + z_3 \cos \theta }{M^2}\right] f(x'_3) d x'_3$ $\bar{(v_1)}_2 (Q_2)$ = $\frac{V'_1(p)}{2 \pi } \xi (z_2, z_3 t)$

Taking inverse Laplace transform

$(v_1)_2 = \frac{V'_1(t_1)}{2 \pi } H(t_1) \xi (z_2, z_3 t)$

$$\begin{aligned} \hbox {where }\xi= & {} \int _0^D \left[ \frac{y_2 \sin \theta - y_3 \cos \theta }{L^2} + \frac{y_2 \sin \theta + y_3 \cos \theta }{M^2}\right] f(x'_3) d x'_3\ \hbox {and} \\ L^2= & {} {x'_3}^2 - 2 x'_3 (z_2 \cos \theta + z_3 \sin \theta ) + {y_2}^2 + {y_3}^2 \\ M^2= & {} {x'_3}^2 - 2 x'_3 (z_2 \cos \theta - z_3 \sin \theta ) + {y_2}^2 + {y_3}^2 \end{aligned}$$