1 Introduction

1.1 Background

The transition from traditional, inelastic, electricity demand to more flexible consumers, means that the paradigm of demand as a passive load is no longer valid since demand can react to price signals. By introducing prosumers, who can both consume and produce electricity, the grid tariffs should provide efficient price signals to align the optimal end-user decisions with efficient utilization of the power system at a larger scale to avoid a sub-optimal outcome as demonstrated in [1].

Grid tariffs are mostly implemented as fixed amounts (€/consumer), volumetric charges (€/kWh), and possibly capacity-based (€/kW) charges. Although variations exist, electricity network tariffs can generally be reduced to these three fundamental structures [2]. A general issue regarding network tariffs is that there does not exist an ideal policy since it is necessary to balance efficiency with other aspects [3]. One principal problem of current grid tariff structures in Europe is that they primarily consist of fixed and volumetric charges. This is, as presented in [4,5,6], not a sufficient proxy for the overall network costs since the main cost driver is the need for sufficient capacity to handle peak loads.

Capacity-based tariffs may be a prospective solution since they more accurately reflect the upstream grid costs than volumetric tariffs as argued in [7, 8]. However, a flat capacity-based tariff scheme provides incentives to stay below the maximum usage in all hours, regardless of the congestion in the network. Furthermore, a flat capacity-based tariff neglects the fact that the grid load usually is well below the capacity.

The overall research question we consider in this paper is: How can we, by using fairly simple network tariffs, incentivize flexible end-users to efficiently adapt their consumption patterns? We address the problems concerning flat tariffs and present a novel approach by formulating the electricity grid tariff design problem with a bilevel structure in the context of prosumers at the end-user level. Various network tariff structures are optimized subject to the prosumers best response in a game theoretical framework, which is benchmarked against a centralized system optimization.

1.2 Literature review

Overall, the existing literature modeling electricity grid tariffs can be assigned to two different groups. One major group focuses on the impact of various tariff structures for specific consumer types and technologies [9,10,11,12]. In general, this line of research is able to assess the impact of various tariff schemes on these stakeholders. The approach in this research area differs from our research because they treat the grid tariffs as exogenous parameters and do not attempt to design the tariffs optimally by considering the consumers and the grid as an integrated system.

The second line of research is more closely related to our work, approaches the subject of electricity grid tariffs by determining an equilibrium between end-users and a grid entity (e.g., DSO). This means that it is necessary to consider a bilevel problem. Using an equilibrium approach, [13,14,15] formulate a problem by defining the lower level as a system of optimization problems and iteratively calculating the tariffs until network costs equal the charges. The aforementioned approaches are limited to selecting the level of flat tariffs, and do not allow for consideration of different scenarios and determining off-peak periods since a loop-based model structure is employed.

Equilibrium models are widely applied to power market research because of the ability to represent various market structures and interactions between market participants. The properties of the tariff design problem addressed in this paper are consistent with Stackelberg-type games [16], which are characterized by a leader who moves first and one or more followers acting optimally in response to the leader’s decisions. Games with a Stackelberg structure can be formulated as mathematical problems with equilibrium constraints (MPECs) [17]. MPEC models are used for investigating aspects such as strategic investment decisions [18,19,20], strategic bidding in electricity markets [21, 22] and for determining optimal generation schedules and prices to minimize total consumer payments [23]

The MPEC approach has recently been used for various forms of indirect load control where some entity tries to induce a change in end-user behaviour through pricing mechanisms. In [24], the Stackelberg relationship between retailers and consumers is formulated as a MPEC where the upper-level retailer tries to maximize its profit by choosing the price-signal subject to the response by consumers. Furthermore, [25] formulate a model of a similiar structure for the interaction between an EV aggregator and EV consumers.

In this paper we consider a DSO as the leader in a Stackelberg-type game. In this context, [26] formulates a DSO interacting with power markets to derive trading strategies. Furthermore the bi-level relationshop between a DSO and aggregators is modeled with direct contracting of the aggregator resources in [27]. The authors in [28] take a top-down approach by formulating a MPEC to determine the optimal DSO policy tailored to control feed-in to the grid. The policy mechanism is modeled directly as a technical limitation on each end-user rather than formulating price signals for indirect load control.

Although the MPEC formulation is increasingly being used in the context of decentralized energy resources, the related literature is limited and the authors have not identified any prior papers which formulate a MPEC approach for investigating indirect load control through grid tariffs to provide incentives for efficient end-user coordination.

1.3 Contributions

Fundamentally, grid tariffs is a price signal that comes on top of the electricity price. However, due to the need for simplicity, it is not possible to tailor the tariff for each time step. Rather, a structure where cost components are predictable for the end-user is needed.

In this work, we address the gap in the literature concerning tariff optimization as a tool for indirect load control and analyze how a fairly simple tariff scheme can be used to activate end-user flexibility and efficiently reduce grid load by developing an MPEC. This paper provides a novel method of determining grid tariffs that can provide more efficient grid pricing and reduce total system costs. The primary contributions of this paper are as follows:

  • Development of a stochastic MPEC model for optimizing electricity network tariffs subject to active end-users. The model formulates end-users responding to the tariffs determined by the DSO. Uncertainty is represented by stochastic demand, market prices, and PV output.

  • Formulation of an electricity network tariff structure capable of incentivizing flexible end-users to efficiently shift their electricity consumption.

  • Analyses that highlight the model features and assess how demand flexibility can be efficiently activated by grid tariffs in a setting with limited grid capacity and decentralized decision-making. The case studies are benchmarked against a system optimal solution with centralized decision-making.

1.4 Structure of paper

The rest of this paper is structured as follows. Section 2 describes the leader and follower optimization problems and how these are coupled in an overall system. A description of both a system optimization model used for benchmarking and the MPEC formulation is provided. Furthermore, Sect. 3 describes reformulations and the computational setup used. Section 4 presents the case study results. Finally, conclusions are drawn in Sect. 5.

2 Model formulation

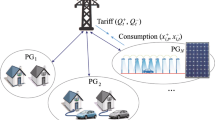
In this section, we formulate the lower-level and upper-level problems considered as part of the MPEC. Then, the resulting MPEC where the DSO decides the tariffs applied to the consumers as depicted in Fig. 1 is formulated.Footnote 1 An explanation of the symbols used is provided in “Appendix 1”.

Fig. 1
figure 1

Structure of the modeled bilevel tariff optimization problem

Full size image

The variables of the lower level (end-user) problems can be adapted for each scenario. This means that the end-users do not consider the stochasticity since all their decisions are scenario-dependent. The uncertainty of the problem is considered in the upper level since the DSO needs to set the tariffs non-anticipatively, based on the different realizations of load, PV generation and power prices. Each realization of the uncertain parameters induce a different response from the lower level. This forms a two-stage stochastic program within the bilevel structure of the MPEC model:

  • Planning stage: The DSO sets tariff levels and off-peak hours.

  • Operational stage: The end-users decides how to operate flexible resources and the DSO decides if load needs to be curtailed.

2.1 Lower-level formulation

The lower level comprise the end-users of electricity, which can be either consumers or prosumers. Lower-level decisions occur at the operational stage. The problem of the individual end-user is described as an optimization problem that is similar for both consumers and prosumers. However, for regular consumers, many of the variables will be zero as there are no generation resources or flexible load. A fully passive consumer will simply exhibit the specified demand on the grid without any decentralized decision-making involved. We indicate the dual variables associated with each of the constraints (5)–(9).

2.1.1 Objective function

We assume the objective of the end-users is to minimize their costs according to (1). Three scenario-dependent cost components are included: cost of purchasing power from the power market, \(Cost_{c,s}^P\), taxes, \(Cost_{c,s}^T\), and grid costs, \(Cost_{c,s}^G\). Note that the actual grid costs are not considered at the end-user level since these costs are imposed indirectly through the network tariffs.

$$\begin{aligned} Min: Cost_{c,s} = Cost_{c,s}^{P} + Cost_{c,s}^T + Cost_{c,s}^{G} \end{aligned}$$
(1)

Where the components of (1) are defined in (2)–(4).

$$\begin{aligned} Cost_{c,s}^{P}= & {} \sum _{h=1}^H(e_{c,s,h}^{I}\times (1+VAT)-e_{c,s,h}^{E})\times P_{s,h} \end{aligned}$$
(2)
$$\begin{aligned} Cost_{c,s}^T= (1+VAT)\times T\times \sum _{h=1}^{H}e_{c,s,h}^{I} \end{aligned}$$
(3)
$$\begin{aligned} Cost_{c,s}^{G}= (1 + VAT)\left( \sum _{h=1}^H(e_{c,s,h}^{I}- NM\times e_{c,s,h}^{E})\times vnt + c_{c,s}^{G}\times cnt\right) \end{aligned}$$
(4)

Note here the NM parameter that quantifies to which extent the electricity exports are subject to net metering:

  • \(NM = 1\): The end-user only pays volumetric charge for net imports.

  • \(NM = 0\): The end-user pays volumetric charge for all imports.

  • \(NM = -1\): The end-user pays volumetric charge for both imports and exports.

2.1.2 Energy balance

The energy balance of the prosumer is described by (5) and states that energy imports subtracted exports must be equal to fixed and flexible demand subtracted generation from PV.

$$\begin{aligned} \forall c, \forall s, \forall h: D_{c,s,h} + d_{c,s,h}^{\varDelta +} - g_{c,s,h} = e_{c,s,h}^{I} - e_{c,s,h}^{E} \quad (\lambda _{c,s,h}^{EB}) \end{aligned}$$
(5)

2.1.3 Flexible load

EV charging requires an amount of electric energy for each day. Therefore, (6) describes the total flexible load for each scenario. This means that a flexible consumer can choose when to consume the flexible load, as long as the total load across all hours in a scenario is equal to the specified amount.

$$\begin{aligned} \forall c, \forall s: D^{\varDelta -}_{c,s} = \sum _{h=1}^Hd_{c,s,h}^{\varDelta +} \quad (\lambda _{c,s}^{FL}) \end{aligned}$$
(6)

The maximum flexible load during each time step is limited by (7). This is analogous to EV charging capacity, which depend on the AC/DC converter.

$$\begin{aligned} \forall c, \forall s, \forall h: d^{\varDelta +}_{c,s,h} \le U^{\varDelta +}_{c,s,h} \quad (\mu _{c,s,h}^{FC}) \end{aligned}$$
(7)

2.1.4 Peak power

The capacity-based part of the grid tariff is based on the measured peak power that is either drawn from or injected to the grid. Therefore, the end-user has to subscribe to the maximum power according to (8). This determines the variable \(c_{c,s}^{G}\) which is subjected to the capacity-based tariff. However, during the off-peak hours set by the DSO (if \(op_{s,h} = 1\)), the constraint is relaxed to allow for increased grid utilization by not including measurements during those hours in the calculation.

$$\begin{aligned} \forall c, \forall s, \forall h: e_{c,s,h}^{I} + e_{c,s,h}^{E} \le c_{c,s}^{G} + D_c^{MAX}\times op_{s,h} \quad (\mu _{c,s,h}^{G}) \end{aligned}$$
(8)

2.1.5 PV generation

PV generation is described by (9) and has the option of curtailing generation in the case of situations with an over-production.

$$\begin{aligned} \forall c, \forall s, \forall h: g_{c,s,h} \le U^{PV}_c\times G_{c,s,h} \quad (\mu _{c,s,h}^{PV}) \end{aligned}$$
(9)

2.2 MCP formulation of lower level

The optimization problems of the end-users are linear and with convex constraints. Due to these properties, the individual optimization problems can be replaced by their Karush–Kuhn–Tucker (KKT) optimality conditions formulated as MCP conditions in (10)–(19) below.

$$\begin{aligned}&\forall c, \forall s, \forall h: (P_{s,h} + T + vnt)\times (1+VAT) - \lambda _{c,s,h}^{EB} + \mu _{c,s,h}^{G} \ge 0 \perp e_{c,s,h}^{I} \ge 0 \end{aligned}$$
(10)
$$\begin{aligned}&\forall c, \forall s, \forall h: -P_{s,h} - NM\times vnt\times (1+VAT) + \lambda _{c,s,h}^{EB} + \mu _{c,s,h}^{G} \ge 0 \perp e_{c,s,h}^{E} \ge 0 \end{aligned}$$
(11)
$$\begin{aligned}&\forall c, \forall s: (1+VAT)\times cnt - \sum _{h=1}^H\mu _{c,s,h}^{G} \ge 0 \perp c_{c,s}^G \ge 0 \end{aligned}$$
(12)
$$\begin{aligned}&\forall c, \forall s, \forall h: \lambda _{c,s,h}^{EB} - \lambda _{c,s}^{FL} + \mu _{c,s,h}^{FC} \ge 0 \perp d_{c,s,h}^{\varDelta +} \ge 0 \end{aligned}$$
(13)
$$\begin{aligned}&\forall c, \forall s, \forall h: -\lambda _{c,s,h}^{EB} + \mu _{c,s,h}^{PV} \ge 0 \perp g_{c,s,h}^{PV} \ge 0 \end{aligned}$$
(14)
$$\begin{aligned}&\forall c, \forall s, \forall h: e_{c,s,h}^{I} - e_{c,s,h}^{E} - D_{c,s,h} - d_{c,s,h}^{\varDelta +} + g_{c,s,h} = 0 \perp \lambda _{c,s,h}^{EB} \end{aligned}$$
(15)
$$\begin{aligned}&\forall c, \forall s, \forall h: c_{c,s}^G + D_c^{MAX}\times op_{s,h} - e_{c,s,h}^{I} - e_{c,s,h}^{E} \ge 0 \perp \mu _{c,s,h}^{G} \ge 0 \end{aligned}$$
(16)
$$\begin{aligned}&\forall c, \forall s, \forall h: U_c^{PV}\times G_{c,s,h} - g_{c,s,h}^{PV} \ge 0 \perp \mu _{c,s,h}^{PV} \ge 0 \end{aligned}$$
(17)
$$\begin{aligned}&\forall c, \forall s: \sum _{h=1}^Hd^{\varDelta +}_{c,s,h} -D^{\varDelta -}_{c,s}= 0 \perp \lambda _{c,j}^{FL} \end{aligned}$$
(18)
$$\begin{aligned}&\forall c, \forall s, \forall h: U^{\varDelta +}_{c,s,h} - d^{\varDelta +}_{c,s,h} \ge 0 \perp \mu _{c,s,h}^{FC} \ge 0 \end{aligned}$$
(19)

2.3 Upper-level formulation

The upper level comprise the DSO which is responsible for connecting the end-users to the electricity grid. Upper-level decisions include determining the grid tariffs at the planning stage and curtailment of load at the operational stage.

2.3.1 DSO costs

The DSO is responsible for building and maintaining the electricity grid. The costs related to the DSO are network losses and load curtailment costs. These costs related to the DSO’s activities are described by (20).

$$\begin{aligned} Cost^{DSO}_{s} = \sum _{h=1}^H(e_{s,h}^{G}\times L^G\times P_{s,h} + ls_{s,h}\times VLL) \end{aligned}$$
(20)

2.3.2 Transmission of electricity

The DSO needs to transfer electricity at each time step according to the total imports or exports generated by the end-users described by (21).

$$\begin{aligned} \forall s, \forall h: e_{s,h}^{G} = \left| \sum _{c=1}^C(e_{c,s,h}^{I} - e_{c,s,h}^{E})\right| \end{aligned}$$
(21)

It should be noted that due to the possibility of exports to the grid, (21) includes an absolute value function, which we handle as described in Sect. 3.1.1.

2.3.3 Interconnection capacity

The interconnection capacity needs to cover the electricity transferred less load curtailment according to (22). It should be noted that the effect of load curtailment is neglected in the lower level problem because it is assumed that the curtailment cost considered by the DSO (VLL) represents the end-user cost of curtailment.

$$\begin{aligned} \forall s, \forall h: F^{G} \ge e_{s,h}^{G} - ls_{s,h} \end{aligned}$$
(22)

In the case of curtailment due to transmission arising from exports to the grid (grid capacity violated and \(e_{s,h}^{G}\) is based on export), the load curtailment is interpreted as generation curtailment.

2.3.4 Total system costs

In the modeled system, costs occur both at the end-user and DSO levels. The total costs in the system are described by (23). The tariff costs are not included since these would be added to consumer costs and subtracted from the DSO’s costs, resulting in zero net contribution towards total costs. Therefore, neglecting cost recovery for the DSO, the grid tariffs are purely tools to incentivize end-user behavior in this model.Footnote 2

$$\begin{aligned} TC = \sum _{s=1}^SA\times W_s\times \left( Cost^{DSO}_{s} + \sum _{c=1}^C(Cost_{c,s}^{P} + Cost_{c,s}^T)\right) \end{aligned}$$
(23)

2.4 System optimization model

The benchmark case is a system optimization where all decisions are made centrally. This would for example be the case if the DSO could directly control EV charging at the consumer level. The system optimization means that the bilevel problem is replaced by a linear problem which considers all costs and technical restrictions both at the DSO and end-user level directly. The system optimization is formulated below:

$$\begin{aligned} \text {Min } TC \end{aligned}$$
(24)

Subject to technical constraints (5)–(9) and (21)–(22).

2.5 Bilevel model

Similar to the system optimization, we consider that the DSO tries to maximize social welfare by minimizing total costs. Therefore, the DSO considers not only it’s own costs, but also the end-user costs. Contrary to the system optimization, the DSO can not directly control resources on the end-user level. Instead, the lower-level response is included indirectly through the complementarity conditions. In this problem the DSO use indirect load control through tariffs to reduce the total system costs.

Using the previously defined equations, the bilevel model formulation becomes:

$$\begin{aligned} \text {Min } TC \end{aligned}$$
(25)

Subject to technical constraints (21)–(22) and complementarity conditions (10)–(19).

Note that the objectives of the end-users and the DSO coincides. Despite this property, it is not possible to translate the bilevel model to a single-level problem since we assume grid costs are passed on through grid tariffs rather than a perfect representation of the true DSO cost structure. Hence, the grid tariffs need to be optimized to provide the most efficient incentives that are possible within the boundary of the tariff design.

2.6 Limitations

This paper aims to tackle a complex issue on that span across different aggregation levels in the power system. The physical modeling of network and loads is simplified since the focus of this paper is on investigating different tariff structures to incentivize efficient temporal shifting of energy. Since we focus on balancing energy on an hourly timescale, voltage constraints are not considered. Furthermore, we consider the flexibility to be represented through flexible EV charging where the specified amount of energy needs to be satisfied for each scenario.

Despite these limitations, the modeling results are insightful for the following reasons:

  • The model is compatible with current pricing mechanisms that work on an hourly basis due to metering limitations. The model can also easily be adapted to subhourly resolutions in the case of more frequent metering.

  • EV charging represent a particularly flexible type of demand and should be considered when determining tariff policies.

  • Realistic grid tariff structures that can potentially be implemented within existing regulatory frameworks are considered.

3 Solution approach

3.1 Linearization methods

The model formulated in Sect. 2.5 contain two sources of nonlinearities:

  • Absolute value term in the upper-level constraint (21).

  • Complementarity conditions (10)–(19) in the MPEC formulation (shown as \(\perp\)).

The following sections will describe how the problem is reformulated to handle these computationally.

3.1.1 Line flow constraint

The amount of transferred electricity is described by an absolute value function (21) since it is the maximum of either imports or exports. However, since losses have nonnegative costs with nonnegative power market prices, a cost minimizing DSO will select the lowest amount of grid transfer possible. Therefore, equality (21) can be replaced by inequalities (26)–(27), which does not include absolute value terms, as long as power market prices are nonnegative.

$$\begin{aligned}&\forall s, \forall h: e_{s,h}^{G} \ge \sum _{c=1}^C(e_{c,s,h}^{I} - e_{c,s,h}^{E}) \end{aligned}$$
(26)
$$\begin{aligned}&\forall s, \forall h: e_{s,h}^{G} \ge \sum _{c=1}^C(e_{c,s,h}^{E} - e_{c,s,h}^{I}) \end{aligned}$$
(27)

3.1.2 Complementarity conditions

The complementarity conditions on the form:

$$\begin{aligned} f(x) \ge 0 \perp x \ge 0 \end{aligned}$$
(28)

Can be replaced by:

$$\begin{aligned} f(x) \ge 0, x \ge 0, f(x) \le \alpha \times M, x \le (1-\alpha )\times M \end{aligned}$$
(29)

Where \(\alpha\) is a binary variable and M is a large enough constant. However, choosing an appropriate value for M is important for numerical stability, but can be a challenging task in itself [29]. To overcome the issues concerning a “big-M” formulation, the complementarity conditions can also be transformed by using SOS type 1 variables as presented in [30]. Hence, (28) can be reformulated into the following:

$$\begin{aligned}&f(x) \ge 0, x \ge 0 \end{aligned}$$
(30)
$$\begin{aligned}&u = \frac{x + f(x)}{2} \end{aligned}$$
(31)
$$\begin{aligned}&v^+ - v^- = \frac{x-f(x)}{2} \end{aligned}$$
(32)
$$\begin{aligned}&u - (v^+ + v^-) = 0 \end{aligned}$$
(33)

Where \(v^+\), \(v^-\) are SOS type 1 variables.

The SOS type 1 based approach provides a global optimal solution in a computationally efficient way. In addition, we avoid having to specify an appropriate value for M to ensure that the complementarity conditions are not violated. Therefore, complementarity conditions (10)–(19) are linearized using the SOS type 1 approach, forming a MILP.

3.2 Computational set-up

The models are implemented in GAMS v27.3.0 and solved as LP for the benchmark case and MILP for the MPEC cases by CPLEX v12.9.0.0 on a personal computer with an Intel(R) Core(TM) i7-8850H 6-core CPU and 32GB of RAM.

3.2.1 System optimization

The system optimization is formulated as a linear problem which with the linearized line flow constraint can be solved directly by off the shelf optimization software.

3.2.2 MPEC

After the linearizations described in Sects. 3.1.1 and 3.1.2, the MPEC is reformulated into a MILP with SOS1 variables to handle the complementarity conditions. The resulting formulation can be directly solved with commercial MILP solvers. A relative gap tolerance of 1% was used in all cases.

The MPEC is computationlly challenging and the tractable problem size is limited. This is mainly due to the following aspects:

  • Linking of hourly problems within each scenario through the flexible charging constraint.

  • Upper-level decisions such as tariff levels which affect all scenarios.

Despite the computational limitations, it is possible to use this framework to investigate the efficiency of various tariff structures with flexible end-users.

4 Case studies

In this section, we present results for the following cases:

  • SO: System optimal solution

  • MPEC-F: MPEC with flat capacity based tariff (\(op_{s,h}\) fixed at zero).

  • MPEC-P: MPEC with capacity-based tariff and scenario dependent off-peak period selection (\(op_{s,h}\) binary and decided by DSO). The off-peak periods does not have to be equal across all scenarios.

  • MPEC-PN: MPEC with capacity-based tariff and off-peak period constrained by nonanticipativity (\(op_{s,h} = op_{h}\) binary and decided by DSO). In this case, the off-peak periods need to be the same in all scenarios.

MPEC-F is the case with the simplest form of a capacity-based tariff, where the measured peak load over all hours within a scenario determines the cost regardless of when it occurs. This creates an incentive for each end-user to flatten their load profile. In the MPEC-P and MPEC-PN case, we introduce the possibility of off-peak hours. Capacity usage during the off-peak hours are not measured so the end-users can have a high load during these hours without incurring extra costs. Off-peak hours creates an incentive for load-shifting to these hours, which can be beneficial in the case of low-load periods or periods with high injection of renewable energy in the distribution grid. The difference between the MPEC-P and MPEC-PN cases is that in the first case the off-peak hours can be different for each scenario while in the latter case, the off-peak hours need to be equal across all scenarios. These cases are benchmarked against the system optimal model (SO) to assess the efficiency of the various tariff schemes.

We assume that end-users pay volumetric charges on imports, but not exports and that the electricity is not net metered. Hence, a parameter setting for NM of zero is used in this paper. This is in line with current practice in several European countries.

4.1 Deterministic example

For simplicity, we first consider a deterministic example of one scenario with a fixed and a flexible load and limited grid capacity. The scenario comprise one day with two segments which are denoted segment 1 and 2, respectively. Segment 1 comprise the first 12 h of the day, while segment 2 comprise the second 12 h. The fixed load is high in the first segment, and low in the second segment. Furthermore, the electricity price is low in the first segment and high in the second segment. This means that we have a situation where fixed demand is high when electricity prices are low and opposite. Therefore, with limited grid capacity, it is beneficial for the grid if most of the flexible load occur in the high-price period to avoid load curtailment. An overview of the input data for the illustrative example is provided in Table 1.

Table 1 Input parameters for illustrative example
Full size table

Since we only consider one scenario, case MPEC-PN is not included in the illustrative example. All cases were solved in less than 1 minute. Results are provided in Table 2 and Fig. 2.

Fig. 2
figure 2

Illustrative example: operational decisions for centralized optimization and two different tariff structures with decentralized decision-making

Full size image

The benchmark case is SO, which takes a central planning approach. The MPEC cases can be compared to the SO case to assess the performance of the different tariff schemes. Regarding total costs, MPEC-P is equal to SO, while MPEC-F has higher total costs due to load curtailment occurring in segment 1. The load curtailment can be explained by the flat tariff scheme in MPEC-F, which means that the prosumer has incentives to keep the maximum load as low as possible in any hour. Hence, the lowest peak load is obtained by dividing the total load of 70kWh by 24 h, resulting in a flat load of 2.92kWh/h for the entire day. This operational pattern can be observed in Fig. 2b. Therefore, since the DSO is unable to provide any time-dependent incentives, case MPEC-F results in load curtailment during the first segment of the day even though the load could be served in segment 2.

Table 2 Illustrative example: key results
Full size table

In contrast to MPEC-F, load curtailment is completely avoided in case MPEC-P since segment 2 is set as off-peak by the DSO. Hence, because of the off-peak period, the prosumer has incentives to shift most of the load towards segment 2, even though the power prices are higher in this segment. These findings highlight a key problem with flat capacity-based tariffs since such tariffs will only incentivize each consumer to flatten their load profile individually. However, the peak grid load is the sum of individual loads which may not be coincident with individual peaks. Another problem with a flat tariff scheme is that it will induce a change in end-user behaviour also when the grid has no need for a such flexibility, creating socio-economic losses due to the associated discomfort for end-users. This suggest that a flat capacity-based tariff do not reflect the true grid costs in an accurate way and that the incentives need to be more efficient. As such, introducing off-peak periods may be a prospective solution to communicate how load should be shifted in a coordinated fashion across multiple end-users.

Next, the aspects of decentralized generation and stochasticity concerning the realizations of load, generation and power prices are considered.

4.2 Stochasticity and decentralized generation

Next, we consider the case of residential load coupled with a PV generation and an EV charging facility. We assume consumer 1 is an inflexible residential load for 1000 m\(^2\) of apartments. Furthermore, consumer 1 also has a PV system with an installed capacity of 50 kW. Consumer 2 is an EV charging facility who shares the grid connection with consumer 1. Since the grid connection is shared between these consumers, coordinated EV-charging can potentially be important for the DSO, because it impacts the total load. However, the restriction on aggregate load can not be imposed directly on the end-users so such coordination need to be achieved through the grid tariffs.

4.2.1 Input data

Input data for the stochastic cases is provided in Table 3. Demand data representing 1000 m\(^2\) of apartments is generated according to the methodology presented in [31]. We cluster the data into two representative days, or scenarios, by applying a hierarchical clustering algorithm. The algorithm minimizes the distance between two days using PV generation, demand, and electricity price for each hour of the day as observations. The scenario-dependent information, presented in Fig. 3, is: (1) load profile for fixed demand, (2) PV generation, and (3) power market prices. Furthermore, we assume that a current interconnection capacity of 25 kW exists, and that is is not possible to increase the interconnection capacity. Scenario 1 has an overall higher load than scenario 2 for consumer 1. Also, there is a significant variation of the fixed demand within the day. Therefore, to avoid load curtailment, it is preferable for the DSO if consumer 2 perform the EV charging when consumer 1 has a low load.

Table 3 Input parameters for the stochastic example
Full size table
Fig. 3
figure 3

Input-data for the two scenarios considered in the stochastic example

Full size image

4.2.2 Results

Computationally, the main difference compared to the illustrative example is that more than one scenario is considered. When increasing the number of scenarios, the computational burden increases because some decisions at the upper level are nonanticipative. Hence, even though the lower-level problems are completely scenario dependent, the overall bilevel problem can not be directly decomposed by the individual scenarios.

Figures 4 and 5 provide information about the operational decisions in scenario 1 with a high fixed load and scenario 2 with a lower fixed load, respectively. Case MPEC-F, with a flat capacity-based tariff, gives a similar result as for the deterministic case since the flexible demand of consumer 2 is simply divided by the number of hours in the day to give the minimum charging capacity during each time step. This operational pattern can be observed in Fig. 4b, where the total load exceeds the interconnection capacity during some time steps. Therefore, with 200 kWh of charging during the day, the flexible load is 8.33 kWh for each hour. This results in load curtailment when the fixed demand is above 16.67 kWh per time step since the total capacity of 25kW would be exceeded. This occurs in scenario 1, but not in scenario 2 as the fixed load of consumer 1 is low enough to allow for 8.33 kWh of charging during all time steps. Another observation is that during the middle of the day, the PV system at consumer 1 produces significant amounts of electricity by PV, which could be directly used for EV charging at consumer 2. However, due to the flat tariff structure, consumer 2 does not have any incentives to try to shift charging to these hours.

Fig. 4
figure 4

Stochastic example: operational decisions in scenario 1

Full size image
Fig. 5
figure 5

Stochastic example: operational decisions in scenario 2

Full size image

Some key results are provided in Table 4. It can be observed that total costs for cases MPEC-P and MPEC-PN comes close to the theoretically optimal result in case SO. The difference between MPEC-P and MPEC-PN is that in MPEC-P, the DSO can select off-peak hours for each scenario individually, whereas for MPEC-PN, the off-peak hours have to be equal for all scenarios. Similiarly to the illustrative example, we observe that the volumetric tariff (vnt) is set to zero in all cases since the DSO is unable to use the volumetric tariff for providing efficient incentives. In the case of a cost-recovery criterion for the DSO, the volumetric tariff could be used for the purpose of collecting residual costs.

Table 4 Case study: key results
Full size table

Operational patterns for case MPEC-P in scenario 1 is provided in Fig. 4c. We see that in contrast to case MPEC-F, the load for consumer 2 changes over time as a response to the off-peak periods set by the DSO. As a result, load curtailment is completely avoided since consumer 2 is incentivized to consume as much as possible when consumer 1 produce significant amounts of electricity from the PV system.

Having off-peak hours depend on the scenario might be unrealistic in practice due to the added complexity and need for frequently communicating the off-peak hours to the end-users. Therefore, Case MPEC-PN ensures that off-peak hours need to be equal for all scenarios by adding nonanticipativity constraints to the off-peak period selection. The nonanticipativity constraint alters the operational patterns slightly as shown in Figs. 4d and 5d, but the overall benefit of including off-peak periods is intact. It should be noted that to simplify the examples, we consider the off-peak periods as a binary variable. In practical applications, a DSO might want to employ this in a partial way, by allowing a limited amount of extra capacity usage during certain hours with a low grid load. This way, potential issues related to rebound effects of load shifting can be reduced.

5 Conclusions

In this paper, a methodology for optimal grid tariff design under decentralized decision-making is presented. The presented bilevel model include a realistic formulation of the interaction between the end-user and distribution system operator. Uncertainty is included in the form of scenarios for fixed demand, PV generation, and electricity market prices. In addition, a centralized decision-making model is provided for benchmarking of the various tariff schemes.

An illustrative example to highlight the model features in a deterministic setting and a stochastic case study is presented. The case studies describes how flexible consumers can be incentivized to change their consumption patterns to reduce overall power system costs. By including off-peak periods, the flexible consumer can effectively be incentivized to shift the charging to off-peak hours and hours with significant PV generation available at the local level. In contrast, a flat capacity-based tariff structure is not able to provide efficient incentives for load shifting.

Therefore, it can be concluded that in light of flexible end-users the electricity network tariff scheme should include a time-dependent capacity-based component such as partial or full off-peak hours to provide efficient incentives for load shifting.

The presented model is tractable, but computationally expensive. Despite this limitation, the model is a novel application of the MPEC formulation, tailored to investigating electicity grid tariffs under decentralized decision-making and uncertainty. Further work is needed to speed up the calculations when increasing the amount of scenarios.