A bi-level model for the design of dynamic electricity tariffs with demand-side flexibility

Abstract

This paper addresses the electricity pricing problem with demand-side flexibility. The interaction between an aggregator and the prosumers within a coalition is modeled by a Stackelberg game and formulated as a mathematical bi-level program where the aggregator and the prosumer, respectively, play the role of upper and lower decision makers with conflicting goals. The aggregator establishes the pricing scheme by optimizing the supply strategy with the aim of maximizing the profit, prosumers react to the price signals by scheduling the flexible loads and managing the home energy system to minimize the electricity bill. The problem is solved by a heuristic approach which exploits the specific model structure. Some numerical experiments have been carried out on a real test case. The results provide the stakeholders with informative managerial insights underlining the prominent roles of aggregator and prosumers.

1 Introduction

In recent years, decentralized and renewable electricity generation has increased all around the world. Residential consumers have been playing an increasingly active role becoming energy producers, typically from renewable energy sources. The term used to denote this new player of the liberalized energy market is “prosumer”. By the deployment of smart meters and taking advantage of the advancement of Information and Communication Technology (ICT) infrastructures, prosumers are now able to dynamically control and optimize their electricity consumption. Harnessing this new potential, a smooth transition from the traditional supply-follows-demand paradigm to a new, demand-follows-supply approach can be already observed. In this context, increasing the demand flexibility represents a very important issue to improve the coordination of the electricity system. Demand Side Management (DSM) is a series of activities that utilities undertake to change habitual users’ consumption pattern to achieve power grid efficiency. With the liberalization of the energy market, the DSM has evolved into two main approaches, namely Energy Efficiency and Demand Response (DR). While the first approach aims to reduce the overall energy consumption (Behrangrad 2015), the DR aims to change consumers’ electricity usage from their habitual consumption patterns in response to economic signals. For an extensive discussion about the DSM, interested readers are referred to Good et al. (2017); Paterakis et al. (2017).

There are two main complementary approaches for the DR classified as explicit and implicit DR. In the explicit case, the result of the DR actions is sold upfront on the market, either directly (for example, in the case of large industrial consumers) or by service providers. This scheme is sometimes called “incentive-based” since consumers receive a specific reward in exchange of their flexibility. In the implicit DR, consumers decide to be exposed to electricity prices that may vary over time. In this case, their flexibility is rewarded by a reduction of the electricity bill. A comprehensive survey on the DR is proposed in Deng et al. (2015) where the authors review the main mathematical models and the potential challenges. Other contributions (see, e.g., Gerami et al. 2020 and the references therein) investigate the challenges of the DR programs in some application contexts.

The definition of proper pricing policies is one of the main factors for the success of the DR programs as consumers could be motivated to change the timing of the load operations as long as a reduction in the electricity bill is guaranteed.

This contribution focuses on pricing problems in electricity supply considering the interaction between two agents, aggregator and prosumer. The aggregator represents a new player in the liberalized electricity market, where the creation of prosumers’ communities is a growing phenomenon (Espe et al. 2018). It can be seen as an agent which aggregates in a collaborative system more customers who decide to act together. Like the classic retailer, the aggregator faces the problem of designing competitive rates compared to those offered by other potential suppliers to ensure that prosumers remain within the coalition. However, unlike the retailer who typically acts as an intermediary, i.e., purchasing energy from the market and reselling it to its customers, the aggregator owns an energy system to optimally manage which guarantees the coverage (at least partial) of the coalition’s demand. As a result, the offered tariffs depend not only on the market prices (as for the retailer), but also on the supply plan that the aggregator decides to implement (see, e.g., Ferrara et al. 2020) This feature makes the pricing problem more involved creating additional challenges, only marginally investigated in the scientific literature. Furthermore, the prosumer is assumed to own local resources, consisting of a system of photovoltaic (PV) panels and a storage device. As a result, demand flexibility is further increased: the storage system can be used to decouple energy production and/or purchasing from consumption and controllable loads may be shifted in response to pricing signals.

Over the last decades, different pricing strategies have been investigated by researchers and practitioners. Interested readers are referred, for example, to the recent contribution (Grimm et al. 2020) where the authors analyze and compare different pricing schemes providing interesting managerial insights. In this paper, we focus on a dynamic pricing scheme, which unlike the static one typically contracted for long periods (e.g., one year) is based on electricity tariffs announced with short antecedence. In particular, we assume that the rates are communicated the day before and are differentiated according to the Time of Use (ToU). The tariffs (e.g., for each hour) are valid for the subsequent day without any variation regardless of the energy demand which, in any case, is assumed to be bounded by contract.

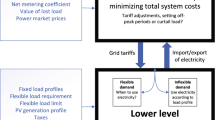
The interaction between the two agents involved in the pricing problem is modeled as a Stackelberg game and formulated as a Bi-Level (BL) problem (Stackelberg et al. 1952). The aggregator represents the Upper Level (UL) decision maker, i.e., the leader, who sets the pricing scheme by optimizing the procurement plan, taking also into account the possible reaction of the prosumer. This latter plays the role of follower, i.e., the Lower Level (LL) decision maker, who may react to the offered rates by optimally managing the home energy system and/or scheduling the flexible loads. Leader and follower have conflicting goals: while the aggregator’s aim is to maximize the total profit, defined as the difference between the revenue obtained from selling energy and procurement costs, the prosumer aims at minimizing the electricity bill.

The inclusion of realistic features, mainly related to the management of local resources, makes the problem very challenging. The UL model is a mixed-integer problem with an objective function including bilinear terms, while the structure of the LL problem prevents the adoption of standard approaches used to derive a single-level reformulation (Gümüş and Floudas 2005). In this paper, we present a simple heuristic approach that exploits the problem structure and is based on the idea of generating a pool of BL feasible solutions from which the best one is chosen. The approach has been tested on a virtual coalition derived from the analysis of a real configuration including different types of prosumers, e.g., residential, commercial, public utilities. For the numerical experiments, only the class of residential prosumers that are similar in terms of energy requirement, demand response profiles and available facilities has been considered.

To summarize, the main contributions of the paper are the following. We propose a new comprehensive BL model for the electricity pricing problem modeling the interaction between aggregator and prosumer; we design and test a simple heuristic approach that exploits the specific structure of the problem; we provide extensive computational experiments carried out a real case study and discuss a number of practical insights that can support the aggregator in the electricity pricing problem.

The rest of the paper is organized as follows. Section 2 reviews the relevant scientific literature on electricity pricing problem. Section 3 describes the problem and presents the mathematical formulation. Section 4 introduces the heuristic solution approach. The results of extensive computational experiments are presented and discussed in Sect.  5. Finally, conclusions and future research directions are drawn in Sect. 6.

2 Literature review

This section is devoted to the review of the most relevant contributions on the BL optimization for the electricity pricing problem. Interested readers are also referred to a recent survey where the authors present a comprehensive review of the main BL models and methods (Antunes et al. 2020). These contributions mainly differ in the nature of the decision makers involved in the pricing problem, i.e., retailer/aggregator and consumer/prosumer, and the possibility to manage local resources and scheduling flexible loads.

In Kovács (2019), the author proposes a BL model for the definition of ToU energy tariffs where the LL problem refers to a prosumer who reacts to the pricing signals by optimally managing the home energy system. The problem is solved by a tailored approach which exploits the primal-dual reformulation of the follower problem used to derive a single-level quadratically constrained problem. A DSM model to determine optimized electricity rates has been proposed in Alekseeva et al. (2018). Here the pricing policy is aimed at modifying the consumer’s behavior by shifting the loads from peak to off-peak hours. A more recent contribution by Aussel et al. (2020) presents a DSM model where four decision makers, including suppliers, local agents, aggregators, and end-users are involved. The authors formulate the problem as a tri-level single-leader-multi-follower model that is transformed into a new BL problem and solved using three different approaches. In Grimm et al. (2020), the authors compare various flexible tariffs, i.e., ToU, critical-peak-pricing, real-time-pricing tariff, and fixed-price. The follower is represented by a prosumer owing an energy generation system and storage facilities who aims to maximize the total revenue from electricity production minus total cost of electricity purchase from the retailer. The problem is reformulated into a single-level model and solved by a commercial solver.

In all the aforementioned contributions, the LL problem contains only continuous decision variables. The introduction of binary variables, typically used to account for the scheduling of flexible loads, makes the problem even more challenging, requiring the design of solution approaches to exploit the specific problem structure.

In Alves and Antunes (2018), the authors propose an extension of the model proposed in Alves et al. (2016), where the LL problem is formulated as a bi-objective mixed-integer model minimizing the consumer consumption costs and the dissatisfaction caused by rescheduling the operation of the flexible appliances. The UL problem only contains continuous decision variables related to the ToU electricity tariffs and maximizes the retailer’s profit. A hybrid genetic algorithm is applied on the UL problem, while the LL subproblem is solved using a commercial solver. In Soares et al. (2020), Soares et al. present a more involved model where the LL problem accounts for the rescheduling of flexible loads (shiftable, interruptible, and thermostatically controlled) in response to the price signals. The authors develop a hybrid approach based on a population-based algorithm that calls a commercial solver to deal with the LL problem. A new solution method based on the optimal-value function reformulation was proposed in Soares et al. (2021) and applied to solve the same problem. The solution strategy consists of generating a series of convergent upper and lower bounds for the UL objective function until the difference between the bounds is below a given threshold. The extension of the model proposed in Soares et al. (2020) to the multi-follower case is presented in Soares et al. (2019) where the authors propose two population-based heuristics (a genetic algorithm and a particle swarm optimization algorithm) to deal with the UL problem both encompassing an exact solver to address the LL problem. We also mention the contribution by Le Cadre et al. (2019) where analyzed the relation between aggregator and consumers joined into a coalition and modeled it as a Stackelberg game. In the model, the aggregator does not own energy assets and aims to maximize the daily revenue gained by selling energy to consumers while no consumer leaves the coalition and a fairness criterion imposed by a cost-sharing mechanism is met. Consumers reacts to pricing signals rescheduling the flexible loads.

The model we propose is linked to the aforementioned contributions since it assumes as, for example, in Grimm et al. (2020), that the follower is equipped with his home energy system and as, for example, in Soares et al. (2020) the presence of flexible appliances whose operations could be rescheduled. Thus, more realistically, the follower is a smart prosumer who can more effectively react to the price signals by integrating the two sources of flexibility. More importantly, the leader is not simply a retailer buying energy from the market and reselling it to the customers, but an entity who possesses generation and storage devices whose optimal management influences the procurement cost and consequently the profit that can be gained.

3 Problem definition and mathematical formulation

We consider a coalition of prosumers managed by an aggregator that faces the problem of defining electricity tariffs for the coalition members. In a real setting, the coalition is composed of heterogeneous prosumers, e.g., residential, commercial, and industrial end-users. Here we model the interaction between the aggregator and the class of residential prosumers. In particular, our reference is a family with a home energy system composed of PV panels and a storage device (battery). The proposed formulation also applies when considering the interaction with other classes of prosumers provided that the follower’s constraints are redefined. The generalization to the multi-follower case, where different classes of prosumers are jointly considered, is the subject of our ongoing research.

In our setting, the aggregator does not have direct access to the prosumers’ resources, but is responsible to ensure the energy supply (Beraldi et al. 2018). To this end, the aggregator should define the procurement plan, optimizing the management of his own resources (conventional production plant and/or renewable energy sources), and/or purchasing energy from the energy market, e.g., the Day Ahead (DA) market and/or using bilateral contracts, if signed in advance.

We consider a dynamic pricing scheme, announced the day before. The planning horizon denoted by the set ${\mathcal {T}}=\{1,..., t, \dots ,T\}$ is divided into time steps of equal length (e.g., one hour). The problem is solved every day using updated data for the market price, the solar production, and the operations of the flexible appliances. Table 4 in Appendix reports the complete nomenclature.

The interaction between aggregator and prosumer is modeled as a Stackelberg game. The aggregator plays the role of leader who has full control on tariff setting considering the prosumer’s response, while the prosumer behaves as a follower who optimally manages the energy resources and schedules the flexible loads reacting to the offered electricity rates. The leader and follower problems are introduced in the next subsections.

3.1 The aggregator problem

The price profile offered by the aggregator depends on the supply strategy. Self-produced energy should be eventually integrated by additional electricity amounts purchased from the market. Besides a system of PV panels with a production profile $\psi ^a_t$, we assume that the aggregator owns a small production plant. For each time period t, we denote by $\alpha _t$ the production level and by $\chi _{t}$ the binary variable related to the state (on/off) of the plant. Constraints (1) impose that whenever the plant is on, the produced amount should be within some bounds depending on the plant’s capacity:

$$\begin{aligned}&\, {\underline{\epsilon }} \chi _{t} \le \alpha _t \le {\overline{\epsilon }} \, \chi _{t} \ \ \ \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(1)

The aggregator is also supposed to own a battery storage device that should be properly managed. Hereafter, we use the superscript a to refer to the variables pertaining to the aggregator. In particular, for each time period t, variables soc$_{t}^a$,  in$_{t}^a$,  out$_{t}^a$ refer to the state of charge and to the amount of energy charged in and discharged from the battery. Moreover, binary variables $\gamma _{t}^{ia}$ and $\gamma _{t}^{oa}$ are introduced to avoid the simultaneous charge and discharge. Constraints (2)-(7) model the management of the aggregator’s storage system. In particular, the flow balance constraints (2) relate the state of charge between two subsequent time periods. Constraint (3) requires that the aggregator’s battery level at the last time period is equal to a specified amount (soc$^a_{0}$) that is supposed to be present at the beginning of the planning horizon. Constraints (4) impose lower and upper bounds on the state of charge. In a similar way, constraints (5) and (6) bound the amount of power charged into and discharged from the battery, respectively. Finally, constraints (7) prevent the simultaneous charge and discharge.

$$\begin{aligned}&\mathrm{soc}^{a}_{t} = \mathrm{soc}^{a}_{t-1} + \eta _i\, \mathrm{in}^a_{t } - \frac{1}{\eta _o}\,\mathrm{out}^a_{t} \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(2)

$$\begin{aligned}&\mathrm{soc}^a_{T} = \mathrm{soc}^a_{0} \ \end{aligned}$$

(3)

$$\begin{aligned}&\, C^a_\mathrm{min}\le \mathrm{soc}^a_{t} \le C^a_\mathrm{max} \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(4)

$$\begin{aligned}&\mathrm{in}^a_t \le \theta _1\, C^a \gamma ^\mathrm{ia}_{t} \ \ \ \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(5)

$$\begin{aligned}&\mathrm{out}^a_t \le \theta _2 \,C^a \gamma ^\mathrm{oa}_{t} \ \ \ \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(6)

$$\begin{aligned}&\gamma ^\mathrm{ia}_{t} + \gamma ^\mathrm{oa}_{t} \le 1 \ \ \ \ \ \ \ \ \forall t\in {\mathcal {T}} \end{aligned}$$

(7)

Besides using self-produced energy, the aggregator may satisfy the prosumer’s demand by purchasing electricity from the DA market and/or by bilateral contracts. For each time period t, we denote by $\beta _t$ and $\delta _t$ the corresponding decision variables. On these latter, bounding conditions can be imposed reflecting contractual and/or aggregator’s previously defined strategies:

$$\begin{aligned}&\underline{\delta _t} \le \delta _t \le \overline{\delta _t} \ \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(8)

The aggregator’s supply should guarantee the satisfaction of the prosumer’s demand, denoted by the variable $r_t$ under the follower control:

$$\begin{aligned}&\alpha _{t} + \beta _t +\delta _t + \psi ^a_t + \mathrm{out}^a_{t} - \ \mathrm{in}^a_{t} \ge r_t \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(9)

The daily aggregator’s expense depends on the individual costs of the different supply sources, that may change from day to day. We denote by $u_t^{\alpha }$, $u_t^{\beta }$ and $u_t^{\delta }$ the unitary production cost, the DA price and the price of bilateral contracts, respectively. Thus, the overall cost, denoted by TC, is defined as:

$$\begin{aligned}&\mathrm{TC}=\sum _{t=1}^T \left( u_t^{\alpha } \alpha _{t} + u_t^{\beta } \beta _t + u_t^{\delta } \delta _t \right) \end{aligned}$$

(10)

The aggregator aims at maximizing the profit defined as the difference between revenue and cost. Clearly, the revenue depends on the electricity rates, denoted by the continuous variables $p_t$. The set of constraints (11)-(12) bound the offered tariff and impose a limit on its daily average value; by imposing the lower bound $\underline{p_t}$, we ensure that a minimum revenue for the aggregator is obtained while imposing the upper bound $\overline{p_t}$ reflects the competitive environment in the energy market. In addition, as in Zugno et al. (2013), we assume that the aggregator and the prosumer have signed an agreement in advance that specifies the lower and the upper bounds and the average value $\varDelta$ that the rates could attain during the day:

$$\begin{aligned}&\underline{p_t}\le {p}_t \le \overline{p_t}\ \ \forall t\in {\mathcal {T}} \end{aligned}$$

(11)

$$\begin{aligned}&\frac{1}{T} \sum _{t=1}^T {p}_t \le \varDelta \end{aligned}$$

(12)

Finally, the aggregator’s objective function is defined as:

$$\begin{aligned} \max z_{A} = \sum _{t=1}^T {p}_t \,r_t - TC \end{aligned}$$

(13)

3.2 The prosumer problem

The prosumer reacts to the tariffs offered by the aggregator by optimizing the management of the local resources and properly scheduling the loads with the aim of minimizing the daily electricity bill. In particular, we classify the prosumer’s loads into two main groups, referred to as base and flexible loads. Lighting, tv, refrigerator, etc., belong to the first group and are not deemed for control. For each period t, $b_t$ denotes the corresponding amount of required electricity. On the contrary, flexible loads are associated with controllable appliances. These, in turn, are divided into shiftable and interruptible loads. The first ones refer to loads having an operation cycle that, once initiated, cannot be interrupted, e.g., dishwasher, washing machine or clothes dryer, while the second ones are loads whose operations can be temporarily interrupted provided that a given amount of energy is supplied during a specified time slot, e.g., the battery of electric vehicle.

The sets of shiftable and interruptible loads are denoted by ${\mathcal {J}}=\{1,\cdots ,J \}$ (indexed by j) and ${{\mathcal {K}}} = \{1,\cdots ,K \}$ (indexed by k), respectively. For each flexible load (either j or k), a comfort time window ($[l_.,u_.]$) reflecting the prosumer’s preferences is specified. Additional data, reported in Table 4, refer to the duration and to energy required.

The scheduling of the flexible loads entails the introduction of binary variables. For each shiftable load j, we introduce the binary variable $z_{jt}$ that takes the value 1 if the appliance starts operating at time t and 0 otherwise. Clearly, each appliance can start operation only one time within its time window and once started, it should be active for the next subsequent $N_j$ periods to complete its cycle. We model this condition by the following constraints:

$$\begin{aligned} \sum _{t=l_j}^{u_j-N_j +1} z_{jt} =1 \ \ \ \ \ \forall j \in {\mathcal {J}} \end{aligned}$$

(14)

We assume that the energy required during each period by appliance j is a constant value denoted by $m_j$. Thus, the quantity of electricity required by appliance j in period t can be expressed as:

$$\begin{aligned} m_j \sum _{s=\max {(l_j, t-N_j)}}^t z_{js} \end{aligned}$$

(15)

We should note that the assumption on the constant energy required by each load within its operation cycle is a very common feature frequently considered in the energy context (see, for example, Liu et al. 2019 and also the references therein). On the other hand, we can model loads for which the operation cycle consists several stages with different power requirements (as in Violi et al. 2022), but this requires the introduction of additional variables and constraints contributing to the model complexity.

To model interruptible load k, we introduce the binary variable $y_{kt}$ corresponding to the state of appliance k. Obviously, these variables assume value 0 outside the time window. By constraints (16) we impose that the total amount of energy consumed by each load k within its comfort window does not exceed the total request $Q_k$:

$$\begin{aligned}&\sum _{t = l_k}^{u_k} m_k y_{kt} \ge Q_k \ \ \ \ \forall k \in {\mathcal {K}} \end{aligned}$$

(16)

where $m_k$ denotes the power required by appliance k for each time period.

Besides rescheduling the flexible loads, the prosumer can react to the price signals optimizing the management of the storage system. Here, we introduce some variables and constraints similar to those considered for the aggregator. In particular, for each time period t, variables $\mathrm{soc}_{t}^p,\, \mathrm{in}_{t}^p,\, \mathrm{out}_{t}^p$ refer to the state of charge and the amount of energy charged in and discharged from the battery. Moreover, the binary variables $\gamma _{t}^\mathrm{ip}$ and $\gamma _{t}^\mathrm{op}$ are introduced to avoid the simultaneous charge and discharge. The following constraints with the same meaning of constraints (2)-(7) are introduced for the prosumer’s side:

$$\begin{aligned}&\mathrm{soc}^{p}_{t} = \mathrm{soc}^{p}_{t-1 } + \eta _i\, \mathrm{in}^p_{t } - \frac{1}{\eta _o}\, \mathrm{out}^p_{t} \ \ \ \forall t \in {\mathcal {T}}\end{aligned}$$

(17)

$$\begin{aligned}&\mathrm{soc}^p_{T} = \mathrm{soc}^p_{0} \ \ \ \end{aligned}$$

(18)

$$\begin{aligned}&C^p_\mathrm{min} \le \mathrm{soc}^p_{t} \le C^p_\mathrm{max}\ \ \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(19)

$$\begin{aligned}&\mathrm{in}^p_t \le \theta _1\, C^p \gamma ^\mathrm{ip}_{t} \ \ \ \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(20)

$$\begin{aligned}&\mathrm{out}^p_t \le \theta _2 \,C^p \gamma ^\mathrm{op}_{t} \ \ \ \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(21)

$$\begin{aligned}&\gamma ^\mathrm{ip}_{t} + \gamma ^\mathrm{op}_{t} \le 1 \ \ \ \ \ \ \ \ \forall t\in {\mathcal {T}} \end{aligned}$$

(22)

The prosumer’s residual demand, $r_t$, to be purchased from the aggregator, is defined by constraint (23):

$$\begin{aligned}&r_t = b_t + \sum _{k=1}^K m_k y_{kt} + \sum _{j=1}^J m_j \sum _{s=\max {(l_j, t-N_j)}}^t z_{js} - \nonumber \\&\psi ^p_t- \mathrm{out}^p_{t}+ \mathrm{in}^p_{t } \ \ \ \ \ \ \ \forall t \in {\mathcal {T}} \end{aligned}$$

(23)

Here the first three terms account for the total amount of base and flexible loads, $\psi ^p_t$ denotes the amount of energy produced by the PV panels within time slot t, and the last two terms are related to the storage system.

The prosumer is asked to provide in advance an estimation of his demand for the next day; obviously, for residential customers, such amount is always below a pre-specified value mentioned in the contract.

The prosumer’s objective function aims at minimizing the total electricity expenses defined as:

$$\begin{aligned}&\min z_P = \sum _{t=1}^T {p}_t\, r_t \end{aligned}$$

(24)

4 Solution approach

The proposed model belongs to the class of the BL problems with mixed integer variables at both the upper and lower levels. In addition, the leader and follower objective functions contain bilinear terms, further increasing the computational complexity. Problems in this class are considered as the most challenging ones since, as shown in Köppe et al. (2010), an optimal solution may not be attainable unless specific assumptions are satisfied (Fischetti et al. 2017). We point out that the nature of the decision variables prevents the application of standard techniques (relying on the Karush–Kuhn–Tucker conditions) to derive a single-level reformulation, calling for the design of tailored solution approaches that may exploit the problem structure. Here, we propose a heuristic scheme relying on the optimal-value-function reformulation. Other approaches as, for example, the one proposed in Soares et al. (2021), rely on the same reformulation. Another class of heuristic approaches is represented by hybrid methods, (see, e.g., Soares et al. 2020, 2019), that integrate metaheuristic algorithms (e.g., genetic algorithm and particle swarm optimization algorithm) to explore the UL search space and apply exact solvers to find optimal LL solutions.

The basic idea of our heuristic scheme is to generate a pool of BL feasible solutions by exploiting the optimal-value-function reformulation (Kleinert et al. 2021). In order to describe the method, we reformulate our BL problem in more general terms:

$$\begin{aligned}&\max _{x^U \in X^U \, x^L \in X^L } F(x^U, x^L) \end{aligned}$$

(25)

$$\begin{aligned}&H(x^U, x^L) \le 0 \end{aligned}$$

(26)

$$\begin{aligned}&x^L \in arg\min _{x'^L \in X^L}\{f(x^U, x'^L): \, h(x'^L)\le 0 \} \end{aligned}$$

(27)

Here, the variables $x^U$, defined on set $X^U$ are the leader’s variables, while the variables $x^L$ defined on set $X^L$ are the follower’s variables, as reported in Table 4 in Appendix. $H(x^U, x^L)$ and $h(x^L)$ are the UL and LL constraint functions defined by the set of constraints (1)-(12) and (14)-(23), respectively. Finally, $F(x^U, x^L)$ and $f(x^U, x^L)$ are the UL and LL objective functions defined by (13) and (24). The BL model (25)-(27) can be equivalently represented as:

$$\begin{aligned}&\max _{x^U \in X^U \, x^L \in X^L } F(x^U, x^L) \end{aligned}$$

(28)

$$\begin{aligned}&H(x^U, x^L) \le 0 \end{aligned}$$

(29)

$$\begin{aligned}&h(x^L)\le 0 \end{aligned}$$

(30)

$$\begin{aligned}&f(x^U, x^L) \le \varPsi (x^U) \end{aligned}$$

(31)

where the follower value function, $\varPsi (\cdot )$, for a given $x^U$, is defined as:

$$\begin{aligned}&\varPsi (x^U) = \min _{x^L \in X^L}\{f(x^U, x^L): \, h(x^L)\le 0 \} \end{aligned}$$

(32)

We note that, in our formulation both the UL and LL objective functions involve bilinear terms resulting from the product of the UL variables related to the tariffs, $p_t$, and the LL variables related to the residual demand $r_t$. Interestingly, once the tariffs are released, the bilinear terms in the LL objective function turn into linear ones allowing to solve the corresponding problem by using off-the-shelf solvers.

Finally, we also point out that we follow an optimistic approach as common in many BL contributions (Soares et al. 2021) to break the tie (in case the LL problem has multiple optimal solutions) in favor of the UL decision maker.

The proposed heuristic approach generates a pool of BL feasible solutions. A solution $({\bar{x}}^{U},{\bar{x}}^{L})$ is said to be BL feasible (Lozano and Smith 2017) if it satisfies the set of constraints (29)–(31). We note that dropping the constraint (31) from model (28)–(31) leads to the so-called High Point Relaxation (HPR) problem. It is easy to clarify that a feasible solution of the HPR problem provides an upper bound (UB) to the BL problem; also, any BL feasible solution $({\bar{x}}^{U},{\bar{x}}^{L})$, is nothing but a lower bound (LB). We remark that the LL constraints do not depend on any UL variables; this property is essential to guarantee the correctness of the proposed algorithm.

At each iteration of the algorithm a BL feasible solution $({\bar{x}}^{U},{\bar{x}}^{L})$, is generated and the LB$=F({\bar{x}}^{U},{\bar{x}}^{L})$ value is computed. The new solution is added to the pool, $\varOmega$, and the incumbent, denoted by $LB_B$, is updated whenever an improving lower bound is obtained ($F({\bar{x}}^{U},{\bar{x}}^{L})>\mathrm{LB}_B$).

The pseudocode of the proposed heuristic scheme is sketched in Algorithm  1. At the first iteration, we find the optimal solution of the HPR, denoted by $({\hat{x}}^U,{\hat{x}}^L)$ and we compute the initial UB$=F({\hat{x}}^U,{\hat{x}}^L)$. The UL decision variables ${\hat{x}}^U$ related to the tariffs are injected into the LL subproblem that is solved to optimality. If the LL optimal solution ${\bar{x}}^L$ amended with ${\hat{x}}^U$ is feasible with respect to the constraints (9), then $({\hat{x}}^U,{\bar{x}}^L)$ is accepted as a BL feasible solution, otherwise we may repay the UL solution to retain feasibility. To this end, we may, for example, modify the exchange with the DA market over some time periods that is the value of the $\beta _t$ variables which are not restricted in the UL constraints. Clearly, in the latter case the UL objective function should be re-evaluated. To move to another BL feasible solution, we add cut (33) into the HPR in order to find another UL solution accounting for the follower’s reaction:

$$\begin{aligned} f(x^U,x^L) \le f(x^U,{\bar{x}}^L) \end{aligned}$$

(33)

where ${\bar{x}}^L$ is the feasible LL solution determined at the previous iteration. Then, we solve the HPR amended with the new constraint (33) and repeat the procedure until a stopping criterion is met. In practice, we could end the algorithm before Iter$_\mathrm{max}$ iterations if at least one of the two following conditions holds: the gap between the initial upper bound value and the current best lower bound falls below a given threshold $\tau$ or for a specified number of consecutive iterations (let say NT), no new BL feasible solution is found.

We finally comment on the bilinear structure of the UL and LL objective functions. The linearization has been carried out by applying the dual reformulation, that it is proved to provide tighter approximation compared to the McCormick’s inequalities (Costa et al. 2017). In particular, we introduce the auxiliary variable $\omega _t$ that replaces the nonlinear term $p_t r_t$, and we add the following constraints:

$$\begin{aligned}&{p}_t= (\lambda _1^t+\lambda _2^t) \, \underline{p_t}+ (\lambda _3^t+\lambda _4^t) \, \overline{p_t} \end{aligned}$$

(34)

$$\begin{aligned}&r_t= (\lambda _1^t+\lambda _3^t) \, \underline{r_t} + (\lambda _2^t+\lambda _4^t) \, \overline{r_t} \end{aligned}$$

(35)

$$\begin{aligned}&\omega _t= \lambda _1^t\, \underline{p_t}\, \underline{r_t} +\lambda _2^t\, \underline{p_t} \, \overline{r_t} +\lambda _3^t\, \, \overline{p_t}\underline{r_t} + \lambda _4^t\, \overline{p_t}\, \underline{r_t} \end{aligned}$$

(36)

$$\begin{aligned}&\sum _{j=1}^4 \lambda _j^t=1 \end{aligned}$$

(37)

$$\begin{aligned}&\lambda _j^t \ge 0,\,\, j=1, ..., 4 \end{aligned}$$

(38)

Here $\underline{p_t}$ and $\overline{p_t}$ are proper bounds on the tariffs (see constraints (11)), whereas for the residual demand, the lower bound $\underline{r_t}$ is typically set to 0, and the upper bound, denoted by $\overline{r_t}$, is fixed by contract.

5 Case study

This section is devoted to the presentation and discussion of the computational experiments carried out to assess the effectiveness of the proposed approach on a real case study. The model and the heuristic scheme have been implemented in GAMS 24.4.6 (Bussieck and Meeraus 2007), and CPLEX has been used to solve, once linearized, the generated mixed integer problems. All the experiments have been performed on an Intel ^®Core i7 2.6 GHz, with 16.0 GB of RAM memory.

In the following, we first introduce the case study and then we present and analyze the numerical results. Finally, we comment on the performance of the proposed solution approach.

5.1 Experimental setting and data

The computational experiments have been carried by using real data collected as part of an Italian-funded research project ”COMESTO: Community Energy Storage”. The proposed model is solved every day by using updated information. In the experiments, we have considered hourly tariffs to reflect the organization of the Italian market taken as reference, but finer granularity (e.g., half-hour intervals) and/or longer time horizons (weekly) can be considered.

The aggregator is assumed to own traditional gas-fueled plants, a system of PV panels and some lithium battery storage devices. The data used in the experiments are reported in Appendix. Besides self-production, the aggregator may satisfy the prosumer’s demand by eventually using bilateral contracts and/or purchasing electricity from the DA market (Beraldi et al. 2017). In the model, the DA electricity prices, increased by a fee accounting for transmission and distribution, have been used as the lower bound values $\underline{p_t}$, whereas the upper bound values, $\overline{p_t}$, have been set by considering the rates offered by potential market competitors. Finally, the value of $\varDelta$ has been set to . Figure 1 reports the hourly DA prices (Single Nationwide Price -PUN) recorded in the Italian market for a winter day (23 Jan 2020) used in the experiments.

Fig. 1

The DA market prices

Fig. 2

Aggregator’s procurement plan

Fig. 3

Aggregator: storage management

Fig. 4

Offered tariff for a working winter day

Fig. 5

Management of the home energy system

Fig. 6

Management of the prosumer’s storage device

Fig. 7

Retailer versus aggregator: offered tariffs

Fig. 8

Retailer versus aggregator: prosumer’s electricity purchase

Fig. 9

Consumer versus Prosumer: purchased energy amount

As regards for the LL problem, the reference prosumer is represented by a family of five persons living in the Southern Italy who owns a home energy system consisting of PV panels and a storage device. The detailed data used in the experiments are reported in Appendix 1. In addition to the base load (e.g., lighting, refrigerator) that cannot be controlled and that amounts on average to $13\,kWh$ per day, flexible loads associated with 5 appliances have been considered. In particular, the first four are labeled as shiftable, i.e., Laundry Machine (LM), Clothes Dryer (CD), Dishwasher (DW) and Vacuum Cleaner (VC), while the last one as interruptible, i.e., Electric Vehicle (EV). For each flexible load, a comfort time window is specified by the end-user based on his specific needs, that may change eventually from day to day. The details are reported in Table 6 of the Appendix 1.

5.2 Numerical results

The numerical results reported hereafter have been collected considering a working day in winter.

We analyze the results from the aggregator’s side first. Figure 2 reports the aggregator’s procurement plan and the prosumer’s residual demand (red line).

Looking at the results, we may observe that during the first hours of the day, when the electricity prices are lower, the market is the only source of procurement. In particular, when the market price reaches the minimum value (at 5 a.m), the aggregator purchases an extra quantity of electricity which is stored and then used to satisfy the demand over the subsequent time periods. The management of the storage device is detailed in Fig. 3 that reports the state of charge and the amounts of electricity charged in and discharged from the system in each time period. We may notice the use of the battery to decouple production from consumption. For example, the unused energy produced during the central hours of the day (10 a.m-2 p.m) is stored and used later in the evening.

Figure 4 shows the offered electricity rates for the considered day. We may notice that the tariffs follow the market trend with lower prices during the early hours of the day when the electricity price in the market is lower. In response to the price signals, the prosumer optimizes the management of the local resources and the scheduling of the flexible loads, as shown in Fig. 5 where the blue line represents the prosumer’s load and the red bars denote the amount of energy purchased from the aggregator.

Looking at the results, we may observe that flexible loads are mainly scheduled (also according to the specified time windows) during the first hours of the day when the offered rates are lower. During some hours, e.g., 5–6 a.m., the prosumer purchases an extra amount over the demand which is kept in the storage system for later use. Production from PV panels is partially used to satisfy the demand, during the central hours of the day, whereas the unused amount is charged into the battery and used later in the evening, as evident in Fig. 6 that reports the management of the prosumer’s storage device.

In what follows, we report the results of some additional tests carried out with the aim of evaluating the impact of different elements on the suggested pricing tariffs and the management plans.

5.2.1 The impact of different interactions

The proposed model is quite general and encompasses, as special cases, other possible configurations, such as the retailer at the UL and the consumer at the lower one. We first discuss the retailer case assuming that the follower is still represented by a prosumer. Retailer-prosumer is a classic interaction presented in other contributions, although typically either the flexibility deriving from the controllable loads or that related to the management of the storage system is considered, but not both. The results provided by our model are meaningful and optimize the prosumer’s response to the retailer’s price signals.

Figure 7 shows the rates offered by the aggregator compared to those applied by the retailer. We may notice that during some time periods the prices are the same whereas during others there is a slight variation. This results in a different response, in terms of the amount of electricity that the prosumer purchases from the leader, as shown in Fig. 8. The cost incurred by prosumer in both the configurations is the same (4.33) whereas, as expected, the profit for the retailer is lower since he actually purchases more electricity from the market. In the case of the aggregator, energy is purchased from the market only if the DA price is lower than the production cost.

When the follower is represented by a consumer, the only response to the price signals is related to the possibility of optimizing the scheduling of the flexible loads. As expected, the aggregator’s profit is higher since the amount of the electricity purchased by the follower increases. In particular, the aggregator’s profit increase is around $21 \%$.

Figure 9 reports the electricity required by the consumer. As evident, during some hours of the day the prosumer buys an amount in excess to the demand to store in the battery and uses it in subsequent time periods. The cost incurred by the consumer is around $30 \%$ higher than that of the prosumer. This result confirms the importance of investing in the home energy system. In addition to the obvious economic advantage, there are environmental benefits which should be considered in the spirit of moving towards sustainable solutions.

Fig. 10

ToU block versus hourly pricing schemes

Fig. 11

Prosumer plan

5.2.2 The impact of the tariff structure

Final experiments have been carried out to assess the impact of the tariff scheme. In particular, we have compared the results of the hourly differentiated tariffs with those of the classic ToU blocks. Following the organization of the Italian market, we have considered three ToU blocks denoted as peak (8 a.m.–6 p.m.), intermediate (7 a.m. and 7–10 p.m.) and off-peak (1–6 a.m. and 11–12 p.m.).

The results are reported in Figs. 10 and 11 that show the proposed ToU rates and the prosumer’s plan. As expected, the prosumer optimizes the consumption pattern in response to the offered tariffs. For the considered test cases, we have observed a slight increase in the profit achieved by the leader and a worsening of the prosumer objective function. This behavior can be explained by observing that in the case of rates differentiated for blocks of hours the prosumer’s reaction might be less effective.

5.3 Managerial insights

The proposed BL model can be used as the core element of a system to support decision makers in dealing with electricity pricing problems. The model allows to consider different stakeholders in the upper and lower levels and various tariff schemes. Since the aim is to provide dynamic rates, the model should be solved in an iterative manner, using updated information on the main parameters involved in the decision-making process in each execution in order to provide more accurate solutions.

The analysis of the large set of numerical results clearly shows that the problem solutions provide the stakeholder with informative managerial insights on how the aggregator can set the electricity rates to maximize the profit and how the prosumer can optimize the home energy system to minimize the electricity bills.

The results underline that greater benefits for the follower side can be observed when considering a prosumer. The greater flexibility, resulting from the possibility of accumulating energy in the storage system in addition to scheduling flexible loads, results in a decrease of the prosumer electricity bill.

To have a more precise idea, we have run the experiments for four typical days (as the representatives of the four seasons) and we have then calculated the annual values by multiplying the daily figures of a typical day for the number of the typical days in each season. We have not considered the difference between working and not working days.

Table 1 Results for all the seasons

Table 2 Numerical results

Fig. 12

BL feasible solutions: aggregator’s profit

Table 1 reports the average values of the aggregator and prosumer objective functions for a typical day in each season.

The results show a slight reduction of the electricity bill for the summer due to the higher production from renewable sources, while higher costs are observed in the winter.

Compared to the values recorded for the consumer, a reduction of the annual electricity bill around $30\%$ can be observed. This substantial saving underscores the importance for the follower to invest in domestic technologies.

5.4 Computational effort

Finally, we comment on the computational effort required for solving the proposed BL problem. The results reported below refer to the test case for the winter day, but similar performance in terms of solution quality and computational effort has been obtained also for the other test cases.

In the experiments, the maximum number of iterations Iter$_\mathrm{max}$ has been set to 50. Table 2 reports the results for the first 6 iterations, after which no improvement of the solution has been registered. In particular, the second and third columns of the table, specified by the headings LB and LB$_B$, report the UL objective function value associated with the BL feasible solutions and the best UL objective value found so far, respectively.

Table 3 Results for all the seasons

The last column shows the prosumer objective function associated with the generated solutions. We should note that the UL objective function value associated with the solution of the initial HPR problem, which provides an upper bound, is equal to 3.578.

Looking at the results, we may note that, as expected, an improvement in the leader’s objective function (i.e., increase in the aggregator’s profit) is associated with the deterioration of the follower’s objective (increase of the prosumer’s electricity bill).

Figure 12 shows the objective function value of the first 30 BL feasible solutions. The solution corresponding to the first iteration clearly shows the reaction of the follower to the originally proposed tariff scheme. A deterioration of around $25 \%$ can be observed.

Table 4 Nomenclature

The plot shows that no trend can be observed in the solutions generated by the heuristic approach. For the considered test, the best solution is registered during the first iterations (red point).

In terms of the computational time, the algorithm is quite fast. For a fixed value of the UL variables, the LL problem becomes a MIP that can be solved by CPLEX in a few seconds. The results for the test cases referring to all seasons are shown in Table 3.

As evident, for all the tested instances, the computational effort is limited and the average solution time is lower than 25 seconds.

6 Conclusions

In this study, we addressed the electricity pricing problem with demand-side flexibility. We have modeled the interaction between an aggregator and a prosumer as a Stackelberg game formulated using a mathematical BL program. At the UL, the aggregator optimizes the daily price profile with the aim of maximizing the total profit. At the LL, the prosumer modifies his consumption pattern by scheduling the flexible loads and exploiting the available resources (PV system and storage device).

The presence of integer variables at the LL prevents us from applying the single-level reformulations that represent a classical approach in the BL optimization literature. We presented a heuristic method based on the optimal-value-function reformulation which consists of generating a pool of BL feasible solutions from which the best is chosen.

A large number of numerical experiments have been carried out on real test cases. The results provide the stakeholders with informative managerial insights and underline the prominent roles of the aggregator and prosumer.

An extension of the proposed model could consider a multi-follower variant where different types of prosumers are jointly managed in the coalition.

Fig. 13

Electricity production from PV panels for a typical day of each season

An interesting research line of research would be the definition of BL formulations that take into account the uncertain nature of some of the parameters involved in the decision-making process, such as the spot market energy price and the production from renewable energy sources.

Appendix

The following table reports the nomenclature used in the proposed BL model.

The data reported below refer to the local resources of the aggregator. In particular, the production plant is assumed to have a capacity of 3.5 kW, with a production cost of / kWh. As for the PV panels, we have considered a system of 3 kW with an average daily production of 11  kWh. Figure 13 reports the energy production for a typical day, one for each season. Table 5 reports the data referring of the storage system. A similar system has been considered for the aggregator.

Data referring to the flexible loads are reported in Table 6.

Table 5 Input parameters: storage system

Table 6 Input parameter: Flexible loads