1 Introduction

The universe is in an accelerating phase, as confirmed by a supernova of type Ia [1]. Quasars are the most persistent sources observed at redshift \(z \approx 7\), and can be used to study the expansion and large-scale structure of the universe [2, 3]. To address the expansion of the universe based on general relativity an exotic form of energy called dark energy (DE) can be introduced. Different models have attempted to understand the nature of dark energy, such as quintessence, phantom, tachyon, and quintom [4], but the Big Rip scenario predicted that it is in the form of phantom energy [5].

Matter in the cosmos is considered as substance that deforms under external forces, such as gravity and pressure. This is essentially the behavior of a fluid that deform with the application of force[6, 7]. The accretion of the phantom test fluid can increase [8] or decrease [9] the mass of the S-AdS BH. A recent study [10] predicted a phantom like DE that is responsible for the rapid expansion of the universe and can prevent black hole formation. According to the evolution equation of state \(\rho _d = a^{-3(1+\omega )}, \; \text {for} \; \omega <-1\) the DE energy density grow in time [11]. The role of repulsive cosmological constant \(\Lambda\) is significant for both the geometrically thin accretion discs [12] and the toroidal discs orbiting supermassive BH [13]. The current carrying string loops in Schwarzschild-AdS and Kerr-AdS spacetimes can reflect the quasi-periodic oscillations and jets originating at the accretion discs as predicted by [14]. These phenomena are very important to understand the complex surrounding of BHs that can accelerate particles to ultra-high-energies (UHE).

The magnetic field plays an important role in the formation of accretion discs [15, 16], accelerating particles to the UHE, and in the evolution of the large-scale structure of the universe. Sgr A\(^*\) is an excellent probe for studying the particle dynamics in the surrounding of BH, its low luminosity put it into an inefficient accretion flow regime [17]. The accretion flow near Sgr A\(^*\) is in magnetically arrested state [18]. The four dimensional analytical solution of AdS, the Schwarzschild-AdS/dS shadow and gray body bounding and BH shadow in Symmergent Gravity is discussed in [19,20,21,22,23,24]. The structure of magnetic field near Sgr A\(^*\) is explained in detail by [25]. This types of BHs are called weakly magnetized BHs such that the magnetic field strength can not change the spacetime geometry but can significantly effect the dynamics of matter in the accretion disc [26, 27]. The magnetic field in the vicinity of these BHs should follow the condition [26]:

$$\begin{aligned} B\ll B_\text {max} \sim 10^{19} \frac{M_{\odot }}{M_\text {BH}} \text {Gauss}. \end{aligned}$$
(1)

This condition is valid for Stellar mass (\(\sim 10^{8}\) Gauss) and supermassive BHs (\(\sim 10^{4}\) Gauss) [28]. The quasinormal modes (QNMs) during the final stage (ringdown) of BH mergers can be well described by BH perturbation theories, especially the time dependant perturbations on the stationary background spacetime [29,30,31,32]. In this work, we focused on the time conformal perturbation in S-AdS spacetime with topological defect. The idea of time conformal spacetimes is discussed in detail by [33,34,35,36,37,38,39,40,41,42,43]. It is defined as the addition of first order expansion of \(e^{\epsilon f(t)}\) in the metric. This perturbation will give rise to first order approximate Noether symmetries of time conformal spacetime see e.g., [38, 44]. The conservation laws associated with the Noether symmetries can be applied further to study the dynamics of charged particles in the surrounding of BHs that admits a temporal factor perturbation.

This work is an extension of our previous work [27], where we discussed the dynamics of charged particles in the vicinity of Schwarzschild anti-de Sitter (S-AdS) BH. In this work, we introduce the time conformal perturbation in the S-AdS BH metric, so we focused on the effect of this perturbation on the geodesic motion of a charged particle in the vicinity of BH. This research work is important to understand the spacetime geometry, especially the timelike geodesics that can be used to predict the paths of binary BHs spiraling in toward each other [45]. Also the QNMs of BHs during the last stage (ringdown) of merging can be studied using the time dependent perturbation theory of spacetimes. Furthermore, the expansion of the universe and evolution of the BH depends on the phantom DE [10], so we explored the effect of DE on the particle dynamics in the surrounding of the mention BH. We may calculate the geodesic of binary black holes, that is, the path of blackholes they would follow while orbiting each other by understanding the curvature of spacetime by modelling these paths one can predict the gravitational waves (GW) they would emit. This is critical in GW astronomy, allowing scientists to analyze GW using instruments such as LIGO and VIRGO [46] etc. To explore the evolution of binary mergers system, understanding the geodesic motion is necessary for instance, numerical relativity simulation [47] uses timelike geodesic to track the motion of blackholes.

2 Time conformal S-AdS BH and their Neother symmetries

Here we considered the physical and mathematical acceptable time conformal form of the S-AdS BH and applied the Noether’s theorem to obtain the symmetries associated with this spacetime. The S-AdS spacetime with topological defect [27] with a general time conformal factor \(e^{\epsilon f(t)}\) [38, 48, 49] is defined as

$$\begin{aligned} ds^2_{con}=e^{\epsilon f(t)}ds^2_e, \end{aligned}$$
(2)

the expanded form of (2) is given as

$$\begin{aligned} ds^2_{con}=(1+\epsilon f(t)+\frac{\epsilon ^2}{2} f(t)^2+\cdots ) ds^2_e \end{aligned}$$
(3)

neglecting the \(\epsilon ^2\) and higher order terms. We obtained the following general time conformal S-AdS line element

$$\begin{aligned} ds^2_{con}= & {} (1+\epsilon f(t)) \left( \Phi (r) dt^2- \Phi (r)^{-1} dr^2\right. \nonumber \\{} & {} \quad \left. - r^2\left( d\theta ^2+ \sin ^2(\theta )d\phi ^2\right) \right) \end{aligned}$$
(4)
$$\begin{aligned} \Phi (r)= & {} 1-\beta ^2-\frac{2M}{r}+\frac{r^2}{a^2}, \end{aligned}$$
(5)

where \(\beta\) is the parameter that is related to the scale of symmetry breaking (topological defect), M is mass of BH assumed to be constant and a is related with cosmological constant as \(a^2 = 3/\lambda\). The grand unification scale \(\beta \equiv 10^{ -6}\) is introduced in the metric tensor which is the fractional topological defect in the spacetime satisfying the condition \(1- \beta ^2 \approx 1\). The time conformal Lagrangian corresponding to (4) takes the following form

$$\begin{aligned} \begin{aligned}&\mathcal {L}_{con}=\mathcal {L}_{ext}+\epsilon \mathcal {L}_{app}=\\ {}&\Phi (r) \dot{t}^2 - \Phi (r)^{-1} \dot{r}^2 -r^2\left( \dot{\theta }^2+ \sin ^2(\theta )\dot{\phi }^2\right) \\&\quad +\epsilon f(t) \left( \Phi (r) \dot{t}^2- \Phi (r)^{-1} \dot{r}^2-r^2\left( \dot{\theta }^2+ \sin ^2(\theta )\dot{\phi }^2\right) \right) \end{aligned}\end{aligned}$$
(6)

The first order approximate Neother symmetry is defined as

$$\begin{aligned} \textbf{X}=\textbf{X}_{ext}+\epsilon \textbf{X}_{app}, \end{aligned}$$
(7)

up to the gauge \(A=A+\epsilon B,\) here

$$\begin{aligned} \textbf{X}_{ext}= \xi _e \partial _s + \eta ^i \partial _{x^i}, ~~~ i=0,1,2,3,\end{aligned}$$
(8)
$$\begin{aligned} \textbf{X}_{app}= \tau _a \partial _s + \eta ^i_a \partial _{x^i}, ~~~ i=4,5,6,7. \end{aligned}$$
(9)

The conformal symmetries must satisfies the following equations

$$\begin{aligned} \epsilon : \,\textbf{X}_{app}^1\mathcal {L}_{ext}+\textbf{X}_{ext}^1\mathcal {L}_{app}+ (D\xi _e) \mathcal {L}_{app} +(D\tau _a) \mathcal {L}_{ext}= & {} DB. \nonumber \\ C:\, \textbf{X}_{ext} \mathcal {L}_{ext} + (D\xi _e) \mathcal {L}_{ext}= & {} DA, \end{aligned}$$
(10)

where D is differential operator, B is gauge function and \(X^1_{app}\) is first order prolongation of the generator

$$\begin{aligned} \textbf{X}_{ext}^1= {\xi _e \partial _s + \eta _{e}^i \partial _{x^i}+ \eta _{ec}^i \partial _{\dot{x}^i}}, ~~~ i=0,1,2,3,\end{aligned}$$
(11)
$$\begin{aligned} \textbf{X}_{app}^1= \tau _a \partial _s + \eta ^i_a \partial _{x^i} + \eta ^i_{ac} \partial _{\dot{x}^i}, ~~~ i=4,5,6,7. \end{aligned}$$
(12)

Combining the solution of exact Noether symmetries of the orginal metric [27], and comparing monomials obatined from (10), we get the following system

$$\begin{aligned}{} & {} \tau _s=\tau _t=\tau _{\theta }=\tau _{\phi }=B_s=0,~~2 \eta ^4_s \Phi -B_t=0,\nonumber \\{} & {} 2 \eta ^5_s \Phi ^{-1}+B_r=0, ~~~ 2 \eta ^6_s r^2 +B_{\theta }=0, \nonumber \\{} & {} 2 \eta ^7_s r^2 \sin ^2 \theta +B_{\phi }=0, ~~~ 2 \eta ^4_{\phi } - \eta ^7_t r^2 \sin ^2 \theta =0, \nonumber \\{} & {} \eta ^4_{\theta } \Phi -r^2 \eta ^6_t=0, ~~~ 2 \eta ^4_{r} \Phi ^2 - \eta ^5_t =0, \nonumber \\{} & {} \eta ^5_{\phi } \Phi ^{-1}-\eta ^7_r r^2 \sin ^2 \theta =0, ~~ \eta ^5_{\phi } \Phi ^{-1}-\eta ^6_r r^2=0,\nonumber \\{} & {} \eta ^6_{\phi } -\eta ^7_{\theta } \sin ^2=0, ~~~\alpha _3 f_t(t)+(2/r) \eta ^5+2\eta ^5_r-\tau _s=0,\nonumber \\{} & {} \alpha _3 f_t(t)-\frac{\Phi _r}{\Phi } \eta ^5+ 2 \eta ^5_r-\tau _s=0,\nonumber \\{} & {} \alpha _3 f_t(t)+\frac{\Phi _r}{\Phi } \eta ^5+ 2 \eta ^5_r-\tau _s=0,\nonumber \\{} & {} \alpha _3 f_t(t)-\frac{2}{r} \eta ^5+ 2\cot \theta \eta ^6+ 2\eta ^7_\phi -\tau _s=0, \end{aligned}$$
(13)

solving the above determining partial differential equations resulting from (10), we will get the following time conformal solution

$$\begin{aligned} \begin{aligned}&\eta ^0_e+\epsilon \eta ^{{4}}_a =c_{2}+\epsilon c_2^{'},~~ \eta ^1_e+\epsilon \eta ^{{5}}_a =0,\\ {}&\eta ^2_e+\epsilon \eta ^{{6}}_a =-c_{3}\,\cos \left( \phi \right) +c_{3}\,\sin \left( \phi \right) +\epsilon (-c_{3}^{'}\,\cos \left( \phi \right) \\&\quad +c_{4}^{'}\,\sin \left( \phi \right) ) ,\\ {}&\eta ^3_e+\epsilon \eta ^{{7}}_a = c_{5}+\cot \left( \theta \right) \left[ c_{3}\ \sin \left( \phi \right) +c_{4} \cos \left( \phi \right) \right] \\&\quad +\epsilon \bigg (c_{5}^{'}+\cot \left( \theta \right) \left[ c_{3}^{'}\ \sin \left( \phi \right) +c_{4}^{'} \cos \left( \phi \right) \right] \bigg ),\\ {}&\xi +\epsilon \tau =\epsilon c_2\frac{s}{\alpha }+c_1^{'},\,A+\epsilon B =c_6+\epsilon c_6^{'} ,\,\, f(t)=\frac{t}{\alpha } +c_{7}^{'}. \end{aligned}\end{aligned}$$
(14)

The time conformal line element is

$$\begin{aligned} ds^2_{con}= & {} \left( 1+\epsilon t/\alpha \right) \left( \Phi (r)\right) dt^2+ \left( \Phi (r)\right) ^{-1} dr^2\nonumber \\{} & {} \quad +r^2\left( d\theta ^2+ \sin ^2(\theta )d\phi ^2\right) , \end{aligned}$$
(15)

where the Neother symmetry generators obtained from (14) are as follows

$$\begin{aligned} \textbf{X}_1= & {} \partial _t + \epsilon \frac{s}{\alpha } \partial _s,~~ \textbf{X}_2= \partial _s,~~ \textbf{X}_3= \partial _{\phi }, \nonumber \\ \textbf{X}_4= & {} \cos {(\phi )}\partial _{\theta } -\cot (\theta ) \sin (\phi )\partial _{\phi }, \nonumber \\ \textbf{X}_{5}= & {} \sin (\phi )\partial _{\theta } + \cot (\theta ) \cos (\phi )\partial _{\phi }. \end{aligned}$$
(16)

The non-trivial case is observed in the generator \(\textbf{X}_6\), which re-scale the energy contents. Corresponding to the Noether symmetries (16) the time conforml conservation laws are given in Table 1.

Table 1 Conservative quantities
Full size table

We applied the Noether’s theorem on arc length Lagrangian 6, as a result, the metric with temporal perturbation admits 5 Noether symmetries which corresponds to different conservation laws. Conserved quantities play a crucial role in expressing the dynamics of isolated systems in the universe since they may be used to comprehend the behavior of phenomena in a variety of fields, including mechanics, chemistry, engineering science, and astrophysics. In general, the conserved quantities corresponding to the \(\textbf{X}_6, \textbf{X}_8\) in Table (1) are time conformal case of energy and momentum. The comparative analysis of the conservation laws obtain in Table I and II, reflects that these quantities are only conserved for \(\epsilon\) equals to zero. Moreover, one can say that the time conformal factor \(e^{\epsilon f(t) }\) does not affect the symmetry structure. Therefore, one may say that with the evolution of time the energy profile may re-scale, locally conserved, thus effect the whole dynamics, as the angular momentum and energy contributes significantly in most of the behaviour of physical theories. Further, it also reflects that the desired ’conserved quantities’ are not conserved in general [50].

2.1 Existence and location of horizon

The time conformal line element is

$$\begin{aligned} ds^2_{con}= & {} \left( 1+\frac{\epsilon }{\alpha } f(t)\right) \left( \Phi (r) dt^2- \Phi (r)^{-1} dr^2\right. \nonumber \\{} & {} \quad \left. - r^2\left( d\theta ^2+ \sin ^2(\theta )d\phi ^2\right) \right) \end{aligned}$$
(17)

where \(\epsilon\) is a dimensionless parameter, the constant \(\alpha\) having dimension equivalent to time leads the term \(t/\alpha\) to a dimensionless factor. Further, the roots of the cubic equation

$$\begin{aligned} -(1+\frac{\epsilon t}{\alpha } ) \Phi (r)=0, \end{aligned}$$
(18)

remain the same because the time conformal perturbation does not effect the horizon so it is same as in the case of S-AdS BH with topological defect (see [27] for detail).

3 Dynamics

In this section, we will discuss the dynamics of a charged particle that is moving around the time conformal S-AdS BH. The conserved energy and total angular momentum are given in Table (1), the conformal energy and angular momentum is calculated by using \(\textbf{X}_6\) and \(\textbf{X}_8\) is as follows

$$\begin{aligned} E_{conf}= & {} (1+\frac{\epsilon t}{\alpha })(E-\frac{\epsilon s}{a}) \end{aligned}$$
(19)
$$\begin{aligned} L^2= & {} (1+\frac{\epsilon t}{\alpha })(r^2 v_{\perp }+\frac{L_z ^2}{\sin ^2 \theta }) \end{aligned}$$
(20)

where \(v_{\perp }=r^2 \dot{\theta }\).

We assume the particle is charged and investigate the motion of particle around time conformal S-AdS BH given in (15). We are focusing on weakly magnetised BHs such as stellar mass and supermassive BH whose magnetic field strength can not change the surrounding geometry, but strongly effect the dynamics of particle in the vicinity of EH. Therefore, a static, homogeneous and axis symmetric magnetic field of strength (B) is considered. We assumed the same magnetic field profile as obtained in [27]. The Lagrangian [56] for charged particle is defined as

$$\begin{aligned} \mathcal {L}=\frac{qA_{\nu }}{m}u^{\mu }+\frac{1}{2} g_{\mu \nu } u^{\mu } u^{\nu }, \end{aligned}$$
(21)

where m is mass of the particle and q is the electric charge. Using the Lagrangian equation, the constants of the motion in the magnetised S-AdS spacetime with the time conformal perturbation are defined as

$$\begin{aligned} \dot{t} =\frac{E(1-\frac{\epsilon t}{\alpha })}{\Phi (r)}, ~~~~ \dot{\phi }=\frac{L_z(1-\frac{\epsilon t}{\alpha })}{r^2 \sin ^2 (\theta ) }-B,~~~~ B=\frac{q\mathbb {B}}{2m}, \end{aligned}$$
(22)

We apply the normalization condition \(\dot{x}^{\mu } \dot{x}_{\nu } =1\), and obtain the equation of motion for charged particle

$$\begin{aligned} \dot{r}^2= & {} E^2 -\left( \Phi (r) \right) r^2 \dot{\theta }^2 -\Phi (r) \left( r^2 sin^2(\theta ) \left( \frac{L_z (1-\frac{\epsilon t}{\alpha })}{r^2 sin^2(\theta ) }-B\right) ^2 \right. \nonumber \\{} & {} \quad \left. +(1-\frac{\epsilon t}{\alpha } ) \right) , \end{aligned}$$
(23)

The effective potential on particle is of the form

$$\begin{aligned} U_{eff}= \left( 1-\beta ^2-\frac{2M}{r}+\frac{r^2}{a^2} \right) \left( (1-\frac{\epsilon t}{\alpha } )+r^2 \left( \frac{L (1-\frac{\epsilon t}{\alpha } )}{r^2}-B\right) ^2\right) \end{aligned}$$
(24)
Fig. 1
figure 1

The plot of effective potential for \(\beta =10^{-6}\), \(a=0.5\), \(B=5\) (see text for detail)

Full size image

In Figs. 1, 2, 3 and 4 we presented the behaviour of effective potential against time (t), topological defects \((\beta )\), angular momentum (L) and dark energy parameter (a). All the parameters used in these Figures are in dimensionless (\(\hat{r}=r/M, L=l/M, B\)) form and the values of both \(\epsilon\) and \(\alpha\) is 1.

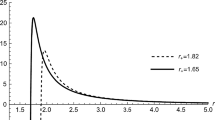
The behaviour of effective potential for different values of time and angular momentum L parameters is shown in Fig. 1. The local minimum for \(t=0\) remains same as S-AdS done in ([27]), wherease for the large value of time, local minima of effective potential shifted away from the EH. This is the indication of shifting of ISCO away from the BH horizon.

Fig. 2
figure 2

The plot of effective potential for \(L=5, \beta =10^{-6}, \;a=0.5\) (see text for detail)

Full size image

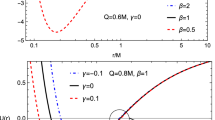
The behaviour of effective potential for different values of time parameter is shown in Fig. 2. For a large value of magnetic field and time parameter, local minima of the effective potential shifted towards the BH horizon. So the presence of magnetic field and temporal perturbation can reduce the radius of ISCO and make it more unstable. If there is no magnetic field and the temporal perturbation then there are more chances for a particle to fall into the BH.

Fig. 3
figure 3

(a): The plot of effective potential for \(L=5, \beta =10^{-5}, B=1, a=0.5.\,\,\) (b): The plot of effective potential for \(L=5, \beta =10^{-6}, B=5\) (see text for detail)

Full size image
Fig. 4
figure 4

The plot of effective potential for \(L=5, \beta =10^{-6}, B=5\) (see text for detail)

Full size image

The plot of effective potential which is reflected in Fig. 3, subfigure 3b showing various values of the DE parameter \((a\propto 1/ \lambda )\) and specific time interval. The typical value of the symmetry breaking paramter is \(\beta =10^{-6}\). The particle escapes easily by increasing the value of time and DE parameters. Fig. 4 represents shifting of the local minima toward the horizon as the value of DE parameter decrease and vice virsa. The position of ISCO is shifting away from the BH as the DE increase (repulsive gravitational force).

Fig. 5
figure 5

The plot of effective potential for \(L=5, \beta =10^{-6}, \; B=5\) (see text for detail)

Full size image

The presence of DE and magnetic field, effects the stability of orbits which inturn is responsible for the chaotic motion in the vicinity of BH. Temporal perturbation also play an important role in this scenario. For small value of time, particles have more chances to fall into the BH, also the DE corresponds to repulsive gravitational force which leads to increase the radius of ISCO. The increase in time rises the effects of dark energy, and also rise the minimum value of effective potential. The increase in the time decreases the stability of orbits as well as the position of ISCO shifts. More elaborative behaviour of effective potential concerning radial and temporal parameters is represented in the three dimensional (3D) surface plot 5. The green surface plot better represents the local minimum of the effective potential. Further, as the dark energy value increases, the local minimum shifts away from the horizon; moreover, in a specific interval of time, the value of effective potential increases rapidly.

3.1 Innermost stable circular orbit

For the existence of circular orbit, the effective potential follow the following conditions:

$$\begin{aligned} E^2 - U_\text {eff} = 0, ~~~~~~ \frac{dU_\text {eff}}{dr} = 0 \end{aligned}$$
(25)

The above equations can be written as,

$$\begin{aligned} \frac{dU}{dr}&= \left( 1 -\beta ^2 -\frac{2 M}{r} + \frac{r^2}{a^2}\right) \left( 2 r \left( \frac{\mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) }{r^2}-B\right) ^2\right. \nonumber \\&\quad \left. -\frac{4 \mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) \left( \frac{\mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) }{r^2}-B\right) }{r}\right) \nonumber \\ {}&+\left( \frac{2 r}{a^2}+\frac{2 M}{r^2}\right) \left( r^2 \left( \frac{\mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) }{r^2}-B\right) ^2-\frac{t \epsilon }{\alpha }+1\right) = 0. \end{aligned}$$
(26)

By solving above equations we can obtain the expression for angular momentum (\(L_o\)) and energy (\(E_o\)) correspond to the ISCO. The equation for the ISCO is,

The second derivative of the effective potential can be written as \(\frac{d^2U_\text {eff}}{d^2 r} =\)

$$\begin{aligned}&-\left( \left( 1 -\beta ^2 -\frac{2 M}{r} + \frac{r^2}{a^2}\right) \left( 2 \left( \frac{\mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) }{r^2}-B\right) ^2\right. \right. \nonumber \\&\quad \left. \left. -\frac{4 \mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) \left( \frac{\mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) }{r^2}-B\right) }{r^2}+\frac{8 \mathcal {L}^2 \left( 1-\frac{t \epsilon }{\alpha }\right) ^2}{r^4}\right) \right) \qquad \nonumber \\&\quad - 2 \left( \frac{2 r}{a^2}+\frac{2 M}{r^2}\right) \left( 2 r \left( \frac{\mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) }{r^2}-B\right) ^2\right. \nonumber \\&\quad \left. -\frac{4 \mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) \left( \frac{\mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) }{r^2}-B\right) }{r}\right) \nonumber \\&-\left( \frac{2}{a^2}-\frac{4 M}{r^3}\right) \left( r^2 \left( \frac{\mathcal {L} \left( 1-\frac{t \epsilon }{\alpha }\right) }{r^2}-B\right) ^2 + \left( 1 -\frac{t \epsilon }{\alpha }\right) \right) =0 \end{aligned}$$
(27)

The above equation (27) can reduced to Schwarzshild-BH case (\(r -6M=0\)) if we exclude other parameters. Also the the condition for stable circular orbits is \(\frac{d^2U_\text {eff}}{d^2 r} > 0\) and for marginally stable ones \(\frac{d^2U_\text {eff}}{d^2 r} = 0\). These conditions only holds for asymptotic flat spacetimes as is the case. These equations reduce to the S-BH case with \(r_{ISCO}=6M\), for \(t=0, \beta =0\) and if we neglect the DE parameter (a).

3.2 Angular velocity

The angular velocity of a particle moving in a stable orbit around a BH can be written as

$$\begin{aligned} \Omega = \frac{\dot{\phi }}{\dot{t}} = \frac{\left( L_z(1-\frac{\epsilon t}{\alpha }) -\mathbb {B} (r^2 \sin ^2 (\theta ))\right) \Phi (r)}{E (1-\frac{\epsilon t}{\alpha }) (r^2 \sin ^2 (\theta ))} \end{aligned}$$
(28)
Fig. 6
figure 6

(a): Angular velocity for different value of parameters \(\mathbb {B}\), L, and t. (b): for different values of DE parameter a (right panel) (see text for detail)

Full size image

The time period of the particle is

$$\begin{aligned} T = \frac{2\pi }{\Omega } = \pm 2\pi \times \frac{E (1-\frac{\epsilon t}{\alpha }) (r^2 \sin ^2 (\theta ))}{\left( L_z(1-\frac{\epsilon t}{\alpha }) -\mathbb {B} (r^2 \sin ^2 (\theta ))\right) \Phi (r)}. \end{aligned}$$
(29)

The time period depends on angular momentum, energy and magnetic field. The time conformal perturbation is also important while estimating the time period. Using the general relativistic magnetohydrodynamic simulations we can probe these properties with more details.

3.3 Effective force

Charged particles in the vicinity of S-AdS BH is under the influence of gravitational and electromagnetic forces. DE can also affect their motion. Therefore, to represents the combined effect of these different influential agents, the effective force is the best way to represent. Therefore, the effective force on particle in this environment is,

$$\begin{aligned} F_{eff}=-\frac{1}{2} \bigtriangledown U_{eff}, ~~\bigtriangledown =\frac{\partial }{\partial r}. \end{aligned}$$
(30)

It can be written as

$$\begin{aligned}{} & {} F = -1/2\, \left( 1-{\beta }^{2}-2\,{\frac{M}{r}}+{\frac{{r}^{2}}{{a}^{2}} } \right) \left( 2\,r \left( {\frac{{\mathcal {L}}^{2}}{{r}^{4}} \left( 1-{ \frac{\epsilon \,t}{\alpha }} \right) ^{2}}-B \right) \right. \nonumber \\{} & {} \quad \left. -4\,{\frac{{\mathcal {L}}^{ 2}}{{r}^{3}} \left( 1-{\frac{\epsilon \,t}{\alpha }} \right) ^{2}} \right) \nonumber \\{} & {} \quad -1/2\, \left( 2\,{\frac{M}{{r}^{2}}}+2\,{\frac{r}{{a}^{2}}} \right) \left( 1-{\frac{\epsilon \,t}{\alpha }}+{r}^{2} \left( {\frac{{\mathcal {L}}^{2} }{{r}^{4}} \left( 1-{\frac{\epsilon \,t}{\alpha }} \right) ^{2}}-B \right) \right) . \end{aligned}$$
(31)
Fig. 7
figure 7

(a): The plot of effective force for \(L=5, \beta =10^{-6}, a=0.1\). (b): The plot of effective force for \(L=5\), \(\beta =10^{-6}\). (see text for detail)

Full size image

The behaviour of effect force for the charged particle varies for different value of B and a which is shown in Fig. 7a, b. The effective force for S-AdS is discussed in [27] and the complete term by term analysis is defined in [51] and[52]. An increase in the temporal parameter and the magnetic field makes the effective force more repulsive as indicated in Fig. 7. Therefore, the time parameter and the strength of the magnetic field are responsible for moving the position of the stable orbit away from the EH. In Figs. 7a, b and 9, we presented the behaviour of effective force with-respect to different parameters. The results for small values of a and temporal parameter t the force is more repulsive, however as we increase the value of the parameters a and t the repulsive force starts decreasing. The effective force also depends on angular momentum (L), if the value of L is high the force is more attractive. Figure 7 shows that for high magnetic field make the force more repulsive, also for large value of a the force is attractive. Time affects the stability of orbits due to which behaviour of effective force as well as effective potential changes continuously. The Fig. 7b reflects the effective force decreases as the temporal parameter and the dark enrgy parameter increases. The Fig. 8a,b shows as the angular momentum, charge on the particle increases the effective potential will become more repulsive over the change in temporal paramter t.

Fig. 8
figure 8

(a) The effects of increasing t and angular momentum on effective potential with \(a=0.2,\) \(\beta =10^{-7}, B=5.\,\,\)   (b) The replusive effects of increasing t, angular momentum and charges (B) on effective potential with \(a=0.2,\) \(\beta =10^{-7}\)

Full size image
Fig. 9
figure 9

The surface plot of effective force for \(L=5\), \(\beta =10^{-6}.\) (see text for detail)

Full size image

3.4 Escape velocity

The expression for escape velocity (v) is obtained as

$$\begin{aligned} v&=\pm \left( \sqrt{{ \left( {E}^{2}- \left( 1-{\beta }^{2}-2\,{\frac{M}{r}}+{\frac{{r}^{2}}{{a}^{2}}} \right) \left( 1-{\frac{\epsilon \,t}{ \alpha }} \right) \right) \left( 1-{\beta }^{2}-2\,{\frac{M}{r}}+{\frac{{r}^{2}}{{a}^{2}}} \right) ^{-1}}}+rB \right) \nonumber \\ {}&\quad \times \left( 1-{\frac{\epsilon \,t}{\alpha }} \right) -{\frac{L_{{z}}}{r}}, \end{aligned}$$
(32)
Fig. 10
figure 10

(a): The plot of effective force for \(L=5, B=5, \beta =10^{-6}.\) (b): The plot of effective force for \(L=5, \beta =10^{-6}\). c: The plot of effective force for \(L=5, \beta =10^{-6}. a=1, B=5\) (see text for detail)

Full size image

the equality in above equation corresponds to \(U_{eff}=1\) and \(\dot{r}=0\), therefore the escape condition after the collision of particle in the presence of magnetic field from the vicinity of BH is given by the equation (32). The mechanism proposed by Blandford-Znajek and Penrose [53,54,55], charged particles can be accelerated up to a large distance from an active galactic nuclei (AGN). Suppose that particle revolving around a BH in the equatorial plane, after collision the particle may escape orthogonally and acquire an escape velocity (v). The trajectory plots for dark energy parameter, magnetic field, angular momentum and temporal parameter with respect to radial component is represented in Fig. 10. In Fig. 10, escape conditions of the particle is shown for large L. For large value of a particles can escape easily, also, the large value of temporal parameter also favour particles to escape.

Suppose a particle escapes from the BH surrounding, since outside the vicinity of BH the gravitational field is negligible. So, practically the charged particle are in flat spacetime such motion is in accordance with [56]. It is important to study the regime where both the dark energy and magnetic field affects velocity/motion of the particle, before it reaches the infinity. Therefore, in the left panel of Fig. 10, we presented the escape velocity behaviour for different values of DE parameter, similarly in the right panel for multiple values of magnetic field B and temporal parameter.

Moreover the influence of dark energy is more near the horizon and motion of particle is chaotic, also temporal parameter does not affect motion of particle near horizon. For the fixed value of B and increase in t the escape probability of particle is very high which is inline with [26, 27] and [38]. However, in contrast to the result of escape velocity [27] for fixed value of a the escape condition of particle is different for increasing value of temporal parameter. The dark energy supports the escape of particle which is mainly dependent on the time. The behavior of a particle’s escape velocity for anticlockwise rotating particles \((L =-10)\) at a long distance is comparable to that of a particle moving in an orbit with a clockwise rotation near BH. However, for co-rotating particles, there is no change in escape velocity for the temporal parameter, as shown in the bottom panel of Fig. 10. Counter-rotating particles have an interesting feature: their escape velocity increases dramatically as time increases. The solid purple curve in the bottom panel of Fig. 10 shows an increase in temporal parameter, indicating a high chances of particles escaping from the BH surrounding. Over time, the dashed, red, and blue curves indicate that the minimum escape velocity will remain constant. Additionally, the bound motion region around the black hole is influenced by time, and for an \(L = -10\), the escape velocity increases with the temporal parameter. As shown in the bottom panel of Fig. 10, the temporal parameter contributes to both the faster escape of anticlockwise rotating particles.

4 Conclusions

In this work, we extended the previous work [27] by introducing the first order time conformal perturbation in the S-AdS metric. Using this approximation we studied the behaviour of the particle rotating around the BH with respect to time. We explored the parametric effects of DE, magnetic field angular momentum, and temporal perturbation on ISCO position, effective force, effective potential and escape velocity. Mainly, we focused to determine the bound and escape conditions for particles moving in the vicinity of BHs. These conditions are discussed under the dynamics of particles.

In general, the motion of charged particles around the BH is not bound. The major question is to find under what condition a particle can escape to infinity or captured by the BH? We found that large magnetic field strength and angular momentum reduce chances for a particle to escape from the BH surrounding. DE is a repulsive force, shift the ISCO position away from the horizon. The introduction of temporal perturbation also shift the ISCO position away from the BH. The significant difference between our results and the work presented in [27], is the shifting of ISCO away from horizon due to temporal perturbation. The effective force become more repulsive due to this perturbation.

We also calculated the escape velocity of charged particle moving in the vicinity of S-AdS BH under the influence of gravito-magnetic forces. The parametric effect of DE is also included in our calculation. The combined effect of temporal perturbation and DE make the effective force more repulsive, therefore increasing the probability of particles to escape. Particle can be captured by the BH, result in increasing its mass [57, 58]. The introduction of the temporal perturbation in the S-AdS BH is necessary for the present day universe, because it is expanding with increasing rate. Various perturbation techniques are employed for a multitude of objectives [59, 60].

Timelike geodesics can be used to predict the paths of binary BHs that are spiraling in [45], which is our potential future work. Further, we will study the distortion of BH during the ringdown stage of merging BHs using this time dependent perturbation theory. We are also interested in exploring null geodesics and their applications e.g., estimating the BH shadow etc.